Introduction

The increasing integration of renewable energy sources (RESs), such as photovoltaic (PV) systems, into traditional power grids has brought new challenges to load frequency control (LFC)1,2,3. The combination of fluctuating renewable energy generation with the inherent dynamics of thermal power plants creates instability in power system frequency4 and tie-line power, leading to potential operational inefficiencies5. This study is motivated by the need to design an advanced control mechanism that can effectively manage the dynamic interactions between renewable and conventional energy sources while maintaining frequency stability and minimizing power fluctuations. By improving the efficiency and reliability of hybrid power systems, the research aims to address critical issues related to the stability and performance of modern power grids.

Related works

The control and optimization of hybrid power systems, particularly in the context of load frequency control (LFC), have garnered significant attention due to the increasing integration of renewable energy sources and the complexities of managing hybrid systems. Dunna et al.6 proposed a super-twisting MPPT control for grid-connected PV/battery systems using higher-order sliding mode observers, emphasizing the enhancement of stability under fluctuating renewable energy conditions. However, their focus on grid stability does not extend to addressing the intricate frequency regulation challenges posed by hybrid systems incorporating thermal power plants. Similarly, Izci et al.7 developed a fractional-order PID plus double-derivative controller for automatic voltage regulation using the mountain gazelle optimizer. While this study demonstrates the potential of advanced fractional-order controllers in improving system stability, it primarily targets voltage regulation, leaving the domain of frequency control in hybrid systems unexplored.

Expanding on controller tuning methodologies, Aribowo et al.8,9 employed gradient-based and modified mountain gazelle optimizers for PID controller tuning in DC motor systems. These studies highlight the critical role of optimization algorithms in enhancing controller performance. While focused on DC motor applications, such optimization approaches resonate with the use of bio-dynamic grasshopper optimization algorithm (BDGOA) in fine-tuning LFC parameters for hybrid power systems. Premkumar et al.10 further explored hybrid power systems by employing a multi-objective optimization approach for stochastic renewable energy sources and FACTS devices, demonstrating the need for sophisticated control strategies to manage system uncertainties. This study contributes to understanding system complexities, yet it focuses on operational optimization rather than specific challenges related to frequency stability and oscillation reduction, as addressed in this research.

Pandya et al.11 introduced a RIME algorithm-based approach for techno-economic analysis in hybrid power systems, accounting for uncertainties in security-constrained load dispatch. This work underscores the significance of managing uncertainties, a challenge also addressed in this study through the robust design of the BDGOA-tuned TDn(1 + PI) controller. Alsmadi et al.12 extended this discussion by integrating fuzzy logic with model order reduction for digital systems, emphasizing the adaptability of intelligent control techniques. While fuzzy logic control enhances system flexibility, the integration of tilt-derivative control with proportional-integral action in the present study achieves superior performance under nonlinear and uncertain conditions.

In the realm of dynamic systems, Abualigah et al.13 and Alrashed et al.14 explored optimized PID controller designs for aircraft pitch control and dynamic voltage restorers, respectively, leveraging novel optimization techniques like the Sinh-Cosh Optimizer and IGWO algorithm. These studies demonstrate the applicability of advanced optimization in diverse fields but lack the focus on hybrid energy systems. Similarly, Fadheel et al.15 proposed a hybrid sparrow search optimization-based fractional virtual inertia control for frequency regulation in microgrids, showcasing the potential of hybrid optimization techniques. While their approach targets microgrid applications, this research addresses the broader challenge of multi-area power systems, enhancing both inter-area frequency stability and tie-line power regulation.

The contributions of Abualigah et al.16,17,18 in refining optimization algorithms, such as the artificial rabbits optimizer and modified artificial hummingbird algorithm, align with the growing trend of employing bio-inspired optimization techniques. These studies focus on improving system stability and efficiency across applications like automatic voltage regulation and cruise control systems. The integration of BDGOA with a multi-stage controller in this study achieves significant reductions in overshoot and settling times in hybrid power systems, representing a distinct advancement. Altawil et al.19 explored the slap swarm algorithm for fractional-order PI controller optimization in grid-connected PV systems, emphasizing the importance of controller adaptability. The current study advances this notion by addressing both transient and steady-state performance in hybrid systems with varying operational conditions.

Finally, Sarayrah et al.20 investigated predictive damping control strategies for inter-area power systems, focusing on improving dynamic stability. Their approach highlights the importance of predictive strategies in modern power grids, a principle mirrored in this study through the use of a multi-stage controller design that anticipates and mitigates frequency fluctuations. Additionally, Sarayrah et al.21 examined a damping control strategy employing predictive modeling for inter-area oscillations in power systems. Their work emphasizes predictive and proactive control mechanisms for enhancing system stability. However, while focused on inter-area oscillations, the study does not delve into hybrid systems with renewable energy sources, where the dynamics of PV and thermal generators significantly complicate control requirements.

Various controllers have been proposed in recent years to enhance the performance of LFC systems3,22. Among these, proportional integral (PI)23 and proportional integral derivative (PID)24 controllers are widely used due to their simplicity and ease of implementation. However, conventional PI and PID controllers often fall short in addressing the nonlinearities and complexities of hybrid power systems25,26. To overcome these limitations, more multi-stage controllers have been developed27,28,29. These controllers not only address steady-state errors but also improve the dynamic response by managing the rate of change, thus providing more robust and efficient solutions for frequency regulation in hybrid systems.

Optimization algorithms play a critical role in tuning the parameters of controllers30,31 to enhance system performance32. Traditional optimization techniques such as genetic algorithm (GA)33, firefly algorithm (FA)34, and salp swarm algorithm (SSA)35,36 have been extensively applied to optimize LFC controllers. However, these methods often struggle with issues like local optima and slower convergence rates. In this research, we propose the bio-dynamic grasshopper optimization algorithm (BDGOA), a novel optimization technique, to optimize the parameters of a newly developed multi-stage TDn(1 + PI) controller.

A variety of controllers have been developed for LFC in hybrid microgrids and interconnected power systems. Notably, traditional controllers like PI and PID are widely used due to their simplicity, but they often fall short in handling the nonlinear dynamics of hybrid systems37. To address these limitations, several multi-stage and fractional-order controllers have emerged. For instance, Shayeghi and Rahnama38 introduced a multistage TDF(1 + FOPI) controller optimized using the bonobo optimization algorithm (BOA). The controller demonstrated superior dynamic performance, particularly in handling uncertainties and sudden load changes, when compared to conventional PI and PID controllers. Similarly, Shayeghi, et al.39 presented a TFODn-FOPI controller, which outperformed standard controllers in islanded microgrid systems by reducing the detrimental effects of time-delay nonlinearities and cyber vandalism.

Optimization algorithms have played a critical role in enhancing the tuning of these controllers. Ekinci et al.40 employed the RIME algorithm to optimize a PI controller for automatic generation control (AGC) in hybrid PV-reheat thermal systems, showcasing its effectiveness in reducing frequency oscillations and tie-line power changes. Moreover, Can and Ayas41 introduced a GTO-based PI controller, which outperformed other optimization techniques like GA and SSA in terms of cutting down on settling times and overshoot values.

Among the most recent approaches, hybrid and intelligent control strategies have gained prominence. Haroun and Li42 proposed a hybrid fuzzy logic intelligent PID (FLiPID) controller, optimized using particle swarm optimization (PSO), for boiler dynamics and physically constrained multi-area power systems that are interconnected (BDs). This approach improved the system’s robustness and dynamic response compared to traditional methods. Additionally, they highlighted the potential of a FLiPID controller to manage LFC more effectively under nonlinear conditions.

In terms of novel optimization techniques, Khadanga, et al.43 introduced an algorithm MWOA to design a PIDF controller for a two-area power system. The MWOA algorithm showed improvements in implementation time and solution quality over traditional whale optimization algorithm (WOA), further contributing to better frequency regulation in hybrid systems.

The performance of these various controllers and optimization techniques highlights the importance of choosing the right combination for specific system dynamics. A study by Arya28, which focused on a multi-stage FPIDF-(1 + PI) controller for AGC, demonstrated that combining advanced control strategies with energy storage systems like capacitive energy storage (CES) units could significantly enhance system stability. Finally, Shayeghi and Rahnama29 proposed a PD-(1 + PI) controller for an entirely renewable microgrid, emphasized the role of demand response programs (DRPs) in achieving robust performance under fluctuating RESs. The main findings from these recent studies are summarized in Table 1.

Table 1 Overview of utilizing controller and optimization method in the recent paper.
Full size table

Research gap and motivation

Despite significant advancements in LFC strategies for hybrid power systems, several critical challenges remain. Most existing studies focus on either PV systems or thermal power plants independently, often neglecting the complex dynamic interactions between these energy sources in hybrid systems. Additionally, while optimization algorithms like GA, SSA, and FA have been extensively applied to tune LFC controllers, they often suffer from limitations such as slow convergence rates and vulnerability to local optima. These drawbacks hinder their performance in addressing the nonlinearities and uncertainties inherent in hybrid power systems, including governor deadband, boiler dynamics, and time delays.

Another gap lies in the lack of comprehensive evaluations of multi-stage controllers that effectively balance transient and steady-state performance in such systems. While multi-stage and fractional-order controllers have shown promise in improving robustness and dynamic responses, their application in hybrid PV-thermal power systems remains underexplored, particularly under nonlinear operating conditions and varying system parameters.

Motivated by these gaps, this research introduces a novel BDGOA to optimize a multi-stage TDn(1 + PI) controller for LFC in a two-area power system with PV and thermal generators. This approach aims to enhance system stability and reliability by addressing the aforementioned challenges, offering superior performance compared to conventional methods. The study evaluates the controller’s robustness under diverse scenarios, including parameter uncertainties and nonlinearities, highlighting its practical applicability for modern power grids.

Contributions

This research offers several significant contributions to the area of LFC in power systems:

  • Development of a novel multi-stage controller: The work presents a novel multi-stage TDn(1 + PI) controller specifically made for LFC in a two-area power system with a PV power plant and a reheat thermal generator. System stability and dynamic response are greatly increased by this controller’s special blend of a PI controller and a TDn filter.

  • Analysis of the PV power plant’s influence: The effects of the PV power plant on frequency control under various operating situations are thoroughly examined in this study. Significant new information on the LFC system’s performance and dynamic behavior with integrated renewable energy is provided by this analysis.

  • Superior performance of the proposed controller: The newly developed multi-stage BDGOA-tuned TDn(1 + PI) controller is compared with several existing methods, such as MWOA-tuned PIDn43, MWOA-tuned PID43, RIME-tuned PI40, BWOA-tuned PI44, SSA-tuned PI45, SFLA-tuned PI46, FA-tuned PI34, GA-tuned PI34, GTO-tuned PI41, and WOA-tuned PI43 controllers from previous research. Results show that the BDGOA-tuned TDn(1 + PI) controller outperforms these controllers, demonstrating superior robustness and efficiency in frequency regulation.

  • Validation of robustness and contribution to system stability: The research proves the robustness of the BDGOA-tuned TDn(1 + PI) controller under various complex operating conditions, including random and stepwise load changes, system parameter variations, and nonlinearities. The controller’s ability to maintain stable performance in these diverse scenarios underscores its reliability and practical application, making it a powerful tool for enhancing overall system stability and ensuring a reliable energy supply in hybrid power systems.

  • Additional contributions: The study also addresses critical nonlinear factors in LFC, including time delay (TD), governor deadband (GDB), and boiler dynamics (BD). While previous studies have explored the effects of GDB and BD in PV-thermal power systems41, this research uniquely investigates the influence of TD as a nonlinear factor. By incorporating these elements, the study provides new insights and a more thorough understanding of LFC in PV-thermal power systems, further increasing the novelty and impact of the research.

Additionally, the paper is organized into six main sections: Sect. 1 offers an introduction, followed by Sect. 2, which presents and explains the specifics of the photovoltaic and thermal power system. In Sect. 3, the proposed TDn(1 + PI) controller is introduced and analyzed. Section 4 addresses the problem formulation and provides an overview of how the BDGOA optimization technique is integrated with the proposed controller. Section 5 presents the results of control strategy evaluations, various scenarios, and comparative analyses. Lastly, Sect. 6 concludes the paper and outlines potential future work.

Modelling of photovoltaic and thermal power system

A test model was used to evaluate the multi-stage TDn(1 + PI) controller’s performance. This model integrates a PV system and reheat thermal system into a two-area power system. The PV system and its related loads make up Area 1 of Fig. 1, whereas the reheat thermal power system and its related loads make up Area 2.

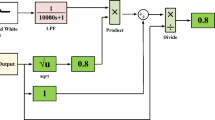
The Eq. (1) represents the transfer function of the solar PV system in area-1, which includes the PV panel, maximum power point tracking (MPPT), converter, and filter.

$$\:{G}_{PV}\left(s\right)=\frac{A-Bs}{{s}^{2}+Cs+D}=\frac{900–18s}{{s}^{2}+100s+50}$$
(1)

The governor, turbine, reheater, and power system are located in Area 2. According to Eqs. (2)–(5), first-order systems are used to express the transfer functions for these components. In these equations, \(\:{\tau\:}_{G}\), \(\:{\tau\:}_{T}\)​, \(\:{\tau\:}_{R}\), \(\:{\tau\:}_{PS}\:\) represent the time constants, while \(\:{K}_{G}\), \(\:{K}_{T}\)​, \(\:{K}_{R}\), \(\:{K}_{PS}\) denote the respective gains for each component of the power system34,40,41,43,44,45,46,47,48. The transfer functions of the governor, turbine, reheater and power system are given respectively as:

$$\:{G}_{G}\left(s\right)=\frac{{K}_{G}}{1+s{\tau\:}_{G}}=\frac{1}{1+0.08s}$$
(2)
$$\:{G}_{T}\left(s\right)=\frac{{K}_{T}}{1+s{\tau\:}_{T}}=\frac{1}{1+0.3s}$$
(3)
$$\:{G}_{R}\left(s\right)=\frac{1+s{K}_{R}{\tau\:}_{R}}{1+s{\tau\:}_{R}}=\frac{1+3.3s}{1+10s}$$
(4)
$$\:{G}_{PS}\left(s\right)=\frac{{K}_{PS}}{1+s{\tau\:}_{PS}}=\frac{120}{1+20s}$$
(5)

Variations in tie-line power and frequency variances are the sources of the area control error (ACE). For Area 1, it is stated in Eq. (6), and for Area 2, in Eq. (7). The ACE for Area 2 accounts for key factors, such as the frequency bias parameter (B) and the change in tie-line power \(\:{\varDelta\:P}_{tie}\)) between the two areas.

$$\:{ACE}_{1}={\varDelta\:P}_{tie}$$
(6)
$$\:{ACE}_{2}=B{\varDelta\:f}_{2}+{\varDelta\:P}_{tie}$$
(7)

To properly evaluate how well the BDGOA-tuned TDn(1 + PI) controller works and make sure it is effective, we need to consider factors like nonlinearities, including GDB and BD, as well as TDs. The model of a two-area PV-thermal power system with these components included is displayed in Fig. 1. In this figure, \(\:{\varDelta\:f}_{1}\) represents the frequency changes in area-1, \(\:{\varDelta\:f}_{2}\) represents the frequency changes in area-2, \(\:{\varDelta\:P}_{tie}\) shows the changes in power between the areas, and R is the regulation droop. The main goal of LFC is to reduce the overall frequency changes in each area and the power deviations between the areas.

Fig. 1
figure 1

Overview of two-area PV-thermal power system with nonlinearity.

Full size image

The transfer function of GDB is detailed in Eq. (8). This study also investigates a different nonlinearity called BD, which denotes a device used for generating steam under pressure. Figure 2 illustrates the BD model and its component transfer functions, which are mathematically represented by Eqs. (9)-(11)41,42.

$$\:{G}_{GDB}\left(s\right)=\frac{0.8-\left(\frac{0.2}{\pi\:}\right)s}{1+s{\tau\:}_{G}}=\frac{0.8-\left(\frac{0.2}{\pi\:}\right)s}{1+0.08s}$$
(8)

The transfer functions of the pressure control, fuel system and boiler storage are given respectively as:

$$\:PC=\frac{{K}_{IB}{T}_{IB}{s}^{2}+{K}_{IB}\left({T}_{RB}+{T}_{IB}\right)s+{K}_{IB}}{0.1{T}_{RB}{s}^{2}+s}=\frac{0.78{s}^{2}+2.85s+0.03}{6.9{s}^{2}+s}\:$$
(9)
$$\:FS=\frac{{e}^{-{T}_{d}s}}{1+{T}_{F}s}=\frac{1}{1+10s}\:$$
(10)
$$\:BS=\frac{1}{{C}_{B}s}=\frac{1}{200s}\:$$
(11)
Fig. 2
figure 2

Block diagram of the BD system.

Full size image

Proposed multi-stage TDn(1 + PI) controller

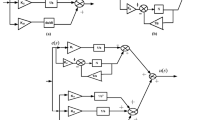
The goal of the suggested multi-stage TDn(1 + PI) controller is to maximize the LFC in a two-area power system that consists of a PV power plant and a reheat thermal generator. This innovative design is structured into two stages, each of which contributes to different aspects of system performance, leading to enhanced dynamic response, frequency stability, and improved control over tie-line power oscillations.

In the first stage, the TDn controller focuses on refining the system’s transient response, particularly in reducing the oscillations that occur during disturbances. The tilt-derivative aspect is a modification of the traditional derivative controller, which not only addresses the rate of change in error but also adjusts the slope of the error signal over time. This allows the system to respond more gradually and effectively to disturbances, preventing abrupt changes that might destabilize the system. By incorporating this tilt function, the controller reduces the amplitude of oscillations, which is crucial when dealing with the inherent fluctuations caused by RESs like PV systems. The inclusion of an N filter in this stage plays a vital role in smoothing out high-frequency noise in the system, which typically arises from the variability of PV power generation. This noise can interfere with control decisions, so filtering it out ensures that the controller reacts only to significant changes in system behavior, rather than responding to spurious signals. The overall effect of the TDn stage is a much smoother and more controlled transition during disturbances, reducing the risk of prolonged oscillations and allowing the system to return to stability more quickly.

The second stage of the controller involves the PI component, which is crucial for correcting both steady-state errors and providing a stable long-term response. The proportional action in this stage delivers an immediate reaction to any frequency deviation by producing a control signal proportional to the magnitude of the error. This helps in providing initial corrective actions as soon as any disturbance occurs, keeping the system from drifting too far from the desired set point. However, while the proportional action helps minimize the immediate deviation, it alone is insufficient to eliminate steady-state errors over time. This is where the integral action becomes critical. The integral part continuously accumulates the error over time and adjusts the control output to ensure that any persistent deviation from the desired frequency is corrected. This process ensures that the system reaches a stable operating point without residual frequency deviations. In combination, the PI controller ensures that both short-term and long-term errors are addressed, providing a balanced response that eliminates steady-state errors while maintaining system stability during dynamic conditions. The block diagram illustrating the proposed controller is depicted in Fig. 3.

Fig. 3
figure 3

Proposed TDn(1 + PI) controller structure.

Full size image

By integrating these two stages, the TDn(1 + PI) controller provides a comprehensive solution that addresses both the dynamic and steady-state requirements of LFC. The TDn stage significantly reduces oscillations and improves the system’s transient response by filtering out noise and managing the rate of change, which is essential in systems with RES prone to fluctuations. The PI stage ensures that steady-state errors are corrected and that the system maintains a stable frequency after disturbances. This multi-stage approach leads to a faster settling time, less oscillatory behavior, and improved long-term stability, making it an ideal solution for modern power systems that combine conventional and RESs. The combined effect of the TDn and PI stages enhances the overall performance of the system, providing faster, more stable, and more accurate LFC. The open-loop transfer function of the first stage controller is shown as Eq. (12):

$$\:{G}_{TDn}\left(s\right)=\frac{{K}_{T}}{{s}^{\frac{1}{n}}}+[{K}_{D}\times\:\left(\frac{Ns}{N+S}\right)]$$
(12)

The open-loop transfer function of the second stage controller is shown as Eq. (13):

$$\:{G}_{(1+PI)}=1+{K}_{P}+\frac{{K}_{I}}{s}$$
(13)

The open-loop representation of the proposed controller can be depicted by Eq. (14).

$$\:{G}_{TDn\left(1+PI\right)}=\left[\frac{{K}_{T}}{{s}^{\frac{1}{n}}}+\left(\frac{{K}_{D}Ns}{N+s}\right)\right]\times\:\left[\frac{\left(1+{K}_{P}\right)s+{K}_{I}}{s}\right]$$
(14)

Finally, Eqs. (15)-(20) illustrate the closed-loop system.

$$\:{G}_{TDn\left(1+PI\right)}=\left[\frac{{K}_{T}\times\:\left(N+s\right)+{K}_{D}\times\:N\times\:{s}^{\frac{1}{n}}\times\:s}{\left(s+N\right)\times\:{s}^{\frac{1}{n}}}\right]\times\:\left[\frac{\left(1+{K}_{P}\right)\times\:s+{K}_{I}}{s}\right]\:$$
(15)
$$\:{G}_{TDn\left(1+PI\right)}=\frac{{[K}_{T}N+{K}_{T}s+{K}_{D}N{s}^{\left(\frac{1}{n}+1\right)}]\times\:(s+{K}_{P}s+{K}_{I})}{\left(s+N\right)\times\:{s}^{\frac{1}{n}}\times\:s}\:$$
(16)
$$\:{G}_{TDn\left(1+PI\right)}=\frac{{[K}_{T}Ns+{K}_{T}{K}_{P}Ns+{K}_{T}{K}_{I}N+{K}_{T}{s}^{2}+{K}_{T}{K}_{P}{s}^{2}+{K}_{T}{K}_{I}s+{K}_{D}N{s}^{(2+\frac{1}{n})}+{K}_{D}{K}_{P}N{s}^{(2+\frac{1}{n})}+{K}_{D}{K}_{I}N{s}^{(1+\frac{1}{n})}]}{{s}^{(2+\frac{1}{n})}+N{s}^{(1+\frac{1}{n})}}\:$$
(17)
$$\:{G}_{TDn\left(1+PI\right)}=\frac{{\left[{(K}_{D}N+{K}_{D}{K}_{P}N\right){s}^{\left(2+\frac{1}{n}\right)}+{K}_{D}{K}_{I}N{s}^{(1+\frac{1}{n})}{+(K}_{T}+{K}_{T}{K}_{P}{)s}^{2}+(K}_{T}N+{K}_{T}{K}_{P}N+{K}_{T}{K}_{I}\left)s{+K}_{T}{K}_{I}N\right]}{{s}^{(2+\frac{1}{n})}+N{s}^{(1+\frac{1}{n})}}\:$$
(18)

If we substitute the optimal parameters of BDGOA-TDn(1 + PI) controller, given in Table 2, into Eq. (18), the following will be obtained.

$$\:{G}_{{TDn\left(1+PI\right)}_{Area-1}}=-\frac{\left(\right(5.0701E+03){s}^{75.5294}+(1.9129E+03){s}^{74.5294}+3.9{s}^{2}+5.0716(E+03)s+1.9129E+03)}{1{s}^{75.5294}+1.3{E}^{+3}{s}^{74.5294}}$$
(19)
$$\:{G}_{{TDn\left(1+PI\right)}_{Area-2}}=-\frac{\left(\right(2.2346E+03){s}^{420.9359}+2.1994(E+03){s}^{419.9359}+3.9156{s}^{2}+4.7028(E+03)s+4.6250E+03)}{1{s}^{420.9359}+1.2001{E}^{+3}{s}^{419.9359}}$$
(20)
Table 2 Optimum gains of proposed and other controllers.
Full size table

Additionally, an overview of the PV-thermal power system and the proposed controller in two-area studied in this research is depicted in Fig. 4.

Fig. 4
figure 4

General scheme of the under-examination model.

Full size image

Optimization method

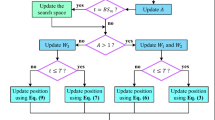
The bio-dynamic grasshopper optimization algorithm (BDGOA) is a modified version of the grasshopper optimization algorithm (GOA) which has been designed to improve the GOA performance in solving the difficult optimization problems. BDGOA addresses the major weaknesses of the original GOA such as, it has a tendency to get stuck in local minima and its convergence rate is slow. Through the introduction of new mechanisms and parameters, BDGOA strikes a better equilibrium between exploration and exploitation. The original GOA is a population-based optimization algorithm inspired by the natural behavior of grasshoppers, particularly their swarming behavior. In GOA, grasshoppers move in the search space under the influence of three main forces: social interaction, gravity, and wind advection. The combination of these forces helps the algorithm find the best solution to a given optimization problem. GOA is divided into two phases:

  • Exploration phase: Grasshoppers move across the search space in large steps to explore different regions.

  • Exploitation phase: Grasshoppers focus on smaller, refined movements to fine-tune their search in areas where promising solutions have been found.

However, despite its potential, GOA suffers from issues like getting stuck in local minima and an imbalanced focus on exploitation too early in the optimization process. This is where BDGOA comes into play. To overcome the limitations of GOA, the BDGOA introduces several enhancements that improve the overall performance of the optimization process. These improvements include:

  • Elimination and replacement mechanism: One of the critical issues in GOA is that poor-performing grasshoppers can slow down the algorithm’s ability to converge to the global best solution. BDGOA addresses this by periodically eliminating a percentage of the worst-performing grasshoppers after a specified number of iterations. These eliminated grasshoppers are replaced with new grasshoppers, which are randomly distributed in the search space. This not only refreshes the population but also helps avoid premature convergence by introducing new potential solutions.

  • Adaptive search space expansion: BDGOA dynamically adjusts the search space as the optimization process progresses. In the early stages, the search space may be relatively confined, allowing for focused exploration of promising regions. However, as the number of iterations increases and certain conditions are met, the search space expands. This gradual expansion helps ensure that the algorithm doesn’t miss out on global solutions by restricting itself to a limited search area. The expansion rate is controlled by the parameter \(\:\omega\:\), which dictates how quickly the search space grows.

  • Exploration-exploitation balance: One of the key challenges in any optimization algorithm is finding the right balance between exploration and exploitation. In BDGOA, this balance is achieved by controlling the rate at which the exploration diminishes and exploitation intensifies. The parameter ccc, which controls this balance, starts with a high value, emphasizing exploration, and gradually decreases over time, allowing the algorithm to focus more on exploitation in the later stages. This helps the algorithm explore new areas early on and refine the best solutions as it nears completion.

Selecting Parameters in BDGOA involves several key factors. The elimination percentage \(\:{\varvec{e}}_{\varvec{p}}\:\)defines the proportion of grasshoppers removed during each elimination phase, while the elimination threshold \(\:{\varvec{e}}_{\varvec{t}}\:\) specifies the number of iterations after which this phase occurs. The threshold for search space expansion \(\:{\varvec{T}}_{\varvec{h}\:}\:\)dictates when the algorithm starts expanding the search space to explore larger regions, and the search space growth rate \(\:\varvec{\omega\:}\:\)controls how quickly the search space expands over time, allowing the algorithm to cover more ground as iterations progress. The BDGOA follows a structured process to solve optimization problems. It begins with initialization, where the objective function (OF) and constraints are defined, and a randomly generated population of grasshoppers represents potential solutions. In the fitness evaluation step, each grasshopper’s position is assessed based on the OF to determine its fitness. The grasshopper positions are then updated using the GOA equation, influenced by factors like social interaction, gravity, and wind forces. After a specified number of iterations, the elimination and replacement phase occur, where the worst-performing grasshoppers are removed and replaced by new ones to maintain diversity and prevent premature convergence. As the algorithm progresses, once a predefined threshold is reached, the search space expands, controlled by the parameter \(\:\omega\:\), allowing the grasshoppers to explore larger areas of the solution space and increasing the likelihood of finding the global optimum. The algorithm iterates through these steps until the maximum number of iterations is reached, continuously updating the best solution. Finally, once the termination criteria are met, the algorithm outputs the best solution found. Table 3 show all steps in optimization process. Figure 5 depicts the schematic of the proposed controller utilizing the BDGOA optimization method in PV-thermal power system.

Table 3 BDGOA steps in optimization process.
Full size table
Fig. 5
figure 5

The schematic of the proposed controller utilizing the BDGOA optimization method in PV-thermal power system.

Full size image

4.1 Objective function definition

The objective function (OF) is a tool used by designers to assess how the system responds dynamically. It aims to guarantee that the control mechanism’s output delivers the best performance across different operating conditions, specifically targeting the minimization of steady-state error. This study aims to carefully adjust the TDn(1 + PI) controller settings using an optimization method called BDGOA to reduce fluctuations in frequency and tie-line power in power systems that include RES. So, OF employed is the ITAE, defined by Eq. (21)40,41.

$$\:{OF}_{min}=\underset{0}{\overset{{t}_{sim}}{\int\:}}t(\left|\varDelta\:{f}_{1}\right|+\left|\varDelta\:{f}_{2}\right|+\left|\varDelta\:{P}_{tie}\right|)dt$$
(21)

Here,\(\:\:t\) and \(\:{t}_{sim}\:\)are present and simulation time, respectively. The OF is restricted by the range of controller coefficients, defining the search space for the optimization problem as presented in Table 4.

Table 4 Range of gains in proposed and other controllers.
Full size table

The BDGOA optimization algorithm was executed in 30 separate rounds, with Table 5 displaying the best, worst, average, and standard deviation (SD) of OF values achieved by different controllers. In addition to the displayed values, the BDGOA has a p-value of \(\:1.7344E-06\) (obtained from Wilcoxon test49,50,51) with respect to all algorithms (BDGOA vs. GEO, BDGOA vs. GOA, BDGOA vs. PSO, BDGOA vs. POA), indicating its superiority.

Table 5 Values of the OF following 20 rounds of optimization algorithms using TDn(1 + PI) controller.
Full size table

Figure 6 compares the effectiveness of five algorithms: BDGOA, golden eagle optimization (GEO), GOA, pelican optimization algorithm (POA), and PSO in minimizing the OF, using boxplots. The boxplot in Fig. 6 clearly shows that the worst result from the BDGOA algorithm is significantly better than the best results from the other four algorithms, highlighting the superior performance of the BDGOA algorithm.

Fig. 6
figure 6

Boxplots of BDGOA, GEO, GOA, PSO and POA algorithms using TDn(1 + PI) controller.

Full size image

The BDGOA algorithm has been run for enough iterations to ensure it converges to the optimal point. We use the BDGOA technique to assess the effectiveness of the proposed controller. Figure 7 shows the results of this optimized approach, which reaches the lowest OF values after 50 iterations, demonstrating the controller’s superior performance.

Fig. 7
figure 7

Convergence profiles of BDGOA, GEO, GOA, PSO and POA algorithms using TDn(1 + PI) controller.

Full size image

Finally, Table 2 shows the optimal controller parameter values in two-area obtained from the best results produced by the BDGOA algorithm.

For a comprehensive numerical comparison, calculations and reports on time-domain evaluation metrics were conducted across various scenarios. These metrics include the integral of square error (ISE), integral of time-weighted square error (ITSE), integral of absolute error (IAE), and integral of time-weighted absolute error (ITAE). The corresponding equations for these metrics are presented in Eqs. (22)-(25).

$$\:ISE={\int\:}_{0}^{x}\left[{\left(\varDelta\:{f}_{1}\right)}^{2}+{\left(\varDelta\:{f}_{2}\right)}^{2}+{\left(\varDelta\:{P}_{tie}\right)}^{2}\right].dt\:$$
(22)
$$\:ITSE={\int\:}_{0}^{x}t.\left[{\left(\varDelta\:{f}_{1}\right)}^{2}+{\left(\varDelta\:{f}_{2}\right)}^{2}+{\left(\varDelta\:{P}_{tie}\right)}^{2}\right].dt\:$$
(23)
$$\:IAE={\int\:}_{0}^{x}\left(\left|\varDelta\:{f}_{1}\right|+\left|\varDelta\:{f}_{2}\right|+\left|\varDelta\:{P}_{tie}\right|\right).dt\:$$
(24)
$$\:ITAE={\int\:}_{0}^{x}t.\left(\left|\varDelta\:{f}_{1}\right|+\left|\varDelta\:{f}_{2}\right|+\left|\varDelta\:{P}_{tie}\right|\right).dt\:$$
(25)

Parameter sensitivity analysis

The performance of the BDGOA is highly influenced by the choice of key parameters, particularly the iteration number and population size. These parameters were systematically analyzed in this study to determine their optimal values for LFC in hybrid power systems. An increase in iteration numbers or population size allows the algorithm to explore the search space more extensively. While this can enhance the chances of finding a global optimum, it comes at the cost of increased computational time. Our experiments show that beyond a certain threshold, further increases in these parameters provide diminishing returns in terms of solution quality, while significantly escalating computational overhead.

Reducing the iteration number or population size below the optimal values limits the algorithm’s ability to sufficiently explore and exploit the search space. This results in suboptimal tuning of the controller parameters, adversely affecting the stability performance of the LFC system. Specifically, inadequate exploration can lead to convergence towards local optima, undermining the algorithm’s robustness in handling system nonlinearities and uncertainties.

To strike a balance, the optimal values of iteration numbers and population size were identified through rigorous trials. These values ensure that the BDGOA achieves high-quality solutions with minimal computational resources. The selected parameters allow for effective convergence within a reasonable time while maintaining the robustness and efficiency of the LFC system.

Simulation and analysis

In this section, the proposed TDn(1 + PI) controller is operationalized and integrated into the PV-thermal power system control mechanism as discussed earlier in Sect. 4. Moreover, these findings show a strong correlation between the results obtained from classical controllers. Subsequently, the closed-loop system is implemented using MATLAB 2023a with Simulink. Using 50 iterations and participation of 20 particles, the BDGOA algorithm effectively identifies the optimal controller coefficient values. The duration of the simulation is 30 s. Although we experimented with higher order approximations, they didn’t significantly alter the results when evaluated in MATLAB. In this system, the parameters are set as follows34,40,41,43,44,45,46,47,48: \(\:{K}_{PS}=120\) Hz/pu.MW, \(\:{\tau\:}_{PS}=20\) s, \(\:{\tau\:}_{R}=10\) s, \(\:{\tau\:}_{G}=0.08\) s, \(\:{\tau\:}_{T}=0.3\:\)s, \(\:{K}_{R}=0.33\) Hz/pu.MW, \(\:{2\pi\:T}_{\text{1,2}}=0.54\) pu.MW / Hz, \(\:B=0.8\) pu.MW / Hz, \(\:R=2.5\) Hz/pu.MW

Analyzed PV-thermal power system in different operation

This section uses simulation experiments to assess the BDGOA-TDn(1 + PI) controller’s performance in various settings. The system’s reaction to load variations in the thermal system demand is evaluated in the first scenario. The behavior of the system is examined for variations in load in both regions in the second scenario. The system is then evaluated by increasing the load in Area 2 step-by-step before both regions see random load variations. The system’s performance is then assessed while taking the power system’s nonlinearities into account. Lastly, the system is assessed using several parameter values; Table 6 has a list of the pertinent BD parameters41,42.

Table 6 Parameters of the boiler dynamic.
Full size table

Scenario I: 10% step change in thermal system demand

In the first scenario, involving a 10% step change \(\:(\varDelta\:{P}_{D1}=0.1\:pu)\) in thermal system demand, the system’s response to a 0.1 pu load change at 0 s is analyzed. The resulting figures compare the proposed controller with the PI, PID, PIDn, FOPID controllers, focusing on frequency variations in area-1 \(\:(\varDelta\:{f}_{1})\), frequency variations in area-2 \(\:(\varDelta\:{f}_{2})\), and tie-line power variations \(\:(\varDelta\:{P}_{tie})\). These comparisons are illustrated in Figs. 8, 9, 10, 11, 12 and 13 respectively. Tables 7 and 8 present detailed numerical data derived from the graphical representations.

Table 7 Numerical results of ST, US, OS and TP for \(\:{\varDelta\:f}_{1}\), \(\:{\varDelta\:f}_{2}\), \(\:{\varDelta\:P}_{tie}\:\)in scenario I
Full size table
Table 8 Comparison of the results for proposed and different controllers in scenario I.
Full size table
Fig. 8
figure 8

Comparison of frequency variation \(\:{\varDelta\:f}_{1}\) for proposed and PI controllers in scenario I

Full size image
Fig. 9
figure 9

Comparison of frequency variation \(\:{\varDelta\:f}_{1}\:\)for proposed and PID, PIDn and FOPID controllers in scenario I.

Full size image
Fig. 10
figure 10

Comparison of frequency variation \(\:{\varDelta\:f}_{2}\) for proposed and PI controllers in scenario I

Full size image
Fig. 11
figure 11

Comparison of frequency variation \(\:{\varDelta\:f}_{2}\) for proposed and PID, PIDn and FOPID controllers in scenario I.

Full size image
Fig. 12
figure 12

Comparison of tie-line power deviation \(\:{\varDelta\:P}_{tie}\) for proposed and PI controllers in scenario I

Full size image
Fig. 13
figure 13

Comparison of tie-line power deviation \(\:{\varDelta\:P}_{tie}\:\)for proposed and PID, PIDn and FOPID controllers in scenario I.

Full size image

Scenario II: both locations see a 10% step change

In the second scenario, which involves a 10% step change \(\:(\varDelta\:{P}_{D1}=0.1\:pu\:\text{a}\text{n}\text{d}\:\varDelta\:{P}_{D2}=0.1\:pu\:)\) in both areas, the system’s response to a 0.1 pu load change at 0s is analyzed. The resulting figures compare the proposed controller with the PI, PID, PIDn, FOPID controllers focusing on frequency variations in area-1 \(\:(\varDelta\:{f}_{1})\), frequency variations in area-2 \(\:(\varDelta\:{f}_{2})\), and tie-line power variations \(\:(\varDelta\:{P}_{tie})\). These fluctuations are depicted in Figs. 14, 15, 16, 17, 18 and 19 respectively. Tables 9 and 10 present detailed numerical data derived from the graphical representations.

Table 9 Numerical results of ST, US, OS and TP for \(\:{\varDelta\:f}_{1}\), \(\:{\varDelta\:f}_{2}\), \(\:{\varDelta\:P}_{tie}\) in scenario II
Full size table
Table 10 Comparison of the results for proposed and different controllers in scenario II.
Full size table
Fig. 14
figure 14

Comparison of frequency variation \(\:{\varDelta\:f}_{1}\) for proposed and PI controllers in scenario II

Full size image
Fig. 15
figure 15

Comparison of frequency variation \(\:{\varDelta\:f}_{1}\) for proposed and PID, PIDn and FOPID controllers in scenario II.

Full size image
Fig. 16
figure 16

Comparison of frequency variation \(\:{\varDelta\:f}_{2}\) for proposed and PI controllers in scenario II

Full size image
Fig. 17
figure 17

Comparison of frequency variation \(\:{\varDelta\:f}_{2}\) for proposed and PID, PIDn and FOPID controllers in scenario II.

Full size image
Fig. 18
figure 18

Comparison of tie-line power deviation \(\:{\varDelta\:P}_{tie}\) for proposed and PI controllers in scenario II

Full size image
Fig. 19
figure 19

Comparison of tie-line power deviation \(\:{\varDelta\:P}_{tie}\) for proposed and PID, PIDn and FOPID controllers in scenario II.

Full size image

Scenario III: stepwise load increase in area 2

The effectiveness of the suggested BDGOA-TDn(1 + PI) controller was assessed in Scenario III with notable variations in load, from 0.1 to 0.5 pu. The simulation results, displayed in Figs. 20 and 21, and 22, demonstrate how well the BDGOA-TDn(1 + PI) controller efficiently reduced the effects of sudden changes in load and rapidly reduced oscillations in both frequency and tie-line power deviations. These results highlight how well the controller keeps the system stable and guarantees dependable performance even in the face of significant load changes.

Fig. 20
figure 20

Comparison of frequency variation \(\:{\varDelta\:f}_{1}\) for proposed controller in scenario III

Full size image
Fig. 21
figure 21

Comparison of frequency variation \(\:{\varDelta\:f}_{2}\) for proposed controller in scenario III

Full size image
Fig. 22
figure 22

Comparison of tie-line power deviation \(\:{\varDelta\:P}_{tie}\:\)for proposed controller in scenario III

Full size image

Scenario IV: both locations see a random load change

This part looks at the dynamics of the system in two different areas under various load circumstances. Figures 23 and 24, and 25 show how the system reacts to combined load variations of 0.05 pu, 0.1 pu, 0.2 pu, 0.3 pu, and 0.5 pu in Area 1 and Area 2. The convergence of oscillation patterns is demonstrated by these images, which also display the frequency fluctuations, and tie-line power variations brought on by synchronized load disturbances in the two sectors. Crucially, a quick and efficient damping reaction is indicated by the oscillations’ quick reduction.

Fig. 23
figure 23

Comparison of frequency variation \(\:{\varDelta\:f}_{1}\) for proposed controller in scenario IV

Full size image
Fig. 24
figure 24

Comparison of frequency variation \(\:{\varDelta\:f}_{2}\:\)for proposed controller in scenario IV

Full size image
Fig. 25
figure 25

Comparison of tie-line power deviation \(\:{\varDelta\:P}_{tie}\:\)for proposed controller in scenario IV

Full size image

Scenario V: non-linear time-delay with random load variation in both locations

In this section, we examine the effects of sudden load changes in both areas, taking into account the impact of time-delay as a non-linearity factor on system dynamics. The system’s responses to these abrupt load variations are presented, highlighting how TDs as a non-linearity factor affect overall performance. In this scenario, it is presumed that the control system’s stimulation signal experiences a 20ms delay on both area controllers. The results in Figs. 26, 27 and 28 show significant changes in frequency and tie-line power, demonstrating that TDs can increase oscillations and make system stabilization more difficult. Although the system eventually stabilizes, the presence of time-delay non-linearity slows down the damping process, resulting in longer-lasting oscillations before the system reaches stability. However, the proposed controller effectively overcomes these challenges, significantly improving system stability and damping oscillations more quickly.

Fig. 26
figure 26

Comparison of frequency variation \(\:{\varDelta\:f}_{1}\) for proposed controller in scenario V

Full size image
Fig. 27
figure 27

Comparison of frequency variation \(\:{\varDelta\:f}_{2}\:\)for proposed controller in scenario V

Full size image
Fig. 28
figure 28

Comparison of tie-line power deviation \(\:{\varDelta\:P}_{tie}\:\)for proposed controller in scenario V

Full size image

Scenario VI: GBD and BD as nonlinearities

The behavior of the system was assessed when there are nonlinearities, such as boiler dynamics (BD) and governor deadband (GDB), to offer a more realistic analysis. When GDB is included, the oscillations in Area 1, Area 2, and the tie-line power deviations are shown in Fig. 29; the oscillations affected by BD are shown in Fig. 30. These graphs show that the tie-line power variations and frequency oscillations of the system are rapidly muted and remain within the specified bounds. In Fig. 31, where both BD and GDB are applied simultaneously, the results confirm that the system remains stable, with the controller effectively handling the more complex nonlinear dynamics. This underscores the effectiveness of the BDGOA-TDn(1 + PI) controller in attenuating oscillations despite the presence of nonlinearities, highlighting its robustness in managing system dynamics and maintaining stability.

Fig. 29
figure 29

Comparison of variation \(\:{\varDelta\:f}_{1}\:,\:{\varDelta\:f}_{2}\:\)and \(\:{\varDelta\:P}_{tie}\:\)for proposed controller with GDB in scenario VI

Full size image
Fig. 30
figure 30

Comparison of variation \(\:{\varDelta\:f}_{1}\:,\:{\varDelta\:f}_{2}\:\)and \(\:{\varDelta\:P}_{tie}\:\)for proposed controller with BD in scenario VI

Full size image
Fig. 31
figure 31

Comparison of variation \(\:{\varDelta\:f}_{1}\:,\:{\varDelta\:f}_{2}\:\)and \(\:{\varDelta\:P}_{tie}\:\)for proposed controller with GDB and BD in scenario VI

Full size image

Scenario VII: fluctuation in parameters

In electrical power systems, sensitivity analysis is essential for anticipating system behavior in unpredictable circumstances and guaranteeing optimal functioning. In this study, a sensitivity analysis was conducted on the power system to evaluate performance under varying conditions. The governor, turbine, reheater, and power system components had their time constants adjusted by ± 25% as part of the analysis. The outcomes, which are shown in Figs. 32 and 33, and 34, show that the suggested controller was able to manage these fluctuations and stabilize the oscillations in the system. This highlights the controller’s robustness and adaptability to changes in system parameters, ensuring reliable stability across different operating conditions.

Fig. 32
figure 32

Comparison of frequency variation \(\:{\varDelta\:f}_{1}\:\)for proposed controller in scenario VII

Full size image
Fig. 33
figure 33

Comparison of frequency variation \(\:{\varDelta\:f}_{2}\:\)for proposed controller in scenario VII

Full size image
Fig. 34
figure 34

Comparison of tie-line power deviation \(\:{\varDelta\:P}_{tie}\:\)for proposed controller in scenario VII

Full size image

Conclusions and scope of future work

In this work, we investigated the use of LFC in a two-area power system comprising a PV power plant and a reheat thermal generator. To address dynamic challenges such as frequency oscillations and tie-line power fluctuations, we developed an advanced multi-stage TDn(1 + PI) controller. The controller’s parameters were optimized using the BDGOA, with an enhanced ITAE serving as the OF. The BDGOA-tuned TDn(1 + PI) controller was compared in detail to a number of other controllers, such as the BDGOA-tuned FOPID, MWOA-tuned PIDn, MWOA-tuned PID, BDGOA-tuned PID, BDGOA-tuned PI, RIME-tuned PI, BWOA-tuned PI, SSA-tuned PI, SFLA-tuned PI, FA-tuned PI, GA-tuned PI, GTO-tuned PI, and WOA-tuned PI controllers. Comprehensive simulation results consistently demonstrated that the BDGOA-tuned TDn(1 + PI) controller outperformed the alternatives, especially when it came to decreasing overshoot/undershoot values and attaining quicker system oscillation settling periods. Moreover, the proposed controller demonstrated excellent performance under different operating conditions, such as random load changes, system parameter variations, stepwise load changes, and the presence of nonlinear factors. The robustness of the BDGOA-tuned TDn(1 + PI) controller was further validated through tests with parameter variations, where it maintained stable performance, confirming its reliability. These results lead us to the conclusion that the BDGOA-tuned TDn(1 + PI) controller dramatically increases power system stability and reliability and is a highly effective LFC solution in two-area PV-thermal systems. Additionally, this study highlights the critical role of LFC in ensuring operational efficiency and reliable energy supply in power systems. We recommend further empirical research using the OPAL-RT simulation platform and anticipate that ongoing development of optimization algorithms will lead to enhanced operational performance, particularly in LFC applications. The BDGOA-tuned TDn(1 + PI) controller emerges as a promising tool for maintaining stable power system operation and reducing oscillations in similar hybrid power systems.