An information gap decision theory and improved gradient-based optimizer for robust optimization of renewable energy systems in distribution network

Abstract

In this paper, a robust fuzzy multi-objective framework is performed to optimize the dispersed and hybrid renewable photovoltaic-wind energy resources in a radial distribution network considering uncertainties of renewable generation and network demand. A novel multi-objective improved gradient-based optimizer (MOIGBO) enhanced with Rosenbrock’s direct rotational technique to overcome premature convergence is proposed to determine the problem optimal decision variables. The deterministic optimization framework without uncertainty minimizes active energy loss, unmet customer energy, and renewable generation costs. The study also examines the impact of dispersed and hybrid renewable resources on solving the problem. In the robust optimization framework considering the deterministic obtained results, the focus is on determining the maximum uncertainty radius (MUR) of renewable resource generation and network demand based on the uncertainty risk. The MURs and system robustness are optimally determined using information gap decision theory (IGDT) and the MOIGBO, considering various uncertainty budgets under worst-case scenarios. The deterministic results indicate that the MOIGBO effectively balances the objectives and identifies the final solution within the Pareto front, according to fuzzy decision-making. The results also reveal that the dispersed case yields better objective values than the hybrid case. Furthermore, the MOIGBO outperforms MOGBO and multi-objective particle swarm optimization (MOPSO) in improving distribution network operations. The robust results show that maximum system robustness is achieved at 30% uncertainty risk due to forecasting errors, with MUR values of 0.54% for resource production and 12.56% for load demand.

Introduction

Motivation

Because of population growth and the process of urbanization, there is at present a significant increase in the electrical energy demand, which is unable to be met by the infrastructure of the present electrical system^1,2. Therefore, more generation may be produced by efficiently using traditional fossil fuel-powered production facilities^1,2. Further power generation via distributed generation (DG), or tiny producing units that may be directly connected to the current distribution system, can be used to provide supplemental assistance³. The distributed generation (DGs) that rely on renewable energy sources (RESs) like wind turbine (WT) and photovoltaic (PV) resources can be placed in the electricity network in close proximity to the end users^4,5. The RES integration into networks has the potential to increase voltage stability, reduce losses, and reduce voltage variation^6,7. To get the most value from the optimization of RESs in the networks, the best site and capacity for these resources should be chosen. Furthermore, because of their inherent uncertainties, both the RES power generation and the network demand should be assessed in light of the distribution network’s RES optimization^8,9.

Related works and research gaps

Numerous researches have been carried out in the area of renewable resource optimization in distribution network optimization, focusing on the objective function (OF), renewable system structure, optimization technique, and uncertainty modeling. In¹⁰, a particle swarm optimization (PSO) is used to optimize a renewable energy resource in the network with the goal of lowering the overall loss. In¹¹, distributed generators are efficiently allocated in distribution networks to minimize power loss, and enhance voltage conditions using a chaotic search method. A method for making decisions for optimizing the storage device in a power plant made up of loads, PV resources, and WT was described in¹² with the aim of lowering the virtual power plant’s overall cost. In order to achieve loss reduction, security, and voltage augmentation, the enhanced spotted hyena optimizer (ISHO) is applied in¹³ to the stochastic optimization of the wind and photovoltaic devices with power uncertainty. In¹⁴, with multiple goals DG optimization is investigated in the restructuring of the network utilizing the enhanced particle swarm optimization approach to preserve improved feeder current and voltage profiles and lower annual energy loss. To maximize the hosting size in¹⁵ under load unpredictability, the Harris Hawks optimization (HHO) is utilized to solve stochastic optimization of the DGs in networks. In order to anticipate the network’s development, the authors of¹⁶ presented a model with multiple levels for the networks possessing significant penetrating of renewable units and storage systems. In¹⁷, an optimization strategy is suggested for a far-off remote household region. The suggested approach is predicated on the utilization of traditional energy resources, WT, and PV. A MINLP approach to DG scheduling that minimizes the fuel cost of wind and traditional power units has been given in¹⁸. The findings demonstrated that determining the best site and capacity for wind units decreased fuel costs and power loss while also improving the network voltage profile. In order to achieve the best possible operation for energy systems, a multi-objective strategy is presented in¹⁹. Power decrease and voltage improvements have also been developed in the networks. In order to decrease overall losses, the renewable systems operation has been optimized in²⁰ using the Cuckoo Search (CS) algorithm and the grasshopper optimization approach. In²¹, a modified sine–cosine algorithm is used to allocate DG resources in networks with the goal of costs and losses minimization while simultaneously increasing voltage consistency. The multi-objective PSO was created in²² is utilized to minimize the loss, enhancing the voltage characteristics, and enhancing stability through the best possible deployment of renewable sources within the network. In order to decrease the losses and voltage fluctuations, an equilibrium optimizer (EO) is suggested in²³ for finding the optimization of WTs in the network. In²⁴, the goal is to increase voltage stability and minimize losses and voltage variations by using an improved spotted hyena optimizer (ISHO) in two deterministic and stochastic WT optimization in the network. With the goal of reducing loss and enhancing voltage stability while accounting for the uncertainty of wind power, the network presents the stochastic optimization of wind energy resources in^25,26 using the Monte Carlo simulation (MCS). A multi-objective multi-verse optimization technique is presented in²⁷ for the concomitant ideal positioning and scaling of energy storage and DG in the networks. The work in question aims to enhance the voltage characteristic while minimizing the expense of the expenditure. The improved spotted hyena optimizer (ISHO) is used in¹³ to distribute PV and WT resources considering generation uncertainty to minimize the losses, and safety and voltage enhancement. In order to examine the financial and ecological consequences of many buildings, a MINLP model is created in²⁸ for the placement of combined power, heat, and cooling systems that are integrated with renewable energy. The outcomes demonstrated the cost-effectiveness of integrating power and heating during periods of high demand for renewable resources.

The research gaps of the previous studies are listed as follows:

• The majority of research relies on multi-objective optimization, and the weighted coefficient approach is applied for problem solving. However, choosing the coefficients in this method is difficult and cannot be done in a way that compromises all objectives.

• The operation of the network can be impacted by the uncertainties created by the demand for the network and generation of renewable resources. If these factors are ignored, conservative scheduling and the avoidance of making wise decisions that are robust to these uncertainties result. Certain studies have not taken into account the impact of uncertainty on the robust network’s energy resource optimization.

• Most research on stochastic optimization of renewable resources in distribution networks uses Monte Carlo simulation, according to a study of the literature. The Monte Carlo approach is computationally demanding and requires data with a probability distribution. Furthermore, the output of this system is very reliant on the described situations and is not capable of offering a reliable solution in unpredictable circumstances.

• Upon reviewing the literature, it is evident that most research has tackled the optimization of renewable resources in distribution networks through statistical methods and meta-heuristic algorithms. Analytical techniques are very intricate and demand a great deal of data. Furthermore, based on the NFL theory²⁹, none of the meta-heuristic algorithms can ensure that the global optimal solution would be achieved; instead, they could get stuck in the local optimal solution. Meta-heuristic algorithms are less time-consuming and easier to develop than statistical methods. As a result, by achieving a precise problem solution, offering an enhanced meta-heuristic method that is more capable than its traditional version can result in an improvement in the distribution network’s performance.

Contributions

The study’s contributions are listed in the following order based on the identified research gaps:

• In order to minimize active energy loss, energy not met by network customers, and renewable generation cost considering two dispersed and hybrid cases, deterministic multi-objective optimization of renewable PV-WT energy resources is demonstrated in radial distribution networks integrated with fuzzy decision-making.

• An information gap decision theory (IGDT) is applied for robust optimization analyzing different uncertainty budgets to calculate the system robustness contrary to the worst scenario of uncertainty circumstances, in contrast to stochastic methods, which are unable to identify the robust solution.

• A new multi-objective improved gradient-based optimizer (MOIGBO) is recommended as a novel solver to discover the decision variables optimally. It is based on Rosenbrock’s direct rotational approach³⁰ to avoid premature convergence.

• Newton’s method’s guiding principles serve as the basis for the traditional GBO³¹. To solve the deterministic issue, the MOIGBO’s efficiency has been contrasted to that of MOGBO and multi-objective particle swarm optimization (MOPSO).

Paper’s organization

“Methodology” section of the ensuing paper presents the technique, which includes the OF, constraints, optimization approach, and renewable generation and demand model, as well as how it was implemented for problem solving. The multi-objective approach suggested by MOIGBO is described in “Proposed optimizer” section. The robust optimization strategy is described in “Robust optimization approach” section. The simulation outcomes for the various scenarios are retrieved in “Simulation results” section. Ultimately, the study’s outcomes are summarized in “Conclusion” section.

Methodology

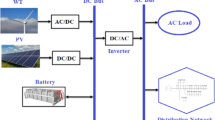
This section presents the formulation of optimizing distributed and hybrid energy systems, which include PV and WT resources, in radial networks to minimize the renewable generation cost, energy not-met, and annual active energy loss by applying the MOIGBO.

Generation and demand model

WT model

The relation between wind speed and the power generated using the WT is nonlinear. The following formula is used to determine each wind turbine unit’s electrical output depending on different types of wind speed^13,23,26:

$$P_{WT} = \left\{ \begin{gathered} 0\begin{array}{*{20}l} {} & {} & {} \\ \end{array} \,\begin{array}{*{20}l} {} & {} & {} \\ \end{array} \mathop {}\limits^{{}} \,\,\,\,\,\,\,\,\,\,\,\,V_{W} \le V_{cutin} ,\,v_{W} \ge V_{cutout} \hfill \\ a \times V_{W}^{3} - b \times P_{WT,rated} \mathop {}\limits^{{}} \mathop {}\limits^{{}} \mathop {}\limits^{{}} V_{cutin} \le V_{W} \le V_{rated} \hfill \\ P_{WT,rated} \begin{array}{*{20}l} {} & {} & {} \\ \end{array} \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \,V_{rated} \le V_{W} \le V_{cutout} \hfill \\ \end{gathered} \right.$$

(1)

$$a = \frac{{P_{WT,rated} }}{{V_{{_{rated} }}^{3} - V_{{_{cutin} }}^{3} }}$$

(2)

$$b = \frac{{V_{{_{cutin} }}^{3} }}{{V_{{_{rated} }}^{3} - V_{{_{cutin} }}^{3} }}$$

(3)

where $P_{WT,rated}$ denotes the nominal power, $V_{W}$ is to the present wind speed, $V_{cutout}$, $V_{rated}$, $V_{cutin}$ are the cutout, nominal and cutin wind speed, respectively.

PV model

The radiation emitted on a PV panel’s surface and the surrounding temperature determine the panel’s production capability. One may compute the output power of every PV panel unit ($P_{PV}$) based on temperature and irradiance using the following formulas^10,12:

$$P_{PV} = P_{PV,rated} \times \frac{S}{{S_{ref} }} \times [1 + N_{T} (T_{c} - T_{STC} )]$$

(4)

$$T_{c} = T_{amb} + \left[\frac{(NOCT - 20)}{{800}} \times S \right]$$

(5)

where, $P_{PV,rated}$ indicates nominal PV power, $S$ and $S_{ref}$ refer to the instantaneously irradiance and standard irradiance, $N_{T}$ is coefficient related to the PV temperature (-3.7 $\times$ 10^–3 (1/°C)), $T_{c}$, $T_{STC}$ and $T_{amb}$ refer to the PV cell, standard condition and temperature of the ambient. $NOCT$ is temperature of the nominal operating cell (°C).

Demand model

Every distribution post has a particular mix of industrial, residential, and commercial loads, and the range of voltages of the post affects how much power is used. The following formula can be used to define active and reactive load and models of the power demand³²:

$$P_{i} = P_{0i} \left| {\overline{V}_{i} } \right|^{\alpha }$$

(6)

$$Q_{i} = Q_{0i} \left| {\overline{V}_{i} } \right|^{\beta }$$

(7)

where, P_i and Q_i refer to the active and reactive load for bus i. $\alpha$ and $\beta$ denote the exponents of voltage-dependent demands³², $P_{0i}$ and $Q_{0i}$ indicate the active and reactive powers at rated voltage, and the voltage amplitude at the terminal to rated quantity ratio is expressed as $\overline{V}$³².

Objective function

The objective function (OF) of the dispersed and hybrid PV and WT resources allocation in distribution networks is formulated as for minimizing the annual active energy loss, energy not-met, and renewable generation cost.

Energy loss

Reducing energy losses is one of the primary aims of the network operations. The active energy losses of the network lines in the simulation period, as described by^9,13,20, equals the active energy losses of the network ($E_{Loss}$) as follows:

$$E_{Loss} = \sum\limits_{t = 1}^{\partial } {P_{Loss} (t)}$$

(8)

$$P_{Loss} = \sum\limits_{i = 1}^{\mathchar'26\mkern-10mu\lambda} {(R_{i} \times Cu_{i}^{2} } )$$

(9)

$$Cu_{i}^{2} = \frac{{P_{i}^{2} + Q_{i}^{2} }}{{\left| {V_{i} } \right|^{2} }}$$

(10)

where,$\partial$ refers to simulation period (8760 h), ${\mathchar'26\mkern-10mu\lambda}$ is the network lines number, $R_{i}$ refers to the ohmic resistance of ith line, $Cu_{i}$ is ith line current, $V_{i}$ is bus i voltage, $P_{i}^{{}}$ is active load flow at transferring the i^th line’s end and $Q_{i}^{{}}$ is real load flow at the ith line’s transmitting end.

Energy not-met

Improving reliability is one of the distribution network’s main goals³³. The distribution network has historically been subject to regular component failures as well as planned and unplanned problems. These events can cause network outages and interfere with the uninterrupted and sufficient provision of the customer’s demand. The equation that follows is used in the present research to improve network reliability by customers energy not met (ENM) minimization:

$$ENM = \sum\limits_{t = 1}^{\partial } {\sum\limits_{i = 1}^{\mathchar'26\mkern-10mu\lambda} {\sum\limits_{j = 1}^{\ell } {\Omega_{i} \times \xi_{i} \times C_{\kappa } \times \tau_{i} \times \phi_{j} } } }$$

(11)

where, $\xi_{i}$ refers to the length of the line, $\ell$ is the loads number that are cut off following the line i outage, $\Omega_{i}$ is the outage value per km in a year, $C_{\kappa }$ denotes the cost of the ENS, $\phi$ clears the disrupted load as a result of the line i outage, and the time it takes to fix the problem is $\tau_{i}$.

Renewable resources cost

Minimizing the power cost of renewable resources is another objective taken into account in this study since it helps determine where those resources should be placed in the the network most effectively³⁴. The overal cost of the initial investment, ongoing operations and maintenance, and the cost of injecting power into the network using the RESs is known as the resource production cost.

$$\begin{gathered} C_{\mu } = ((C_{PV\Upsilon }^{{}} + C_{{PVO{\rm M}}}^{{}} ) + (C_{WT\Upsilon }^{{}} + C_{{WTO{\rm M}}}^{{}} )) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, + C_{PV}^{{}} \times \sum\limits_{t = 1}^{\partial } {P_{PV} } (t) + C_{WT}^{{}} \times \sum\limits_{t = 1}^{\partial } {P_{WT} } (t) \hfill \\ \end{gathered}$$

(12)

where, $C_{PV\Upsilon }^{{}}$ and $C_{{PVO{\rm M}}}^{{}}$ are primary investment and operation and maintenance costs. $C_{WT}^{{}}$ and $C_{PV}^{{}}$ are cost of per kW transferred power of WT and PV to the network.

Constraints

The OF must be satisfied while taking into account the following constraints in order for solving the optimization issue^9,13,20:

Voltage constraint

The voltage of the bus ought to fall between the permitted lower and upper limits.

$$\upsilon_{i,min} \le \upsilon_{i} \le \upsilon_{i,max}$$

(13)

Whereas, $\upsilon_{i,min}$ and $\upsilon_{i,max}$ denote the bus voltage’s lower and upper bounds.

RESs capacity penetration

The following guidelines should be followed in order to restrict the quantity of resource penetration and the capacity of RESs:

$$\sum\limits_{i = 1}^{\gamma } {P_{RES,i} } \le \varphi \times \sum\limits_{i = 1}^{\chi } {P_{Load,i} }$$

(14)

where, $\gamma$ is the energy resources number, $\chi$ is the buses number, and $\varphi$ is the degree of RES penetration in the network.

Every RES resource’s chosen capacity should also fall between the standard values and be fewer than the recommended size.

$$P_{RES,i}^{\min } \le P_{RES,i}^{{}} \le P_{RES,i}^{\min } \,\,\,\,\,i = 1,2,...,N_{RES}$$

(15)

Power balance

In Eq. (16), power balance constraint brought on by the generation of RESs, consumers, losses, and network power:

$$P_{Post} + P_{RES} = P_{Loss} + \sum\nolimits_{n = 1}^{\chi } {P_{Load,n} }$$

(16)

where, P_Post is the active power transferred to the network by the post, P_RES is the total generating capacity of the renewable energy sources, and demand is the amount of power used by each bus.

Current constraint

The following is the maximum current that can be obtained by the network lines:

$$Cu_{\min } \le Cu_{i} \le Cu_{\max } ;\,\,\,\,\,\,\,i = 1,2,...,\partial$$

(17)

where, $Cu_{\min }$ and $Cu_{\max }$ refer to the highest and lowest permitted currents flowing via the branch k, respectively.

Proposed optimizer

Overview of GBO

The concepts behind Newton’s approach serve as the basis for the gradient based-optimizer (GBO)³¹. To achieve equilibrium between the pursuit of knowledge and profit, the gradient search rule (GSR) and the local escape operator (LEO) are the two primary operators used by the technique.

Gradient search rule (GSR): By including an unpredictable nature in the optimization approach, the proposed GSR can improve the optimization locally during the exploration and escape stages. An efficient local search is established using a method known as Direct Motion (DM) to increase the convergence rate of the GBO. The following formula, which is used to update the present vector’s location (${x}_{n}^{m}$)³¹, is produced by combining GSR and DM.

$${X1}_{n}^{m}={x}_{n}^{m}-randn\times {\rho }_{1}\times \frac{2\Delta x\times {x}_{n}^{m}}{({x}_{\text{worst}}-{x}_{best}+\varepsilon )}+rand\times {\rho }_{2}\times ({x}_{best}-{x}_{n}^{m})$$

(18)

where,

$${\rho }_{1}=2\times rand\times \alpha -\alpha$$

(19)

$$\alpha =\left|\beta \times \text{sin}\left(\frac{3\pi }{2}+\mathit{sin}\left(\beta \times \frac{3\pi }{2}\right)\right)\right|$$

(20)

$$\beta ={\beta }_{min}+\left({\beta }_{max}-{\beta }_{min}\right)\times {\left(1-{\left(\frac{m}{M}\right)}^{3}\right)}^{2}$$

(21)

In this case, ${\beta }_{min}$ and ${\beta }_{max}$ have quantities of 0.2 and 1.2. M is the maximum iterations number, and the variable m denotes the number of iterations. An arbitrary number taken from a normal distribution is denoted by the word randn, and ε is a tiny quantity in the interval [0, 0.1]. The process used to calculate ${\rho }_{2}$ is³¹.

$${\rho }_{2}=2\times rand\times \alpha -\alpha$$

(22)

$$\Delta x=rand(1:N)\times |step|$$

(23)

$$step=\frac{({x}_{best}-{x}_{r1}^{m})+\delta }{2}$$

(24)

$$\delta =2\times rand\times \left(\left|\frac{{x}_{r1}^{m}+{x}_{r2}^{m}+{x}_{r3}^{m}+{x}_{r4}^{m}}{4}-{x}_{n}^{m}\right| \right)$$

(25)

where, an N-dimensional randomized number collection is represented by $rand(1:N)$. Randomly selected unique numbers from the interval [1, N] are the values $r1, r2, r3, r4 (r1\ne r2\ne r3\ne r4\ne n$. The size determined by ${x}_{best}$ and ${x}_{r1}^{m}$ is the step. The process³¹ below can be used to create the new vector (${X2}_{n}^{m}$) by replacing the current vector (${x}_{n}^{m}$) at the optimal vector location (${x}_{\text{best}}$):

$${X2}_{n}^{m}={x}_{\text{best}}-randn\times {\rho }_{1}\times \frac{2\Delta x\times {x}_{n}^{m}}{({yp}_{n}^{m}-{yq}_{n}^{m}+\varepsilon )}+rand\times {\rho }_{2}\times ({x}_{r1}^{m}-{x}_{r2}^{m})$$

(26)

$${yp}_{n}=rand\times \left(\frac{\left[{z}_{n+1}{+x}_{n}\right]}{2}+rand\times \Delta x \right)$$

(27)

$${yq}_{n}=rand\times \left(\frac{\left[{z}_{n+1}{+x}_{n}\right]}{2}-rand\times \Delta x \right)$$

(28)

The solution that will be offered in the next iteration (${x}_{n}^{m+1}$) can be obtained by via the positions of ${X1}_{n}^{m}$, ${X2}_{n}^{m}$, and the present location (${X}_{n}^{m}$)³¹.

$${x}_{n}^{m+1}={r}_{a}\times \left({r}_{b}\times {X1}_{n}^{m}+\left(1-{r}_{b}\right)\times {X2}_{n}^{m}\right)+\left(1-{r}_{a}\right){\times X3}_{n}^{m}$$

(29)

$${X3}_{n}^{m}={X}_{n}^{m}-{\rho }_{1}\times ({X2}_{n}^{m}-{X1}_{n}^{m})$$

(30)

Improving Productivity using Local Escape Operator (LEO): In order to enhance the suggested GBO’s operation in handling complex issues, the LEO is described. To find the best-performing solution (${X}_{LEO}^{m}$), LEO uses several solutions. These include the one with the greatest performance (${x}_{\text{best}}$), solutions ${X1}_{n}^{m}$ and ${X2}_{n}^{m}$, two randomly chosen solutions, ${x}_{r1}^{m}$, and ${x}_{r2}^{m}$, as well as a new arbitrary solution, ${x}_{k}^{m}$. The following procedure is used to create the answer ${X}_{LEO}^{m}$³¹:

(31)

whereas ${f}_{2}$ is an arbitrary number taken from a normally distributed distribution with a median and a standard deviation of 1, ${f}_{1}$ denotes a constant value falling between − 1 and 1 at random. Pr is an abbreviation for likelihood. Furthermore, as stated following³¹, ${u}_{1}$, ${u}_{2}$, and ${u}_{3}$ represent three different arbitrary numbers:

$${u}_{1}=\left\{\begin{array}{ll}2\times rand & \quad if \; {\mu }_{1}< 0\text{.}5 \\ 1 & \quad otherwise\end{array}\right.$$

(32)

$${u}_{2}=\left\{\begin{array}{ll}rand & \quad if \; {\mu }_{1}<0\text{.}5 \\ 1 & \quad otherwise\end{array}\right.$$

(33)

$${u}_{3}=\left\{\begin{array}{ll}rand & \quad if \; {\mu }_{1}<0\text{.}5 \\ 1 & \quad otherwise\end{array}\right.$$

(34)

where, ${\mu }_{1}$ denotes a value between the bounds of [0, 1], and $rand$ denotes an arbitrary number within the interval [0, 1]. The approach listed below can be used to simplify the given formulas³¹:

$${u}_{1}={L}_{1}\times 2\times rand+(1-{L}_{1})$$

(35)

$${u}_{2}={L}_{1}\times rand+(1-{L}_{1})$$

(36)

$${u}_{3}={L}_{1}\times rand+(1-{L}_{1})$$

(37)

${L}_{1}$ is a binary parameter in this context that can have a value of either 0 or 1. The value of ${L}_{1}$ is altered to 0 otherwise; it becomes 1 when the parameter ${\mu }_{1}$ is less than 0.5. The following method is described as a means of identifying the solution ${x}_{k}^{m}$³¹:

$${x}_{k}^{m}=\left\{\begin{array}{ll}{x}_{rand} & \quad if \; {\mu }_{2}<0\text{.}5 \\ {x}_{p}^{m} & \quad otherwise\end{array}\right.$$

(38)

$${x}_{rand}={X}_{min}+rand\left(0, 1\right) \times \text{(}{X}_{max}-{X}_{min})$$

(39)

A unique solution is indicated by ${x}_{rand}$, an arbitrary solution chosen from the population (where $p\in [1\text{, 2,}\dots \text{, }N$) is represented by ${x}_{p}^{m}$, and ${\mu }_{2}$ is an arbitrary number falling between [0, 1]. The following method can be used to simplify Eq. (38):

$${x}_{k}^{m}={L}_{2}\times {x}_{p}^{m}+(1-{L}_{2})\times {x}_{rand}$$

(40)

In this case, the binary parameter ${L}_{2}$ has two possible values: 0 and 1. ${L}_{2}$ gets a value of 0 otherwise, and is altered to 1 when ${\mu }_{2}$ is lower than 0.5.

Overview of IGBO

Two issues with the standard GBO are that it becomes trapped in early convergence and exhibits an unequal distribution of discovery and extraction. In this study, Rosenbrock’s direct rotational (RDR) approach³⁰ is used to improve the efficiency of the traditional GBO in these situations. The coordinate axes serve as a starting point for the RDR local search technique’s rotation as it moves to a fresh designated point where successful steps are produced till a minimum of one successful procedure and one failed step are found in every search orientation.

In this instance, the current stage is completed, and the identifying foundation is examined to determine the total impact of all completed stages across each dimension³⁰. The following updates have been made to the orthonormal foundation:

$$x^{k + 1} - x^{k + } = \sum\limits_{i = 1}^{n} {\lambda_{i} .d_{i} }$$

(41)

A series of directions is given in the following equation. where ${x}^{k+1}-{x}^{k+}$ denotes the location with the greatest advantageous search direction, and λ_i stands for the overall number of accurate variables. As a result, the search direction has been adjusted.

$$pi = \left\{ \begin{gathered} d_{i} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\lambda_{i} = 0 \hfill \\ \sum\limits_{j = 0}^{n} {\lambda_{j} .d_{j} \,\,\,\,\,\,\,\,\,\,\lambda_{i} \ne 0} \hfill \\ \end{gathered} \right.$$

(42)

The following equation represents the updated search results derived from the Gram-Schmidt normalization technique.

$$qi = \left\{ \begin{gathered} p_{i} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i = 1 \hfill \\ p_{i} - \sum\limits_{j = 1}^{i - 1} {\frac{{q_{j}^{T} .p_{i} }}{{q_{j}^{T} .q_{j} }}\,\,\,\,\,\,\,\,\,\,i \ge 2} \hfill \\ \end{gathered} \right.$$

(43)

The following is a definition of the adjusted and normalized search instructions:

$$d_{i} = \frac{{q_{i} }}{{\left\| {\left. {q_{i} } \right\|} \right.}},\,i = 1,2,3,...,n.$$

(44)

This technique searches till the convergence criterion is satisfied in the entirely reverse direction, during which it updates the local search.

Overview of MOIGBO

The multi-objective optimization issue^33,35 has multiple conflicting OFs and constraints that need to be optimized simultaneously. This problem is defined by

$$Min F\left(x\right)={\left[{f}_{1}\left(x\right) {f}_{2}\left(x\right) \dots {f}_{n}\left(x\right)\right]}^{T}$$

(45)

$$Subject\; to{:} \; \left\{\begin{array}{ll}{g}_{i}\left(x\right)<0 & \quad i=\text{1,2},\dots ,{N}_{ueq}\\ {h}_{i}\left(x\right)=0 & \quad i=\text{1,2},\dots ,{N}_{eq}\end{array}\right.$$

(46)

where, n denotes the OFs number, F(x) refers to the vector representation of OFs, and ${g}_{i}\left(x\right)$ and ${h}_{i}\left(x\right)$ are the restrictions of inequality and equality. A multi-objective optimization issue has two alternative answers: x and y. Either one will be superior to the other, or no one of the other selections will be. Therefore, if the next two requirements are satisfied, Answer x to an optimization issue is going to win over answer y.

$${\forall j\in \left\{\text{1,2},\dots ,n\right\}, f}_{j}\left(x\right)\le {f}_{j}\left(y\right)$$

(47)

$${\exists k\in \left\{\text{1,2},\dots ,n\right\}, f}_{k}\left(x\right)<{f}_{k}\left(y\right)$$

(48)

So, Pareto set answers may be determined using non-dominated solutions in the space of search. Eventually, the last stored non-dominated solutions including the answer. To determine the best response between the optimum selections, the fuzzy decision process is evaluated via a function of membership whereby the accurate several variables could be input. The OF i best possible quantity among the answers that are Pareto optimum k is represented by ${\mu }_{i}^{k}$, which has the following definitions^33,35:

$$\mu_{i}^{k} = \left\{ \begin{array}{ll} 1 & \quad {\text{ f}}_{i} \le f_{i}^{\min } \hfill \\ \frac{{f_{i}^{\max } - {\text{f}}_{i} }}{{f_{i}^{\max } - f_{i}^{\min } }} & \quad f_{i}^{\min } \le {\text{f}}_{i} \le f_{i}^{\max } \hfill \\ 0 & \quad {\text{f}}_{i} \ge f_{i}^{\max } \hfill \\ \end{array} \right.$$

(49)

The highest and smallest amounts of the OF i are denoted by ${f}_{i}^{max}$ and ${f}_{i}^{min}$. The proposed approach for calculating these numbers takes advantage of the optimization outcomes for each OF. The number ${\mu }_{i}^{k}$ ranges from 0 to 1. A value of 0 indicates incompatibility within the outcome and the operator’s objectives, whereas an amount of 1 indicates total compliance.

For each of the k Pareto solutions, the normalized membership function is calculated the following way:

$$\mu_{{}}^{k} = \frac{{\sum\nolimits_{i = 1}^{m} {\mu_{i}^{k} } }}{{\sum\nolimits_{z = 1}^{n} {\sum\nolimits_{i = 1}^{m} {\mu_{i}^{k} } } }}$$

(50)

In this case, m denotes the OF’s number and n represents the non-dominated solutions number. Utilizing the membership function’s highest possible value is the recommended course of action.

The MOIGBO implementation

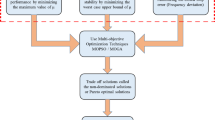
According to the defined objective functions (Eqs. (8)–(12), (50)) and the constraints (Eqs. (13)–(17)) of the optimization problem, the optimal values of the decision variables are determined by the MOIGBO multi-objective optimizer. The procedure for solving the optimization problem is depicted in Fig. 1. In this way, MOIGBO seeks to determine the best optimization variables within their minimum and maximum limits in such a way that, in addition to achieving the best compromise between each of the objectives, the constraints of network operation and the capacity of renewable resources are also satisfied. To eliminate impractical solutions, a penalty function is considered, which is added to the objective function in case of violation of any of the constraints of the problem. Thus, in an iterative process based on MOIGBO, the optimal values of the optimization variables, including the capacity and installation location of photovoltaic sources and wind turbines, have been determined.

Fig. 1

Flowchart of the MOIGBO application to solve the deterministic optimization problem.

The MOIGBO implementation process is given in following.

Step 1::

initializing the data. The techno-economic data of PV and WT resources, as well as data on irradiance, wind speed, temperature, and network loading, loads, and lines of the network, are all included in this stage of the system data. In addition, the algorithm’s parameters—the population, the greatest iterations number, and the programs operating independently number —are started.

Step 2::

For every algorithm population, select at random a set of variables defined as site and capacity of renewable units in the network during a given time frame.

Step 3::

Compute the OF for the collection of variables considered in Step 2.

Step 4::

After determining which answers are non-dominated, isolate them and save them in an archive.

Step 5::

Select the optimal algorithm member from the collection of non-dominant answers.

Step 6::

Refresh the algorithm population.

Step 7::

Sort the non-dominated solutions and archive them after determining the population’s OF for the optimizer-updated population. Next, relocate the better member from the non-dominated answer archive employing the best algorithm member found in Step 5.

Step 8::

Update the algorithm population using the direct rotational approach proposed by the RDR.

Step 9::

The OF is computed for the revised population of the algorithm following the steps of modifying the population in step 8, sorting out the non-dominant solutions, archiving them, and transmitting the best algorithm member from the non-dominant answer archive with the best algorithm member determined in step 7.

Step 10::

Archive the current solutions that aren’t prevalent.

Step 11::

Remove the dominant solutions from the archive.

Step12::

Evaluating the convergence requirements. If convergence is reached and the maximum number of iterations is completed, the optimization process is ended. Return to step 6 if not.

Step 13::

Select the best interactive answer and bring the MOIGBO to an end.

Robust optimization approach

By taking into account the uncertainty worst-case scenario, the IGDT is a reliable technique for decision-making that can determine the biggest uncertainty radius. By using this method, the system becomes robust to forecasts that are inaccurate due to uncertainty^36,37. The application of the risk averse method suggests that the goals of lowering annual active energy losses and the ENM are harmed by the growing OF. A higher uncertainty budget in the risk-averse strategy results in higher energy losses and ENM, which drives down PV and WT production and increases network load. The process is robust versus predicting mistakes caused by uncertainties when the upper uncertainty radius values for uncertainty changes to the budget take into account the annual active energy losses and the ENM increase. Determining the upper radius of uncertain parameters according to the system’s robustness enables robust decision-making. Here is how the IGDT is put together^36,37:

$$\begin{gathered} \mathop {\max }\limits_{X,\alpha } \mathop {}\limits^{{}} \alpha \hfill \\ \eta_{i} (X,\overline{\mathchar'26\mkern-10mu\lambda} ) \le 0,\mathop {}\limits^{{}} \forall i \in \Omega_{I} \hfill \\ \kappa_{i} (X,\overline{\mathchar'26\mkern-10mu\lambda} ) = 0,\mathop {}\limits^{{}} \forall j \in \Omega_{E} \hfill \\ f(X,{\mathchar'26\mkern-10mu\lambda} ) \le \psi_{C} \hfill \\ \psi_{C} = f(X,\gamma ).(1 + \sigma ),\mathop {}\limits^{{}} {\mathchar'26\mkern-10mu\lambda} \in \Gamma \,\,\& \,\,0 \le \sigma \le 1 \hfill \\ \left| {\frac{{{\mathchar'26\mkern-10mu\lambda} - \overline{\mathchar'26\mkern-10mu\lambda} }}{{\overline{\mathchar'26\mkern-10mu\lambda} }}} \right| \le \alpha \hfill \\ \end{gathered}$$

(51)

In this case, $\alpha$ denotes the uncertain parameters uncertainty radiuses, which include load demand, PV and WT energy resources, and so on. $\psi_{C}$ stands for the OF’s critical value, which the decision-maker determines. $\sigma$ pays off the budget for uncertainty. According to several factors, cost value is the foundation valued in deterministic optimization. In contrast to deterministic optimization, this study takes into account uncertain network demand as well as PV and WT generation. As a consequence, when taking risk aversion into account, increased objectives are negatively impacted by increases in network demand and decreases in the production of renewable resources. As such, network demand (α_Load) as well as PV and WT generation (α_RES) are considered questionable. The formula for uncertain parameters radius maximizing is as follows:

$$\begin{gathered} \,\,\max \alpha_{Load} ,\alpha_{RES} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,s.t.\,\,\,OF_{IGDT} \le (1 + \sigma ) \times OF_{Deter\min istic} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,P_{PV}^{i,t} \in \Omega \,(\alpha_{PV} ,P_{PV*}^{i,t} ) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,P_{WT}^{i,t} \in \Omega \,(\alpha_{WT} ,P_{WT*}^{i,t} ) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,P_{Load}^{i,t} \in \Omega \,(\alpha_{Load} ,P_{Load*}^{i,t} ) \hfill \\ \Omega \,(\alpha_{PV} ,P_{PV*}^{i,t} ) = \left\{ {P_{PV}^{i,t} :\,\,\left| {\frac{{P_{PV}^{i,t} - P_{PV*}^{i,t} }}{{P_{PV*}^{i,t} }}} \right| \le \alpha_{PV} } \right\},\,\alpha_{PV} \ge 0 \hfill \\ \Omega \,(\alpha_{WT} ,P_{WT*}^{i,t} ) = \left\{ {P_{WT}^{i,t} :\,\,\left| {\frac{{P_{WT}^{i,t} - P_{WT*}^{i,t} }}{{P_{WT*}^{i,t} }}} \right| \le \alpha_{WT} } \right\},\,\alpha_{WT} \ge 0 \hfill \\ \Omega \,(\alpha_{Load} ,P_{Load*}^{i,t} ) = \left\{ {P_{Load}^{i,t} :\,\,\left| {\frac{{P_{Load}^{i,t} - P_{Load*}^{i,t} }}{{P_{Load*}^{i,t} }}} \right| \le \alpha_{Load} } \right\},\,\alpha_{Load} \ge 0 \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(13) - (17)\, \hfill \\ \end{gathered}$$

(52)

where, respectively, $\alpha_{Load}$ and $\alpha_{RES}$ stand for the network demand, PV, and WT production upper uncertainty radius. The network load and wind maximum capacity are denoted by the letters $P_{LD*}^{i,t}$, $P_{PV*}^{i,t}$ and $P_{WT*}^{i,t}$. $OF_{Deter\min istic}$ indicates the value of the OF that is found when the deterministic issue was solved. The risk aversion technique states that when the uncertainty budget increases, network load increases and PV and WT power generation decreases by

$$P_{PV}^{i,t} = P_{PV*}^{i,t} \times (1 - \alpha_{PV} ),\,\,P_{WT}^{i,t} = P_{WT*}^{i,t} \times (1 - \alpha_{WT} )\,\,\& \,\,P_{LD}^{i,t} = P_{LD*}^{i,t} \times (1 + \alpha_{LD} )$$

(53)

Simulation results

System data

A 33-bus IEEE network³⁸ is utilized to accomplish the robust multi-objective allocation of PV and WT via the MOIGBO; this network is demonstrated in Fig. 2. This network has a total active and reactive demand equal to 3.72 MW and 2.3 MVAr. The suggested approach is programmed using MATLAB 2015b on a desktop computer running 64-bit Windows 7 featuring an Intel Core i7-4510U that can reach 3.1 GHz and 8 GB of RAM. The network’s line data and load data for residential (RL), commercial (CL), and industrial (IL) use are obtained from³⁸. The temperature, irradiance, and wind speed (WS) information on the weather are taken from^38,39,40. Figures 3, 4, 5, 6 show the variations in temperature, wind speed, irradiance, and network loading percentage. Additionally, Tables 1, 2, 3^32,38,39,40 provide load coefficients for the models as well as PV array and WT techno-economic data.

Fig. 2

Schematic of 33-bus network considering different loads.

Fig. 3

Variations of irradiance during 24 h.

Fig. 4

Variations of wind speed during 24 h.

Fig. 5

Changes of temperature during 24 h.

Fig. 6

Variations of different loadings during 24 h.

Table 1 Load model coefficients³².

Table 2 Techno-economic WT data^38,39,40.

Table 3 Techno-economic PV data^38,39,40.

The outcomes of the PV and WT resources multi-objective allocation in the 33-bus distribution network are extracted with fuzzy decision-making for minimizing the energy losses, energy not-met of subscribers additionally to the renewable units power cost using the MOIGBO in the following scenarios.

Scenario#1: Optimal deterministic allocating the PV and WT in the network without uncertainty.

• Case I: Dispersed Energy resources

• Case II: Hybrid Energy resources

Scenario#2: Optimal robust allocating the PV and WT in the network with uncertainty.

Results of Scenario#1 (deterministic approach)

For minimization of the annual losses, ENM, and the cost of generating electricity from renewable resources utilizing the MOIGBO, the results of deterministic optimization of PV and WT energy sources in the 33-bus network are provided in this part. Figures 6 and 7 depict the Pareto-front solution set curve that was acquired via MOIGBO in order to solve scenario 1 in cases I and II, respectively. The MOIGBO has developed a compromise among all of the objectives based on Figs. 7 and 8. The set of solutions has been increased among all of the objectives, and the ultimate solution (green point) has been identified utilizing the fuzzy decision-making procedure.

Fig. 7

Pareto front solution set to solve the Case I, Scenario#1 using the MOIGBO.

Fig. 8

Pareto front solution set to solve the Case II, Scenario#1 using the MOIGBO.

Table 4 presents the final fuzzy solution’s findings, which include the optimal variables and the values of each goal for Cases I and II derived from the MOIGBO and contrasted with the conventional MOGBO and PSO approaches. Based on the outcomes of Case I, all MOIGBO, MOGBO, and MOPSO algorithms have been successful in raising subscriber reliability and lowering annual energy losses for optimization of the location and size of renewable energy sources in the 33-bus distribution network. The optimization program has installed 628.18 kW of photovoltaic power and 978.63 kW of wind power in buses 16 and 33, respectively, based on the MOIGBO. As a result, the annual energy losses in the base network have decreased from 603,362.93 kWh to 302,751.62 kWh. The data reveals that ENM had a decline from 214.03 MWh to 118.64 MWh, indicating an improvement in network reliability. However, using the MOIGBO, the optimization program in Case II has also installed 102.27 kW of photovoltaic power and 845.05 kW of hybrid wind power in bus 16. As a result, the annual loss in the base case is reduced from 603,362.93 kWh to 427,565.88 KWh, and the ENM is decreased from 214.03 MWh to 144.64 MWh. Furthermore, by lowering ENM, Case II significantly improves network reliability. Therefore, it has been established that the suggested method is superior in achieving lower yearly energy loss and ENM by comparing the MOIGBO results with the MOGBO and MOPSO in both circumstances. Table 4 presents the outcomes of examples I and II. It is evident that case 1 has enhanced the network’s performance and achieved a higher quantity of all the objectives. Stated differently, Case I yields lower (better) yearly energy loss and ENM values than Case II. According to the load requirement, the energy sources in Case I are used in the network in a distributed way. on Case II, on the other hand, it is anticipated that renewable energy sources would function as a hybrid system that could be integrated into the power distribution network and installed on a bus that is similar to it. The distribution of optimal power distribution within the network has proven to be more successful in enhancing network performance, as indicated by the acquired results.

Table 4 Fuzzy final solution and results of solving the Scenario#1.

Figure 9 displays the power changes of PV and WT units for Cases I and II based on data from MOIGBO. The PV peak power in Cases I and II is 628.18 kW and 102.27 kW, respectively, and the WT peak power in cases I and II is 978.63 kW and 845.05 kW, respectively, according to the figures that have been presented. As a result, while Case I has less production capacity limitations, Case II has more due to hybridization and the requirement to meet operational requirements.

Fig. 9

PV and WT power changes for Scenario#1 during 24-h (a) Case I (b) Case II.

Changes in losses and ENM of the basic network and cases I and II during 24 h are depicted in Figs. 10 and 11, respectively. As it is clear, in each of the cases, the power loss as well as ENM values have decreased in all hours compared to the base values. The results illustrated that the losses and ENM values in Case I are lower than the results compared to the Case II. Figure 8 shows a greater improvement of reliability in Case I than in Case II, which clears the superior capability of Case I in reducing ENM of the network subscribers.

Fig. 10

Active and reactive power loss of the network without and with the RES for Scenario#1 during 24-h.

Fig. 11

Energy not-met changes of the network without and with the RES for Scenario#1 during 24-h.

Results of Scenario#2 (robust approach)

The results of the PV and WT sources robust allocation in the 33-bus network are shown in this section. The objective is to use the MOIGBO for minimizing the annual energy losses, ENM, and the cost of power generation from renewable resources while taking network demand and renewable generation uncertainties into account. To model the uncertainty, and determine the higher level of the uncertain parameters radius and the system robustness, the IGDT with the risk-averse strategy is employed. The value of the network demand’s uncertainty radius and the value of the PV and WT renewable resource production’s uncertainty radius are shown in Table 5 and are determined using evaluating the various uncertainty budgets or risk values. It is evident that as the quantity of uncertainty budget is increased or the risk of the OF value is raised, the behavioral network’s load increases and energy resource production tends to decline. The behavior of changes in the resource generation and network load uncertainty radius with respect to the uncertainty budget amount is depicted in Figs. 12 and 13. Analyzing the impact of varying uncertainty budget values has demonstrated that the operating constraints are not met and the system is not robust to risk values beyond 30%. As a result, 30% is the maximum risk for the system’s robustness under uncertainty. The findings demonstrated that resource production and network load uncertainty radius values are reached at 0.54% and 12.56%, respectively, at 30% risk. In other words, the system is robust against forecasting errors in the worst uncertainty scenario with a 30% increase in the uncertainty budget.

Table 5 Optimal results of the uncertainty radius with respect to different uncertainty budgets in scenario 2.

Fig. 12

Changes of generation uncertainty radius versus uncertainty budget increasing.

Fig. 13

Changes of load uncertainty radius versus uncertainty budget increasing.

Tables 6 and 7 give the values of the annual active energy loss and energy not-met goals for various uncertainty budget values up to 30%, respectively, after establishing the uncertainty radius value of unknown parameters. It is evident that each of the aforementioned goals now has a higher level of uncertainty due to the increase in the uncertainty budget. The value of annual active energy loss and energy not met is found to be 389,490.39 kW and 161.15 kWh, respectively, in the greatest level of budget risk.

Table 6 Annual energy loss of the network with respect to the different uncertainty budgets in scenario 2.

Table 7 Energy not-met of the network with respect to the different uncertainty budgets in scenario 2.

Table 8 presents a comparison of the outcomes obtained from deterministic and robust optimization for each aim. It is evident by comparing the robust optimization to the deterministic optimization that the uncertainty circumstances have led to an rise in the cost of losses and the ENM. Hence, even in the most uncertain circumstances, the system’s robustness is ensured by taking uncertainty into account and implementing robust optimization.

Table 8 Energy not-met of the network with respect to the different uncertainty budgets in scenario 2.

Figure 14 shows the increase in annual active energy loss from 32,041.88 to 389,490.39 kW and Fig. 15 demonstrates the increase in energy not-met value from 125.43 to 161.15 kWh due to risk increase from 5 to 30%.

Fig. 14

Changes of annual active energy loss versus uncertainty budget increasing.

Fig. 15

Changes of energy not-met versus uncertainty budget increasing.

The deterministic approach (scenario #2) without taking uncertainty into account is contrasted with the robust approach (scenario #1) taking uncertainty into consideration in terms of power losses and energy not met in a 24-h period in Figs. 16 and 17. In comparison to the deterministic scenario, the robust scenario showed an increase in power losses and energy not-met in the majority of hours, as illustrated in Figs. 16 and 17. The circumstances of the uncertainty parameters are to blame for this growth. Conversely, higher uncertainty budget values have led to a larger rise in power losses and energy not-met.

Fig. 16

Power loss changes of the in deterministic and robust approaches during 24-h.

Fig. 17

Energy not-met changes of deterministic and robust approaches during 24-h.

Results comparison with previous studies

This section compares Ref.³⁴, which uses single-objective turbulent flow of water-based optimization (TFWO) for the best distribution of WT and PV resources in the 33-bus network, with the robust approach via the MOIGBO. It should be mentioned that uncertainty modeling with the Monte Carlo simulation technique is developed in Ref.³⁴. Tables 9, 10 offer a comparison of the outcomes of the suggested robust strategy with Ref.³⁴, both with and without taking uncertainty into account. It is evident that the suggested robust method based on MOIGBO has obtained lower active power loss and energy not-met, demonstrating its superior performance.

Table 9 Results comparison with previous studies without uncertainty.

Table 10 Results comparison with previous studies with uncertainty.

Conclusion

In this research, deterministic and robust optimization of PV and WT energy resources was presented in the networks using the MOIGBO. At first, the deterministic optimization without considering uncertainty in two dispersed and hybrid cases for minimizing the active energy loss, energy not-met of the network customers and the renewable generation cost. Then, according to the obtained objective results of the deterministic problem, robust optimization was implemented to find the renewable generation and network demand MURs and the system robustness value. The findings of the research are presented as follows

• The MOIGBO has created a compromise within all the aims, a set of answers has been expanded among all the objectives, and finally, via the fuzzy decision-making, the final solution has been determined.

• Also, the results have shown that the dispersed case has obtained a better value for each of the objectives compared to the hybrid case of renewable resources. The annual energy loss as well as the ENM values in dispersed cases are obtained lower (better) than the other case.

• The MOIGBO superior performance was proved compared to MOGBO and MOPSO in further improving the distribution network operation in achieving lower annual energy loss and ENM.

• The robust optimization results based on the IGDT showed that at 30% uncertainty budget risk, the MURs of renewable production and network load were achieved at 0.54% and 12.56%, respectively. In other words, the outcomes cleared that the system is robust against forecasting errors in the worst uncertainty scenario with a 30% rise in the budget for uncertainty. Also, the annual active energy loss and ENM were obtained at 389,490.39 kW and 161.15 kWh, respectively at 30% uncertainty budget risk.

• Considering that the production energy of photovoltaic and wind sources are inherently unpredictable and have uncertainty, the greater penetration of these sources in the electrical network can cause technical challenges and limitations without integration with proper and sufficient storage system. On the other hand, one of the existing limitations is the hard access to meteorological data of solar radiation and wind speed for the studied areas for accurate knowledge of the energy operators of the actual production of these resources.

• The robust fuzzy multi-objective optimization of PV and WT energy resources with multi-energy storage such as battery and hydrogen in radial distribution networks is suggested for future work.