Introduction

As agricultural water conservancy engineering projects expand and become more complex, accurate construction cost prediction is essential for evaluating project feasibility and selecting optimal design schemes, which directly influences the economic viability and overall quality of the project. Due to the inherent complexity and uncertainty of these projects, personnel and machinery costs fluctuate, making construction costs difficult to control and often leading to significant cost overruns1. Consequently, developing an accurate method for predicting construction costs is essential.

There are two fundamental approaches to predicting construction costs: (1) traditional mathematical and statistical methods and (2) machine learning methods2,3. Traditional mathematical and statistical methods encompass linear regression analysis4,5, grey prediction6, and time series analysis7,8, which have notable limitations. Their prediction accuracy is often constrained, and they struggle to model non-linear relationships in data, making it difficult to meet the industry’s increasing demands for better accuracy and efficiency. Furthermore, these methods fail to quickly adapt to changes in the market or project progress9,10,11. In contrast, the rapid advancement of artificial intelligence has led to the growing adoption of machine learning (ML) for construction cost prediction. ML is particularly effective at extracting data features from high-dimensional, non-linear datasets12,13,14, enabling it to capture complex relationships between input and output data. By leveraging past project data, ML can generate reliable and swift cost estimates15,16,17,18. Kim et al. demonstrated that artificial neural networks (ANNs) outperform traditional statistical methods based on limited historical data for long-term forecasts19. Cheng et al.20 highlighted the challenges of predicting construction costs due to fluctuations in building prices. They proposed a hybrid model combining least squares support vector machines (LS-SVMs) and differential evolution (DE) to predict the construction cost index, achieving a root mean square error of just 1.354% on the test dataset. This model holds promise as a valuable tool to aid decision-makers in construction management. Chou et al.21 developed an ANN model to predict project bidding prices, finding that a model with three neurons in the hidden layer outperformed traditional or case-based reasoning methods, with an average absolute percentage error of 13.09%. El Kholy et al.22 and Tijani ć et al.23 summarized that ANNs represent a promising approach for estimating construction costs, providing more accurate results and reducing estimation errors. Furthermore, ML models have demonstrated significant applicability across diverse domains. For instance, Kennedy et al. employed ML models to predict the compressive strength of concrete and granular sand, achieving robust predictive performance24,25.

In the practical application of neural network models, prediction performance is often influenced by the values of hyperparameters. To address this issue, some scholars have adopted intelligent optimization algorithms to enhance the performance of cost prediction models. For instance, AI et al.26 developed a model for predicting environmental governance costs by optimizing the parameters of a support vector machine using the particle swarm optimization algorithm. Their findings revealed that this method achieved higher prediction accuracy compared to the BP neural network and LSSVM models, making it more suitable for predicting costs prior to environmental governance. More recently, Zheng et al.27 constructed a random forest (RF) prediction model optimized with the bird swarm algorithm (BSA) to predict construction costs. Compared to backpropagation neural networks and support vector machines, their model demonstrated superior prediction accuracy and efficiency, providing a solid basis for optimizing construction project cost management.

Despite advancements in using artificial neural networks (ANNs) for cost prediction, these models still face challenges in practical engineering applications. There is an urgent need to integrate advanced information technology and artificial intelligence methods to improve the accuracy and real-time performance of engineering cost prediction28. In recent years, the emergence of Building Information Modeling (BIM) technology has opened up new possibilities for improving construction cost forecasting. BIM integrates geometric, material, time, and cost data, providing a powerful data source for accurate cost predictions29,30. Abanda et al.31 emphasized that BIM technology can automate the cost estimation process using standard measurement methods, thereby addressing the inaccuracy of cost prediction. Wang et al.32 explored the feasibility of using BIM for cost estimation in the construction industry, while Yang et al.33 highlighted the importance of cost analysis in the early stages of construction project planning and proposed a method combining cost estimation models with BIM technology for more accurate cost predictions, supported by case studies. Li et al.34 combined BIM data with intelligent modeling to improve the coordination of prefabricated shear wall structures, enhancing design and construction integration. Additionally, some scholars have explored the integration of BIM with machine learning or neural networks. For instance, Hong et al.35 used BIM technology combined with neural network methods to predict net costs. In addition, Abbasnejad et al.36 further evaluated the effectiveness of integrating BIM with neural networks through mathematical modeling, demonstrating enhanced decision-making efficiency and improved cost prediction accuracy.

Research by various scholars has consistently highlighted the significant potential of neural networks in predicting construction costs. When combined with data from BIM technology, neural networks can further enhance the accuracy and efficiency of these predictions. This integration offers strong theoretical and practical foundations for future applications in architecture and related engineering fields. However, a notable limitation of these studies is their narrow focus on construction projects within a single domain, which limits their universality and applicability. Therefore, there is an urgent need for comprehensive research to develop scientifically sound construction cost prediction models specifically tailored to the field of agricultural water conservancy engineering.

The Grey BP Neural Network (PGNN), a prominent machine learning model, is renowned for its exceptional capabilities to process time series data and identify patterns. It has proven highly effective in addressing complex, nonlinear problems, making it a valuable tool for predicting the temporal fluctuations in construction costs37. Furthermore, PGNN has shown remarkable proficiency in predicting building factor prices38,39. Consequently, the objective of this study is to develop and validate a construction cost prediction model for agricultural water conservancy projects that integrates BIM and PGNN neural networks, referred to as the BIM-PGNN model. Additionally, the introduction of the Sparrow Optimization Algorithm (SSA) facilitates the optimization of weights and threshold hyperparameters within the PGNN neural network, overcoming issues like local optima and overfitting, which are common in traditional neural networks. This study aims to provide a theoretical basis and technical support for predicting the construction costs of agricultural water conservancy projects.

Research method

Digital analysis of intelligent buildings based on BIM technology

Currently, BIM technology involves the creation and use of digital information models for design management, construction management, and operational maintenance of construction projects. This technology integrates building data and information models, enabling efficient information sharing and transmission across the entire lifecycle of a project, from design to operation and maintenance. The comprehensive application of BIM technology throughout the lifecycle of engineering projects represents the current development trajectory of the construction industry and the dominant trend for future advancements. Fully utilizing BIM technology can significantly enhance project management capabilities and production efficiency within construction enterprises, driving sustainable development across various sectors, including water conservancy engineering. BIM technology is characterized by key features such as visualization, coordination, simulation, and optimization. The BIM methodology facilitates the digitization and visualization of building information through a structured workflow encompassing planning and design, conceptual design, preliminary design, analysis, drawing production, prefabricated components, 4D/5D construction simulation, construction logistics, operation and maintenance, and renovation and demolition.

In this study, BIM5D technology, an extension of BIM, was utilized to extract construction quantities for agricultural water conservancy projects. BIM5D technology primarily relies on the BIM platform to establish a three-dimensional model of water conservancy projects, forming a five-dimensional building information model that integrates 3D (three-dimensional model), 1D (schedule), and 1D (cost budget). The specific construction workflow of the BIM5D model is shown in Fig. 1. In the context of cost prediction for agricultural water conservancy engineering construction, BIM5D technology provides essential data, including project progress, costs, funds, resources, and construction organization, enabling coordinated and shared change information with high visualization accuracy. By dynamically extracting precise data on construction quantities for fixed periods, different materials, and various flow segments, BIM5D technology lays the foundation for accurate cost prediction.

Fig. 1
figure 1

BIM5D modeling process diagram.

Full size image

PGNN neural network model and its optimization

The BP neural network is the most widely used multi-layer feed-forward neural network model in machine learning. Trained on sample data using the error back-propagation algorithm offers advantages such as good fault tolerance and strong associative memory, particularly for solving nonlinear problems and handling limited sample data40. This network typically consists of input, hidden, and output layers, with the propagation process primarily divided into forward propagation and back-propagation.

The PGNN model, also known as the Grey BP Neural Network model, combines the Grey GM (1,1) model and the BP Neural Network (BPNN) model. It incorporates the grayscale features of Grey System Theory and the self-learning adaptability of the BP Neural Network, enabling effective handling of nonlinear data sequences41,42. The formulation of the time series material unit price prediction problem based on PGNN is as follows: Let the original data sequence of material unit price eigenvalues for n months be denoted as \({X}^{(0)}=\left\{{x}^{(0)}(1),{x}^{(0)}(2),\cdots ,{x}^{(0)}(n)\right\}\). After applying the GM (1,1) model, the predicted unit price sequence is obtained as follows:

$${x}^{(0)}(t+1)=(1-{e}^{\alpha })\left({x}^{(0)}(1)-\frac{\mu }{\alpha }\right){e}^{-\alpha t}$$
(1)

where α is the development coefficient; and μ is the grey action quantity.

The specific steps for predicting material unit prices using the Grey BP Neural Network model are as follows: ① Preprocess the material unit price data and establish a Grey GM (1,1) model to obtain the unit price prediction sequence; ② Subtract the predicted unit price sequence from the original sequence to obtain the residual sequence of material unit prices; ③ Use the residual sequence as the output sample to train a Grey BP Neural Network model, which generates the unit price correction sequence; ④ Add the predicted unit price sequence to the correction sequence to obtain the final predicted material unit prices using the Grey BP Neural Network model.

The PGNN neural network model offers distinct advantages, particularly in modeling dynamic changes in sequence data, a key feature for intelligent construction cost prediction. Construction costs are influenced by various factors, such as market fluctuations and material price changes, which often exhibit temporal variation. The grey model effectively captures these time series characteristics, providing more accurate and real-time predictions. Furthermore, BP neural networks are highly effective in processing nonlinear and dynamic data, making them particularly useful for addressing challenges in the construction field, where projects often involve complex nonlinear relationships and dynamic fluctuations43.

While PGNN neural networks can simulate dynamic data changes and predict the prices of agricultural water conservancy construction materials in real-time, they face challenges in practical applications, such as slow convergence, low computational efficiency, and difficulty in achieving global optimality. To enhance the global optimization ability of the network, the Sparrow Search Algorithm (SSA) is introduced to optimize the PGNN neural network. The SSA algorithm optimizes the weights and thresholds of the PGNN network by simulating the hunting and anti-hunting behavior of sparrow populations, thereby improving the training efficiency and predictive performance of the network44. Additionally, the SSA algorithm avoids the random assignment of network weights and thresholds, guiding the network away from local minima toward a global or near-global optimal solution45,46.

This algorithm adopts two behavioral strategies: searching and following. Searchers actively seek food sources, while followers obtain food from the searchers. When sparrows detect a predator, they emit an alarm signal and move to a safer location. Sparrows that find better food sources may transition to searchers, while the overall ratio of searchers to followers remains constant.

1) Search behavior.

Searchers with higher fitness values are responsible for locating food and guiding the entire population’s actions. They find food more quickly and cover a larger search area than followers during the hunting process. The location of the searcher is updated using formula (2):

$${X}_{i,j}^{t+1}=\left\{\begin{array}{c}{X}_{i,j}^{t}\cdot exp\left(\frac{-i}{\alpha \cdot ite{r}_{max}}\right) if{R}_{2}<ST\\ {X}_{i,j}^{t}+QL if{R}_{2}\ge ST\end{array}\right.$$
(2)

where Xi, j represents the position of the j-th dimension of the i-th search sparrow; t is the current iteration number; α is a random number between 0 and 1; itermax is the maximum number of iterations of the algorithm; Q is a random number that following a normal distribution; L is a 1 × d-dimensional matrix; R2 is the warning value within the range of 0 to 1; and ST is the safe value ranging from 0.5 to 1.

2) Following behavior.

Followers constantly monitor the searchers during the hunting process and compete for high-quality food discovered by the searchers. The position of the follower is generated by formula (3):

$${X}_{i,j}^{t+1}=\left\{\begin{array}{c}Q\cdot exp\left(\frac{{X}_{worst}^{t}-{X}_{i,j}^{t}}{{i}^{2}}\right)ifi>\frac{n}{2}\\ {X}_{P}^{t+1}+\left|{X}_{i,j}^{t}-{X}_{P}^{t+1}\right|\cdot {A}^{+}\cdot L otherwise\end{array}\right.$$
(3)

where Xtworst represents the worst position of the searcher; Xt+1P represents the best position of the searcher; and A is a 1 × d-dimensional matrix randomly assigned −1 or 1.

Some sparrows in the population serve as"warning signs,"guiding others to safer hunting areas. These sparrows position themselves between the edge and the safe zones. The location of a warning sparrow is randomly generated according to formula (4):

$${X}_{i,j}^{t+1}=\left\{\begin{array}{cc}{X}_{best}^{t}+\beta \cdot \left|{X}_{i,j}^{t}-{X}_{best}^{t}\right|& if{f}_{i}>{f}_{g}\\ {X}_{i,j}^{t}+K\cdot \left(\frac{\left|{X}_{i,j}^{t}-{X}_{worst}^{t}\right|}{({f}_{i}-{f}_{w})+\varepsilon }\right)& if{f}_{i}={f}_{g}\end{array}\right.$$
(4)

where Xtbest is the optimal position of the sparrow population; β is a random number that follows a normal distribution (0,1); K is a random number with a value range of −1–1; ε is a constant. \({f}_{i}\) is the current individual fitness value of the sparrow in the algorithm; \({f}_{g}\) is the optimal fitness value of the sparrow in the algorithm; and \({f}_{w}\) is the worst fitness value.

The process of optimizing the PGNN neural network using the SSA algorithm is illustrated in Fig. 2, and the specific steps involved are as follows:

Fig. 2
figure 2

Flowchart of PGNN model optimized by SSA algorithm.

Full size image

1) Neural Network Structure Determination and Initialization Parameter Setting: Establish the population size, maximum iteration count, the proportion of searchers and followers within the population, and the warning values. The topology of the PGNN neural network is determined based on the input and output data from the training unit price sample.

2) Fitness Function Calculation: The average mean square error between the output values of the training and testing samples and the expected values is used as the fitness value for the sparrow algorithm to determine the current optimal initial position:

$$fitness=\frac{\sum_{i=1}^{n} \left[({Y}_{i}-{Z}_{i}{)}^{2}+{\left({Y}_{i}{\prime}-{Z}_{i}{\prime}\right)}^{2}\right]}{2n}$$
(5)

where n is the number of samples; \({Y}_{i}\) and \({Z}_{i}\) are the output and expected values of the training samples for unit price; and \({Y}_{i}\) and \({Z}_{i}\) are the output and expected values of the testing samples for unit price.

3) The iterative process is initiated to adjust the weights and thresholds. Continuously update the position coordinates of each functional sparrow using Eqs. (2)-(4), and optimize the optimal individual position of the population at various iterations. Use the best individual and the global optimal solution from the sparrow population in the current iteration to determine the weights and thresholds of the PGNN model.

4) Network Training: Repeat steps (2) to (3) until the maximum number of iterations is reached, outputting the minimum fitness value to obtain the optimal weights and thresholds for the network. Alternatively, continue the process until either the iteration limit is reached or the training results meet the specified error accuracy requirements.

To verify the superiority of the Sparrow Search Algorithm (SSA) in hyperparameter optimization, performance tests were conducted using benchmark functions, including unimodal test functions (F1, F2) and high-dimensional multimodal functions (F10, F13). The unimodal functions were selected to evaluate the exploitation ability of the algorithm, i.e., rapidly locating the optimal solution, while the high-dimensional multimodal functions aimed to assess its exploration capability for avoiding local optima. The mathematical definitions of these benchmark functions are provided in Table 1. This study compares SSA with three other metaheuristic algorithms: Genetic Algorithm (GA)47, Particle Swarm Optimization (PSO)48, and Whale Optimization Algorithm (WOA). To ensure statistical robustness, all algorithms were configured with identical parameters: a population size of 30, a maximum iteration count of 200, and 20 independent runs. The average results were adopted as final performance metrics, with convergence curves illustrated in Fig. 3.

Table 1 Selected benchmark function.
Full size table
Fig. 3
figure 3

Convergence curves for different algorithms.

Full size image

As illustrated in Fig. 3, SSA demonstrated superior performance in two critical dimensions: (1) For unimodal test functions (F1, F2), SSA exhibited faster convergence speed and final solutions closer to the theoretical optimum, confirming its enhanced optimization efficiency; (2) In high-dimensional multimodal functions (F13, F15) characterized by complex search spaces, SSA achieved global optima with minimal iterations, whereas comparative algorithms frequently stagnated in local optima or exhibited slower search dynamics. These empirical findings substantiate that SSA effectively balances exploration and exploitation mechanisms compared to GA, PSO, and WOA, thereby improving both search precision and convergence acceleration, which contribute to elevated predictive accuracy in subsequent model.

Construction cost prediction model for agricultural water conservancy engineering based on BIM and SSA-PGNN

To effectively predict the construction cost of agricultural water conservancy projects, this study established a prediction model that integrates BIM technology and the SSA- PGNN neural network. After normalizing the data, the model consists of two key components: extracting actual engineering quantities using BIM and constructing an SSA-PGNN unit price prediction model. Firstly, a 3D model of the agricultural water conservancy engineering is established. Based on this model, the scheduling plan and cost budget are imported to construct the BIM5D database, and the required engineering quantities are extracted based on specific criteria. Subsequently, the PGNN neural network model, optimized using the SSA algorithm, is utilized to predict the unit price for labor and machinery, facilitating real-time, dynamic cost predictions for agricultural water conservancy projects. The specific process framework is shown in Fig. 4.

Fig. 4
figure 4

Analysis and modelling process framework.

Full size image

Case study and result analysis

Data acquisition and pre-processing

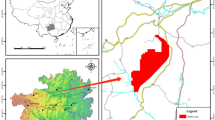
To assess the performance of the proposed construction cost prediction model for agricultural water conservancy projects based on BIM and the SSA-PGNN neural network, an agricultural water conservancy project in Yanghe Town, Anshan City, Liaoning Province, was used as a case study. The primary focus of our study was on the construction period of specific structures, including"mortar masonry rectangular groove","concrete road (3 m wide)","agricultural bridge (6 m × 4 m × 1.5 m)","agricultural bridge (6 m × 6 m × 2 m)","agricultural culvert (φ 1000 × 4 m)","agricultural culvert (φ 600 × 6 m)", and"high mortar masonry retaining walls (1.2 m and 1.5 m)."Due to the substantial contribution of steel reinforcement and concrete to the direct construction cost, the study concentrated on evaluating the total construction cost of grade III seismic steel bars (HRB400 φ 18-25 mm) and C25 and C30 concrete materials. The data was sourced from open data platforms of the government and industry, encompassing a total of 62 material information prices for C25, C30 concrete, and HRB400 steel bars in Liaoning Province from January 2016 to February 2021, as shown in Fig. 5.

Fig. 5
figure 5

Monthly average price chart of concrete and steel bars.

Full size image

The sample input data comprised the prices of concrete and steel bars over the first 12 months, with the corresponding output data representing the price in the 13th month. A PGNN neural network model, optimized using the SSA algorithm, was then developed. The 62 material information price data points were divided into 50 groups, with the randperm function used to randomly assign 40 groups as the training set and 10 groups as the testing set in the ratio of 8:2. Additionally, K-fold cross-validation with K = 5 was implemented on the training set, where different subsets of the training data were alternately utilized for model training and validation, thereby enabling a more reliable assessment of the model’s generalization performance.

The original unit price data were normalized to the interval [0, 1] using Min–Max normalization as specified in Eq. (6), a preprocessing step implemented to mitigate significant errors caused by substantial discrepancies in input data magnitudes. This transformation accelerated both the convergence rate and prediction accuracy of the training network by eliminating dimensional heterogeneity and standardizing data scales across measurement units.

$$x^{\prime}_{i}=\frac{{x}_{i}-{x}_{min}}{{x}_{max}-{x}_{min}}$$
(6)

where \(x^{\prime}_{i}\) is the normalized data; \({x}_{i}\) is the unit price data before normalization; \({x}_{max}\) is the maximum value of each group of unit price data, and \({x}_{min}\) is the minimum value.

Extracting agricultural water conservancy engineering quantities based on BIM technology

Revit design software is currently the most widely used BIM modeling platform, supporting tasks such as 3D modeling, 3D visualization, and interaction between drawings and models. The family library function enables the integration of pre-built components from various projects, thereby reducing the modeling workload through the utilizing of shared family libraries and improving modeling efficiency. Revit-generated 3D models of individual agricultural water conservancy projects are shown in Fig. 6a.

Fig. 6
figure 6

BIM model of each project.

Full size image

After establishing the Revit3D models for each individual project, the 3D models are exported as E5D files using the BIM5D plugin and imported into the digital project management platform. Individual engineering models of roads, bridges, and culverts are imported, as shown in Fig. 6b. Following the import process, project schedules from the scheduling plan and cost budgets from pricing software are integrated into the platform to establish the BIM5D model.

The construction simulation function in the BIM + technology management system simulates the planned construction period for each project. It dynamically displays the construction status of each project component over time, providing real-time updates to facilitate progress adjustments and ensure timely completion.

After completing the simulation construction, the BIM5D platform allows dynamic querying of quantities for each project component. The BIM5D platform extracts data for all components, classifies them, and efficiently determines the required quantities. Associating construction progress with the model facilitates real-time calculation of work quantities, material usage, and flow period in real-time. Table 2 shows the usage of steel bars and concrete for each project during the construction period from March 20th to September 20th, 2021, as extracted from the BIM5D platform.

Table 2 Quantity of reinforcement and concrete in each project.
Full size table

Parameter setting and model evaluation

In this study, the computer configuration used for network training and testing is based on Matlab2023b software running on a Windows 10 64 bit operating system environment. The system is equipped with an NVIDIA GeForce GTX1650 graphics card with 4 GB of graphics memory, 16 GB of RAM, a 1 TB of hard drive, and an Intel (R) Core (TM) i5-9300H CPU operating at 2.40 GHz.

Firstly, the data are normalized to generate a training dataset with random numbers between 0 and 1. This preprocessing step minimized material cost data oscillation during gradient updates, accelerated network convergence, and reduced training time. Based on empirical equations, the number of hidden layer nodes was calculated using a trial-and-error approach, with the selection range determined to be5,14. Simulation experiments were performed with varying node counts to determine the optimal number that minimized deviation. Table 3 shows the average relative error values for different node counts after network training, indicating that the grey BP neural network achieved the best fitting performance when the hidden layer nodes were set to 13. Based on these results, the PGNN neural network topology was finalized as 12–13-1.

Table 3 Average relative error values corresponding to the number of nodes in different hidden layers.
Full size table

The runtime performance of the SSA algorithm depends on the population size and the number of iterations. The population size was tested within the range of 10 to 80, and the number of iterations ranged from 80 to 150. The fitness function error, defined as the mean square error (MSE) of the training set, was used to identify the optimal parameters. As shown in Table 4, the minimum errors of 1.2069 and 0.0514 were achieved when the population size was set to 30 and the number of iterations to 100. At these values, the algorithm converged.

Table 4 Comparison of algorithm errors for different population sizes and number of iterations.
Full size table

To evaluate the performance of the SSA- PGNN model proposed in this study, Random Forest (RF), XGBoost, PGNN and SSA-BP models were established as comparative models using the same dataset. Specifically, Random Forest (RF) employs an ensemble of multiple decision trees, where the final output is derived from averaging all individual tree predictions, effectively mitigating overfitting while ensuring stable predictions. XGBoost, as a representative gradient boosting framework-based ensemble learning algorithm, achieves high-precision predictions through the integration of multiple weak learners, demonstrating particular efficacy in processing large-scale datasets. These two models were selected as baseline representatives of traditional machine learning (ML) approaches for comparative validation. All machine learning models underwent systematic parameter optimization through a trial-and-error approach to identify optimal parameter combinations, and the specific parameter settings for each model are shown in Table 5.

Table 5 Quantity of reinforcement and concrete in each project.
Full size table

Finally, to assess the model’s performance, we use the following metrics: root mean square error (RMSE), mean absolute percentage error (MAPE), and coefficient of determination (R2). Lower RMSE and MAPE values indicate higher prediction accuracy of the model. R2 values range from 0 to 1, and values closer to 1 indicate a better fit between the predicted and actual values, suggesting superior model performance. The formulas for calculating RMSE, MAPE and R2 are provided below:

$$RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n} {\left({Y}_{i}-\widehat{{Y}_{i}}\right)}^{2}}$$
(7)
$$MAPE=\frac{1}{n}\sum_{i=1}^{n} \left|\frac{{Y}_{i}-\widehat{{Y}_{i}}}{{Y}_{i}}\right|\times 100\text{\%}$$
(8)
$${R}^{2}=1-\frac{\sum_{i=1}^{n} {\left({Y}_{i}-\widehat{{Y}_{i}}\right)}^{2}}{\sum_{i=1}^{n} {\left({Y}_{i}-\overline{{Y }_{i}}\right)}^{2}}$$
(9)

where \({Y}_{i}\) is the real values; \(\widehat{{Y}_{i}}\) is the predicted values; and \(\overline{{Y }_{i}}\) is the average of the predicted values.

Results and discussion

Prediction results for both the training and testing sets of all five models demonstrated no significant signs of overfitting or underfitting. In the unit price prediction of C25 concrete, C30 concrete, and HRB400 steel bars, the predicted values of the five models were compared with the true values, and the results are depicted in Fig. 7. The comparison of performance evaluation indicators for various prediction models is shown in Table 6.

Fig. 7
figure 7

Comparison between predicted and actual values of different model.

Full size image
Table 6 Comparison of performance evaluation index of different models.
Full size table

Figure 7 demonstrates that the proposed SSA-PGNN model provides superior fitting to the nonlinear changes in unit prices for agricultural water conservancy materials, including C25 concrete, C30 concrete, and HRB400 steel bars, compared to the PGNN and SSA-BPNN models. Its predicted unit price curves align more closely with actual values, achieving the highest degree of fitting and the most accurate prediction performance.

Furthermore, the statistical results of the performance evaluation indicators in Table 6 indicate that the SSA-PGNN prediction model proposed in this study has the smallest RMSE and MAPE values, with an R2 value closest to 1, thus outperforming other prediction models. Under the same conditions, the PGNN model demonstrates superior predictive performance compared to traditional ML models (RF, XGBoost), indicating that PGNN exhibits smaller overall prediction deviations and more stable accuracy, particularly showing significant advantages in handling nonlinear temporal data such as material unit prices. Simultaneously, the SSA-PGNN model exhibits significantly improvements in performance evaluation metrics compared to the SSA-BPNN model. For the C25 concrete unit price prediction model, its RMSE and MAPE decreased by 35% and 17%, respectively, while R2 increased by 2%. In the C30 concrete unit price prediction model, its RMSE and MAPE decreased by 15% and 18%, respectively, while R2 increased by 1%. In the HRB400 steel reinforcement unit price prediction model, its RMSE and MAPE decreased by 9% and 32%, respectively, while R2 increased by 1%. These results confirm that incorporating grey GM(1,1) processing of historical material price data into the BP neural network effectively extracts temporal fluctuation trends, mitigates data randomness, and achieves higher prediction accuracy and operational efficiency by synergistically correcting nonlinear errors through neural networks.

Under the same conditions, the SSA- PGNN model shows significant improvements in evaluation metrics such as RMSE, MAPE, and R2 compared to the PGNN model. In the C25 concrete unit price prediction model, its RMSE and MAPE decreased by 64% and 25%, respectively, while R2 increased by 4%. In the C30 concrete unit price prediction model, its RMSE and MAPE decreased by 39% and 18%, respectively, while R2 increased by 4%. In the HRB400 steel reinforcement unit price prediction model, its RMSE and MAPE decreased by 20% and 54%, respectively, while R2 increased by 3%. Regarding computational costs, training durations for non-optimized models (RF, XGBoost, PGNN) ranged between 40–60 s, whereas SSA-optimized models (SSA-BP, SSA-PGNN) achieved reduced training times of approximately 10 s. These improvements highlight the importance of using optimization algorithms to optimize the weights and thresholds of the PGNN model, which significantly enhances predictive performance and efficiency, as randomly generated hyperparameters can negatively impact the model’s generalization ability, training times and prediction accuracy, preventing it from reaching optimal performance.

This study employed SPSS software to conduct independent samples t-tests on the prediction results of the SSA-PGNN and PGNN models, with the confidence interval set at 95% for significance analysis of test set results. The computational results for different materials are presented in Table 7. We observed that the Sig values for all three materials exceeded 0.05, indicating that the prediction results of the two models met the homogeneity of variance test. Subsequently, the t-test results revealed that the sig (Bilateral) values were all below 0.05, demonstrating a statistically significant difference between the predicted values of the two models.

Table 7 The calculation results of t-test.
Full size table

In summary, the comparative analysis demonstrates that the SSA-PGNN model outperforms other models in key metrics such as prediction accuracy, RMSE, and R2. The SSA-PGNN prediction model has better accuracy and stability in unit price prediction, confirming its scientific validity.

The prediction results of HRB400 steel bars, C25 concrete, and C30 concrete unit prices from March 2021 to September 2021, based on the established SSA-PGNN prediction model, are shown in Fig. 8. Combined with the steel bars and concrete consumption extracted from the BIM5D platform, the main material cost information of the actual project was obtained. Subsequently, the BIM-SSA-PGNN model developed in this study was utilized to predict the construction cost of the actual project in Yanghe Town, Anshan City, Liaoning Province. These predictions were then compared with those of the PGNN model and the SSA-BPNN model, with the results presented in Table 8.

Fig. 8
figure 8

Comparison of PGNN, SSA-BP and SSA-PGNN prediction results.

Full size image
Table 8 Comparison of construction cost prediction results of different models.
Full size table

Performance analysis of the BIM-SSA-PGNN model revealed that its prediction accuracy remained consistently high across different months, achieving a MAPE of only 2.99%. This accuracy surpasses that of the BIM-ANN model proposed by Zhang et al.49, which reported a MAPE of 4.29% when predicting the price of HRB400 steel bars. The data spanned from April 2019 to October 2022, while this study employed a broader temporal range, demonstrating the importance of data sample size for neural network model performance. This also validates the perspective of Cheng et al.20, who emphasized that construction prices fluctuate over time, leading to difficulties in predicting construction costs, thus highlighting the criticality of prediction models’ capability to capture temporal data variations. On the other hand, Baduge et al.50 argued that neural network models could be extensively applied in performance prediction of construction materials including concrete, steel, and timber to optimize cost-effectiveness. These findings substantiate the feasibility and applicability of the BIM-SSA-PGNN prediction model established in this study, particularly in generating satisfactory outcomes for material price forecasting.

Furthermore, the BIM-SSA-PGNN model demonstrates optimal performance among the compared models, with an R2 value of 0.9819 and an RMSE of 0.1358, underscoring its stability in cost prediction, effectiveness in capturing cost fluctuations, and viability for supporting intelligent construction cost management. Compared with the SSA-BP model, this model reduced RMSE by 19% and improved R2 by 2%, demonstrating superior performance. This conclusion aligns with the viewpoints of Pham et al.51 and Alshboul et al.52, indicating that the proposed model effectively captures construction cost fluctuations and explains that such variations primarily originate from historical price volatility.

Therefore, the BIM-SSA-PGNN model exhibits significant advantages over traditional methods in construction cost prediction. The digital and visualization capabilities of BIM technology enable accurate extraction of engineering data information from projects. Combined with the rapid processing capacity of the SSA-PGNN model for time-series data, it achieves precise prediction of construction costs for agricultural water conservancy projects, providing the agricultural water conservancy industry with more accurate and reliable cost management tools.

Practical application and future work

Practical application

Management application aspect. The proposed BIM-SSA-PGNN model provides a scientific decision-making tool for the whole-lifecycle management of agricultural water conservancy projects. By integrating engineering data (e.g., quantities, schedules, and resource demands) through BIM5D technology with the predictive capabilities of the SSA-PGNN model, managers can dynamically generate cost baselines during the planning phase, monitor cost deviations in real time during construction, and adjust resource allocation strategies based on prediction results. Specifically, the model can combine construction schedule simulations to predict the cost impacts of different schedule compression schemes, assisting managers in achieving multi-objective optimization among quality, cost, and schedule. Furthermore, the high-precision prediction results generated by the model can support budget preparation and contract risk allocation during the bidding phase, reducing claims risks caused by cost estimation deviations and enhancing the standardization and foresight of project management processes.

Technical application aspect. The technical value of this model lies in the innovative integration of BIM and machine learning. By automatically extracting structured quantity data (e.g., concrete volume, steel reinforcement specifications) via BIM5D technology and combining it with the SSA-optimized PGNN network, an end-to-end automated workflow from data acquisition to predictive analysis is achieved. The model synchronizes BIM component attributes with real-time market price databases, allowing technical teams to visualize the impact weights of material price fluctuations on costs and inversely optimize designs. This integration overcomes limitations in traditional cost estimation, enabling self-updating prediction models with enhanced real-time adaptability.

Economic application aspect. The model effectively controls hidden cost overrun risks in agricultural water conservancy projects through accurate predictions. The SSA-PGNN model can forecast material price fluctuations across different construction seasons, helping financial departments optimize cash flow scheduling and reduce financial costs caused by advance project payments.

Scalability aspect. By adjusting BIM models and parameters, the model can adapt to diverse engineering scenarios such as bridges, tunnels, and residential buildings. Combined with real-time market prices of materials and machinery in different regions, it enables cross-engineering domain and cross-regional application capabilities. For instance, by constructing a BIM model for residential building projects, concrete quantity data can be automatically extracted, and the SSA-PGNN model can predict concrete prices in the target region, ultimately deriving concrete costs for regional residential projects.

Future work

Dataset quality and quantity critically influence machine learning model performance. Limited by the current dataset size, this study has not yet employed deep learning models such as LSTM and Transformer, which excel in handling complex, large-scale datasets. Future studies should prioritize systematic collection and organization of engineering-related data to improve cost prediction accuracy using deep learning. Integrating SHAP value analysis could further visualize the contribution of engineering features to cost predictions, enhancing project planning and management.

Additionally, future research will focus on integrating IoT with BIM models, with a particular emphasis on exploring real-time data interaction mechanisms among on-site sensor networks, inspection systems, and BIM5D platforms. To achieve this, researchers should develop a predictive system architecture capable of synchronizing multi-source heterogeneous data—such as construction progress, resource consumption, and market price fluctuations—thereby supporting dynamic cost control throughout project lifecycles. By extending this framework to diverse project types, intelligent prediction systems can be established across engineering domains, ultimately advancing the construction industry toward real-time collaboration and autonomous decision-making.

Conclusion

This study addresses the complexity of predicting construction costs in agricultural water conservancy projects by developing a construction cost prediction model based on BIM technology and a PGNN neural network. The model’s accuracy and generalization ability are further enhanced through the integration of the SSA algorithm. The following conclusions are drawn from case studies:

  1. 1)

    By utilizing BIM technology to create a 3D model of an actual project, introducing the schedule plan and cost budget to establish the BIM5D model, and dynamically extracting key engineering quantity information within the required time period, a reasonable adaptation between BIM5D technology functions and cost prediction task requirements is achieved.

  2. 2)

    To address the nonlinear and periodic characteristics of unit price fluctuations in agricultural water conservancy projects, the grey GM (1,1) model combined with the BP neural network was selected as the prediction model. The SSA algorithm is employed to swiftly search for model weights and thresholds, adjusting the population positions to minimize errors, resulting in an optimized process. Experimental results demonstrate that the SSA-PGNN model outperforms the PGNN model in prediction accuracy.

  3. 3)

    Using the agricultural water conservancy project in Yanghe Town, Anshan City, Liaoning Province, as a case study, the BIM-SSA-PGNN model was employed to quickly and accurately process relevant engineering quantity data. The model’s performance yielded an average prediction accuracy of 97.01% across different months, with an RMSE of 0.1358 and an R2 of 0.9819. The model evaluation indicators surpass those of the PGNN model and SSA-BPNN model, verifying its high accuracy and reliability. This model can provide reference and technical support for predicting the construction cost of agricultural water conservancy projects, while enhancing the efficiency and effectiveness of construction cost management and project decision-making.

  4. 4)

    The proposed construction cost prediction model has significant practical implications for the agricultural water conservancy industry. The model effectively captures the dynamic trends in cost changes, accounting for complex factors such as design modifications and market price fluctuations, while enhancing the real-time accuracy of predictions. This model allows project managers to optimize project planning, adjust labor, modify work hours, and reallocate tasks as needed, thereby providing more comprehensive decision support and optimization solutions.