Implicit Runge-Kutta based sparse identification of governing equations in biologically motivated systems

Abstract

Identifying governing equations in physical and biological systems from datasets remains a long-standing challenge across various scientific disciplines. Common methods like sparse identification of nonlinear dynamics (SINDy) often rely on precise derivative approximations, making them sensitive to data scarcity and noise. This study presents a novel data-driven framework by integrating high order implicit Runge-Kutta methods (IRKs) with the sparse identification, termed IRK-SINDy. The framework exhibits remarkable robustness to data scarcity and noise by relying on the A-stability of IRKs and consequently their fewer limitations on stepsize. Two methods for incorporating IRKs into sparse regression are introduced: one employs iterative schemes for numerically solving nonlinear algebraic system of equations, while the other utilizes deep neural networks to predict stage values of IRKs. The performance of IRK-SINDy is demonstrated through numerical experiments on synthetic data in benchmark problems with varied dynamical behaviors, including linear and nonlinear oscillators, the Lorenz system, and biologically relevant models like predator-prey dynamics, logistic growth, and the FitzHugh-Nagumo model. Results indicate that IRK-SINDy outperforms conventional SINDy and the RK4-SINDy framework, particularly under conditions of extreme data scarcity and noise, yielding interpretable and generalizable models.

Introduction

Discovering differential equations holds significant importance for understanding and predicting complex systems in science and engineering^1,2,3,4. In traditional modeling approaches, early research efforts were fundamentally based on deriving equations analytically from first principles, such as conservation laws. Numerous modeling frameworks have been developed to address diverse problems, including the characterization of interaction networks among cells and proteins⁵, metabolic networks⁶, dynamics of tumor growth⁷, complex tumor-immune interactions⁸, population dynamics^9,10,11, the propagation of diseases^12,13,14, as well as pharmacokinetic-pharmacodynamic models^15,16. However, It is clear that this approach faced substantial limitations due to its requirement for complete physical knowledge of the system. As an illustrative example, governing equations of a dynamical system from observed data, for oscillatory and chaotic dynamics¹⁷, is challenging across diverse scientific disciplines. For instance, predator-prey dynamics^18,19 and competition models^20,21 are fundamental in systems biology of cancer²², yet creating realistic models (accurately describing the interactions) from empirical data is challenging. Even in scenarios where there exists a partial knowledge of the phenomenon under investigation, it is impractical to rely exclusively on first principles²³.

In recent years, the remarkable advancements in machine learning for regression and classification^24,25,26,27 have led to effective data-driven frameworks, particularly in systems biology^28,29 to capture underlying structures in biological systems^28,30,31. However, due to the black-box nature of e.g. neural networks and their substantial data requirements, these algorithms suffer from interpretability limitations^32,33,34,35. On the other hand, while many data-driven techniques such as eigensystem realization algorithms³⁶ (ERA) and autoregressive models³⁷ (ARX) lead to black-box models in system identification, recently, machine learning frameworks have gained special attention for addressing parsimonious white-box modeling with lowest complexity, constituting a burgeoning field of research. Towards developing interpretable models, based on classical system identification techniques while utilizing neural networks, some techniques aim to fit datasets to predefined model structures. Frameworks like physics-informed machine learning^38,39,40,41, and universal differential equations⁴², employ physical and biological knowledge (i.e. first principles) into model training, focusing less on knowledge discovery.

In fact, these methods leverage existing physical knowledge. However, due to intrinsic needs, we pursue methodologies to uncover the physical knowledge underlying the data. In this context, for linear systems, there exists a well-established set of highly efficient techniques accompanied by a relatively complete theoretical framework such as autoregressive moving average (ARMA) and autoregressive moving average with exogenous input (ARMAX)^43,44. In contrast, nonlinear systems face numerous challenges and fundamental limitations. Symbolic regression techniques utilize evolutionary computation methods- most notably genetic programming-to discover governing equations of dynamical systems. From a computational perspective, these algorithms are prohibitively expensive, while their inductive bias makes them particularly vulnerable to overfitting. Subsequent attempts to combine symbolic regression with deep neural networks^45,46 improved its performance slightly, but its main disadvantages remained. Thus, sparsity emerges as a critical consideration, driving the development of modeling frameworks centered on this principle. This methodology gains further significance as physical system dynamics are fundamentally characterized by a set of few nonlinear terms, thereby facilitating the development of highly interpretable models.

Differently, Brunton et al⁴⁷. proposed sparse identification of nonlinear dynamics, SINDy, employing sparse regression^48,49 that leverages the principle of parsimony⁵⁰, resulting in interpretable and generalizable models¹. SINDy has predominantly been developed along two main directions. Derivative-based SINDy techniques, depend on the direct computation of derivatives from observed data. Following that, and based on the type of optimization used, certain methods were proposed. Sequentially thresholded least-squares (STLSQ) method is employed in⁴⁷ to obtain parsimonious models of differential equations by considering it as a linear combination of nonlinear candidate functions. Other similar approaches, such as least absolute shrinkage and selection operator⁵¹, LASSO, and elastic net⁵², have been employed in SINDy through $\ell _{p}-\text {regularization}$⁴⁹ techniques. Along these lines, further SINDy extensions have been proposed to handle challenges in physics⁵³, chemistry⁵⁴, biology⁵⁰, and engineering⁵⁵. Although SINDy initially designed for ordinary differential equations⁴⁷ (ODEs) and its performance was evaluated on different benchmark problems, it has been subsequently adapted for partial differential equations⁵⁶ (PDEs). SINDYc^57,58was developed to account for control input. Prokop et al¹⁷. provide a comprehensive categorization of employing SINDy on biological systems and its challenges. While the effectiveness of SINDy variants has been validated with synthetic datasets, empirical cases have also been explored^18,19,59,60. Implicit-SINDy⁵⁰ was presented to handle dynamical systems with rational functions but exhibited noise sensitivity. Modifications to the optimization problem formulation and its transformation into a convex problem led to SINDy-PI⁶¹, improved the performance of the method against noise, but its robustness to noise is on a low scale. Most of these extensions are implemented in the open-source module PySINDy⁶².

These SINDy variants require accurate derivative approximations, which impose significant limitations on the sampling time steps. In addition to the fact that data scarcity yields inaccuracy in computations of derivatives, the presence of noise also adds to their severity⁶³. Schaeffer and McCalla⁶⁴ introduced integral formulation of SINDy to overcome numerical instability in derivative approximations. Messenger and Bortz^65,66 by proposing Weak SINDy (WSINDy) extended this integral (or weak) formulation to provide better robustness to noise. Goyal and Benner⁶⁷, by conceptualizing the integration of sparse identification with the classical fourth-order Runge-Kutta method⁶⁸-termed RK4-SINDy-have reduced the requirement for derivative approximation. Similar study conducted on linear multistep methods by Chen⁶⁹.

However, beyond the aforementioned classification of SINDy variants into derivative-approximation-based and integral-form approaches, other generalized extensions of SINDy also exist. As representative examples, Fasel et al⁷⁰. addressed data scarcity utilizing bootstrap aggregating techniques and proposed Ensemble-SINDy. Their approach improves robustness to noise and allows for uncertainty quantification and probabilistic predictions, however, it does not address the challenge of derivative approximations. The fundamental limitation of SINDy and its prior variants lies in their reliance on numerical methods with bounded stability regions, rendering them unusable for e.g. stiff problems⁷¹ that can arise in the optimization process. Consequently, A-stable methods (methods whose stability region includes the entire left half-plane of coordinates) are necessary for effectively addressing many nonlinear problems, encompassing oscillators and stiff systems^71,72. Implicit Gauss methods constitute the A-stable class of fully implicit Runge-Kutta methods exhibiting the highest accuracy^72,73, thus establishing them as an ideal choice for addressing stiff problems.

In this paper, we aim to discover data-driven models by combining the SINDy technique with A-stable Runge-Kutta methods. Given the implicit nature of these methods, we introduce and evaluate two potential approaches to facilitate data-driven discovery of governing differential equations. The first approach is based on computation of stage values of IRKs by solving the nonlinear system of algebraic equations. The second approach is founded on the prediction of stage values of IRKs by leveraging the universal approximation capabilities of deep neural networks. The aforementioned advantages of IRKs, combined with the sparsity-promoting properties of SINDy, render our derivative-free proposed algorithms remarkably robust against both data scarcity and measurement noise. This is convincingly demonstrated across a range of benchmark problems and comprehensive comparisons with conventional SINDy and RK4-SINDy.

The subsequent sections of the paper are organized as follows: Methods section provides two approaches based on IRKs for the purpose of learning governing equations through sparse regression techniques. Additionally, Results section evaluates the performance of the proposed frameworks utilizing synthetic datasets through a series of numerical experiments, while also comparing the results with existing approaches. Finally, conclusions and discussion are presented in last section, accompanied by a brief summary of prospective research directions.

Methods

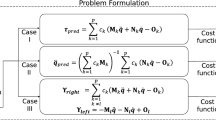
Problem statement and background

In this work, we consider data-driven discovery for nonlinear dynamical systems governed by ODEs of the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t) = f(x(t)),\\ x(t_{0}) = x_{0}, \end{array}\right. } \end{aligned}$$

(1)

where the vector $x(t) = \begin{bmatrix} x_{1}(t)&\dots&x_{d}(t) \end{bmatrix}^{T}$ indicates the state variables and $f: \mathbb {R}^{d} \rightarrow \mathbb {R}^{d}$ represents the unknown vector field. The goal is to determine the function f(x(t)) from measurement data. The SINDy algorithm⁴⁷ addresses this problem using sparse regression, relying on the fact that many systems can be described by relatively few active terms in the eq. (1). The essential step in SINDy involves the generation of a large library of candidate nonlinear features, denoted as $\Phi = [\phi _{1}(x), \phi _{2}(x), \cdots , \phi _{N}(x)]$, which encompasses potential nonlinear functions that can play a role in the right hand side of the governing equations. It is assumed that the function f(.) can be expressed as a linear combination of a few selected terms derived from the library⁴⁷. Illustratively, one could opt for a collection of polynomials, exponential functions, as well as trigonometric functions within the library. Upon considering the vector $x=[x_{1}, \dots , x_{d}]^{T}$, a library may be given as:

$$\begin{aligned} \Phi (x) := [1, x, x^{\mathscr {P}_{2}}, \dots , x^{\mathscr {P}_{d}}, \dots , \sin (x), \cos (x), \dots , \exp (-x), \exp (-2x), \dots ], \end{aligned}$$

(2)

where $x^{\mathscr {P}_{i}}$ represents polynomials of the degree i. To exemplify, in the scenario where $d=2$, $x^{\mathscr {P}_{2}}$ is given as follows:

$$\begin{aligned} x^{\mathscr {P}_{2}} = [x_{1}^{2}(t), x_{1}(t)x_{2}(t), x_{2}^{2}(t)]. \end{aligned}$$

Each element within the $\Phi$ library stands as a suitable candidate for representing f. Moreover, depending on the specific context, a collection of meaningful features can be systematically or empirically devised for inclusion within the library. To determine the governing ODE with fewest terms in function f, it is assumed that state variables x are known and the data $\{ x(t_{k}) \}_{k=0}^{m}$ can be sampled at times $\{ t_{0}, t_{1}, \dots , t_{m}\}$ with stepsizes $h_{k} = t_{k+1}-t_{k}$. We can represent data in measurement matrix $X = [x(t_{0}) x(t_{1}) \cdots x(t_{m})]^{T}\in \mathbb {R}^{(m+1)\times d}$ and library matrix $\Phi (X) = [\phi _{1}(X), \phi _{2}(X), \cdots , \phi _{N}(X)]^{T}\in \mathbb {R}^{(m+1)\times N}$ that allow us to form the sparse regression problem (3) to select a limited number of candidate functions from the library:

$$\begin{aligned} \xi = \mathop {\mathrm {\arg \min }}\limits _{\hat{\xi }} \{\Vert \dot{X}-\Phi (X)\hat{\xi } \Vert _{2} + \lambda \Vert \hat{\xi } \Vert _{0} \}, \end{aligned}$$

(3)

where $\xi = [\xi _{1} \xi _{2} \cdots \xi _{d}]$ represents the sparse coefficient matrix to select active terms in resulting model. $\lambda$ is called thresholding parameter that controls the amount of sparsity promotion through penalizing the number of nonzeros term by $\ell _{0}$-regularization.

Despite the possession of an extensive library, numerous choices for candidates will inevitably arise. The primary objective, however, revolves around identifying the minimal feasible candidate subset for the nonlinear representation of the function f^47,67. Since $\ell _{0}\text {-regularization}$ is recognized as an NP-hard problem⁷⁴, alternative regularized optimization problems such as $\ell _{p}\text {-regularization}$ are formulated:

$$\begin{aligned} \xi = \mathop {\mathrm {\arg \min }}\limits _{\hat{\xi }} \{\Vert \dot{X}-\Phi (X)\hat{\xi } \Vert _{2} + \mathscr {R}(\xi , \lambda )\}, \end{aligned}$$

(4)

In practice, derivatives in matrix $\dot{X}=[\dot{x}(t_{1}) \dot{x}(t_{2}) \cdots \dot{x}(t_{m})]^{T}$ are not typically available. These quantities can be approximated from the measurement matrix X. For example, finite difference methods such as

$$\begin{aligned} \dot{x}(t_{k}) \approx {x(t_{k}) - x(t_{k-1}) \over t_{k} - t_{k-1}}, \end{aligned}$$

are used for this purpose in conventional SINDy⁴⁷. After determinig the sparse matrix $\xi$ through solving the optimization problem (4), kth component in the righthand side of discovered model must be $f_{k}(x) \approx \sum _{j}^{N} \Phi _{j}(x)\xi _{j,k} = \Phi (x)\xi _{k}$. Alternatively, in a more comprehensive manner:

$$\begin{aligned} \dot{x} = f(x) \approx \Phi (x) \xi , \end{aligned}$$

(5)

The main disadvantage of standard methods is that to accurately calculate the derivative matrix $\dot{X}$, the distance between the measurement data ($h_{K}$) must be small, which may require a very large number of measurements to discover the governing equations. Another disadvantage of this method is that finite difference methods approximate the derivative with low order and thus sensitive to noise.

Implicit Runge-Kutta methods

Runge-Kutta methods are extensively utilized to solve initial value problems due to the capability to construct them from any specified order^71,72,75. Implicit Runge-Kutta methods exhibit A-stability properties and are widely recognized as a highly suitable candidate for addressing issues associated with stiffness^71,72. Higher order IRKs impose fewer limitations on the stepsize, can therefore play a crucial role in the sparse identification of dynamical systems with constrained data availability.

Inspired by recent development in combining numerical integration schemes with sparse identifcation techniques^67,69, our approach compares the observed data $x(t_{k+1})$ with its predicted value obtained by applying an IRK method to the data at time $t_{k}$. Hence, let us utilize the general form of Runge-Kutta methods with s stages⁷² to approximate the solution of eq. (1):

$$\begin{aligned} x(t_{k+1})&\approx x(t_{k}) + h_{k}\sum _{j=1}^{s}b_{j} f(\chi _{j}^{f}(t_{k})), \end{aligned}$$

(6a)

$$\begin{aligned} \chi _{i}^{f}(t_{k})&= x(t_{k}) + h_{k} \sum _{j=1}^{s}a_{ij}f(\chi _{j}^{f}(t_{k})), \quad i=1, \dots , s, \end{aligned}$$

(6b)

where $\chi _{i}^{f}(t_{k}) \approx x(t_{k} + c_{i}h_{k})$ denotes the stage values. This system can also be rewritten in vectorized form using following notations:

$$\begin{aligned}&\chi = \begin{bmatrix} \chi _{1}^{f}\\ \vdots \\ \chi _{s}^{f} \end{bmatrix}, \quad F(\chi ) = \begin{bmatrix} f(\chi _{1}^{f})\\ \vdots \\ f(\chi _{d}^{f}) \end{bmatrix}, \end{aligned}$$

(7a)

$$\begin{aligned}&\begin{bmatrix} \begin{array} {c} \chi (t_{k})\\ \hline x(t_{k+1}) \end{array} \end{bmatrix} \approx \begin{bmatrix} \begin{array} {c|c} A\otimes \mathbb {I}_{d} & {\textbf {1}}_{s} \otimes \mathbb {I}_{d}\\ \hline b^{T}\otimes \mathbb {I}_{d} & 1 \end{array} \end{bmatrix} \begin{bmatrix} \begin{array} {c} h_{k} F(\chi (t_{k}))\\ \hline x(t_{k}) \end{array} \end{bmatrix}, \end{aligned}$$

(7b)

where $\mathbb {I}_{d}$ denotes $d\times d$ identity matrix, ${\textbf {1}}_{s}$ is s-element unit vector, and $\otimes$ represents Kronecker product. Depending on the structure of the matrix A, this formulation yields either implicit or explicit time-stepping schemes. If A is a strictly lower triangular matrix, then the method is called the explicit Runge-Kutta method. Otherwise, the method is called the implicit Runge-Kutta method. Gauss IRK methods, which we employ in this work, are implicit schemes that can achieve up to order 2s with s stages^71,72,75. The key idea is to reconstruct future data from stage values and minimize the discrepancy with observed data. This discrepancy is encoded in a loss function, which guides the optimization process during training. Through this framework, we refine the identified vector field without relying on explicit derivative estimation.

Discovering nonlinear differential equations with IRKs

The finite difference method for approximating derivative is equivalent to the Euler method for numerically solving the initial value problem (1). The stability region of the Euler method is limited–a unit disk in the complex plane–which makes it unsuitable for stiff systems⁶⁸. To address this limitation, Goyal et al⁶⁷. introduced RK4-SINDy, which integrates the well-known fourth-order Runge-Kutta scheme (RK4) with sparse identification. Due to its higher accuracy ($O(h_{k}^{4})$) and larger stability region compared to Euler’s method, RK4-SINDy showed greater robustness to data scarcity and noise. However, similar to the Euler method, RK4 still suffers from a bounded stability region and performs poorly on stiff systems. In contrast, IRKs (such as Gauss methods) are A-stable and have unbounded stability region that contains the entire left half of the complex plane. This property allows for greater flexibility in the stepsize without compromising numerical stability⁷². Here, we generalize the use of Runge-Kutta methods, particularly IRKs, to enhance the accuracy and stability of the sparse identification.

The s-stage Gauss IRK method achieves local error of order $O(h_k^{2s})$⁷². For sufficiently small stepsizes, $h_{k}$, this leads to high-accurate approximations of $x(t_{k+1})$ from $x(t_{k})$. Let us denote by $\mathscr {F}_{irk}$ the right hand side of eq. (6a) as a function of f, $x(t_{k})$ and $h_{k}$:

$$\begin{aligned} \mathscr {F}_{irk}(f, x(t_{k}), h_{k}) := x(t_{k}) + h_{k}\sum _{j=1}^{s}b_{j}f(\chi _{j}^{f}(t_{k})), \end{aligned}$$

(8)

where, it is possible to predict both $x(t_{k+1})$ and $x(t_{k-1})$ values with high accuracy using IRKs based on $x(t_{k})$ by the fact that the correctness of $x(t_{k+1}) \approx \mathscr {F}_{irk}(f, x(t_{k}), h_{k})$ follows directly. o formulate the IRK-SINDy framework, we aim to identify the most parsimonious representation of the vector field f(x(t)) by leveraging the time series data of x(t) at the time instances $\{ t_{0}, \dots , t_{m}\}$ that was previously assumed. For this purpose, we consider the data matrices in the following manner:

$$\begin{aligned} X^{L} : = \begin{bmatrix} x^{T}(t_{0})\\ x^{T}(t_{1})\\ \vdots \\ x^{T}(t_{m-1}) \end{bmatrix},\quad X^{R} : = \begin{bmatrix} x^{T}(t_{1})\\ x^{T}(t_{2})\\ \vdots \\ x^{T}(t_{m}) \end{bmatrix}, \end{aligned}$$

(9)

and the corresponding predicted values:

$$\begin{aligned} X_{\mathscr {F}}^{R}(f) = \begin{bmatrix} \mathscr {F}_{irk}(f, x(t_{0}), h_{0})\\ \mathscr {F}_{irk}(f, x(t_{1}), h_{1})\\ \vdots \\ \mathscr {F}_{irk}(f, x(t_{m-1}), h_{m-1}) \end{bmatrix}, \quad X_{\mathscr {F}}^{L}(f) = \begin{bmatrix} \mathscr {F}_{irk}(f, x(t_{0}), -h_{0})\\ \mathscr {F}_{irk}(f, x(t_{1}), -h_{1})\\ \vdots \\ \mathscr {F}_{irk}(f, x(t_{m-1}), -h_{m-1}) \end{bmatrix}. \end{aligned}$$

(10)

where the kth row of the matrix $X_{\mathscr {F}}^{R}$ is a prediction of the value of $x(t_{k})$ given the information $x(t_{k-1})$ using IRKs. Similarly, the kth row of the $X_{\mathscr {F}}^{L}$ matrix is a prediction of the value of $x(t_{k-1})$ given the information $x(t_{k})$ and with a negative stepsize. This idea is similar to the work used in RK4-SINDy⁶⁷. Consequently, appropriately selecting candidate functions from the library determines the governing equations. Special attention must be given to eq. (11) while formulating the appropriate optimization problem:

$$\begin{aligned} X^{i} = X^{i}_{\mathscr {F}}(f),\quad \text {where}\quad f(x) \approx \Phi (x)\xi , \end{aligned}$$

(11)

for $i=L, R$. Now, independently of calculating the derivative matrix $\dot{X}$, according to eqns. (5) and (11), we can define the loss function (12) as a function of the coefficient matrix $\xi$ for training:

$$\begin{aligned} \mathscr {L}(\xi ) = \alpha \Vert X^{L} - X^{L}_{\mathscr {F}}(\Phi (.)\xi ) \Vert _{2}^{2} + (1 - \alpha ) \Vert X^{R} - X^{R}_{\mathscr {F}}(\Phi (.)\xi ) \Vert _{2}^{2}, \end{aligned}$$

(12)

with trade-off parameter $0 \le \alpha \le 1$. To encourage sparsity of resulting coefficient matrix, similar to^67,69, the corresponding regularized optimization problem (13) can be formulated as:

$$\begin{aligned} \xi = \mathop {\mathrm {\arg \min }}\limits _{\hat{\xi }} \{ \mathscr {L}(\hat{\xi }) + \mathscr {R}(\hat{\xi }, \lambda )\}, \end{aligned}$$

(13)

where, $\mathscr {R}(\hat{\xi }, \lambda )$ represents the regularization term with thresholding parameter $0 \le \lambda \le 1$. A choice is the utilization of $\ell _{1}\text {-regularization}$^51,52, defined as $\mathscr {R}(\hat{\xi }, \lambda ) = \lambda \Vert \hat{\xi } \Vert _{1}$.

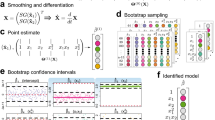
To implement the algorithm, it is crucial to acquire the stage values, $\chi _{i}(t_{k}), i=1, \dots , s$, within the context of IRKs. In the classical implementation of IRKs, these values are computed by solving the nonlinear system of algebraic equations (6b) employing iterative schemes such as fixed-point iteration and Newton’s method⁷². We note that, in our implementation based on Newton’s method, automatic differentiation tool⁷⁶ exploited to calculate required Jacobean matrix. In light of this foundational framework, as illustrated in Figure 1, we propose a novel sparse identification process of differential equations inspired by IRKs. Within this approach, we perform predictive analyses of the quantities $X^{L}$ and $X^{R}$ to address the optimization problem in (13), which is achieved by obtaining the sd stage values through the aforementioned iterative techniques and subsequently substituting them into eq. (6a). It is crucial to emphasize that in the context of fixed point methods, the convergence condition for calculating the solution of the system represented by iteration map $\Psi (x) = 0$ is depended on Lipschitz constant associated to $\Psi$. Conversely, for an initial guess in proximity to the stage values, Newton’s method exhibits a rapid convergence to the solution of the system^71,72. Therefore, given the limitations of fixed-point methods in solving nonlinear and stiff problems^73,75, they are inefficient for the sparse identification of nonlinear dynamical systems.

Fig. 1

Overview of the IRK-SINDy framework: (a) For each benchmark problem, we perform measurements that incorporate noise and, thereafter form a dataset. Our objective is to construct a model that is parsimonious, interpretable, and possesses generalizability, capable of accurately forecasting reference dynamics. (b) Given an appropriate initial guess (e.g., $X(t_{k})$), the stage values of the IRKs are approximated by solving the system of nonlinear equations (6b) through iterative schemes. In this context, we employ two iterative approaches: (i) fixed point iteration and (ii) Newton’s method. (c) With the stage values established the subsequent step values are computed according to eq. (8). This computational process is depicted as the systematic IRK network. (d) Within this structured representation of IRK-SINDy, the dataset is classified into two categories: forward and backward, followed by the formation of a symbolic features library comprising candidate nonlinear functions. To solve a nonlinear sparse regression problem using the forward and backward predictions illustrated in (b) and (c), an IRK step is applied, and the loss function is minimized by choosing a suitable optimizer. Following a certain number of epochs, a sparsity-promoting algorithm is employed. Finally, every non-zero element in the coefficient matrix $\xi ^{*}$ signifies an active term within the feature library, thereby representing the resultant discovered model.

Despite the efficiency of this approach, the necessity of solving the system of nonlinear equations at each epoch significantly slows down the overall optimization process⁷⁷. Moreover, to enhance the accuracy of the predictions, it is essential to employ higher-order IRKs, and therefore an increased number of stage values. As sincreases, the corresponding computational cost increases exponentially associated with these calculations. Inspired by Raissi et al³⁹., we address this computational challenge using an auxiliary deep neural network to approximate stage values efficiently. This leads to a linear computational cost scaling with respect to s, dramatically accelerating training.

Discovering nonlinear differential equations through combining DNNs and IRKs

Here we make use of an auxiliary DNN that is parameterized as a nonlinear mapping from time $t_{k}$, along with the corresponding state variable x evaluated at $t_{k}$, i.e. $x(t_{k})$, to the stage values of IRKs in the approximation of $x(t_{k+1})$ with stepsize $h_{k}$. Therefore, we denote this neural network by $\chi ^{\theta } = [\chi ^{\theta }_{1}, \dots , \chi ^{\theta }_{s}]$, wherein $\theta$ represents the trainable parameters of the DNN. As elucidated in Figure 2, the DNN is trained to approximate the true IRK stage values $\chi ^{f}$ governed by the underlying dynamical system, aiming to satisfy:

$$\begin{aligned} \chi ^{\theta }_{i}(t_{k}) \approx \chi ^{f}_{i}(t_{k}), \quad i=1, \dots , s, \quad k=0,1, \dots , m-1. \end{aligned}$$

To effectively integrate the auxiliary DNN and IRKs within the framework of the optimization process, it becomes imperative to reformulate eq. (8). Thus, by subtracting eq. (6a) from eq. (6b), we obtain:

$$\begin{aligned} \hat{\mathscr {F}}_{irk}^{L}(f, x(t_{k}), h_{k}, i)&:= \chi _{i}(t_{k}) - h_{k}\sum _{j=1}^{s}a_{ij} f(\chi _{j}(t_{k})), \quad i=1, \dots , s, \end{aligned}$$

(14a)

$$\begin{aligned} \hat{\mathscr {F}}_{irk}^{R}(f, x(t_{k}), h_{k}, i)&:= \chi _{i}(t_{k}) + h_{k} \sum _{j=1}^{s}(b_{j} - a_{ij})f(\chi _{j}(t_{k})), \quad i=1, \dots , s, \end{aligned}$$

(14b)

It subsequently becomes evident that:

$$\begin{aligned} x(t_{k})&\approx \hat{\mathscr {F}}_{irk}^{L}(f, x(t_{k}), h_{k}, i), \quad i=1,\dots , s, \end{aligned}$$

(15a)

$$\begin{aligned} x(t_{k+1})&= x(t_{k}+h_{k}) \approx \hat{\mathscr {F}}_{irk}^{R}(f, x(t_{k}), h_{k}, i),\quad i=1,\dots , s. \end{aligned}$$

(15b)

Fig. 2

Overview of the deep IRK-SINDy framework: (a) The dataset is prepared for the purpose of training the neural network. (b) The inputs to the neural network are assigned into two distinct variables: time and state variables. The neurons located in the output layer of the network are partitioned into s segments, each containing d neurons. The i’th segment predicts the d stage values corresponding to the $\chi _{i}$. (c) Through the process of forward propagation within the DNN, the stage values are predicted, and these predictions are subsequently employed in the IRK steps, i.e. eq. (8), facilitating both forward and backward predictions. (d) By comparing the predictions against the data, the loss is computed, followed by the optimization step. Upon reaching a specified number of epochs, at which point the loss is sufficiently minimized, the sparsity-promotion algorithm is exclusively applied to the coefficient matrix $\xi$. Finally, the non-zero coefficients of the $\xi$ denote the active terms in the nonlinear feature library.

In a manner similar to eqns. (9) and (10), the IRK network can be systematically defined as eq. (16):

$$\begin{aligned} \hat{X}_{\hat{\mathscr {F}}}^{i}(f) = \begin{bmatrix} \hat{\mathscr {F}}^{i}_{irk}(f, x(t_{0}), h_{0}, 0) & \dots & \hat{\mathscr {F}}^{i}_{irk}(f, x(t_{0}), h_{0}, s)\\ \hat{\mathscr {F}}^{i}_{irk}(f, x(t_{1}), h_{1}, 0) & \dots & \hat{\mathscr {F}}^{i}_{irk}(f, x(t_{1}), h_{1}, s)\\ \vdots & & \vdots \\ \hat{\mathscr {F}}^{i}_{irk}(f, x(t_{m-1}), h_{m-1}, 0) & \dots & \hat{\mathscr {F}}^{i}_{irk}(f, x(t_{m-1}), h_{m-1}, s) \end{bmatrix}, \quad i=L,R. \end{aligned}$$

(16)

Now, to select the most active terms among the nonlinear features of the $\Phi$ library, the loss function is formulated in eq. (17) through the integration of three ingredients, including sparse identification, IRKs, and the auxiliary DNN, with the aim of simultaneously determining the parameters associated with the neural network as well as the coefficient matrix:

$$\begin{aligned} \hat{\mathscr {L}}(\xi ) = \alpha \Vert X^{L} - \hat{X}^{L}_{\hat{\mathscr {F}}}(\Phi (.)\xi ) \Vert _{2}^{2} + (1 - \alpha ) \Vert X^{R} - \hat{X}^{R}_{\hat{\mathscr {F}}}(\Phi (.)\xi ) \Vert _{2}^{2}, \end{aligned}$$

(17)

where $0 \le \alpha \le 1$ controls the trade-off between forward and backward prediction accuracy. Similar to problem (13), in accordance with eq. (17) the corresponding regularized optimization problem can be formulated in the following manner^67,69 to obtain the sparse coefficient matrix $\xi$ alongside the DNN parameters $\theta$:

$$\begin{aligned} \xi = \mathop {\mathrm {\arg \min }}\limits _{\hat{\xi }, \theta } \{ \hat{\mathscr {L}}(\hat{\xi }, \theta ) + \mathscr {R}(\hat{\xi }, \lambda )\}, \end{aligned}$$

(18)

This integrated framework, referred to as deep IRK-SINDy, enables data-driven discovery of governing differential equations without requiring explicit derivative computations. Notably, it demonstrates strong robustness against noise and performs effectively even with limited data availability (data scarcity)^65,66,70.

Sparsity-promoting procedure

When the nonlinear optimization problems delineated in eqns. (13) and (18) are rigorously formulated, the goal is to seek an approximate sparse solution denoted as $\xi$⁶⁷. Although several sparse regression techniques–such as LASSO⁴⁸ or elastic net⁵²– (which modify the loss function by sparsity-promoting penalties of the form $loss + \lambda _{1} \Vert \xi \Vert _{1} + \lambda _{2} \Vert \xi \Vert _{2}$ and continuously drive coefficients toward zero) are frequently employed to promote the sparsity in the resultant solution, it is crucial to note that a significant number of these algorithms are predominantly tailored for linear and convex optimization problems^78,79. While $\ell _{p}$-regularization with $p \in \mathbb {N}$ can approximate the ideal but non-convex $\ell _{0}$ penalty⁴⁹, in practice, thresholding methods offer a more tractable alternative for model discovery^47,67,80. In order to select the active terms in governing equations within the frameworks of eqns. (13) and (18), we adopt a gradient-based sequential thresholding procedure, inspired by the sequential thresholding least squares algorithm utilized in conventional SINDy⁴⁷, and adapted for non-convex scenarios⁶⁷. Unlike prevalent sparse regression methods^48,52,81, the sequential thresholding approach directly enforces sparsity by hard-thresholding coefficients. This procedure is schematically outlined in Figures 1 and 2.

During each iteration of the procedure, the loss function articulated in eq. (12) (for IRK-SINDy) or eq. (17) (for deep IRK-SINDy) is first minimized through the application of a gradient-descent method during the training phase⁸². This optimization is conducted with respect to the coefficient matrix $\xi$ and also, in the case of deep IRK-SINDy, the neural network parameters $\theta$. Our proposed procedure initiates with the establishment of an initial guess for $\xi$ coupled with setting a threshold value $\lambda$. Following a certain number of epochs in each iteration, sparsity-promoting modifications are applied to obtain a sparse $\xi$: all coefficients in $\xi$ with absolute value smaller than $\lambda$ are set to zero. This procedure is iterated until convergence. In practice, when reasonable values of $\lambda$ are employed, the sequential thresholding surprisingly requires a few number of iterations to achieve convergence, ultimately leading to the derivation of the optimal coefficient matrix $\xi$. The pseudocode in Algorithm 1 provides a technical exposition of this sparsity-promoting optimization process within the IRK-SINDy framework. For deep IRK-SINDy, the same steps are applied, with the addition of optimizing $\theta$ alongside $\xi$ during gradient descent.

Algorithm 1

Psudocode for sequential thresholding procedure in IRK-SINDy

It is imperative to underscore the point that when we set $\lambda$ to zero, every term within the nonlinear feature library is recognized as an active term; this scenario is particularly pronounced in instances characterized by measurement errors and numerical round-off effects, which can be deemed non-physical in nature. Furthermore, by specifying $\lambda =1$, the regularization term effectively overcomes the loss function, compelling $\xi$ to approach zero and, consequently, the model to $\dot{x}=0$. Therefore, the reasonable determination of the sparsity-promoting parameter $\lambda$ through concepts such as cross-validation⁸³ and the analysis of the Pareto front⁸⁴, which aims to balance the trade-off between loss minimization and model complexity, play a pivotal role in correctly identifying the reference dynamics. In this context, our objective is to impose a penalty on the number of terms within the model, while simultaneously striving to minimize the loss function, thereby yielding the most parsimonious model. To achieve this end, we can utilize the information criterion for model selection delineated in^84,85,86, a process that has been successfully applied across various sparse identification problems, with each case resulting in the correct identification of the reference model.

Results

In this section, the efficacy of the proposed methodologies for the data-driven discovery of governing differential equations is demonstrated and examined through a series of numerical experiments on benchmark problems exhibiting varying classified complexity, from linear and nonlinear oscillators to noisy measurement of predator-prey dynamics. The robustness to noise and data scarcity is illustrated in comparison with conventional SINDy⁴⁷ (referred to as Conv-SINDy) and RK4-SINDy⁶⁷ without access to derivative information. The two proposed methodologies have implemented in the PyTorch deep-learning module⁸⁷ utilizing a gradient descent optimization method alongside Gauss methods up to 500 stages³⁹, as IRKs with the highest accuracy, to address the optimization problems delineated in eqns (13) and (18). In this implementation, the Adam optimizer⁸⁸ has employed to iteratively update the coefficient matrix $\xi$ and the parameters of the neural network $\theta$. All models have trained using an Core i5-7400 CPU with 8 GB memory. Synthetic data are generated by forward-solving the system of differential equations utilizing numerical methods, specifically the fourth-order Runge-Kutta method and Backward Differentiation Formulas (BDF)^68,71,72, as implemented in the solve$\_$ivp function of SciPy module, followed by introducing various levels of noise into the dataset. Finally, after the model discovery process, the identified model is subjected to a comparative analysis against a reference model in each numerical experiment by evaluating the solutions corresponding to distinct initial conditions.

Linear damped oscillator

As a first illustrative example, we consider discovering the governing equations of a two-dimensional linear damped oscillatory system using data with different levels of noise and data availability. The reference dynamics is given by ():

$$\begin{aligned} \dot{x}_{1}(t) = -0.1 x_{1}(t) + 2.0 x_{2}(t), \end{aligned}$$

(19a)

$$\begin{aligned} \dot{x}_{2}(t) = -2.0 x_{1}(t) - 0.1 x_{2}(t). \end{aligned}$$

(19b)

To initiate the data collection process, we establish the initial condition as $\begin{bmatrix} x_{1}(0)&x_{2}(0) \end{bmatrix}^{T} = \begin{bmatrix} 2.0&0.0 \end{bmatrix}^{T}$, and uniformly sample a total of $m+1$ data points utilizing a fixed stepsize 20/m, within the time interval $t\in [0, 20]$. In the first scenario, we use a variety of values for m, with the objective of rigorously assessing the robustness of the proposed methodologies to data scarcity, without adding noise to measurements. It is noteworthy to mention that the algorithm is also flexible for data with variable stepsize, however, for the sake of simplicity and clarity in our analytical framework, we have opted to utilize a constant stepsize in the current analysis. The data from the sampling process are plotted in Figure 3a.

Fig. 3

Linear damped oscillator: Comparing identified models under various levels of data scarcity with reference model. (a) Data, (b) sample size $m=801$, (c) sample size $m=201$, (d) sample size $m=51$, (e) sample size $m=31$.

We systematically explore the desired model in the model space of possible descriptions of the dynamical system under investigation, which, in the specific case of this particular example, is restricted to the space of polynomials up to degree 3. Upon the careful selection of the nonlinear feature library, we proceed to set the threshold value across all approaches to constant value $\lambda =0.05$. Within the frameworks of the IRK-SINDy and RK4-SINDy approaches, we use a learning rate of $lr=0.01$ for updating coefficient matrix $\xi$ and regularly conduct sequential thresholding every 1000 epochs. It is crucial to point out that in the context of the deep IRK-SINDy approach, the first approximation of stage values may require potentially more epochs initially to facilitate effective sequential thresholding. This requirement arises due to the need of the DNN to undergo adequate training in order to accurately predict the stage values corresponding to IRKs, which subsequently allows for the prediction of both next and preceding step values via eq. (). Thus, it follows that the more rapidly the network acquires proficiency in learning the $\chi ^{\theta }$ values, the fewer epochs will be necessitated by the algorithm for the procedure of sequential thresholding. It is imperative to emphasize again that within the framework of the deep IRK-SINDy approach, the Adam optimizer updates $\xi$ and $\theta$ simultaneously, while, the endeavor to learn the stage values imposes a limit on the permissible learning rate. For this reason, in the deep IRK-SINDy framework, we set two different learning rates of $10^{-3}$ and 0.01 for the DNN parameters and the coefficient matrix $\xi$, respectively. In the first iteration, 15, 000 epochs and in subsequent iterations, 1, 000 epochs are employed to train the network. In this configuration, we use 4 hidden layers, each comprising 32 neurons, utilizing the $\tanh$ activation function within the architecture of the fully connected DNN. At the end of each iteration, the learning rate values are updated by multiplying them by a number between 0 and 1. We use 4 fixed-point iterations and 3 Newton’s iterations, respectively.

Figure 3 depicts a qualitative evaluation of the accuracy associated with the discovered dynamical systems by providing a comparative analysis between the reference trajectories and the predicted trajectories, alongside the resultant phase portrait. It reveals that all approaches, including the two versions of IRK-SINDy, are able to capture the dynamical evolution of the system given sufficient and clean data. As delineated in Table 1 and Table 2, the equations derived from these approaches demonstrate a remarkable consistency with the reference dynamics. Furthermore, Figure 3 confirms that for a limited amount of data, the two innovative proposed approaches exhibit superior performance relative to the previously mentioned approaches. For instance, in the scenario where $m = 31$, both the IRK-SINDy and deep IRK-SINDy approaches successfully capture the governing equations, outperforming the other approaches. Additionally, as anticipated, Figure 3 and Table 2 show that applying IRK-SINDy with Newton’s itiration yields superior results when compared to its utilization with fixed-point iteration. Table 1 indicates that the two approaches Conv-SINDy and RK4-SINDy have encountered challenges in identifying correct and sparse models, particularly under conditions of significant data scarcity.

Table 1 Linear damped oscillator: the discovered governing equations using deep IRK-SINDy, RK4-SINDy, and Conv-SINDy for various sample-size m.

Table 2 Linear damped oscillator: the discovered governing equations using IRK-SINDy in the approach of Newton’s iterations and fixed point iterations for various sample-size m.

In the second scenario, m is kept constant and equal to 551, while various levels of noise are introduced to the measurements in order to examine the robustness of the proposed methodologies to noise. Herein, we utilize $\sigma \in \{0.01, 0.04, 0.08, 0.16\}$ to produce Gaussian noise $\mathscr {N}(\mu , \sigma ^{2})$ with a zero mean $\mu = 0$ and variance $\sigma ^{2}$, whereby the noise level is controlled by the standard deviation sigma. We employ 3 thresholding iterations with 2, 000 epochs per iteration, using a thresholding parameter of $\lambda = 0.06$. For deep IRK-SINDy, 20, 000 epochs are allocated in the first iteration and, 2, 000 epochs in the subsequent iterations, employing the identical DNN architecture. Before the training process, we employ the Savitzky-Golay⁸⁹ filter for data preprocessing to obtain denoised data^67,90. This preprocessing phase is employed by default in the PySINDy module⁶². For unbiased comparative analysis, we apply the finite difference derivative approximation in the Conv-SINDy simulation step.

Fig. 4

Linear damped oscillator: Comparing the response of identified models under various noise levels in measurements with reference model. (a) Noisy data, (b) noise level $\sigma = 0.01$, (c) nise level $\sigma = 0.04$, (d) noise level $\sigma =0.08$, (e) noise level $\sigma =0.16$.

Our simulations demonstrate that our methodology is robust to noise. As illustrated in Figure 4 and Table 3, our approach is more robust to noise than previous approaches. Table 4 distinctly indicates that the application of Newton’s iterative method in the implementation of IRK-SINDy surpasses fixed point methods concerning noise. Despite the efficiency of the IRK-SINDy framework against noise, taking into account the capabilities of DNNs, appropriate architectures may be developed to enhance the network’s noise resistance, which can be the subject of future studies.

Table 3 Linear damped oscillator: the discovered governing equations using deep IRK-SINDy, RK4-SINDy, and Conv-SINDy for various noise level $\sigma$.

Table 4 Linear damped oscillator: the discovered governing equations using IRK-SINDy in the approach of Newton’s iterations and fixed point iterations for various noise levels $\sigma$.

Cubic damped oscillator

Now, let us consider the two-dimensional damped harmonic oscillator characterized by cubic dynamics given in eq. ():

$$\begin{aligned} \dot{x}_{1}(t) = -0.1 x_{1}^{3}(t) + 2.0 x_{2}^{3}(t), \end{aligned}$$

(20a)

$$\begin{aligned} \dot{x}_{2}(t) = -2.0 x_{1}^{3}(t) - 0.1 x_{2}^{3}(t). \end{aligned}$$

(20b)

In this experiment, we employ the initial condition $\begin{bmatrix} x_{1}(0)&x_{2}(0) \end{bmatrix}^{T} = \begin{bmatrix} 2.0&0.0 \end{bmatrix}]^{T}$ to collect data across the temporal interval $t \in [0, 20]$ for the cases where m is assumed the values of 801, 401, 101, and 51. The objective is to successfully recover the governing equations that dictate nonlinear behavior of the system, utilizing both a sufficient and scarce data. The architecture of DNN comprises a total of four hidden layers, each incorporating 32 neurons. Furthermore, we establish a thresholding value of $\lambda =0.05$, alongside a learning rate $lr=10^{-3}$ for the parameters associated with the DNN, while concurrently applying a learning rate of $10^{-2}$ for the coefficient matrix $\xi$. Throughout this simulation, we incorporate a total of three thresholding iterations, each consisting of 1, 000 epochs conducted within the polynomial space up to degree 3. 15, 000 epochs are used for the first iteration in the deep IRK-SINDy training process.

In the subsequent analysis presented in Figure 5, we provide a comprehensive comparison between IRK-SINDy, RK4-SINDy, and Conv-SINDy. It becomes readily apparent that the IRK-SINDy aaproach accurately identify the dynamics of system (), whereas the Conv-SINDy approach exhibits considerable difficulties when confronted with smaller values of m. Moreover, it is noteworthy that IRK-SINDy demonstrates a superior capability in discovering interpretable equations in comparison to RK4-SINDy, particularly in scenarios characterized by scarce data availability. This capability can be attributed to the A-stability properties in Gauss methods^71,72, which ensures that the stability region of these methods contains the entire left half-plane of the coordinate system, in contrast to the finite stability region associated with explicit methods such as RK4. It is pertinent to mention that, for the purposes of this comparative analysis, we employ an IRK method of the same order as the RK4 algorithm.

Fig. 5

Cubic damped oscillator: Comparing identified models under various levels of data scarcity with reference model. (a) Phase portraits, (b) coefficient matrices for $m\in \{ 801, 401, 101, 51 \}$. IRK-SINDy provides a more parsimonious and generalizable model compared to RK4-SINDy and Conv-SINDy.

FitzHugh-Nagumo

The subsequent benchmark problem pertains to a relatively simple (in its formulation) yet important model in the field of mathematical neuroscience that characterizes the oscillatory and nonlinear dynamics in the electrical activity of neurons, known as the FitzHugh-Nagumo model⁹¹, commonly abbreviated as FHN model. In spite of its simplicity, this mathematical model is utilized in various neuroscience applications, particularly in illustrating how neurons are capable of generating action potentials in response to stimuli. FHN can simulate the periodic oscillatory behavior observed in neuronal activity, such as brain rhythms, and the propagation of electrical waves in a network of neurons. FHN serves as a foundational framework, establishing a basis for the subsequent development of more sophisticated models that seek to capture the complexities associated with neuronal activity. The system of differential equations that encapsulates the underlying dynamics of this model is expressed in eq. ():

$$\begin{aligned} \dot{v}(t) = v(t) - w(t) - {1 \over 3}v^{3}(t) + 0.5, \end{aligned}$$

(21a)

$$\begin{aligned} \dot{w}(t) = 0.04 v(t) -0.028w(t) +0.032. \end{aligned}$$

(21b)

By employing the initial condition $\begin{bmatrix} v(0)&w(0) \end{bmatrix}^{T} \begin{bmatrix} 0.0&0.0 \end{bmatrix}^{T}$, we generate time-series data on the interval $t \in [0, 200]$. We use deep IRK-SINDy with a fully connected neural network architecture characterized by a periodic activation function, SIREN⁹², consisting of 3 hidden layers each containing 32 neurons, thereby providing a robust framework for capturing the periodic dynamics of the system on the long time intervals. We establish the thresholding value to be $\lambda =0.01$ and proceed to learn the governing equations in the space of polynomials up to degree 3, employing a total of 8 sequential thresholding iterations with 20, 000 epochs allocated for the first iteration, followed by 5, 000 epochs for each subsequent iteration, with a learning rate of $10^{-4}$ and $10^{-3}$ (Except for the case $m = 101$ that we utilize $5\times 10^{-4}$) for the DNN and the coefficient matrix $\xi$ in the first iteration, respectively.

Fig. 6

Fitz-Hugh Nagumo model: a comparison of the reference model and recovered models using data collected at constant time stepsize. (a) Phase portraits, (b) coefficient matrices for $m\in \{ 2001, 401, 201, 101 \}$. IRK-SINDy results a parsimonious and generalizable model for biologically motivated models such as FHN even in data scarcity.

In Figure 6, we present a comparative analysis of our proposed methodology against the performance of Conv-SINDy and RK4-SINDy, for various values of m. The incorporation of a periodic activation function within the DNN architecture significantly enhances the model’s capability to effectively learn from periodic data⁹³, which is of paramount importance for accurately predicting the stage values associated with the IRKs. Consequently, as illustrated in Figure 6, it becomes evident that deep IRK-SINDy demonstrates a markedly reduced dependence on the quantity of data points compared to the two alternative methodologies, thus revealing its superior efficacy in reconstructing the dynamics of the FHN model.

Lorenz attractor

Here, to explore the efficacy of deep IRK-SINDy in identifying chaotic dynamics, we examine the nonlinear 3D Lorenz system⁹⁴ as the next illustrative example. A distinctive characteristic of this system is its sensitivity to initial conditions, which makes it a prominent candidate within the field of data-driven discovery of dynamical systems. The governing equations of this system are given as eq. ():

$$\begin{aligned} \dot{x}(t) = 10 (y(t) - x(t)), \end{aligned}$$

(22a)

$$\begin{aligned} \dot{y}(t) = x(t) (28 - z(t)) - y(t), \end{aligned}$$

(22b)

$$\begin{aligned} \dot{z}(t) = x(t) y(t) - {8 \over 3} z(t). \end{aligned}$$

(22c)

Utilizing the initial condition$\begin{bmatrix} x(0)&y(0)&z(0) \end{bmatrix}^{T} = \begin{bmatrix} -8&7&27 \end{bmatrix}^{T}$, we conduct measurements on the time interval $t \in [0, 10]$ with different sample sizes m. We employ a DNN comprising one hidden layer with 256 neurons to represent the nonlinear dynamics at the stage values of IRKs with the periodic activation function SIREN. For the sequential thresholding procedure, we use 10 thresholding iterations, commencing with 20, 000 epochs in the first iteration and 2, 000 epochs in the subsequent iterations, with a thresholding parameter set at $\lambda =0.5$. During the training phase, we adopt a learning rate of $10^{-3}$ for the DNN parameters and a learning rate of $10^{-2}$ for the coefficient matrix while searching for active terms in the space of polynomials up to degree 2. Moreover, at the end of each iteration, both learning rates are diminished by specific scales. It is important to note that due to the very large standard deviation of the state variables (significantly exceeding 1), the library of polynomials may become ill-conditioned, thereby disrupting the optimization process. Therefore, prior to initiating the learning process, it is necessary to preprocess the data through scaling or normalization. This procedure is conducted such that the transformed data exhibits a mean of 0 and a variance of 1⁶⁷. It is crucial that the scaling of the data does not influence the interaction among the state variables, thus, the sparsity of the identified dynamics remains consistent with that of the reference dynamics. Under the same configuration, we repeat this numerical experiment for the scenario where $1\%$ noise is added to the data.

Fig. 7

Lorenz attractor model: a comparison of the reference model and recovered models using data collected at constant time stepsize in the cases (a) noise free, (b) 1 percent noise $\sigma =0.01$,.

All three approaches IRK-SINDy, RK4-SINDy and Conv-SINDy are able to correctly identify the active nonlinear features, while the coefficient matrix obtained from IRK-SINDy is closer to the coefficients of the reference model. However, the Lorenz system has a positive Lyapunov exponent and small differences between the reference and discovered models cause exponential growth in the forecasted differences. As evidenced in Figure 7, although small deviations in the dynamic coefficients significantly affect the dynamics due to the highly chaotic behavior of the system, the bi-stable structure of the attractor is well captured even in presence of noise. While Figure 7 shows that IRK-SINDy discovers more robust and parsimonious models against noise.

Lotka-Volterra predator-prey model

Next, we examine the Lotka-Volterra equations, which describe the predator-prey dynamics, and have recently been employed extensively as a significant biologically motivated benchmark problem in the data-driven discovery of the governing equations in biological systems^19,23,95. This is crucial due to the fact that the predator-prey dynamics serve as the cornerstone for numerous mathematical models within the investigation of biological systems, particularly in the field of systems biology of cancer (where cancer cells are conceptualized as prey and the immune system as the predator)^21,22. In this context, we demonstrate the usefulness of proposed approach in identifying the Lotka-Volterra equations given by eqns. () that describe the interaction between two species, denoted as u for prey and v for predator:

$$\begin{aligned} \dot{u}(t) = \alpha u(t) - \beta u(t) v(t), \end{aligned}$$

(23a)

$$\begin{aligned} \dot{v}(t) = - \gamma v(t) + \delta u(t) v(t), \end{aligned}$$

(23b)

The time-series data are generated through solving the reference differential equation by parameters $\{\alpha = {2 \over 3}, \beta = {4 \over 3}, \gamma = \delta = 1\}$ on the time interval $t \in [0, 10]$ with the initial condition $[u(0), v(0)]^{T} = [1.8, 1.8]^{T}$. By setting the thresholding value $\lambda =0.1$, we employ deep IRK-SINDy using the SIREN periodic activation function alongside an architecture comprising 2 hidden layers, each containing 64 neurons, to discover the governing differential equations across different data quantities m. This approach, incorporating learning rates of $10^{-3}$ and $10^{-4}$ during the first iteration for $\xi$ and $\theta$, respectively, through sequential thresholding with 3 iterations that is employed 6, 000 epochs in each iteration (except 25, 000 epochs for the first iteration), successfully captures the correct active terms within the nonlinear feature library, which in this illustrative example is selected as a polynomial space of up to degree 2. In Figure 8, the obtained models are tested on the time interval $t \in [0, 20]$ and the efficacy of deep IRK-SINDy under data scarcity is depicted.

Fig. 8

Lotka-Volterra model: a comparison of the reference model and recovered models using data collected at constant time stepsize. (a) Phase portraits, (b) coefficient matrices for $m\in \{ 801, 101, 51, 31 \}$. Compared to Conv-SINDy and RK4-SINDy, IRK-SINDy produces a sufficiently sparse, interpretable and generalizable model.

Logistic growth model

In the last numerical experiment, we study the discovery of the governing equations for tumor growth. Despite the extensive advancement of various effective mathematical models within the realm of mathematical oncology, in this context, we exclude the high dimensionality and the consideration of complex tumor-immune interactions, directing our attention exclusively towards the well-established logistic growth model. This nonlinear model is a modified exponential growth model by taking into account the carrying capacity of the system, which is particularly crucial for accurately modeling the mechanisms underlying tumor growth⁹⁶. The general form of this nonlinear dynamical system is given by eq. (24):

$$\begin{aligned} \dot{T}(t) = r T(t) (1 - {T(t) \over K}) = a T(t) - b T^{2}(t), \end{aligned}$$

(24)

where T(t) signifies the temporal evolution of tumor concentration, while r and K represent the growth rate and carrying capacity, respectively. To generate data, we assign tumor-specific parameters of $r=0.31$ and $K=2$, conducting measurements under the initial condition $T(0)=0.1$ over the time interval $t \in [0, 50]$. We set the thresholding value to $\lambda =0.025$ and consider the polynomial space of up to order 5 to serve as our nonlinear feature library. Throughout four successive thresholding iterations, with 20, 000 epochs allocated to the first iteration and 5, 000 epochs to each of the subsequent iterations, we simultaneously identify the active terms in the library while training the neural network. The DNN employed in this experiment comprises 3 hidden layers, each containing 32 neurons, utilizing the $\tanh$ activation function. We use a learning rate of $10^{-3}$ in learning $\xi$ and a learning rate of $10^{-4}$ in learning $\theta$ to discover the governing equations with varying values of m. Figure 9 depicts the superior efficacy of deep IRK-SINDy in comparison to the RK4-SINDy and Conv-SINDy methodologies. All hyperparameters and neural network architectures in these six illustrative examples are detailed in Table 5.

Fig. 9

Logistic growth model: a comparison of the reference model and recovered models using data collected at constant time stepsize. (a) Phase portraits, (b) coefficient matrices.

Table 5 Summary of hyperparameters and neural network configurations for all numerical experiments.

Conclusion

We have proposed an implicit Runge-Kutta based sparse identification of nonlinear dynamics, representing a new class of data-driven methods for discovering the governing equations of nonlinear dynamical systems from sparse and noisy datasets. Our innovative methodology, by integrating Gauss methods as a subclass of A-stable IRK methods by the highest accuracy with sparse regression, has demonstrated an impressive capability to directly encode the physical laws and biological mechanisms governing a specified dataset into a system of differential equations. In this work, we develop data-driven algorithms that are independent of derivative information and exhibit high robustness to data scarcity. The major challenge of these algorithms pertains to the computation of the stage values of IRKs, which has led to two general approaches: (a) iterative schemes for solving systems of nonlinear algebraic equations, including fixed-point and Newton’s iterations, and (b) deep neural networks. The resultant algorithms have evidenced promising outcomes across a diverse family of benchmark problems in the field of data-driven discovery of differential equations, particularly those with biological motivation. This framework opens a new path for applying the integration of three pivotal techniques-numerical methods for solving differential equations, sparse regression, and deep learning-to directly model physical and biological phenomena from datasets.

Nevertheless, it is essential to acknowledge that the application of these algorithms to benchmark problems has revealed impracticality of approach (a) due to the computational complexity and the execution time of the algorithm. This is why approach (b) was designed and has successfully demonstrated its efficacy through the appropriate selection of neural network architecture. Deep IRK-SINDy, when applied to benchmark problems such as the two-dimensional damped harmonic oscillatory systems, FitzHugh-Nagumo model, Lorenz attractor, predator-prey dynamics, and logistic growth, has outperformed RK4-SINDy, which was similarly introduced by integrating the fourth-order Runge-Kutta method with sparse regression, as well as the conventional SINDy in the case of data scarcity. Throughout this study, it was revealed that these algorithms are resistant to noise. In this work, the Savitzky-Golay filter was employed to reduce noise and enhance the fidelity of the discovered equations.

Although this work has produced highly promising results, it is likely that the reader would concur that the number of questions engendered by this investigation significantly exceeds the answers it provides. Which neural network architecture is optimally suited for a particular dataset? How can parametric dynamical systems, dynamical systems incorporating control terms, and equations including rational terms be effectively identified using the IRK-SINDy framework? How can this method be used to discover the governing equations for systems involving partial derivatives? Is the mean-squared error the most appropriate choice for the loss function? How can we develop algorithms that maintain robustness in the face of high noise levels within scenarios characterized by data scarcity, particularly considering the recent advancements in neural network architectures?

Certainly, in light of the numerous challenges present, further research is needed to establish a robust foundation in this field. Finally, the principal factor contributing to the robustness of IRK-SINDy n the context of data scarcity is related to the reduced stepsize constraints in A-stable methods and the high accuracy of IRK methods. In the future, we would like to extend the proposed framework through employing alternative high-order implicit methods that possess lower computational cost and data-independent implementations, thereby facilitating integration with sparse identification in such a way that approach (a) becomes practical and approach (b) more efficacious. Furthermore, data-driven discovery of governing PDEs using IRK-SINDy could be a possible research direction in e.g. pattern formation.