Multi-scale spatio-temporal graph neural network for urban traffic flow prediction

Abstract

The Urban traffic flow is affected by both internal supply and demand changes and external random disturbances, and during its continuous spatiotemporal propagation, these factors overlap with each other, presenting a highly non-linear and complex spatiotemporal pattern, which poses a huge challenge to traffic flow prediction. In response to the above challenges, this paper proposes a novel Spatio-Temporal Graph neural network with Multi-timeScale (abbreviated as STGMS). In STGMS, a multi-timescale feature decomposition strategy was designed to decompose the traffic flow into signals at multiple timescales and residuals. A unified spatio-temporal feature encoding module was designed to integrate the spatiotemporal features of traffic flow and the interaction features of multi-timescale traffic flows. Finally, the mapping from the multi-timescale spatiotemporal feature encoding to the future traffic flow was learned. We conducted numerous experiments on four real-world datasets and compared them with eleven baseline models from the past three years. The results show that the performance of our model outperforms the current state-of-the-art baseline models. On the four datasets, the average improvement rates of the three prediction accuracy metrics, namely the Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE), reach 17.69%, 15.65%, and 10.30% respectively.

Introduction

Urbanization and the fast-growing urban population have led to traffic congestion in major global cities. This not only causes inconvenience to people’s work and life but also brings issues such as a higher accident rate, a less reliable travel time, higher fuel consumption, air pollution, and the degradation of social health. To solve these problems, countries are looking for ways to ease traffic congestion. Analyzing the spatio-temporal evolution law of historical traffic flow to predict the future trend of urban traffic flow, thereby assisting people in planning travel routes reasonably and helping traffic management departments to formulate traffic control and emergency guidance plans, etc., is one of the important means to alleviate traffic congestion^1,2.

With the development of intelligent transportation technology, urban road traffic flow prediction research has attracted scholars. In urban traffic, flow spreads in time and space, with road traffic flows interacting and coupling spatio-temporally, showing complex correlations¹. Road traffic flow contains multi-scale temporal signals and random external-factor-disturbed signals³, resulting in highly non-linear and non-stationary features, which pose great challenges to urban traffic flow prediction.

In the process of exploring the complex spatio-temporal evolution characteristics of traffic flow, scholars have proposed numerous methods, striving to accurately extract and simulate its temporal and spatial dependence relationships. In the early stage, some scholars regarded road network traffic flow as a multi-dimensional time series⁴. By means of statistical models¹ and machine learning models², they attempted to study the temporal variation patterns of traffic flow. However, such methods overlooked spatial information, making it difficult to effectively simulate the complex and dynamic changes of urban traffic flow. With the rise of neural network technology, its powerful feature extraction and non-linear fitting capabilities have attracted attention in the field of traffic flow prediction. Scholars use RNN⁵, GRU^6,7, or LSTM⁸ to construct temporal models to explore the temporal correlations of traffic flow; and adopt GCN^7,9,10 or GAT^11,12,13,14 to design spatial models to capture the spatial dependence characteristics of traffic flow. To capture both temporal and spatial dependence characteristics simultaneously, scholars combine temporal and spatial models to construct combined spatio- temporal models, such as DeepSTUQ⁷, ST-PEF+¹¹, Auto-DSTSGN¹⁵, and IST-Net¹⁶. These models use independent networks to extract temporal and spatial characteristics respectively and then integrate them for prediction. However, they do not consider the correlation between the two from the perspective of spatio-temporal integration, and some of them also have the problem of low late-stage integration efficiency. Therefore, researchers start from the network structure and design fusion spatio- temporal models that deeply integrate spatio-temporal dependence, such as STJGCN¹⁷, ST-Ware¹⁸, STGSA¹⁹, and DSTAGNN²⁰. Compared with combined spatio-temporal models, fusion spatio-temporal models can learn the interdependent characteristics of time and space and simulate a more realistic traffic flow evolution trend. However, most current research still ignores the multi-periodicity of traffic flow.

In recent years, the powerful feature extraction, multi-source information fusion, and knowledge reasoning capabilities of large language models (LLMs) have also attracted widespread attention in the field of traffic flow prediction. Some traffic flow prediction models^21,22,23,24 that apply large language models have been successively proposed. The powerful data processing and knowledge reasoning capabilities of large language models can help complete the missing traffic data and extract complex patterns in traffic, which can contribute to improving the prediction accuracy of the models. Nevertheless, large language models also have problems such as high computational complexity leading to large latency, poor interpretability, and difficulty in handling complex spatio-temporal dependency relationships.

To analyze the complex multi-periodicity of traffic flow, scholars have proposed various decomposition strategies. The Seasonal-Trend Decomposition method³ aims to reveal the internal laws of data by decomposing traffic flow time series into seasonal, trend, and residual components. However, this method is based on the assumption of linearity and stationarity of time series, which fundamentally contradicts the nonlinear and non-stationary characteristics of traffic flow. Additionally, it suffers from limitations such as insufficient capability to handle aperiodic features, difficulty in separating the superposition effects of different cycles, and a high dependence on the statistical characteristics of historical data during decomposition, leading to restricted application scenarios. As an adaptive decomposition technique for nonlinear and non-stationary sequences, the Empirical Mode Decomposition method²⁵ possesses advantages such as strong adaptability, multi-scale analysis, and prominent nonlinear fitting capability. Nevertheless, since this method still relies on the statistical characteristics of historical data for decomposition, it cannot ensure the consistency of time scales in modal decomposition of traffic flow time series across different time windows, thus limiting its applicability in continuous traffic flow prediction tasks. Furthermore, some studies represent traffic flow as sequences of fixed time scales (e.g., ”week”, ”day”, ”hour”) through statistical analysis²⁶, but this fixed division fails to effectively distinguish the internal periodicity of traffic flow from random fluctuations caused by external factors. Another category of methods, such as decomposing traffic flow into fixed flow and diffusion flow²⁷, or using wavelet transform²⁸ to achieve multi-scale feature analysis through decomposition from time-domain signals to frequency-domain signals: the former faces issues of insufficient adaptability to nonlinear traffic flow and model failure in dynamic scenarios, while the latter encounters challenges such as difficulty in basis function selection and failure in nonlinear signal analysis.

To address urban traffic flow prediction challenges and research gaps, we innovatively propose STGMS, a spatio-temporal graph neural network for accurate prediction. In order to capture the spatio-temporal features in the continuously generated traffic data promptly and accurately, and further achieve the continuous prediction of traffic flow, we design an online-decomposing algorithm that splits data into multi-timescale traffic flow feature sequences and an external random-disturbance signal. Then, we apply spatio-temporal attention and graph convolutional neural networks to these multi-scale features, comprehensively learning their complex interactions and capturing spatial dependencies. Finally, a fully-connected neural network maps the multi-timescale spatio-temporal feature encoding to future traffic flow sequences, enabling accurate prediction. In summary, the main contributions of this paper are as follows:

• We designed a multi-time decomposition strategy capable of dynamically configuring time scales, and organically integrated the attention mechanism and graph convolutional networks, thus constructing a STGMS suitable for continuous traffic flow prediction.

• We developed a unified spatio-temporal feature encoding module, which is used to handle the spatio-temporal dependency relationships of traffic flow under different time scales and the correlation relationships of traffic flow across time scales.

• On four real-world datasets, STGMS outperforms benchmark models, with average improvements of 17.69%, 15.65%, and 10.30% on MAE, RMSE, and MAPE respectively.

Concepts and problem definition

In this section, we will first introduce the basic concepts of urban traffic flow prediction and then put forward the problem to be studied.

Definition 1

(Urban traffic network) An urban traffic network consists of intersections and connecting roads, with the vehicle allowed passing direction on a road being its direction.

Definition 2

(Road traffic graph G) We use a directed graph $G=(V,E,A)$ for the topological structure of an urban road traffic network. $V=\{v_1,v_2,\dots ,v_N\}$ are the N intersections in G, $E\subset V\times V$ is the set of roads, and $A\in {0,1}^{N\times N}$ is the adjacency matrix. If $e=\langle v_i,v_j\rangle \in E$, $A_{ij}=1$ (a road from $v_i$ to $v_j$); if not, $A_{ij}=0$ .

In an urban traffic network, traffic sensors at each intersection monitor road traffic. The number of vehicles passing through an intersection per unit time is the traffic flow on the corresponding road. Continuous observation gives a traffic flow sequence for each intersection over time.

Definition 3

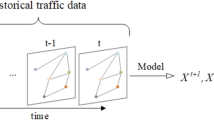
(Traffic flow tensor X) We use the tensor $X_{t-T+1:t}\in R^{N\times D\times T}$ to represent the continuous traffic flow observations at each intersection in G over T consecutive time units up to time t. $X_t\in R^{N\times D}$ is the traffic flow set at time t, D is the number of traffic flow features, initially $D=1$.

Based on the above concepts, our goal is to study an encoder $f(\cdot )$ and a spatiotemporal decoder $g(\cdot )$ that capture the spatiotemporal characteristics of urban traffic flow. We aim to learn spatiotemporal dependencies and predict the urban network’s traffic flow in the next H time units. The encoder $f(\cdot )$ learns from $X_{t-T+1:t}$ to get $Y_{t-T+1:t}\in R^{N\times D\times T}$, which describes traffic flow evolution, and $D'$ represents the number of feature channels in the encoding of traffic flow features. The decoder $g(\cdot )$ predicts $\hat{Y}_{t:t+H}$ based on $Y_{t-T+1:t}$.

Given the loss function $\mathcal {L}(\cdot )$, the urban traffic flow prediction problem can be formally represented as follows Eq. 1:

$$\begin{aligned} f^*,g^*=\mathop {\arg \min }{f,g}\sum _{h=1}^{H}{\mathcal {L}\Big (g\big (f(X_{t-T+1:t}),X_{t+1:t+H}\big )\Big )} \end{aligned}$$

(1)

Here, $f^*$ and $g^*$ are optimized encoder and decoder. $g\big (f(X_{t-T+1:t})\big )=\hat{Y}_{t+1:t+H}$ is the predicted traffic flow, and $X_{t+1:t+H}$ is the observed one.

Spatio-temporal graph network with multi-timescale

Overall framework

In urban traffic networks, the multi-periodicity of road traffic demands and random external disturbances interact, endowing traffic flow time series with highly nonlinear and non-stationary characteristics. To differentially analyze the spatio-temporal evolution of various road traffic demands under different cycles and effectively simulate traffic flow’s inherent spatio-temporal features, we propose the Spatio-Temporal Graph network with Multi-timeScale (abbreviated as STGMS).

Fig. 1

The overall framework of STGMS.

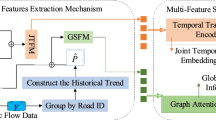
As in Fig. 1, the STGMS model has three main components: data Preparation, continuous spatio-temporal encoding, and spatio-temporal decoding. Given an urban traffic flow tensor $X_{t-T+1:t}$ and topological features of the traffic network $G=(V,E,A)$, we first decompose the traffic flow time series features based on $[P_1,\cdots ,P_m]$ for multi-timescale feature representation, and generate Chebyshev polynomial coefficients from the adjacency matrix A. Then, the multi-layer STBlock extracts and encodes the traffic flow’s inherently coupled spatio-temporal dependent features. It mines hidden relationships using the spatio-temporal attention network and Chebyshev graph convolution network, generating a multi-timescale spatio-temporal feature encoding of historical traffic flow. Finally, based on this encoding, we predict the traffic flow volume in the next H time units. Next, we’ll detail each model component.

Data preparation

Time feature decomposition

Due to the operational characteristics of urban transportation systems and diversified travel demands, multiple periodic trend features often overlap and are interfered by random factors, causing traffic flow to exhibit significant nonlinear and non-stationary characteristics. To analyze the internal trends of traffic flow under different time cycles, it is necessary to decompose various periodic sequences and residual components from complex and changeable traffic flow signals. However, existing seasonal trend decomposition methods and empirical mode decomposition methods both assume that time series signals are linear and stationary, which contradicts the actual non-stationary characteristics of traffic flow. In addition, these two types of algorithms rely on the statistical characteristics of historical data, making them only suitable for offline processing of static traffic flow sequence data. To overcome the limitations of the above methods, this paper proposes a trend decomposition method based on moving average of sliding time windows. This method can real-time capture random fluctuations caused by external factors such as traffic incidents and holidays, and is not constrained by the statistical characteristics of long-term historical data. It can online decompose nonlinear and non-stationary traffic flow sequences into the superposition of multi-time scale periodic sequences and residuals.

Given the urban traffic flow tensor $X\in R^{N\times D\times T}$ (where N is the number of traffic network nodes like intersections, D is the number of traffic feature channels, and T is the input traffic flow length), and a set of periods $P=[P_1,\cdots ,P_m]$ sorted in descending order of magnitude, we can decompose m periodic time features $X^1,\cdots ,X^m$ representing different time scales and a residual $S^m$ from the original traffic flow sequence X in the order from the largest to smallest period.

$$\begin{aligned} {\left\{ \begin{array}{ll} X_t^i=\frac{1}{P_i}\sum _{k=t-P_i+1}^{t}{S_k^{i-1}}\\ S^i=S^{i-1}-X^i \end{array}\right. } , where\ i=1,\cdots ,m \end{aligned}$$

(2)

Initially, let $S^0=X$. As shown in Eq. 2, we first use the moving average method to calculate the mean of all data in the time window $[t-P_1+1,t]$ of the traffic flow data sequence $S^0$, so as to obtain the value, $X_t^1$, of the traffic flow time feature with period $P_1$ at time t, and then obtain the traffic flow time feature sequence $X^1$ with period $P_1$. Subsequently, we define $S^1=S^0-X^1$, which represents the residual after the first periodic feature decomposition of the traffic flow. By repeating the above steps, we can sequentially decompose the periodic time feature sequences $X^2,\cdots ,X_m$ with periods $P_2,\cdots ,P_m$ from the traffic flow, and finally obtain the residual $S^m$.

After getting m periodic features $X^1,\cdots ,X^m$ and the residual $S^m$, they are concatenated as in Eq. 3 to obtain the traffic flow’s multi-timescale feature representation.

$$\begin{aligned} Y=concat(X^1,\cdots ,X^m,S^m) \end{aligned}$$

(3)

Based on this multi-periodic spatiotemporal feature representation, we design a unified spatiotemporal feature extraction module. It can encode traffic spatiotemporal features of different time cycles and learn cross-temporal and spatial interaction features of traffic flows in different time cycles.

Generate Chebyshev polynomial coefficients

In graph convolutional neural networks, in order to simplify the computational complexity of the eigenvalue decomposition of the Laplacian matrix $L_G$ of the traffic network G, we use the K order Chebyshev polynomial to approximately replace the eigenvalue polynomial of the matrix $L_G$. As shown in Eq. 4 below, the K order Chebyshev polynomial can be generated through iterative computation.

$$\begin{aligned} Ch_i(L_G)=2L_GCh_{i-1}(L_G)-Ch_{i-2}(L_G) \end{aligned}$$

(4)

In the above formula, $i=1,2,\cdots ,K$, and the i-th order Chebyshev polynomial coefficient $Ch_i$ is only related to the $i-1$-th and $i-2$-th order coefficients and the graph Laplacian matrix $L_g$, and initially $Ch_1(L_G)=L_g$, $Ch_0(L_G)=0$.

STBlock: spatio-temporal feature encoding with multi-timescale

During traffic flow’s continuous spatio-temporal propagation, its temporal and spatial features interweave, forming complex correlations. Next, we’ll analyze these spatio-temporal correlations in traffic flow and design methods for extracting and encoding its spatio-temporal features.

Definition 4

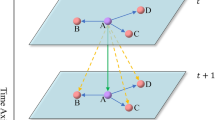
(Spatio-temporal Correlation Relationship) The relationship where traffic flows at each intersection in transportation network G interact and are interdependent in temporal and spatial dimensions is defined as the spatio-temporal correlation relationship among traffic flows.

Based on spatio-temporal scale differences in interaction and interdependence, we divide traffic flow’s spatio-temporal correlation into local and global ones. The local one characterizes traffic flow dependence within the local spatio-temporal scope of the transportation network, while the global one describes similarity across the entire network and observed time span.

Spatio-temporal feature fusion

In the STGMS model, we use the spatio-temporal attention network and graph convolutional neural network to design the STBlock module for extracting traffic flow’s spatio-temporal correlation features. This module extracts and integrates global temporal, global spatial, and local spatial dependencies in traffic flow.

First, with the temporal attention mechanism, we learn and integrate multi-timescale traffic flow feature interdependencies in the global time domain. Given $Y\in R^{N\times D\times (m+1)T}$, we design $Tan(Y)=V_t\cdot \sigma ((YW_t^1)W_t^2(W_t^3Y)^T+b_t)$ to learn time-domain similarity, where , $W_t^1\in R^N$, $W_t^2\in R^D\times N$, $W_t^3\in R^D$, $V_t\in R^{(m+1)T\times (m+1)T}$ and $b_t\in R^{(m+1)T\times (m+1)T}$ are the parameters to be learned. Then, $Att_t=softmax(Tan(Y))$ and $Y_1=Y\cdot Att_t$ integrates global temporal correlations.

Next, for $Y_1\in R^{N\times D\times (m+1)T}$, we use the spatial attention mechanism. Design $San(Y_1)=V_s\cdot \sigma ((Y_1W_s^1)W_s^2(W_s^3Y_1)^T+b_s)$ to learn spatial-domain similarity, where $W_s^1\in R^{(m+1)T}$, $W_s^2\in R^D\times {(m+1)T}$, $W_s^3\in R^D$, $V_s\in R^{N\times N}$ and $b_s\in R^{N\times N}$ are parameters to be learned. Then, $Att_s=softmax(San(Y_1))$ and $Y_2=Att_s\cdot Y_1$ integrates global spatial correlations.

Finally, for $Y_2\in R^{N\times D\times (m+1)T}$, we use the Chebyshev graph convolutional network $ChebNet(Y_2,K,G)=\sum _{i=0}^{K}{\theta _iCh_i(L_G)Y_2}$ to aggregate local-space traffic flow features, where K represents the order of the Chebyshev polynomial, $Ch_i$ represents the i-th order Chebyshev polynomial coefficient, $L_G$ represents the Laplacian matrix of the road traffic network G, and $\theta _i$ is the parameter to be learned.

In summary, in the STBlock module, we extract and fuse global time-space correlations and local spatial dependencies in urban traffic flow using the spatio-temporal attention mechanism and graph convolutional neural network, getting a multi-timescale spatio-temporal feature representation Z. We define this process as $\Phi (\cdot )$ in Eq. 5.

$$\begin{aligned} Z=\Phi (Y,G,K,Ch,\Theta ) \end{aligned}$$

(5)

where $\Theta =\{\theta , W_t^1, W_t^2, W_t^3, V_t, b_t, W_s^1, W_s^2, W_s^3, V_s, b_s\}$ is the set of all parameters to be learned.

In urban traffic, upstream traffic disperses into downstream roads by weights. After merging with downstream traffic, it continues flowing, affecting traffic in a wider spatio-temporal range.

To extract high-order non-linear spatio-temporal features, we build a deep neural network using multiple STBlock modules. It can simulate spatio-temporal dependencies and alleviates the gradient vanishing problem via a residual network between adjacent STBlock modules. The output of the i-th layer is $Z^{(i)}=\Phi ^{(i)}(Z^{(i-1)},G,K,Ch,\Theta ^{(i-1)})$, with $Z^{(0)}=Y$ (multi-timescale traffic flow features) at initialization.

Spatio-temporal feature decoding

After deep fusion, we get multi-cycle deep spatio-temporal feature encoding $Z\in R^{N\times (m+1)T}$. A fully-connected neural network learns a weight matrix $U\in R^{(m+1)T\times H}$ to map Z to future traffic flow prediction $\hat{Z}\in R^{N\times H}$ ($\hat{Z}=Z\cdot U$). To improve accuracy, we use the loss function $\mathcal {L}(\cdot )$ for training:

$$\begin{aligned} \mathop {\arg \min }_{f,g,\Theta _f,\Theta _g} \mathcal {L}(f^*,g^*,\Theta _f^*,\Theta _g^*)=\frac{1}{N}\!\frac{1}{H} \sum _{i=1}^{N}{\!\sum _{h=1}^{H}{\mathcal {L}\Big ( g_h^i\big ( f(X_{t-T+1:t},G,\Theta _f),\Theta _g \big ),X_{t+h}^i \Big )}} \end{aligned}$$

(6)

Here, $f(X_{t-T+1:t},G,\Theta _f)$ is the multi-timescale spatio-temporal feature encoding of historical traffic flow; $g_h^i(\cdot )$ is the future traffic flow prediction at the i-th intersection, and $X_{t+h}^i$ is the observed value. $\Theta _f$ and $\Theta _g$ are the parameters for the encoding function f and the decoding function g respectively. $f^*$, $g^*$, $\Theta _f^*$ , and $\Theta _g^*$ represent the optimized encoder, decoder, encoder parameters, and decoder parameters respectively.

Experimental study

Experimental dataset and setup

We validate STGMS on four publicly available traffic network datasets: PEMS03, PEMS04, PEMS07, and PEMS08, from the Caltrans Performance Measurement System (PeMS). Aggregated into 5-minute intervals, each dataset has 288 daily traffic flow data points. To ensure a fair comparison, we split each dataset into training, validation, and test sets at a 6:2:2 ratio, and then randomly batch the data. The main default model parameters include: traffic flow input and prediction length of 12, 2 layers in the spatio-temporal feature encoding network, Chebyshev polynomial order 3, batch size 32, graph convolutional network kernel size 64. During the model training phase, consistent with the methods in^11,20,29, we employed the Adam optimizer to conduct the training of the model. The learning rate was set at 0.001, and the number of training epochs was set to 200. Additionally, to enhance the model’s nonlinear fitting ability, we introduced Sigmoid and ReLU as activation functions into the model and applied the Dropout regularization technique. To evaluate the performance of the STGMS model, as shown in Table 1 below, we selected eleven representative models from the research conducted in the past three years as baseline methods and compared them with the STGMS model.

Table 1 The Computation cost on the PEMS04 dataset.

All experimental programs were implemented based on Python 3.1.2 and Torch 2.5.0, and the servers used were from the AutoDL cloud service platform (www.autodl.com). Specifically, for the PEMS03, PEMS04, and PEMS08 datasets, we selected Linux servers equipped with Intel Xeon(R) Gold 6430 CPUs and NVIDIA RTX 4090 GPUs. For the PEMS07 dataset, however, we adopted servers equipped with Intel Xeon(R) Gold 6430 CPUs and NVIDIA A800 GPUs. For each dataset, we conducted at least 10 independent experiments and reported the average performance. In the experiments, the Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE) were used to evaluate the accuracy of the model.

Effectiveness of periodic feature decomposition

We designed and conducted experiments to analyze traffic flow time-feature decomposition. By comparing the impact of feature decomposition on traffic flow prediction accuracy across different time periods or combinations, we aimed to assess its effectiveness. The time periods included 1-hour, 2-hour, 4-hour, 8-hour, daily, and weekly, denoted as ‘1’, ‘2’, ‘4’, ‘8’, ‘D’, and ‘W’ respectively. We used ‘o’ to represent no periodic feature decomposition for comparison, exploring the impact of periodic features on model performance.

Fig. 2

Model accuracy under different time-scale feature decompositions: (a) Model accuracy with single or no time-scale feature decomposition operation; (b) Model accuracy with gradually increasing larger time scales starting from smaller one; (c) Model accuracy with gradually increasing smaller time scales starting from larger one; (d) Model accuracy when arbitrarily selecting three time scales. The time scales used in this experiment cover 1H, 2H, 4H, 8H, D, and W.

First, we performed feature decomposition with a single time period to analyze each period’s effectiveness. Results in Fig. 2a show that the use of any single time period to decompose traffic flow time features can improve model prediction accuracy to some extent. This indicates traffic flow has multi-timescale features. Separating periodic time features effectively enhances the ability to learn traffic flow spatio-temporal features.

Secondly, we constructed time-period sets in two ways: adding long-term periods starting from short-term ones, and vice versa. Then, we used each set for traffic flow time-feature decomposition to explore multi-timescale feature decomposition effectiveness. Results in Fig. 2b,c show that either way can improve traffic flow prediction accuracy. Also, starting from short-term periods to add long-term ones leads to a faster accuracy increase. We draw two conclusions: multi-time-period decomposition uncovers more traffic flow spatio-temporal features for higher accuracy, and short-period combinations are better for learning these features than long-period ones.

Although multi-time-period decomposition boosts accuracy, more time periods mean more training parameters and longer training. To balance accuracy and efficiency, we group the six time periods into long-term ‘W’, ‘D’, medium-term ‘8’, ‘4’, and short-term ‘2’, ‘1’. Then, we pick one from each group to form a three-time-period set. We analyze prediction accuracy for all eight combinations through experiments. Figure 2d shows that the combination {‘W’, ‘4’, ‘1’} gives the highest accuracy. So, in subsequent experiments, the default time-period set for traffic flow time-feature decomposition is {‘W’, ‘4’, ‘1’}.

Computational performance

To evaluate the computational performance of the STGMS model, we conducted a series of experiments on the PEMS04 dataset. We compared the computational performance of the STGMS model with that of multiple baseline models, and the results are shown in Table 2. Through comparison, it was found that the STGMS model demonstrated certain advantages in terms of training time and average prediction time compared to the four baseline models.

Table 2 Computational cost of five methods on PEMS04 dataset.

By analyzing the technical frameworks adopted by each model, it can be seen that for the dynamic spatio-temporal attention part of the DSTAGNN model, its computational complexity has a quadratic relationship with both the length of the traffic flow sequence and the number of nodes. Therefore, its computational complexity is much higher than that of the other four models. Both the PDFormer and DEC-Former models employ a self-attention mechanism with relatively high computational complexity, which leads to their performance being slightly inferior to that of the STGMS model. When the ISTNet model realizes the interaction of spatio-temporal features through matrix operations, its computational complexity is relatively high, and it usually has a quadratic relationship with the number of nodes and the number of feature channels. As for the STGMS model proposed by us, its computational complexity mainly stems from the relatively long time required for the spatial graph convolution operation.

Comparison and result analysis

Table 3 presents the data prediction accuracy of the proposed STGMS model and eleven baseline models on four datasets. The best results are in bold, and the second-best are underlined. From the comparative experiments, we can draw the following conclusions:

Table 3 Performance comparison of different approaches on four datasets.

STGMS superiority: STGMS outperforms all benchmark methods in all dataset indicators. Compared to the second-best results on four datasets, STGMS’s average improvement rates in MAE, RMSE, and MAPE are 17.69%, 15.65%, and 10.30% respectively, showing its outstanding performance in traffic flow prediction.

Modeling method comparison: Enhanced spatio-temporal feature modeling methods outperform traditional ones in prediction accuracy, indicating that improving spatio-temporal feature modeling and increasing information extraction can boost model prediction ability.

Enhanced vs preprocessing methods: Despite enhancing spatio-temporal feature learning by increasing feature dimensions, enhanced methods have lower prediction accuracy than data preprocessing methods. This shows that data preprocessing or feature decomposition can better excavate data potential and offer a higher-quality data base for modeling.

In summary, traffic flow preprocessing or feature decomposition is crucial for prediction, as it can enhance spatio-temporal feature learning and prediction accuracy. Also, increasing the dimension of spatio-temporal feature learning without preprocessing can still improve the ability to learn dependeny features and prediction accuracy.

Ablation study

To fully verify the effectiveness of different components in STGMS, we carefully designed four variants of this method and conducted ablation experiments on the PEMS03, PEMS04, and PEMS08 datasets. Specifically, STGMS w/o TA, w/o SA, and w/o CN remove the temporal attention mechanism, the spatial attention mechanism, and the Chebyshev graph neural network respectively. These three variants explore the efficacy of the spatio-temporal attention mechanism and the Chebyshev graph convolutional network in spatio-temporal feature extraction and encoding. Also, we created STGMS w/o MP, which excludes multiple-period time feature decomposition, to verify its effectiveness in traffic flow prediction.

Table 4 Results of ablation experiments conducted on the dataset PEMS03, PEMS04 and PEMS08.

Table 4 shows the accuracy of different STGMS variants on PEMS03, PEMS04, and PEMS08 datasets. From the table: First, STGMS without multi-timescale feature decomposition (MP) performs much worse than the other three variants. This shows that multi-timescale feature decomposition significantly boosts STGMS’s ability to learn traffic flow’s internal spatio-temporal dependency features. Second, STGMS without the temporal attention network (TA) performs worse than those without the spatial attention network (SA) and the Chebyshev graph convolutional network (CN). This indicates that the temporal attention network is crucial for learning and encoding traffic flow spatio-temporal features. It can capture correlations among multi-timescale features and in the time dimension, vital for improving traffic flow prediction accuracy. Third, on the three datasets, the performance of STGMS without SA and without CN varies, but their performance change relative to the complete STGMS is small. This implies that while traffic flow spatial attention and spatial feature aggregation contribute to learning spatio-temporal dependencies, their contribution is much less than multi-timescale feature decomposition and the temporal attention mechanism.

In summary, the superior performance of multi-timescale feature decomposition validates our design. It analyzes traffic flow’s multi-periodicity to learn its internal spatio-temporal evolution features.

Traffic flow prediction errors analysis

To systematically explore the dynamic evolution mechanism of traffic flow prediction errors, this section is based on the PEMS08 dataset. A road intersection is randomly selected as the research object to compare and analyze the error characteristics between the predicted values and real values when the prediction horizons are set to 1, 4, 8, and 12, respectively. The specific results are shown in Fig. 3.

Fig. 3

Traffic flow prediction errors across different forecasting horizons.

First, from the analysis of the overall trend, regardless of the adjustment of the prediction horizon, the traffic flow prediction sequence output by the model can well fit the change trend of the real data. This indicates that the model has a good ability to capture the traffic flow trend and can effectively learn and reproduce the periodic fluctuation characteristics of traffic flow. Second, a statistical analysis of errors under different prediction horizons shows that when the horizon is 1, 4, 8, and 12, the mean absolute errors are 9.86, 12.77, 20.80, and 20.49, respectively, and the maximum absolute errors are 100.89, 148.82, 281.72, and 274.11 in sequence. The change trends of the two error indicators are consistent with the general laws of time series prediction. It is worth noting that when the prediction horizon increases from 8 to 12, the error growth rate slightly narrows, indicating that the model has stable anti-error accumulation capability in long-term prediction scenarios. Third, visual analysis of the error distribution reveals that the prediction error significantly increases when the traffic flow is in the peak-valley transition stage. This phenomenon mainly stems from two reasons: firstly, the traffic flow at peak-valley extreme points has significant nonlinear mutations, which puts forward higher requirements for the model’s nonlinear modeling capability; secondly, compared with the traffic flow changes in conventional periods, peak-valley points have sparse samples in the time series, making it difficult for the model to fully learn the traffic flow change patterns in extreme states. The combined effect of the above factors leads to the decline of prediction accuracy when the model processes the peak-valley transition area.

Parameters sensitivity study

In addition to exploring the impact of the set of time periods used for the time-feature decomposition of traffic flow, we also carried out several groups of experiments to analyze the effects of several key parameters in STGMS on the model’s prediction accuracy. These parameters include the number of layers of the STBlock module, the order of the Chebyshev polynomial, the prediction length , and the size of the graph convolution kernel, etc. The experimental results are shown in Fig. 4, from which we have the following findings:

Fig. 4

Sensitivity of key model parameters: (a) influence of the number of layers in the STBlock module on model accuracy; (b) influence of the number of Chebyshev polynomial coefficients on model accuracy; (c) influence of prediction horizon on model accuracy; (d) influence of the size of the convolution kernel in the graph convolutional network on model accuracy.

• (1) When the number of layers of the STBlock module increases from 1 to multiple layers, the model’s prediction accuracy improves significantly. However, when the number of layers of the STBlock module exceeds 2, the change in the model’s accuracy is not obvious, and it may even slightly decrease. This is because using multiple layers of the STBlock module can capture the spatio-temporal features of traffic flow in a broader time and space domain, thus helping to improve the prediction accuracy. But as the number of layers of the STBlock module continues to increase, problems such as gradient vanishing become more and more serious. The negative impacts brought about by this gradually offset or even exceed the learning advantages brought by the multi-layer network.

• (2) As the order K of the Chebyshev polynomial increases, the prediction accuracy of the model begins to improve significantly. When $K>3$, the model accuracy fluctuates slightly within a certain range. This is because when the Chebyshev polynomial is used to approximately replace the eigenvalue decomposition of the graph Laplacian matrix, the high-order coefficients represent the ability of the graph convolutional network to learn the detailed spatio-temporal features in traffic flow. When K increases starting from 2, due to the model learning more detailed spatio-temporal features, the prediction accuracy can be significantly improved. However, after the value of increases to a certain extent, if the high-order coefficients are continuously increased, although the Chebyshev graph convolutional network can learn more and more detailed spatio-temporal features, these newly learned spatio-temporal features may be either effective or ineffective, thus causing a slight fluctuation in the prediction accuracy of traffic flow.

• (3) When predicting the traffic flow in the next H time units based on the traffic flow data of the past one hour (with an input length of 12), if the value of H is less than 12 (i.e., within one hour), the model can learn the spatio-temporal variation characteristics of the traffic flow within H time units from the historical traffic flow data. Therefore, a relatively good prediction accuracy can be achieved. However, when the value of H is greater than 12, the one-hour historical traffic flow data input is insufficient to enable the model to learn the spatio-temporal characteristics of the traffic flow within H time units. Thus, as the value of H increases, the prediction accuracy will decrease rapidly. Even so, compared with other baseline methods in the comparative experiments, the accuracy of our STGMS model in predicting the traffic flow in the next 16, 18, and 32 time units is still higher than that of most baseline methods in predicting the traffic flow in the next 12 time units.

• (4) When the size of the convolution kernel in the graph convolutional network starts to increase from 1, the accuracy of traffic flow prediction initially shows a rapid upward trend, and then the rate of increase gradually slows down. When the size of the convolution kernel reaches 64, the accuracy reaches its optimal value. If the convolution kernel is further increased after this, the accuracy will slightly decrease. In the architecture of the graph convolutional network, the size of the convolution kernel is specifically characterized by the number of nodes participating in the local spatial feature aggregation. When the size of the convolution kernel is small, although the model can capture local detailed features, there are certain limitations in learning the traffic flow features of surrounding nodes. As the size of the convolution kernel increases, the model can aggregate the spatio-temporal features of traffic flow from more nodes, thus enhancing the feature representation ability of the model. However, after the convolution kernel is increased to a certain extent, if it is increased further, it may incorporate some features of nodes that are farther away and have no effect on traffic flow prediction, thus leading to a certain decline in the accuracy of traffic flow prediction.

Conclusion

In the field of urban transportation, the complex traffic supply-demand relationship and the characteristics of spatio-temporal propagation lead to highly nonlinear characteristics of traffic flow, which pose a severe challenge to accurate traffic flow prediction. To effectively address this problem, we propose a novel spatio-temporal graph neural network model, STGMS. The STGMS model can be deeply integrated with mainstream navigation systems such as Baidu Maps, Google Maps, and Bing Maps. By accurately predicting the future trends of urban traffic, it can scientifically and rationally plan travel routes for users, improving travel efficiency. Additionally, it can be integrated into the urban traffic management system to help traffic management departments anticipate potential traffic congestion in advance and provide strong support for urban traffic planning.

The time feature decoupling method applied to the STGMS model can perform online feature decomposition on continuously arriving traffic flow data, demonstrating certain advantages. However, STGMS still relies on the physical topological structure of the road traffic network. This, to a certain extent, restricts the applicability of the STGMS model. Looking ahead, we plan to improve the STGMS model from the following two aspects: Firstly, we will study the data-driven method for constructing the traffic network to reduce the model’s dependence on the physical topological structure of the traffic network. Secondly, we will explore the internal correlations among various traffic modes in urban transportation to enhance the model’s ability to predict traffic flow under mixed traffic modes.