Leveraging hybrid deep learning with starfish optimization algorithm based secure mechanism for intelligent edge computing in smart cities environment

Abstract

The Internet of Things (IoT) now appears in each domain, from smart cities to home applications. The widespread use of IoT is making its security a real concern. The past few years have revealed an extraordinary increase in computer-intensive applications. Such applications always make huge volumes of data that demand severe latency-aware computational processing abilities. While edge computing is one of the attractive technologies for balancing severe latency-related problems, its deployment produces novel tasks. Edge computing is an innovative model distinguished mainly by its mobility support, geo-distributed process, low latency, and context awareness. However, recent edge computing developments have begun to explore novel IoT potentials that are leveraged from a security perspective. Methods depend upon artificial intelligence (AI) and its subgroups, machine learning (ML) and deep learning (DL), are generally employed to develop a safe Intrusion Detection System (IDS) for IoT. This study proposes a Hybrid Deep Learning-Based Intrusion Detection for Edge Computing Using Starfish Optimization Algorithm (HDLID-ECSOA) technique. The main goal of the HDLID-ECSOA technique is to provide intelligent edge computing in smart cities using advanced optimization models. Initially, the data pre-processing employs the min-max normalization to convert and standardize raw data to improve the efficiency of models. Furthermore, the dingo optimizer algorithm (DOA) technique detects and chooses the most relevant features from input data. Moreover, integrating a convolutional neural network and bidirectional gated recurrent unit with a cross-attention mechanism (CNN-BiGRU-CrAM) technique is implemented for the classification process. To enhance model performance, the starfish optimization algorithm (SFOA) is used for hyperparameter tuning to select the optimal parameters for improved accuracy. A comprehensive experimentation analysis of the HDLID-ECSOA model is performed under the Edge-IIoT and ToN-IoT datasets. The experimental validation of the HDLID-ECSOA model portrayed superior accuracy values of 99.35% and 99.33% over existing techniques under the dual dataset.

Introduction

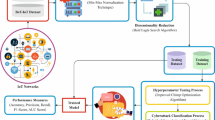
Smart cities are metropolitan regions utilizing data-driven technology to enhance residents’ sustainability, efficiency, and living standards¹. The concept of smart cities has recently attained substantial traction owing to the progression of IoT, AI, and big data. It has experienced a phenomenal increase in domain-specific applications, namely smart agriculture, healthcare, industry, and smart transportation systems, to enhance socio-economic improvement in recent times². These IoT methods are formed by various actuators, interconnected sensors, and network-enabled gadgets that can interchange diverse kinds of information through either Internet infrastructure or private networks³. The evolution of IoT gadgets has also improved the data system bandwidth. Nevertheless, IoT gadgets have constrained resources, making it challenging to perform the conventional security models for protecting systems against cyber-threats⁴. Thus, it is vital to present the multi-access edge computing (MEC), which permits the computation to be conducted at the edge of a system for tackling the resource-constrained issue in IoT networks. Figure 1 illustrates the architecture of edge computing in smart cities.

Fig. 1

Architecture of edge computing in smart cities.

Edge computing is an effective method of refining the execution of machines and gadgets, tackling the drawback of cloud computing (CC)⁵. Edge computing is a structure that combines storage, network services, and computing, which extends from CC to the edges of the network. In comparison with the services of CC, edge computing increases computing speed, reduces storage, improves data security, lowers latency bandwidth, and decreases location limitations by offloading certain computations to edge devices⁶. In edge computing, multiple gadgets will create vast amounts of data; edge computing offers effective, secure services for several end-users. IoT has turned the driving force of the existing industrial revolution and the method to gather live dependent information, making it crucial to take cybersecurity seriously⁷. Thus, there is a requirement for an IDS which can identify existing and upcoming threats to safeguard the IoT systems and networks made by it. The IDS for edge computing settings identifies intruders using signature-based and anomaly-based methods. The normal behaviour of this method is anomaly-based recognition that inspects the behaviour of incoming traffic and classifies it as both abnormal and normal depending on the constructed technique. Conversely, signature-based recognition relates incoming traffic to pre-determined guidelines⁸. Recently, various investigation report articles have advanced in the field of IDS for edge computing (EC) settings. Earlier investigations focused on DL and ML methodologies⁹. There have also been endeavours to apply sophisticated applications, namely a traditional recognition technique that permits the integration of outcomes of multiple classifications to enhance the performance of IDS effectively. Traditional ML models are unsuitable for utilizing large volumes of data, owing to the absence of annotated trained data and the higher prominence on recovered features gained by users¹⁰. DL, an innovative technology in ML, employs artificial neural networks (ANN) and exceeds classical models.

This study proposes a Hybrid Deep Learning-Based Intrusion Detection for Edge Computing Using Starfish Optimization Algorithm (HDLID-ECSOA) technique. The main goal of the HDLID-ECSOA technique is to provide intelligent EC in smart cities using advanced optimization models. Initially, the data pre-processing employs the min-max normalization to convert and standardize raw data to improve the efficiency of models. Furthermore, the dingo optimizer algorithm (DOA) technique detects and chooses the most relevant features from input data. Moreover, integrating a convolutional neural network and a bidirectional gated recurrent unit with cross-attention mechanism (CNN-BiGRU-CrAM) technique is implemented for the classification process. To enhance model performance, the starfish optimization algorithm (SFOA) is used for hyperparameter tuning to select the optimal parameters for improved accuracy. A comprehensive experimentation analysis of the HDLID-ECSOA model is performed under the Edge-IIoT and ToN-IoT datasets. The key contribution of the HDLID-ECSOA model is listed below.

• The HDLID-ECSOA method applies min-max normalization to scale input features within a consistent range, ensuring balanced input for the learning process. This improves training stability and accelerates convergence. It also mitigates the risk of bias from dominant features, improving the model’s more accurate and reliable performance.

• The HDLID-ECSOA technique utilizes the DOA method to effectually select the most relevant features from the dataset, eliminating redundant and irrelevant data. This enhances learning efficiency and mitigates overfitting risks. By reducing feature space, it also improves computation and model generalization.

• The HDLID-ECSOA approach effectively captures spatial and sequential patterns by combining a hybrid CNN-BiGRU technique with the CrAM model. This incorporation strengthens feature representation and context understanding. Concentrating on the most informative features significantly enhances classification accuracy, particularly in intrinsic data scenarios.

• The HDLID-ECSOA methodology implements the SFOA method to fine-tune hyperparameters, ensuring the selection of optimal values that improve performance. This adaptive tuning process enhances model accuracy and generalization. It also mitigates manual intervention and speeds up convergence during training, resulting in a more efficient learning process.

• This HDLID-ECSOA method introduces a novel methodology by integrating DOA-based feature selection, a CNN-BiGRU classifier enhanced with CrAM, and SFOA-based hyperparameter tuning. This integration enables more accurate, efficient, and context-aware classification, demonstrating significant novelty in model design.

Review of literature

Chen et al.¹¹ proposed a model to overcome over-parameterization in present optimization-based heuristic models, the geometrized task scheduling concern is handled by changing the distribution of clustered challenges into a regional partition concern in a 2-D graph and implementing a Tetris-like challenge offloading approach for edge-cloud co-operation. An online learning model is used to fine-tune the sliding window length based on the developing circumstances. Al-Quayed et al.¹² introduce a secure decision-making technique employing reinforcement learning (RL) with the integration of BC to improve data protection and trust. The presented approach raises the system efficacy for deploying sources and communication gadgets with security. It offers a dependable and more flexible model by investigating learning models to handle the instability and inaccuracy of cognitive methods. Sahu et al.¹³ advanced a multi-objective optimizer framework for smart parking integrating digital twin (DT) technology, Markov decision process (MDP), particle swarm optimization (PSO), and pareto front optimizer (PFO). Thus, the projected structure employs DT. Additionally, PSO enhances the solution initiated from the Pareto front for a higher distribution. Chen et al.¹⁴ developed an improved geospatial sensor web (GSW), integrating spatio-temporal modelling (STM) techniques and IoT protocols. Validated over the city sensing base station (CSBS), a pilot experiment exhibited that the architecture incorporates different sensing sources through 8 protocols, accomplishing more than five stages with faster aerial-ground system formation in an emergency. In¹⁵, a probability-based hybrid whale-dragonfly optimizer (p-H-WDFOA) edge-computing technique is proposed for smart urban vehicle transportation, decreasing edge-computing’s wait and latency to tackle these problems. The 5G localized MEC servers. Tian et al.¹⁶ developed a comprehensive security framework integrating an ELM-based replicator neural network (ELM-RNN) with the deep RL-based Deep Q-Networks (DRL-DQN) technique. Additionally, a secure trust-aware philosopher privacy and authentication (STAPPA) and garson algorithm (GA) is utilized for optimization to strengthen data protection and mitigate security breaches. Xu, Nagothu, and Chen¹⁷ proposed an autonomous and resilient edge (AR-EC) framework that integrates SDN, blockchain (BC), and AI technologies. Software-defined networking (SDN) enables effective edge resource optimization and coordination with the assistance of AI methodologies like large language models (LLM). Moreover, a federated microchain fabric safeguards edge networks’ resilience and security in a decentralized manner. Finally, a primary proof-of-concept prototype of an intelligent transportation system (ITS) data shows the possibility of implementing AR-Edge in real-time settings. In¹⁸, a resource allocation method for hierarchical EC depending on attention mechanism (AM) is projected, to remove a smaller number of aspects that may depict services from a vast amount of data gathered from edge nodes. The AM is employed to define the precedence of service rapidly.

Wang et al.¹⁹ developed NeuroSpatialIOT, an intuitive smart home control system that combines 2D spatial mapping, eye tracking, and DL to accurately interpret user intent. Far et al.²⁰ investigated the integration of BC and deep RL (DRL) models to optimize mobile transmission and secure data exchange in Iot-assisted smart cities, improving privacy, security, and system efficiency. Khan et al.²¹ developed and evaluated energy-efficient parallel computation offloading mechanism through DL (EPCOD) and energy efficient DL-based offloading scheme (EEDOS) techniques, optimizing latency and energy usage in multi-task, multi-server mobile EC environments. Mishra and Chaurasiya²² developed a hybrid DL LSTM-SVM approach integrating long short-term memory (LSTM) and support vector machine (SVM) classifiers. The system integrates min-max normalization for data preprocessing, feature selection using the reptile search algorithm (RSA), and BC technology to detect and prevent cyber-attacks effectively. Ficili et al.²³ explored and analyzed the integration of IoT, CC/EC, and AI to enable real-time decision-making and advance pervasive environmental intelligence. Wang et al.²⁴ proposed an AI-enhanced multi-stage learning-to-learning (MSLL) approach by utilizing MMStransformer for secure, efficient load management in IoT networks of smart cities, improving load forecasting accuracy while ensuring data security and privacy. Lilhore et al.²⁵ proposed a hybrid deep Q-network (DQN)-proximal policy optimization (PPO)-graph neural network (GNN)-RL model for optimizing resource allocation in dynamic IoT environments, enhancing efficiency, reducing costs, and improving performance in real-time applications. Ahmed and Elena²⁶ explored the integration of AI techniques such as ML, federated learning (FL), and intelligent orchestration frameworks with EC to enhance real-time decision-making, reduce latency, and improve scalability in smart cities, industrial IoT, and 5G/6G networks. Qasim Jebur Al-Zaidawi and Çevik²⁷ proposed a technique by utilizing hybrid grey wolf optimization with PSO (HGWOPSO) and hybrid world cup optimization with Harris Hawks optimization (HWCOAHHO) to symmetrically balance global exploration and local exploitation, optimizing DL models for real-time anomaly detection in IoT networks. Additionally, a multi-criteria decision-making (MCDM) framework integrating the analytic hierarchy process (AHP) and technique for order preference by similarity to ideal solution (TOPSIS) is employed to effectively evaluate and rank the proposed methods. Kumar and Neduncheliyan²⁸ developed an ensemble DL methodology integrating self-attention CNN, BiGRU, and shark smell optimized feed forward networks (SSOFFN) techniques for improved cybersecurity in IoT-based smart cities, utilizing fog computing (FC) to mitigate latency and computational overhead. Table 1 summarizes the existing studies on intelligent EC using DL and optimization techniques.

Table 1 Performance comparison of the proposed ensemble DL model with existing methods for IoT cyber-attack detection in smart City environments.

The existing studies on IoT-based smart city applications exhibit crucial improvements in security, resource optimization, and load management. However, several approaches concentrate on optimizing a single aspect, such as energy consumption or security, without considering a holistic, multi-objective optimization. The integration of AI, BC, and EC remains fragmented, with restricted exploration of their coordination. Furthermore, several techniques, such as DQN-PPO-GNN and EPCOD, show limitations in addressing the scalability problems when dealing with massive, dynamic IoT environments. Moreover, the adaptability of hybrid models like LSTM-SVM in real-time anomaly detection is often unexamined in diverse urban contexts. Another research gap is the lack of standardized frameworks for secure and effective data exchange in multi-server, multi-task settings across various IoT applications. Additionally, existing models often fail to integrate privacy-preserving mechanisms crucial for protecting sensitive data in decentralized IoT networks. The absence of unified evaluation benchmarks also affects objective comparison and validation of proposed approaches across diverse smart city scenarios.

The proposed method

This manuscript presents the HDLID-ECSOA model. This technique’s main goal is to provide intelligent EC in smart cities using advanced optimization models. It contains data pre-processing, a DOA-based FS process, hybrid classification, and a parameter fine-tuning process. Figure 2 depicts the entire flow of the HDLID-ECSOA technique.

Fig. 2

Overall flow of HDLID-ECSOA model.

Data normalization: Min-Max

Initially, the data pre-processing employs the min-max normalization method to convert and standardize raw data to improve the efficiency of models²⁹. This model is chosen due to its simplicity and efficiency in scaling data within [0, 1]. This technique ensures that all features contribute equally to the model, preventing any single feature from dominating due to differences in scale. This technique is less sensitive to outliers and performs well when the data is not normally distributed, compared to other normalization techniques, such as Z-score normalization. This benefits datasets with varied feature ranges, like those found in IoT applications. Furthermore, this normalization method is computationally efficient, making it ideal for massive datasets, ensuring faster model convergence during training.

Min-max normalization is carried out on the data to scale the vectors in standardization. Equation (1) provides the design of min-max normalization.

$${y}^{{\prime\:}}=\frac{(V-\text{m}\text{i}\text{n})}{(\text{m}\text{a}\text{x}-\text{m}\text{i}\text{n})}$$

(1)

Here, $\:y$ denotes a set of features, $\:\text{m}\text{a}\text{x}$ signifies the maximal value from the features, and min denotes the minimal value in the features of the dataset $\:{V}^{{\prime\:}}$. This characterizes the standardized data, which holds values from $\:(0$−1).

Feature selection: DOA

Furthermore, the DOA implements a subset of the FS process to detect and choose the most relevant features from the input data³⁰. This model is selected for its capability to effectively explore the search space and detect the most relevant features. This population-based optimization technique replicates the natural behaviour of dingo packs, which assists in avoiding local minima and finding optimal feature subsets. Unlike conventional methods such as genetic algorithms or PSO, DOA is prevalent because of its faster convergence and capability to handle high-dimensional data. Its flexibility in balancing exploration and exploitation makes it appropriate for feature selection tasks in complex datasets. Moreover, DOA does not require gradient data, making it suitable for nonlinear and non-convex feature selection problems. This approach improves the model’s performance by eliminating redundant or irrelevant features, enhancing accuracy and reducing computational cost. Figure 3 illustrates the workflow of the DOA technique.

Fig. 3

Working flow of the DOA methodology.

DOA simulates the social behaviour of Australian dingos. This model is stimulated by dingoes’ searching tactics, which are attacked by scavenging behaviour, grouping tactics, and persecution. Three search approaches related to the four rules are established to increase the model’s efficacy and performance.

The initial approach is a group attack. Predators frequently utilize very intellectual searching methods. Dingoes generally search for smaller prey like rabbits separately; however, they collect in groups after hunting larger prey like kangaroos. It may discover the prey position and encircle it, like wolves; this behaviour is characterized by the succeeding Eq. (2):

$${\overrightarrow{x}}_{i}\left(t+1\right)={\beta\:}_{1}{\sum\:}_{k=1}^{n\alpha\:}\frac{\left[\overrightarrow{{\varphi\:}_{\text{k}}\left(t\right)}-\overrightarrow{{x}_{i}}\left(t\right)\right]}{na}-\overrightarrow{{x}_{*}}\left(t\right)$$

(2)

Whereas $\:{\overrightarrow{x}}_{i}(t+1)$ refers to the new location of the searching agent, $\:na$ denotes a randomly generated integral number in the range [2, SizePop/2]. In contrast, SizePop stands for total dimensions (dingoes that assault). At the same time, $\:{\varphi\:}_{k}\left(t\right)$ denotes sub-set of searching agent, $\:X$ refers to dingoes’ population randomly made, $\:x\left(t\right)$ signifies present search iteration, and $\:\beta\:1$ signifies uniformly generated random number from interval $\:[-\text{2,2}],$ $\:x\left(t\right)$ symbolize top searching agent identified from the preceding iteration. The second tactic is Persecution. Dingos generally search for smaller prey that is hunted till it is captured separately. The following Eq. (3) models this behaviour:

$$\:{\overrightarrow{x}}_{i}(t+1)={\overrightarrow{x}}_{*\left(t\right)+{\beta\:}_{1}*{e}^{{\beta\:}_{2}}*(}{\overrightarrow{x}}_{{r}_{1}}\left(t\right)-{\overrightarrow{x}}_{i}\left(t\right))$$

(3)

Whereas $\:{\beta\:}_{2}$ denotes uniformly generated random numbers within the range [− 1, 1], $\:{r}_{1}$ refers to randomly generated numbers from 1 to the dimensions of a maximum of search agents (dingoes), and $\:i\ne\:{r}_{1}.$

The third tactic is Scavenger, whose behaviour is described as the action once dingos discover corpses to feed on after arbitrarily walking in their environment. The succeeding Eq. (4) models this behaviour:

$$\:{\overrightarrow{x}}_{i}(t+1)=\frac{1}{2}[{e}^{{\beta\:}_{2}}*{\overrightarrow{x}}_{{r}_{1}}(t)-(-1{)}^{\sigma\:}*{\overrightarrow{x}}_{i}(t)]$$

(4)

Whereas $\:\sigma\:$ denotes a binary number randomly$\:\:\epsilon\:\:\left\{\text{0,1}\right\}$, and $\:i\ne\:{r}_{1}.$

Fourth tactic: Survival Rates of Dingos: Dingo dogs are at risk of extinction because of illegal hunting. The dingoes’ survival rate value is provided by the succeeding Eq. (5):

$$\:{\overrightarrow{x}}_{i}\left(t\right)={\overrightarrow{x}}_{*}\left(t\right)+\frac{1}{2}\left[{\overrightarrow{x}}_{{r}_{1}}\right(t)-\left(-1{)}^{\sigma\:}*{\overrightarrow{x}}_{{r}_{2}}\left(t\right)\right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(5)

The fitness function (FF) reflects the accuracy of classification and the number of selected features. It utilizes classification accuracy and reduces the preferred features’ dimensionality. Hence, the FF below is deployed to assess discrete solutions.

$$\:Fitness=\alpha\:*\:ErrorRate+\left(1-\alpha\:\right)*\frac{\#SF}{\#All\_F}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(6)

Here, $\:ErrorRate$ is the classifier rate of error utilizing the chosen features. $\:ErrorRate$ is calculated as the proportion of improperly classified to several classifications prepared among 0 and 1. $\:\#SF$ means several preferred features, and $\:\#\:All\_F$ refers to the complete number of features in the original dataset. $\:\alpha\:$ is employed to control classifier excellence and subset length. The value of $\:\alpha\:$ is 0.9.

Classification process: CNN-BiGRU-CrAM

Besides, the proposed HDLID-ECSOA model employs the CNN-BiGRU-CrAM technique for the classification process³¹. This model was chosen for its capability of effectively capturing both spatial and sequential dependencies in data. The CNN shows excellence in extracting hierarchical features from raw input, particularly for tasks comprising spatial patterns, such as image or time-series data. The BiGRU layer is appropriate for processing sequential data, as it captures context from past and future time steps, improving temporal feature representation. Integrating the CrAM enhances the model’s focus on the most relevant features by allowing it to learn contextual relationships between diverse input parts. This integration of CNN, BiGRU, and CrAM outperforms conventional methods by giving a more holistic representation of data. It also improves classification accuracy by addressing spatial and temporal dimensions in intrinsic datasets, making it ideal for IoT and IIoT applications. Figure 4 depicts the infrastructure of CNN-BiGRU-CrAM method.

Fig. 4

Structure of CNN-BiGRU-CrAM model.

CNN is a deep-structured feedforward NN that contains a convolution calculation. The sparsity of links among layers and sharing the hidden layer (HL)’s convolutional kernel framework permit CNN to remove features with minimum calculation. The fully connected (FC), convolutional, input, and pooling layers are presented in the complete architecture of CNN. During this input layer, the removed attributes are provided as input. In contrast, the convolutional layer utilizes convolution calculations on the input with the convolutional kernel to obtain feature mapping. The integration involving $\:Z$ convolutional kernels is indicated by $\:[{Q}_{1},\:{Q}_{2},\:{Q}_{3},\dots\:,\:{Q}_{Z}]$, whereas $\:{Q}_{Z}$ imitates the $\:Zth$ kernel size of the convolution or the longitudinal dimension of the convolution kernel window. There would be $\:Z$ feature mapping vectors afterwards, computing $\:Z$ convolutional kernels. The size of the convolution window was provided as $\:I$. To remove the local attributes, the convolutional kernel is applied to perform the convolution process on the input windows $\:{y}_{1}^{H},$ $\:{y}_{2}^{H},$ $\:{y}_{3}^{H},$ $\:{y}_{p-H+1}^{p}$. Assuming that the input $\:D$ contains $\:p$ feature vectors, $\:{y}_{1},$ $\:{y}_{2},$ $\:{y}_{3},$ $\:{y}_{p}$, that is represented as

$$\:{z}_{j}=g\left(X.{y}_{j:j+H-1}+B\right)$$

(7)

.

Whereas $\:g\left(\right)$ indicates the nonlinear function, $\:H$ suggests the kernel size of the convolution, and $\:B$ and $\:X$ indicate the biased vector and weighted matrix. The vector’s incorporation is signified by $\:{y}_{j:j+H-1}.$

After the extraction of the convolutional kernel, the eigen-vector $\:z$ is gained as:

$$\:z=\left\{{z}_{1},\:{z}_{2},\:{z}_{3},\dots\:,\:{z}_{p-H+1}\right\}$$

(8)

Following the convolution process, every eigen-vector is vulnerable to pooling processing using the pooling layer. The multi-dimensional vectors are converted into a value afterwards; pooling is applied as the pooled vector component. The larger component in the series $\:{z}_{1},{z}_{2},{z}_{3},{z}_{p-H+1}$ should be selected by the maximal pooling model, which would lastly give novel vectors $\:z$:

$$\:z=\text{m}\text{a}\text{x}\left({z}_{j}\right)$$

(9)

A kind of RNN, such as LSTM, is considered GRU. RNNs implement recursion in the progressive direction of the sequence by inputting sequential data. Therefore, RNN contains memory and parameter sharing. Moreover, RNNs perform well while learning nonlinear features from sequential data. LSTM can learn data of correlation between long-term and short-term sequential data. Subsequently, GRU was recognized as the solution to the LSTM problem, using a slow convergence rate and extreme parameters. The inner modules of GRU contain the reset and update gates.

This framework allows the Bi-GRU to successfully handle the flow of information by establishing which feature to retain or discard. Compared with LSTM, GRU exchanges the input and forget gates of the LSTM using an update gate. The value of the greater update gate imitates the greater influence degree. The succeeding equation is applied to describe the HL component $\:B$:

$$\:{Z}_{u}=\delta\:\left({w}_{Z}.\left[{H}_{u-1},\:{y}_{u}\right]\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(10)

$$\:{R}_{u}=\delta\:\left({w}_{R}.\left[{H}_{u-1},\:{y}_{u}\right]\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(11)

$$\:{\stackrel{\sim}{H}}_{u}=\text{t}\text{a}\text{n}\text{h}\left(w\left[{R}_{u}*{H}_{u-1},\:{y}_{u}\right]\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(12)

$$\:{H}_{u}=\left(1-{Z}_{u}\right)*{H}_{u-1}+{Z}_{u}*{\stackrel{\sim}{H}}_{u}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(13)

Whereas $\:\delta\:$ specifies the function of Sigmoid, $\:\text{t}\text{a}\text{n}\text{h}$ indicates the function of hyperbolic tangent, and $\:{Z}_{u}$ and $\:{R}_{u}$ identify the reset and update gates. $\:{w}_{R},{v}_{R},wz,vz$, and $\:v$ imply each of the training parameter matrices. The reset $\:{R}_{u}$, the input gate $\:{Y}_{u}$, in the present sample, the output $\:{H}_{u-1}$ of the HL neuron at the previous instant, and the matrices of training parameters $\:v$ and $\:u$ work together to determine the activation state of the candidate $\:{\stackrel{\sim}{H}}_{u}$ at the current instant. The Bi-GRU network is superior for learning the connections among present, previous, and upcoming determinant factors. It is measured as

$$\:{z}_{2}=g\left(v{B}_{2}+{v}^{{\prime\:}}{B}_{2}^{{\prime\:}}\right)$$

(14)

.

and $\:{B}_{2}^{{\prime\:}}$ are calculated utilizing

$$\:{B}_{2}=g\left(w{B}_{1}+u{y}_{2}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(15)

$$\:{B}_{2}^{{\prime\:}}=g\left({w}^{{\prime\:}}{B}_{3}^{{\prime\:}}+u{y}_{2}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(16)

.

The HL value $\:{S}_{u}$ in the forward computation is related to $\:{S}_{u-1}$. The HL value $\:{S}_{u}$ in the backwards calculation is associated with $\:{S}_{u-1}$. The forward and reverse calculations determine the last outcome. The computation process of the bi-directional RNN is provided as shown:

$$\:{O}_{u}=g\left(v{S}_{u}+{v}^{{\prime\:}}{S}_{u}^{{\prime\:}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(17)

$$\:{S}_{u}=f\left(u{y}_{u}+w{S}_{u-1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(18)

$$\:{S}_{u}^{{\prime\:}}=f\left({u}^{{\prime\:}}{y}_{u}+{w}^{{\prime\:}}{S}_{u-1}^{{\prime\:}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(19)

Cross-entropy (CE) loss function is applied for the classification difficulty within the NN.

The AM is designed to reduce the intervention of incorrect data and assist make the most promising results. The AM works well in dual methods: Initially, it spontaneously recognizes the local data which needs to be focused on the global input. Due to these dual advantages, AM is often applied to enhance local data features. Moreover, the attention region and the task objective are dissimilar. The significant data is used effectively after local information is collected. The attention network output is specified as shown:

$$\:{Z}_{u}=g\left({z}_{u-1},\:{m}_{u-1},\:{D}_{u}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(20)

Here, $\:{Z}_{u}$ symbolizes the AM’s output at a sample $\:u,$ $\:g$ indicates the dense layer, $\:{Z}_{u-1}$ suggests the AM’s output at time $\:u-1$, and $\:{m}_{u-1}$ defines the label at instant $\:u-1.$

$$\:{D}_{u}={\sum\:}_{k=1}^{{U}_{y}}{b}_{uk}{i}_{k}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(21)

.

$\:{D}_{u}$ symbolizes the following stage output, $\:{i}_{k}$ involves the AM’s $\:kth$ input, and $\:{b}_{uk}$ describes the attention weights.

$$\:{b}_{uk}=\frac{\text{e}\text{x}\text{p}\left({e}_{uk}\right)}{{\sum\:}_{k=1}^{{U}_{y}}\text{e}\text{x}\text{p}\left({e}_{ul}\right)}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(22)

$$\:{e}_{uk}=h\left({z}_{u-1},\:{i}_{k}\right)=w\times\:\text{t}\text{a}\text{n}\text{h}\left(X\times\:{i}_{k}+v\times\:{Z}_{u-1}+c\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(23)

Meanwhile, $\:h$ is applied to calculate the area of relation between $\:{Z}_{u-1}$ and $\:{i}_{k}$, and $\:{b}_{uk}$ defines the amount to which the present AM is associated with the $\:kth$ input.

Parameter Fine-Tuning: SFOA

The SFOA model is utilized for hyperparameter tuning to optimize model performance to ensure that the optimum hyperparameters are selected for enhanced accuracy³². This model is chosen due to its robust global search capability and efficiency in finding optimal solutions. The model is inspired by the foraging behaviour of starfish, which makes it perform well in balancing exploration and exploitation effectively, making it less likely to get trapped in local minima than conventional optimization techniques like gradient descent. Unlike grid or random search methods, SFOA can adaptively adjust its search process to find the optimum hyperparameters with fewer iterations. This results in an enhanced optimization accuracy and mitigated computational cost. Additionally, this model is appropriate for high-dimensional, complex parameter spaces commonly found in DL models. Its flexibility and robustness across diverse tasks make it an ideal choice for fine-tuning parameters, ensuring the model attains optimal performance without excessive computational overhead. Figure 5 represents the framework of the SFOA approach.

Fig. 5

SFOA framework.

Meta-heuristic methods frequently balance exploitation (local search refinement) and exploration (global search capability). Efficient optimization must be the best tradeoff among these dual stages to avoid early convergence to sub-optimal solutions. As meta-heuristic tactics depend on randomized searching mechanisms, they do not guarantee the best solutions for all problems. The bio-inspired design for SFOA is acquired from starfish’s hunting, movement, and regenerating capabilities. Starfish, otherwise named sea stars, usually show a five-arm radial symmetry extending from the primary disk.

The exploration stage of SFOA imitates the starfish’s foraging behaviour, whereas exploitation is modelled through regeneration and predation tactics. SFOA uses a hybrid searching mechanism that combines:

• For 5-dimensional search $\:(L>5)$, stimulated by the five arms of the starfish, for different exploration.

• Increasing convergence if the feature area is small for a 1-dimensional search (L ≤ 5).

The optimizer procedure of SFOA contains three main phases:

Initialization: At the start of the optimizer procedure, starfish locations are randomly made inside the pre-defined design area, expressed as:

$$X=\left[\begin{array}{llll}{\chi}_{11}&{x}_{12}&\dots&{x}_{1L}\\{x}_{21}&{x}_{22}&\dots&{x}_{2L}\\{\chi}_{31}&{x}_{32}&\dots&{x}_{3L}\\\:\vdots&\:\vdots&\:\ddots\:&\:\vdots\\{x}_{N1}&{x}_{N2}&\:\dots&{x}_{NL}\end{array}\right]$$

(24)

Whereas $\:N$ denotes the size of the population, $\:L$ refers to the design variable counts, and the primary locations are calculated as:

$$\:{x}_{ij}=\text{l}o{w}_{j}+random\left(uppe{r}_{j}-\text{l}o{w}_{j}\right),\:i=\text{1,2},\:\dots\:,N,\:j=\text{1,2},\:\dots\:,\:L\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(25)

The fitness score of all starfish is estimated according to the objective function, allowing an adaptive searching process.

Exploration: SFOA uses dissimilar tactics according to the dimensionality of the problem:

• For $\:L>5$, a 5-dimensional search is applied for larger‐scale optimization.

• For $\:L\le\:5$, a 1-dimensional search was utilized for enhanced local refinement.

The location updated rule in the exploration stage is expressed as:

$$\:{X}_{i,p}^{t+1}=\left\{\begin{array}{l}{X}_{i,p}^{t}+a\left({X}_{best,p}^{t}-{X}_{i,p}^{t}\right)\:\text{c}\text{o}\text{s}\theta\:,\:if\:rn\le\:0.5,\\\:{X}_{i,p}^{t}+a\left({X}_{besi,p}^{t}-{X}_{i,p}^{t}\right)\:\text{s}\text{i}\text{n}\theta\:,\:if\:rn>0.5.\end{array}\right.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(26)

Whereas $\:rn$ denotes randomly generated numbers $\:e\left(\text{0,1}\right)$, and $\:{X}_{i,p}^{t+1},{X}_{i,p}^{t}$, and $\:{X}_{besi,p}^{t}$ characterize the computed, present, and best locations, correspondingly. The parameters $\:a$ and $\:\theta\:$ are provided by:

$$\:a=\left(2r-1\right)\pi\:,\:\theta\:=\frac{\pi\:}{2}\cdot\:\frac{t}{{t}_{\text{m}\text{a}\text{x}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(27)

When the modified position is outside the borders of the model parameters, the arms are given to stay in the preceding location instead of migrating. The exploration stage upgrades the area utilizing the unidimensional search design if $\:L\le\:5$. In such a case, a starfish uses location data from others to move one of its arms toward the food resource:

$$\:{X}_{i,p}^{t+1}={E}_{t}{X}_{i,p}^{t}+{a}_{1}\left({X}_{k1,p}^{t}-{X}_{i,p}^{t}\right)+{a}_{2}\left({X}_{k2,p}^{t}-{X}_{i,p}^{t}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(28)

Here, $\:{X}_{k1,p}^{t}$ and $\:{X}_{k2,p}^{t}$ are randomly chosen $\:P$-dimensional positions from dual starfish, $\:{a}_{1}$ and $\:{a}_{2}$ are randomly generated numbers $\:e\left(-\text{1,1}\right)$, and $\:{E}_{t}$ is measured as:

$$\:{E}_{t}=\frac{{t}_{\text{m}\text{a}\text{x}}-t}{{t}_{\text{m}\text{a}\text{x}}}\:\text{c}\text{o}\text{s}\:\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(29)

Exploitation: The exploitation stage consists of regeneration and hunting tactics. The location of the starfish is upgraded according to the best position:

$$\:{d}_{n}={X}_{best}^{t}-{X}_{{n}_{p}}^{t},\:n=\text{1,2},\:\dots\:,5\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(30)

The new location is calculated utilizing:

$$\:{X}_{i}^{t+1}={X}_{i}^{t}+r{n}_{1}{d}_{n1}+r{n}_{2}{d}_{n2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(31)

Here, $\:r{n}_{1}$ and $\:r{n}_{2}$ signify randomly generated values in $\:\left(\text{0,1}\right)$, and $\:{d}_{n1},{d}_{n2}$ denote randomly selected distances.

Moreover, in the regeneration stage, if a starfish loses an arm to prevent predators, the position is upgraded utilizing:

$$\:{X}_{i}^{t+1}=\text{e}\text{x}\text{p}\left(-t\times\:\frac{N}{{t}_{\text{m}\text{a}\text{x}}}\right){X}_{i}^{t}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(32)

The last upgrade guarantees that values remain inside limits:

$$\:{X}_{i}^{t+1}=\left\{\begin{array}{ll}{X}_{i}^{t+1},&\:if\:lo{w}_{i}\le\:{X}_{i}^{t+1}\le\:uppe{r}_{j},\\\:lo{w}_{j,}&\:if\:{X}_{i}^{t+1}<lo{w}_{j,}\\\:upper,&\:if\:{X}_{i}^{t+1}>uppe{r}_{i}.\end{array}\right.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(33)

The SFOA generates a feature set (FF) to improve the classification accuracy. It defines an optimistic number to signify the better productivity of the candidate solution. The classifier rate of error minimization was measured as FF, as set in Eq. (34).

$$fitness\left( {{x_i}} \right) = ClassifierErrorRate\left( {{x_i}} \right) = \frac{{no.\;of\;misclassified\;instances}}{{Total\;no.\;of\;instances}} \times 100\;\;\;$$

(34)

Experimental validation

The simulation validation of the HDLID-ECSOA model is examined under the Edge-IIoT dataset³³. This dataset holds 36,000 records under 12 types of events, as depicted in Table 2. There are 63 features, but only 47 are selected.

Table 2 Details of Edge-IIoT dataset.

Figure 6 presents the confusion matrix created by the HDLID-ECSOA technique using the Edge-IIoT dataset under an 80:20 training phase (TRAPHA), testing phase (TESPHA), and 70:30 TRAPHA/TESPHA. The outcomes specify that the HDLID-ECSOA method efficiently identifies and detects all classes precisely.

Fig. 6

Edge-IIoT dataset (a-b) 80%TRAPHA and 20%TESPHA and (c-d) 70%TRAPHA and 30%TESPHA.

Table 3; Fig. 7 illustrate the intrusion detection of the HDLID-ECSOA methodology under the Edge-IIoT dataset. Depending on 80% TRAPHA, the proposed HDLID-ECSOA approach attains an average $\:acc{u}_{y}$ of 99.35%, $\:pre{c}_{n}$ of 96.11%, $\:rec{a}_{l}$ of 96.11%, $\:{F}_{Measure}\:$of 96.11%, $\:{AUC}_{Score}$of 97.88%, and Kappa of 97.95%. Besides, based on 20% TSAPHA, the proposed HDLID-ECSOA approach achieves an average $\:acc{u}_{y}$ of 99.32%, $\:pre{c}_{n}$ of 95.95%, $\:rec{a}_{l}$ of 95.95%, $\:{F}_{Measure}\:$of 95.94%, $\:{AUC}_{Score}$of 97.79%, and Kappa of 97.86%. Likewise, based on 70% TRAPHA, the proposed HDLID-ECSOA approach attains an average $\:acc{u}_{y}$ of 98.42%, $\:pre{c}_{n}$ of 90.49%, $\:rec{a}_{l}$ of 90.49%, $\:{F}_{Measure}\:$of 90.48%, $\:{AUC}_{Score}$of 94.81%, and Kappa of 94.88%. Also, based on 30% TSAPHA, the proposed HDLID-ECSOA approach attains an average $\:acc{u}_{y}$ of 98.47%, $\:pre{c}_{n}$ of 90.82%, $\:rec{a}_{l}$ of 90.81%, $\:{F}_{Measure}\:$of 90.80%, $\:{AUC}_{Score}$ of 94.99%, and Kappa of 95.06%.

Table 3 Intrusion detection of HDLID-ECSOA approach under Edge-IIoT dataset.

Fig. 7

Average of HDLID-ECSOA method under Edge-IIoT dataset.

In Fig. 8, the training (TRAN) $\:acc{u}_{y}$ and validation (VALN) $\:acc{u}_{y}$ outcomes of the HDLID-ECSOA methodology under the Edge-IIoT dataset below 80:20 are demonstrated. The figure highlights that both values of $\:acc{u}_{y}$ demonstrate rising trends that informed the capability of the HDLID-ECSOA methodology with maximum performance over several iteration counts. Besides, both $\:acc{u}_{y}$leftovers closer over the epochs, which indicates minimal overfitting and exhibits superiority of the HDLID-ECSOA model, guaranteeing consistent prediction on unseen instances.

Fig. 8

$\:Acc{u}_{y}$ analysis of HDLID-ECSOA method under Edge-IIoT dataset below 80:20.

In Fig. 9, the TRAN loss (TRANLOS) and VALN loss (VALNLOS) graph of the HDLID-ECSOA model under the Edge-IIoT dataset below 80:20 is exhibited. It is indicated that both values illustrate a falling trend, notifying the capacity of the HDLID-ECSOA model to balance a tradeoff between generalization and data fitting. The constant reduction in loss values further ensures the improved effectiveness of the HDLID-ECSOA model and refines the prediction outcomes.

Fig. 9

Loss graph of HDLID-ECSOA technique under Edge-IIoT dataset below 80:20.

Table 4; Fig. 10 show the comparative results of the HDLID-ECSOA methodology under the Edge-IIoT dataset with existing methods^{19,35,36,37,38}. The outcomes emphasized that the LSTM, Random Forest (RF), FL, FedMLDL-Bayesian HPO, LDA, Gradient Boosting (GB), and J48 methodologies obtained lesser performance. The CNN-LSTM, DBN, and NeuroSpatialIOT methodologies also attained slightly lesser results. However, the proposed HDLID-ECSOA method reported superior performance with higher $\:acc{u}_{y}$, $\:pre{c}_{n}$, $\:rec{a}_{l}\:$and $\:{F}_{Measure\:}$of 99.35%, 96.11%, 96.11%, and 96.11%, correspondingly.

Table 4 Comparative analysis of HDLID-ECSOA model under Edge-IIoT dataset^{19,35,36,37,38}.

Fig. 10

Comparative analysis of HDLID-ECSOA model under Edge-IIoT dataset.

Table 5; Fig. 11 specifies the computational time (CT) analysis of the HDLID-ECSOA approach with existing models under Edge-IIoT dataset. The HDLID-ECSOA approach demonstrates the fastest performance with a CT of 7.63 s, outperforming all other approaches. LSTM records 10.93 s, RF at 11.12 s, and LDA model at 11.03 s, indicating relatively efficient CT with nearly equal CT. In contrast, FL takes 15.61 s, and CNN-LSTM attains 15.74 s, suggesting moderate computational efficiency. Among the slower models, DBN shows 16.79 s while FedMLDL-Bayesian HPO illustrates the highest CT of 17.20 s. NeuroSpatialIOT, J48, and GB record 12.70, 13.20, and 12.39 s respectively.

Table 5 CT evaluation of HDLID-ECSOA approach with existing models under Edge-IIoT dataset.

Fig. 11

CT evaluation of HDLID-ECSOA approach with existing models under Edge-IIoT dataset.

Table 6; Fig. 12 portrays the error analysis of the HDLID-ECSOA technique with existing methods under Edge-IIoT dataset. The GB model achieves the highest $\:acc{u}_{y}$ of 10.96% with a $\:rec{a}_{l}$ of 10.98% but a relatively low $\:pre{c}_{n}$ of 5.45%, indicating it identifies relevant cases but struggles with $\:pre{c}_{n}$. The RF method exhibits an $\:acc{u}_{y}$ of 6.62% and the highest $\:{F}_{Measure\:}$ of 7.91%, suggesting balanced but modest performance. The LSTM model depicts an $\:acc{u}_{y}$ of 5.17% with a $\:pre{c}_{n}$ of 10.97% and $\:rec{a}_{l}$ of 10.07%, highlighting robust detection capability despite low overall correctness. FedMLDL-Bayesian HPO and NeuroSpatialIOT illustrate $\:rec{a}_{l}$ values of 10.98% and 10.45% respectively, showing potential in capturing relevant positives. However, the HDLID-ECSOA model significantly underperforms with only an $\:acc{u}_{y}$ of 0.65% and equal $\:pre{c}_{n}$, $\:rec{a}_{l}$, and $\:{F}_{Measure\:}$ values of 3.89%, indicating limited utility in classification tasks within this context. Overall, while some models excel in specific metrics, none achieve uniformly robust performance across all indicators, highlighting challenges in IIoT error detection.

Table 6 Error analysis of HDLID-ECSOA technique with existing methods under Edge-IIoT dataset.

Fig. 12

Error analysis of HDLID-ECSOA technique with existing methods under Edge-IIoT dataset.

Table 7; Fig. 13 demonstrate the ablation study of the HDLID-ECSOA technique under the Edge-IIoT dataset. The baseline DOA approach attains an $\:acc{u}_{y}$ of 97.23%, a $\:pre{c}_{n}$ of 94.27%, a $\:rec{a}_{l}$ of 94.01%, and an $\:{F}_{Measure}$ of 94.14%. Enhancing the optimization strategy with SFOA attains an $\:acc{u}_{y}$ of 97.75%, a $\:pre{c}_{n}$ of 94.79%, a $\:rec{a}_{l}$ of 94.73%, and an $\:{F}_{Measure}$ of 94.69%. Incorporating DL with the CNN-BiGRU-CRAM model attains an $\:acc{u}_{y}$ of 98.55%, a $\:pre{c}_{n}$ of 95.57%, a $\:rec{a}_{l}$ of 95.41%, and an $\:{F}_{Measure\:}$of 95.33%. Finally, the proposed HDLID-ECSOA model attains the highest performance, with an $\:acc{u}_{y}$ of 99.35%, a $\:pre{c}_{n}$ of 96.11%, a $\:rec{a}_{l}$ of 96.11%, and an $\:{F}_{Measure}$ of 96.11%, illustrating the strength of the integrated architecture in improving detection efficiency in IIoT environments.

Table 7 Result analysis of the ablation study of the HDLID-ECSOA technique.

Fig. 13

Result analysis of the ablation study of the HDLID-ECSOA technique.

Also, the proposed HDLID-ECSOA technique is verified under the ToN-IoT dataset³⁴. It contains 119,957 samples below nine classes. 42 features are reachable, but only 35 are selected. Table 8 shows the complete particulars of the ToN-IoT dataset.

Table 8 Details of the ToN-IoT dataset.

Figure 14 signifies the confusion matrix created by the HDLID-ECSOA technique under the ToN-IoT dataset. The outcomes specify that the HDLID-ECSOA method efficiently recognizes and detects all classes.

Fig. 14

ToN-IoT dataset (a-b) 80%TRAPHA and 20%TESPHA and (c-d) 70%TRAPHA and 30%TESPHA.

Table 9; Fig. 15 present the intrusion detection of the HDLID-ECSOA methodology under the ToN-IoT dataset. Based on 80% TRAPHA, the proposed HDLID-ECSOA methodology presents an average $\:acc{u}_{y}$ of 99.29%, $\:pre{c}_{n}$ of 91.52%, $\:rec{a}_{l}$ of 86.78%, $\:{F}_{Measure}\:$of 88.33%, $\:{AUC}_{Score}$of 93.10%, and Kappa of 93.16%. Also, based on 20% TSAPHA, the proposed HDLID-ECSOA technique presents an average $\:acc{u}_{y}$ of 99.33%, $\:pre{c}_{n}$ of 91.37%, $\:rec{a}_{l}$ of 87.07%, $\:{F}_{Measure}\:$of 88.54%, $\:{AUC}_{Score}$of 93.26%, and Kappa of 93.33%. Besides, depending on 70% TRAPHA, the proposed HDLID-ECSOA technique presents an average $\:acc{u}_{y}$ of 99.14%, $\:pre{c}_{n}$ of 88.73%, $\:rec{a}_{l}$ of 82.60%, $\:{F}_{Measure}\:$of 83.18%, $\:{AUC}_{Score}$ of 90.98%, and Kappa of 91.04%. Finally, based on 30% TSAPHA, the proposed HDLID-ECSOA technique presents an average $\:acc{u}_{y}$ of 99.12%, $\:pre{c}_{n}$ of 89.48%, $\:rec{a}_{l}$ of 82.28%, $\:{F}_{Measure}\:$of 82.79%, $\:{AUC}_{Score}$ of 90.80%, and Kappa of 90.87%.

Table 9 Intrusion detection of HDLID-ECSOA approach under ToN-IoT dataset.

Fig. 15

Average of HDLID-ECSOA approach under ToN-IoT dataset.

Figure 16 demonstrates the TRAN $\:acc{u}_{y}$ and VALN $\:acc{u}_{y}$ results of the HDLID-ECSOA approach under the ToN-IoT dataset below 80:20. The figure highlights that both $\:acc{u}_{y}$ values exhibit a growing trend, which indicates the HDLID-ECSOA approach’s ability to improve performance across several iterations. Simultaneously, both $\:acc{u}_{y}$ remains closer over the epochs, which means lower overfitting and displays greater performance of the HDLID-ECSOA methodology.

Fig. 16

$\:Acc{u}_{y}$ analysis of HDLID-ECSOA approach under ToN-IoT dataset below 80:20.

Figure 17 shows the TRANLOSS and VALNLOSS analysis of the HDLID-ECSOA approach under the ToN-IoT dataset below 80:20. Both values prove a reducing tendency, informing the capacity of the HDLID-ECSOA model to balance a tradeoff between data fitting and simplification. The incessant decrease in loss values highlights the improved performance of the HDLID-ECSOA model.

Fig. 17

Loss graph of HDLID-ECSOA approach under ToN-IoT dataset below 80:20.

The comparative results of the HDLID-ECSOA technique under ToN-IoT dataset with existing techniques are shown in Table 10; Fig. 18^{21,35,36,37,38}. The results emphasized that the LSTM, RF, AdaBoost, kNN, XGBoost, CART, and 1D CNN techniques have gained minimal performance. However, the proposed HDLID-ECSOA method reported an optimal performance with improved $\:acc{u}_{y}$, $\:pre{c}_{n}$, $\:rec{a}_{l}\:$and $\:{F}_{Measure\:}$of 99.33%, 91.37%, 87.07%, and 88.54%, respectively.

Table 10 Comparative analysis of HDLID-ECSOA model under ToN-IoT dataset^{21,35,36,37,38}.

Fig. 18

Comparative analysis of HDLID-ECSOA model under ToN-IoT dataset.

Table 11; Fig. 19 indicates the CT assessment of the HDLID-ECSOA methodology with existing techniques under ToN-IoT dataset. The HDLID-ECSOA methodology attained the fastest CT of 9.69 s, outperforming models like LSTM at 20.08 s, RF at 24.00 s, and EPCOD at 29.67 s. Other approaches such as AdaBoost and DNN recorded even higher CTs of 27.88 s and 28.98 s, respectively. Compared to widely used methods like XGBoost and 1D CNN, which had 12.45 s and 14.87 s respectively, the HDLID-ECSOA model illustrated superior efficiency. This reduced CT makes the HDLID-ECSOA model highly appropriate for real-time and resource-constrained IIoT environments.

Table 11 CT assessment of HDLID-ECSOA methodology with existing techniques under ToN-IoT dataset.

Fig. 19

CT assessment of HDLID-ECSOA methodology with existing techniques under ToN-IoT dataset.

Table 12; Fig. 20 shows the error analysis of the HDLID-ECSOA method with existing models under ToN-IoT dataset. The error analysis on the ToN-IoT dataset reveals that most models showed moderate to low accuracy, with RF achieving 10.47%, AdaBoost 10.08%, and XGBoost 8.05%. These models also exhibited relatively higher $\:pre{c}_{n}$, $\:rec{a}_{l}\:$and $\:{F}_{Measure\:}$ values, such as XGBoost with $\:pre{c}_{n}$ of 10.25%, $\:rec{a}_{l}$ of 18.79%, and $\:{F}_{Measure\:}$ of 21.39%. In contrast, the HDLID-ECSOA model achieved the lowest $\:acc{u}_{y}$ at 0.67%, along with $\:pre{c}_{n}$ of 8.63%, $\:rec{a}_{l}$ of 12.93%, and $\:{F}_{Measure\:}$ of 11.46%, exhibiting that while it was computationally efficient, its predictive performance was significantly lower. Overall, conventional ensemble methods and tree-based algorithms outperformed others in balancing precision and recall across this dataset.

Table 12 Error analysis of HDLID-ECSOA method with existing models under ToN-IoT dataset.

Fig. 20

Error analysis of HDLID-ECSOA method with existing models under ToN-IoT dataset.

Table 13; Fig. 21 represent the ablation study of the HDLID-ECSOA approach under the ToN-IoT dataset. The DOA method attains an $\:acc{u}_{y}$ of 97.22%, $\:pre{c}_{n}$ of 89.47%, $\:rec{a}_{l}$ of 84.94%, and an $\:{F}_{Measure}$ of 86.42%. The SFOA approach attains an $\:acc{u}_{y}$ of 97.86%, $\:pre{c}_{n}$ of 90.02%, $\:rec{a}_{l}$ of 85.66%, and an $\:{F}_{Measure\:}$of 87.18%. The CNN-BiGRU-CRAM model attains an $\:acc{u}_{y}$ of 98.53%, $\:pre{c}_{n}$ of 90.76%, $\:rec{a}_{l}$ of 86.28%, and an $\:{F}_{Measure}$ of 87.83%. The proposed HDLID-ECSOA model attains an $\:acc{u}_{y}$ of 99.33%, achieving a precision of 91.37%, $\:rec{a}_{l}$ of 87.07%, and an $\:{F}_{Measure}$ of 88.54%, highlighting its superior detection capability.

Table 13 Result analysis of the ablation study of the HDLID-ECSOA approach.

Fig. 21

Result analysis of the ablation study of the HDLID-ECSOA approach.

Conclusion

In this study, the HDLID-ECSOA technique was presented. The HDLID-ECSOA technique used advanced optimization models to provide intelligent EC in smart cities. Initially, the data pre-processing employed the min-max normalization method to convert and standardize raw data to improve the efficiency of models. Furthermore, the DOA implemented a subset of the FS process to detect and choose the most relevant features from the input data. Besides, the HDLID-ECSOA model utilized CNN-BiGRU-CrAM for the classification process. A comprehensive experimentation analysis of the HDLID-ECSOA model is performed under the Edge-IIoT and ToN-IoT datasets. The experimental validation of the HDLID-ECSOA model portrayed superior accuracy values of 99.35% and 99.33% over existing techniques under the dual dataset. The limitations of the HDLID-ECSOA model comprise its focus on a limited set of datasets, which may affect the generalizability of the results to other IoT or IIoT environments. Furthermore, the existing evaluation only considers clean data, without examining the robustness of the model against adversarial attacks or noisy data, which are critical in real-world applications. The model does not address privacy and security concerns like data leakage or adversarial evasion strategies. Future work should consider incorporating more diverse datasets, comprising real-world IoT traffic, to validate the performance of the model across diverse scenarios. Additionally, the study may be extended by assessing the model under adversarial conditions to analyze its robustness in hostile environments. Integrating privacy-preserving techniques to enhance security and exploring the scalability of the model in large-scale IoT networks will also be significant areas for future development.