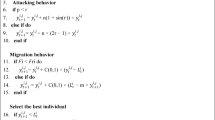A black-winged kite optimization algorithm enhanced by osprey optimization and vertical and horizontal crossover improvement

Abstract

This paper addresses issues of inadequate accuracy and inconsistency between global search efficacy and local development capability in the black-winged kite algorithm for practical problem-solving by proposing a black-winged kite optimization algorithm that integrates the Osprey optimization algorithm and Crossbar enhancement (DKCBKA). Firstly, the adaptive index factor and the fusion Osprey Optimization Algorithm approach are incorporated to enhance the algorithm’s convergence rate, and the probability distribution factor is updated throughout the attack stage. Second, the stochastic difference variant method is implemented to prevent the method from entering the local optima. Lastly, the longitudinal and transversal crossover technique is incorporated to enhance the algorithm’s convergence accuracy and to dynamically alter the population’s global and individual optimal solutions. Fifteen benchmark functions are chosen to test the effectiveness of the enhanced algorithm and to compare the optimization efficiency of each technique. Simulation experiments are performed on the CEC2017 and CEC2019 test sets, revealing that the DKCBKA algorithm surpasses five standard swarm intelligence optimization methods and six improved optimization algorithms regarding solution accuracy and convergence speed. The superiority in meeting real optimization challenges is further demonstrated by the optimization of three real engineering optimization problems by DKCBKA, with optimization capabilities 18.222%, 99.885% and 0.561% higher than BKA, respectively.

Introduction

Optimization challenges are becoming significant in disciplines such as engineering, economics, bioinformatics, and artificial intelligence, and others as human civilization, science, and technology improve. Historically, optimization approaches have been widely utilized across numerous fields, including medical problems^1,2, engineering optimization³, machine learning⁴, image processing⁵, offshore wind generation⁶, and many more. However, many real-world issues are highly nonlinear, multimodal, and unpredictable⁷, making it challenging to solve them using classic optimization strategies.

Meta-heuristic algorithms are categorized into four types according to their sources of motivation: group intelligence algorithms, evolution-based algorithms, human-based algorithms, and physics and chemistry-based algorithms. Optimization algorithms employing population intelligence are utilized to emulate the behavioral traits of biological populations to get the global optimal solution. In accordance with this algorithm, every group is a biological group that can complete tasks that are impossible for individuals to do due to the synergistic behavior of its members. Its features include excellent robustness, ease of implementation, and a simple structure^8,9,10. For example, Spider-Tailed Horned Viper Optimization(STHVO)¹¹, Orangutan Optimization Algorithm (OOA)¹², Pied Kingfisher Optimizer (PKO)¹³, Fossa Optimization Algorithm (FOA)¹⁴, Secretary Bird optimization algorithm (SBOA)¹⁵, Addax Optimization Algorithm (AOA)¹⁶.

The study of metaheuristic algorithms is an area that is always changing to meet the demands of practical applications and ever-morE−complex global optimization issues. The principle of “there is no free lunch” posits that not one algorithm may achieve optimal performance across all optimization and search tasks. Thus, many researchers are now concentrating on improving the approach of metaheuristic algorithms. To address the inadequate optimization efficacy of the conventional Beluga Whale Optimization Algorithm in complex multidimensional issues, a mixed multi-strategy improved Beluga Whale Optimization Algorithm was developed in the literature¹⁷. Similarly, literatur¹⁸ presented a mixed multi-strategy enhanced Sparrow Search Algorithm (MISSA) to resolve the traveling salesman problem, addressing deficiencies in its fundamental Sparrow Search Algorithm (SSA), such as delayed convergence, local optimum, and convergence speed, among other issues. literature¹⁹ proposed a hybrid cuckoo search algorithm (LHCS) utilizing a linearly declining population to enhance the system’s local search capabilities and expedite convergence. A novel sparrow search method (IBSSA), founded on beetle antenna searches, was proposed in the literature²⁰ to enhance the efficacy for the sparrow search algorithm in tackling intricate optimization issues. In order to solve problems like reduced population diversity and To address issues such as diminished varied populations and the inclination to converge towards local optima towards the conclusion of algorithm iterations, a multi-strategy amalgamation of the enhanced Osprey Optimization Algorithm (IOOA) was developed in the literature²¹. To rectify the algorithm’s flaws, including its constrained accuracy, slow convergence rate, and susceptibility to local optima, and performance that depends on parameter selection during the optimization process, literature²² developed an enhanced seagull optimization method with multi-strategy merging.

In practical engineering, swarm intelligent optimization algorithms have been used. For example, Jin et al.²³ combined the Boids model inspired by the bird swarm algorithm with deep reinforcement learning in the UAV pursuit task. Zhu et al.²⁴ proposed an IM algorithm based on Phase Evaluation Enhancement (PHEE) for social network analysis. Sun et al.²⁵ employed a BFC deployment optimization algorithm that is based on breadth-first search to determine the shortest path between the source node and the destination node. They subsequently verified that the algorithm is optimized in terms of end-to-end latency and bandwidth resource consumption.

Asha et al.²⁶ modified the parameters of the recurrent neural network (RNN) utilizing the enhanced Honey Badger Algorithm (SA-HBA) to forecast the optimal efficacy of the RNN. And Gai et al.²⁷ developed a modified YOLO-V4 deep learning method for the detection of cherry fruits Saravanan et al.²⁸ suggested an improved technique for scheduling efficiency to resolve the job scheduling issue in cloud computing.

The main structure of this paper is as follows: Chapter 2 is a literature review, Chapter 3 introduces the basic BKA optimization process, and chapter 4 introduces the enhanced DKCBKA method. As part of the improvement strategy, 1) update the probability factor Ps, introduce dynamic exponential factor, and integrate Osprey optimization algorithm (OOA)²⁹ to improve the attack behavior; 2) Stochastic differential variance strategy is introduced in the migration stage to improve the overall optimization ability; 3) The accuracy and convergence speed of the algorithm are improved by using crossbar method. Horizontal crossing improves the global search ability of the method, while vertical crossing enables the system to escape local optimization. In Chapter 5, the optimization performance of several improvement strategies is evaluated and compared using a total of 15 benchmark functions. The test assesses performance metrics including ideal values, mean values, standard deviations, and convergence curves. In Chapter 6, using the CEC 2017 test function set with 19 functions and the CEC 2019 test function set with 10 functions, the effectiveness of the DKCBKA method is evaluated by comparing it with 6 enhancement algorithms and 5 swarm intelligence optimization algorithms. In the engineering application part of Chapter 7, three traditional engineering situations are used to evaluate the feasibility of the proposed algorithm DKCBKA in the actual engineering environment. Chapter 8 is the discussion and chapter 9 is the conclusion.

Literature review

Overview of existing research

The Black-winged Kite Algorithm (BKA)³⁰, a novel swarm intelligence optimization technique, was initially introduced by Jun Wang et al. and drew inspiration from the natural behaviors and hunting strategies of black-winged kite, and is characterized by strong adaptability, few adjustable parameters, and high convergence accuracy. Despite combining the leader approach and the Cauchy variation method, BKA performs well in determining the best function optimization when compared to other intelligent optimization algorithms³¹. BKA still has a lot of flaws, though. First, there are issues like low population variety, a lackluster ability to search globally, and a tendency to rely too much on local optimization in the end, among other things.

To address the aforementioned issues, Zhang et al.³² suggested a method that integrates a population initiated by logistic chaos map with the osprey optimization algorithm, which altered the initialized population’s random distribution, enhanced population diversity, and sped up the program’s rate of convergence; Xue et al.³³ integrated the BKA approach with the artificial rabbit optimization algorithm to maximize the advantages of the two algorithms for collaborative search. They utilized the master–slave model technique and incorporated effective point sets to initialize the population, hence enhancing the algorithm’s search efficiency and optimizing its performance; Fu et al.³⁴ introduced an improved black-winged kite optimization method (IBKA) by substituting the Gompertz growth model for the attack phase parameter n. This algorithm achieves a balanced approach between local and global search, while exhibiting a reduced rate of step decay; Mu et al.³⁵ used enhanced Circle mapping, fused hierarchical reverse learning, and introduced the Nelder—Mead method to improve the BKA, which improved the optimization performance of the original algorithm; Zhao et al.³⁶ proposed an improved black-winged kite algorithm based on chaotic mapping and adversarial learning, which improves the optimization speed and accuracy of the original algorithm.

This work suggests a black-winged kite approach that integrates multi-strategy improvement (DKCBKA) to address these drawbacks of BKA.

A comparative analysis of this study and recent developments

In this section, we compare and analyze the algorithm DKCBKA proposed in this paper with recent relevant studies, including IM algorithm based on phase evaluation enhancement (PHEE), DRL method of pursuit based on Boids model (BOIDS-PE), Improved SADEKTS algorithm(ISADEKTS)³⁷, optimization algorithm based on breadth-first search (SFCDO) and an improved heuristic algorithm combining ClarkE−Wright saving algorithm and adaptive large neighborhood search, and introducing Q learning to adjust operator weights(IHA)³⁸. The comparison dimensions are algorithm improvement strategies, application problems, advantages and limitations respectively, and the results are shown in Table 1.

Table 1 Comparison of DKCBKA with recent studies.

Black-winged kite optimization algorithm

Black-winged kites nest in wide fields with trees and bushes, farmland, sparse woodlands, and grasslands. They eat field mice, insects, small birds, rabbits, and reptiles. Their hunting style consists primarily of perching on telephone poles and tall trees, waiting for passing birds and insects, and then diving down to catch them. Another strategy is to silently circle, glide, and monitor the ground for hours in the skies before diving down to catch their prey when it appears. Black-winged kites migrate to their breeding areas in the spring (April–May) and leave in the autumn (October–November). An algorithm model inspired by black-winged kites’ hunting abilities and migrating behaviors has been developed.

Initialization stage

The Black-winged Kite algorithm, like other methods, uses a random initialization mechanism.

$$\begin{array}{c}{X}_{i}={BK}_{lb}+rand\left({BK}_{ub}-{BK}_{lb}\right)\end{array}$$

(1)

where rand represents an arbitrary value within the range of [0, 1], i is an integer within the range of 1 to N, ${X}_{i}$ is the starting black-winged kite set, and ${BK}_{lb}$ and ${BK}_{ub}$ denote the lower and higher limits of the $i$-th black-winged kite in the $j$-th dimension, respectively.

Attacking behavior

Birds typically act aggressively because they need to defend their area and for self-defense. They might squawk, peck, and flap their wings in an aggressive manner when they feel threatened. During flight, black-winged kites modify the angle of their wings and tails to suit the speed of the wind. They then hover silently to examine their prey before swiftly diving and attacking. The black-winged kite’s assault behavior can be mathematically modelled as follows:

When p < r, at a great pace, the black-winged kite charges at its target, and the position update equation is

$$\begin{array}{c}{X}_{t+1}={X}_{t}+n\left(1+\mathit{sin}\left(r\right)\right)\times {X}_{t}\end{array}$$

(2)

When p > r, the most recent formula for the black-winged kite’s attack state position when it is hovering in midair is

$$\begin{array}{c}{X}_{t+1}={X}_{t}+n\left(2r-1\right)\times {X}_{t}\end{array}$$

(3)

$$\begin{array}{c}n=0.05\times {e}^{-2\times {\left(\frac{t}{T}\right)}^{2}}\end{array}$$

(4)

where the locations of the black-winged kite in the $t$-th and $(t+1)$-th iterations are indicated by ${X}_{t}$ and ${X}_{t+1}$, respectively, p is an integer valued at 0.9, and r is a stochastic constant inside the interval [0, 1]. T represents the maximum amount of iterations, whereas t is the amount of iterations that have been completed to date.

Migration behavior

Bird migration represents an instinctual behavior in which birds navigate according to environmental cues. The migration behavior of BKA integrates Cauchy’s mutation with the leader’s strategy: The leader relinquishes their position and integrates into the migrating population if the current group’s fitness value is inferior to that of a random population. The current population will maintain its leadership and guidance until it reaches its objective, provided its fitness value exceeds that of the random population. The following mathematical model illustrates the BKA’s dynamic migration conduct:

$$\begin{array}{*{20}c} {X_{{t + 1}} = \left\{ {\begin{array}{*{20}c} {X_{t} + C\left( {{\text{0,1}}} \right) \times \left( {X_{t} - L_{t} } \right)\;\;\;\;} & {F_{i} < F_{{ri}} } \\ {X_{t} + C\left( {{\text{0,1}}} \right) \times \left( {L_{t} - m \times X_{t} } \right)} & {else\;\;\;\;\,} \\ \end{array} } \right.} \\ \end{array}$$

(5)

$$\begin{array}{c}m=2\times \mathit{sin}\left(r+\frac{2}{\pi }\right)\end{array}$$

(6)

${L}_{t}$ symbolizes the commander of the black-winged kite during the $t$-th iteration to date. ${X}_{t}$ and ${X}_{t+1}$ reflect the location of the black-winged kite during the $t$-th and $(t+1)$-th iterations, respectively. ${F}_{i}$ denotes the fitness score of an individual in the $t$-th iteration. ${F}_{ri}$ reflects the fitness value of a black-winged kite during the $t$-th iteration. C(0, 1) symbolizes the Cauchy mutation.

Two parameters define the continuous probability distribution known as the onE−dimensional Cauchy distribution. The density function of probability of the a onE−dimensional Cauchy distribution is shown by the given formula.

$$\begin{array}{c}f\left(x,\delta ,\mu \right)=\frac{1}{\pi } \frac{\delta }{{\delta }^{2}+{\left(x-\mu \right)}^{2}},-\infty <x<+\infty \end{array}$$

(7)

The probability distribution function acquires standard form when δ = 1 and µ equals 0. The following are the formulas that follow:

$$\begin{array}{c}f\left(x,\delta ,\mu \right)=\frac{1}{\pi } \frac{\delta }{{x}^{2}+1},-\infty <x<+\infty \end{array}$$

(8)

Enhanced optimization algorithm for the black-winged kite

The basic black-winged kite optimization algorithm exhibits limitations in its attack phase, where the dynamic selection strategy does not fully enhance adaptive capability. Furthermore, the algorithm’s global search ability is insufficient, resulting in a propensity to converge on local optima. Additionally, the position update formula for alternative members of the population generates new candidates in proximity to the current individual and the best individual, potentially diminishing population diversity and contributing to local optima entrapment and reduced convergence efficiency. Building on previous research, this work suggests a fusion multi-strategy black-winged kite optimization methods to improve the analytical algorithm’s optimization efficiency. The particular strategies are delineated in the following order:

Dynamic exponential factoring and fusion osprey algorithm strategy

The black-winged kite optimization technique employs a dynamic selection strategy for global search during the attack phase; however, it encounters difficulties in properly balancing worldwide search capabilities with local exploitation, rendering it susceptible to local optimization. To augment the method’s improvement efficacy for seeking, this work integrates the Osprey algorithm’s method for updating the black-winged kite’s place with a dynamic index factor and selection strategy.

The nonlinear probability element $\upomega$ is introduced to modify the original linear segmentation factor $\omega$, as expressed below:

$$\begin{array}{c}\omega ={-e}^{{\left(1-\frac{t}{T}\right)}^{3}}\end{array}$$

(9)

The dynamic exponential factor is crucial in optimizing the objective function, as an appropriate dynamic factor can enhance algorithm convergence and effectively balance domestic and international search. In the initial phase of iteration, a dynamic exponential factor is incorporated into the positional iteration formula to improve the targeted search capabilities of the method. This adjustment facilitates effective exploration of the ideal outcome, compensates for the initial limitations in local optima, and improves overall search efficacy in subsequent stages. The formula for the dynamic exponential factor is presented below:

$$\begin{array}{c}\alpha = \left ({e}^{\left(1-\left(\frac{t}{T}\right)^{2}\right)}\right)^{2kt}\end{array}$$

(10)

If k represents a random variable in an exponential distribution, t represents the current number of iterations, and t represents the maximum number of iterations.

During the attack phase, the exploration strategy of the osprey optimization method can expand the target region, inhibit the technique from converging on an individual optimum, and augment the global search capabilities of the BKA.

$$\begin{array}{c}{X}_{i,j}^{{p}_{1}}={X}_{i,j}+{r}_{i,j}\cdot \left(S{F}_{i,j}-{I}_{i,j}\cdot {X}_{i,j}\right)\end{array}$$

(11)

where $S{F}_{i,j}$ is the fish chosen from $i$-th osprey during the $j$-th dimension, ${r}_{i,j}$ is an arbitrary value in [0, 1], ${I}_{i,j}$ is a random value in the collection {1, 2}, and ${X}_{i,j}^{{p}_{1}}$ is the new position of the $i$-th osprey in the $j$-th dimension.

A dynamic exponential factor is incorporated into the assault phase of the black-winged kite, which enhances the swarm intelligence algorithm’s robustness, global search capability, and convergence speed by dynamically modifying the parameters to prevent premature convergence. Meanwhile, fusing the osprey optimization algorithm in the attack phase improves the fusion of the two swarm intelligence algorithms, which can combine the advantages of each and make up for the shortcomings of a single algorithm, thus enhancing the overall effectiveness. The Black-winged Kite algorithm’s precision in searching in the local area can be enhanced by the fusion, which also concentrates on fine search during the attack phase of the osprey optimization algorithm, thereby facilitating the discovery of a superior solution.

The subsequent formula delineates the position upgrade for the enhanced algorithm during the attack phase.

$$\begin{array}{*{20}c} {X_{{t + 1}} = \left\{ {\begin{array}{*{20}c} {\alpha \times X_{t} + n\left( {1 + sin\left( r \right)} \right) \times X_{t} } & {\omega < r} \\ {X_{t} + r_{{i,j}} \cdot \left( {SF_{{i,j}} - I_{{i,j}} \cdot X_{t} } \right)\;} & {else\;} \\ \end{array} } \right.} \\ \end{array}$$

(12)

Differential variation randomized

An examination of the relocation process of the black-winged kite reveals that the positional adjustment of individuals within the population occurs in proximity to the current individual ${X}_{t}$ and the optimal individual ${L}_{t}$, indicating that other individuals are directed to migrate towards the optimal area represented by ${L}_{t}$. When ${L}_{t}$ represents a locally optimal solution, the population will likely converge around this solution as iterations advance, resulting in diminished population variety, which may induce untimely convergence and decrease the precision with the algorithm’s convergence. To ensure convergence, the population intelligence algorithm implements an optimal preservation strategy following each iteration. To address this challenge, it is customary to implement mutation operations to enhance population variety and prevent convergence to local optima. Literature³⁹ introduced an enhanced whale optimization algorithm utilizing stochastic differential mutation, drawing inspiration from the differential evolutionary algorithm.

This idea is adopted in this paper by incorporating a stochastic differential mutation strategy during the migration phase. This technique employs the present individual, the most effective private, and randomly selected individuals from the community to generate a new individual. By incorporating this strategy into the migration phase of the black-winged kite algorithm, the search diversity can be enhanced, the global search capability can be enhanced, and the algorithm can be prevented from entering the local optimal state, as illustrated by the subsequent expression:

$$\begin{array}{c}{X}_{t+1}=r\times \left({L}_{t}-{X}_{t}\right)+r\times \left({X}_{p}^{\prime}\left(t\right)-{X}_{t}\right)\end{array}$$

(13)

where ${\text{X}}_{\text{t}+1}$ represents a novel entity acquired through stochastic differential evolution, and r is a variable constrained inside the interval of 0 to 1. ${\text{L}}_{\text{t}}$ is the best person’s present location. ${\text{X}}_{{\text{p}}}^{\prime} \left( {\text{t}} \right)$ designates the position of a randomly chosen member from a cohort.

Vertical and horizontal crossover strategy

The black-winged kites in the population exhibit a tendency to congregate around optimal individuals as the amount of repetitions grows. The method’s ability to find the best solution is hampered by this trend, which gradually reduces population variety. This paper presents a crossover strategy that incorporates both vertical and horizontal elements, specifically detailing horizontal and vertical crossover methods. In the literature^40,41, the vertical and horizontal crossover technique serves to enhance the method’s convergence efficiency and international inquiry capabilities while reducing local optimality. The horizontal crossover operation facilitates an expansion of the search range and diminishes search blind spots, thereby further improving the algorithm’s international inquiry ability. Premature convergence in many population-based intelligent search algorithms frequently results from the stagnation of certain dimensions within the population. By making it easier to activate these stagnant dimensions, vertical crossover enables the algorithm to circumvent local optimal solutions.

Crossover strategy can provide a better balance between exploration and development of algorithms, and effectively improve the convergence accuracy. Applying it after the migration phase can help the algorithm explore new regions while also digging deeper into areas of potential that have been found. In addition, the crossover operation effectively enhances population diversity. The vertical and horizontal crossover strategy incorporates a competitive mechanism that facilitates population updates by evaluating the relative strengths and weaknesses of offspring compared to their parents. Sequential execution of horizontal and vertical crossover improves the algorithm’s convergence speed and solution correctness. A quick explanation of these two crossover processes is given below.

A transverse crossover is an arithmetic crossover that involves two separate persons across all dimensions. Members of the population are originally partnered randomly, followed by the execution of a transverse crossover between the two paired individuals, as represented by the following equation.

$$\begin{array}{c}{X}_{i,d}^{hc}={a}_{1}*X\left(i,O\right)+\left(1-{a}_{1}\right)*X\left(j,O\right)+{c}_{1}*\left(X\left(i,O\right)-X\left(j,O\right)\right)\end{array}$$

(14)

$$\begin{array}{c}{X}_{j,d}^{hc}={a}_{2}*X\left(j,O\right)+\left(1-{a}_{2}\right)*X\left(i,O\right)+{c}_{2}*\left(X\left(j,O\right)-X\left(i,O\right)\right)\end{array}$$

(15)

where ${a}_{1}$, ${a}_{2}$ are [0,1] random numbers, ${c}_{1}$, ${c}_{2}$ are [− 1,1] random numbers, $X\left(i,O\right)$ and $X\left(j,O\right)$ are the parent individuals after pairing of $X\left(i\right)$ and $X\left(j\right)$ in the d-dimension, and ${X}_{i,d}^{hc}$ and ${X}_{j,d}^{hc}$ stand for the d-dimensional $X\left(i,O\right)$ and $X\left(j,O\right)$ produced by lateral crossover, respectively. offspring. Individuals with lower objective function values are kept after the produced children are compared to their parents.

A longitudinal crossover refers to a crossover variant involving all individuals across two distinct dimensions. The BKA algorithm may demonstrate a propensity to converge to a local optimal value in subsequent iterations, typically resulting from the formation of a local optimum in a specific dimension during the update process. Each individual executes a longitudinal crossover to modify a single dimension while maintaining the integrity of the other dimensions. This approach allows the stagnant dimension to escape a local optimum without compromising the potential of another dimension that may also represent a local optimum. Two distinct dimensions, ${d}_{1}$ and ${d}_{2}$, are randomly chosen for longitudinal crossover to produce offspring using the subsequent formula:

$$\begin{array}{c}{X}_{i,{D}_{1}}^{vc}=b*X\left(i,{D}_{1}\right)+\left(1-b\right)*X\left(j,{D}_{2}\right)\end{array}$$

(16)

where $b$ is a stochastic variable inside the interval [0,1] and ${X}_{i,{D}_{1}}^{vc}$ is the parent generating offspring by longitudinal crossover in ${D}_{1}$ and ${D}_{2}$ dimensions. Individuals exhibiting lower objective function values are retained following the comparison of the offspring with their progenitors.

DKCBKA implementation procedure and pseudo-code

The pseudo-code and complete implementation procedure of DKCBKA are detailed below, and Fig. 1 illustrates the algorithm’s flowchart.

Fig. 1

DKCBKA flow chart.

Step 1 Initialize the location of individual black-winged kites, within the search range, randomly generate an N × D dimensional matrix to store the place information of the population; set the algorithm related parameters, assigning values to the population size N, the maximum iterations T, the dimensionality D, and the population search boundaries $lb$, ub, and so on.

Step 2 Compute and order the fitness ${X}_{t}$ of every individual within the population. and record the current best fitness value noted as ${L}_{t}$.

Step 3 update the parameters ω and α according to Eqs. (9) and (10).

When $\omega$<rand, a dynamic exponential factor is introduced to update the black-winged kite position throughout the attack stage according to the improved position update formula (12).

When $\omega$>rand, the position update formula (12) of the fundamental osprey optimization algorithm is used to revise the location of the black-winged kite; the fitness value of the black-winged kite is computed, and a determination is made regarding the revision of the desired position and target fitness score.

Step 4 Update the black-winged kite migration stage position in accordance with the judgment condition of Eq. (5).

Step 5 Update the black-winged kite position in accordance with the random difference variant of Eq. (13); calculate the black-winged kite fitness value and determine whether to update the target position and target fitness value.

Step 6 Select random positional crossover mutations to update black-winged kite positions according to the longitudinal crossover Eqs. (14)–(16).

Step 7 Ascertain the necessity of updating the optimal position by calculating the fitness score.

Step 8 Evaluate whether the algorithm satisfies the termination criterion; if it does, terminate the main iteration and display the target place and target value; if not, back to step 3.

Algorithm 1

Improved the pseudocode of black-winged kite algorithm

Analysis of the DKCBKA algorithm’s time complexity

This paper examines the temporal complexity of the DKCBKA algorithm. Population initialization, location updates, fitness assessment during iterations, and vertical and horizontal crossover operations are the main parts for the method. The initialization process exhibits a temporal challenge of O(N × D), with N representing the group’s size and D denoting the problem’s dimension. In each iteration, the time complexity for computing the fitness values within the population is O(N × D). The dynamic exponential factor in the attack strategy is enhanced based on the original linear factor. The original attack phase formula is replaced by the Osprey optimization algorithm’s global search technique. Both modifications maintain the algorithm’s temporal challenge at O(N × D). Additionally, the temporal challenge of the stochastic difference variant during the migration phase is O(N × D). The longitudinal and transversal crossover operation is segmented into two components, horizontal and vertical, with respective time complexities of O(N/2 × D) and O(N × D). The overall temporal challenge for each iteration is O(2.5 × N × D). The algorithm executes T iterations, resulting in a temporal challenge of O(2.5 × T × N × D). The simplified time challenge is typically expressed as O(T × N × D),disregarding the constant factor. The DKCBKA algorithm described in this study has a time complexity that is comparable to the BKA algorithm.

Algorithm abbreviation

The acronyms for each method and comparison algorithm used in this study are displayed in Table 2.

Table 2 Algorithm abbreviation table.

Analysis of experimental simulation results

Experimental environment

The computer configuration employed for the simulation tests in this study is an Intel(R) Core(TM) i5-10210U processor operating at 1.60 GHz, with 12.0 GB of RAM, running the Windows 11 operating system, and utilizing the Matlab2020(b) computational environment.

Introduction to test functions

This study evaluates the algorithm’s optimization capabilities and efficacy by conducting simulated tests that employ 15 established benchmark test functions. The standard test functions’ names, dimensions, value ranges, and theoretically ideal values are presented in “Supplementary information”. The singlE−peak evaluation functions F1–F7 assess the algorithm’s precision and convergence rate. The multi-peak evaluation functions F8–F13 are designed to evaluate the algorithm’s global search capability. The composite evaluation functions F14 and F15, with a singular global optimum and several local optima, the assessment of the algorithm’s stability and local development capabilities is conducted. N = 50 is the population size, T = 1000 is the maximum amount of iterations, the dimension is D = 30, and 30 iterations are carried out to determine the ideal value, standard deviation, and mean for comparison analysis.

Comparison of optimization performance of each improvement strategy

Three improvement strategies—BKA (DBKA) with the addition of dynamic exponential factor and fusion of osprey algorithm strategy, BKA (KBKA) with the addition of stochastic differential variance strategy, and BKA (CBKA) with the addition of longitudinal and transversal crossover strategy—are employed in this paper to confirm the accuracy and efficacy of the algorithms. BKA, DBKA, KBKA, CBKA, and DKCBKA were evaluated using 15 benchmark functions exhibiting various optimization characteristics. To assess how well the aforementioned algorithms find the best solution, the population size is set at N = 50, the maximum iteration at T = 1000, the dimensionality of a search space is D = 30. The experiment is conducted independently 30 times, with results presented as optimal value, mean, and standard deviation.

The ideal value, the average, and deviation from the mean of DKCBKA at 30 dimensions are substantially superior to those of BKA, according to Table 3. DKCBKA demonstrates convergence to the ideal value in theory in both simple single−peak functions F1–F6 and multiple−peak functions F9 and F11. The mean outcomes closely align with the theoretical desired values of the corresponding functions, exhibiting a standard deviation of 0. This indicates that DKCBKA exhibits superior optimization performance and enhanced robustness. While DKCBKA does not attain convergence to the hypothetical optimal value in F7–F8 and F14–F15, it has the utmost convergence precision when compared to other techniques. The complex multi-peak functions F12 and F13 indicate that the desired value, mean, deviation from the mean of DKCBKA and CBKA outperform the original approach by more than 26 orders of magnitude. This means that the addition of the vertical and horizontal crossover techniques significantly enhances the method’s ability to ascertain this ideal result and avoid neighborhood optima. DKCBKA surpasses the fundamental algorithm regarding optimization capability. The addition of a dynamic index component, together with the osprey optimization algorithm method and stochastic difference variant strategy, significantly enhances both method rate and convergence precision. Additionally, a balance between regional investigation capabilities and worldwide inquiry is made possible by the introduction of longitudinal and transversal crossover tactics. When these three tactics are combined, the original algorithm’s performance in finding the best answers is significantly improved.

Table 3 Compares the optimization outcomes of 15 benchmark functions (F1–F15) utilizing different approaches to improvement.

Figure 2 illustrates the linear image iteration curves produced by the DKCBKA for functions F1–F2, F5–F7, F9, F11–F13, and F15. This demonstrates that the fitness values derived from the enhanced method at the initial stages of iteration are closely aligned with the optimal fitness values achieved at final convergence. The convergence curves of functions F4, F10, and F14 exhibit rapid convergence, albeit with slight fluctuations. The DKCBKA convergence curve in the F8 function shows several inflection points, suggesting that the suggested strategy can more easily exit the local most effective than the original technique. The global most effective is reached at the quickest rate in the F3 function image, and the DKCBKA’s convergence rate is noticeably higher than the basic BKA’s. The DKCBKA clearly shows the best optimization performance out of all the function images in Fig. 2.

Fig. 2

Convergence graph for comparison between strategies.

In conclusion, DKCBKA offers numerous advantages for identifying the best possible answer of a function and has superior performance in convergence and optimization search efficiency.

Comparison of DKCBKA with other improved algorithms

The DKCBKA algorithm is evaluated against the initial BKA algorithm and six superior enhanced optimization techniques.to further validate its effectiveness: the sand cat swarm optimization algorithm combining elite decentralization and crossover strategy and its application (CWXSCSO)⁴², the whale optimization algorithm based on elite dyadic and cross-optimization (ECWOA)⁴³, the multi-strategy chimpanzee optimization algorithm and its application to engineering problems (EOSMICOA)⁴⁴, the nonlinear parametric grey wolf optimization algorithm based on elite learning (IGWO)⁴⁵, the subtractive optimizer algorithm incorporating golden sines (GSABO)⁴⁶, and the improved golden jackal optimization algorithm based on hybrid strategy (IWKGJO)⁴⁷. In order to fairly examine the performance of DKCBKA in high dimensions, the total population size for every method in this experiment is established at N = 50, iteration T = 1000, and dimensions are 30 and 100 dimensions, respectively. Each experiment is carried out independently 30 times. Table 4 displays the parameter configurations of the algorithms that are the subject of this paper.

Table 4 Algorithmic parameter.

CEC2017 test function information

Nineteen of the twenty-nine functions in the CEC2017 test set were chosen to assess DKCBKA’s optimization performance. The algorithm’s speed and efficiency in identifying a singular optimal solution can be accurately assessed, as F1 and F3 are single−peak operates with one ideal solution. Conversely, the straightforward multi-peak functions F4–F10, that have numerous local optimum answers, are employed in evaluating the method’s capacity to evade local optima. The algorithm’s ability to address more complex optimization challenges is evaluated using the hybrid functions F11–F20, which combine the characteristics of single−peak and multi-peak functions. These functions complicate the optimization of algorithms and evaluate their flexibility and resilience across many contexts. “Supplementary information” presents the essential information regarding the CEC2017 test function.

Analysis of experimental results

Table 5 contains the optimization indexes, which are denoted as min., avg., and std., the optimal value, average value, and standard deviation, respectively. Examining the comparative statistics presented in Table 5 at a dimension of 100 shows that DKCBKA outperforms the original BKA algorithm and performs better regarding optimization than the other six improved optimization techniques. The DKCBKA shows better optimal and average fitness values in functions C1 and C3, having an average deviation ranking somewhat lower than those of the CWXSCSO and GSABO. However, in functions C4, C11–C15, and C17–C19, the DKCBKA outperforms comparative algorithms, including IWKGJO, across all three optimization indices. The standard deviation of the algorithm described in this study is lower than that of the GSABO in C5, C7, C8, and F20, and it ranks second to the CWXSCSO in C9 and C11, and third in C10. Furthermore, in C16, the IWKGJO outperforms DKCBKA. The proposed approach attains the highest optimum value and a mean fitness score among the given functions. The efficiency of the DKCBKA is subpar compared to the ECWOA concerning function C6. The DKCBKA exhibits a comparative advantage, signifying its capacity to tackle intricate optimization challenges in high-dimensional spaces, as well as remarkable adaptability and resilience in diverse contexts.

Table 5 100-dimensional optimization metrics for CEC2017.

The 100-dimensional convergence image in Fig. 3 demonstrates that the DKCBKA has greater convergence accuracy compared to advanced methods such as the IWKGJO, particularly in functions C1–C20. In contrast to previous comparison algorithms and the initial method, the DKCBKA can converge rapidly before 200 iterations in C5–C10, C13, C15–C17, and C19–C20. Additionally, each function’s convergence curves experience slight oscillations during the prE−convergence phase, demonstrating the algorithm’s capacity to diverge from its regional optimum.

Fig. 3

Convergence curve of the 100-dimensional function for CEC2017.

The optimization results of the DKCBKA on 19 CEC2017 test functions demonstrate enhanced performance relative to the initial method and six other advanced sophisticated algorithms for solution precision, convergence velocity, and stability.

CEC2017 Wilcoxon rank sum test

The effectiveness and precision of different approaches are illustrated by executing the ideal fitness values, typical fitness values, and average deviations of the seven compared methods independently for 30 iterations. However, this does not confirm whether DKCBKA and the seven algorithms above differ significantly in their capacity to resolve intricate optimization challenges. This section evaluates the optimization effectiveness of the BKA, GSABO, ECWOA, EOSMICOA, IGWO, CWXSCSO, and IWKGJO by applying the DKCBKA to the Wilcoxon rank-sum test for the 19 test functions in the test set CEC2017 in different dimensions. Relevant Wilcoxon rank sum test results and values for P are shown in Table 6. For hypothesis testing, 5% is the crucial amount, which is the significance level. The two comparison methods are thought to differ significantly if the P-value is less than 5%; if it is larger than 5%, the distinction between DKCBKA and the comparison algorithm with regard to of optimization results is not immediately evident. The performance of the DKCBKA is “far superior than,” “the same to,” or “lower to” other comparison algorithms, as shown by the symbols “+ ”, “ = ”, and “−”.

Table 6 Wilcoxon rank-sum test results for the 100-dimensional problem in CEC2017.

From Table 6, comparing the DKCBKA to the GSABO, IGWO, and EOSMICOA, it has a 95% chance of producing a significant difference in the overall optimization results. In C20, it performs marginally inferior than the BKA and IWKGJO algorithms, and in C5 and C8, it performs inferior than the ECWOA and IWKGJO, respectively. The ECWOA and CWXSCSO outperform the DKCBKA in C16 and C17, respectively.

Analysis of CEC2019 test function results

For thoroughly assess the optimization effectiveness of the DKCBKA, we selected 10 CEC2021 test functions characterized by distinct optimization features. “Supplementary information” displays the fundamental details of the CEC2019 test function. The DKCBKA was compared with five traditional optimization algorithms: GOOSE Algorithm (GO)⁴⁸, Nutcracker Optimization Algorithm (NOA)⁴⁹, Parrot Optimization Algorithm (PO), Seagull Optimization Algorithm (SOA)⁵⁰, and Sparrow Search Algorithm (SSA)⁵¹. The following settings are set: population size N = 50, maximum iterations T = 1000, and dimensionality D = 10. Table 7 shows the parameter settings of the comparison algorithm.

Table 7 Algorithmic parameter.

The optimization indexes in Table 8 are respectively the optimal value, average value and standard deviation represented by min, avg and std. Table 8 demonstrates it, relative to six other advanced optimization algorithms, the DKCBKA exhibits enhanced performance in FC1–FC10 and achieves the optimal value. Across all 10 functions, the enhanced method, DKCBKA, has a significantly higher convergence accuracy than the comparison approach. Additionally, the average fitness value ranks first. However, in functions FC2 and FC10, the DKCBKA performs somewhat worse than the SSA approach regarding standard deviation. In FC1, FC3, FC5, and FC9, the performance is notably robust. The SSA outperforms the DKCBKA in FC2 and FC10. The NOA in FC4, FC6, FC7, and FC8 is slightly more effective than the enhanced technique described in this study.

Table 8 CEC2019 different function optimization indicators.

Figure 4 illustrates that the DKCBKA has enhanced optimization performance relative to the other methods. In FC1-FC3, the DKCBKA demonstrates a rapid convergence speed, facilitating its attainment of the global optimum with efficiency. In the FC6, FC9, and FC10 test routines, the initial value of the DKCBKA at the start of the iteration is nearly equivalent to the worldwide ideal In comparison to the other algorithms, the DKCBKA demonstrates superior optimization accuracy, as evidenced by the results from FC4, FC7, and FC8.

Fig. 4

CEC2019 function convergence curves.

In conclusion, the CEC2019 test set demonstrates that the DKCBKA outperforms five traditional optimization algorithms.

CEC2019 Wilcoxon rank sum test

The rank sum check is a quantitative statistical method that is used to determine whether there is a significant variation in the distribution locations of two distinct samples. The rank sum test is effective in assessing performance differences among various algorithms on specific functions in optimization studies of method performance comparison. This section of the article compares the results of the CEC2019 test benchmark. The optimization efficacy of the GO, NOA, PO, SOA, and SSA algorithms is statistically assessed against the performance of the DKCBKA algorithm employing the Wilcoxon rank sum test.

Table 9 indicates that the DKCBKA outperforms both the NOA and SOA, but DKCBKA is inferior to PO and SSA algorithm in FC1, and inferior to PO and GO in the functions FC2 and FC10, respectively, but it surpasses the comparison technique utilized in the other functions, and the optimization performance is substantial. The findings indicate that DKCBKA possesses a substantial optimization superiority compared to the five swarm intelligence methods.

Table 9 CEC2019 Wilcoxon rank-sum test results.

Application examples

Mathematical models and mechanical optimization problems are strongly related, determining the design variables, objective functions, and constraints is essential to developing the optimal design mathematical model. In this section, DKCBKA is chosen to be run 30 times for comparative analysis with WOA⁵², HHO⁵³, GWO⁵⁴, OOA, SO⁵⁵, and BKA for three common engineering problems: the pressure vessel design problem, the triplE−bar truss design problem, and the speed reducer design problem. To assess the optimization efficacy of DKCBKA in engineering applications, the group size is established at 30, and the total number of iterations is fixed at 1000.

Pressure vessel design issues

The pressure vessel is designed as efficiently as possible to reduce the overall production cost. Shell thickness (Ts), head thickness (Th), inner radius (R), and cylinder length (L) are four of the optimization variables. Figure 5 illustrates the convergence diagram of its optimization of structure. The upper and lower limits of the above size parameters are set in DKCBKA, and the penalty function method is used, when the design exceeds these limits, the algorithm will give a large penalty. The cost function is considered as part of the optimization problem, and the cost is controlled by minimizing $minf\left(\overrightarrow{x}\right)$ by the objective function. The following is the pressure vessel design’s mathematical model:

Fig. 5

Optimization convergence plot for pressure vessel design problem.

Variant

$$\overrightarrow{x}=\left[{x}_{1}{x}_{2}{x}_{3}{x}_{4}\right]=\left[{T}_{s}{T}_{h}RL\right]$$

Function

$$minf\left(\overrightarrow{x}\right)=0.6224{x}_{1}{x}_{3}{x}_{4}+1.7781{x}_{2}{x}_{3}^{2}+3.1661{x}_{1}^{2}{x}_{4}+19.84{x}_{1}^{2}{x}_{3}$$

Subject to

$${g}_{1}\left(\overrightarrow{x}\right)=-{x}_{1}+0.0193{x}_{3}\le 0$$

$${g}_{2}\left(\overrightarrow{x}\right)=-{x}_{3}+0.00954{x}_{3}\le 0$$

$${g}_{3}\left(\overrightarrow{x}\right)=-\pi {x}_{3}^{2}-\frac{4}{3}\pi {x}_{3}^{3}+1296000\le 0$$

$${g}_{4}\left(\overrightarrow{x}\right)={x}_{4}-240\le 0$$

design variable

$${x}_{\text{1,2}}\in [\text{0.1,99}]$$

$${x}_{\text{3,4}}\in [\text{10,200}]$$

Figure 5 illustrates the optimal convergence rate and precision of the DKCBKA. Table 10 indicates that the total cost of the optimized design, achieved by DKCBKA is 6037.613549, which is 15.619% less than the base BKA and lowers the production cost by 18.222% when compared to WOA, HHO, GWO, OOA, and SO algorithms by 18.222%, 12.146%, 10.951%, 96.328%, and 11.488%, respectively. According to the results, DKCBKA has clear advantages over existing algorithms and can reduce the overall cost of pressure container design.

Table 10 Optimization results for pressure vessel design problems.

Gear train design problem

In mechanical engineering, designing gear trains is a complex combinatorial optimization challenge. The main goal is to minimize the gear ratio—the ratio of input shaft rotation to output wheel speed—to reduce overall transmission cost. This involves determining the optimal number of teeth for each gear. Specifically, ${N}_{a}({x}_{1})$, ${N}_{b}({x}_{2})$, ${N}_{d}({x}_{3})$, and ${N}_{f}({x}_{4})$ represent the number of teeth on gears A, B, D, and F. The geometric constraint problem is that the size and shape of the gear need to meet specific geometric standards, so a reasonable range of gear parameters should be set in the optimization model, and the penalty function or constraint optimization algorithm is used to deal with these constraints. Finding the best combination of these variables is crucial for achieving the lowest gear ratio while maintaining functionality and efficiency.

Function

$$minf\left(x\right)=\left(\frac{1}{6.931}-\frac{{x}_{2}{x}_{3}}{{x}_{1}{x}_{4}}\right)^{2}$$

Value range

$$12\le {x}_{i}\le 60,i=\text{1,2},\text{3,4}$$

The optimization challenge for the gear train design problem is effectively addressed by DKCBKA, demonstrating strong stability and convergence, as illustrated in Table 11 and Fig. 6. According to the information provided in Table 11, the adaptation value determined by the DKCBKA calculation is the lowest. This lowers construction costs to varying degrees in comparison to the comparative algorithms, demonstrating the validity and potential usefulness of DKCBKA in real-world engineering applications.

Table 11 Optimization results of the gear train design problem.

Fig. 6

Optimization convergence plot for gear train design problem.

Reducer design issues

The speed reducer design issue is a mechanical optimization challenge aimed at minimizing the weight of the speed reducer by optimizing seven parameters while adhering to constraints related to shaft stresses, bending stresses on gear teeth, transverse shaft deflections, and surface pressures. The seven design variables are facial breadth (b), quantity of gear teeth (p), tooth component (m), length of the initial shaft between the bearings (${l}_{1}$), length of the secondary shaft between the bearings (${l}_{2}$), diameter of the initial shaft (${d}_{1}$), and diameter of the secondary shaft (${d}_{2}$) denoted as ${x}_{1}$-${x}_{7}$. In order to ensure that the transmission ratio and efficiency of the reducer meet the design requirements, the target range of transmission ratio and efficiency is set in the optimization model, and the optimization algorithm is used to find the design that meets these conditions. The following delineates the mathematical treatment of the challenge:

Variant

$$\overrightarrow{x}=\left[{x}_{1}{x}_{2}{x}_{3}{x}_{4}{x}_{5}{x}_{6}{x}_{7}\right]=[bmp{l}_{1}{l}_{2}{d}_{1}{d}_{2}]$$

Function

$$minf\left(x\right)=(0.7854{x}_{1}{x}_{2}^{2}\left(3.3333{x}_{3}^{2}+14.9334{x}_{3}-43.0934\right)-1.508{x}_{1}\left({x}_{6}^{3}+{x}_{7}^{2}\right)+7.4777\left({x}_{6}^{3}+{x}_{7}^{3}\right)+0.7854({x}_{4}{x}_{6}^{2}+{x}_{5}{x}_{7}^{2})$$

Subject to

$${g}_{1}\left(x\right)=\frac{27}{{x}_{1}{x}_{2}^{2}{x}_{3}}-1\le 0$$

$${g}_{2}\left(x\right)=\frac{397.5}{{x}_{1}{x}_{2}^{2}{x}_{3}}-1\le 0$$

$${g}_{3}\left(x\right)=\frac{1.93{x}_{5}^{3}}{{x}_{1}{x}_{6}^{4}{x}_{3}}-1\le 0$$

$${g}_{4}\left(x\right)=\frac{1.93{x}_{5}^{3}}{{x}_{2}{x}_{7}^{4}{x}_{3}}-1\le 0$$

$${g}_{5}\left(x\right)=\frac{\left[\left(745\left(\frac{{x}_{4}}{{x}_{2}{x}_{3}}\right)\right)^{2}+16.9\times {10}^{6}\right]^{1/2}}{110{x}_{6}^{3}}-1\le 0$$

$${g}_{6}\left(x\right)=\frac{\left[\left(745\left(\frac{{x}_{5}}{{x}_{2}{x}_{3}}\right)\right)^{2}+157.5\times {10}^{6}\right]^{1/2}}{85{x}_{7}^{3}}-1\le 0$$

$${g}_{7}\left(x\right)=\frac{{x}_{2}{x}_{3}}{40}-1\le 0$$

$${g}_{8}\left(x\right)=\frac{5{x}_{2}}{{x}_{1}}-1\le 0$$

$${g}_{9}\left(x\right)=\frac{5{x}_{1}}{12{x}_{2}}-1\le 0$$

$${g}_{10}\left(x\right)=\frac{1.5{x}_{6}+1.9}{{x}_{4}}-1\le 0$$

$${g}_{11}\left(x\right)=\frac{1.1{x}_{7}+1.9}{{x}_{5}}-1\le 0$$

Value range

$$2.6\le {x}_{1}\le 3.6$$

$$0.7\le {x}_{2}\le 0.8$$

$$17\le {x}_{3}\le 28$$

$$7.3\le {x}_{4}$$

$${x}_{5}\le 8.3$$

$$2.9\le {x}_{6}\le 3.9$$

$$5.0\le {x}_{7}\le 5.5$$

Table 12 displays the experimental findings for resolving the gearbox design’s minimum weight issue. The gearbox design problem’s optimization convergence plot is displayed in Fig. 7. According to Table 8’s data, the DKCBKA algorithm’s minimum weight is 2994.4711, indicating a good optimization accuracy and a 0.561% reduction over the traditional BKA. The convergence graph in Further evidence that DKCBKA is more capable of solving mechanical optimization problems comes from Fig. 7, which shows that it has a higher convergence efficiency than other methods.

Table 12 Optimization results of the gear train design problem.

Fig. 7

Optimization convergence plot for the reducer design problem.

Discussions

Improvements in a black-winged kite algorithm that incorporates a osprey optimization algorithm with a longitudinal crossover strategy can be attributed to the following. First, the black-winged kite algorithm’s assault phase is enhanced by the dynamic exponential factor, and the osprey optimization algorithm is incorporated to enhance the algorithm’s global search capability and convergence speed, as well as to prevent premature convergence. Following the migration phase, a stochastic differential mutation strategy is implemented to enhance the diversity of the population and balance the algorithm’s global search and local exploration capabilities. This strategy is based on the mutation behavior in the differential evolution algorithm. Lastly, the algorithm’s convergence accuracy is enhanced by the inclusion of the vertical and horizontal crossover strategy at the end. This strategy includes both horizontal and vertical crossover.

Secondly, the superiority between the strategies was compared through 15 functions in the benchmark test set, the superiority of DKCBKA in comparison with 6 good improved algorithms was tested through the CEC2017 test set as well as the performance of DKCBKA in comparison with 5 swarm intelligence algorithms through the CEC2019 test set.

Lastly, the efficacy of DKCBKA in real-world problems is evaluated using three real-world engineering examples: pressure vessel design issues, gear train design problems, and reducer design issues.

The above experimental analysis can be obtained:

• (1) The improved algorithm DKCBKA proposed in this paper occupies a relative advantage over the 15 compared algorithms, and the optimization performance improves significantly and has a good overall performance.

• (2) DKCBKA shows an absolute advantage in the 15 benchmark functions, and the optimization performance is greatly improved compared to the original algorithm. The optimization accuracy of DKCBK is known to be better than 6 improved optimization algorithms in 95% of the cases by 20 functions in CEC2017, and the optimization accuracy of DKCBKA is better than other 5 swarm intelligence algorithms in all 10 functions in CEC2019. And the nonparametric statistical verification of the simulation results by Wilcoxon rank sum test shows that DKCBKA dominates the disadvantage in absolutely few cases. Finally three engineering examples show that the optimization performance of DKCBKA is improved by 18.222%, 99.885% and 0.561% respectively compared to the original algorithm.

Although the algorithm proposed in this paper significantly enhances the optimization performance of the original algorithm, it still has certain constraints. Specifically, using the maximum number of iterations to test functional performance may lack fairness and can be used instead of using the objective function to evaluate the number of iterations. The application of DKCBKA in practical engineering can be more novel.

Future research may apply the DKCBKA to novel engineering examples, including offshore wind turbine structural foundation optimization and other related issues, while further verifying the algorithm’s performance through practical applications. Other test sets, such as CEC2011, can also be used to evaluate algorithm performance in the future. CEC2011, CEC2017, and CEC2019 test sets can be used to test the performance of the improved algorithm, including unimodal, multi-modal, composite problems, and support multiple dimensional testing. The difference is that CEC2011 has fewer problems and less complexity, which is suitable for preliminary algorithm verification; CEC2017 adds more composite and rotation problems, significantly improving the complexity, suitable for medium-complexity algorithm evaluation; CEC2019 further increases the complexity of the problem, making it more challenging and suitable for high-complexity algorithm evaluation.

Conclusion

This study provides a BKA that enhances the optimization power by integrating the Osprey optimization process with vertical and horizontal crossover techniques. The algorithm first alters the position update equation in the assault phase by integrating the dynamic index factor and the Osprey optimization technique. This approach enhances the method’s precision and convergence rate. The program employs the mutation principle from the differential evolution algorithm to improve population variety and promote movement away from local optima via random differential variation during the migration phase. A vertical and horizontal crossover technique is introduced for improving group variety and boost the accuracy of algorithm convergence. To assess the optimization efficacy using the improved technique, the DKCBK is evaluated against the original algorithm across 15 benchmark functions from CEC2005. This is further validated by analyzing 19 functions from CEC2017 alongside 10 functions from CEC2019, utilizing six improved algorithms, including IWKGJO, and five swarm intelligence optimization algorithms, including GO. Practical illustrations in the design of pressure tanks, gear train, and reducers exemplify DKCBKA’s engineering efficiency proficiency. The results show that the proposed DKCBKA has higher convergence speed and robustness, and the global search and local exploration capabilities are improved.