Introduction

The development of neural networks is an amazing feat of nature that results in the emergence of collective ionic activity, and in much of the animal kingdom, these rhythms ultimately support the emergence of thinking and consciousness. Much of the previous literature on neural networks has a neuron-centric focus and measures electrical excitability within neurons. This neuron-centric, electrically-focused view of neural network excitability overlooks two key aspects of the brain: (1) the development of the brain involves a variety of cell types, the most common among them astrocytes that act as modulators of neuronal cells, and (2) neural network development also encompasses biophysical morphological changes of neural cells and networks, raising the question of the role of biomechanics in the emergence and sustainment of collective ionic activity1,2,3,4,5,6. In the past couple decades, more research has investigated other forms of excitability and the role of glial cells and their impacts on and regulation of neurons and brain activity2,7,8,9,10,11,12.

A starting point for studying neural network development is neural precursor cells (NPC), a mixed population of cells containing both neural stem cells and neural progenitor cells, which differentiate downstream into populations of mature neurons, astrocytes, and oligodendrocytes within the brain13. During differentiation, profound changes occur within each cell as the cytoskeleton rearranges from immature NPCs to the differentiated, mostly post-mitotic state that characterizes more mature neural cells1,14,15,16. At the same time, cell groups develop communications that characterize networks of mature neural cells.

Neurons, differentiated from NPCs, are the canonically “electrically active” cells that undergo rapid changes in transmembrane potential related to communication known as action potentials (AP)17,18,19. Neuronal APs occur primarily in response to communication between cells from the presence of small molecules. One such group of small molecules are known as neurotransmitters, which are released by and taken up by communicating neuronal cells. Neuronal APs are tightly regulated through the influx and efflux of sodium and potassium ions that regulate the transmembrane potential of the cells rapidly, on timescales of milliseconds. Other ions also transit across the membrane during the AP, including Ca2+, which moves into the cell in tens to hundreds of milliseconds, making it a useful tool for monitoring neuronal activity in real-time without the need for millisecond timescale imaging20,21,22. Several technologies take advantage of these slower Ca2+ transients, namely calcium-sensitive dyes (like Fluo-4, X-Rhod, and CalBryte) and genetically encoded calcium indicators (like the GCaMP family of proteins)23,24. Coordinated networks of neurons work together, communicating and synchronizing APs to convey information. Ion transit across neuronal membranes plays a key role in coordinating this activity, for example, with pacemaker HCN channels being crucial for generating spontaneous rhythmicity, such as in the heart and thalamic neurons. These HCN channels respond to specific thresholds and modulate neuronal excitability and cell-cell communication transmission25,26,27.

Astrocytes, which are also differentiated from NPCs, perform a variety of tasks such as maintaining the cells that form the blood-brain barrier, releasing gliotransmitters in response to calcium and neuronal signaling, and forming scar tissue in response to infection and damage within the Central Nervous System1. Healthy astrocytes have a star-like morphology, with the star’s tips thought to modulate and interact with the synapses of neurons1,2,3. While astrocytes, unlike neurons, do not depolarize, recent studies have shown that they are not “silent” and instead show oscillations and waves in intracellular calcium levels, indicating an excitable character of astrocytic Ca2+ signaling2,7. Network-wide Ca2+ signaling in NPCs can form the basis for communication in more mature neural networks28. This Ca2+ signaling in astrocytes can be modulated by some of the same physiologically-relevant inputs that also alter neuronal activity, such as ATP, glutamate, and noradrenaline3,7,29.

Glial cells, often overlooked in traditional neuron-centric views of the brain, play a pivotal role in modulating neuronal networks30. Through their diverse functions, including neurotransmitter uptake, ion homeostasis, and synaptic pruning, glial cells actively contribute to shaping neural circuits and information processing1,2,9,31,32. Astrocytes, for instance, regulate extracellular ion concentrations and neurotransmitter levels, impacting synaptic strength and plasticity. Microglia, the immune cells of the brain, engage in synaptic remodeling and influence neuronal connectivity. Understanding the dynamic interplay between glial cells and neurons is essential for unraveling the intricate mechanisms underlying neural network function and dysfunction.

The development of an active neural network also involves cellular biomechanical machinery. Driving much of neural morphological change is actin cytoskeletal polymerization and depolymerization33,34,35. Mature neurons are not generally migratory; however, they still exhibit intracellular actin dynamics36,37,38,39. Previous research on other cell types had shown that actin dynamics can be driven by Ca2+ dynamics in several contexts, including calcium-dependent actin reorganization in chondrocytes, receptor-induced calcium mobilization mediating actin rearrangement in B lymphocytes, and increases in intracellular calcium leading to actin reorganization and migration in breast cancer cells in response to propofol40,41,42. Within a neural context, a number of studies have shown typically localized coupling between actin dynamics and calcium signaling in dendritic spines—with calcium influx regulating dendritic spine plasticity43,44.

However, recent studies have discovered that the dynamics of the actin cytoskeleton do not necessarily require a specific signaling input, but that the biomechanical actin polymerization machinery acts as an excitable system capable of generating waves or oscillations2,45,46,47,48,49. The key characteristics of biomechanical excitability are the same as for electrical excitability: (1) the system has multiple distinct states, (2) there is some threshold for activation, and (3) there is a refractory period following activation in which another activation is suppressed. Moreover, these recent studies have even suggested that biomechanics and mechanical cues can play a key role in neuronal communication, such that mechanical cues like pressure can lead to dynamic structural changes of actin in synaptic spines that can leave longer-lasting (tens of seconds) impacts on the neurotransmission of glutamate and therefore neuronal communication36.

Since actin dynamics exhibit excitability, it opens the possibility that biomechanical waves and oscillations may contribute to the information contained within neural networks. In neuronal cells, the dynamics of actin play a role in multiple functionalities: In axons, dynamic actin is found in growth cones during axonogenesis and in small actin patches and waves, which can propagate perpendicular to the axon. In dendrites, dynamic actin-rich structures can form along the length of the dendrite and evolve into dendritic spines, important structures for neuronal synaptic communication50. Recent work has demonstrated that the dynamic character of actin remains important in synapses, with drugs affecting actin dynamics also affecting the modulation of synapses and preventing important synapse functions like long-term potentiation51,52. In terms of network populations, recent work on co-cultures of neurons and astrocytes has shown rhythmic actin dynamics in astrocytes, specifically in subcellular local hotspots. The presence of neurons increases astrocytic actin dynamics, which may suggest these two cells might impact each other’s biomechanical systems during communication53.

Therefore, the goals of our study are to characterize the changes in intracellular actin dynamics during neural cell differentiation and to elucidate the potential coupling and the impacts that arresting intracellular actin dynamics has on cell-scale Ca2+ activity by measuring changes in the slower calcium dynamics, such as like those found primarily astrocytes54,55.

Results

To investigate actin dynamics and Ca2+ in neural cells, we use live optical imaging of immortalized NPCs with genetically labeled actin probes and calcium fluorescent indicators throughout their differentiation56.

Controlled differentiation in neural progenitor cells with stable lifeactTagGFP2 expression

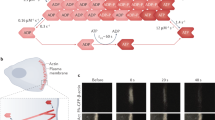
The goals of this work are to observe NPCs at three time points in their differentiation process, to analyze changes in intracellular actin dynamics using optical flow, and to identify impacts of actin arrest on cell-scale calcium dynamics (Fig. 1A). We established an NPC line with a commonly used genetic actin probe, LifeactTagGFP2, using a commercially available human NPC (hNPC) line immortalized through V-MYC transduction. The hNPC line used shows immature neural stem cell markers nestin and sox2 in the undifferentiated state as assayed by immunohistochemistry (Fig. 1B). Differentiation initiated by the removal of growth factors leads to a mixed population of differentiated cells with mutually exclusive expression of beta-3-tubulin (TUBB3) or glial fibrillary acidic protein (GFAP), which are neuron and astrocyte expression markers, respectively (Fig. 1C). During differentiation, cell morphology of hNPCs changes dramatically. Undifferentiated cells show polygonal morphology characteristic of many adherent epithelial cell lines. Differentiated cells show a reduction in cell body size, as well as longer processes. Differentiated populations achieve around 25% (24.4 ± 3.1) TUBB3 positive neurons (n = 8 with at least 7 FOV per sample containing ~20 cells) (Fig. 1D). Lentiviral transduction was used to obtain stable expression of LifeactTagGFP2 within the undifferentiated cells, and this expression is retained throughout the induction of differentiation (Fig. 1E).

Fig. 1: Model hNPC line workflow and differentiation capability.
figure 1

Workflow for the proposed work (A), starting with time course of hNPC differentiating towards matured neurons and astrocytes, followed by analysis of calcium and actin dynamics. Cells are considered “naïve differentiated” at 4–10 days post-differentiation initiation and “mature differentiated” at 14–28 days post-differentiation initiation. Representative immunofluorescence image of undifferentiated hNPC (B) with expression of Nestin (green) and Sox2 (red). Immunofluorescence on naïve differentiated (4 days post-differentiation initiation) hNPC (C) with expression of TUBB3 (green) or GFAP (red) with nuclear staining (blue). Box plot representing the percentage of TUBB3 positive cells after 4 days differentiation (n = 8 biologically independent experiments; error bars represent the standard deviation across experiments) (D). Representative confocal fluorescent image of lifeact-GFP stable transduction of a mature differentiated (21 days post-differentiation initiation) cell derived from hNPC (E).

Full size image

Actin dynamics of hNPC have characteristic rhythm and change scale to match functional needs throughout differentiation; soma directionality unchanged throughout differentiation

We analyzed actin dynamics of hNPC throughout differentiation by looking at three specific time periods during their maturation: 1) during the undifferentiated cell state, 2) during the early/naive differentiated cell state (4–10 days post differentiation), and 3) during the late/mature differentiated cell state (14–28 days post differentiation). Actin was imaged for 5 min with frames captured at 0.25 or 0.125 Hz. Qualitatively, we observed a change in the scale of the actin dynamics during these three stages of differentiation. To observe differences temporally, images were constructed representing temporal max-projections—where each frame is represented by a different color and is collapsed into a single image. White or grey areas represent persistent regions, while colored areas show dynamic regions that are only notable for short time intervals (Fig. 2). Therefore, temporal max-projections can be used to visualize dynamics. Colored regions can be influenced by both actin dynamics parallel to the cell boundary as well as actin dynamics that changes the cell shape itself. However, hNPC cells are not known to move or change shape rapidly, so actin dynamics independent of cell shape changes are expected to dominate. Before differentiation, smaller transient protrusions are observed around the edges of the cells (Fig. 2A, B). During the early stages of differentiation, actin is organized in more wave-like flows, which seem to propagate down and along developing processes (Fig. 2C, D), indicated by gradations of color in a rainbow-like progression along a process. Finally, during the late stage of differentiation, we instead see most of the dynamics localized not along the processes but instead perpendicular to the cell processes (Fig. 2E, F).

Fig. 2: hNPC actin dynamics change scale over differentiation: increasing during naïve differentiated states before decreasing in mature differentiated states.
figure 2

Images represent temporal max projections from 5 min of actin imaging. hNPC in an undifferentiated state (A, zoom in on B). hNPC early differentiation, 5 days post-differentiation initiation (C, zoom in on D). hNPC in mature differentiated cells, 21 days post-differentiation initiation (E, zoom in on F).

Full size image

To measure the directionality of actin flow throughout differentiation, we employed optical flow (Fig. 3A–F)57,58,59. Optical flow is a computer vision algorithm that compares subsequent frames of an image sequence and interprets the directionality and magnitude of flow based on the pixel intensities. Subsequent frames (Fig. 3A) from a population of undifferentiated cells demonstrate how optical flow is used to analyze actin dynamics, showing the optical flow vectors, histogram of actin speed, magnitude, and orientation in the subsequent frames (Fig. 3B–E, respectively) as well as analysis of the entire film sequence showing the orientation of optical flow vectors over time (Fig. 3F). It is important to note that the detected optical flow speed matches known speeds of actin polymerization waves, with the typical waves reported to travel approximately 1 micron per minute57. Optical flow was implemented on undifferentiated, early differentiated, and mature differentiated cell time series (n = 7, 7, 8, respectively across N = 3–4 biologically independent experiments per condition). The top 15% of magnitude flow vectors from each frame were retained and used to construct images that show how often each pixel exhibits the highest optical flow magnitude (Fig. 3G–I are representative images from each differentiation stage). Magenta arrows highlight key observations: Undifferentiated cells show that actin dynamics, as measured by optical flow, covers broad areas mainly within the cell body (Fig. 3G). Early differentiated cells show regions of activity along processes (Fig. 3H), while late differentiated cells show most activity distributed among a larger number of small punctate regions that appeared along and perpendicular to processes (Fig. 3I). This fits well with the generally accepted view that neuronal cells show morphologically dynamic outer lamellipodial-like structures during early development (akin to Fig. 3G), then pivot more towards pathfinding during neurite outgrowth stages by extending processes (akin to Fig. 3H), and finally show smaller dynamics and branching once neurites are developed during later stages (akin to Fig. 3I)60,61,62. Propagation of actin waves would be expected to be seen during the projection of axon and dendrite growth cones away from the soma, similar to our observed actin flows along processes (Fig. 2C, D)37,63. Finally, smaller dendritic branches and synapses form after contact between processes, potentially leading to dynamics more like the punctate actin activity observed.

Fig. 3: Optical flow as a tool to study actin dynamics with top 15% optical flow vectors show distinct regions of activity throughout differentiation.
figure 3

Actin dynamics within hNPC can be captured using optical flow algorithm (A–F). To visualize optical flow’s use, a single analysis time point of two subsequent frames from a 7-minute movie (with 0.06255 Hz acquisition) showing intracellular actin is labeled (A, B). Overlay of two subsequent frames analyzed with time gradient shown (A). Optical flow vectors (green) overlaid on the second of the two subsequent frames from (A, B). Probability distribution of optical flow vectors of detected actin speeds between subsequent frames (C). The magnitude calculated by optical flow algorithm is overlaid on the masked cell region (D). Orientation of optical flow vectors displayed on the overlaid cell region; color shown is indicative of directionality of optical flow vectors detected as displayed by circular map showing directionality in radians (E). Kymograph that captures the probability (as indicated by color) of directional actin flow (as indicated on the y-axis) over time (along the x-axis) (F). Max projection of actin image time-series showing top 15% magnitude flow vectors over all frames from 5-min movies at specific differentiation time points (G–I). Colorscale indicates the proportion of frame pixels that were found to be in the top 15% magnitude throughout the entire film. Examples of undifferentiated cells (G), naive differentiated cells (H), and mature differentiated cells (I). All scale bars represent 50 microns.

Full size image

To further illustrate the changes in actin dynamics throughout differentiation using optical flow, we analyzed actin flow directionality along the major axis (as identified by eye) of the cell in our movies (images captured at 0.25 or 0.125 Hz). Optical flow detects the directionality of actin flow by analyzing actin dynamics from frame to frame to interpret the direction of an actin polymerization (Fig. 3A–F). When analyzing our image sequences of individual cells, we found that actin flow is biased along the cell’s major axis in most cases [undifferentiated = 4/6, naïve differentiated = 4/5, mature differentiated = 4/7] (Fig. 4A and Supplementary Fig. 1) throughout the different stages of differentiation when including all optical flow vectors as well as only including those in the top 15% magnitude (Fig. 4B–D top and bottom respectively). Using one-way ANOVA, we determined there were significant differences for the mean actin speeds based on the differentiation stage for hNPC (p = 1.98E-8). Applying multiple comparisons test with the Holm–Bonferroni correction, we found that, when taking an entire film into account, only the mature differentiated cells had significantly slower mean actin speeds compared to the undifferentiated and naive differentiated cells (mature differentiated p = 1.5E-7 compared to undifferentiated and p = 5.9E-8 compared to naïve differentiated) (Fig. 4E). This was also true when only looking at the optical flow vectors within the top 15% highest magnitude (mature differentiated p = 2.7E-5 compared to undifferentiated and p = 4.0E-6 compared to naïve differentiated) (Fig. 4F). When looking over individual frames for the image sequences, we see that most cells consistently show actin flow along the cell’s major axis throughout time (Fig. 4D–F and Supplementary Fig. 1). Along with biased actin flow along the major axis, one key feature seen in the analyzed kymographs is that, throughout hNPC development, actin dynamics appear to have a rhythmic character that is maintained throughout differentiation in some cells (Fig. 4G–I). We analyzed this rhythm in the vertical directions using Fourier analysis of the optical flow magnitudes and found that all cells appear to have some rhythmic character to their actin dynamics over time as seen via hotspots on the kymographs in the x-axis (Supplementary Fig. 1). Additionally, we investigated the characteristic frequency of the highest amplitude Fourier analysis, allowing us to reveal that both undifferentiated and naïve differentiated cells have a rhythmic frequency around 0.4 cycles per minute, while mature differentiated cells have a dominant frequency around 1.3 cycles per minute (Supplementary Fig. 1D).

Fig. 4: Actin dynamics are generally oriented along the cell’s major axis and show a rhythmic character throughout differentiation.
figure 4

Schematic with an arrow showing orientation along a cell’s major axis (A). Analysis from actin imaging captured at 0.25 or 0.125 Hz (n = 17). Representative cell samples under various stages of differentiation: Undifferentiated (B, G), naïve differentiated (C, H), and mature differentiated (D, I) showing either all vectors (top) or using vectors within the of top 15% magnitude (bottom). Rose plots (B–D) show probability of optical flow vector orientation over entire films. Dot plots of mean actin speed at various stages of differentiation using all vectors (E) and using vectors within the top 15% magnitude (F). Conditions marked with asterisk have significantly different means from the others (n = 17 time-lapse movies obtained across N = 3 biologically independent experiments; error bars represent the standard deviation across experiments). Kymographs (G–I) show directional probability over time of all vectors (top) or of the highest 15% magnitude vectors (bottom). Hotter colors indicate a higher probability.

Full size image

Automated analysis and representation of population-level calcium dynamics in hNPC

Calcium dynamics within developing hNPC are associated with proliferation, signaling, and developing cell-to-cell communication. To investigate the communication and coordination of calcium signaling throughout differentiation, calcium dynamic data from hNPCs are visualized using the cell-permeant dye Calbryte590, a calcium fluorescent dye that increases in intensity with increases in intracellular calcium concentration. Calbryte590, a non-ratiometric probe, was chosen due to its brightness, intracellular retention, and compatibility with the experimental protocols. Actin and calcium dynamics were not followed in parallel in any of these experiments since these dynamics are on different timescales (actin over tens of seconds, calcium over hundreds of milliseconds) and distinct length-scales (intracellular for actin vs. cell-scale for calcium), calling for separate analysis. Populations of about 100–300 cells in each field of view were imaged (Fig. 5A). This methodology and our automated analysis pipeline allowed us to look at individual cells and extract the fluorescent intensity over time. Individual cells can be identified either in an automated or manual fashion and labeled at the cell center (Fig. 5B). Fluorescent intensity over time is collected at 3 Hz with 100 ms exposure time (Fig. 5C) and represented in a kymograph (Fig. 5D). This frame rate is fast enough to yield multiple data points for each observed calcium transient. Using this automated workflow, the kymograph representation allows us to then plot all cells along the y-axis with time represented along the x-axis and look at the dynamic changes in calcium intensity over time for large populations of cells (Fig. 5E, F). The representative kymograph obtained from the analysis in Fig. 5 shows a mixture of active and inactive cells detected during analysis, which is standard for our in vitro hNPC neural populations (Fig. 5). This disparity of active and inactive cells is seen in previous research, and our downstream analysis excludes non- or low spiking cells64.

Fig. 5: hNPC calcium dynamics can readily be quantified at the population level.
figure 5

Microscope field of view of naïve differentiated (10 days post-differentiation initiation) hNPCs; scale bar representing 50 microns (A). Zoom in from (A), highlighting individual cell #151 in magenta; scale bar representing 50 microns (B). Trace of calcium fluorescent data over time from cell #151 (C). Kymograph representation of trace from C for cell #151; time on the x-axis, fluorescent intensity indicated as color (D). Automated cell centers are displayed as dots and numbered from the entire microscope field of view from (A); scale bar representing 50 microns (E). Kymograph representing all cell fluorescent intensities over time (F).

Full size image

Pharmacological arrest of hNPC actin modulates calcium dynamics

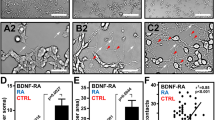
Finally, to understand the impacts of actin dynamics on the calcium transient dynamics within developing hNPCs, we use a pharmacological cocktail of drugs to inhibit actin dynamics during the naïve differentiation stage of our cells ie: day 4–5 after differentiation initiation (n = 14 time-lapse movies, collected across N = 3–4 biologically independent experiments per condition). The pharmacological cocktail we used contains the ROCK inhibitor Y-27632, latrunculin A, and jasplakinolide (JLY cocktail), and it has been shown previously to arrest actin dynamics over a period in multiple cell types, while still allowing for other excitable dynamics like calcium signaling65. To arrest dynamics, initially the ROCK inhibitor is added for 10 min, before the addition of latrunculin A and jasplakinolide (Supplementary Fig. 2). For this study, we were able to show the arrest of actin dynamics in 4–5 days post differentiation initiation hNPCs using the JLY cocktail, and we correspondingly observed the impact of actin arrest on the ionic calcium dynamics within hNPCs (Fig. 6). In control conditions, temporal color-coded max projections display regions of color, suggesting activity over time (Fig. 6A), whereas cells treated with the JLY cocktail show stark black and white images (Fig. 6B), indicating static structures. These results suggest JLY cocktail addition works well in stabilizing actin structures and inhibiting dynamics. In control conditions, using temporal color-coded max projections show calcium dynamics observed for a 1-min interval show few colors, suggesting less dynamic calcium activity (Fig. 6C), whereas the same interval of time in JLY, actin arrested condition shows many more colors, which suggests an increase in activity (Fig. 6D). These changes are further quantified and illustrated in the population level kymograph representations of individual cells’ calcium fluorescent intensities over time (Fig. 6E, F). Control conditions (Fig. 6E) show less activity compared to the JLY, actin arrested condition (Fig. 6F), as indicated by an increase in the number of blue peaks that occur, representing activity in the kymographs—which look more like an oscillatory phenotype. We chose to look further at these slower scale calcium dynamics that would primarily represent astrocytes54,55. In summary, actin dynamics within actin-arrested conditions show decreased activity, as indicated by more white regions in the actin-arrest condition compared to the control condition (Fig. 6A, B). Calcium dynamics within actin-arrested conditions show more increased activity, as indicated by more colored regions in the actin-arrest condition (Fig. 6C, D), and a potentially increased frequency of spikes within the kymograph compared to the control condition (Fig. 6E, F).

Fig. 6: Pharmacological actin arrest in naive differentiated hNPC increases calcium dynamics.
figure 6

Temporally color-coded max projections from naïve differentiated (4–5 days post-differentiation initiation) hNPCs of LifeactTagGFP2 over 4 min films captured at 0.5 Hz during control or actin arrest; scale bars represent 50 microns (A, B, respectively). Temporally color-coded max projections from Calbryte590 over 1 min films captured at 3 Hz during control or actin arrest; scale bars represent 50 microns (C, D, respectively). Kymographs showing calcium dynamics over 9 min captured at 3 Hz with fluorescent intensity indicated by the color bar on the right-hand side, and individual cells indexed along the y-axis during control or actin-arrested conditions (E, F, respectively [same scale used]).

Full size image

Actin arrest and excitable Tyrode’s solution decrease correlations in hNPC network calcium dynamics

To quantify the impact of actin arrest on the slower timescale calcium dynamics, we examined hNPCs under four conditions. The first condition was differentiation medium (the solution the cells matured in and supports long term growth/survival). The second condition was differentiation medium with pharmacological actin arrest. To assess the impact of actin arrest on cells at different levels of natural activity, for the third and fourth condition, we observed the cells either with or without pharmacological actin arrest in an excitable Tyrode’s solution (a modified version of Tyrode’s solution supplemented with extra sodium hydroxide). Tyrode’s solution is an isotonic solution often used for short-term assessment of neural activity due to its ability to replicate physiologically-relevant conditions. Tyrode’s is well tolerated at moderate exposure (up to four hours) and has been found to be compatible with neural cells66,67,68,69,70,71, with no noted impacts on cell health on the timescales of our measurements (1–2 h)66,67,68,72,73,74.

We first analyze how the four conditions affect calcium spike width (length of time) and spike prominence (amplitude) as calculated based on the quantified ΔF/F calcium signal (Fig. 7A–C). We find that actin arrest via JLY leads to decreases in calcium spike widths (p = 0.021) (Fig. 7A) (see Supplementary Table 2) compared to cells in medium alone. This is similar to the effect of excitable Tyrode’s solution (p = 0.0057) (Fig. 7B), with comparable spike widths and prominence (p = 0.52 and p = 0.77, respectively) (Supplementary Table 2). Interestingly, the combination of actin arrest and excitable Tyrode’s solution does not lead to further shortening of spikes but rather to a higher spike amplitude [p = 3.6e-4] (Fig. 7C).

Fig. 7: Comparing the effects of excitable Tyrode’s solution and actin arrest on calcium dynamics.
figure 7

Probability histograms of spike width and prominence of calcium spikes [~15,000 individual spikes, compiled from n = 14 time-lapse movies across N = 3–4 biologically independent experiments] in various conditions (A–C). Spike width and prominence of cells in medium with or without actin arrest (JLY) (A). Spike width and prominence of cells in either medium (Ctrl) or Tyrode’s solution (B). Spike width and prominence of cells in Tyrode’s solution with or without actin arrest (C). Conditions marked with asterisk are significantly different from one another (A–C). Dot plots showing the proportion of active cells (D) or spiking frequency (E) under tested conditions—control condition in medium, control condition in excitable Tyrode’s solution, actin arrest in medium, and actin arrest in excitable Tyrode’s solution (n = 1 4 time-lapse movies each with at least 50 cells per field of view, across N = 3–4 biologically independent experiments; error bars represent the standard deviation across experiments). Histograms showing the relative probability of max cross correlation values from all cells pairs under the same conditions as in (A and B) on a logarithmic y-axis (F). Schematic representation of calcium fluctuations in the context of conditions applied within this work (G). Conditions marked with asterisk are significantly different from one another.

Full size image

Next, we looked at active cells under all four conditions. We define active cells as those with at least three transients during our imaging time and measured both the proportion of active cells (Fig. 7D) and their spiking frequency (Fig. 7E). We find an increase in the proportion of active cells under excitable Tyrode’s conditions but no statistically significant increase from actin arrest in growth medium. We applied a one-way ANOVA on both the proportion of active cells as well as the impact on spiking frequency (as assayed per field of view), where we found there were significant differences between our conditions (p = 4.3e-6 and p = 1.4e-5 respectively; alpha = 0.05) (all comparisons in Supplementary Table 3). Following ANOVA, we performed pairwise tests between samples for the mean proportion of active cells as well as mean spiking frequency. For the proportion of active cells, both Levene’s and Bartlett’s test for unequal variance found there to be no significant difference. Therefore, we performed Tukey’s HSD to compare the proportion of active cells with a Holm–Bonferroni correction for significance for multiple comparisons.

When looking at spiking frequency of active cells, we found that cells with actin arrest in medium had a significantly higher spiking frequency (p = 0.011) (Fig. 7E and Supplementary Table 3) compared to cells in media alone. Excitable Tyrode’s solution further increased spiking frequency to similar levels both with and without actin arrest (p = 0.36) (Fig. 7E). We performed Welch’s test to compare our four conditions with a Holm–Bonferroni correction for significance, since both Levene’s and Bartlett’s test for unequal variance show significant differences in variance.

To further characterize network activity on the slower timescales of astrocytic calcium dynamics54,55, we calculate the maximum cross-correlation with a time lag of ± 10 s (Fig. 7F). For the four conditions, we found that activating cells with actin arrest, excitable Tyrode’s, or both, decreases the cross-correlation statistics in similar ways compared to media alone.

A possible explanation for our findings in Fig. 7 lies in the excitable systems character of calcium dynamics, which we illustrate in a schematic in Fig. 7G. In our control medium, calcium dynamics appear dampened with few active cells. Actin arrest and excitable Tyrode’s solution appear to make the system more excitable, supporting more spontaneous activity. Combining both perturbations increases the amplitude of the spontaneous oscillations, as illustrated schematically in Fig. 7G.

Discussion

This work investigates the changes in biomechanical activity during the development of neural networks and includes two key aspects of neural networks that are missed in the typical neuron-centric and action potential-centric view of brain communication: that the composition of neural networks includes non-neuronal cells, and that neural cell excitability is not only electrical in nature. The contribution of this work is twofold:

First, this study demonstrates that neural cells have reproducible actin dynamics and that the characteristic scale of actin dynamics changes with cell differentiation in a way that can be simply connected to changes in cell function. We show that actin dynamics change the spatial scale as a function of the differentiation stage—first being localized to emerging protrusions in undifferentiated cells, spanning developing neurites and processes during early stages of differentiation, and finally becoming smaller, on synaptic or perisynaptic scales, in late stages of differentiation (Figs. 2 and 3). In addition to these well-known roles of actin dynamics at the leading edges of protrusions, growth cones, and synaptic scales, we find that the dynamics also occur away from such leading edges and that the dynamics have characteristics of an excitable system with rhythmic actin dynamics observed throughout differentiation38,39,45,75,76,77 (Fig. 4). Future work should look to further characterize the rhythmic actin dynamics within neural populations of cells and to determine if the amplitude or frequency of that rhythm is associated with specific cell states or diseases. Future work should also seek to understand how modulating this rhythm may enhance neural cell differentiation, development, and communication.

Second, our study suggests that the biomechanical excitability of actin dynamics is an active participant in neural information flow as measured via calcium dynamics. Our results suggest actin dynamics dampen calcium dynamics—decreasing the frequency and increasing the spike width (Figs. 6 and 7). The effect of actin arrest resulted in a similar effect as excitable Tyrode’s solutions alone, leading to a similar increase in the proportion of active cells (Fig. 7). When applied together, actin arrest and excitable Tyrode’s act synergistically and further increase the excitability of the system, resulting in increased amplitude, increased frequency, and decreased widths of oscillations (Fig. 7). The comparable decrease in cross-correlations for both actin arrest and excitable Tyrode’s (Fig. 7E) indicates that actin arrest increases the intrinsic calcium dynamics of cells. Our results are inconclusive regarding the impact of actin arrest on synaptic connectivity as an increase in spontaneous activity alone is consistent with a decrease in cross-correlations.

There are some limitations to keep in mind within this body of work. One potential caveat is the impact of LifeActGFP2 on nascent intracellular actin dynamics. LifeAct is a small peptide sequence that binds to actin (akin to other actin-binding proteins) often used in live-cell imaging to track F-actin structures78. While LifeAct is commonly used to study live intracellular actin dynamics, it is known that the addition of this small protein probe can perturb actin (though less so than a direct fusion protein like actin-GFP)79,80,81. Another potential study limitation pertains to calcium buffering, which might be influenced by the presence of calcium indicators. These indicators, crucial for monitoring calcium dynamics, can subtly impact actual calcium concentrations in cells, potentially affecting result accuracy82.

Nevertheless, our findings that the actin and calcium dynamics of hNPCs affect each other raises the possibility that mechano-chemical excitability, in the form of actin dynamics, can play an active role in information flow in neural networks. Indeed, we have recently developed a model based on the slow biomechanical rhythms observed here, and we find that these rhythms can give neural networks powerful information processing capabilities, most notably the ability to adapt quickly and extrapolate to unseen dynamics83. Thus, it may be valuable to consider mechano-chemical excitability in future studies of neural network function.

Methods

Cell culture

The hNPC line was derived from human fetal brain tissue from the ventral mesencephalon (Millipore Sigma #SCC008), which includes the v-myc transgene, and was cultured in accordance with previous methods56. Briefly, cells were expanded on Matrigel-coated plates or tissue culture flasks (NEST and Corning). Cells were maintained in growth medium composed of DMEM:F12 + GlutaMax (Thermo Fischer Scientific) supplemented with 2% v/v B-27 plus neural cell supplement (Thermo Fischer Scientific), 1% v/v P4333 penicillin-streptomycin solution (Sigma-Aldrich; final concentration 100 U/mL penicillin & 100 μg/mL streptomycin), 50 mM heparin (Stemcell Technologies), in the presence of 10 ng/mL bFGF (Stemcell Technologies) and 20 ng/ml EGF (Stemcell Technologies). Differentiation medium was composed of the same components as growth medium, excluding the growth factors (bFGF and EGF). Cells were maintained in a cell culture incubator at 37 °C in a humidified environment with 5% CO2. Cells were passaged at around 95% confluency. Briefly, cells were rinsed with DPBS, and cells were detached using a brief incubation with accutase (Stemcell Technologies). After 5–10 min, one volume of DMEM:F12 + GlutaMax was added. The cells are centrifuged at 500 × g for 5 min. The cell pellet was resuspended in fresh growth medium before being plated on Matrigel-coated plates. All experiments were carried out on cells between passages 5 and 30.

Generation of LifeactGFP cell line

hNPC line was cultured as described above. rLV-Ubi-LifeAct-TagGFP2 lentivirus, purchased from Ibidi technologies (catalog no. 60141), was used according to supplier instructions, with the addition of viral transduction reagent on cell cultures around 50% confluent at desired MOI (2 and 4). After 48 h of incubation for viral uptake, media containing viral particles was replaced. Cell samples were then checked under a confocal fluorescence microscope for the presence of a GFP signal. Cells were subjected to antibiotic selection using 5 ug/mL puromycin to establish stable polyclonal lines. After 2–7 days of selection, cells were expanded with samples cryopreserved for future use. Lifeact-generated lines were used between passages 7 and 30.

Calcium labeling and imaging

Intracellular calcium labeling was accomplished using Calbryte-590 AM (AAT Bioquest) following manufacturer-provided protocol. A stock solution is prepared in anhydrous DMSO. Briefly, appropriate dilution of Calbryte-590 AM was added to cell medium to achieve 1 uM final working concentration. Cells were then incubated for 30–60 min in a 37 °C incubator. The cell sample was then incubated at room temperature for another 15 min. Afterward, the cell sample medium was replaced with an appropriate imaging solution (either cell culture growth medium, or Tyrode’s solution with supplemented sodium [Tyrode’s solution from Alfa Aesar J67607; supplemented pH 7.8 using NaOH]). Samples were then immediately imaged on a system with temperature, humidity, and CO2-controlled environments at 37 °C, 90%, and 5% CO2, respectively, using 561 nm lasers to excite fluorescent indicators.

Pharmacological arrest of actin

The pharmacological arrest of actin was performed according to previous literature using modified concentrations65. For the JLY treatment, first, hNPC are incubated with 10 μM Y-27632 for 10 min. Next jasplakinolide (3 μM) and latrunculin B (5 μM) were added, at which point the JLY cocktail is considered fully active. For calcium imaging with actin arrest, cells are preincubated with Calbryte-590 AM for 30–60 min as described above before having the medium replaced, after which Y-27632 is added for 10 min before the addition of jasplakinolide and latrunculin B.

Immunocytochemistry

At the specified endpoints, cell samples were removed from the incubator, the medium was removed, and cells were rinsed with PBS for 5 min. Cell samples were then fixed in 4% paraformaldehyde/PBS for 15 min, followed by rinsing three times in PBS for 5 min each. Cells were then permeabilized with 0.1% Triton × 100 + 1% BSA in PBS for 1 h at room temperature. Direct immunofluorescence was then performed using specific antibodies incubated overnight at room temperature. Nestin was probed using anti-nestin-AF-488 at 5:1000 (Santa Cruz Biotechnology, catalog no. sc-23927 AF546, 10c2 clone). Sox2 was probed using anti-sox2-AF-546 at 5:1000 (Santa Cruz Biotechnology, catalog no. sc-365823 AF546, E-4 clone). βIII-tubulin was probed using anti-TUBB3-AF-640 at 5:1000 (BD Pharmingen, catalog no. AB_1645400, TUJ1 clone). GFAP was probed using anti-GFAP-AF-546 at 2:1000 (Santa Cruz Biotechnology, catalog no. sc-58766 AF546, GA5 clone). After direct antibody staining overnight, the antibody solution was removed, and cells were rinsed in PBS for 5 min. Samples from Fig. 1C that required nuclear staining were stained with Hoechst (bisBenzimide H 33342 trihydrochloride, Millipore Sigma B2261-25MG) at 1:2000 in PBS for 2 to 4 min followed by an additional PBS wash.

Imaging fixed cell cultures

Image sequences of fixed cell cultures for immunocytochemistry and live imaging of actin and calcium dynamics were captured on a PerkinElmer spinning disk microscope using 405, 488, 561, and 640 nm wavelength lasers at 10% power. Live cultures were maintained using a Tokai Hit environmental chamber with temperature, CO2, and humidity control. Actin imaging was acquired every 4 s (0.25 Hz).

Image analysis

All image analysis used either the ImageJ processing package FIJI or Matlab. FIJI (ImageJ) was used to obtain temporal color-coded max projection images. First, image sequences from the microscope were opened using ImageJ and converted into 8-bit. Next, the temporal color code plugin by Kota Miura applied. On images of actin dynamics, jitter is removed using the image registration plugin “Linear Stack Alignment with SIFT” to remove translational motion. Movies with these artifacts are then cropped before downstream analysis. Looking at images, most drift or jitter was identified as translational motion, and therefore, the expected transformation option was selected to be translational. In noisy images, the FIJI plugin “remove outliers” was used with a radius of 2 pixels to remove bright outliers.

To analyze actin dynamics, optical flow was implemented in Matlab using the “estimateflow” function using the “opticalFlowFarneback” object with the following parameters: the number of pyramid layers 7, filter size 20, neighborhood size 1, pyramid scale 0.5. Optical flow vectors from samples at various stages of differentiation were then used to create the plots in Figs. 3 and 4. Within Figs. 3 and 4 and Supplementary 1, kymographs are generated using either all optical flow vectors or those vectors within the top 15% highest magnitude sorted into 10° width bins (36 in total). Kymographs in Fig. 3 have no averaging across time, whereas kymographs in Fig. 4 use an averaging across time from the individual frame and the two adjacent frames on either side (this allows one to see the periodicity better). Finally, kymographs in Supplementary Fig. 1 are shown without time averaging, with 3 frames time averaging, and with 5 frames time averaging. To obtain FFTs, specific orientations (pi/2, 0, and -pi/2) were chosen as centers with 40° on either side averaged to get a mean trace/activity. FFT is run using this mean trace and then plotted in the FFT shown for each direction for supplementary Fig. 1A–C. For supplementary Fig. 1D, kymographs were used to find the six 10°-width bins with the highest amplitude, which were then averaged and run with FFT to obtain the maximum values for the frequency of rhythm represented in actin images.

In Matlab, Tiff image sequences are loaded. Cell centers are then identified automatically using a difference of Gaussian approach and then identifying cell centers as local maxima. An expected cell radius size is used to record ROI of fluorescent activity over time. Fluorescent activity for each cell is normalized by dividing the raw fluorescent intensity by the maximum value. Moving average baseline subtraction is performed to compute the delta F over F (ΔF/F). These ΔF/F traces for each cell correspond to plots in Figs. 5C, D, F and 6E, F. Calcium spikes are detected using the “findpeaks” function with the stipulations for the minimum prominence value of 20 of the normalized ΔF/F value and maximum spike width of 10 s. The number of peaks found was then used to calculate the proportion of active cells (with more than 3 peaks) under specific conditions as well as the frequency of spiking activity under specific conditions. Peak width and height/prominence were also detected via the use of “findpeaks” function.

Plots for the observed probability of spike widths and prominence in Fig. 7A–C were plotted using Matlab’s “histogram” function with bin widths of 2 for spike width plots and bin widths of 10 for prominence/intensity plots.

Probability distributions of the maximum cross correlation values allowing a 10 s lag shown in Fig. 7G were plotted using Matlab’s “histogram” function with bin widths of 0.025.

Statistics and reproducibility

Data in Fig. 1 represent n = 8 biologically independent experiments In Fig. 1D, error bars indicate the standard deviation across experiments. Data in Figs. 2, 3, and 4 represent n = 17 time-lapse movies obtained across N = 3 biologically independent experiments. Statistical analysis for Fig. 4E, F shows error bars representing the standard deviation across experiments; significance was determined using one-way ANOVA followed by Tukey’s HSD test, with Holm–Bonferroni correction applied. Data in Figs. 6 and 7 represent n = 14 time-lapse movies across N = 3–4 biologically independent experiments. For Fig. 7A–C, statistical comparisons of the histogram datasets were performed using Kolmogorov–Smirnov test, with significance set using Holm–Bonferroni correction (results in Supplementary Table 2). For Fig. 7D, E, error bars represent the standard deviation across experiments; significance was determined using one-way ANOVA, with homogeneity of variance evaluated by both Levene’s and Bartlett’s tests. Depending on outcome, either Tukey’s HSD or Welch t-test was implemented for pairwise comparison, with significance set at either p < 0.05 and Holm–Bonferroni correction (results in Supplementary Table 3). Histogram data from Fig. 7F applied Matlab’s “kstest2” function to perform two-sample Kolmogorov–Smirnov tests on all pairs of distributions with Holm–Bonferroni correction applied for significance (results in Supplementary Table 4). Data for dot plots and box plots in Figs. 1, 4, and 7 in Supplementary Data 1.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.