Causal spatially heterogeneous Bayesian networks with GPs and normalizing flows for seismic multi-hazard estimation

Abstract

Post-earthquake hazard and impact estimation are critical for effective disaster response, yet current approaches face significant limitations. Traditional models employ fixed parameters regardless of geographical context, misrepresenting how seismic effects vary across diverse landscapes, while remote sensing technologies struggle to distinguish between co-located hazards. We address these challenges with a spatially-aware causal Bayesian network that decouples co-located hazards by modeling their causal relationships with location-specific parameters. Our framework integrates sensing observations, latent variables, and spatial heterogeneity through a novel combination of Gaussian Processes with normalizing flows, enabling us to capture how same earthquake produces different effects across varied geological and topographical features. Evaluations across three earthquakes demonstrate Spatial-VCBN achieves Area Under the Curve (AUC) improvements of up to 35.2% over existing methods. These results highlight the critical importance of modeling spatial heterogeneity in causal mechanisms for accurate disaster assessment, with direct implications for improving emergency response resource allocation.

Introduction

Earthquakes cause harm not only through direct ground shaking but also by triggering secondary ground failures such as landslides and liquefaction. These combined effects lead to devastating consequences, including structural damage and human casualties. A striking illustration is the 2021 Haiti earthquake, which initiated over 7000 landslides covering more than 80 square kilometers. This catastrophic event resulted in damage or destruction to over 130,000 buildings, claimed 2248 lives, and left more than 12,200 people injured¹. Rapidly identifying where and how severely ground failures and structural damage have occurred following an earthquake is essential for effective victim rescue operations within the crucial “Golden 72 Hour” window, and plays a vital role in developing effective post-disaster recovery plans^2,3.

Over the years, researchers have developed various approaches for estimating the location and intensity of earthquake-induced ground failures and building damage. Traditional approaches to seismic hazard assessment fall into two main categories: physical and statistical models^4,5,6,7. Physical models apply fundamental geotechnical principles, such as the Newmark displacement method for landslides or liquefaction potential indices. While foundational, these approaches require detailed geotechnical data often unavailable during rapid response and frequently oversimplify complex physical dynamics. Statistical models estimate hazards using geospatial susceptibility indicators paired with ground motion data, calibrated on historical events. However, current approaches employ fixed parameters regardless of location. This one-size-fits-all approach misrepresents how seismic effects vary across different geological compositions, topographical features, and infrastructure, leading to significant estimation inaccuracies.

Remote sensing technologies, particularly Interferometric Synthetic Aperture Radar (InSAR), have revolutionized rapid post-earthquake assessment capabilities. InSAR works by comparing phase differences between radar signals captured at different times, enabling detection of surface deformation with high-resolution precision⁸. Damage Proxy Maps (DPMs) generated by the NASA’s Advanced Rapid Imaging and Analysis (AIRA) team, which is a state-of-the-art InSAR product, identify ground changes by analyzing radar measurement disparities before and after seismic events⁹. Although remote sensing technologies facilitate expedited hazard evaluation¹⁰, these approaches typically address individual hazards and face challenges in differentiating between overlapping signals from multiple hazard types while filtering out environmental noise¹¹. This limitation creates a critical information gap for emergency responders who need a comprehensive understanding of multiple concurrent hazards.

Recent advances have introduced causal Bayesian networks to address the limitations of remote sensing technologies by disentangling cascading earthquake impacts^{12,13,14,15,16,17,18,19}. These probabilistic models leverage variational inference to track causal chains from initial earthquake events through multiple hazards to ultimate building damage. A recent approach²⁰ attempted to account for spatial variations using bilateral filters, which is a technique that creates weighted averages based on proximity between locations^21,22. While this improved upon uniform-parameter models, bilateral filtering fundamentally treats spatial dependency as a simple averaging operation without modeling how the underlying causal mechanisms themselves vary across different geological settings^23,24. For example, the same level of ground shaking might have a much stronger causal effect on triggering landslides in areas with steep slopes and loose soil compared to flat areas with stable bedrock²⁵. Similarly, building damage resulting from liquefaction will vary dramatically depending on foundation types and subsurface conditions. These location-specific causal relationships cannot be captured by simple spatial averaging²⁶.

To address these limitations, we propose a spatially-aware variational causal Bayesian network (Spatial-VCBN) that represents a fundamental shift in approach: rather than modeling spatial correlation as an afterthought, we directly model the variation in causal mechanisms themselves. The distinction is crucial because while previous approaches might apply spatial smoothing to already-estimated parameters, our framework incorporates spatial heterogeneity directly into the causal structure itself. Such integration captures the reality that the same earthquake generates dramatically different effects depending on local conditions. The physical intuition behind Spatial-VCBN is that causal relationships in earthquake scenarios are fundamentally location-dependent, a principle well-established in geophysics but rarely incorporated into predictive models. While simpler approaches like linear spatial interpolation or kernel smoothing might seem sufficient, the highly non-linear and potentially multi-modal nature of earthquake causal effects demands more sophisticated methods. Our framework consists of three key components: (1) observable variables including geospatial features and DPMs derived from satellite imagery; (2) latent hazard/impact variables representing unobserved landslides, liquefaction, and building damage; and (3) spatially-varying causal coefficients that quantify the strength of causal relationships at each location.

A key innovation in Spatial-VCBN is the modeling of these spatially-varying causal coefficients using a combination of Gaussian Processes (GPs) with normalizing flows. GPs serve as spatial priors that ensure causal relationships vary smoothly across regions based on geophysical similarities²⁷, while normalizing flows provide flexible, non-linear transformations that capture complex^3,18,28, non-Gaussian distributions of causal effects. Conceptually, normalizing flows transform simple probability distributions into more complex ones through a sequence of invertible mappings, allowing us to represent the richly varied ways that earthquake forces translate into surface effects across different terrains. The use of Gaussian Processes is particularly well-suited for this problem because they naturally model spatial correlation while allowing for location-specific variations. Normalizing flows complement this approach by transforming simple distributions into more complex ones through a series of invertible mappings, enabling Spatial-VCBN to capture the highly non-linear and potentially multi-modal nature of causal effects in earthquake scenarios. Our ablation studies reveal that an optimal flow number of K = 6 is required to adequately model these complex relationships, confirming that simpler distributional assumptions would fail to capture the physical reality of earthquake impacts. This is crucial because the relationships between geological features, seismic waves, and resulting hazards often follow complex, non-Gaussian patterns that simpler distributional assumptions would fail to capture.

By combining GPs with normalizing flows, our framework can represent complex, non-Gaussian distributions of causal effects that better reflect the physical reality of how earthquake impacts propagate through diverse environments. This probabilistic approach also enables principled quantification of uncertainty in hazard estimates, which is crucial for effective disaster response planning. For inference, we implement a stochastic variational approach with an expectation-maximization algorithm that alternates between updating posteriors of unobserved variables and refining model parameters. To handle large geographical regions efficiently, we apply a local pruning strategy that exploits the natural sparsity in real-world causal networks, achieving processing speeds of ~0.94 s/km² with GPU acceleration, making Spatial-VCBN viable even for large-scale events like the Haiti earthquake (15,970 km²).

Our empirical evaluations demonstrate that this spatially-variant approach significantly improves hazard and impact estimation accuracy, with AUC improvements of up to 35.2% over prior probability baselines and 5.5% over state-of-the-art methods across three earthquake events (Haiti, Puerto Rico, and Turkey-Syria). These substantial improvements are not merely incremental advances but represent a step-change in our ability to rapidly assess complex disaster scenarios with the precision needed for effective emergency response. The model shows remarkable robustness in signal-constrained environments, successfully extracting coherent hazard patterns even from noisy DPM signals, as demonstrated in mountainous and coastal regions. Particularly noteworthy is the strong performance of Spatial-VCBN at low false positive rates, which is crucial for effective resource allocation in disaster response operations where false alarms can waste limited resources. These results highlight the critical importance of modeling spatial heterogeneity in the actual causal mechanisms themselves, rather than merely accounting for spatial proximity, for effective disaster assessment and response planning.

Results

Data description

We evaluate our framework on three earthquake events: the 2020 Puerto Rico earthquake (M6.4), 2021 Haiti earthquake (M7.2), and 2023 Turkey-Syria earthquake sequence (M7.8).

The 2020 Puerto Rico earthquake A magnitude 6.4 earthquake hit the southwest part of Puerto Rico on January 7, 2020. The ARIA team created DPMs using SAR images from the Sentinel-1 satellite to identify potentially damaged areas²⁹. Researchers from the USGS, the University of Puerto Rico Mayagüez, the GEER team, and the StEER team later conducted field reconnaissance to collect ground truth observations^30,31,32. Post-earthquake reports documented that at least 300 landslides were triggered near the epicenter³⁰.

The 2021 Haiti earthquake On August 14, 2021, a magnitude 7.2 earthquake struck the southern peninsula of Haiti. The StEER team and GEER team later collected ground truth inventories for landslides and building damage^33,34,35. According to post-disaster reports, the earthquake resulted in at least 2248 human fatalities, destroyed 53,815 buildings, and damaged 83,770 structures throughout Grand Anse, Nippes and Sud^36,37.

The 2023 Turkey-Syria earthquake sequence On February 6, 2023, an earthquake of Mw 7.8 and its aftershocks caused unparalleled destruction in Turkey and Syria. This disaster resulted in more than 55,000 deaths, displaced 3 million people in Turkey and 2.9 million in Syria, and caused damage or destruction to at least 230,000 buildings^14,17. The ARIA team generated DPM derived from synthetic aperture radar (SAR) images on Feb. 10, 2023 by the Copernicus Sentinel-1 satellites operated by the European Space Agency³⁸. Ground truth was later collected and reported by the Turkish Ministry of Environment^14,39.

Evaluation metrics and benchmarks

We evaluate our framework using multiple complementary metrics to provide a comprehensive assessment of performance. The primary evaluation is based on the receiver operating characteristics (ROC) curve and its area under curve (AUC) metric⁴⁰. ROC curves plot True Positive Rate against False Positive Rate (FPR) across varying decision thresholds, providing a threshold-independent assessment that is particularly valuable in disaster contexts where optimal classification thresholds may vary by event type, geographic region, or hazard category. This approach aligns well with the probabilistic nature of our framework, as both our spatially-aware causal model and the benchmark methods produce confidence scores rather than hard classifications.

To complement the AUC metric, we also employ the F1 score, which is the harmonic mean of precision and recall. The F1 score is calculated as $F1=2\times \frac{precision\times recall}{precision+recall}$, where precision represents the ratio of correctly identified hazards to all predicted hazards, and recall captures the proportion of actual hazards that were correctly identified. Unlike AUC, which evaluates performance across all possible thresholds, F1 score requires selecting a specific classification threshold. For consistent comparison, we use the threshold that maximizes the F1 score for each model and hazard type. This metric is particularly informative for disaster response applications, where balancing false alarms (precision) with missed hazards (recall) is critical for effective resource allocation.

Although our framework is fundamentally an unsupervised model that approximates true posteriors through variational inference, these evaluation metrics enable objective comparison with supervised approaches. Additionally, we utilize the variational bound as an internal metric to optimize model parameters and determine the optimal flow length for the normalizing flow component.

Spatially-varying causal influence mapping between multi-hazards and structural damage

Figure 1 illustrates the complex spatial relationships between different types of hazard, their causal influence, and surface deformation patterns following the 2020 Puerto Rico earthquake with an extent of −66.945°W, 17.956°N to −66.876°W, 17.998°N. The DPM (Fig. 1b) captures surface deformation and ground changes, serving as an observable proxy that Spatial-VCBN interprets through causal relationships.

Fig. 1: Spatial distribution of hazards, causal parameters, and damage following the 2020 Puerto Rico earthquake.

a Google satellite imagery of the study area with extent of −66.945°W, 17.956°N to −66.876°W, 17.998°N. b DPM derived from satellite imagery. c Spatial distribution of γ_LS values, showing the causal parameter strength from landslides (LS) to building damage (BD). d Spatial distribution of γ_LF values, showing the causal parameter strength from liquefaction (LF) to building damage (BD). e Posterior probability of landslide occurrence. f Posterior probability of building damage occurrence. g Posterior probability of liquefaction occurrence.

The spatial distribution of the causal parameters γ_LS and γ_LF, which are shown in Fig. 1c, d, reveals how different hazard mechanisms contribute to the damage of buildings throughout the landscape. Areas with elevated γ_LS values indicate locations where landslides have a stronger causal influence on building damage, predominantly in the hillier portions of the study area. These high-coefficient regions align well with areas showing a high posterior probability of landslide occurrence (Fig. 1e), suggesting that Spatial-VCBN successfully captures the spatial specificity of landslide impacts.

The effects of liquefaction show distinctly different spatial patterns, with high values of γ_LF concentrated in the central lowlands and coastal areas. This clear spatial separation between high γ_LS and high γ_LF regions validates Spatial-VCBN assumption that landslides and liquefaction generally do not co-occur at the same location due to their different geological requirements. The posterior probability of building damage (Fig. 1f) represents the result of our causal network, showing how the model integrates information from both types of hazard. Importantly, the model does not simply translate DPM signals directly into damage estimates but interprets these signals through the learned causal structure and spatially varying parameters.

These results demonstrate the ability of Spatial-VCBN to decouple different causal mechanisms contributing to observed surface changes, providing a more nuanced understanding of disaster impacts than would be possible from DPM interpretation alone. This capability forms the foundation for our subsequent analysis of how these causal parameters influence remote sensing observations.

Building on our understanding of causal relationships between hazards and structural damage, we now examine how these mechanisms present in DPM signals under varying conditions. We analyze both high-fidelity signal regions and challenging signal-constrained environments to demonstrate the robustness of Spatial-VCBN.

Robust spatially-varying causal inference between hazards and remote sensing observations

Figure 2 reveals the complex spatial relationships between different hazard mechanisms and their contributions to the observed DPM signals in an area with significant surface deformation in the study area with an extent of −66.946°W, 17.958°N to −66.890°W, 18.009°N. The DPM presented in Fig. 2a shows a concentrated area with high deformation values. The spatial distribution of the causal parameters provides insight into the primary mechanisms that drive these changes.

Fig. 2: Spatial distribution of causal parameters and DPM signals in a high-deformation area.

a Damage Proxy Map (DPM) showing surface deformation with brighter areas indicating higher change detection values in the study area with extent of −66.946°W, 17.958°N to −66.890°W, 18.009°N. b Spatial distribution of λ_LF, quantifying the causal relationship strength from liquefaction to DPM signals. c Spatial distribution of λ_LS, quantifying the causal relationship strength from landslides to DPM signals. d Spatial distribution of λ_BD, quantifying the causal relationship strength from building damage to DPM signals.

In this region, we observe spatial heterogeneity in how different hazards influence the DPM signals. The liquefaction causal parameter λ_LF (Fig. 2b) shows stronger values in the lower portion of the deformation area, suggesting that liquefaction processes are a dominant contributor to the DPM signals in that specific zone. This pattern is consistent with the typical geographic distribution of liquefaction in low-lying areas with specific soil conditions. Conversely, the landslide causal parameter λ_LS shown in Fig. 2c exhibits higher values in scattered patches, particularly in the right portion of the image where several high-intensity areas appear. This indicates locations where landslide mechanisms have a stronger influence on the observed DPM signals, likely corresponding to areas with steeper slopes or unstable terrain.

Figure 2d displays the building damage parameter λ_BD. It shows a distinct spatial pattern with moderate to high values in several discrete clusters. These areas represent locations where building deformation and structural impacts most strongly contribute to the DPM signals, which often correspond to zones with higher density of built structures. This spatial segregation of causal parameters demonstrates the ability of Spatial-VCBN to decouple multiple contributing factors to DPM signals, providing insights into the dominant hazard mechanisms at different locations within the affected area.

This capability to decouple in high-signal regions establishes a baseline for comparison with more challenging signal-constrained environments, which we examine next to demonstrate the robustness of Spatial-VCBN under varying conditions.

While Spatial-VCBN performs well in areas with strong DPM signals, real-world disaster assessment often involves regions with weak, noisy, or ambiguous observational data. We now demonstrate the ability of Spatial-VCBN to extract meaningful causal parameters even in these challenging signal-constrained environments. Figure 3 highlights the robust capability of Spatial-VCBN to identify meaningful landslide patterns even in challenging conditions where DPM signals are weak, inconsistent, or contaminated by noise. The areas shown exhibit noisy DPM readings, shown in Fig. 3c, g that likely result from environmental factors such as snow cover or the complex reflectance properties of mountainous terrain, which can introduce artifacts in satellite-based change detection. Despite these challenging conditions, our spatially-aware causal Bayesian network successfully extracts coherent landslide susceptibility patterns. The distributions of landslide causal parameter λ_LS shown in Fig. 3a, e display distinct spatial organization with higher values concentrated along features that correspond to terrain characteristics associated with landslide risk. This demonstrates that Spatial-VCBN can effectively filter signal from noise by leveraging spatial correlation structures through its Gaussian Process component.

Fig. 3: Spatial pattern learning in areas with noisy DPM signals following the 2020 Puerto Rico earthquake.

This figure demonstrates the ability of Spatial-VCBN to detect landslide patterns even in areas with weak or noisy DPM signals. Top row (a–e) and bottom row (f–j) show two different regions following the 2020 Puerto Rico earthquake: a, f Spatial distribution of λ_LS, quantifying the causal relationship strength from landslides to DPM; b, g Posterior probability of landslide occurrence; c, h Uncertainty of landslide posterior distributions; d, i Damage Proxy Map (DPM) showing noisy surface deformation signals (0–1); e, j Google satellite imagery showing the corresponding terrain.

Notably, the uncertainty maps for landslide occurrence (Fig. 3c, h) reveal important patterns that complement our posterior probability estimates. Areas with high landslide probability in Fig. 3b, g generally exhibit low uncertainty (darker regions in the uncertainty maps), indicating high confidence in these estimations. Conversely, transitional zones between high and low probability areas show elevated uncertainty levels. This uncertainty quantification provides critical decision support information, as emergency responders can prioritize areas with both high hazard probability and low uncertainty for immediate intervention, while areas with high uncertainty might warrant additional monitoring or investigation.

The posterior probability maps for landslide occurrence presented in Fig. 3b, f reveal a refined understanding of landslide risk that transcends the limitations of the noisy DPM data. These posterior estimates incorporate both the learned causal strengths and the underlying geophysical context, resulting in coherent spatial patterns that align with landslide-prone landscape features visible in the satellite imagery (Fig. 3d, h). This ability to maintain signal fidelity in challenging conditions is particularly important for comprehensive hazard assessment in mountainous regions, where environmental factors typically confound traditional analysis methods.

Similar resilience is observed in building damage estimation, as shown in Fig. 4. Several factors can introduce noise in building damage estimation from satellite-based DPM, including variable building materials and construction types that respond differently to deformation, vegetation coverage partially obscuring buildings, complex urban geometries creating shadows and radar reflection artifacts, temporal variations in atmospheric conditions affecting satellite measurements, and pre-existing structural modifications unrelated to disaster impacts. Despite these challenges, our spatially-aware causal Bayesian network successfully extracts coherent building damage patterns. The distributions of building damage causal parameter λ_BD shown in Fig. 4a, e exhibit clear spatial structure with higher values concentrated along what appear to be developed corridors visible in the satellite imagery. These patterns follow the distribution of built environments rather than appearing randomly distributed, suggesting that Spatial-VCBN is able to capture true building-related signals despite the noise.

Fig. 4: Building damage estimation in areas with noisy DPM signals following the 2020 Puerto Rico earthquake.

This figure demonstrates the ability of Spatial-VCBN to detect building damage patterns despite weak DPM signals. Top row (a–e) and bottom row (f–j) show two different regions. a, f Spatial distribution of λ_BD, quantifying the causal relationship strength from building damage to DPM; b, g Posterior probability of building damage occurrence; c, h Uncertainty of building damage posterior; d, i DPM showing noisy surface deformation signals; e, j Google satellite imagery showing developed areas with building structures.

The uncertainty maps for building damage (Fig. 4c, h) show particularly low uncertainty values (typically below 0.2) in both developed and undeveloped areas, with slightly higher uncertainty in transition zones. This spatial consistency in uncertainty estimates further validates our model’s robustness. The uncertainty is generally lower for building damage estimation compared to landslide estimation (maximum of 0.2 versus 0.25), suggesting that building damage signatures may be more distinctly identifiable in the DPM signals. This has important implications for disaster response prioritization, as resources can be more confidently allocated to areas with predicted building damage.

The posterior probability maps for building damage presented in Fig. 4b, f show improved spatial patterns that are more structured than what might be inferred from the noisy DPM alone. The larger posterior probabilities appear primarily in areas with visible building clusters in the satellite imagery (Fig. 4d, h), demonstrating that Spatial-VCBN effectively incorporates contextual information about the built environment.

The robustness of Spatial-VCBN extends to different earthquake events and hazard types, as demonstrated in Fig. 5 for liquefaction estimation in the 2021 Haiti earthquake. Even when DPM signals are compromised by various confounding factors such as water level fluctuations, coastal erosion processes, wave action affecting shoreline appearance, soil moisture variations in near-shore environments, and varying sediment compositions that respond differently to seismic shaking, Spatial-VCBN successfully identifies coherent liquefaction patterns across different coastal areas. The distributions of liquefaction causal parameter λ_LF, which is presented in Fig. 5a, e, show distinctive spatial patterns with higher values concentrated in areas near coastlines where geological conditions favor liquefaction. The consistency of these patterns across different coastal regions within the same earthquake event suggests that Spatial-VCBN is able to capture fundamental physical relationships rather than location-specific anomalies.

Fig. 5: Liquefaction estimation in coastal areas of the 2021 Haiti earthquake.

Top row (a–e) and bottom row (f–j) show two different coastal areas. a, f Spatial distribution of λ_LF, quantifying the causal relationship strength from liquefaction to DPM; b, g Posterior probability of liquefaction occurrence; c, h Uncertainty of liquefaction posterior; d, i DPM showing noisy surface deformation signals; e, j Google satellite imagery showing coastal areas susceptible to liquefaction.

The uncertainty maps for liquefaction (Fig. 5c, h) exhibit the lowest overall uncertainty values among the three hazard types (maximum of 0.15), particularly near shorelines where liquefaction is most likely to occur. This lower uncertainty for liquefaction estimation likely reflects the stronger geophysical constraints on where liquefaction can occur, primarily in saturated, unconsolidated sediments near water bodies. The clear spatial correlation between low uncertainty and coastal proximity offers valuable information for risk-aware decision making, as emergency responders can confidently prioritize resources for coastal communities where liquefaction risk is both high and certain.

The posterior probability maps for liquefaction, shown in Fig. 5b, f, exhibit refined spatial patterns that align with coastal geomorphology visible in the satellite imagery (Fig. 5d, h). Higher probabilities appear in low-lying coastal areas with likely unconsolidated sediments that are typically more susceptible to liquefaction during seismic events. This correspondence between model estimations and physical geography further validates the ability of Spatial-VCBN to capture meaningful hazard patterns despite noisy observations.

Our comprehensive uncertainty quantification extends beyond spatial visualizations to the performance metrics themselves, as shown in Table 1. By incorporating standard deviation values alongside mean AUC metrics, we provide a robust assessment of model reliability. Spatial-VCBN consistently achieves the highest AUC values with relatively small standard deviations (between ±0.0076 and ±0.0124), demonstrating both superior performance and reliability. The standard deviations tend to be smaller for building damage estimation compared to landslide estimation, which aligns with our spatial uncertainty observations. This performance consistency across different hazard types and earthquake events, coupled with explicit uncertainty quantification, enhances the practical utility of our framework for real-world disaster response applications where decision-makers must consider both hazard likelihood and estimation confidence.

Table 1 AUC values comparison across earthquake events

These qualitative assessments across different hazard types, signal conditions, and earthquake events demonstrate the robust nature of our spatially-aware causal framework. In the following section, we provide quantitative evaluation metrics that further validate these observations.

Figure 5 demonstrates the effectiveness of Spatial-VCBN in detecting liquefaction patterns across different coastal regions affected by the 2021 Haiti earthquake, even when DPM signals are compromised by various confounding factors such as water level fluctuations, coastal erosion processes, wave action affecting shoreline appearance, soil moisture variations in near-shore environments, and varying sediment compositions that respond differently to seismic shaking. Despite these challenges, our spatially-aware causal Bayesian network successfully identifies coherent liquefaction patterns across different coastal areas. The distributions of liquefaction causal parameter λ_LF, which is presented in Fig. 5a, e, show distinctive spatial patterns with higher values concentrated in areas near coastlines where geological conditions favor liquefaction. The consistency of these patterns across different coastal regions within the same earthquake event suggests that Spatial-VCBN is able to capture fundamental physical relationships rather than location-specific anomalies. The posterior probability maps for liquefaction, shown in Fig. 5b, f, exhibit refined spatial patterns that align with coastal geomorphology visible in the satellite imagery (Fig. 5d, h). Higher probabilities appear in low-lying coastal areas with likely unconsolidated sediments that are typically more susceptible to liquefaction during seismic events. This correspondence between model estimations and physical geography further validates the ability of Spatial-VCBN to capture meaningful hazard patterns despite noisy observations. The ability of Spatial-VCBN to produce consistent, physically plausible liquefaction assessments in challenging coastal environments, where traditional DPM analysis would be heavily compromised by noise, demonstrates its value for comprehensive multi-hazard assessment in diverse settings.

Cross-event validation and baseline comparison

Our evaluation framework includes a comprehensive array of comparative methods across multiple hazard types. For our landslide (LS) and liquefaction (LF) estimation performance, we evaluate against several established approaches: the ground failure models developed by the USGS^41,42, the VBCI methodology proposed by¹², as well as both the Artificial Neural Network (ANN) and Gradient Boosting Machine (GBM) techniques outlined by⁴³. In assessing building damage (BD) estimation capabilities, we contrast Spatial-VCBN with conventional building fragility curves, the VBCI framework¹², ensemble methodology⁴⁴, and the bilateral filtering approach recently introduced by²⁰. Figure 6 and Tables 1 and 2 demonstrate the superior performance of our spatially-aware causal Bayesian network across multiple hazard types and earthquake events. The consistently higher metric values achieved by Spatial-VCBN validate the effectiveness of Spatial-VCBN in accurately identifying disaster impacts.

Fig. 6: ROC (Receiver Operating Characteristic) curves and AUC (Area Under the Curve) values comparing the performance of Spatial-VCBN against baselines for different hazard types across three recent earthquakes.

a–c Building damage, Landslide, and Liquefaction ROC curves of the 2020 Puerto Rico earthquake. d Building damage for 2023 Turkey-Syria earthquake, e, f Building damage and Landslide ROC curves of the 2021 Haiti earthquake. Each plot compares three approaches: prior probability^41,42 (blue dotted line), posterior from VBCI baseline¹² (red dashed line), and posterior from Spatial-VCBN (solid yellow line).

Table 2 F1 score comparison across earthquake events

For the 2020 Puerto Rico earthquake, Spatial-VCBN achieves remarkable improvements in building damage (Fig. 6a), with an AUC of 0.9532 compared to 0.9145 for the VBCI and only 0.7050 for the prior. This represents a substantial 35.2% improvement over the prior probability baseline. As shown in Table 1, Spatial-VCBN consistently outperforms six competitive baselines, including both traditional statistical approaches and deep learning methods. The F1 score results shown in Table 2 further validate these findings, with Spatial-VCBN achieving 0.9167 for building damage in Puerto Rico, compared to the next best performer (Bilateral filter²⁰) at 0.8945. This performance gain is particularly noteworthy for building damage, where distinguishing between different damage mechanisms can be challenging. For landslides (Fig. 6b), Spatial-VCBN also outperforms competitors with an AUC of 0.9527, though the margin is smaller as all methods perform relatively well on this hazard type. Looking at Table 1, we observe that the closest competitor for landslide estimation is the Bilateral filter approach (0.9413), which still falls short of the performance of our method by 1.2%. The consistency between AUC and F1 metrics (0.9173 for Spatial-VCBN versus 0.9031 for Bilateral filter) indicates that our performance improvements are robust across different evaluation criteria. Liquefaction estimation (Fig. 6c) shows intermediate improvements, with Spatial-VCBN achieving an AUC of 0.9489, representing a 9.5% improvement over the prior (0.8662). Table 2 shows a similar pattern for F1 scores, with Spatial-VCBN achieving 0.9107 compared to 0.8815 for Bilateral filter and 0.8714 for VBCI, highlighting the balanced performance of Spatial-VCBN in both estimation accuracy and false alarm reduction.

The cross-event evaluation further substantiates the robustness of Spatial-VCBN. For the 2023 Turkey-Syria earthquake (Fig. 6d), Spatial-VCBN achieves an impressive AUC of 0.9874 for building damage, significantly outperforming the prior (0.9051) with improvement of 9.1%. Tables 1 and 2 reveal that this superiority is maintained across metrics, with our F1 score of 0.9412 substantially outperforming all alternatives including the Bilateral filter (0.9089). Notably, Spatial-VCBN demonstrates particularly strong improvements over learning-based methods such as the Ensemble approach, which achieves only F1 score of 0.8213 for the Turkey-Syria earthquake, highlighting the advantage of our causal framework over pure statistical learning approaches. Similar improvements are observed for the 2021 Haiti earthquake, with Spatial-VCBN achieving AUCs of 0.9703 for landslide (Fig. 6e) and 0.9774 for building damage (Fig. 6f), representing improvements of 26.0% over the prior (0.7755) for building damage, and 5.15% over the prior (0.9228) for landslide. Table 1 shows that even compared to the stronger Bilateral filter approach, Spatial-VCBN maintains advantages of 2.0% and 3.9% for landslide and building damage estimation, respectively.

A comprehensive examination of Tables 1 and 2 reveals several additional insights not immediately apparent from the ROC curves alone. First, the performance gap between Spatial-VCBN and alternatives is consistently larger for building damage than for landslide estimation across all earthquake events, suggesting that our spatial-causal modeling approach particularly excels at capturing the complex mechanisms underlying building vulnerability. Second, machine learning methods like ANN and GBM show substantially worse performance than causal modeling approaches across all metrics, with AUC differences of up to 0.1475 (comparing Spatial-VCBN to ANN for landslide estimation in Puerto Rico) and F1 score differences of up to 0.2041 (comparing Spatial-VCBN to GBM for liquefaction estimation in Puerto Rico). This highlights the limitations of purely data-driven approaches when physical causal mechanisms are not explicitly modeled.

These results highlight three key strengths of Spatial-VCBN. First, Spatial-VCBN demonstrates consistent performance advantages across different hazard types, with particularly notable improvements for building damage estimation where distinguishing between different damage mechanisms is especially challenging. Second, Spatial-VCBN shows strong transferability across different earthquake events in diverse geographical settings, maintaining its performance edge in the Puerto Rico, Haiti, and Turkey-Syria earthquakes despite their varying geological contexts and built environment characteristics. Third, Spatial-VCBN achieves robust performance improvements particularly at low FPRs, which is crucial for practical deployment in disaster response scenarios where false alarms can waste limited resources and undermine confidence in automated hazard assessments. The consistent outperformance across multiple events, hazard types, and evaluation metrics demonstrates that modeling spatially-varying causal relationships through combined Gaussian Processes and normalizing flows provides a powerful framework for disaster impact assessment that generalizes well across different scenarios. This performance advantage is from the ability of Spatial-VCBN to capture both the spatial correlation structure inherent in disaster impacts and the complex, non-Gaussian distributions of causal effects that characterize real-world hazard-damage relationships. By learning location-specific causal parameters rather than assuming uniform relationships across the study area, Spatial-VCBN can adapt to the unique geological, structural, and environmental factors that influence how different hazards manifest in different locations.

Ablation study and model robustness

Computational efficiency analysis

Table 3 provides insights into the computational requirements of our framework across three earthquake events with varying affected areas. We implement a pruning strategy that maintains efficiency by focusing computational resources on active nodes while eliminating inactive ones from the processing pipeline. For the Haiti earthquake with the largest affected area (15,970 km²), Spatial-VCBN required 15,029 s (~4.2 h), while the smaller Puerto Rico earthquake area (1305 km²) was processed in just 1198 s (~20 min). This near-linear scaling (with a processing rate of ~0.94 s/km²) indicates that our framework maintains computational efficiency as the geographical scope increases.

Table 3 This table shows the time cost of running our framework using the same batch size in three earthquake events using real-world data

The consistency in processing time per unit area across different earthquake events suggests that the computational demands of Spatial-VCBN are primarily determined by the spatial extent rather than being affected by the complexity or specific characteristics of different regions. This predictable scaling behavior is particularly valuable for emergency response scenarios where estimation of required computational resources is crucial for timely deployment. Our implementation leverages GPU acceleration, equipped with an NVIDIA Tesla T4 GPU (15 GB VRAM) and 51 GB of RAM, enabling rapid parallel processing of spatial data. The results indicate that even for large-scale events like the Turkey-Syria earthquake (4676 km²), analysis can be completed within reasonable timeframes (~1.3 h), making our approach practical for operational use in disaster response.

Hyperparameter sensitivity

Table 4 presents a systematic evaluation of the sensitivity of Spatial-VCBN to the flow number K in the normalizing flow component, which directly affects the expressiveness of the spatially-varying causal parameter distributions. The results reveal several important patterns across different earthquake events and hazard types. For all hazard types and earthquake events, performance improves substantially as K increases from 2 to 6, with the significant improvements observed in the early stages. For example, in the Haiti earthquake building damage estimation, AUC increases from 0.8915 with K = 2–0.9774 with K = 6, an improvement of 9.6%. This pattern indicates that the spatial distribution of causal parameters in disaster scenarios exhibits complexity that cannot be adequately captured by simpler flow architectures.

Table 4 Ablation study on flow number K in normalizing flows

Notably, we observe that K = 6 represents an optimal balance point across all hazards and events, achieving the highest AUC values for landslide estimation in Haiti (0.9703), building damage in Haiti (0.9774), landslide in Puerto Rico (0.9527), liquefaction in Puerto Rico (0.9489), building damage in Puerto Rico (0.9532), and building damage in Turkey-Syria (0.9874). Beyond K = 6, we observe a slight performance degradation, with AUC decreasing marginally for K = 7 and K = 9. This pattern suggests a form of overfitting when the flow becomes too expressive relative to the available constraints.

The impact of K varies across different hazard types, with building damage showing the highest sensitivity to flow complexity. For the Puerto Rico earthquake, increasing K from 2 to 6 improves building damage AUC by 0.0818, compared to improvements of 0.0514 for landslide and 0.0593 for liquefaction. This difference likely reflects the more complex causal mechanisms involved in building damage, which depends on both the primary hazards and structural characteristics. Cross-event comparison reveals consistent patterns in hyperparameter sensitivity, with all three earthquake events showing similar optimal flow complexity despite their geographical and geological differences. This consistency suggests that Spatial-VCBN architecture captures fundamental aspects of the spatially-varying causal relationships in disaster scenarios rather than simply fitting to dataset-specific patterns.

Normalizing flow architecture evaluation

To justify our choice of planar flows in the Spatial-VCBN framework, we conducted a comparative analysis of several normalizing flow architectures, evaluating their performance, computational efficiency, and memory requirements. Table5 presents the results of this comparison across five different flow architectures: Planar Flows (our implemented approach), RealNVP, Masked Autoregressive Flows (MAF), Radial Flows, and Inverse Autoregressive Flows (IAF).

Table 5 Comparison of normalizing flow architectures

While more complex architectures such as MAF demonstrate slightly higher performance with AUC improvements of 0.0016 (0.17%) for Haiti landslide detection and 0.0024 (0.25%) for Puerto Rico building damage detection, these marginal gains come at substantial computational costs. MAF requires 4.7× the memory of planar flows and 3.2× longer running time. Similarly, RealNVP and IAF show modest performance improvements (less than 0.2% AUC increase) while requiring significantly more computational resources. For our spatially-aware causal modeling framework, which often needs to process large geographical regions, computational efficiency is a critical consideration. The landslide detection area for the Haiti earthquake alone covers ~15,970 km², making efficient processing essential for practical deployment in time-sensitive disaster response scenarios. Planar flows provide an optimal balance between model expressiveness and computational efficiency, enabling our framework to handle large-scale disaster events while maintaining high accuracy (AUC ≥ 0.95 across all test cases). Radial flows, despite their comparable computational efficiency to planar flows, demonstrated slightly lower performance in our experiments. This suggests that the specific transformation properties of planar flow, which are well-suited for capturing the spatial causal relationships in earthquake-induced hazard scenarios. Based on this analysis, we selected planar flows for our final implementation, prioritizing practical application while maintaining performance for multi-hazard estimation.

Discussion

The development of a spatially-aware causal Bayesian network with normalizing flows represents a significant advancement in multi-hazard disaster impact assessment. Our results demonstrate that this approach not only improves estimation accuracy across multiple hazards and impacts induced by different earthquake events, with AUC improvements of up to 35.2% over prior probability baselines and 5.5% over state-of-the-art VBCI methods. Additionally, it provides interpretable insights into the complex causal mechanisms underlying disaster impacts. In this discussion, we contextualize our findings within the broader disaster science literature and examine their implications for both theoretical understanding and practical applications.

Traditional approaches to hazard assessment often rely on either purely data-driven methods that lack causal interpretability or physical models that struggle to incorporate the complex spatial heterogeneity of real-world disaster contexts. Our framework bridges this gap by explicitly modeling spatially-varying causal relationships through a combination of Gaussian Processes and normalizing flows. This innovation allows us to capture both the spatial correlation structure inherent in disaster impacts and the non-Gaussian, potentially multimodal distributions of causal effects that characterize real-world hazard-damage relationships.

The spatial patterns observed in our causal parameters (γ_LS, γ_LF, λ_LS, λ_LF, and λ_BD) highlight the fundamental importance of accounting for spatial heterogeneity in disaster modeling. For instance, in the Puerto Rico earthquake (Fig. 1), the clear differentiation between landslide-dominated hillsides and liquefaction-dominated lowlands demonstrates how terrain characteristics fundamentally alter causal mechanisms. This spatial variability, along with the distinct patterns of building damage influence, suggests that assuming spatial homogeneity in causal relationships, as many existing models do, may lead to substantial inaccuracies in hazard assessment. The optimal flow number of K = 6 identified in our ablation study (Table 4) suggests that real-world causal relationships in disaster contexts exhibit complexity that cannot be adequately captured by simpler distributional assumptions, underscoring the importance of our methodological innovation.

Remote sensing plays a crucial role in disaster response, but the interpretation of complex signals like DPM remains challenging. The ability of Spatial-VCBN to decouple multiple contributing factors to DPM signals addresses a significant gap in existing approaches. As demonstrated in Fig. 2, our framework can identify distinct causal pathways from different hazard types to observed DPM signals within the same geographic region, providing critical insights that would be lost in approaches that treat DPM as a uniform indicator of damage. The results demonstrating robust causal parameter extraction even in signal-constrained environments (Figs. 3 and 4) highlight the potential of causal modeling to enhance the utility of remote sensing data in challenging conditions. For example, in mountainous regions where snow cover and complex topography introduce noise into DPM measurements, Spatial-VCBN successfully extracts coherent landslide susceptibility patterns that align with terrain characteristics visible in satellite imagery. The consistent performance across different hazard types and earthquake events suggests that our approach captures fundamental physical relationships rather than only fitting to dataset-specific patterns. This is particularly notable given the diverse geological and built environment contexts represented in our study areas (Puerto Rico, Haiti, and Turkey-Syria), as evidenced by the comparable AUC values achieved across these events (Table 1). The transferability of Spatial-VCBN suggests that the spatially-varying causal relationships we identify reflect genuine physical processes that generalize across different disaster scenarios.

The practical implications of our work extend beyond theoretical advancements to offer tangible benefits for disaster risk reduction and emergency response. Particularly noteworthy is the strong performance of Spatial-VCBN at low FPR, as shown in the ROC curves (Fig. 6). In practical disaster response, false alarms can waste limited resources and undermine stakeholder confidence in automated assessment systems. The ability of our approach to maintain high detection rates while minimizing false positives addresses this crucial operational concern. The reasonable computational requirements demonstrated in our efficiency analysis (Table 3), with processing times of ~0.94 s/km² with GPU acceleration, suggest that our approach is viable for operational deployment, even for large-scale events. The near-linear scaling with geographical area provides predictable resource requirements for emergency management agencies planning post-disaster assessments. For example, our results indicate that even a large-scale event like the Haiti earthquake (15,970 km²) can be analyzed in ~4.2 h using modest computational resources. Beyond immediate response applications, our spatially-explicit causal framework offers valuable insights for long-term disaster risk reduction planning. The identification of areas where specific hazard mechanisms dominate could inform targeted mitigation strategies. For example, authorities might prioritize slope stabilization in regions with high γ_LS values or focus on liquefaction-resistant foundation designs in areas with elevated γ_LF parameters.

While we focused on seismic events in this study, the fundamental design of Spatial-VCBN makes it readily adaptable to non-seismic hazards and multi-hazard scenarios. The causal Bayesian network architecture is inherently flexible and can be reconfigured to model alternative causal chains, such as those involved in rainfall-induced landslides, flooding, or hurricane impacts. For instance, in modeling rainfall-triggered landslides, precipitation intensity could replace seismic shaking as the primary triggering node, while retaining similar geophysical feature nodes. The key requirement for applying our framework to other hazard types is the availability of (1) relevant remotely sensed coherence change products similar to DPMs, (2) geospatial features that influence the hazard mechanisms, and (3) a conceptual understanding of the causal relationships between triggers, environmental conditions, and resulting impacts. Our spatially-varying approach using Gaussian Processes with normalizing flows would be particularly valuable for modeling non-seismic hazards like hurricanes or floods, where impacts often show strong spatial heterogeneity based on topography, infrastructure quality, and socioeconomic factors. Extending Spatial-VCBN to these scenarios would primarily require adapting the causal graph structure and incorporating hazard-specific geospatial features, while the core inference methodology would remain applicable.

The spatially-varying causal parameters identified by our framework could serve as valuable calibration or validation data for detailed physical simulations, potentially improving their spatial accuracy. Conversely, insights from physical models could inform prior distributions in our Bayesian framework, creating a virtuous cycle of model improvement. This integration of data-driven causal inference with physical understanding represents a promising direction for advancing multi-hazard assessment methodologies. The ability of Spatial-VCBN to identify meaningful patterns even in areas with weak or noisy DPM signals suggests that it could extend the utility of physics-based models to regions where observational data is limited or compromised by environmental factors. This is particularly relevant for global-scale hazard assessment, where data quality varies substantially across different regions.

While our approach complements rather than replaces physics-based hazard models, the identified spatially-varying causal parameters could serve as valuable calibration data for physical simulations. Conversely, insights from physical models could inform prior distributions in our Bayesian framework. Despite promising results, limitations remain. Future work should validate our approach across a broader range of disaster types and incorporate temporal dynamics of hazard evolution.

In conclusion, our spatially-aware causal Bayesian network advances disaster impact assessment through its ability to capture spatially heterogeneous causal relationships, maintain robust performance under varying signal conditions, and provide interpretable insights into complex disaster mechanisms. The framework addresses critical limitations in existing approaches that either lack causal interpretability^43,44 or struggle with spatial heterogeneity^3,12. Our integration of Gaussian Processes with normalizing flows builds upon advances in spatially-varying coefficient models⁴⁵ while extending their applicability to non-Gaussian posterior distributions. The performance improvements demonstrated across multiple hazard types and earthquake events, particularly the substantial gains in building damage assessment, validate the practical utility of our approach for disaster response operations.

Methods

Prior geospatial models

Earthquake shaking intensity serves as the fundamental catalyst for structural damage and geohazards like landslides and liquefaction. We incorporate this critical factor through USGS ShakeMap data, which provides comprehensive shaking metrics. The composite ShakeMap effectively captures maximum ground motion intensities, enabling more accurate assessments of structural and geologic impacts, which is an invaluable resource for post-earthquake forensic analysis.

Beyond basic shaking information, USGS expanded their rapid post-earthquake information products in 2018 to include ground-failure estimations⁴⁶. These specialized models predict the likelihood and distribution of earthquake-triggered landslides and liquefaction³⁰. The modeling framework integrates multiple environmental factors including terrain slope, geological susceptibility, and soil characteristics to generate probability maps^41,42. An illustrative example appears in Fig. 7, showing the USGS ground failure projections following the 2023 Turkey-Syria earthquake. Within our Bayesian network architecture (Fig. 9), these established USGS ground failure products are incorporated as prior probability distributions for landslide and liquefaction occurrence, represented by nodes α_LS and α_LF respectively.

Fig. 7: Ground Failure Probability Maps Generated by the USGS.

After the 2023 Turkey-Syria earthquake sequence, the USGS produced example ground failure models for liquefaction (shown in panel b) and landslide (shown in panel a)⁶⁰. The probability of ground failure models is what the legend colors represent.

InSAR data and damage proxy maps

For our analysis, we utilized DPMs, which are specialized remote sensing products derived from InSAR data. DPMs identify ground surface changes by analyzing coherence differences between radar signals captured before and after seismic events⁹. These maps were generated by NASA’s ARIA team following three major earthquakes: the 2020 Puerto Rico earthquake (M6.4), the 2021 Haiti earthquake (M7.2), and the 2023 Turkey-Syria earthquake sequence (M7.8).

This InSAR product works by measuring changes in radar coherence, which represents the consistency of radar reflections from Earth’s surface between two time periods. Earthquake-induced changes to the surface disrupt this coherence, allowing detection of surface deformation. The resulting DPMs, shown in Fig. 8, represent these coherence changes where brighter pixels indicate greater surface disruption potentially caused by landslides, liquefaction, or building damage. While DPMs provide valuable high-resolution (30-m pixel) observations, they present interpretation challenges as they cannot inherently distinguish between different hazard types and contain environmental noise. In this work, the Spatial-VCBN framework addresses these limitations.

Fig. 8: Damage proxy maps (DPM) generated by the ARIA team following major earthquakes.

a 2021 Haiti earthquake (M7.2) with red boxes highlighting areas of significant surface deformation; b 2020 Puerto Rico earthquake (M6.4) with red boxes indicating concentrated damage zones; c 2023 Turkey-Syria earthquake sequence (M7.8). Brighter areas in all maps indicate greater surface deformation detected by InSAR. The geographical extents of these DPMs define our study regions.

Our study regions include (a) from −74.771°W to −72.581°W, from 18.118°N to 18.719°N for the 2021 Haiti earthquake (Fig. 8a); (b) from −67.022°W to −66.570°W, from 17.908°N to 18.153°N for the 2020 Puerto Rico earthquake (Fig. 8b); (c) from 36.681°E to 37.467°E, from 37.075°N to 37.676°N for the 2023 Turkey-Syria earthquake sequence (Fig. 8a).

Geophysical features

We incorporate seven geophysical features in Spatial-VCBN: (1) Vs30, (2) Slope from DEM, (3) Land Cover, (4) DEM (Elevation), (5) CTI (Compound Topographic Index), and (6) Water Body Distance, and (7) Lithology. Below, we provide a brief rationale for including each feature.

• Vs30 (Shear-Wave Velocity over 30 m): Vs30 is widely recognized as a key parameter for characterizing local site conditions and capturing near-surface amplification effects in seismic hazard assessments. Higher Vs30 values generally correspond to stiffer soils or rocks, reducing the likelihood of significant ground amplification^47,48.

• Slope from DEM: Slope, derived from a Digital Elevation Model (DEM), is crucial in identifying areas susceptible to landslides and other mass-movement hazards triggered by seismic activity. Regions with steep slopes tend to experience higher landslide hazard potential^49,50.

• Land Cover: Land cover information helps discern the presence of vegetation, urban infrastructure, or water bodies. Different land cover classes (e.g., dense vegetation vs. built-up areas) can significantly influence ground response and post-earthquake soil stability⁵¹.

• DEM (Elevation): The base elevation data from DEM are essential for capturing broader topographic variations. Elevation can affect not only slope angle but also local climate, drainage patterns, and material properties, all of which have implications for earthquake-induced geophysical hazards⁵².

• CTI (Compound Topographic Index): CTI, sometimes referred to as the Topographic Wetness Index, quantifies the potential for water accumulation in the terrain. High CTI values often indicate persistently wetter soils, influencing both liquefaction susceptibility and potential post-seismic runoff or slope failure⁵³.

• Water Body Distance: Proximity to the Water Body plays a significant role in liquefaction evaluations because saturated coastal regions and near-shore sediments are more prone to ground failure under strong seismic shaking^41,54.

• Lithology: Lithology plays a crucial role in assessing earthquake-related hazards as it directly influences seismic wave propagation, amplification, and ground shaking intensity. Different rock types exhibit varying mechanical properties such as stiffness, strength, and porosity, which affect the degree of energy dissipation and resonance during an earthquake. Additionally, lithological features control the susceptibility of slopes to landslides and liquefaction in earthquake-prone areas. Understanding lithology is therefore essential for accurate hazard zoning and designing resilient infrastructure in seismically active regions^42,55.

These geophysical features collectively represent critical factors governing seismic hazard distributions, spanning soil stiffness, topography, hydrology, and land use. By explicitly modeling their spatial variations and interactions, we aim to more accurately capture the localized nature of seismic impacts across heterogeneous terrains.

Causal modeling for disaster impacts

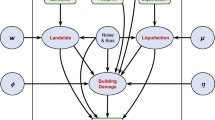
Disasters propagate through complex chains of causation, where initial events trigger cascading hazards that ultimately result in observable impacts. To accurately model these processes, we develop a spatially-aware causal Bayesian network that captures both the structural relationships between variables and the spatial heterogeneity of these relationships. Figure 9 presents our causal Bayesian network architecture, which consists of three key component types: (1) observable variables (represented as orange rectangles) including geospatial features (GF) and DPMs; (2) latent hazard/impact variables (shown as blue circles) representing unobserved landslides (LS), liquefaction (LF), and building damage (BD); and (3) spatially-varying causal coefficients that quantify the strength of causal relationships at each location.

Fig. 9: Overview of our causal Bayesian inference framework for seismic multi-hazard and impacts estimation.

l in the figure refers to the lth location in a target area. Blue circles refer to latent hazard/impact variables. Green cirles refer to the spatial-varying causal coefficients. Orange rectangles refer to the observations or known information.

For each location l in our study area, we define the leaf node y^l as the damage proxy map observation. Its relationship with parent nodes follows a log-linear model:

$$\log {y}^{l}| {\mathcal{P}}({y}^{l}),{\epsilon }_{y}^{l},{{\boldsymbol{\lambda }}}_{{\bf{{\mathcal{P}}}}({{\boldsymbol{y}}}^{{\boldsymbol{l}}})}^{l} \sim N\left({w}_{0y}+\sum _{k\in {\mathcal{P}}({y}^{l})}{\lambda }_{k}^{l}{x}_{k}^{l},{w}_{{\epsilon }_{y}}^{2}\right)$$

(1)

where ${x}_{k}^{l}$ represents the hidden hazard/damage variables, ${{\boldsymbol{\lambda }}}_{{\bf{{\mathcal{P}}}}({{\boldsymbol{y}}}^{{\boldsymbol{l}}})}^{l}$ denotes the spatially-varying causal coefficients that quantify the causal relationship from latent variables x_k ∈ {LS, LF, BD} to y, and ϵ_y accounts for environmental noise. The hidden nodes ${x}_{i}^{l}\in \{0,1\}$ for i ∈ {LS, LF, BD} are binary variables indicating hazard occurrence, with activation probabilities governed by their respective parent nodes and spatially-varying coefficients ${\gamma }_{i}^{l}$ that quantify the causal relationship from the parent nodes ${\mathcal{P}}(x)$ to x:

$$\begin{array}{l}\log \frac{p({x}_{i}^{l}=1| {x}_{{\mathcal{P}}({x}_{i}^{l})},{\epsilon }_{i}^{l},{\gamma }_{{\mathcal{P}}({x}_{i}^{l})})}{1-p({x}_{i}^{l}=1| {x}_{{\mathcal{P}}({x}_{i}^{l})},{\epsilon }_{i}^{l},{\gamma }_{{\mathcal{P}}({x}_{i}^{l})})}=\sum\limits_{k\in {\mathcal{P}}({x}_{i}^{l})}{\gamma }_{k}^{l}{x}_{k}^{l}+{w}_{{\epsilon }_{i}}{\epsilon }_{i}+{w}_{0i}\\ p({x}_{i}^{l}| {x}_{{\mathcal{P}}({x}_{i}^{l})},{\epsilon }_{i}^{l},{\gamma }_{{\mathcal{P}}({x}_{i}^{l})})={[p({x}_{i}^{l} = 1| {x}_{{\mathcal{P}}({x}_{i}^{l})},{\epsilon }_{i}^{l},{\gamma }_{{\mathcal{P}}({x}_{i}^{l})})]}^{{x}_{i}^{l}}\times {[1-p({x}_{i}^{l} = 1| {x}_{{\mathcal{P}}({x}_{i}^{l})},{\epsilon }_{i}^{l},{\gamma }_{{\mathcal{P}}({x}_{i}^{l})})]}^{1-{x}_{i}^{l}}\end{array}$$

(2)

Modeling spatially heterogeneous causal effects using normalizing flows with Gaussian process

A key innovation in Spatial-VCBN is the modeling of spatially-varying causal coefficients λ^l and γ^l using Normalizing Flows with Gaussian Process. This combination allows us to capture both the spatial correlation structure inherent in these coefficients while accommodating potentially complex, non-Gaussian posterior distributions. The following sections detail our methodology for posterior inference in this model and demonstrate its effectiveness for multi-hazard impact estimation.

To capture the complex spatial variation in causal coefficients ${v}^{l}\in \{{\lambda }_{a}^{l},{\gamma }_{b}^{l}\}$ where a ∈ {LS, LF, BD} and b ∈ {α_LS, α_LF, LS, LF}, we propose a novel approach that combines Gaussian Processes (GPs) with normalizing flows. This approach effectively captures both the spatial correlation structure and the complex, potentially non-Gaussian distributions of causal effects.

We introduce latent spatial variables ${z}_{v}^{l}$ which serve as the building blocks for our spatially varying causal coefficients. These latent variables represent underlying spatial patterns that, after transformation, will yield the causal parameters used in Spatial-VCBN. By working with these latent variables rather than directly modeling the coefficients, we gain mathematical tractability while maintaining expressiveness.

We model these latent variables ${z}_{v}^{l}$ across different locations using a Gaussian Process prior, which naturally captures correlations between locations with similar geophysical characteristics:

$${{\bf{z}}}_{v} \sim {\mathcal{GP}}({m}_{v}({\bf{GF}}),{k}_{v}({\bf{GF}},{{\bf{GF}}}^{{\prime} }))$$

(3)

where ${{\bf{z}}}_{v}=[{z}_{v}^{1},{z}_{v}^{2},\ldots ,{z}_{v}^{L}]$ is the vector of latent variables across all locations, m_v(GF) is the mean function that depends on the geophysical features GF at all locations, and ${k}_{v}({\bf{GF}},{{\bf{GF}}}^{{\prime} })$ is the kernel function that defines the covariance structure between different geophysical features. We use a Matern kernel, which is a widely used covariance function in spatial statistics whose smoothness parameter ν directly controls the mean-square differentiability of the process^56,57,58, with ν = 3/2:

$${k}_{v}({{\bf{GF}}}_{i},{{\bf{GF}}}_{j})={\sigma }_{v}^{2}\frac{{2}^{1-\nu }}{\Gamma (\nu )}{\left(\sqrt{2\nu }\frac{| | {{\bf{GF}}}_{i}-{{\bf{GF}}}_{j}| | }{{\ell }_{v}}\right)}^{\nu }{K}_{\nu }\left(\sqrt{2\nu }\frac{| | {{\bf{GF}}}_{i}-{{\bf{GF}}}_{j}| | }{{\ell }_{v}}\right)$$

(4)

where ${\sigma }_{v}^{2}$ controls the variance, ℓ_v is the length scale parameter, K_ν is the modified Bessel function, and GF_i, GF_j represent the geophysical feature vectors at locations i and j. This formulation ensures that locations with similar geophysical features will have similar coefficients, which better captures the underlying physical relationships in Spatial-VCBN.

To allow for complex non-Gaussian distributions of causal coefficients, we transform the GP latent variables through a series of invertible normalizing flow transformations:

$${v}^{l}={f}_{{K}_{v}}\circ \cdots \circ {f}_{2}\circ {f}_{1}({z}_{v}^{l})$$

(5)

where ${f}_{1},\ldots ,{f}_{{K}_{v}}$ are invertible transformations and K_v is the number of flow layers. This combination allows us to model both spatial correlation (through the GP) and distributional complexity (through the normalizing flow).

For inference, we approximate the true posterior of the GP latent variables with a multivariate Gaussian variational distribution:

$$q({{\bf{z}}}_{v})={\mathcal{N}}({{\boldsymbol{\mu }}}_{v},{{\bf{\Sigma }}}_{v})$$

(6)

where μ_v represents the posterior mean vector and Σ_v the posterior covariance matrix across all locations. For computational efficiency, we parameterize Σ_v as a low-rank plus diagonal structure:

$${{\bf{\Sigma }}}_{v}={{\bf{L}}}_{v}{({{\bf{L}}}_{v})}^{T}+{\rm{diag}}({{\boldsymbol{\delta }}}_{v})$$

(7)

where L_v is a lower-triangular matrix of rank r ≪ n (with n being the number of spatial locations), and δ_v is a vector of positive diagonal elements.

To enable efficient gradient computation during optimization, we employ the reparameterization trick:

$${{\bf{z}}}_{v}={{\boldsymbol{\mu }}}_{v}+{{\bf{L}}}_{v}{{\boldsymbol{\epsilon }}}_{1}+{\rm{diag}}(\sqrt{{{\boldsymbol{\delta }}}_{v}}){{\boldsymbol{\epsilon }}}_{2},\quad {{\boldsymbol{\epsilon }}}_{1} \sim {\mathcal{N}}({\bf{0}},{{\bf{I}}}_{r}),{{\boldsymbol{\epsilon }}}_{2} \sim {\mathcal{N}}({\bf{0}},{{\bf{I}}}_{n})$$

(8)

This allows us to sample from q(z_v) while maintaining differentiability with respect to the variational parameters μ_v, L_v, and δ_v.

When transforming the GP latent variables through the normalizing flow, we apply the change of variables formula to compute the density of the transformed variables:

$$\log q({v}^{l}| GF)=\log q({z}_{v}^{l})-\mathop{\sum }\limits_{k=1}^{{K}_{v}}\log \left\vert \det \left(\frac{\partial {f}_{k}}{\partial \mathop{z}\nolimits_{v,k-1}^{l}}\right)\right\vert$$

(9)

where ${z}_{v,k-1}^{l}$ represents the output of the (k − 1)-th transformation, with ${z}_{v,0}^{l}={z}_{v}^{l}$.

Computing expectations under the transformed distribution is done via Monte Carlo sampling:

$$\begin{array}{l}{{\mathbb{E}}}_{q({v}^{l})}[h({v}^{l})]={{\mathbb{E}}}_{q({z}_{v}^{l})}[h({f}_{{K}_{v}}\circ \cdots \circ {f}_{2}\circ {f}_{1}({z}_{v}^{l}))]\\\qquad\qquad\quad\;\approx \frac{1}{M}\mathop{\sum }\limits_{m=1}^{M}h({f}_{{K}_{v}}\circ \cdots \circ {f}_{2}\circ {f}_{1}({z}_{v}^{l,(m)}))\end{array}$$

(10)

where ${z}_{v}^{l,(m)}$ are samples drawn from $q({z}_{v}^{l})$ using the reparameterization in Equation (8), and M is the number of Monte Carlo samples.

In our implementation, we utilize planar flows of the form:

$${f}_{k}({z}^{l};{u}_{k},{c}_{k},{b}_{k})={z}^{l}+{u}_{k}h({c}_{k}^{T}{z}^{l}+{b}_{k})$$

(11)

where h is a tanh activation function with derivative ${h}^{{\prime} }(\cdot )$, and u_k, c_k, b_k are learnable parameters of the k-th flow. The log-determinant of the Jacobian for this transformation is:

$$\log \left\vert \det \left(\frac{{\rm{d}}{f}_{k}}{{\rm{d}}\mathop{z}\nolimits_{k-1}^{l}}\right)\right\vert =\log | 1+{u}_{k}^{T}\psi ({z}_{k-1}^{l})|$$

(12)

where $\psi (z)={c}_{k}\cdot {h}^{{\prime} }({c}_{k}^{T}z+{b}_{k})$.

We parameterize the mean function m_v(GF) as a function of the geophysical features:

$${m}_{v}({{\bf{GF}}}_{l})={{\rm{NN}}}_{v}({{\bf{GF}}}_{l})$$

(13)

where NN_v is a neural network that maps geophysical features at location i to the mean of the corresponding GP latent variable ${z}_{v}^{l}$.

This GP-Normalizing Flow approach provides several advantages for modeling spatially heterogeneous causal effects: (1) it naturally captures spatial correlation through the GP prior, (2) it allows for complex, non-Gaussian distributions through the normalizing flow transformation, and (3) it provides a principled way to incorporate uncertainty in the causal parameter estimates.

Stochastic variational inference with spatial-variant causal parameters

The ultimate goal is to jointly infer the true posteriors of multiple unobserved target variables x_i ∈ X, which represents the target hazards and impacts with unknown parameters of causal dependencies, and the unknown spatial-varying causal parameters ${\lambda }_{a}^{l},{\rm{where}}\,a\in \{LS,LF,BD\}$, and ${\gamma }_{b}^{l},{\rm{where}}\,b\in \{{\alpha }_{LS},{\alpha }_{LF},LS,LF\}$, across different locations that quantify the causal dependencies among parent nodes and child nodes. Therefore, we use variational inference to approximate the true posteriors of X^l using q(X^l) by optimizing the variational lower bound. Since the variable X^l is binary, we can further factorize q(X^l) over hidden (unobserved) nodes by:

$$q({X}^{l})=\prod _{i\in \{LS,LF,BD\}}q({x}_{i}^{l})=\prod _{i\in \{LS,LF,BD\}}{({q}_{i}^{l})}^{{x}_{i}^{l}}{(1-{q}_{i}^{l})}^{1-{x}_{i}^{l}}$$

(14)

where ${q}_{i}^{l}$ is defined to approximate the posterior probability that node i is active in location l.

We derive the lower bound of the marginal log-likelihood of the observed Y by Jensen’s inequality as follows:

$$\log\,P(Y, GF) = \underbrace{{\mathbb{E}}_{q(X^l,\epsilon^{l},{\mathbf{z}}^{l})}[\log\,p(y^{l}, GF, X^{l}, {\mathbf{z}}^{l})]}_{[1]} - \underbrace{{\mathbb{E}}_{q(X^l,\epsilon^{l},{\mathbf{z}}^{l})}[\log\,q(X^l,\epsilon^{l},{\mathbf{z}}^{l})]}_{[2]}$$

(15)

Here z^l represents the latent Gaussian Process variables, which are transformed through a normalizing flow to produce the spatially-varying parameters λ^l and γ^l shown in Equation (5).

The item [1] is further expanded as:

$$\begin{array}{rcl} {\mathbb{E}}_{q(X^l,\epsilon^{l},{\mathbf{z}}^{l})}[\log\,p(y^{l}, GF, X^{l}, {\mathbf{z}}^{l})] & =& \underbrace{{\mathbb{E}}[\log\,p(y^{l} | x_{{\mathcal{P}}(y)}^{l}, f_{K_{\lambda}} \circ \cdots \circ f_2 \circ f_1 ({\mathbf{z}}^{l}_{\lambda}), \epsilon_{y}^{l}, GF)]}_{[3]} \\ & +& \underbrace{\sum\limits_{i \in \{LS, LF, BD\}} {\mathbb{E}}[\log\,p(x_{i}^{l}|f_{K_{\gamma}} \circ \cdots \circ f_2 \circ f_1({\mathbf{z}}^{l}_{\gamma {\mathcal{P}}(x_{i}^{l})}), {\mathcal{P}}(x^{l}), \epsilon_{i}^{l}, GF ) ]}_{[4]}\\ & +& \underbrace{{\mathbb{E}}[\log\,p({\mathbf{z}}^{l}_{\lambda}|GF)]}_{[5]} + \underbrace{{\mathbb{E}}[\log\,p({\mathbf{z}}^{l}_{\gamma}|GF)]}_{[6]}\\ & +& \underbrace{\sum\limits_{i \in \{LS, LF, BD\}} {\mathbb{E}}[\log\,p(\epsilon_{i}^{l})] + {\mathbb{E}}[\log\,p(\epsilon_{y}^{l})]}_{C_{1}} \end{array}$$

(16)

Where $p({{\bf{z}}}_{\lambda }^{l}| GF)$ and $p({{\bf{z}}}_{\gamma }^{l}| GF)$ are Gaussian Process priors shown in Equation (3). As for item [2], we have:

$$\begin{array}{rcl} {\mathbb{E}}_{q(X^l,\epsilon^{l},{\mathbf{z}}^{l})}[\log\,q(X^l,\epsilon^{l},{\mathbf{z}}^{l})] & = & \underbrace{\sum\limits_{i} {\mathbb{E}}(x_{i}^{l})\log\,q_{i}^{l} + \sum\limits_{i} {\mathbb{E}}(1- x_{i}^{l})\log\,(1-q_{i}^{l})}_{[7]}\\ & +& \underbrace{{\mathbb{E}}[\log\,q({\mathbf{z}}^{l}_{\lambda})]}_{[8]} + \underbrace{{\mathbb{E}}[\log\,q({\mathbf{z}}^{l}_{\gamma})]}_{[9]}\\ & +& \underbrace{\sum\limits_{i} {\mathbb{E}}[\log\,q(\epsilon_{i}^{l})] + {\mathbb{E}}[\log\,q(\epsilon_{y}^{l})]}_{C_{2}} \end{array}$$

(17)

where C₁ and C₂ cancel out. $q({{\bf{z}}}_{\lambda }^{l})$ and $q({{\bf{z}}}_{\gamma }^{l})$ are Gaussian Process posteriors presented in Equation (6).

For terms [5], [6], [8], and [9] involving the Gaussian Process, we apply the KL divergence formula for multivariate Gaussians:

$$\begin{array}{rcl}[5]-[8]&=&-KL[q({{\bf{z}}}_{\lambda }^{l})| | p({{\bf{z}}}_{\lambda }^{l}| {\bf{GF}})]\\ &=&-\displaystyle\frac{1}{2}\left[{\rm{tr}}({{\bf{K}}}_{\lambda }^{-1}{{\bf{\Sigma }}}_{\lambda })+{({{\boldsymbol{\mu }}}_{\lambda }-{{\bf{m}}}_{\lambda })}^{T}{{\bf{K}}}_{\lambda }^{-1}({{\boldsymbol{\mu }}}_{\lambda }-{{\bf{m}}}_{\lambda })+\log | {{\bf{K}}}_{\lambda }| -\log | {{\bf{\Sigma }}}_{\lambda }| -{n}_{\lambda }\right]\end{array}$$

(18)

$$\begin{array}{lll}[6]-[9]&=&-KL[q({{\bf{z}}}_{\gamma }^{l})| | p({{\bf{z}}}_{\gamma }^{l}| {\bf{GF}})]\\ &=&-\displaystyle\frac{1}{2}\left[{\rm{tr}}({{\bf{K}}}_{\gamma }^{-1}{{\bf{\Sigma }}}_{\gamma })+{({{\boldsymbol{\mu }}}_{\gamma }-{{\bf{m}}}_{\gamma })}^{T}{{\bf{K}}}_{\gamma }^{-1}({{\boldsymbol{\mu }}}_{\gamma }-{{\bf{m}}}_{\gamma })+\log | {{\bf{K}}}_{\gamma }| -\log | {{\bf{\Sigma }}}_{\gamma }| -{n}_{\gamma }\right]\end{array}$$

(19)

where K represents the prior covariance matrices derived from the Matern kernel over geophysical features, Σ denotes the variational posterior covariance matrices, μ and m are the posterior and prior mean vectors respectively, and n is the dimensionality of the corresponding latent variable vectors. These equations quantify the divergence between our variational approximation and the true GP prior distributions for both λ and γ coefficients.

Based on our conditional distribution assumptions for ${y}^{l}| {\mathcal{P}}({y}^{l}),{\epsilon }_{y}^{l},{{\boldsymbol{\lambda }}}_{{\bf{{\mathcal{P}}}}({{\boldsymbol{y}}}^{{\boldsymbol{l}}})}^{l}$ as defined in Equation (1), we can calculate item [3] in Equation (16) as:

$$\begin{array}{lll}{\mathbb{E}}[\log p({y}^{l}| {\mathcal{P}}({y}^{l}),{\epsilon }_{y}^{l},{{\boldsymbol{\lambda }}}_{{\bf{{\mathcal{P}}}}({{\boldsymbol{y}}}^{{\boldsymbol{l}}})}^{l})]\,=\,-\log {y}^{l}-\log | {w}_{{\epsilon }_{y}}| -\displaystyle\frac{(\log {y}^{l})+{w}_{0y}^{2}+{\sum }_{k\in {\mathcal{P}}({y}^{l})}{\mathbb{E}}[{({\lambda }_{k}^{l})}^{2}]{q}_{k}^{l}-2\log {y}^{l}\cdot {w}_{0y}}{2{w}_{{\epsilon }_{y}}^{2}}\\\qquad\qquad\qquad\qquad\qquad\qquad\quad\;\, -\,\displaystyle\frac{{\sum }_{j\ne k}{\mathbb{E}}({\lambda }_{k}^{l})\cdot {\mathbb{E}}({\lambda }_{j}^{l})\cdot {q}_{k}^{l}\cdot {q}_{j}^{l}+({w}_{0y}-\log {y}^{l})\left({\sum }_{k\in {\mathcal{P}}({y}^{l})}{\mathbb{E}}({\lambda }_{k}^{l})\cdot {q}_{k}^{l}\right)}{{w}_{{\epsilon }_{y}}^{2}}\end{array}$$

(20)

As for item [4] in Equation (16), we consider two scenarios—when x_i is a leaf node and a non-leaf node. First we can describe the conditional distribution of LS, LF, and BD as follows:

$$\begin{array}{l}p({x}_{i}^{l}| {x}_{{\mathcal{P}}({x}_{i})}^{l},{\epsilon }_{i}^{l},{{\boldsymbol{\gamma }}}_{{\bf{{\mathcal{P}}}}({{\boldsymbol{x}}}_{{\boldsymbol{i}}}^{{\boldsymbol{l}}})}^{l})=\\ {\left[\displaystyle\frac{1}{1+\exp \left(-{\sum }_{k\in {\mathcal{P}}({x}_{i})}{\gamma }_{k}^{l}{x}_{k}^{l}-{w}_{{\epsilon }_{i}}{\epsilon }_{i}^{l}-{w}_{0i}\right)}\right]}^{{x}_{i}^{l}}\cdot {\left[\displaystyle\frac{1}{1+\exp \left({\sum }_{k\in {\mathcal{P}}({x}_{i})}{\gamma }_{k}^{l}{x}_{k}^{l}+{w}_{{\epsilon }_{i}}{\epsilon }_{i}^{l}+{w}_{0i}\right)}\right]}^{1-{x}_{i}^{l}}\end{array}$$

(21)

The expectation of Equation (21) can be formulated as:

$$\begin{array}{rcl}{\mathbb{E}}[\log p({x}_{i}^{l}| {x}_{{\mathcal{P}}({x}_{i})}^{l},{\epsilon }_{i}^{l},{{\boldsymbol{\gamma }}}_{{\bf{{\mathcal{P}}}}({{\boldsymbol{x}}}_{{\boldsymbol{i}}}^{{\boldsymbol{l}}})}^{l})]&=&{q}_{i}^{l}{\mathbb{E}}\left[-\log \left(1+\exp \left(-\sum\limits_{k\in {\mathcal{P}}({x}_{i})}{\gamma }_{k}^{l}{x}_{k}^{l}-{w}_{{\epsilon }_{i}}{\epsilon }_{i}^{l}-{w}_{0i}\right)\right)\right]\\ &+&(1-{q}_{i}^{l}){\mathbb{E}}\left[-\log \left(1+\exp \left(\sum\limits_{k\in {\mathcal{P}}({x}_{i})}{\gamma }_{k}^{l}{x}_{k}^{l}+{w}_{{\epsilon }_{i}}{\epsilon }_{i}^{l}+{w}_{0i}\right)\right)\right]\end{array}$$

(22)

However, the distribution of $-\log \left[1+\exp \left({\sum }_{k\in {\mathcal{P}}({x}_{i})}{\gamma }_{k}^{l}{x}_{k}^{l}+{w}_{{\epsilon }_{i}}{\epsilon }_{i}^{l}+{w}_{0i}\right)\right]$ is intractable, as it involves a log-sum-exp function that mixes both discrete and continuous variables. Consequently, we need to derive a tight lower bound for its expectation. Without loss of generality, we begin with the case where node i has a single active parent. Given that the function $-\log x$ is convex, Jensen’s inequality, combined with Taylor’s theorem, allows us to establish the following relationship:

$${\mathbb{E}}[-\log (1+\exp (x))]\ge -\log (1+{\mathbb{E}}[\exp (x)])$$

(23)

Therefore, we obtain the lower bound of Equation (22) as:

$$\begin{array}{rcl}{\mathbb{E}}[\log p({x}_{i}^{l}| {x}_{{\mathcal{P}}({x}_{i})}^{l},{\epsilon }_{i}^{l},{{\boldsymbol{\gamma }}}_{{\bf{{\mathcal{P}}}}({{\boldsymbol{x}}}_{{\boldsymbol{i}}}^{{\boldsymbol{l}}})}^{l})]&\ge &{q}_{i}^{l}\left[-\log \left(1+{\mathbb{E}}\left[\exp \left(-\sum\limits_{k\in {\mathcal{P}}({x}_{i})}{\gamma }_{k}^{l}{x}_{k}^{l}-{w}_{{\epsilon }_{i}}{\epsilon }_{i}^{l}-{w}_{0i}\right)\right]\right)\right]\\ &+&(1-{q}_{i}^{l})\left[-\log \left(1+{\mathbb{E}}\left[\exp \left(\sum\limits_{k\in {\mathcal{P}}({x}_{i})}{\gamma }_{k}^{l}{x}_{k}^{l}+{w}_{{\epsilon }_{i}}{\epsilon }_{i}^{l}+{w}_{0i}\right)\right]\right)\right]\\ &=&-{q}_{i}^{l}\left\{\log \left[1+\left(\prod\limits_{k\in {\mathcal{P}}({x}_{i})}\left[(1-{q}_{k}^{l})+{q}_{k}^{l}{\mathbb{E}}[\exp (-{\gamma }_{k}^{l})]\right]\right)\cdot \exp \left(\frac{{w}_{{\epsilon }_{i}}^{2}}{2}-{w}_{0i}\right)\right]\right\}\\ &-&(1-{q}_{i}^{l})\left\{\log \left[1+\left(\prod\limits_{k\in {\mathcal{P}}({x}_{i})}\left[(1-{q}_{k}^{l})+{q}_{k}^{l}{\mathbb{E}}[\exp ({\gamma }_{k}^{l})]\right]\right)\cdot \exp \left(\frac{{w}_{{\epsilon }_{i}}^{2}}{2}+{w}_{0i}\right)\right]\right\}\end{array}$$

(24)

As for item [7] in Equation (17), we have:

$$\sum _{i}{\mathbb{E}}({x}_{i}^{l})\log {q}_{i}^{l}+\sum _{i}{\mathbb{E}}(1-{x}_{i}^{l})\log (1-{q}_{i}^{l})=\sum _{i}{q}_{i}^{l}\log {q}_{i}^{l}+\sum _{i}(1-{q}_{i}^{l})\log (1-{q}_{i}^{l})$$

(25)

Given a map containing a set of locations, l ∈ L, we further derive a tight lower bound for the log-likelihood as follows:

$$\begin{array}{rcl}{\mathcal{L}}&=&\log P(Y,GF)\\ &=&-\log {y}^{l}-\log | {w}_{{\epsilon }_{y}}| -\frac{(\log {y}^{l})+{w}_{0y}^{2}+{\sum }_{k\in {\mathcal{P}}({y}^{l})}{\mathbb{E}}[{({\lambda }_{k}^{l})}^{2}]{q}_{k}^{l}-2\log {y}^{l}\cdot {w}_{0y}}{2{w}_{{\epsilon }_{y}}^{2}}\\ &&-\displaystyle\frac{{\sum }_{j\ne k}{\mathbb{E}}({\lambda }_{k}^{l})\cdot {\mathbb{E}}({\lambda }_{j}^{l})\cdot {q}_{k}^{l}\cdot {q}_{j}^{l}+({w}_{0y}-\log {y}^{l})\left({\sum }_{k\in {\mathcal{P}}({y}^{l})}{\mathbb{E}}({\lambda }_{k}^{l})\cdot {q}_{k}^{l}\right)}{{w}_{{\epsilon }_{y}}^{2}}\\ &&-\sum\limits_{i\in \{LS,LF,BD\}}\left[{q}_{i}^{l}\left\{\log \left[1+\left(\prod\limits_{k\in {\mathcal{P}}({x}_{i})}\left[(1-{q}_{k}^{l})+{q}_{k}^{l}{\mathbb{E}}[\exp (-{\gamma }_{k}^{l})]\right]\right)\cdot \exp \left(\frac{{w}_{{\epsilon }_{i}}^{2}}{2}-{w}_{0i}\right)\right]\right\}\right.\\ &&-\left.(1-{q}_{i}^{l})\left\{\log \left[1+\left(\prod\limits_{k\in {\mathcal{P}}({x}_{i})}\left[(1-{q}_{k}^{l})+{q}_{k}^{l}{\mathbb{E}}[\exp ({\gamma }_{k}^{l})]\right]\right)\cdot \exp \left(\frac{{w}_{{\epsilon }_{i}}^{2}}{2}+{w}_{0i}\right)\right]\right\}\right]\\ &&-\sum\limits_{a\in \{LS,LF,BD\}}\displaystyle\frac{1}{2}\left[{\rm{tr}}({{\bf{K}}}_{{\lambda }_{a}}^{-1}{{\bf{\Sigma }}}_{{\lambda }_{a}})+{({{\boldsymbol{\mu }}}_{{\lambda }_{a}}-{{\bf{m}}}_{{\lambda }_{a}})}^{T}{{\bf{K}}}_{{\lambda }_{a}}^{-1}({{\boldsymbol{\mu }}}_{{\lambda }_{a}}-{{\bf{m}}}_{{\lambda }_{a}})+\log | {{\bf{K}}}_{{\lambda }_{a}}| -\log | {{\bf{\Sigma }}}_{{\lambda }_{a}}| -{n}_{{\lambda }_{a}}\right]\\ &&-\sum\limits_{b\in \{{\alpha }_{LS},{\alpha }_{LF},LS,LF\}}\displaystyle\frac{1}{2}\left[{\rm{tr}}({{\bf{K}}}_{{\gamma }_{b}}^{-1}{{\bf{\Sigma }}}_{{\gamma }_{b}})+{({{\boldsymbol{\mu }}}_{{\gamma }_{b}}-{{\bf{m}}}_{{\gamma }_{b}})}^{T}{{\bf{K}}}_{{\gamma }_{b}}^{-1}({{\boldsymbol{\mu }}}_{{\gamma }_{b}}-{{\bf{m}}}_{{\gamma }_{b}})+\log | {{\bf{K}}}_{{\gamma }_{b}}| -\log | {{\bf{\Sigma }}}_{{\gamma }_{b}}| -{n}_{{\gamma }_{b}}\right]\\ &&-\left.\sum\limits_{i}{q}_{i}^{l}\log {q}_{i}^{l}-\sum\limits_{i}(1-{q}_{i}^{l})\log (1-{q}_{i}^{l})\right\}\end{array}$$

(26)

Training and stochastic optimization with sparse Gaussian processes

We aim to minimize our loss function in order to find optimal combinations of posteriors and parameters of causal dependencies (including the weights of parent nodes, and parameters of the normalizing flows). To achieve this, we develop an expectation-maximization (E–M) algorithm that alternates between updating the posteriors of unobserved variables (e.g., LS, LF, BD) with causal effects, and flow parameters.

To manage computational complexity when working with large geographical regions, we employ a sparse Gaussian Process formulation using inducing points. Rather than modeling the GP latent field directly at every location, we introduce a set of M inducing points u_v at strategic locations in feature space. This approach reduces the computational complexity from O(N³) to O(NM²), where N is the number of locations and M ≪ N is the number of inducing points.

We model spatial correlation in the causal parameter field using a Gaussian Process with a Matern kernel operating in feature space rather than geographical space. This approach allows the model to capture correlations between locations with similar geophysical characteristics (elevation, slope, lithology, etc.) even when they are not physically adjacent. This is motivated by the observation that similar feature combinations tend to exhibit similar causal relationships in earthquake-triggered hazard scenarios regardless of their geographic proximity.

Within each iteration, we sample a mini-batch of locations and perform the following two steps:

• Expectation step: Update the posterior probability estimates of the unobserved latent variables (LS, LF, BD) at each location by conditioning on the current GP parameters, neural network weights, and the most recent samples of causal coefficients derived from the GP latent variables through normalizing flows. The posterior probabilities are updated according to the causal dependencies encoded in the Bayesian network structure.

• Maximization step: Update the parameters of the sparse Gaussian Process, specifically the variational parameters for inducing points u_v, along with the neural network parameters that map geophysical features to the mean function of the GP. Specifically, for iteration t + 1, these parameters are updated as

  $${{\boldsymbol{\mu }}}_{u}^{(t+1)}={{\boldsymbol{\mu }}}_{u}^{(t)}+\rho {\bf{A}}\,\nabla {\mathcal{L}}({{\boldsymbol{\mu }}}_{u}),\quad {{\bf{\Sigma }}}_{u}^{(t+1)}={{\bf{\Sigma }}}_{u}^{(t)}+\rho {\bf{A}}\,\nabla {\mathcal{L}}({{\bf{\Sigma }}}_{u}),$$

  (27)
  $${{\boldsymbol{\theta }}}_{NN}^{(t+1)}={{\boldsymbol{\theta }}}_{NN}^{(t)}+\rho {\bf{A}}\,\nabla {\mathcal{L}}({{\boldsymbol{\theta }}}_{NN}),$$

  (28)

  where μ_u and Σ_u are the parameters of the variational distributions over inducing points, θ_NN represents the neural network parameters, A is a positive definite preconditioner, ρ is the learning rate, and $\nabla {\mathcal{L}}(\cdot )$ denotes gradients of the loss function with respect to the corresponding parameters. The causal coefficients at observed locations are then derived through conditioning on the inducing points and applying normalizing flow transformations to the resulting GP latent variables. This gradient update scheme is guaranteed to converge to a local maximum of ${\mathcal{L}}$ if ρ satisfies appropriate decay conditions.

Our variational evidence lower bound (ELBO) with inducing points can be formulated as:

$$\begin{array}{l}{\mathcal{L}}={{\mathbb{E}}}_{q}[\log p({\bf{y}}| {\bf{X}},{{\bf{z}}}_{v})]+{{\mathbb{E}}}_{q}[\log p({\bf{X}}| {{\bf{z}}}_{v})]-KL[q({{\bf{u}}}_{v})| | p({{\bf{u}}}_{v})]\\\qquad-\,{{\mathbb{E}}}_{q}[\log q({\bf{X}})]\end{array}$$

(29)

where q(X, z_v, u_v, ϵ) = q(X) × p(z_v∣u_v) × q(u_v) × p(ϵ) is our variational distribution. By using the exact conditional p(z_v∣u_v) in our variational approximation, we ensure that the model maintains valid probabilistic semantics over the entire spatial field while only needing to represent distributions at the inducing points explicitly.

Once the model converges, we obtain the final posterior estimates of LS, LF, and BD for each location, and also the causal effects between hidden hazards and observations, reflecting the spatially heterogeneous causal relationships inferred from the observed data.

We also apply a local pruning algorithm to accelerate the computation over a large region. This strategy is motivated by the observation that real-world causal graphs are typically sparse: only a small subset of nodes stay active. For example, locations without building footprints will not have damaged buildings, i.e., building damage nodes are inactive. Therefore, we can prune these inactive nodes while keeping the active ones crucial for parameter updates^3,12.