Introduction

As a tangible testament to history, architectural heritage is highly vulnerable to the ravages of time, mainly when constructed with wood, which is susceptible to weathering, moisture, and the effects of prolonged exposure to the elements. This often results in structural degradation, such as cracks, tilting, and other forms of damage1,2,3. Particularly susceptible are ancient wooden pagodas and Ming and Qing official buildings, such as the Yingxian Wooden Pagoda—China’s oldest and tallest wooden tower—which possesses distinctive structural characteristics and significant historical value, making it an essential focus for cultural heritage preservation4. Since its construction, the Yingxian Wooden Pagoda has endured numerous natural disasters, including earthquakes and storms. However, due to inadequate restoration efforts, the pagoda has suffered irreversible structural tilts, with the second floor being the most severely damaged, thereby jeopardizing the structure’s overall stability5. These deformations have exacerbated localized stress concentrations within the structure and compromised the tower’s mechanical integrity, heightening the risk of potential safety hazards6,7,8. Consequently, the real-time monitoring and analysis of deformation inbuilt heritage are critical for assessing its current state of health and predicting future risks to its structural integrity.

To ensure the long-term safety and preservation of wooden architectural heritage, national authorities have consistently enacted laws and regulations to safeguard architectural heritage. Concurrently, researchers have pursued advanced restoration techniques and protection strategies for such heritage. However, most current preservation efforts predominantly focus on emergency response and post-damage salvage, often neglecting the critical need for continuous monitoring and proactive, preventive conservation9. The emergence of digital twin technology offers innovative solutions and new perspectives for conserving architectural heritage, providing a transformative approach to long-term preservation and risk mitigation10. Digital twin technology leverages multi-dimensional virtual models and real-time data integration to offer a wide array of practical and functional services, including monitoring, simulation, prediction, and optimization, all facilitated through closed-loop interactions between the physical and virtual environments. By employing the digital twin model, advanced data analysis and simulations can be conducted to forecast the future state of a building, enabling predictive maintenance and enhancing the proactive management of structural integrity11. Although digital twin technology has demonstrated distinct advantages across various domains, its application in conserving architectural heritage remains exploratory. Vuoto et al.12 investigated its potential for preserving the structural integrity of architectural heritage, yet their study lacked practical validation. Similarly, Grigor Angjeliu et al.13 proposed a digital twin model development program aimed at predicting the structural behavior of masonry heritage based on the response of the Milan Duomo. However, a comprehensive theoretical framework for applying digital twin technology in the preventive conservation of built heritage has yet to be established.

Behavioral models can be mainly divided into mechanistic principles and behavioral changes, and this study will focus on model construction in terms of behavioral change prediction14. Architectural heritage, a complex system influenced by multiple interconnected factors, benefits from behavioral models, enabling digital twin technology to simulate and reflect the real-time condition of physical entities15. By precisely modeling the behavior and responses of these entities, behavioral models not only facilitate a deeper understanding of the system’s current state but also allow for the prediction of future conditions and potential issues based on historical and real-time data16. This capability provides a valuable platform for architectural heritage conservation, enabling the testing and validating of new strategies or modifications without directly affecting the physical structures themselves.

In the realm of behavioral models, there exist two distinct components: mechanism principle and behavior prediction. The present study will specifically concentrate on developing a model for behavior prediction. There are two aspects to consider when selecting the model substrate: the characteristics of the surface displacement data of architectural heritage components that are nonlinear, non-stationary, dynamic, and complex17,18. The second is that given the dynamics and uncertainty of time series data, a prediction network is needed to capture these complex changes effectively. Conventional approaches to sequence analysis, such as ARIMA and VAR19,20, mostly rely on linear assumptions and have limitations in fully capturing nonlinear dynamics. To date, deep learning has substantially advanced predictive modeling21. Within deep learning models, backpropagation (BP) neural networks, which are conventional neural networks, do not transmit information between neurons in their network layers22. This limitation restricts the network’s ability to comprehend the semantic connections between data points in a sequence. Conversely, conventional recurrent neural networks (RNNs) incorporate inter-layer node connections into BP neural networks, enabling the transmission of information along the sequence, therefore merging past information with the present time23,24. However, the RNN gradient concatenation method encounters the issue of vanishing or bursting gradients when used to long sequence data, which restricts the duration of its predictions. To solve the prediction challenges of time series data with long-term dependencies, GRU was introduced as a variant of LSTM that uses hidden units to record historical data25,26. Ju et al.27 used a GRU neural network to deal with long-term structural temperature prediction of an ancient building in China and solved the problem of low accuracy due to the time lag effect. Furthermore, extensively researched by scholars, convolutional neural networks (CNNs) can efficiently capture local characteristics in time-series data28,29. Nevertheless, these findings do not apply to data that rely on long-term monitoring of relationship building. A temporal convolutional network (TCN) is proposed based on CNN to study and predict the feature relationships in time series30,31. Nevertheless, more than those mentioned above, a single predictive network model is required to fulfill the application needs due to the intricate architecture of existing heritage and the growing amount of data on intricate component behaviors. Therefore, several hybrid models are suggested to fully exploit each approach’s benefits. The CNN-LSTM hybrid model proposed by Wu et al. demonstrates superior performance compared to a single CNN and a single LSTM approach in the prediction mode32. However, in this model, all features are treated equally, which may result in the underappreciation of key features that play a critical role. Babak Alizadeh et al.33 introduced an LSTM model integrated with the attention mechanism and Bayesian optimization. This LSTM-Attention model enhances complex time series data processing by focusing on pivotal time points. Similarly, Wen et al.34 proposed a deep learning model for predicting displacement deformation based on SA-LSTM. Their SA-LSTM model demonstrated superior performance in predicting long-term sequence data compared to a single LSTM network. However, this model cannot address abrupt anomaly data. Given that the digital preservation of architectural heritage is still in its early stages, and considering the complexity and uncertainty of surface displacement data for architectural components, no existing research has yet proposed a time series prediction network model that can be effectively applied to architectural heritage conservation.

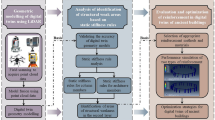
Facing the demand for preventive protection of architectural heritage, this study aims to provide a digital solution for accurate cognition of the health status of architectural heritage from the perspective of a digital twin. Through an in-depth analysis of the architectural heritage digital twin framework and the comprehensive integration of various deep learning techniques, this study combines TCN and LSTM neural networks. TCN is particularly adept at capturing long-range dependencies in time series data. At the same time, LSTM excels at detecting more minor, abrupt fluctuations or local nonlinear features, especially when dealing with data characterized by long-term dependencies. Fusing these two models enables a more robust handling of complex relationships within extended time series data. Furthermore, this study incorporates the self-attention mechanism, which allows each element in the input sequence to focus on the relevance of other elements and account for its relationship within the sequence. This mechanism assigns weights to different features, enabling the network to prioritize the most pertinent aspects of the input data for the current task. Additionally, the PSO algorithm is employed to optimize the parameters of the network model, providing a practical and flexible approach to fine-tuning and identifying the optimal model solution. This study centers on developing behavioral models for architectural heritage digital twins, utilizing the designed TLSA-PSO deep learning neural network. A digital twin system for architectural heritage was created to visualize and display the predicted outcomes of the behavioral model, thereby enabling the shift from reactive salvage conservation to proactive preventive conservation.

Methods

Digital twin behavioral model

The core concept of the digital twin is to create a complete virtual model to mirror a real-world object or system, so constructing a digital twin model of architectural heritage is the key to the preventive conservation of architectural heritage, and the construction of a behavioral model is at the core of the implementation of digital twin technology. The digital twin behavioral model can be described by the Eq. (1):

$$BM=\{BAT,BLA,BF\}$$
(1)

Where \(BAT\) denotes behavioral attribute, \(BLA\) denotes behavioral algorithm, and \(BF\) denotes behavioral function.

Behavioral models mainly describe the real-time behaviors of architectural heritage physical entities under different temporal and spatial scales, such as evolutionary behaviors and performance degradation behaviors over time under the coupling of the external environment and internal causes. Such models are based on physical laws, statistical data and machine learning algorithms. They can predict and simulate architectural heritage entities’ possible behaviors and changes under realistic and specific conditions. In the preventive conservation of architectural heritage, historical data and on-site monitoring data are used to train the models to predict the future deformation of the building by simulating the environmental impacts it is subjected to, to guide the maintenance of the architectural heritage, and to prioritize the parts that may suffer serious consequences due to environmental changes or physical wear and tear, to achieve predictive maintenance.

TLSA-PSO network model design

In this paper, a TLSA deep learning neural network is designed, and the PSO algorithm is used to optimize the prediction network model to construct the TLSA-PSO model used for predicting the digital twin behaviors of wooden tower components. The structure of the TLSA-PSO model is shown in Fig. 1.

Fig. 1
figure 1

Structure of the TLSA-PSO network model.

Full size image

The architecture consists of an input layer, a TCN layer, stacked LSTM modules, an attention layer, and an output layer. The input layer receives the data in the form of a three-dimensional tensor with dimensions of (batch_size, look_back, input_features). Through the fully connected layer, the output layer converts this data into a two-dimensional tensor of (batch_size, output_features). Here, batch_size denotes the overall sample size, and the dataset is partitioned into training and testing sets with an 80% to 20% ratio.

The TCN module primarily comprises a series of residual units, including two types of one-dimensional dilated causal convolution units, weight normalization, activation functions, and a discard layer. TCN is a specific convolutional neural network developed for analyzing time series data. It achieves this using convolutional layers, such as causal and dilated convolution, significantly enhancing the receptive field. This enables TCN to capture long-term dependencies in time series data efficiently. Conventional causal convolution is limited to analyzing a small quantity of historical data. The receptive field’s size grows linearly even when several hidden layers are included. Within dilation convolution, the dilation basis, denoted as d, governs the distance between input data points in the layer. The receptive field of a causal convolution in one dimension is equivalent to the size of the kernel. To augment the magnitude of the receptive field, it is essential to incorporate the dilation base, represented as b. There is a mathematical equation \(d={b}^{i}\), where \(i\) represents the number of layers below. It should be noted that the kernel size must be greater than or equal to the value of the dilation base b. As shown in the Fig. 2, a multilayer dilation convolution with b equal to 2 and kernel size equal to 3 is schematically illustrated. In general, adding one layer of dilation convolution will increase the size of the receptive field \((k-1)\ast d\), and the expression for the size of the receptive field \({\rm{s}}\) is shown in Eq. (2):

$$s=1+\sum _{i=0}^{n-1}(k-1)\ast {b}^{i}=1+(k-1)\ast \frac{{b}^{n}-1}{b-1}$$
(2)

Where \({\rm{n}}\) is the number of layers of the extended convolution, \(k\) is the kernel size, and \({\rm{b}}\) is the expansion base.

Fig. 2
figure 2

Schematic diagram of dilated causal convolution structure.

Full size image

The equation demonstrates that the magnitude of the sensory field increases exponentially as the number of layers increases. Minimizing the number of layers required to ensure comprehensive data coverage is possible for time series data with substantial quantities. Causal convolution in TCN is unidirectional, meaning that the output at time t in the model is solely influenced by the inputs at time t and before time t in the preceding layer. This ensures that the model retains historical information and is not sensitive to future information, preserving the time series properties of the data. The residual linking unit converts the causal convolution between one dimension into residual block linking. Every residual block is represented by the numerical values\((k,d)\), where\({\rm{k}}\) represents the size of the relevant kernel. The input for the next block is generated by augmenting each residual block with two convolutional layers. The network demonstrates fast convergence, and the extended convolution ensures the extraction of all intrinsic properties of the data.

The LSTM layer is typically positioned after the TCN output to facilitate the continued processing of sequence data and extract valuable temporal characteristics for long-term memory. Due to its capacity to accommodate nonlinear entities and regulate the flow of information by incorporating “gate” structures (input gates, oblivion gates, and output gates), the LSTM model is especially well-suited for analyzing and forecasting events with extended time intervals in a time series.

Figure 3 shows the LSTM cell’s structure, including the three gates’ working mechanism and the information flow path between different parts. t-1 moment of the memory cell state value\({C}_{t-1}\), t-1 moment of the hidden state information\({h}_{t-1}\), and the current moment of the input \({x}_{t}\) are the inputs of the LSTM cell, and the current moment of the cell state value \({C}_{t}\) and the current moment of the hidden state \({h}_{t}\) are the outputs of the LSTM cell. The LSTM When the network is running, the input \({x}_{t}\) of the current moment and \({h}_{t-1}\) of the previous moment are input to the network together; firstly, some information is forgotten through the forgetting gate; then the input gate is used to update the state of the storage cell, realizing the update of the cell state variable; the cell state value \({C}_{t}\) of the current moment is determined through the forgetting gate and the input gate; finally, the updated hidden state \({h}_{t}\) is obtained through the output gate to use it as an input for the next moment.

Fig. 3
figure 3

LSTM cell structure and working mechanism.

Full size image

After multiple rounds of experimentation and validation, it was determined that the optimal structure in the PSO optimization network process consisted of three stacked LSTM modules. The first LSTM layer processes the raw input data, while the intermediate LSTM layer enhances feature extraction and transfers the processed information to the final LSTM layer. The last LSTM layer generates the prediction results. Following PSO optimization, the number of neurons in each layer was set to 100, 200, and 300, respectively. This configuration demonstrated the highest prediction accuracy and network stability in the experimental trials. In order to mitigate the risk of overfitting, the Dropout layer decreases the complexity of the model by randomly eliminating (zeroing) a fraction of the neuron outputs throughout the training phase. TCN and LSTM models may undergo a progressive loss of predictive information when predicting long-term sequences. The self-attention structure establishes a direct connection between each time step of the input sequence and the output, preventing information from weakening during the layer-by-layer transfer process. The purpose of the self-attention layer is to allocate weights to the outputs of the LSTM layer to augment the model’s capacity to discern the crucial information of the input sequence. This enables the model to concentrate on the specific portions of the input data that need more emphasis, enhancing the prediction’s accuracy and the model’s response speed.

TLSA-PSO model includes several hyperparameters, including the convolutional kernel, number of convolutional layers, and learning rate, that substantially influence the model’s performance. The ideal combination of these parameters often requires rigorous experimentation and fine-tuning. PSO aims to generate the optimal combination of parameters for TLSA. The pseudocode representation of the PSO algorithm is shown in Table 1.

Table 1 PSO optimization network process
Full size table

PSO algorithm can find the best solution in a hyperparametric multidimensional space by mimicking the search behavior of a flock of birds. Its objective is to minimize the loss function. The algorithm systematically modifies the location of each “particle” by exchanging information and updating positions among all participants, thereby nearing the ideal solution on a global scale. This dynamic process may be mathematically represented by Eq. (3):

$$\begin{array}{c}{V}_{i}^{k+1}=\omega {V}_{i}^{k}+{C}_{1}{r}_{1}({p}_{best,i}^{k}-{X}_{i}^{k})+{C}_{2}{r}_{2}({g}_{best,i}^{k}-{X}_{i}^{k})\\ {X}_{i}^{k+1}={X}_{i}^{k}+{V}_{i}^{k+1}\end{array}$$
(3)

Where \({X}_{i}^{k}\) is a vector with N dimensions that represents the position information of the ith particle at the Kth iteration, \(\omega\) is the weight of inertia, \({V}_{i}^{k}\) is the current velocity of the particle, \({r}_{1}\) and \({r}_{2}\) are random numbers in the range of \([0,1]\); \({C}_{1}\) and \({C}_{2}\) are coefficients of social acceleration, \({P}_{best,i}\) is the local optimal position of the ith particle up to this point, and d is the global optimal position of the particle swarm.

This study used three statistical indicators—mean absolute error (MAE), mean square error (MSE), root mean square error (RMSE), and goodness of fit (R2)—to measure the deviation between the evaluation model’s predicted values and the actual observed values. These indicators reflect the model’s performance and prediction accuracy level.

Mean Absolute Error (MAE) measures the average absolute error between a model’s projected value and its actual value. It represents the average level of all prediction errors. A smaller MAE value indicates a better prediction effect. Minimum Mean Square Error (MSE) is a metric used to evaluate the extent of the difference between a model’s predicted values and the actual value. A smaller MSE value indicates that the model’s prediction results are closer to the actual value, enhancing the model’s accuracy. On the other hand, Root Mean Square Error (RMSE) is the standard deviation of the prediction error, which is more responsive to prediction errors. A smaller number indicates the model’s superior prediction performance. The R2 statistic quantifies the level of agreement between the projected value and the actual value in the prediction model. A higher R2 value indicates a more accurate model. Explicit computations are shown in Eq. (4).

$$\left\{\begin{array}{c}MAE=\frac{1}{n}\mathop{\sum}\limits_{i=1}^{n}|{y}_{i}-{\hat{y}}_{i}|\\ \mathrm{MSE}=\frac{1}{n}\mathop{\sum}\limits_{i=1}^{n}{({y}_{i}-{\hat{y}}_{i})}^{2}\\ RMSE=\sqrt{\frac{1}{n}\mathop{\sum}\limits_{i=1}^{n}{({y}_{i}-{\hat{y}}_{i})}^{2}}\\ {R}^{2}=1-\frac{S{S}_{res}}{S{S}_{rot}}\end{array}\right.$$
(4)

Where \(n\) is the number of samples, \({y}_{i}\) and \({\hat{y}}_{i}\) are the actual and predicted values, respectively, \(S{S}_{res}\) and\(S{S}_{rot}\) are the residual sum of squares and the total sum of squares, respectively, \(S{S}_{res}={\sum }_{i=1}^{n}{({y}_{i}-{\hat{y}}_{i})}^{2}\), \(S{S}_{rot}={\sum }_{i=1}^{n}{({y}_{i}-\bar{y})}^{2}\), and \(\bar{y}\) denotes the mean of all actual values.

Data cleaning

To enhance the prediction accuracy and generalization performance of the TLSA-PSO model, a set of data-cleaning preprocessing procedures on the input displacement data sequences is necessary. These procedures include data screening, vacancy filling, and data standardization. These operations aim to simplify the computational process, reduce the computation time, and guarantee that the implemented model can effectively reveal the fundamental laws of the data.

The data must meet the specified equal interval criteria when conducting time series modeling and analysis. Hence, extracting the relevant data from the raw data at regular intervals is fundamental to constructing a dataset. Owing to the data transmission issues of the automated monitoring robot, there will inevitably be some missing values in the series data. To guarantee the validity and precision of the data, it is necessary to employ suitable techniques for its completion. The often employed techniques for handling missing values can be broadly classified into three categories: direct rounding, filling fixed values (such as sample mean, median, plurality, etc.), and proximity interpolation (including linear interpolation and k proximity interpolation, etc.). In this study, the direct rounding approach was excluded due to the need to analyze the time-series data for each monitoring point. The filling of fixed values method was also prohibited as it would reduce the overall randomness of the data. Additionally, the continuity of the monitoring point data in this study was improved, with fewer missing values, making linear interpolation sufficient for filling them in. This approach presupposes a linear relationship between data points, so enabling the computation of missing values between two known data points, so appropriately preserving the continuity and trend of the data. The method of linear interpolation is represented by Eq. (5):

$${V}_{\mathrm{int}erpolated}={V}_{start}+\frac{({V}_{end}-{V}_{start})\times ({T}_{\mathrm{int}erpolated}-{T}_{start})}{({T}_{end}-{T}_{start})}$$
(5)

where\({V}_{\mathrm{int}erpolated}\) is the data point after interpolation; \({V}_{start}\) and \({V}_{end}\) are the known data points before and after interpolation, and \(T\) represents the corresponding time point.

Since the TLSA-PSO model is susceptible to the scale and range of the data, it is necessary to scale all the features to the same range, i.e., data normalization, to speed up the model iteration and enhance the convergence speed during model training while reducing the model error, which is usually [0,1] or [−1,1]. This study uses the Min-Max scaling method to normalize the data set (x,y,z), which is transformed according to Eq. (6) to lie between [0,1].

$${y}_{i}=\frac{{x}_{i}-\,\min }{\max \,-\,\min }$$
(6)

Where \(\min\) is the minimum value among the sample series data and \(\max\) is the maximum value among the sample series data.

Results

Analysis of behavioral prediction results

In this study, the proposed network model is applied to real-world monitoring data from the Muta architectural heritage to evaluate its performance. The dataset selected for this analysis originates from displacement monitoring conducted at the Yingxian Wooden Pagoda in China, spanning the period from July 2023 to October 2023. The study used an automated monitoring robot to deploy monitoring prisms on the outer columns of each floor of the Yingxian Wooden Pagoda, as shown in Fig. 4. The coordinates of the fixed monitoring points of the Yingxian Wooden Pagoda and the displacements (in millimeters) covering the longitudinal, transverse, and vertical directions were collected.

Fig. 4
figure 4

Location of monitoring prisms at the Yingxian Wooden Pagoda.

Full size image

The automatic monitoring robot is equipped with high-precision measurement capabilities, offering an accuracy of 0.5”. It is designed to operate reliably in outdoor environments, ensuring the precision and consistency of data collection. Data is acquired every four hours, a frequency chosen after considering factors such as the rate of structural change in the building and the robot’s power consumption. The displacement and deformation processes of wooden buildings occur relatively slowly and diffusely over time. Due to environmental factors, this acquisition frequency balances capturing structural changes and minimizing resource wastage. The collected data is wirelessly transmitted directly to the monitoring cloud platform for storage and subsequent processing. This wireless transmission method effectively reduces data transmission delays and ensures the real-time nature and continuity of the data. Nearly all the Yingxian Wooden Pagoda columns exhibit deformation, with the columns on all sides tilting towards the northeast at varying degrees. From a longitudinal perspective, the degree of tilting differs across the layers, with the deformation becoming progressively more severe towards the lower sections. The tilting in the second and third layers is markedly more significant than that in the upper two layers, with the second layer displaying the most significant tilt, as shown in Fig. 5.

Fig. 5
figure 5

Schematic diagram of column structure longitudinal tilt analysis.

Full size image

Within the second layer, column No. 223 is identified as the most deformed. Therefore, this study focuses on the data from monitoring point No. 223, which exhibits the most significant variation for modeling and analysis. The outer column No. 323 in the third layer is also selected for a validation experiment to assess the predictive model’s ability to generalize across different data sets. The distribution of the monitoring points for the outer column is illustrated in Fig. 6.

Fig. 6
figure 6

Distribution of monitoring stations inYingxian Wooden Pagoda.

Full size image

A comparison of the performance of the displacement prediction models based on TLSA-PSO and TLSA for monitoring point 223 in Muta, Yingxian County, China, in the training and test sets is shown in Fig. 7. In the figure, the True value is the actual monitoring data, train is the prediction result of the training set of the TLSA network, test is the prediction data of the test set given by the TLSA model, and pso-train is the optimized TLSA-PSO training set prediction results, and pso-test is the network test set prediction data of TLSA-PSO. In the comparison results of the test set, the blue bar surrounds the actual value curve and indicates the standard deviation of the true value, which is used to compare the degree of conformity of the predicted values with the actual values and the accuracy of the prediction model can be assessed by observing whether the predicted value curves (test and pso-test) fall within the blue bar most of the time. As shown in Fig. 7, the prediction results of both TLSA and TLSA-PSO are roughly in line with the trend of the actual values. However, the pso-test results predicted with the TLSA-PSO network are closer to the actual values, and almost all results fall within the blue bars. On the contrary, most of the prediction result values of the TLSA network deviate more and are farther away from the blue bars. The results show that the accuracy of the prediction results of the TLSA-PSO network is generally higher than that of the TLSA network.

Fig. 7: Comparison of training set and test set prediction results for TLSA-PSO and TLSA models.
figure 7

a Transverse deformation: comparison of TLSA and TLSA-PSO predictions. b Longitudinal deformation: comparison of TLSA and TLSA-PSO predictions. c Vertical deformation: comparison of TLSA and TLSA-PSO predictions.

Full size image

The accuracy of the TLSA-PSO prediction results was compared with the TLSA model accuracy and the simple LSTM model accuracy results. Table 2 lists the results of the respective comparisons in the horizontal, vertical, and longitudinal directions. The results show that the TLSA model outperforms the simple LSTM model in all evaluation metrics in all three deformation directions. The prediction accuracy of the TLSA-PSO network model is again significantly better than that of the TLSA model, and it is the most effective and accurate among the three network models.

Table 2 Comparison of TLSA-PSO and TLSA and LSTM model prediction result error
Full size table

Visualization of behavioral model predictions

Considering the vulnerability of architectural heritage and its high sensitivity to environmental changes, real-time monitoring of component displacement is particularly important. By deploying high-precision sensors such as automatic monitoring robots to non-destructively collect quantitative data on the displacement and deformation of architectural heritage components and relying on the displacement behavior prediction model constructed in this study, this system will realize the long-term monitoring and short-term prediction of component displacement status, and visualize the monitoring data. The prediction results are presented through charts so that the management personnel can obtain the most updated information at any time and take preventive measures according to the prediction results promptly.

To ensure the stability of this research system and facilitate its maintenance and development at a later stage, the whole system is constructed based on the B/S architecture. The front-end and back-end separation of technical solutions is selected, and the front-end interface is developed using the HTML and CSS framework for data visualization. The front-end and back-end use Fetch API to complete the data interaction, and the back-end uses a spatial database to manage and store the system data.

In this study, the displacement monitoring data, collected in real-time by sensors, are gathered by an automatic total station and directly transmitted to the cloud platform for preliminary storage. The cloud platform offers highly scalable storage and processing capabilities, ensuring secure storage and backup of large-scale real-time data. The monitoring data are stored on the cloud server in the form of time series, with an efficient time series database employed for optimal data management. To enhance data access efficiency and system response speed, this study also utilizes MySQL to establish a local database, which is synchronized with the cloud platform via an interface to facilitate data retrieval and updates from the cloud. Once the monitoring data are imported into the local database from the cloud platform, the system performs data querying, management, and visualization through the local database. The TLSA-PSO prediction model periodically analyzes the historical monitoring data within the local database, extracting displacement trends and underlying patterns. Based on this analysis, the model generates future displacement predictions, calculates the prediction accuracy against the actual monitoring data, and stores these predicted values alongside the historical data in the local database.

Unique identifiers (IDs) are systematically assigned to the components of the Yingxian Wooden Pagoda model within the system. The model is efficiently loaded and interactively displayed via the web interface. When a user selects a component on the web page, the system promptly highlights the chosen element to differentiate it from others visually. Concurrently, the system transmits a request to the server, embedding the component’s unique identifier (ID). In response, the server retrieves the real-time monitoring data and predicted displacement trend data from the database, delivering this information to the front end through an API. The front end then generates a line graph representing the data. It presents the model’s prediction accuracy metrics in a tabular format, ensuring transparency and verifiability of the prediction results, as illustrated in Fig. 8.

Fig. 8
figure 8

Digital twin behavioral model visualization system.

Full size image

Validation of model generalization capabilities

To evaluate the generalization capability of the TLSA-PSO model across data from diverse monitoring points, a validation experiment was conducted in this study using column 323, which was chosen from the three outer columns exhibiting the second highest degree of inclination. These validation experiments aim to assess the model’s applicability and accuracy within varying structural contexts, thereby confirming the reliability and practical applicability of the model.

The validation experiment primarily contrasts the prediction outcomes of two models, TLSA and TLSA-PSO, by evaluating the performance of monitoring site 323 in Muta, Yingxian County, China, across both the training and test sets, as illustrated in Fig. 9. In this figure, “True value” represents the actual monitoring data, “train” denotes the prediction results from the TLSA model applied to the training set, and “test” corresponds to the prediction data from the TLSA model for the test set. “Pso-train” refers to the optimized prediction results of the TLSA-PSO model for the training set, while “pso-test” represents the test set predictions generated by the TLSA-PSO model. Upon analyzing the prediction result plots, both the TLSA and TLSA-PSO models demonstrate a strong alignment with the long-term trends of the monitoring data, thereby confirming the models’ ability to capture the overarching patterns of complex time series data. Notably, the result plots reveal that the “pso-test” curve is significantly closer to the actual monitoring data curve, underscoring the model’s enhanced accuracy and sensitivity in predicting transient fluctuations of the actual values. Even in regions where the data exhibit pronounced fluctuations, the predicted values from TLSA-PSO remain close to the true values, a marked improvement over the accuracy limitations of the unoptimized TLSA model.

Fig. 9: Comparison of training and test set predictions for TLSA-PSO and TLSA models for column 323.
figure 9

a Transverse deformation: comparison of TLSA and TLSA-PSO predictions. b Longitudinal deformation: comparison of TLSA and TLSA-PSO predictions. c Vertical deformation: comparison of TLSA and TLSA-PSO predictions.

Full size image

The validation experiment compares the prediction accuracy of the TLSA-PSO model for column 323 with that of the TLSA model. The results of these comparisons for column 323 across the transverse, longitudinal, and vertical directions are presented in Table 3. The findings demonstrate that, in all three deformation directions, the TLSA-PSO network model consistently outperforms the TLSA model, achieving a prediction accuracy as high as 0.99.

Table 3 Comparison of the accuracy of TLSA-PSO and TLSA model prediction results for column 323
Full size table

An analysis of the predictive accuracy of columns 323 and 223 reveals that the disparity in accuracy is primarily attributable to the data’s dynamic variations and nonlinear properties. The second level of the wooden tower housing column 223 is significantly more damaged and distorted, resulting in pronounced data fluctuations, particularly along the z-axis of vertical deformation, which displays evident nonlinear variations. The nonlinearity and pronounced fluctuations make it more challenging for the prediction algorithm to effectively forecast these rapidly changing segments. The deformation at the third level, where column 323 is situated, is marginally more uniform than that at the second level, with relatively little data changes. Consequently, the model is more adept at adapting to these changes, leading to enhanced prediction accuracy in the x and y axes. Despite minor discrepancies in predictions due to varying levels of undulation in the data, the model’s undulation trends closely align with the actual monitoring data, significantly enhancing accuracy compared to traditional prediction models. The TLSA-PSO model’s stability and dependability in intricate time series prediction tasks are evidenced.

Discussion

Based on the proposed TLSA-PSO behavioral prediction model, a predictive analysis was conducted for the columns exhibiting the most significant deformation among the outer columns on the second floor of the corresponding county wooden tower. The prediction accuracy of the TLSA-PSO model was compared to that of the TLSA and a single LSTM model, with the comparative results presented in Radar Fig. 10. The Mean Absolute Error (MAE) for TLSA-PSO shows a maximum reduction of 0.0404, 0.0676, and 0.0318 across the three directions, indicating that the model’s predictions are now closer to the actual values. The Root Mean Square Error (RMSE) also demonstrates a maximum decrease of 0.0495, 0.0807, and 0.0389 across the three directions, suggesting a reduction in the overall prediction error and more excellent stability in the model’s results. Furthermore, the R² values show increases of up to 0.0968, 0.1658, and 0.0453, respectively, highlighting that the TLSA model, optimized by the PSO algorithm, has significantly improved its data-fitting capability and is now better able to capture the underlying patterns and trends in the time series.

Fig. 10: Radar plot comparing the prediction accuracy of TLSA-PSO with TLSA and LSTM models.
figure 10

a Comparison of accuracy of lateral deformation prediction. b Comparison of accuracy of longitudinal deformation prediction. c Comparison of accuracy of vertical deformation prediction.

Full size image

As the columns on all sides of the Yingxian Wooden Pagoda are tilted to varying degrees toward the northeast, the TLSA-PSO prediction results enable the advanced identification of key components that may undergo significant deformation or damage, offering a proactive warning of potential structural risks. For instance, the outer columns of the tower and the roof structure connected to them exhibited substantial deformation trends during the displacement process, particularly in the transverse and longitudinal directions. The displacements of these components are crucial to the structure’s overall stability. The deformation of the outer columns, which serve as the foundational support for the entire tower, could precipitate a broader range of structural issues, potentially compromising the tower’s overall safety. For components predicted to experience severe deformation or damage, researchers and conservators can implement targeted preventive measures based on the TLSA-PSO model’s forecasts. Feasible protection recommendations for the more seriously damaged key conservation areas of the pagoda, especially the peripheral columns on the second and third floors of the pagoda, are as follows:

Structural reinforcement

For components predicted to experience increased deformation, such as external columns or support beams, reinforcement measures can be implemented to enhance their load-bearing capacity and stability, thereby preventing further deterioration or damage. Generally, reinforcement for wooden structures is divided into two types: the strengthening reinforcement method and the damage repair reinforcement method.

Localized repair

The model accurately predicts the specific areas and extent of deterioration for components exhibiting localized damage, thereby guiding targeted repair efforts. By addressing the damage at an early stage, further propagation can be prevented, thereby ensuring the building’s long-term structural integrity and safety.

Long-term monitoring and assessment

By regularly updating forecast data and integrating real-time monitoring feedback, the health status of architectural heritage components is continuously evaluated. This dynamic approach allows for the adjustment of conservation strategies based on the latest forecast results, ensuring the ongoing effectiveness of preservation measures.

The TLSA-PSO deep learning model proposed in this study offers more accurate prediction results for architectural heritage components’ long-term behavior than traditional single-network prediction methods. By optimizing model parameters through the PSO algorithm, the model not only enhances prediction efficiency and accuracy but also strengthens its ability to adapt to complex data patterns. While the model demonstrates excellent performance in prediction accuracy, its current reliance solely on deformation data from the built heritage, without incorporating other sensor data, may introduce some bias in predicting the overall health status of the heritage. Therefore, the model can be enhanced in the future by integrating additional sensor data, such as temperature, humidity, vibration, and other multi-source inputs. Moreover, applying the model to other types of architectural heritage, such as Ming and Qing official buildings, could further improve the accuracy and comprehensiveness of the predictions.