Spectral properties of two superconducting artificial atoms coupled to a resonator in the ultrastrong coupling regime

Abstract

We experimentally investigate a superconducting circuit composed of two flux qubits ultrastrongly coupled to a common LC resonator. Owing to the large anharmonicity of the flux qubits, the system can be described well by a generalized Dicke Hamiltonian containing spin–spin interaction terms. In the experimentally measured spectrum, we observed two key phenomena. First, an avoided level crossing provides evidence of the exotic interaction that allows the simultaneous excitation of two artificial atoms by absorbing one photon from the resonator. Second, we identified a pronounced spectral asymmetry that is a clear signature of light-matter decoupling. This multi-atom ultrastrongly coupled system opens the door to studying novel processes for quantum optics and quantum-information tasks on a chip.

Introduction

Superconducting circuits provide a versatile and flexible platform for modeling various quantum systems^1,2,3,4,5,6. In this platform, artificial atoms can be designed to have tailored energy transitions and controllable interactions with microwave photons². Moreover, superconducting circuits have also become one of the main platforms for scalable quantum information processing and quantum simulation^2,3,4,5,6.

Taking advantage of the high electromagnetic field in a one-dimensional resonator and the huge dipole moment of artificial atoms, these systems achieve a stronger light–matter interaction than those at bare atomic or resonator frequencies^{7,8,9,10,11,12,13}. This ultrastrong (deep-strong) interaction might lead to promising applications, such as high-speed and high-efficiency quantum information processing devices^{14,15,16,17,18,19}. In this coupling regime, several unique physical phenomena have been predicted, and now, some of these are realized experimentally.

Important theoretical predictions include, for example, quantum vacuum radiation and entanglement from the ground state^{20,21,22,23,24}; multi-excitation exchanges between qubits and resonators²⁵; or physical processes analogous to parametric down-conversion^26,27. In 2016, a theoretical work showed that one photon can simultaneously excite two atoms^28,29. This effect should be observable if the atoms are ultrastrongly coupled with a cavity mode and the parity symmetry of the atoms is broken. Similar to Rabi oscillations, this is a coherent and unitary process where the atoms can jointly absorb or emit one photon^27,28.

The first realization of the ultrastrong coupling regime in circuit QED⁷ was evidenced by an avoided level crossing, indicating the exchange of excitations between the qubit and two cavity modes; namely, the multi-excitation exchange between one flux qubit and a waveguide resonator. Later, it was shown^30,31 that, when the parity symmetry is broken in an atom-light system in the ultrastrong coupling regime, the light field acquires a coherence in the ground state that induces symmetry breaking in an ancillary flux qubit weakly coupled to the same field.

Here, we experimentally investigate a circuit composed of two flux qubits ultrastrongly coupled to a common LC resonator. Flux qubits, which form artificial atoms, share the same inductor with the LC resonator, consequently they interact with each other. This system is described by the Dicke Hamiltonian, generalized to include atomic longitudinal couplings and spin–spin interaction terms.

In the measured spectrum, away from the flux qubit optimal point (where the parity symmetry of the system is broken), we observe an energy-level anticrossing, which indicates hybridization between the states $\left\vert gg1\right\rangle$ and $\left\vert ee0\right\rangle$, where $\left\vert g\right\rangle$($\left\vert e\right\rangle$) and $\left\vert 0\right\rangle$ respectively indicate the atomic ground (excited) and zero photon states. This is the fingerprint of the interaction that allows one photon to simultaneously excite two atoms, as well as the reverse process. Here, when the system is set up in the one-photon state, the artificial atoms and the resonator can exchange excitations exhibiting Rabi-like oscillations.

Since the atom–light and atom–atom interactions are very strong, the system states should be strongly hybridized, and the clear observation of the “one–photon–exciting–two–atoms” effect would not be straightforward. However, by studying the generalized Dicke Hamiltonian, we found (i) a partial suppression of the transverse interaction given by a competition between the spin–spin interaction and the spins–light interaction and (ii) the “decoupling” of the longitudinal interaction that depends on the sign of the external flux bias. The decoupling justifies the asymmetry in the measured spectrum.

While a multimode cavity coupled to a single atom, as in⁷, allows frequency-selective interactions, its photon conversion capability is limited by mode spacing. In contrast, multiple atoms coupled to a single cavity (as in our work) can facilitate the conversion of a single photon into multiple lower-frequency excitations. Despite superficial similarities, these two circuits are different in configuration and serve distinct roles.

On the other hand, a recent experiment³² based on many-body localization (MBL), not studied in our work, shows the suppression of the photon down-conversion, due to MBL. This is in stark contrast to our system, which is designed to actively promote both down- and up-conversion processes. Moreover, ref. ³² operates in what they call superstrong coupling regime, which arises when the atomic linewidth exceeds the cavity mode spacing. The resulting three-wave mixing interaction induces multiphoton processes across many modes, which is not our case.

Furthermore, ultrastrong coupling, as realized in our work, occurs in a different regime: when the light-matter coupling strength exceeds 10% of the cavity photon energy. This system is described by a generalized Dicke Hamiltonian including counter-rotating terms, leading to strong hybridization of the qubits with a cavity mode.

Results

Device

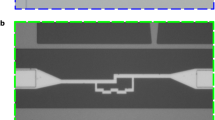
Figure 1a shows an optical microscopy image of the artificial-atom–resonator circuit. The LC resonator is composed of an interdigital capacitor and a line inductor made of a superconducting thin film^33,34. The two flux qubits are inductively coupled to the LC resonator via a Josephson junction (Fig. 1b), which increases the strength of couplings to the ultrastrong regime. Small dots around the two qubits are flux traps that prevent vortex fluctuations during the measurements³⁵. The energies of the flux qubits³⁶ can be changed by applying an external magnetic flux to the loop from a global coil and using an on-chip bias line. Figure 1c shows the equivalent circuit with lumped elements and Josephson junctions.

Fig. 1: Device.

a Optical microscopy image of the measured sample. The sample holder has a coil to bias a uniform magnetic field from the back surface of the chip. Qubit 1 has a local bias line that changes the magnetic flux of the qubit loop. The spectrum is measured using a vector network analyzer (VNA) for probing and reading from the transmission line shown below the circuit. b False-color SEM images of qubits 1 and 2. The design parameters of both qubit junctions are the same. Different colors represent different layers of aluminum deposited via double-angle shadow evaporation. c Equivalent circuit diagram of the sample. The symbols α_i, β_i, a_i, and b_i (i ∈ {1, 2}) label each Josephson junction, while φ denotes the phase difference across a circuit component.

The Hamiltonian of the entire system is^37,38,39

$${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{tot}}}}}={\hat{{{{\mathcal{H}}}}}}_{{{{\rm{q1}}}}}+{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{q2}}}}}+{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{r}}}}}+{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{int}}}}}\,,$$

(1)

where ${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{q}}}}k}$ (k = 1, 2), ${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{r}}}}}$, and ${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{int}}}}}$ represent the qubits, resonator, and atom–resonator plus atom–atom couplings, respectively. The Hamiltonian of the resonator is ${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{r}}}}}=\hslash {\omega }_{{{{\rm{r}}}}}({\hat{a}}^{{{\dagger}} }\hat{a}+1/2)$, where ${\omega }_{{{{\rm{r}}}}}\equiv 1/\sqrt{{L}_{{{{\rm{r}}}}}{C}_{{{{\rm{r}}}}}}$ is the resonance frequency, $\hat{a}\equiv ({\hat{\phi }}_{{{{\rm{r}}}}}-i{Z}_{{{{\rm{r}}}}}{\hat{q}}_{{{{\rm{r}}}}})/\sqrt{2\hslash {Z}_{{{{\rm{r}}}}}}$ is the annihilation operator, ${Z}_{{{{\rm{r}}}}}=\sqrt{{L}_{{{{\rm{r}}}}}/{C}_{{{{\rm{r}}}}}}$ is the characteristic impedance of the LC resonator, and ${\hat{q}}_{{{{\rm{r}}}}}$ is the conjugate variable of ${\hat{\phi }}_{{{{\rm{r}}}}}={\Phi }_{0}{\hat{\varphi }}_{{{{\rm{r}}}}}$. Here, Φ₀ is the flux quantum and the flux φ_r is defined in Fig. 1c. The Hamiltonian of the k-th artificial atom is

$${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{q}}}}k}\equiv 4{E}_{{{{\rm{c}}}}k}{\hat{{{{\bf{q}}}}}}_{k}^{{{{\rm{T}}}}}{{{{\bf{M}}}}}_{k}^{-1}{\hat{{{{\bf{q}}}}}}_{k}+{E}_{{{{\rm{Lr}}}}}{\hat{\varphi }}_{\beta k}^{2}+{\hat{{{{\mathcal{U}}}}}}_{{{{\rm{J}}}}k}\,,$$

(2)

where E_ck is the charging energy of the Josephson junction a_k (see Fig. 1b and 1c), φ_βk represents the phase differences in each β-junction of qubits, M_k is the normalized mass matrix, ${E}_{{{{\rm{Lr}}}}}={\Phi }_{0}^{2}/(2{L}_{{{{\rm{r}}}}})$, and ${\hat{{{{\mathcal{U}}}}}}_{{{{\rm{J}}}}k}$ is the qubit potential energy of Josephson junctions:

$$\begin{array}{rc} \,\,{\hat{{{{\mathcal{U}}}}}}_{{{{\rm{J}}}}k}({\hat{\varphi }}_{{{{\rm{e}}}}k})=& -\,{E}_{{{{\rm{J}}}}k}\,\left[\,{\beta }_{k}\cos ({\hat{\varphi }}_{\beta k})\,+\,\cos ({\hat{\varphi }}_{ak})\,+\,\cos ({\hat{\varphi }}_{bk})\right.\\ &\left.+{\alpha }_{k}\cos ({\varphi }_{{{{\rm{e}}}}k}-{\hat{\varphi }}_{ak}-{\hat{\varphi }}_{bk}-{\hat{\varphi }}_{\beta k})\right]\,.\end{array}$$

(3)

Here, E_Jk is the current energy of the Josephson junction a_k, φ_ik (i = α, a, b) are the phase differences in each junction α_k, a_k, and b_k, and φ_ek represents the external flux for the loop of each atom. The interaction Hamiltonian

$${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{int}}}}}=-{E}_{{{{\rm{Lr}}}}}({\hat{\varphi }}_{\beta 1}{\hat{\varphi }}_{{{{\rm{r}}}}}-{\hat{\varphi }}_{\beta 2}{\hat{\varphi }}_{{{{\rm{r}}}}}+{\hat{\varphi }}_{\beta 1}{\hat{\varphi }}_{\beta 2})$$

(4)

is obtained from the boundary condition (Kirchhoff’s voltage law) of the loop forming the resonator with the elements L_r and C_r.

By approximating each atom as a two-level system⁴⁰ on the basis of persistent currents of the superconducting loop, we obtain the total Hamiltonian in Eq. (1) as

$${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{tot}}}}}/\hslash \simeq \,\,{\omega }_{{{{\rm{r}}}}}{\hat{a}}^{{{\dagger}} }\hat{a}\,+\,\frac{{\varepsilon }_{1}}{2}{\hat{\sigma }}_{z1}\,+\,\frac{{\Delta }_{1}}{2}{\hat{\sigma }}_{x1}\,+\,\frac{{\varepsilon }_{2}}{2}{\hat{\sigma }}_{z2}\,+\,\frac{{\Delta }_{2}}{2}{\hat{\sigma }}_{x2}\\ -({g}_{1}{\hat{\sigma }}_{z1}-{g}_{2}{\hat{\sigma }}_{z2})({\hat{a}}^{{{\dagger}} }+\hat{a})-\frac{2{g}_{1}{g}_{2}}{{\omega }_{{{{\rm{r}}}}}}{\hat{\sigma }}_{z1}{\hat{\sigma }}_{z2}\,,$$

(5)

where ε_k is the persistent current energy of each qubit, Δ_k is the qubit energy gap when ε_k = 0, while ${\hat{\sigma }}_{zk}$ and ${\hat{\sigma }}_{xk}$ are the Pauli matrices for the k-th qubit. We define ε_k > 0 when the qubit current flows anticlockwise and vice versa.

After a unitary transformation that diagonalizes the atomic Hamiltonians ${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{qk}}}}}$, we obtain a generalized Dicke Hamiltonian⁴¹ with spin–spin interaction:

$${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{tot}}}}}/\hslash \simeq \,\,{\omega }_{{{{\rm{r}}}}}{\hat{a}}^{{{\dagger}} }\hat{a}+\frac{{\omega }_{{{{\rm{q1}}}}}}{2}{\hat{\sigma }}_{z1}+\frac{{\omega }_{{{{\rm{q2}}}}}}{2}{\hat{\sigma }}_{z2}\\ -({g}_{1}{\hat{{{\Lambda }}}}_{1}-{g}_{2}{\hat{{{\Lambda }}}}_{2})({\hat{a}}^{{{\dagger}} }+\hat{a})-\frac{2{g}_{1}{g}_{2}}{{\omega }_{{{{\rm{r}}}}}}{\hat{{{\Lambda }}}}_{1}{\hat{{{\Lambda }}}}_{2}\,,$$

(6)

where ${\omega }_{{{{\rm{q}}}}k}={{{\rm{sgn}}}}({\varepsilon }_{k}){({\varepsilon }_{k}^{2}+{\Delta }_{k}^{2})}^{1/2}$ is the qubit frequency and ${\hat{{{\Lambda }}}}_{k}=(\cos {\theta }_{k}\,{\hat{\sigma }}_{xk}+\sin {\theta }_{k}\,{\hat{\sigma }}_{zk})$ gives the direction of the interaction, with ${\theta }_{k}\simeq -\arctan ({\varepsilon }_{k}/{\Delta }_{k})$ (see Methods for more details). For θ_k = 0 (ε_k = 0), the interaction is purely transverse. When θ_k ≠ 0, the interaction has a longitudinal component and the one–photon–exciting–two–atoms effect is allowed.

Energy spectrum

Figure 2a shows the raw data of the measured spectrum as a function of the persistent current energy ε₁ of qubit 1, which are obtained after fixing the value of ε₂/2π at  −3.22 GHz when ε₁ = 0. In Fig. 2b, the spectrum is fitted with the numerically calculated transition frequencies ω_ij between the i-th and j-th eigenstates of the total Hamiltonian ${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{tot}}}}}$. The persistent current energy for qubit 2 and the resonator frequency are affected by the external magnetic flux applied to qubit 1⁸. Thus, to derive the transition frequencies ω_ij, we substitute ε₂  →  ε₂ + Aε₁ and ω_r  →  ω_r(1 + B_±ε₁) in Eq. (5), where A and B_± are small fitting parameters listed in Table 1. We use two different values for B_± because the spectrum is asymmetric with respect to the sign of ε₁, i.e., B₊ is used when ε₁≥0 and vice versa. Including A and B_±, we use 11 parameters in total for the fit. These also include the bias current offset I_b0, when ε₁ = 0, and the persistent current coefficient ${\tilde{\varepsilon }}_{0}$ to derive $\hslash {\varepsilon }_{1}={I}_{{{{\rm{p}}}}}{\Phi }_{0}({\varphi }_{{{{\rm{e1}}}}}-0.5)=\hslash {\tilde{\varepsilon }}_{0}({I}_{{{{\rm{b}}}}}-{I}_{b0})$, where I_p is the persistent current of qubit 1, and I_b is the bias current from the room-temperature current source. We use a photo-processing technique to obtain peak points from the spectrum^37,42,43 and the quantum toolbox in Python for numerical calculations^44,45.

Fig. 2: Transmission spectra.

Pump frequency ω_p from the vector network analyzer versus the persistent current energy ε₁ of qubit 1. a Raw data of the observed single-tone spectrum of the sample shown in Fig. 1. b Observed single-tone spectrum with fitted curves corresponding to the state transition frequencies ω_ij between the i-th and j-th eigenstates of Hamiltonian (6). The fit parameters are g₁/2π = 3.33, g₂/2π = 3.45, Δ₁/2π = 1.31, Δ₂/2π = 1.27, ω_r/2π = 5.15, and ε₂/2π = −3.22 GHz. At around ω_p/2π = 5.09 GHz and 5.57 GHz, parasitic modes can be seen, which originate from, for example, sample ground planes and/or the measurement environment, which includes the sample holder and microwave components coupled to the system.

Table 1 List of the fitting parameters used in Figs. 2 and 3

Flux qubits 1 and 2 are almost identical except for the loop size; consequently, they have similar fitting parameters; i.e., Δ_q1 ≃ Δ_q2 ≃ 0.25 ω_r. We find atom-resonator coupling rates of g₁/ω_r = 0.67 and g₂/ω_r = 0.69, indicating that the artificial atoms are ultrastrongly coupled with the resonator.

One photon simultaneously excites two atoms

We indicate with $\left\vert {\psi }_{i}\right\rangle$ the eigenstate of the system Hamiltonian ${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{tot}}}}}$ with eigenenergies ℏω_i0. The ${\omega }_{{{{\rm{q}}}}i}{\hat{\sigma }}_{zi}/2$ terms in Eq. (6) define the ground $\left\vert g\right\rangle$ and excited $\left\vert e\right\rangle$ atomic bare states.

In Fig. 3a, which is an enlarged view of the red dashed rectangle in Fig. 2b, the black arrow indicates the anticrossing between the eigenstates $\left\vert {\psi }_{3}\right\rangle$ and $\left\vert {\psi }_{4}\right\rangle$ (see Fig. 3b), with eigenfrequencies ω₃₀ and ω₄₀. In agreement with this anticrossing, Fig. 3c shows the numerically calculated projection ${P}_{j}^{(i)}\equiv {| \left\langle {\psi }_{i}| j\right\rangle | }^{2}$ of the third and fourth eigenstates $\left\vert {\psi }_{i}\right\rangle \,(i=3,4)$ on the bare states $\left\vert j\right\rangle=\{\left\vert gg1\right\rangle,\left\vert ee0\right\rangle \}$ as a function of ε₁. Here, it is possible to see that the third and fourth eigenstates are the approximate symmetric and antisymmetric superpositions of $\left\vert gg1\right\rangle$ and $\left\vert ee0\right\rangle$, respectively. Considering also that the sum of the dressed qubit frequencies is nearly equal to the dressed resonator frequency, the anticrossing is the signature of the one–photon–exciting–two–atoms effect (see Methods for more details). Half of the minimum split between ω₃₀ and ω₄₀ in the spectrum gives the effective coupling between $\left\vert gg1\right\rangle$ and $\left\vert ee0\right\rangle$, that is 22.8 MHz (see Supplementary Information).

Fig. 3: Anticross between $\left\vert gg1\right\rangle$ and $\left\vert ee0\right\rangle$.

a Enlarged view of the central part of the spectrum in Fig. 2b with fitting curve. The fitting reproduces the spectrum well. b Enlarged image of the anticrossing between ω₃₀ and ω₄₀. The white lines represent the eigenmodes of $\left\vert gg1\right\rangle$ and $\left\vert ee0\right\rangle$ in the non-interacting Hamiltonian (see Methods for more details). c Projection of the third and fourth eigenstates calculated using Hamiltonian in Eq. (6) with the fitting parameters to the bare states $\left\vert gg1\right\rangle$ and $\left\vert ee0\right\rangle$.

With respect to the theoretical prediction in ref. ²⁸ (g/ω_r ≃ 0.1–0.2), our system has a much larger coupling (g/ω_r ≃ 0.7). This implies that the system eigenstates should have a strong dressing, and in principle we could not observe a clean “one–photon–exciting–two–atoms” effect. On the contrary, Fig. 3c shows that the dressing is low for those states, and, as shown in Fig. 5, our system can still be considered formed by two separated two-level atoms and one cavity mode with shifted eigenfrequencies. This behavior is heuristically justified by the fact that spin–spin and spins–light couplings are competing interactions and that the longitudinal interaction “decouples” for specific values of the signs of ε₁ and ε₂. The signature of this “longitudinal decoupling” is given by the asymmetry in the spectrum with respect to the sign of ε₁. Assuming that there are only longitudinal couplings, in the interaction part of Eq. (6), the operator $({\hat{a}}^{{{\dagger}} }+\hat{a})$ should generate coherent states of light in the ultrastrong coupling regime⁴⁶. However, considering ε₁ < 0 and ε₂ < 0, the atomic states are not associated with coherent states if M = m₁ − m₂ = 0, where m_k = ± 1 is the eigenstate of ${\hat{\sigma }}_{zk}\,(k=1,2)$ (see Methods for more details). As a result, the ground $\left\vert gg\right\rangle$ and excited $\left\vert ee\right\rangle$ states, which have M = 0, have no coherent states associated with them. Nevertheless, the transverse interactions still affect our system, generating a small dressing that reduces the projections ${P}_{gg1}^{(4)}$ and ${P}_{ee0}^{(3)}$ to almost 0.8 at ε₁/2π = −2.4 GHz.

Discussion

We measured the spectrum of a circuit composed of two artificial atoms ultrastrongly coupled to an LC resonator. The generalized Dicke Hamiltonian with spin–spin interaction correctly describes the measured spectrum. At the energy where the sum of the atomic energies almost matches that of the resonator, we observed one anticrossing between the states $\left\vert gg1\right\rangle$ and $\left\vert ee0\right\rangle$. This experimentally confirms the recent theoretical prediction that one photon can simultaneously excite two atoms²⁸, opening a new chapter in quantum nonlinear optics.

Clearly, only the avoided-level crossing and not the excitation process itself have been experimentally observed, because our experiment was not designed to observe Rabi oscillations. However, our spectroscopic observations prove the existence of this excitation. Future work will involve reading out the qubit and photon states⁴⁷ as well as observing the one–photon–exciting–two–atoms dynamics. Theoretically, the reduction of dressing and the asymmetry in the spectrum could be further investigated. These studies could also be extended to explore, for example, photon down- and up-conversions^27,48 and ultrafast two-qubit gates^14,17.

Methods

Circuit Hamiltonian

Here, we describe the circuit Hamiltonian calculation in detail. The branch fluxes across the circuit elements, which are Josephson junctions, the inductance L_r, and the capacitance C_r, follow Kirchhoff’s voltage laws:

$${\varphi }_{\beta 1}+{\varphi }_{\alpha 1}+{\varphi }_{a1}+{\varphi }_{b1}={\varphi }_{{{{\rm{e}}}}1}\,,$$

(7)

$${\varphi }_{\beta 2}+{\varphi }_{\alpha 2}+{\varphi }_{a2}+{\varphi }_{b2}={\varphi }_{{{{\rm{e}}}}2}\,,$$

(8)

$${\varphi }_{{{{\rm{cr}}}}}+{\varphi }_{{{{\rm{\ell r}}}}}+{\varphi }_{\beta 1}-{\varphi }_{\beta 2}=0\,,$$

(9)

where φ_cr and φ_ℓr represent fluxes between the resonator capacitor and the inductor. The total Lagrangian of the circuit is

$$\begin{array}{r}{{{{\mathcal{L}}}}}_{{{{\rm{tot}}}}}={{{{\mathcal{K}}}}}_{{{{\rm{J1}}}}}+{{{{\mathcal{K}}}}}_{{{{\rm{J2}}}}}-{{{{\mathcal{U}}}}}_{{{{\rm{J1}}}}}-{{{{\mathcal{U}}}}}_{{{{\rm{J2}}}}}+{{{{\mathcal{L}}}}}_{{{{\rm{r}}}}}\,,\end{array}$$

(10)

where

$${{{{\mathcal{K}}}}}_{{{{\rm{J}}}}k}= \frac{{C}_{{{{\rm{J}}}}}}{2}\left[\,\beta {\dot{\phi }}_{\beta k}^{2}+{\dot{\phi }}_{ak}^{2}+{\dot{\phi }}_{bk}^{2}\right.\\ \left.+{\alpha }_{i}{({\dot{\phi }}_{\beta k}+{\dot{\phi }}_{ak}+{\dot{\phi }}_{bk})}^{2}\right]\,,$$

(11)

$$\begin{array}{r}\begin{array}{ll}{{{{\mathcal{U}}}}}_{{{{\rm{J}}}}k}=-{E}_{{{{\rm{J}}}}}&\left[{\beta }_{i}\cos ({\varphi }_{\beta k})+\cos ({\varphi }_{ak})+\cos ({\varphi }_{bk})\right.\\ &\left.+{\alpha }_{i}\cos ({\varphi }_{{{{\rm{e}}}}k}-{\varphi }_{\beta k}-{\varphi }_{ak}-{\varphi }_{bk})\right]\,,\end{array}\end{array}$$

(12)

$$\begin{array}{r}{{{{\mathcal{L}}}}}_{{{{\rm{r}}}}}=\frac{{C}_{{{{\rm{r}}}}}}{2}{\dot{\phi }}_{{{{\rm{cr}}}}}^{2}-\frac{1}{2{L}_{{{{\rm{r}}}}}}{({\phi }_{{{{\rm{cr}}}}}+{\phi }_{\beta 1}-{\phi }_{\beta 2})}^{2}\,.\end{array}$$

(13)

Here, k ∈ {1, 2} indicates the qubit, and the sub-index cr indicates the capacitor of the resonator. The qubit kinetic energy part of the Lagrangian in Eq. (10) becomes

$${{{{\mathcal{K}}}}}_{{{{\rm{J}}}}i}=\frac{1}{2}\dot{{{\phi }}}^{{{{\rm{T}}}}}{{{\rm{M}}}}\dot{{{\phi }}}\,,$$

(14)

where ${{{{\boldsymbol{\phi }}}}}_{k}\equiv {\left({\phi }_{\beta k}{\phi }_{ak}{\phi }_{bk}\right)}^{{{{\rm{T}}}}}$ and the mass matrix is given by

$${{{{\bf{M}}}}}_{k}={C}_{{{{\rm{J}}}}}\left(\begin{array}{ccc}{\beta }_{k}+{\alpha }_{k}&{\alpha }_{k}&{\alpha }_{k}\\ {\alpha }_{k}&1+{\alpha }_{k}&{\alpha }_{k}\\ {\alpha }_{k}&{\alpha }_{k}&1+{\alpha }_{k}\end{array}\right)\,.$$

(15)

Using the canonical conjugate ${q}_{i}=\partial {{{\mathcal{}}}}{L}_{{{{\rm{tot}}}}}/\partial {\dot{\phi }}_{i}$ for ${\dot{\phi }}_{i}$, where i ∈ {β_k, a_k, b_k}, we can rewrite Eq. (14) as

$${{{{\mathcal{K}}}}}_{{{{\rm{J}}}}k}=\frac{1}{2}{{{{\bf{q}}}}}_{k}^{{{{\rm{T}}}}}{{{{\bf{M}}}}}^{-1}{{{{\bf{q}}}}}_{k}\,.$$

(16)

Then, we obtain the total Hamiltonian of the circuit as

$${{{{\mathcal{H}}}}}_{{{{\rm{tot}}}}}= {\sum}_{k}{{{{\bf{q}}}}}_{k}^{{{{\rm{T}}}}}{\dot{{{{\boldsymbol{\phi }}}}}}_{k}-{{{{\mathcal{L}}}}}_{{{{\rm{tot}}}}}\\= {\sum}_{k}(4{E}_{{{{\rm{c}}}}}{\tilde{{{{\bf{q}}}}}}_{k}^{{{{\rm{T}}}}}{\tilde{{{{\bf{M}}}}}}_{k}^{-1}{\tilde{{{{\bf{q}}}}}}_{k}+{E}_{{{{\rm{Lr}}}}}{\varphi }_{\beta k}^{2}+{{{{\mathcal{U}}}}}_{{{{\rm{J}}}}k})\\ \,\, +{{{{\mathcal{H}}}}}_{{{{\rm{r}}}}}+{{{{\mathcal{H}}}}}_{{{{\rm{int}}}}}\,,$$

(17)

where $2e\tilde{q}=q$ and ${C}_{{{{\rm{J}}}}}\tilde{{{{\bf{M}}}}}={{{\bf{M}}}}$. The term E_Lrφ_βk originates from Eq. (13) since we define

$$\begin{array}{r}{{{{\mathcal{H}}}}}_{{{{\rm{r}}}}}\equiv \frac{{C}_{{{{\rm{r}}}}}}{2}{\dot{\phi }}_{{{{\rm{cr}}}}}^{2}+\frac{1}{2{L}_{{{{\rm{r}}}}}}{\phi }_{{{{\rm{cr}}}}}^{2}\,\end{array}$$

(18)

as a bare LC resonator. We now replace the canonical values with the operators $\varphi \to \hat{\varphi }$ and $q\to \hat{q}$ and impose their relation $[\hat{\varphi },\hat{q}]=i$. For the resonator, we introduce the creation and annihilation operators. Thereafter, we expand the quantized total Hamiltonian using the eigenvectors ${\left\vert i\right\rangle }_{i}$ ($i\in {\mathbb{N}}$) of the atom Hamiltonians (${\hat{{{{\mathcal{H}}}}}}_{{{{\rm{tot}}}}}-{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{r}}}}}-{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{int}}}}}$),

$$\,\,{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{tot}}}}}= \hslash {\sum}_{i}({\Omega }_{i}^{(1)}{\left\vert i\right\rangle }_{1}{\left\langle i\right\vert }_{1}+{\Omega }_{i}^{(2)}{\left\vert i\right\rangle }_{2}{\left\langle i\right\vert }_{2})+{\hat{{{{\mathcal{H}}}}}}_{{{{\rm{r}}}}}\\ \, -\hslash {\sum}_{i,j}({g}_{ij}^{(1)}{\left\vert i\right\rangle }_{1}{\left\langle j\right\vert }_{1}\,\,-{g}_{ij}^{(2)}{\left\vert i\right\rangle }_{2}{\left\langle j\right\vert }_{2})({\hat{a}}^{{{\dagger}} }\,+\hat{a})\\ -{E}_{{{{\rm{L}}}}}{\sum}_{i,j}{g}_{ij}^{(1)}{g}_{ij}^{(2)}{\left\vert i\right\rangle }_{1}{\left\vert i\right\rangle }_{2}{\left\langle j\right\vert }_{1}{\left\langle j\right\vert }_{2}\,,$$

(19)

where $\hslash {\Omega }_{i}^{(k)}$ is the i-th eigenenergy of atom k and $\hslash {g}_{ij}^{(k)}={I}_{{{{\rm{zpf}}}}}{\Phi }_{0}\left\langle i\right\vert {\hat{\varphi }}_{\beta k}\left\vert \, j\right\rangle$ is the coupling matrix element (${I}_{{{{\rm{zpf}}}}}=\sqrt{\hslash {\omega }_{{{{\rm{r}}}}}/2{L}_{{{{\rm{r}}}}}}$). After truncating the higher state of the flux qubits, we obtain the Hamiltonian of two two-level atoms and a resonator, Eqs. (5) and (6). In Eqs. (5) and (6), the spin–spin interaction reduces the current flowing in the resonator loop, which in this system is the ferromagnetic coupling.

One–photon two–atoms energy exchange

Figure 4 shows numerically calculated transition frequencies of the system using the fit parameters over a wider range. For comparison, we overlaid the eigenvalues of the Hamiltonian in Eq. (6) with the eigenvalues calculated when g₁ = g₂ = 0. In the latter case, we shifted the atoms and cavity frequencies to consider the dressing effect. From Fig. 4, it is possible to notice that the eigenvalues of the interacting and non-interacting (g₁ = g₂ = 0) Hamiltonians almost coincide, proving that our system, operating in the ultrastrong coupling regime, can still be considered composed of two independent atoms and a resonator that interact in the crossing points. Figure 5a is an enlarged image of Fig. 4, with the range around the anticrossing between ω₃₀ and ω₄₀(ε₁ < 0). In our circuit, ω₀₁ and ω₀₂ are the frequencies of dressed qubits 1 and 2, respectively. From the enlarged image of the anticrossing in Fig. 5a, b, it is possible to see that the transition frequency of $\left\vert gg1\right\rangle$ at the anticrossing point is 5.312GHz, which is close to the sum of the frequencies of the dressed qubits, ω₀₁ + ω₀₂ = 5.318GHz.

Fig. 4: Comparison between the lowest eigenstates of the Hamiltonian in Eq. (6) and the non-interacting Hamiltonian (light pink curves).

The non-interacting Hamiltonian is derived from Eq. (6) with g₁ = g₂ = 0, shifting the atom frequencies. The shifts are chosen such that ${\Delta }_{1,2}\,\to \,{\Delta }_{1,2}\exp -2{({g}_{1,2}/{\omega }_{{{{\rm{r}}}}})}^{2}$. For simplicity, we ignore the qubit bias current crosstalk, A = 0.

Fig. 5: Energy levels at the bias point of the anticross.

a Numerically calculated spectrum as a function of ε₁ around the anticross point between ω₃₀ and ω₄₀(ε₁ < 0). b Enlarged image of the purple dashed square in a. Black lines show ω₃₀ and ω₄₀ derived from the non-interacting Hamiltonian.

It has been shown that when an atom interacts longitudinally with light, the atomic states are associated with coherent states of light⁴⁶. In our system, the generation of coherent states, given by the longitudinal coupling of the atoms with the resonator, depends on the signs of ε₁ and ε₂. In the following derivation, we show that when ε₁ < 0 and ε₂ < 0, the atomic states $\left\vert ge\right\rangle$ and $\left\vert eg\right\rangle$ are associated with the coherent states of light, while states $\left\vert gg\right\rangle$ and $\left\vert ee\right\rangle$ are not associated with those.

Considering the system Hamiltonian [Eq. (6)] with Δ_k = 0, g₁ = g₂ = g, and substituting σ_zk with its eigenvalue m_k = ± 1, we can write the following:

$${\hat{{{{\mathcal{H}}}}}}_{s}/\hslash=\frac{| {\varepsilon }_{1}| }{2}{m}_{1}+\frac{| {\varepsilon }_{2}| }{2}{m}_{2}+{\omega }_{{{{\rm{r}}}}}{\hat{a}}^{{{\dagger}} }\hat{a}+gM({\hat{a}}^{{{\dagger}} }+\hat{a})\,,$$

(20)

with $M={{{\rm{sgn}}}}({\varepsilon }_{2}){m}_{2}-{{{\rm{sgn}}}}({\varepsilon }_{1}){m}_{1}$. Performing the substitution $\hat{a}=\hat{b}-Mg/{\omega }_{{{{\rm{r}}}}}$, we obtain

$${\hat{{{{\mathcal{H}}}}}}_{s}/\hslash={\omega }_{{{{\rm{r}}}}}{\hat{b}}^{{{\dagger}} }\hat{b}+\frac{| {\varepsilon }_{1}| }{2}{m}_{1}+\frac{| {\varepsilon }_{2}| }{2}{m}_{2}-{M}^{2}\frac{{g}^{2}}{{\omega }_{{{{\rm{r}}}}}}\,,$$

(21)

which is the Hamiltonian of a harmonic oscillator. By applying the annihilation operator $\hat{b}$ to its ground state ${\left\vert 0\right\rangle }_{M}$ (i.e., $\hat{b}{\left\vert 0\right\rangle }_{M}=0$), we have

$$\hat{a}{\left\vert 0\right\rangle }_{M}=-M\frac{g}{{\omega }_{{{{\rm{r}}}}}}{\left\vert 0\right\rangle }_{M}\,.$$

(22)

From Eq. (22), we see that atomic states with M = 0 are associated with the zero-photon state; while atomic states with M = ±2 are associated with photonic coherent states $\left\vert \pm \alpha \right\rangle$. In turn, M depends on the signs of ε₁ and ε₂. If ε₁ < 0 and ε₂ < 0, then M₋ ≡ M = m₁ − m₂. If ε₁ > 0 and ε₂ < 0, then M₊ ≡ M = − (m₁ + m₂). Table 2 shows the eight possible states as a function of the sign of ε₁ when the interaction is longitudinal. This explains the asymmetry of the spectra with respect to the sign of ε₁.

Table 2 Possible values of M and relative states. We consider ε₂ < 0