Abstract
The lateral geniculate nucleus (LGN) of the thalamus, a major retinal target, processes and relays visual information, including direction selectivity (DS) and orientation selectivity (OS). However, the organization of DS and OS in the LGN, including the extent to which the information is directly inherited from the retina or generated within the LGN, remains poorly understood. Using high-density recordings from across the mouse LGN, we reveal two distinct organization patterns: LGN DS responses are scarce in the central visual field and are topographically aligned to translatory optic flow dynamics around it, whereas OS responses span the visual field. In transgenic mice lacking retinal DS, we find that only LGN DS, but not LGN OS responses are eliminated. Our results suggest that LGN DS is inherited from the retina, although the retinogeniculate transfer is topography-dependent and potentially optimized for representations that support visually-guided behaviors.
Similar content being viewed by others
Introduction
Visual information is initially parsed into separate channels in the retina via the retinal ganglion cells (RGC). Each RGC subtype encodes a different feature in the visual field, such as contrast, color, motion or orientation1,2. Direction-selective RGCs (DSRGCs) encode the direction of motion and respond to a stimulus moving in a preferred direction but are inhibited by motion in the opposite direction. Orientation-selective RGCs (OSRGC) respond strongly to stimuli of a preferred orientation and weakly to stimuli of orthogonal orientation3,4. The tuning preferences of DSRGC and OSRGC arise through distinct mechanisms. In particular, ablation of retinal interneurons called starburst amacrine cells (SACs) eliminates the directional tuning of DSRGCs5,6,7 but does not affect the orientation tuning of OSRGCs5.
Distinct DSRGC and OSRGC subtypes differ in their polarity preferences (On, Off, or On-Off) and in their preferred directions and orientations. Traditionally, DSRGCs show a preference for one of four cardinal directions. OSRGCs typically prefer either the horizontal or vertical cardinal axes. Each RGC subtype is thought to tile the retina so the feature it represents is encoded across the entire visual field8,9,10. However, recent studies in mice demonstrate that various features are non-uniformly represented in the retina but rather organized in a topography-dependent manner11,12,13,14. Specifically, the preferred directions and orientations of DSRGCs and OSRGCs may deviate from the cardinal axes depending on their retinal location15,16,17,18.
The On-Off DSRGC subtypes (here referred to as DSRGCs) project to the lateral geniculate nucleus (LGN) of the thalamus. This major retinorecipient brain center consists of dorsal (dLGN) and ventral (vLGN) subregions, separated by a thin interlayer (intergeniculate leaflet; IGL). dLGN neurons constitute the thalamocortical pathway, commonly thought of as the image-forming pathway19,20. In contrast, IGL and vLGN neurons convey information to brain nuclei involved in non-image-forming functions, including circadian rhythms21 and defensive behaviors22,23.
Anatomical tracing studies identified the dLGN-shell (superficial dLGN) as a major recipient of vertical and nasal DSRGC projections24,25,26. In accordance, in vivo physiological recordings mapped DS-dLGN responses primarily to the dLGN-shell27. Meanwhile, the dLGN-core mostly lacks afferents from DSRGCs, and only vertical DSRGC terminals were traced to deeper parts of the dLGN25,28,29. In some of these tracing studies, the IGL and vLGN were also shown to receive considerable inputs from DSRGCs24,26,28, and functional imaging of vLGN terminals identified DS responses30.
In general, the abovementioned anatomical traces cannot fully predict response properties in the visual thalamus, since the information transfer from the retina to the LGN is not limited to simple relays31,32,33,34,35. Synaptic convergence and divergence between distinct DSRGCs and their targets in the LGN could give rise to new tuning properties. For example, a large-scale imaging study of RGCs’ axonal boutons at the dLGN-shell demonstrated that neighboring DS boutons tend to be tuned to equal or opposite motion directions36. This wiring scheme predicts the presence of DS in the dLGN, as well as the emergence of axis-selectivity (AS)37. While AS responses are indeed reported in the dLGN-shell27,38,39,40, most studies have not really distinguished them from OS responses, and it remains untested if they are in fact generated from integration of oppositely-tuned DS retinal inputs.
To map the organization pattern of DS and AS/OS responses in the LGN, we here extensively surveyed the LGN by way of extracellular in vivo recordings from anesthetized mice using Neuropixels probes. As predicted based on anatomical projections, we found DS responses in the dLGN-shell and vLGN, but not in the dLGN-core. Yet, although DSRGCs are thought to tile the retina, we found DS in the dLGN-shell to display a distinct spatial pattern: DS is scarce in the central visual field but present around it, where preferred directions are aligned to match optic flow dynamics of forward self-motion. AS/OS is found across the visual field, and we also show that a stimulus edge can induce these responses as previously described in the superior colliculus41. To determine the extent to which LGN DS and AS/OS responses are generated from retinal DS, we applied genetic techniques to specifically abolish SACs in the retina. We demonstrate the critical contribution of SACs to sustaining DS, but not AS/OS responses, both in the retina and across all LGN subregions. Our results demonstrate that LGN AS/OS is not generated via the integration of two oppositely-tuned DSRGCs and we therefore refer to them simply as OS neurons, aligning with the original terminology used by Hubel and Wiesel42 and that used today for both the retina and visual cortex. Overall, our findings suggest that retinogeniculate transfer functions display a selective relay mode that is topography-dependent.
Results
To reveal organization patterns of DS and OS responses in the LGN, we performed in vivo Neuropixels recordings in anesthetized, wild-type C57bl mice (Fig. 1a). Animals were centered in front of a screen and presented with a binary noise stimulus for receptive field estimation and moving gratings in 8 directions, based on which we assessed the direction and orientation tuning of the units using accepted parameters (e.g., global direction- and orientation-selective index, gDSI and gOSI, respectively (Methods section Direction, axis- and orientation selectivity)). The gOSI and gDSI populations formed two relatively distinct populations and allowed us to determine direction and orientation tuning of recorded LGN units (Supplementary Fig. 1). Recorded units’ spatial coordinates were histologically mapped to identify their corresponding brain subregion (Fig. 1b, c, Supplementary Fig. 2, Supplementary Fig. 3) (Methods section Brain histology and probe alignment). Taking advantage of the densely packed Neuropixels probe, we were able to acquire a total of 2152 well-isolated, visually responsive single units from across the LGN (20 recordings). We only included visually responsive units in our analysis, which we defined as units that had a defined receptive field and/or responded to moving gratings (for example, response quality index (RQI) > 0.25; see Methods section Light-responsive units, Supplementary Fig. 4a–d).
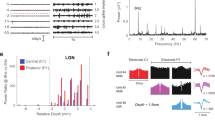
a Schematic of the recording setup: A head-fixed anesthetized mouse is presented with visual stimuli on a screen. b Left: Example of histology with probe track after recording. Middle: Close-up of LGN area. Right: Schematic of LGN subregions (dLGN-shell, dLGN-core, IGL and vLGN) and reconstructed probe track. c 3D reconstruction of all probe tracks (N = 20) in a standard mouse brain (registered to the Allen Common Coordinate Framework 3D space). LGN areas are colored as in b, right. d Examples of DS units recorded from each LGN subregion. Polar plot indicates spike count during 4 s grating presentation for single trials (thin lines) and mean spike count (bold line). Colored arrow points in the cell’s preferred direction and arrow length represents gDSI (outer circle represents 1). Raster plots show spiking response in eight directions (time of grating presentation is indicated by gray shaded area). Bottom left for each polar plot: Example spike shapes of the same unit (200 randomly selected spikes shown in gray) and mean spike shape overlaid (black). Bottom right: Inter-spike interval (ISI) distribution. e Percentages of DS units in dLGN-shell, dLGN-core, IGL and vLGN. Bar height represents weighted mean ± SEM. Single dots indicate individual recordings, dot size represents the number of units per recording. Number of recordings (N) and number of DS units out of total units are indicated below each bar. f Distribution of preferred directions of all DS units in dLGN-shell, dLGN-core, IGL and vLGN. g Cumulative distribution of tuning width of all DS units recorded in each subregion. Inset: Schematic of tuning width calculation. Maximum and half-maximum responses are marked, as well as tuning width (pink line). P: posterior, A: anterior, S: superior; I: inferior. sp: spikes. (Allen CCF dataset (version 2017) was downloaded from https://download.alleninstitute.org/informatics-archive/current-release/mouse_ccf/annotation/)88.
Direction-selective responses in the LGN
We first investigated DS responses across LGN subregions. We found that DS responses in the dLGN were more prominent in the dLGN-shell (13.73 ± 3.19% of total recorded units in that subregion) compared to the dLGN-core (2.59 ± 1.00%), confirming previous findings27 and in line with existing tracing studies of DSRGCs24,25,26 (Fig. 1d, e). The majority of recorded DS dLGN-shell units preferred postero-inferior motion (Fig. 1f). The few DS dLGN-core units we did capture displayed a bias toward the postero-inferior as well as the superior directions (Fig. 1f). This observation aligns with previous reports that ventral-DSRGCs (corresponding to superior motion) project to the dLGN-core25,28. We also found DS responses in the IGL (8.06 ± 3.59%) and vLGN (15.64 ± 7.00%) (Fig. 1d, e). Similar to the dLGN-shell, DS units of the vLGN overrepresented the postero-inferior direction, while those of the IGL did not readily display any clear bias (Fig. 1f). There was no significant difference in the cumulative tuning width distributions (Methods section Tuning width) of DS units across LGN subregions (Fig. 1g). These results confirm that the dLGN-core generally lacks DS responses. Moreover, they reveal that DS responses are present in both the dLGN-shell and the vLGN, both of which show a representation bias towards postero-inferior directions.
Direction-selective responses in the dLGN are topography-dependent
We went on to investigate the organization of DS units in the dLGN. We assessed the receptive fields of recorded units based on their responses to the binary noise stimulus, and found that dLGN units (shell and core combined) generally cover the mouse frontal field of view (Fig. 2a, b; Supplementary Fig. 5). As opposed to the dLGN, IGL and vLGN units rarely displayed a classic compact receptive field, inline with43. We therefore focused on dLGN units for this analysis. In line with previous reports27,44,45,46, dLGN neurons showed a retinotopic organization, with units recorded from neighboring electrodes on the probe having nearby receptive fields in the visual field (Fig. 2c, d and Supplementary Fig. 6). To visualize the retinotopic organization in the dLGN, we embedded the 3D coordinates of recorded units into a volumetric model of the LGN. We noticed a gradual arrangement according to the depth of the units, with more dorsal units having receptive fields in the central-superior region of the screen, and more ventral units having receptive fields in the lateral-inferior regions of the screen (Fig. 2e, f, Supplementary Fig. 7, Supplementary Videos 1, 2).
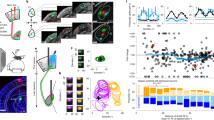
a Receptive field of example unit. Positive and negative values represent On and Off responses, respectively. b Locations of receptive field centers of dLGN units (n = 1108), aligned to contralateral/ipsilateral visual fields. Red dot is example unit from a. c Receptive fields of one example recording colored by depth from pia. d Pairwise receptive field distance vs. distance along probe track for dLGN units. 3D model of histologically derived locations (e) and receptive field locations (f) of dLGN units, color-coded as in (c). These panels include units from Figs. 2b and 4c. g Left: Receptive field locations of non-DS (gray) and DS (red) units of dLGN-shell. Some receptive fields were estimated according to neighboring units (Methods). Binocular border is shown as mean ± SD (shaded area). Right: Proportion of DS units out of all units from the dLGN-shell. Significance was tested against shuffled data (two-sided; see Methods). p-values are indicated according to higher (§) or lower (*) percentage than chance. Gray asterisks indicate bins with <5 units. No corrections for multiple comparisons were made. h Like g for dLGN-core. i Left: Arrows of PDs of DS units from the dLGN-shell plotted on their receptive field, for DS units with PD in postero-inferior quadrant. Right: PD vs. elevation, colored by PD. R and p-value according to Pearson correlation. Shaded area indicates 95% confidence interval of fit. j Translatory optic flow during forward motion. k Calculated optic flow (black) at each visual field location corresponding to DS units’ receptive fields. PDs from i are overlaid. Close-ups show example regions. l Same as k but after rotating optic axis downward by 34°. m Distribution of angular difference between PDs and expected translatory optic flow at each unit’s receptive field location for the vertical optic axis positions shown in k and l. n Optic axis measured during experiment (blue), and its position after changing the optic axis elevation in a calculation (yellow). PD preferred direction, AP antero-posterior, ML medio-lateral, DV dorso-ventral. */§: p < 0.05, **/§§: p < 0.01, ***/§§§: p < 0.001, ****/§§§§: p < 0.0001.
Some dLGN units showed a clear response to the moving gratings but poor responses to the white noise. Hence, we could not directly calculate their receptive field (34.8% of non-DS dLGN units, 62.9% of DS units). The lack of clear receptive fields may occur when a cell with strong surround antagonism is presented with a white noise stimulation. Such strong surround was reported for DSRGCs47,48, probably masking responses to stimuli in the center receptive field. For these units, we relied on the dLGN’s retinotopic organization, and estimated their receptive field center position based on receptive fields of their close neighbors along the probe track (Methods section Estimation of missing receptive fields). We validated this approach using units with identified receptive fields, and confirmed that our estimation was near the receptive field center that was calculated based on the white noise (median error between estimated and real receptive field: 7.4° (Supplementary Figs. 6c, d)). Therefore, in subsequent analyses, we combined receptive fields obtained using both direct measurement and estimation methods.
We analyzed the receptive field locations of all DS units and found that they were not uniformly distributed in the dLGN. First, DS units were mainly found in the monocular field of view (Fig. 2g, h). Although units in the central visual field were abundant, DS units were scarce in this area, which corresponds to the binocular region (Methods section Assessment of binocular field). The low percentages of DS units in the core could originate from units in the ipsilateral patch, which tends to lack DSRGC inputs24,26,28. We therefore separated the core units into ipsilateral and contralateral regions according to their assignment and found that DS units in each region comprised less than 3% of the cells (Supplementary Fig. 8). While most (75%) of the units assigned to the ipsilateral patch had receptive fields in the binocular zone, a quarter had receptive fields in the monocular zone. It was shown that dendrites of dLGN neurons may cross eye-specific boarders and integrate inputs from both eyes33,34,35,49,50,51,52, which may explain the peripheral receptive fields. Yet, these units may also reflect the limitation of our approach to assign units belonging to particularly small brain regions such as the ipsilateral patch. Second, DS units in the dLGN-shell displayed a gradual shift in their preferred direction along the elevation axis: posterior-DS dominated the top end of the screen (40° above eye-level horizon), postero-inferior DS the mid ranges, and inferior-DS the bottom (-20° below horizon) (Fig. 2i, Supplementary Fig. 9a). Raising the RQI threshold did not change these findings (Supplementary Fig. 4e, f).
Since it was shown that in the retina DSRGCs’ preferred directions align with optic flow15, we examined whether the organization of DS units in the dLGN is related to optic flow representation, too. We calculated translatory optic flow generated when the mouse is moving forward (Fig. 2j), and calculated a projection of the resulting optic flow vectors onto a plane (defined by the screen’s location in space) (Methods section Analysis of optic flow). As expected, the central visual field, where DS units are scarce, contains the least optic flow. We first quantified the match between DS units’ preferred direction and the optic flow at their receptive field center using the location of receptive fields that we measured (Fig. 2k). For some DS units their preferred directions matched the local optic flow, but for others it did not (Fig. 2k, inset 1 vs. 2). We then asked how the match between optic flow and preferred directions would change for different gaze positions of the mice. For that, we performed calculations where we changed the elevation of the optic axis, and calculated the resulting receptive field position for each optic axis elevation (Supplementary Fig. 10). For each theoretical optic axis elevation, we quantified the match between DS units’ preferred direction and the optic flow direction (Fig. 2k-n; Supplementary Fig. 10). We found that the optimal matching between DS receptive fields and optic flow directions requires a vertical offset of ~34°, resulting in an alignment of the optic axis with the horizon (Fig. 2l, m, Supplementary Fig. 10e, f). We then independently measured the optic axis positioning in anesthetized mice (Methods section Optic axis measurements, Supplementary Fig. 11) and found that their optic axes display a similar vertical offset (elevation: 36.7 ± 0.7°, azimuth: 73.6 ± 5.5°, mean ± SD, n = 4 mice).
SAC ablation in the retina eliminates DS responses in the LGN
The lack of DS representation in the central visual field is unexpected to derive from the retina, as DSRGCs are thought to be distributed across the entire retinal surface, including the temporal region which represents the center visual field12,15,53,54. Moreover, while DSRGCs projecting to the LGN are reported to be On-Off RGCs that often exhibit balanced On and Off responses, we found that DS units of the dLGN tend to display stronger On- than Off responses, with some cells responding exclusively to On stimuli (Supplementary Fig. 12). These divergences led us to investigate whether DS responses in the LGN are generated de novo, independent of retinal DS, or, despite the discrepancy, are inherited from the retina. For this purpose, we used a ChATCre;iDTR transgenic mice crossbreed that expresses diphtheria toxin receptors (DTR)55 in cells encoding Choline acetyltransferase (ChAT). Since in the mouse retina, ChAT is exclusively expressed in SACs, this setup allowed us to disrupt SAC inhibition of DSRGCs, thereby diminishing retinal DS (Fig. 3a). Two weeks after intraocular injection of diphtheria toxin (DT), mice were sacrificed and their retinas extracted for multielectrode array recordings and histological verification of successful SAC ablation (Fig. 3b). Quantifications of SAC density in WT and control mice (ChATCre(-);iDTR(+), DT injected) vs. ChATCre(+);iDTR(+) mice injected with DT reflected the great efficacy of this method (Supplementary Fig. 13a–c). Upon SAC ablation, we observed acute loss of directional tuning in the retina (Fig. 3c–e). Importantly, retinas of ChATCre(+);iDTR(+) mice injected with DT displayed otherwise normal light responses and baseline physiological properties, with the exception of elevated baseline firing rates (Supplementary Fig. 13d–f). These effects align with previous studies using this technique5,56,57, and are to be expected with the removal of SAC inhibition.
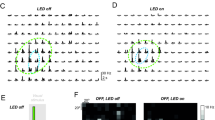
a Schematic of a cross-section of a control and a ChATCre;iDTR retina injected with diphtheria toxin (DT). b Schematic of experimental method: DT is intraocularly injected into ChATCre;iDTR mice. After 14 days, multi-electrode array (MEA) recordings are performed; a schematic of a retina on a multi-electrode array is shown. c Polar plots of an example DS cell from a wild-type retina (left) and an untuned light-responsive cell from a DT retina (right). Notations as in Fig. 1d. Retinal coordinates are shown. d Cumulative distribution of gDSI for wild-type control and DT condition. p-value according to two-sided Wilcoxon rank-sum test (p = 1.9·10−47). e Proportion of DS cells in wild-type control and DT conditions. Notations as in Fig. 1e. Bar height represents weighted mean ± SEM. N = 25/8 retina recordings for WT Control and DT conditions, respectively. p-values according to bootstrapping analysis (two sided; p = 0). D dorsal, V ventral, T temporal, N nasal; sp spikes. ****:p < 0.0001.
Following the successful ablation of SACs and elimination of retinal DS, we conducted in vivo LGN recordings in ChATCre(+);iDTR(+) DT-injected mice. As before, recorded units’ spatial coordinates were histologically reconstructed, and retinal explants were verified for SACs elimination after each recording (Fig. 4a–c). We found a significant reduction of DS responses in SAC-ablated mice, which was robust to RQI threshold (Supplementary Fig. 4g), suggesting that DS responses across the visual thalamus are SAC-dependent (Fig. 4d, e). We compared the cumulative gDSI distributions for each subregion as an unbiased measure of population-level changes in directional tuning. The dLGN-shell, IGL and vLGN exhibited population-level widening of directional tuning (Fig. 4f). Conversely, dLGN-core units displayed only a minor (but significant) change in their tuning width, which reinforces our finding with regard to the scarcity of DS units in that subregion (Fig. 4f).
a Schematic of experimental method for in vivo recording: After the experiment, the probe track is reconstructed and retinas are stained for ChAT to confirm successful SAC ablation. b 3D reconstruction of all probe tracks in DT condition (N = 9) in a standard mouse brain (registered to the Allen Common Coordinate Framework 3D space). c Locations of all receptive fields recorded in DT condition. d Examples of untuned units from all LGN subregions. Notations as in Fig. 1d. e Percentage of DS units in the dLGN-shell, core, IGL and vLGN in control and DT conditions. Notations as in Fig. 1e. Bar height represents weighted mean ± SEM. Number of recordings (N) and number of DS units out of total units are indicated below each bar. p-values according to bootstrapping analysis (one-sided). f Cumulative distribution of gDSI for each LGN subregion for control (solid lines) and DT (dashed lines) condition. p-values according to two-sided Wilcoxon rank-sum test. P posterior, A anterior, S superior; I inferior. sp: spikes. *p < 0.05; ****p < 0.0001. (Allen CCF dataset (version 2017) was downloaded from https://download.alleninstitute.org/informatics-archive/current-release/mouse_ccf/annotation/)88.
Orientation-selective responses in the LGN
Next, we investigated OS responses in the LGN. These responses were determined based on drifting gratings. For the orientation preference, we refer to the orientation of the gratings and not to their movement direction, which is orthogonal. We found that OS responses are more common in the LGN than are DS responses (23.5% and 8.4%, respectively) and that they are prevalent across all LGN subregions (dLGN-shell, 25.90 ± 3.45%; dLGN-core, 24.43 ± 3.22%; IGL, 12.1 ± 4.2%; vLGN, 14.53 ± 6.83%) (Fig. 5a, b). We compared the cumulative tuning width distributions of OS units across LGN subregions and found no significant differences (Fig. 5c, see also Supplementary Fig. 14a) (Methods section Tuning width). The LGN OS population exhibited general orientation tuning biases towards horizontally, vertically and diagonally oriented gratings (mostly postero-superior to antero-inferior) (Fig. 5d).
a Example of OS units recorded from the LGN subregions. Colored line denotes the cell’s preferred orientation, and its length the gOSI. Note that angles here refer to the grating orientation and not the motion’s direction (unlike Figs. 1, 3 and 4). Bottom left for each polar plot: Example of spike shapes of the same unit (200 randomly selected spikes shown in gray) and the mean spike shape overlaid (black). Bottom right: Inter-spike interval (ISI) distribution. b Percentages of OS units in the dLGN-shell, core, IGL and vLGN. Number of recordings (N) and number of OS units out of total units are indicated below each bar. Bar height represents weighted mean ± SEM. Notations as in Fig. 1e. c Cumulative distributions of tuning width of OS cells in all subregions. Inset: Schematic of tuning width calculation. Tuning width (pink) is calculated as the mean width of responses at half-maximum response ((θ1 + θ2)/2). d Distribution of preferred orientations of all OS units for each LGN subregion. P: posterior, A: anterior, S: superior; I: inferior, vert: vertical, hor: horizontal, sp.: spikes. n.s.: not significant.
Edge-induced orientation-selective responses in the dLGN
Next, we searched for topographic trends in the orientation preference of LGN units. Unlike DS responses, OS responses were spread throughout the visual field. We observed that a majority of OS units with receptive fields near the edge of the screen were tuned to an orientation parallel to that edge (Fig. 6a–d). These findings were robust even at higher RQI thresholds (Supplementary Fig. 4h–k). To verify that these OS responses were edge-induced and not topography-dependent, we performed additional experiments with the mouse rotated, and the screen’s edge presented in the central visual field (azimuth 0°) (Fig. 6e). We found that the preferred orientations of OS responses in the central visual field differed between the two conditions. Specifically, more vertical-preferring OS responses appeared when the screen’s edge was in the corresponding region (compare light gray area in Figs. 5b, c to 5f, g). These results suggest that OS responses at the borders of the screen are induced by the screen edge itself, and not the specific location in the visual field. Similar edge-induced OS responses were recently described in the mouse superior colliculus41. After excluding the edge units from the population, the orientation preference of LGN OS units fell along the diagonal and horizontal axes (Fig. 6d), and we observed no area in the visual field having over- or underrepresentation of OS units (Supplementary Fig. 15a–c). When grouping the OS units based on preferred orientation, we did notice some subtle trends of spatial organization along the horizon and around the center visual field (Supplementary Fig. 15d–g).
a Schematic of recording setup. b Lines of preferred orientations of all LGN OS cells plotted on their receptive field center. Color legend is shown below with two schematics of vertical and horizontal gratings. Dashed lines mark 5° from the screen borders. c Distribution of preferred orientations of all OS units located in different areas of the visual field shown above: (1) within 5° of the vertical edge (pink), (2) within 5° of the horizontal edge (purple), (3) in the remaining central screen (dark gray) or (4) between azimuths −5 and 0° (light gray). d Distribution of preferred orientations like in Fig. 5d but only for units with a receptive field in the central area of the screen (from c; gray). n indicates number of OS units from central screen out of all OS units with receptive fields. e Schematic of recording setup where the screen’s edge is located at azimuth 0° (compared to azimuth −47° as in (a–d). The 5° threshold is marked. f Like (b) for experimental setup shown in (e). Gray shaded area encompasses azimuths −5°− 0°. g Preferred axes of OS units with receptive fields located between azimuths −5° and 0° (within 5° of stimulus edge; from (e, f); compare to the same area in visual space shown in (b), (c) (light gray, no edge present)). P posterior, A anterior, S superior, I inferior.
Orientation-selective responses in the LGN persist despite SAC ablation
Previously, it was suggested that a combination of two oppositely-tuned retinal DSRGCs can create an AS response in the LGN36,37. Given the interchangeable use of AS/OS, we used the ChATCre;iDTR mouse model to test whether LGN axis/orientation selectivity is dependent on retinal DS (Fig. 7a). In our ex vivo retinal recordings, the percentages of OSRGCs did not statistically differ between control and DT mice (1.95 ± 0.6% and 1.59 ± 0.6%, respectively) (Fig. 7b–d). In our in vivo LGN recordings, we found that, unlike DS cells, OS-LGN cells retain their proportion within the total of LGN responsive units (Fig. 7e, f). OS-dLGN units also maintained their orientation preference bias towards horizontally oriented gratings (Fig. 7g). Moreover, comparisons of tuning width distributions for control vs. DT conditions revealed no change across all LGN subregions (Fig. 7h, Supplementary Fig. 14b). These findings, which held true across RQI threshold values (Supplementary Fig. 4l), demonstrate that SACs, and thereby DSRGCs, do not provide fundamental inputs to sustain OS (nor AS) responses in the LGN. Finally, as we found in wild-type mice, we also noted edge-induced OS responses in SAC-ablated mice (Supplementary Fig. 16).
a Hypothesized model of creating AS responses by convergence of two DS inputs. b Schematic of experimental method. DT-injected mice were either used for MEA recording of the retina (c-d) or in vivo Neuropixels recordings of the LGN (e-h). c Polar plots of example OSRGCs from a wild-type control retina (left) and a DT retina (right). d Proportion of OSRGCs in wild-type control and DT conditions. N = 25/8 retina recordings for WT Control and DT conditions, respectively. Bar height represents weighted mean ± SEM. p-value according to bootstrapping analysis (one-sided; p = 0.41). e Example of OS units from all four LGN subregions. Notation as in Fig. 5a. f Percentage of OS units in control and DT conditions. Notation as in Fig. 4e. Number of recordings (N) and number of OS units out of total units are indicated below each bar. Bar height represents weighted mean ± SEM. p-values according to bootstrapping analysis (one-sided). g Polar histogram showing the preferred orientations of all OS cells recorded in DT conditions in the dLGN-shell, core, IGL and vLGN. h Cumulative distribution of tuning width (in degrees) for all OS units recorded in the control and DT condition per area. p-values according to two-sided Wilcoxon rank-sum test. D dorsal, T temporal, N nasal, V ventral, P posterior, A anterior, S superior, I inferior, sp spikes. ****p < 0.0001. n.s.: not significant.
Discussion
Our survey of the LGN sheds new light on motion and orientation representation across its subregions. First, we demonstrate that DS responses are rare in the dLGN-core, while OS responses are prevalent in both dLGN-shell and core. Second, we reveal that the distribution of DS cells in the dLGN is non-uniform and biased to represent the translatory optic flow. Third, we give estimates of DS and OS populations in the vLGN and IGL, providing context to help characterize the LGN’s feature space as a whole. Finally, we show that DS responses across the LGN are eliminated in SAC-ablated mice, while AS/OS responses remain intact. Our findings show that the connectivity map between the retina and LGN is topography-dependent, suggesting an efficient representation of retinal channels at the LGN level that is adjusted to fit the animal’s behavioral needs.
Direction selectivity and orientation selectivity show distinct organization patterns in the dLGN
We found two distinct distribution principles for the receptive fields of DS and OS units we recorded in the dLGN. The receptive fields of DS units in the dLGN-shell are scarce in the center of the mouse’s visual field but present in the monocular visual fields, where they show a clear tendency towards the postero-inferior direction. Further, we noted a gradient in directional preference along the elevation arc. This topographic variation of DS in the dLGN-shell suggests a rigid encoding regime for these units, adjusted to the translatory optic flow dynamics of the mouse15,58. The central visual field is expected to have lowest levels of optic flow59, which fits with the low incidence of DS responses in this area. Receptive fields of posterior-DS units of the dLGN-shell mostly reside at ~30–40° above the horizon, matching our measurements of optic axis elevation in anesthetized mice. It follows that when the mouse aligns its gaze to the horizon during forward running, dLGN DS cells would be maximally activated by optic flow motion.
A somewhat different topographic variation of DS in the visual field of mice was previously demonstrated in the superior colliculus60, where anterior- and posterior-DS responses were found to be overrepresented in the binocular and monocular zones. Thus, our results suggest that DS in the dLGN is aligned to translatory optic-flow, while DS in the superior colliculus refers to the binocular-monocular boundary as a symmetrical meridian.
The organization pattern of DS in the dLGN, specifically its scarce representation in the center visual field, is distinct from that in the retina, as DS is thought to be represented across all retinal regions. Yet, there are also similarities between the organization of retinal and LGN DS, as the overrepresentation of posterior direction in the retina15,53 is somewhat similar to the postero-inferior overrepresentation we and others57 have found in the LGN. In fact, the topographic organization of the preferred directions of DS dLGN cells may be partly inherited from the retina according to the tilt of preferred directions that match the translatory optic flow along the body axis15. Other DSRGCs were shown to match the gravitational axis, which we find to be underrepresented in the dLGN. However, the optic flow generated along the body axis and along gravitational axis overlap in specific areas in the visual field (Supplementary Fig. 9b-d), and we therefore cannot rule out the possibility that both representations are transferred to the dLGN, at least for these specific areas. Indeed, given the known topographic variation in the mouse retina12 it is possible that retina-dLGN projection rules are also topography-dependent. These rules may range, depending on DSRGC type and location, from one DSRGC that provides the dominant input to a DS unit in the LGN, through a DSRGC that combines with many other RGCs and forms weak synapses with its target neuron25,61,62, to a DSRGC that completely avoids the LGN.
For orientation representation, we found that a majority of OS units with a clear receptive field near the screen’s edge encode orientations parallel to that edge. These edge-induced OS responses were recently described in the superior colliculus of awake mice41, and we show here that they are also prevalent in the dLGN. This feature follows a dynamic encoding principle, independent of innate retinotopic organization, and was suggested to encode stimulus saliency. Notably, our recordings were performed in anesthetized mice, suggesting that dynamic edge detection is a fundamental property encoded in the early visual processing stages of mice. This edge-induced OS preference may be generated by partially masking the receptive field, thereby effectively creating an elongated ‘functional’ (or unmasked) receptive field. This remaining ‘functional’ receptive field is more likely to align with the stripes of the gratings in orientations matching those of the screen’s edge, giving rise to OS responses. Indeed, elongated receptive fields are suggested as the primary mechanism for generating OS responses, as we describe in the next section.
Orientation selectivity vs axis selectivity
Due to the symmetry of AS responses, they are often indistinguishable from OS responses, in spite of the distinct features they encode. Initially characterized in the cat visual cortex, OS responses were suggested to be generated by an elongated receptive field formed due to the spatial summation of classical center-surround thalamic inputs42. Such input organization may evoke responses to both static and moving stimuli, as long as they have the matching orientation. However, Hubel and Wiesel also reported that half the units they recorded were mostly characterized using moving stimuli, due to their poor responsiveness to static stimuli. Since then, specific circuit models were described, providing various examples for spatio-temporal arrangements of inputs and how they may encode stimuli’s motion or shape, orthogonal to or along their receptive fields’ major axes38,40,63,64.
The term axis selectivity became popular with respect to mouse LGN units. We think that this is partly because of the hypothesis that two DSRGCs with opposing preferred directions converge onto one LGN neuron, which would consequently encode motion along a specific axis36,37. Since our recordings from control and SAC-ablated mice dispute this hypothesis by identifying similar percentages of AS/OS units in the LGN of the two groups, we chose to refer to these units as OS rather than AS. However, only with additional stimuli – such as static orientations or non-oriented motion patterns – can the true nature of these cells, as either axis- or orientation-selective, be determined. Note that there are important implications in terms of terminology. For example, we would consider a neuron tuned to horizontal gratings moving in superior and inferior directions not as a vertical AS cell but as a horizontal OS cell.
Transfer of retinal channels along the primary visual pathway
Our results support the widespread observation that retinal DS readout is eliminated in SAC-ablated mice5,6,7. Notably, we did not find any residual DS responses in any LGN subregion of SAC-ablated mice. This differs slightly from results obtained in SAC-disrupted mice, in which the horizontal component of DS is specifically eliminated57,65. There, imaging of thalamocortical terminal boutons in the superficial layers of the primary visual cortex (V1) showed that posterior-DS units were only partially affected. The differences may originate from the full SAC abolishment we used vs. specific abolishment of horizontal DS. Nonetheless, DS responses were clearly described in cortical neurons of both SAC-ablated and -disrupted mice5,57. Taken together, our results suggest that SAC-independent DS responses emerge at – and not prior to – the cortical stage. These DS responses may emerge from spatiotemporal integration of non-DS thalamic inputs (63).
Our finding that OS-LGN responses are SAC-independent puts into question previous suggestions of the DSRGC combination serving as a facilitator of thalamic axis selectivity36,37. Rather, they support recent studies. One study genetically isolated subsets of cortical V1 neurons, physiologically characterized them and traced back their dLGN and retinal neuronal sources66. Results from this effort indicated that DSRGCs and OSRGCs may form separate transmission lines all the way to the visual cortex66. Another study, working from the bottom up, used a transgenic mouse line to evaluate the extent of functional convergence between ventral and dorsal DSRGCs in the dLGN. Results from that study suggest that vertical-preferring DSRGCs with opposing preferred directions most likely do not functionally converge onto dLGN neurons25. In addition, via measurement of the functional connectivity between DSRGCs and LGN cells, it was shown that vertical-preferring DSRGCs are more likely to form strong synaptic connections with a DS-LGN, but not an AS/OS-LGN cell62. These findings, combined with our results, support the notion of labeled lines, where specific retinal channels remain segregated at the LGN level and perhaps, at least to some degree, at the V1 level.
Role of direction and orientation selectivity in visually-guided behaviors
Two main types of RGCs encode motion direction, On-DSRGCs and On-Off DSRGCs (which we refer to as DSRGCs). While On-DSRGCs are known to target the accessory optic system and mediate the optokinetic reflex7,67,68,69, the behavioral role of DSRGCs remains largely unknown. DSRGCs project to the two major retinal targets, the dLGN and the superior colliculus24,26,28, and both brain regions exhibit DS responses27,37,38,40,60,70,71,72. DSRGCs were shown to mediate DS responses in the superior colliculus73, a visual hub for directed behaviors such as predator evasion and prey capture74,75. Nevertheless, SAC-ablated mice hunt prey as efficiently as wild-type mice do56, implying that locomotion strategies assumed by the mouse during a chase are independent of retinal DS.
The dLGN is generally referred to as the main relay for the image-forming pathway. Under this assumption, diverse features represented in the dLGN, including DS, should highlight specific components of the visual image. Contingent on our results, we hypothesize that the dLGN is involved in translational optic-flow perception, which directly relies on DSRGCs. Interestingly, the primary visual cortex and other higher cortical visual areas have neurons that specialize in encoding translational and rotational optic flow, and these responses were also shown to rely on DS information from the retina65. Together with previous results, our findings strengthen the hypothesis that retinal DS serves as a sensor of optic flow15 and relays this information via the dLGN to visual cortices65,76.
We also found that horizontal OS cells are somewhat denser around 30° elevation – the altitude corresponding to the horizon. These cells may therefore contribute to orienting during navigation. In addition, we identified a streak of higher density of diagonal preferring OS units, the functional significance of which remains unclear and requires further investigation.
Limitations of the study
Our study was limited to the central visual field (Supplementary Fig. 5), and wider investigation of the complete visual field and the entire dLGN would further reveal the topography of DSRGC-dLGN projection patterns and additional representations of DS in the periphery of the visual field. Therefore, we cannot know if DS responses exist in brain regions we did not record from, or if the central visual field has additional representation in dLGN regions which we did not target.
We also note that small errors in anatomical localization may occur, particularly in compact regions such as the ipsilateral patch or the IGL; however, none of our key conclusions depend on precise unit assignment within these compartments.
Our study demonstrates that DS in the dLGN fully depends on retinal DS, but it remains unclear whether other properties, such as polarity preference, are inherited from DSRGCs. Several factors may underlie the observed differences in polarity preference (Supplementary Fig. 12), including differences in On-Off stimulus parameters between MEA and in vivo recordings, such as light level, which was shown to influence RGC polarity77,78. Light level–dependent surround effects may also differentially impact On and Off responses48. Thus, while dLGN DS units likely inherit some of their polarity preference from DSRGCs, contributions from non-DS ON-RGCs or LGN interneurons cannot be excluded.
In this study we optimized the stimulus for canonical DSRGCs. Additional types of non-canonical DSRGCs are thought to be independent of SACs and to project to the LGN13,79 and their contribution to DS and AS/OS in the LGN was not tested here. Lastly, as for any recording technique for extracellular population recordings, our results may be biased towards specific cell types and sizes, and we may have missed cell types of very low frequencies.
Methods
Animals
For wild-type mice we used C57Bl/6 J mice (purchased from Charles River Breeding Laboratories). ChATCre mice, which express Cre in SACs80, were purchased from Jackson Laboratory (#006410, B6;129S6-Chattm2(cre)Lowl/J). ROSA26iDTR mice were obtained from Jackson Laboratories (#007900, C57BL/6-Gt(ROSA)26Sortm1(HBEGF)Awai/J). For ChATCre;iDTR crossings, we used mice heterozygous for ChATCre and iDTR. Mice were housed in groups of no more than 5 mice at 25 °C, at a 12 h/12 h light/dark cycle, with water and food provided ad libitum. For all experiments, we used mice of both sexes. For in vivo Neuropixels recordings we used mice aged between P30-90. Intraocular DT injections were performed on mice aged between P38-67. MEA recordings were performed 14 days after intraocular injections, i.e., mice were aged between P52-81. Control experiments were performed on mice of the same age. All procedures were approved by the Institutional Animal Care Use Committee (IACUC) at the Weizmann Institute of Science (protocols 01490224-2 and 00580123-2).
In vivo surgical procedure
For the purpose of acute electrophysiological recordings, mice were initially sedated with an intraperitoneal injection of Chlorprothixene (8 μg/gr bodyweight, Sigma-Aldrich/Merck, Darmstadt, Germany), then anesthetized with Urethane (intraperitoneal, 1–1.5 mg/gr, Sigma-Aldrich/Merck). Once unconscious, the animal was kept on a feedback-controlled heating pad at 33 °C, and monitored throughout the experiment for breathing rate/quality and absence of foot withdrawal reflex. After securing the mouse onto a stereotactic device, Lidocaine 0.2% (2 μg/gr, VetMarket, Shoham, Israel) was subcutaneously administered to the scalp. The scalp was then removed to expose the skull and all connective tissue was cleared away from its surface. To keep the eyes from drying, a thin layer of paraffin based transparent ophthalmic ointment was applied (Duratears, Alcon-Couvreur, Puurs, Belgium). Following horizontal alignment of the pitch and roll head axes, a metal frame was glued to the skull by cyanoacrylate glue and dental cement. Once the headplate firmly affixed to the skull, a craniotomy of 1–2 mm in diameter was drilled, located 2.3–2.8 mm posterior to bregma and 1.2–2.4 mm lateral. The exposed brain was covered with a layer of saline throughout the recording.
In vivo Neuropixels recordings
Anesthetized mice were head-fixed, centered 25 cm away and in front of a screen. As above, breathing rate and body temperature were monitored throughout the recording session. Recordings were carried out using Neuropixels probes (1.081), which were dipped in fluorescent dye (DiI, Sigma-Aldrich/Merck) for histological reconstruction of their trajectory. Acquisition was performed with SpikeGLX (billkarsh/SpikeGLX @ GitHub). The probe was lowered by a motorized micromanipulator (Luigs & Neumann, Ratingen, Germany) at 10 μm/sec, with a full-field flashing stimulus running meanwhile. Evoked visual responses around 3–4 mm below pia indicated accurate placement of the probe in the LGN, and once the probe had crossed beyond visually responsive areas it was retracted by 50 μm. Recording protocol resumed 15 min later, to allow for resettling of the brain tissue around the probe. In total, we conducted 20 recording sessions from 18 wild-type mice and 9 recordings from 7 DT injected mice (in both groups there were two animals in which we performed 2 insertions of the probe and therefore two recording sessions).
Visual coordinate system for in vivo recordings
We defined visual coordinates using azimuth and elevation. The point of zero azimuth and elevation was defined by a horizontal plane passing through the mouse’s eyes (elevation 0°), and a midsagittal plane orthogonal to it (azimuth 0°). The elevation angle of a point in the visual field was defined as the angle formed between a plane passing through it and the horizontal reference plane. The azimuth angle was defined as the angle formed with the midsagittal plane.
Optic axis measurements
Angular eye orientations of anesthetized mice were obtained as previously described by82 and others. In short, a LED-girdled camera (Dino-Lite Edge) was mounted on a two-axis gimbal (azimuth and elevation, Luigs & Neumann, Ratingen, Germany), and its rotation center was manually adjusted to the pupil by minimizing pupil slippage within the frame (Supplementary Fig. 11). A series of photos taken at different angles were annotated (Fiji) to locate the [X,Y] coordinates of the pupil center as well as the center of the LED-ring corneal reflection (indicating the intersection between the optic axis of the camera and the cornea). Next, horizontal and vertical eye positions were computed as \(E=\arcsin (\frac{{CR}-P}{{Rp}})\), where CR is the position of the corneal reflection, P the position of the pupil center and Rp is the pupil’s rotation radius. Rp was estimated as \({Rp}=\frac{(C{R}_{1}-{P}_{1})-(C{R}_{2}-{P}_{2})}{\alpha }\), where \(\alpha\) is the known angle traversed by the camera (<30°), separating coordinate pairs 1 and 2.
Assessment of binocular field
To calculate the borders of each eye’s field of view, we assumed a field of view of 180° per eye15,83. We calculated the binocular border based on the optic axis position obtained by our measurements (−73.63 ± 5.5° azimuth, 36.7 ± 0.7° elevation, mean ± SD, n = 4 mice) and displayed the range of mean ± SD as a shaded area in Fig. 2g, h.
Transformation to retinal coordinates
To transform coordinates of the visual world (e.g., screen outlines, receptive fields of recorded units) to retinal coordinates for Supplementary Fig. 5, we assumed a point-symmetric mirroring around the optic axis (achieving a ‘flipping’ of the image through the lens). Points in the world had the same coordinates in azimuth and elevation in a modeled 3D retina. To calculate their coordinates on a flattened retina, we transformed their coordinates from a 3D retina into polar coordinates (with the angle theta defining nasal, dorsal, temporal or ventral). We calculated each point’s distance to the optic disc in a 3D curved retina using the Haversine formula, and plotted them at the same distance in a 2D flattened polar plot.
Visual stimuli for in vivo recordings
The visual stimulation LCD screen (24”, 1280/720, LG) was placed 25 cm away from, and centered in front of the mouse. At this distance and positioning, the screen covered +46.66°-46.66° (horizontally, i.e., azimuth) and +40°-19.8° (vertically, i.e., elevation) of the mouse’s visual field. The mice viewed the screen with both eyes.
All stimuli were written in MATLAB R2019a using PsychToolbox84,85. We used two basic visual stimulations: pixelated binary white noise to determine receptive fields, and square wave moving gratings to assess directional preference. Full-field binary white noise was displayed for 15 min at a temporal frequency of 15 Hz. Each square covered 3.7° of the mouse’s visual space (as measured at elevation & azimuth = 0). Moving gratings had a spatial frequency of 0.085 cycles/° and moved at a temporal frequency of 2 Hz (speed of 23.5 °/s), presented in 8 directions in a pseudo-random order for 5 repetitions, with 2 s of mean gray intensity between directions. ¼ phase-shift was applied to even-numbered repetitions. The full-field spot stimulus used to assess light responsiveness (Supplementary Fig. 2) consisted of a 4 s white screen, preceded and followed by black background, presented for five repetitions.
Brain histology and probe alignment
Once recording had concluded, mice were deeply anesthetized with a terminal intraperitoneal injection of thiopental (CTS, Kiryat Malachi, Israel), then intracardially perfused with 4% phosphate-buffered saline (PBS, Biological Industries Israel, 02-023-1 A, pH 7.4) and 4% paraformaldehyde (PFA, ChemCruz, Santa Cruz Biotechnology, Inc., CAS: 30525-89-4) for brain and eyes extraction. Brains were fixed further in 4% PFA for 24 h, then rinsed and suspended in 4% PBS until dissection. We used a Vibratome (Campden Instruments, Loughborough, Leicestershire, UK) to produce 40 μm slices, which were DAPI stained and mounted on slides for imaging. Image acquisition was performed with a slide scanner (OLYMPUS BX61VS), and further image processing was done with FIJI (ImageJ86). A semi-automatic aligning algorithm (87, cortex-lab/allenCCF @GitHub using the Allen mouse brain common coordinate framework88 (version 2017) downloaded from https://download.alleninstitute.org/informatics-archive/current-release/mouse_ccf/annotation/) was used to reconstruct the trajectory traversed by the probe and list the brain areas along that trace. Alignment output was then manually curated against physiological activity landmarks along the probe, and finally recording electrodes and units were assigned their corresponding brain region. We included the following acronyms according to the Allen Brain Atlas in each of our defined recording regions: dLGN-shell: LGd-sh; dLGN-core: LGd-co and LGd-ip, IGL: IntG and IGL, vLGN: LGv. We validated the assigned brain areas by quantifying light responsiveness and found that, as expected, visual areas displayed light responses while adjacent, non-visual areas, did not (Supplementary Fig. 2). Three-dimensional rendering of recorded units’ locations in the LGN was done in Matlab and the Mayavi module @ Python and combines recordings from the control and DT dataset.
Analysis of Neuropixels recordings
Spike sorting was conducted in Kilosort 2.089 (cortex-lab/KiloSort @GitHub), and manually curated using Phy290,91 (cortex-lab/phy @GitHub). We only included well-isolated single units in all further analysis. Single units were defined as units with <1% of spikes falling into the refractory period (1.5 ms). All further analysis was performed in Matlab (R2019b, The MathWorks) using custom-written scripts.
Light-responsive units
We only included light-responsive units in our analysis. A unit was defined as light-responsive if it had a defined receptive field (see below), or was visually responsive to moving gratings. To determine if units were responsive to moving gratings, we calculated a response quality index1 as \({RQI}=\frac{{Var}{\left[{\left\langle R\right\rangle }_{r}\right]}_{t}}{{\left\langle {Var}{\left[R\right]}_{t}\right\rangle }_{r}}\) where R is the firing rate in response to the 4 s presentation of the moving gratings (repetitions r × time t; calculated in time bins of 50 ms), and 〈 〉x and []x represent the mean and variance over dimension x, respectively. Units were classified as responsive if their RQI exceeded 0.25, or if their mean firing rate during grating presentation exceeded the baseline±2 SD (each in the motion direction with the highest firing rate). We verified that the results were independent of the RQI threshold.
Receptive fields
Receptive fields were calculated as the spike-triggered average (STA) in response to the white noise as the average stimulus preceding a spike, extracted from a time window 666.6 ms before the spike containing 10 frames in time steps of 66.6 ms (based on a stimulus frequency of 15 Hz). Averaged spatial receptive fields were then upsampled by a factor of 4 to a resolution of 0.94° and smoothed using a 2D Gaussian smoothing kernel (Matlab function imgaussfilt with σ = 2). The background was defined as the mean STA 666.6 ms before the spike and subtracted from all frames. We only included STAs whose peak response exceeded 2 SD of the background signal for fitting receptive field contours. We performed a contour fit on the frame with the maximum absolute STA amplitude using Matlab’s contourc function with a threshold of 25% of the absolute peak amplitude to account for both ON and OFF responses (adapted from92). The receptive field center was calculated as the weighted center of mass of all pixels included in the contour, using their STA amplitude as the weight (Matlab function regionprops with parameter WeightedCentroid). In a final step, contour fits that resulted in many small contour areas were removed (often due to noisy STAs). In one recording, the white noise stimulus was not presented, and we therefore exclude it from receptive field analysis.
For simplicity of visualization, we defined the left field of view as the contralateral one to the recording hemisphere. Receptive fields recorded from the right hemisphere are plotted in their original location on the screen, and receptive fields recorded from the left hemisphere (originally in the right field of view) were mirrored along the vertical axis at azimuth 0° to appear in the left field-of-view.
Estimation of missing receptive fields
We found that a substantial proportion of DS units did not display clear receptive fields (62.9% of all dLGN DS units). For the analysis of preferred directions across the visual field of the dLGN-shell we therefore estimated receptive field positions of units without receptive fields based on the receptive fields of their neighboring units along the electrode track. Due to the retinotopic organization of receptive fields in the dLGN, units with close-by receptive fields in the visual field will be located close-by along the probe track in the dLGN (Fig. 2c, d; Supplementary Fig. 6). We estimated missing receptive field locations in several steps. First, if one other unit was recorded on the same site and showed a receptive field, we estimated the missing receptive field center to be in the same location. If multiple units were recorded on the same site, we calculated the missing receptive field as the average of all receptive fields of units from the same site. If there were no other units recorded on the same site, we successively increased the distance along the probe to find neighboring units (up to a distance of ±70 μm along the probe). If a unit had one or more neighboring units along the probe, we calculated the estimated receptive field center as the average of all neighbors’ receptive fields, if the maximum pairwise distance between all considered neighbors was <34°. We obtained this value as the 95th percentile of all pairwise distances of neighboring units with known receptive fields within 140 μm along the probe track. We did not estimate receptive fields of units that had no neighboring units with defined receptive fields within 70 μm along the probe.
We validated this method by estimating receptive field centers of units with a known receptive field and calculated the error between the real and estimated receptive field location, resulting in a median error of 7.4° (Supplementary Fig. 6c-d)).
Direction, axis and orientation selectivity
Direction- and orientation-selectivity were determined based on the responses to moving gratings. Direction-selectivity was quantified using a global direction-selectivity index (gDSI), which was calculated as the normalized vector sum according to \({gDSI}=\frac{|\sum {{R}_{\theta }}^{i\theta }|}{\sum {R}_{\theta }}\), where Rθ represents the mean spike count during 4 sec of grating presentation in direction θ. The gDSI can take values between 0 and 1, with higher values corresponding to more sharply tuned cells. The preferred direction was defined as the phase of the complex number of the vector sum.
We additionally calculated a direction selectivity index (DSI) as \({DSI}=\frac{{R}_{{PD}}-{R}_{{ND}}}{{R}_{{PD}}+{R}_{{ND}}}\), where RPD represents the mean spike count in the direction closest to the preferred direction, and RND the spike count in the direction opposite to it. Orientation-selectivity was quantified similarly using a global orientation-selectivity index (gOSI) calculated as, \({gOSI}=\frac{|\sum {{R}_{\theta }}^{2i\theta }|}{\sum {R}_{\theta }}\), where the preferred orientation was defined as half the phase of the complex number. Additionally, we calculated an orientation-selectivity index (OSI) as \({OSI}=\frac{{R}_{{PO}}-{R}_{{NO}}}{{R}_{{PO}}+{R}_{{NO}}}\), where RPO is the mean spike count in the orientation closest to the preferred orientation (defined by two directions 180° apart), and RNO the mean spike count in the orientation orthogonal to it. Note that for direction-selectivity, we consider the motion direction and present polar plots according to the motion, while for orientation-selective cells we consider the stimulus orientations (orthogonal to the motion direction), and therefore present orientations in the figures. Motion directions are represented in world coordinates as posterior, anterior, inferior and superior in all figures.
Units were classified as DS if they filled all following criteria: (1) their gDSI of the mean response exceeded 0.15; (2) they were significantly DS based on a permutation shuffling test (ɑ=0.01); (3) their DSI exceeded 0.3; (4) their mean firing rate and maximum firing during stimulus presentation rate each exceeded 1 Hz, (5) they had a gDSI>0.15 in at least 4/5 trials to ensure consistently tuned responses across trials, and (6) a gDSI>gOSI. OS units were defined analogously, with gOSI≥0.15 and OSI ≥ 0.3. When removing criterion #6, the results of the study did not change.
To calculate proportions of DS and OS units in each LGN subregion, we only included recordings with at least 5 responsive units in each respective area. Percentages of DS or OS units were calculated from the total number of light-responsive single units, and were calculated as the weighted mean, where each recording was weighted by the total number of light-responsive units in it. Statistical comparisons between control and DT percentages were performed using bootstrapping analysis. For that, we drew 1000 random samples of n = 200 units each out of the entire control population (spanning all recordings), and calculated the percentage of DS or OS units for each sample. p-values were calculated as the percentile of the sampling distribution defined by the percentage of DS (or OS) units in DT condition.
Tuning width
To quantify tuning width of DS cells in degrees, we aligned each unit’s tuning curve to its preferred direction. We calculated the response amplitude as the difference between minimum and maximum response and calculated the width of the curve at half-maximum response amplitude using an upsampled response. Similarly for OS units, we calculated the tuning width of both components of the preferred orientation, and report the average of both as the tuning width. Statistical comparison was done using Wilcoxon rank sum test.
Spatial binning and statistical comparison of proportion of DS and OS units
To create spatial bins in the visual field, we divided the visual field into bins of 10°. To calculate the proportion of DS units out of all units in the dLGN-shell (Fig. 2g right), we included units with receptive fields as well as those units where we estimated the receptive fields center based on neighboring units along the probe track (see above). The proportion of DS units was calculated as the proportion of DS units out of the total number of units with receptive fields located in each bin. Spatial bins without any recorded units are displayed in gray. To quantify whether certain bins had a higher or lower proportion of DS units than what would be expected by chance, we performed shuffling analysis. For that, we randomly assigned DS identity (1 or 0) according to the known total percentage of DS units to existing receptive fields, and obtained a distribution of DS percentages for each spatial bin as expected by chance from 1000 shuffles. p-values were calculated as the percentile of the shuffled distribution of DS percentages determined by the observed percentage. Accordingly, we labeled bins with a significant over- or under-representation compared to chance level in the figure as § and *, respectively, using a threshold of α = 0.025 for two-sided comparison. For bins with <5 units the asterisks are shown in gray.
The same analysis was performed for OS units after excluding units within 5° of the screen’s edge (see Analysis of Edge induced OS responses). For Supplementary Fig. 15b, c we used a bin size of ~10°. For Supplementary Fig. 15d–g, we separated OS units into subgroups based on their preferred orientation (using equally sized bins of ±22.5° around the orientations 0, 45, 90 and 135°) and used smaller spatial bins of ~8°.
Analysis of optic flow
To model translatory optic flow we considered a spherical, 3-dimensional coordinate system with the mouse located at the origin (Fig. 2j). For purely translational optic flow, the flow vector field will emanate from the focus of expansion and follow the lines of longitude15,59,93 (Fig. 2j, red lines). The focus of expansion was defined as the point on the sphere along the vector of motion. We then projected the optic flow vectors onto a 2-dimensional plane defined by the screen by calculating their points of intersection with a plane defined by the screen and calculated the optic flow specifically at each DS unit’s receptive field center location (Fig. 2k, black arrows). We then performed vertical shifts (defined by angles) of DS units’ receptive field centers and the vectors defining their preferred directions, and projected the shifted points back onto their new location on the 2D-plane (e.g., Fig. 2l; Supplementary Fig. 10). For each gaze elevation we then calculated the angular difference between DS units’ preferred direction and the expected translatory optic flow at their receptive field center location (Fig. 2m, Supplementary Fig. 10).
Translatory optic flow along the gravitational axis (Supplementary Fig. 9c, d) was calculated analogously, but with the focus of expansion placed above the mouse.
Analysis of edge induced OS responses
To analyze the effect of the screen’s edge on preferred orientations, we set a threshold of 5° around the screen’s edges. We separately analyzed the preferred orientations of units whose receptive field center was located within 5° of the vertical and the horizontal edges. For later analyses, we only included units with receptive fields located in the screen center (>5° distance from all edges). For Fig. 6e–g, we compare preferred orientations of OS units whose receptive fields are located in the same area in visual space (−5-0° azimuth).
MEA recordings
Multi-electrode array (MEA) recordings of the isolated retina were performed using MEAs from MultiChannel Systems (MultiChannel Systems, Reutlingen, Germany; 252 electrodes, 30 μm diameter, 100 μm minimal electrode spacing). Before the recording, mice were dark adapted for at least 30 min. All procedures were performed in darkness or under dim red light or infrared illumination. Mice were anesthetized with isoflurane (Terrell, Piramal Critical Care Inc.) and decapitated. Immediately after, eyes were enucleated and placed in Ames solution (8.8 g/l, USBiological, Salem, MA, USA, CAT: A1372-25) supplemented with 1.9 g/l sodium bicarbonate (Sigma-Aldrich/Merck, Darmstadt, Germany, CAT: S5761-500G) and saturated with carboxygen (95% O2 and 5% CO2). The lens was removed, and the retina was cut in two halves along the naso-temporal axis using retinal landmarks for orientation94. The retina was then removed from the eyecup, and placed on a MEA (precoated with poly-D-lysine for 1 hour (PDL, 1.0 mg/ml in H2O, Merck-Millipore, CAT: A-003-E) with ganglion cells facing down (previously described in95,96,97,98). Throughout the dissection, the orientation of the retina was tracked to allow for the alignment of stimulus directions to retinal coordinates.
The MEA was placed in the headstage, a constant perfusion of oxygenated Ames solution was set up, and the bath temperature was maintained at 32–33 °C. Retinas were allowed to adapt for 1 hour before the start of the recording. Extracellular voltage signals were amplified and digitized at 20 kHz and saved for offline analysis.
Visual stimuli in MEA experiments
Visual stimuli were created using a custom-written GUI in Matlab using PsychToolbox (The MathWorks, Natick, MA, USA; Psychophysics Toolbox84,85). Visual stimuli were projected onto the retina via a monochromatic OLED display (eMagin, EMA-100309-01 SVGA+ , 600 × 800 pixels, 60 Hz refresh rate) through a telecentric lens (Edmund optics, Barrington, NJ USA, ×2.0, no. 58-431) focused onto the photoreceptor layer, resulting in a pixel size of 7.5 μm on the retina. At maximum brightness, the irradiance was 2.6 μW/cm2, resulting in 2.43 × 104 mouse rod isomerizations (R*rod−1s−1, corresponding to photopic regime), whereas minimum brightness was 70.4 R*rod−1s−1.
A battery of full-field visual stimuli was presented to characterize RGC responses. To probe directional responses, we presented square wave sinusoidal moving gratings of 0.075 cycle/°, moving at 2 Hz in eight different directions in a pseudo-random order. Gratings were presented for 4 s, with 2 s of mean gray intensity between each presentation. We additionally presented a full-field ‘chirp’ stimulus96 (adapted from 1), consisting of 2 s steps of varying contrasts, a full-field flicker of increasing contrast presented at 2 Hz, and a full-field flicker of maximum contrast with increasing temporal frequency (0.5–8 Hz) to quantify the quality of light responses in DT injected mice. All stimuli were presented for 5 repetitions.
MEA analysis
Spike sorting of MEA data was performed using Kilosort 2.089 with subsequent manual curation in Phy90,91. We only included well separated single units (see above for in vivo Neuropixel recordings).
Cells were defined as light responsive if their mean firing rate exceeded 1 Hz and their RQI calculated for moving gratings and the ‘chirp’ stimulus (see above) exceeded 0.25 for at least one of the stimuli.
Direction-and orientation-selectivity for MEA recordings
For ex vivo retinal recordings, the presented directions were aligned according to retinal cardinal directions (nasal, dorsal, temporal, ventral) according to a picture of the retina on the MEA taken after each experiment. In all figures presenting retinal recordings, directions are presented in retinal coordinates as opposed to world coordinates (dorsal, ventral, nasal, temporal on the retina, corresponding to inferior, superior, posterior and anterior in world coordinates, respectively, as used for in vivo recordings). Direction- and orientation-selectivity in the retina were quantified the same as those for LGN units, and the same criteria were used to define DS and OS cells (see above). Statistical comparison between control and DT retinas was done using bootstrapping analysis as for the Neuropixel recordings.
Intraocular injections
Intraocular injections were performed to P38-67 mice of both sexes. Mice were anesthetized using isoflurane, and anesthesia was maintained using a nose cone (SomnoSuite, Kent Scientific, 1.5–1.8% isoflurane, flow rate 25–35 ml/min). Eye drops with local anesthetic were applied (Localin, Dr. Fischer, Fischer Pharmaceutical Labs, Tel Aviv, Israel). Using a 32 G hypodermic needle, a small hole was poked at the area of the ora serrata. A glass pipette (Sutter Instrument, Novato, CA, USA, Cat: BF150-86-10) containing diphtheria toxin (1 ng DT (Merck/Sigma-Aldrich, Darmstadt, Germany; D0564-1MG) in 2 μl PBS) was then inserted through the hole using a handheld micromanipulator, and the solution was slowly injected using pressurized air controlled by a PicoPump (PV 820, World Precision Instruments, Sarasota, FL, USA). 14 days after injection, retinas were processed for immunohistochemistry and/or MEA experiments. For Supplementary Fig. 13, wild-type control retinas were not injected, and DT control retinas were obtained from ChATCre(-);DTR(+) mice injected with DT.
Retina immunohistochemistry
For IHC, retinas were dissected similarly to those for MEA experiments. For wholemount retinal staining, the lens was removed and a small cut was made according to retinal landmarks to keep track of the orientation. Retinas from MEA experiments were carefully removed from the MEA after the recording for verification of SAC ablation. Retinas were fixed in 4% paraformaldehyde (PFA; ChemCruz, Santa Cruz Biotechnology, Inc., CAS: 30525-89-4) at 4 °C for 1 hour, and then washed in phosphate buffered saline (PBS; Biological Industries Israel, 02-023-1 A, pH 7.4). Retinas were then blocked in 0.25% PBST (PBS + Triton X-100, Sigma, CAS: 9002-93-1) with 3% bovine serum albumin (BSA; MP Biomedicals, Cat no. 160069) for 3 h at room temperature on shaker, and then incubated for 3–5 days in primary antibody solution (1% BSA and 0.1% Triton X-100 in PBS) with primary antibody (anti-Choline Acetyltransferase Antibody, Merck, Darmstadt, Germany; CAT: AB144-P-200UL, dilution: 1:150) at 4 °C on shaker. The next day, retinas were washed in PBS (4x, >1 hour each), and were then incubated in PBS with secondary antibody (Alexa Fluor 488 AffiniPure Donkey Anti-Goat IgG (H + L), Jackson ImmunoResearch Laboratories Inc., Code: 705-545-147; dilution: 1:200) overnight at 4 °C. The next day, retinas were washed in PBS (4x, >1 hour each) and mounted on microscope slides using anti-fade mounting medium (Vectashield HardSet Antifade mounting medium with DAPI, Vector Laboratories Inc., Newark, California, USA, no H-1500-10).
Retinal wholemounts were imaged using an inverted laser scanning confocal microscope (Zeiss LSM 880 confocal, Zeiss, Oberkochen, Germany) using the software ZEN. Whole-mount retinal scans were recorded as a tile-scan and z-stack using a 10x EC Plan-Neofluar 10x/0.30 M27 objective. Close-ups were recorded using a 25x LD LCI Plan-Apochromat 25x/0.8 Imm Korr DIC M27 objective. Further image processing was performed in Fiji86.
Cell segmentation and density analysis
Cell segmentation was performed using Cellpose version 2.099. We first created maximum intensity projections of wholemount retinal tile scans in Fiji, which included SACs of both the ON and OFF layer. In Matlab, we created masks for each retina using a custom-written algorithm and cropped each masked image into smaller tiles of 512×512 px to allow for better processing through Cellpose. We ran Cellpose on the small images (using the pretrained model with model_type=‘cyto’). Resulting masks were loaded into Matlab for counting the number of cells and calculating resulting mean densities for each retina. Statistical comparison of SAC densities was performed using one-way ANOVA.
Statistical analysis
Statistical tests are mentioned where applicable. Statistical significance was accepted at α = 0.05. Notation of p-values is according to *p < 0.05, **p < 0.01, ***p < 0.001; ****p < 0.0001. For Neuropixel recordings, we report the number of units as n, and the number of recordings as N.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
Source data are provided with this paper. The data generated in this study have been deposited in the Zenodo database under accession code https://doi.org/10.5281/zenodo.16983454100. Source data are provided with this paper.
Code availability
We prove the code to generate the figures together with the data in the Zenodo database under accession code https://doi.org/10.5281/zenodo.16983454100.
References
Baden, T. et al. The functional diversity of retinal ganglion cells in the mouse. Nature 529, 345–350 (2016).
Masland, R. H. The fundamental plan of the retina. Nat. Neurosci. 4, 877–886 (2001).
Nath, A. & Schwartz, G. W. Cardinal orientation selectivity is represented by two distinct ganglion cell types in mouse retina. J. Neurosci. 36, 3208–3221 (2016).
Nath, A. & Schwartz, G. W. Electrical synapses convey orientation selectivity in the mouse retina. Nat. Commun. 8, 2025 (2017).
Hillier, D. et al. Causal evidence for retina-dependent and -independent visual motion computations in mouse cortex. Nat. Neurosci. 20, 960–968 (2017).
Vlasits, A. L. et al. Visual stimulation switches the polarity of excitatory input to starburst amacrine cells. Neuron 83, 1172–1184 (2014).
Yoshida, K. et al. A key role of starburst amacrine cells in originating retinal directional selectivity and optokinetic eye movement. Neuron 30, 771–780 (2001).
Dhande, O. S., Stafford, B. K., Lim, J.-H. A. & Huberman, A. D. Contributions of retinal ganglion cells to subcortical visual processing and behaviors. Annu. Rev. Vis. Sci. 1, 291–328 (2015).
Masland, R. H. The neuronal organization of the retina. Neuron 76, 266–280 (2012).
Wässle, H. Parallel processing in the mammalian retina. Nat. Rev. Neurosci. 5, 747–757 (2004).
Gupta, D. et al. Panoramic visual statistics shape retina-wide organization of receptive fields. Nat. Neurosci. 26, 606–614 (2023).
Heukamp, A. S., Warwick, R. A. & Rivlin-Etzion, M. Topographic variations in retinal encoding of visual space. Annu. Rev. Vis. Sci. 6, 237–259 (2020).
Kim, I.-J., Zhang, Y., Yamagata, M., Meister, M. & Sanes, J. R. Molecular identification of a retinal cell type that responds to upward motion. Nature 452, 478–482 (2008).
Warwick, R. A., Kaushansky, N., Sarid, N., Golan, A. & Rivlin-Etzion, M. Inhomogeneous encoding of the visual field in the mouse retina. Curr. Biol. 28, 655–665.e3 (2018).
Sabbah, S. et al. A retinal code for motion along the gravitational and body axes. Nature 546, 492–497 (2017).
Tiriac, A. & Feller, M. B. Roles of visually evoked and spontaneous activity in the development of retinal direction selectivity maps. Trends Neurosci. 45, 529–538 (2022).
Vita, D. J., Orsi, F. S., Stanko, N. G., Clark, N. A. & Tiriac, A. Development and organization of the retinal orientation selectivity map. Nat. Commun. 15, 4829 (2024).
Laniado, D. D., Maron, Y., Gemmer, J. A. & Sabbah, S. A spherical code of retinal orientation selectivity enables decoding in ensembled and retinotopic operation. Cell Rep. 44, 115373 (2025).
Kerschensteiner, D. Feature detection by retinal ganglion cells. Annu. Rev. Vis. Sci. 8, 135–169 (2022).
Monavarfeshani, A., Sabbagh, U. & Fox, M. A. Not a one-trick pony: Diverse connectivity and functions of the rodent lateral geniculate complex. Vis. Neurosci. 34, E012 (2017).
Delogu, A. et al. Subcortical visual shell nuclei targeted by ipRGCs develop from a Sox14+-GABAergic progenitor and require Sox14 to regulate daily activity rhythms. Neuron 75, 648–662 (2012).
Fratzl, A. et al. Flexible inhibitory control of visually evoked defensive behavior by the ventral lateral geniculate nucleus. Neuron 109, 3810–3822.e9 (2021).
Salay, L. D. & Huberman, A. D. Divergent outputs of the ventral lateral geniculate nucleus mediate visually evoked defensive behaviors. Cell Rep. 37, 109792 (2021).
Huberman, A. D. et al. Genetic identification of an On-Off direction-selective retinal ganglion cell subtype reveals a layer-specific subcortical map of posterior motion. Neuron 62, 327–334 (2009).
Jiang, Q. et al. Functional convergence of on-off direction-selective ganglion cells in the visual thalamus. Curr. Biol. 32, 3110–3120.e6 (2022).
Rivlin-Etzion, M. et al. Transgenic mice reveal unexpected diversity of on-off direction-selective retinal ganglion cell subtypes and brain structures involved in motion processing. J. Neurosci. 31, 8760–8769 (2011).
Piscopo, D. M., El-Danaf, R. N., Huberman, A. D. & Niell, C. M. Diverse visual features encoded in mouse lateral geniculate nucleus. J. Neurosci. 33, 4642–4656 (2013).
Kay, J. N. et al. Retinal ganglion cells with distinct directional preferences differ in molecular identity, structure, and central projections. J. Neurosci. 31, 7753–7762 (2011).
Kim, I.-J., Zhang, Y., Meister, M. & Sanes, J. R. Laminar restriction of retinal ganglion cell dendrites and axons: subtype-specific developmental patterns revealed with transgenic markers. J. Neurosci. 30, 1452–1462 (2010).
Vega-Zuniga, T. et al. A thalamic hub-and-spoke network enables visual perception during action by coordinating visuomotor dynamics. Nat. Neurosci. 28, 627–639 (2025).
Hammer, S., Monavarfeshani, A., Lemon, T., Su, J. & Fox, M. A. Multiple retinal axons converge onto relay cells in the adult mouse thalamus. Cell Rep. 12, 1575–1583 (2015).
Morgan, J. L., Berger, D. R., Wetzel, A. W. & Lichtman, J. W. The fuzzy logic of network connectivity in mouse visual thalamus. Cell 165, 192–206 (2016).
Morgan, J. L. & Lichtman, J. W. An individual interneuron participates in many kinds of inhibition and innervates much of the mouse visual thalamus. Neuron 106, 468–481.e2 (2020).
Müllner, F. E. & Roska, B. Individual thalamic inhibitory interneurons are functionally specialized toward distinct visual features. Neuron 112, 2765–2782.e9 (2024).
Rompani, S. B. et al. Different modes of visual integration in the lateral geniculate nucleus revealed by single-cell-initiated Transsynaptic tracing. Neuron 93, 767–776.e6 (2017).
Liang, L. et al. A fine-scale functional logic to convergence from retina to thalamus. Cell 173, 1343–1355.e24 (2018).
Marshel, J. H., Kaye, A. P., Nauhaus, I. & Callaway, E. M. Anterior-posterior direction opponency in the superficial mouse lateral geniculate nucleus. Neuron 76, 713–720 (2012).
Scholl, B., Tan, A. Y. Y., Corey, J. & Priebe, N. J. Emergence of orientation selectivity in the Mammalian visual pathway. J. Neurosci. 33, 10616–10624 (2013).
Sun, W., Tan, Z., Mensh, B. D. & Ji, N. Thalamus provides layer 4 of primary visual cortex with orientation- and direction-tuned inputs. Nat. Neurosci. 19, 308–315 (2016).
Zhao, X., Chen, H., Liu, X. & Cang, J. Orientation-selective responses in the mouse lateral geniculate nucleus. J. Neurosci. 33, 12751–12763 (2013).
Liang, Y., Lu, R., Borges, K. & Ji, N. Stimulus edges induce orientation tuning in superior colliculus. Nat. Commun. 14, 4756 (2023).
Hubel, D. H. & Wiesel, T. N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol. 160, 106–154 (1962).
Ciftcioglu, U. M., Suresh, V., Ding, K. R., Sommer, F. T. & Hirsch, J. A. Visual information processing in the ventral division of the mouse lateral geniculate nucleus of the thalamus. J. Neurosci. 40, 5019–5032 (2020).
Reese, B. E. Hidden lamination” in the dorsal lateral geniculate nucleus: the functional organization of this thalamic region in the rat. Brain Res. 472, 119–137 (1988).
Reese, B. E. & Jeffery, G. Crossed and uncrossed visual topography in dorsal lateral geniculate nucleus of the pigmented rat. J. Neurophysiol. 49, 877–885 (1983).
Pfeiffenberger, C. et al. Ephrin-As and neural activity are required for eye-specific patterning during retinogeniculate mapping. Nat. Neurosci. 8, 1022–1027 (2005).
Chan, Y.-C. & Chiao, C.-C. Effect of visual experience on the maturation of ON-OFF direction selective ganglion cells in the rabbit retina. Vis. Res. 48, 2466–2475 (2008).
Ankri, L., Riccitelli, S. & Rivlin-Etzion, M. A new role for excitation in the retinal direction-selective circuit. J. Physiol. https://doi.org/10.1113/JP286581 (2024).
Krahe, T. E., El-Danaf, R. N., Dilger, E. K., Henderson, S. C. & Guido, W. Morphologically distinct classes of relay cells exhibit regional preferences in the dorsal lateral geniculate nucleus of the mouse. J. Neurosci. 31, 17437–17448 (2011).
Howarth, M., Walmsley, L. & Brown, T. M. Binocular integration in the mouse lateral geniculate nuclei. Curr. Biol. 24, 1241–1247 (2014).
Zhu, J. J., Uhlrich, D. J. & Lytton, W. W. Properties of a hyperpolarization-activated cation current in interneurons in the rat lateral geniculate nucleus. Neuroscience 92, 445–457 (1999).
Seabrook, T. A., Krahe, T. E., Govindaiah, G. & Guido, W. Interneurons in the mouse visual thalamus maintain a high degree of retinal convergence throughout postnatal development. Neural Dev. 8, 24 (2013).
Tiriac, A., Bistrong, K., Pitcher, M. N., Tworig, J. M. & Feller, M. B. The influence of spontaneous and visual activity on the development of direction selectivity maps in mouse retina. Cell Rep. 38, 110225 (2022).
El-Danaf, R. N. & Huberman, A. D. Sub-topographic maps for regionally enhanced analysis of visual space in the mouse retina. J. Comp. Neurol. 527, 259–269 (2019).
Buch, T. et al. A Cre-inducible diphtheria toxin receptor mediates cell lineage ablation after toxin administration. Nat. Methods 2, 419–426 (2005).
Krizan, J. et al. Predation without direction selectivity. Proc. Natl. Acad. Sci. USA 121, e2317218121 (2024).
Rasmussen, R., Matsumoto, A., Dahlstrup Sietam, M. & Yonehara, K. A segregated cortical stream for retinal direction selectivity. Nat. Commun. 11, 831 (2020).
Holmgren, C. D. et al. Visual pursuit behavior in mice maintains the pursued prey on the retinal region with least optic flow. Elife 10, e70838, (2021).
Longuet-Higgins, H. C. & Prazdny, K. The interpretation of a moving retinal image. Proc. R. Soc. B: Biol. Sci. 208, 385–397 (1980).
de Malmazet, D., Kühn, N. K. & Farrow, K. Retinotopic separation of nasal and temporal motion selectivity in the mouse superior colliculus. Curr. Biol. 28, 2961–2969.e4 (2018).
Litvina, E. Y. & Chen, C. Functional convergence at the retinogeniculate synapse. Neuron 96, 330–338.e5 (2017).
Sonoda, T., Jiang, Q., Ledesma, H. A., Wei, W. & Chen, C. Transmission of mixed convergent signals at the mouse retinogeniculate synapse. BioRxiv https://doi.org/10.1101/2024.08.01.606255 (2024).
Lien, A. D. & Scanziani, M. Cortical direction selectivity emerges at convergence of thalamic synapses. Nature 558, 80–86 (2018).
Suresh, V. et al. Synaptic contributions to receptive field structure and response properties in the rodent lateral geniculate nucleus of the thalamus. J. Neurosci. 36, 10949–10963 (2016).
Rasmussen, R. N., Matsumoto, A., Arvin, S. & Yonehara, K. Binocular integration of retinal motion information underlies optic flow processing by the cortex. Curr. Biol. 31, 1165–1174.e6 (2021).
Wang, H. et al. Parallel pathways carrying direction-and orientation-selective retinal signals to layer 4 of the mouse visual cortex. Cell Rep. 43, 113830 (2024).
Osterhout, J. A., Stafford, B. K., Nguyen, P. L., Yoshihara, Y. & Huberman, A. D. Contactin-4 mediates axon-target specificity and functional development of the accessory optic system. Neuron 86, 985–999 (2015).
Sun, L. O. et al. Functional assembly of accessory optic system circuitry critical for compensatory eye movements. Neuron 86, 971–984 (2015).
Yonehara, K. et al. Congenital nystagmus gene FRMD7 is necessary for establishing a neuronal circuit asymmetry for direction selectivity. Neuron 89, 177–193 (2016).
Inayat, S. et al. Neurons in the most superficial lamina of the mouse superior colliculus are highly selective for stimulus direction. J. Neurosci. 35, 7992–8003 (2015).
Ito, S., Feldheim, D. A. & Litke, A. M. Segregation of Visual Response Properties in the Mouse Superior Colliculus and Their Modulation during Locomotion. J. Neurosci. 37, 8428–8443 (2017).
Reinhard, K. et al. A projection specific logic to sampling visual inputs in mouse superior colliculus. Elife 8, e50697, (2019).
Shi, X. et al. Retinal origin of direction selectivity in the superior colliculus. Nat. Neurosci. 20, 550–558 (2017).
Cang, J., Savier, E., Barchini, J. & Liu, X. Visual function, organization, and development of the mouse superior colliculus. Annu. Rev. Vis. Sci. 4, 239–262 (2018).
Li, C. et al. Pathway-specific inputs to the superior colliculus support flexible responses to visual threat. Sci. Adv. 9, eade3874 (2023).
Rasmussen, R. & Yonehara, K. Contributions of retinal direction selectivity to central visual processing. Curr. Biol. 30, R897–R903 (2020).
Pearson, J. T. & Kerschensteiner, D. Ambient illumination switches contrast preference of specific retinal processing streams. J. Neurophysiol. 114, 540–550 (2015).
Tikidji-Hamburyan, A. et al. Retinal output changes qualitatively with every change in ambient illuminance. Nat. Neurosci. 18, 66–74 (2015).
Rousso, D. L. et al. Two pairs of ON and OFF retinal ganglion cells are defined by intersectional patterns of transcription factor expression. Cell Rep. 15, 1930–1944 (2016).
Ivanova, E., Hwang, G. S. & Pan, Z. H. Characterization of transgenic mouse lines expressing Cre recombinase in the retina. Neuroscience 165, 233–243 (2010).
Jun, J. J. et al. Fully integrated silicon probes for high-density recording of neural activity. Nature 551, 232–236 (2017).
Stahl, J. S., van Alphen, A. M. & De Zeeuw, C. I. A comparison of video and magnetic search coil recordings of mouse eye movements. J. Neurosci. Methods 99, 101–110 (2000).
Sterratt, D. C., Lyngholm, D., Willshaw, D. J. & Thompson, I. D. Standard anatomical and visual space for the mouse retina: computational reconstruction and transformation of flattened retinae with the Retistruct package. PLoS Comput. Biol. 9, e1002921 (2013).
Brainard, D. H. The Psychophysics Toolbox. Spat. Vis. 10, 433–436 (1997).
Pelli, D. G. The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat. Vis. 10, 437–442 (1997).
Schindelin, J. et al. Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682 (2012).
Shamash, P., Carandini, M., Harris, K. D. & Steinmetz, N. A. A tool for analyzing electrode tracks from slice histology. BioRxiv https://doi.org/10.1101/447995 (2018).
Wang, Q. et al. The allen mouse brain common coordinate framework: A 3D reference atlas. Cell 181, 936–953.e20 (2020).
Pachitariu, M., Steinmetz, N., Kadir, S., Carandini, M. & Harris, K. D. Kilosort: realtime spike-sorting for extracellular electrophysiology with hundreds of channels. BioRxiv https://doi.org/10.1101/061481 (2016).
Rossant, C. & Harris, K. D. Hardware-accelerated interactive data visualization for neuroscience in Python. Front Neuroinform. 7, 36 (2013).
Rossant, C. et al. Spike sorting for large, dense electrode arrays. Nat. Neurosci. 19, 634–641 (2016).
Karamanlis, D. et al. Nonlinear receptive fields evoke redundant retinal coding of natural scenes. Nature 637, 394–401 (2025).
Warren, W. H. in The senses: A comprehensive reference 219–230 (Elsevier, 2008). https://doi.org/10.1016/B978-012370880-9.00311-X.
Wei, W., Elstrott, J. & Feller, M. B. Two-photon targeted recording of GFP-expressing neurons for light responses and live-cell imaging in the mouse retina. Nat. Protoc. 5, 1347–1352 (2010).
Karamanlis, D. & Gollisch, T. Nonlinear spatial integration underlies the diversity of retinal ganglion cell responses to natural images. J. Neurosci. 41, 3479–3498 (2021).
Warwick, R. A., Heukamp, A. S., Riccitelli, S. & Rivlin-Etzion, M. Dopamine differentially affects retinal circuits to shape the retinal code. J. Physiol. 601, 1265–1286 (2023).
Warwick, R. A. et al. Top-down modulation of the retinal code via histaminergic neurons of the hypothalamus. Sci. Adv. 10, eadk4062 (2024).
Riccitelli, S., Yaakov, H., Heukamp, A. S., Ankri, L. & Rivlin-Etzion, M. Retinal ganglion cells encode the direction of motion outside their classical receptive field. Proc. Natl. Acad. Sci. USA 122, e2415223122 (2025).
Stringer, C., Wang, T., Michaelos, M. & Pachitariu, M. Cellpose: a generalist algorithm for cellular segmentation. Nat. Methods 18, 100–106 (2021).
Rivlin-Etzion, M. Dataset: Differential topographic organization and retinal inheritance of direction and orientation selectivity in the visual thalamus. Zenodo https://doi.org/10.5281/zenodo.16983454 (2025).
Acknowledgements
We thank Meital Oren-Suissa for providing her confocal microscope, Rony Dahan for providing the ROSA26iDTR mouse line, Sasha Devore, Yaniv Ziv and members of the Rivlin lab for helpful comments on the manuscript. This work was supported by research grants from the European Research Council (ERC starter No. 757732), the Israel Science Foundation (2449/20), the Minerva Foundation with funding from the Federal German Ministry for Education and Research. In addition, this research was generously supported by the Nella and Leon Benoziyo Center for Neurological Diseases, the Sagol Weizmann-MIT Bridge Program, the Swiss Society Center for Research on Perception and Action, and Mike and Valeria Rosenbloom Center for Research on Positive Neuroscience, the Azrieli Institute for Brain and Neural Sciences, and the Zuckerman Center for Research on Learning, Memory, and Cognition. A.S.H. was supported by the Minerva Fellowship, S.R. was supported by a Dean Fellowship of the Weizmann Institute of Science.
Author information
Authors and Affiliations
Contributions
H. Y., A. S. H. and M. R.-E. designed the experiments. H. Y. performed the in vivo experiments and brain histologies. A. S. H. and S. R. performed initial retinal experiments. A. S. H. performed the ex vivo experiments, intraocular injections and retinal IHC. A. S. H. and H. Y. conducted the analyses. H. Y., A. S. H. and M. R.-E. wrote the manuscript. All authors edited the manuscript and approved the final version.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Alexandre Tiriac who co-reviewed with Kaylee Yeager; and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Yaakov, H., Heukamp, A.S., Riccitelli, S. et al. Differential topographic organization and retinal inheritance of direction and orientation selectivity in the visual thalamus. Nat Commun 16, 9303 (2025). https://doi.org/10.1038/s41467-025-64321-1
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41467-025-64321-1