Introduction

Human Leukocyte Antigen (HLA) haplotype1, genetic risk score2, and family history3 are all strongly associated with T1D risk (AUC: 0.7–0.82)4. The concordance rate for monozygotic twins is about 50%, and perhaps that unknown environmental factors are also important for predicting T1D2,5 and may trigger the disease. Bovine serum albumin, from cow’s milk6,7 vitamin D8,9, and introduction of gluten10,11 are associated with onset of T1D. Bacteria and viruses such as enterovirus12 and respiratory infections were both associated with T1D and development of islet antibodies13, and the microbiome has been shown to potentially drive type one diabetes in NOD (non-obese diabetic) mice via hormone regulation14 and molecular mimicry15.

We hypothesized it is possible to predict type one diabetes with participant gut microbiota before autoantibodies become present. There is some evidence for microbiome predictors of inflammatory bowel disease16,17. The microbiome has also been associated with development of islet autoantibodies18 and T1D19,20 in retrospective case-control cohort scenarios. To our knowledge, one other study has attempted to predict future type one diabetes risk21. However, it only predicted T1D for children older than 30 months of age and had very modest predictive ability (AUC 0.58–0.63).

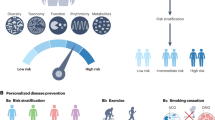
Often, the design of machine learning predictors focuses on developing a single predictor that optimizes prediction accuracy, such as area under the curve; however, in observational datasets, the study design parameters may be flexible, and flexibility may lead to over-optimistic predictions. Specification curves analysis is a method of comparing different results based on different analytical choices or specifications. Specification curve analysis has been used extensively to evaluate the effect that analytical choices and confounders can have on the reproducibility of results22,23. This is especially important in T1D where three studies on the same subjects gave different results due to methodological and analytical choices in the analysis18,19,24 (Supplementary Table 1). Here, we predicted T1D and autoantibodies for subjects of different ages and HLA haplotypes with different machine learning algorithms, clinical features, and feature selection methods (Fig. 1A).

Fig. 1: Analytical Pipeline Overview and an illustration of all specifications used in the study.
figure 1

A The step by step analytical pipeline performed for each specification. In bold are the different steps in the pipeline we vary for each specification. These include the phenotype being predicted, age, and HLA of the subject, the proportion of data being used for training, the feature selection method, and the machine learning model used for prediction. B A stacked bar-plot illustrating the specifications. The x-axis is the category of analytical choice made, and the y-axis is the percent of specifications that use a given analytical method in each stacked box. The boxes are colored by one of three studies previously done that associated type one diabetes with the microbiome (Supplementary Table 1) to illustrate the analytical choices other studies have done previously. Acronyms: fdr (is a first degree relative of someone with Type 1 Diabetes) grs2 (genetic risk score) healthy_pre-sero (specification in which seroconverters are compared to healthy individuals) number_AAs (number of autoantibodies) BRF (balanced random forest) RFQ (Random Forest Quantile Classifier).

Full size image

In this study, we aimed to test a bevy of microbiome characteristics and study designs to predict type one diabetes and antibody status. Microbiome characteristics included microbial genes, species, or pathways for 783 individuals longitudinally sampled from the TEDDY cohort19. To query the space of all possible predictors, we performed a specification curve analysis14,25. 72.5% of models in the specification curve analysis that only use microbial features as predictors has an area under the curve (AUC) of 0.5, and the “best” model has an AUC of 0.78. Together, these results show a large amount of variation in the predictive ability of the microbiome dependent on the choice of specifications.

Results

Creation of 11,189 specifications for robust prediction of future type 1 diabetes risk

To evaluate whether the microbiome’s ability to predict type one diabetes depends on different analytical choices (specifications) or is robust to them, we performed a specification analysis. With this method we chose a set of theoretically justified, statistically valid, and non-redundant specifications, predicted T1D and related phenotypes, and visualized results from all specifications together to evaluate how model and analytical choices affected prediction. At each stage in our machine learning pipeline we made different, equally valid, analytical choices. We predicted T1D, presence of one of three autoantibodies and seroconversion for all ages and for each of the following age groups: 6, 12, 18, 24 months, 6–12 months, 12–18 months, or 18–24 months old. We also chose all subjects regardless of HLA haplotype, or those only with one of the following HLAs: DR4/DR8, DR4/DR4, DR4/DR3, DR3/DR3. Due to the stratification, different specifications had different sample sizes (Supplementary Fig. 1). The average number of samples was 103 ∓ 71 and only specifications with at least 10 cases and 10 controls were used in the analysis. We also trained our models on either 50, 66, or 80 percent of the data, optionally performed feature selection with a t test, and used six different machine learning models to perform prediction: binary lasso regression, random forests, lasso regression using the cox model, random survival forests, logistic regression, and cox-regression. Due to the unbalanced nature of our cases and controls we also ran every model after either weighting or unweighting cases and controls by the proportion of samples they made up. We also used different features for prediction. For the microbiome, we used either gene, species, or pathway abundances, and for clinical variables we used family history, genetic risk score, number of autoantibodies, and sex. For binary models we predicted whether a subject would or would not get T1D, seroconvert, or obtain any one of the three major autoantibodies. For survival models we predicted whether a subject would get the condition one or three years in the future (Figs. 1B, 2). In total we varied eight different parameters in our pipeline, resulting in 11,189 specifications (Fig. 3A). Only 3.58% of these specifications have been performed in previous prospective association studies between T1D and the microbiome (Figs. 1B, 3A).

Fig. 2: Example specification curve.
figure 2

20 randomly sampled specifications to demonstrate a specification curve. The bottom panel is a heatmap where columns represent specifications and rows represent choices made in each specification. Purple cells represent the presence of a choice in a specification. The next panel “Study” shows specifications performed by other studies. The next panel “Sample Size” shows the number of samples in each specification. The top panel is a scatterplot where each red dot is the area under the receiver operating characteristic (ROC) curve for a specification, which measures how well a specification distinguishes cases from controls. The lines represent the 95% confidence intervals. Acronyms: fdr (is a first degree relative of someone with Type 1 Diabetes) grs2 (genetic risk score) healthy_pre-sero (specification in which seroconverters are compared to healthy individuals) BRF (balanced random forest) RFQ (Random Forest Quantile Classifier).

Full size image
Fig. 3: Specification curve and association between AUC and different analytical choices.
figure 3

A The specification curve. The bottom panel is a heatmap where each column is a different specification. Purple indicates the choice made for the specification. The panel labeled “Study” illustrates the specifications made by previous studies shown in Supplemental Table 1 that associate the microbiome with T1D. The panel labeled Sample Size represents the number of samples per specification. The top panel represents the AUC for each specification. The red dots represent the AUC-ROC. The top of the black line and bottom of the black line represent the 95% confidence interval of the AUC. B A forest plot illustrating the beta coefficients and significance of a linear model where the dependent variable is AUC and the independent variables are the choices made in each specification (i.e., row labels of the plot). *p < 0.05. **p < 0.01. ***p < 0.001. Blue text and lines indicate specification choices positively associated with AUC and red text and lines indicate specification choices negatively associated with AUC. Acronyms: fdr (is a first degree relative of someone with Type 1 Diabetes) grs2 (genetic risk score) healthy_pre-sero (specification in which seroconverters are compared to healthy individuals) BRF (balanced random forest) RFQ (Random Forest Quantile Classifier).

Full size image

Heterogeneity in type 1 diabetes predictions for all specifications

Through the specification curve analysis, we can evaluate how robust predictions are to changes in analytical choices and understand how each choice effects the predictions. We found large heterogeneity in type one diabetes and antibody predictions (Fig. 3A). The average AUC of the receiver operating characteristic (ROC) for all specifications was 0.60 and the average AUC for microbiome only models was 0.517. To quantify the predictive ability of each analytical choice in our specifications, we associated the AUC with the presence of each choice, where each choice was quantified as a categorical variable except sample size (Fig. 3B). We found that adding the number of autoantibodies as a predictor resulted in an increase in AUC of 0.15 (p = 3.69e-97) compared to our reference model where family history and genetic risk score were used as predictors. Furthermore, using only microbial features resulted in a decrease in AUC of 0.23 (p < 2.2e-16) compared to using family history and genetic risk score together (Supplementary Table 2). This pattern also held true when performing a specification analysis on specifications with over 300 samples (Supplementary Fig. 2A). The average AUC for microbiome only specifications was 0.52 and using microbial features only results in a decrease in AUC of 0.23, p < 2.2e-16, (Supplementary Fig. 2B). We also used Wilcoxon signed rank tests to directly compare specifications that shared all the same analytical choices except for the features used in prediction (i.e., microbial or clinical features). We found that microbiome only models have significantly lower AUCs (p < 2.3e-13) than complementary models that predict T1D with number of autoantibodies, family history, and genetic risk score (Supplementary Fig. 3). Together these data show that using the microbiome decreases predictive ability compared to methods that can be evaluated at birth.

In addition to the microbiome, we also checked how the size of our training dataset affected prediction. To interrogate how the percent of training data impacted prediction, we compared the AUC between specifications with all the same model choices except for the percentage of training data used to train the models. We found that using 66% and 80% of data for training gave a small but significant increase in AUC compared to using 50% of data for training (p = 2.3e-07 mean difference: 0.007 and p = 0.031; mean difference 0.006). However, there was no significant difference in AUC when comparing models using 66% and 80% of data for training (p = 0.2 mean difference 0.0007; Supplementary Fig. 4). We also compare the AUC between models similar in all other specification choices except whether to correct for imbalanced data by weighting observations based on the number of cases and controls. There was no significant difference in AUC between weighted and unweighted models in Random Forest methods (p = 0.72 and p = 0.68). For non-random forest methods, there was a significant difference in AUC (p = 9.3e-06), but the mean difference was −0.0017 indicating that weighting decreased AUC by a very small amount (Supplementary Fig. 5).

While the microbiome does not predict T1D, microbial genes consistently associated with type one diabetes and related phenotypes could be useful to understand the etiology of T1D. We counted the proportion of specifications that chose different microbial genes as significant predictors (absolute value of beta coefficient or importance greater than 0 in lasso regression or random forest models respectively). No microbiome genes, pathways, or taxa were found in greater than 50% of models (Fig. 4; Supplementary Fig. 6) providing evidence that the microbiome is not robustly associated with T1D before onset.

Fig. 4: The top microbial gene and taxonomy predictors.
figure 4

A The top 50 genes that were significant predictors of any T1D related phenotype (T1D, seroconversion, MIAA, IA2A, GAD autoantibody). The x-axis represents the proportion of total specifications the gene was significant in. B The top 50 taxa that were significant predictors of any T1D related phenotype (T1D, seroconversion, MIAA, IA2A, GAD autoantibody). The x-axis represents the proportion of total specifications the taxa was significant in.

Full size image

Discussion

Here we predicted future type one diabetes risk as a function of the gut microbiome. Instead of reporting one or a few models, we used a “specification curve analysis”, an approach to parameterize and systematically test all possible study design specifications25. We found a large amount of heterogeneity in our predictions that are dependent on clinical features used in the model, and, in general, that the microbiome is not predictive of prospective type one diabetes or seroconversion. Specifically, predicting T1D with the number of autoantibodies resulted in the most accurate predictions4, while predicting with the microbiome alone was less accurate than using family history and genetic risk factors.

Specification curve analysis allows investigators to quantify the role of participant level characteristics and variables (e.g., age) that influences predictions. This allows us to quantify the influence of all feasible study specifications and variables on prediction. In fact, we found that the metagenome led to worse prediction capability on average compared to the number of autoantibodies, which is part of the current best model for T1D prediction4. We believe prospective clinical predictions are therefore not enhanced by the microbiome.

The main drawback of this study was that low sample size left us underpowered to systematically probe all specifications. These could lead to findings that are biased, and lack of generalizability in new cohorts. Indeed, our power analysis showed that we would need 1783 samples to be well powered to make predictions using Cox regression models, but the gain in the AUC over variables such as family history would likely be modest. While increasing the sample size may have allowed us to detect subtle associations between the microbiome and T1D, they still pale in comparison to baseline predictors that can be taken at birth such as family history and genetic risk score4.

Similarly to sample size, low sequencing depth may also render us unable to detect lowly abundant genes or microbes. There is an average of 13.3 million reads per sample which is not enough to capture the full diversity of the microbiome26. This may cause us to miss lowly abundant but important microbes that could influence T1D risk27. However, given that lowly abundant microorganisms are less likely to be in the entire population, this is unlikely to influence prediction. Another factor that can influence our view of the microbiome is the clustering method we use to create the gene catalog. This step consists of finding open reading frames within the metagenomic samples and clustering them at a specific percent identity. Here we use 30% because homologous proteins can diverge up to 30% identity and at least one other gene catalog reports high quality clusters with 30% identity28,29. However, there is no consensus on the percent identity to use as no single cutoff can capture all biological boundaries and the number of genes in a gene catalog can differ based on the percent identity used for clustering30,31. As a result of the hard cutoff, some clusters may have genes with multiple functions, while other clusters should be combined together because they hold genes with the same functions. In previous work we showed that clustering at 30% captures all KEGG pathways, thus, we do not expect clustering thresholds to drastically change the interpretation of this manuscript30,31.

It is also important to note that the specification curve analysis is only as good as the specifications or analytical choices deemed feasible. As in any other computational analysis, it is possible we are missing an unknown microbial feature or potential interaction between different microbial features that would successfully predict type one diabetes.

Just because the metagenome cannot predict future T1D, does not mean the microbiome has no link to T1D. This manuscript is specifically focused on using gut metagenomics to prospectively predict T1D among high risk individuals two years of age and younger. Prediction naturally assumes that the metagenome predisposes individuals to diabetes. However, it is often thought that genetics predispose individuals, while environmental factors (such as the microbiome) trigger the disease32,33. To test this hypothesis one could perform a case only analysis where the microbiome is compared early in life to a period right before T1D onset. Thus, future work could focus on understanding acute changes in the microbiome right before onset rather than changes early in life that may predispose an individual to T1D.

In this manuscript, we saw a large heterogeneity in results based on the specification used for prediction. This begs the question, is there a “best” specification. This work was specifically designed to test if the microbiome could reliably predict type one diabetes despite different analytical choices. However, one could instead use a Specification Curve to test what analytical choices give the best predictions. Such a study could be used to evaluate the best analytical choices for a study that uses the microbiome to predict a phenotype, similarly to Le Goallec et al.34. This could lead to a list of “best practices” in microbiome analyses that could advance the reproducibility of methods used in the field and be a helpful resource for other researchers that want to perform microbiome association studies but are unsure of the best methods to use.

Associations between T1D and the microbiome are difficult to reproduce. A recent study was unable to replicate any of the 34 associations found in two different T1D cohorts35. Similarly three different studies on the TEDDY cohort18,19,24 found different taxa associated with islet autoantibodies and T1D (Supplemental Table 1). Each study made different analytical choices including sequencing method and microbial features being analyzed, phenotype being evaluated, computational model and confounding variables adjusted for, and age of subjects being studied, any or all of which could be responsible for variations in results (Figs. 1,  3A). As a result the clinical applicability of the microbiome is unclear. Here we show that the microbiome is not a useful predictor of future type one diabetes and, with small sample sizes, is on average, more likely to decrease predictive accuracy in comparison to clinical predictors such as family history, genetic risk score, or seroconversion.

Methods

Specifications

In a specification curve analysis, one tests how results change based on the use of different, theoretically justified, and statistically valid analytical choices, or specifications. Here we tested how the predictive ability of the microbiome changes based on the age and genetic susceptibility of individuals to T1D, the machine learning method used, and the type of microbial features used for prediction, along with many other analytical choices detailed below.

We predicted T1D and four related phenotypes including future seroconversion and presence of three different islet autoantibodies (GAD, IA2A, and MIAA). Metadata was customized for each phenotype being predicted and the age of the subjects we were predicting on. We also stratified the data based on the HLA haplotype of individuals. To evaluate variation in prediction due to train-test split proportions, we made three additional variations of our data, one where 50% of the subjects were put into the train group, and another where 66% of subjects were put into the train group, and a third where 80% of subjects were put into the train group. We used four different machine learning algorithms to evaluate variation in prediction due to machine learning algorithms. The four methods were LASSO cox-regression, random survival forests, LASSO logistic regression, and random forests. Weighted and unweighted versions of each algorithm were implemented as well (Supplementary Materials).

Age specifications and landmark-horizon analysis for longitudinal data

To incorporate the longitudinal aspect of the data into the modes we used landmark-horizon cox-regression models as done in a previous manuscript by the TEDDY Study Group4. In a landmark-horizon analysis, we train our data using samples under a certain age (landmark ages). Then we make predictions whether that subject will have the predicted phenotype at specific years in the future (horizons). This allows us to make full use of the longitudinal data by evaluating the age a child needs to be to accurately predict their risk of type 1 diabetes.

Specifically, we created different models where we only trained on samples from subjects in a specific age range. These age ranges were less than or equal to 3 months, 6 months, 12 months, 18 months, and 24 months or between 6 and 12 months of age, 12 to 18 months of age, and 18 to 24 months of age. These age ranges are called landmark ages. Then we made predictions on whether a subject will get Type 1 Diabetes or will have an autoantibody 1 or 3 years into the future, which are the horizons. This landmark-horizon analysis allows us to evaluate how well we can predict T1D 1 or 3 years in the future in children of different ages.

For the binary classification methods, we used different baseline ages as done for the cox-regression, but instead of predicting at specific years in the future, we predicted whether that subject would have T1D in the future or not.

For microbial features, the microbiome abundances from the same subject during the baseline age range were averaged together. Microbiome abundances from the same subject after the baseline age were also averaged together, such that we trained our models on the abundances during the baseline age and predicted using microbial abundances after the baseline age.

Machine learning model specifications

We used six different machine learning algorithms for each dataset to evaluate variation in prediction due to machine learning algorithms. These six machine learning methods can be separated into two main categories, binary classification and survival analysis. These two categories address slightly different questions. Survival analysis allows us to predict if someone will get a disease while accounting for time to that individual being “censored” (leaving the study as someone without T1D) or having T1D. Binary classification only predicts whether the subject will ever get the disease, regardless of the time of followup. The binary classification is simpler but does not take into account the varied times that an individual can get a disease, such as T1D. Therefore, we chose to incorporate both classification and survival approaches into this study.

As a baseline model for the survival method, we used a standard Cox regression model to fit clinical risk factor variables known to be predictive of T1D4 such as number of autoantibodies, genetic risk score, and family history of T1D. As a baseline model for binary classification, we fit a logistic regression model with the same clinical risk factor variables. These two models are meant to be used as baselines to test if models incorporating microbiome data improved the state of the art baseline model. To demonstrate whether microbiome models improved prediction accuracy over the clinical baseline we have plotted the difference in AUC between the baseline model and its respective microbiome model in predicting T1D using a Wilcoxon signed rank test (Supplementary Fig. 3).

In addition, we also wanted to compare the performance of non-linear models to linear models. For non-linear modeling, we used random forest models, specifically, random forests and random survival forests to perform binary and survival analysis respectively. To represent linear models, we used binary lasso regression and lasso-regularized cox-regression for binary classification and survival analysis respectively. Lasso regression was used to perform feature selection during training to (1) ovoid overfitting models during training and (2) to make accurate predictions even if features are correlated. LASSO accomplishes this by penalizing models that include more features, thus promoting sparse models. One consequence of this is that given two or more correlated variables, the LASSO algorithm will only choose one variable to represent the correlated set of variables36,37.

Feature selection specifications

Feature selection was performed in the training set (Fig. 1A). We performed the feature selection in two different ways: (1) by using lasso regression, where all features with a coefficient of greater than 0 were included in the model or (2) via t-test where we input genes significantly associated (BY adjusted p-value < 0.05) with T1D or autoantibodies into the model for training. In specifications where both lasso regression and t-tests were used, we first performed a t-test, inputting genes significantly associated (BY adjusted p-value < 0.05) with T1D or autoantibodies into the lasso-regularized model for training. In random forest methods, we only input genes significantly associated (BY adjusted p-value < 0.05) into the random forest model. If more than 100 genes were significantly associated with T1D or autoantibodies the top 100 features were chosen, ranked by p-value.

Specifications for imbalanced data

On the random forest models, we used two different types of weighting procedures. One was down sampling and the other was the random forests quantile-classifier38.

For the other models, we estimated weights by computing the frequencies of case to controls. Control observations received the weights of #cases/#controls while cases received the weight of 1- (#cases/#controls). As a result, the more unbalanced the dataset, the more influence the cases had over the model. We only used weights during the training procedure, and not when estimating the test data AUC.

T1D outcomes and predictors

We predicted T1D and related phenotypes with microbial and clinical features. Microbial features included species, pathways, and gene abundances. Clinical features include family history, genetic risk score, and sex (Supplementary Materials). All statistical analyses were performed in R, version 4.2.2. We visualized the AUC for all specifications using the ComplexHeatamp package. Any AUC values below 0.5 were rounded to 0.5 for downstream analysis and visualization.

Description of the specification curve figures

In Fig. 2 we display an example of our Specification Curve from Fig. 3A. This was constructed by randomly sampling 20 specifications and creating a Specification Curve from them (Fig. 2). In this example figure (as in Fig. 3A) the bottom panel displays a heatmap where column is a specification (model created for prediction) and the rows are the choices we make (e.g., the condition we are predicting, the machine learning method we use for prediction). The purple color in each cell represents the presence of the choice in the specification. For example, in the rightmost specification, the model is predicting the presence of a MIAA autoantibody as indicating by the purple color. The topmost panel is the “curve” in specification curve. This is a scatterplot where the red dots represent the area under the ROC curve for each prediction made by a specification. The lines extending from each red dot represents the 95% confidence interval. The confidence intervals are made through cross-validation on three train-test splits.

Statistical analysis

We performed all analyses using R version 4.1. Using multivariate regression models, we evaluated analytical choices that influence prediction as measured by AUC. We included the condition being predicted (T1D or autoantibodies) baseline age, HLA of subjects, the proportion of data used during training, the model used for prediction, the feature selection method, the type of microbiome features (species, gnes, or pathways) whether samples were weighted or unweighted, the number of samples, the type of features used for prediction (clinical or microbial) and the horizon time as covariates in the model. The equation is described below.

$${{{\rm{A}}}}{{{\rm{U}}}}{{{\rm{C}}}}\,= {\beta }_{{{{\rm{c}}}}{{{\rm{o}}}}{{{\rm{n}}}}{{{\rm{d}}}}{{{\rm{i}}}}{{{\rm{t}}}}{{{\rm{i}}}}{{{\rm{o}}}}{{{\rm{n}}}}}({{{{\rm{X}}}}}_{{{{\rm{c}}}}{{{\rm{o}}}}{{{\rm{n}}}}{{{\rm{d}}}}{{{\rm{i}}}}{{{\rm{t}}}}{{{\rm{i}}}}{{{\rm{o}}}}{{{\rm{n}}}}})+\\ {\beta }_{{{{\rm{b}}}}{{{\rm{a}}}}{{{\rm{s}}}}{{{\rm{e}}}}{{{\rm{l}}}}{{{\rm{i}}}}{{{\rm{n}}}}{{{\rm{e}}}}{{{\rm{a}}}}{{{\rm{g}}}}{{{\rm{e}}}}}({{{{\rm{X}}}}}_{{{{\rm{b}}}}{{{\rm{a}}}}{{{\rm{s}}}}{{{\rm{e}}}}{{{\rm{l}}}}{{{\rm{i}}}}{{{\rm{n}}}}{{{\rm{e}}}}{{{\rm{a}}}}{{{\rm{g}}}}{{{\rm{e}}}}})+\\ {\beta }_{{{{\rm{H}}}}{{{\rm{L}}}}{{{\rm{A}}}}}({{{{\rm{X}}}}}_{{{{\rm{H}}}}{{{\rm{L}}}}{{{\rm{A}}}}})+\\ {\beta }_{{{{\rm{p}}}}{{{\rm{r}}}}{{{\rm{o}}}}{{{\rm{p}}}}{{{\rm{o}}}}{{{\rm{r}}}}{{{\rm{t}}}}{{{\rm{i}}}}{{{\rm{o}}}}{{{\rm{n}}}}{{{\rm{t}}}}{{{\rm{r}}}}{{{\rm{a}}}}{{{\rm{i}}}}{{{\rm{n}}}}{{{\rm{i}}}}{{{\rm{n}}}}{{{\rm{g}}}}{{{\rm{d}}}}{{{\rm{a}}}}{{{\rm{t}}}}{{{\rm{a}}}}}({{{{\rm{X}}}}}_{{{{\rm{p}}}}{{{\rm{r}}}}{{{\rm{o}}}}{{{\rm{p}}}}{{{\rm{o}}}}{{{\rm{r}}}}{{{\rm{t}}}}{{{\rm{i}}}}{{{\rm{o}}}}{{{\rm{n}}}}{{{\rm{t}}}}{{{\rm{r}}}}{{{\rm{a}}}}{{{\rm{i}}}}{{{\rm{n}}}}{{{\rm{i}}}}{{{\rm{n}}}}{{{\rm{g}}}}{{{\rm{d}}}}{{{\rm{a}}}}{{{\rm{t}}}}{{{\rm{a}}}}})+\\ {\beta }_{{{{\rm{m}}}}{{{\rm{o}}}}{{{\rm{d}}}}{{{\rm{e}}}}{{{\rm{l}}}}}({{{{\rm{X}}}}}_{{{{\rm{m}}}}{{{\rm{o}}}}{{{\rm{d}}}}{{{\rm{e}}}}{{{\rm{l}}}}})+\\ {\beta }_{{{{\rm{f}}}}{{{\rm{e}}}}{{{\rm{a}}}}{{{\rm{t}}}}{{{\rm{u}}}}{{{\rm{r}}}}{{{\rm{e}}}}{{{\rm{s}}}}{{{\rm{e}}}}{{{\rm{l}}}}{{{\rm{e}}}}{{{\rm{c}}}}{{{\rm{t}}}}{{{\rm{i}}}}{{{\rm{o}}}}{{{\rm{n}}}}{{{\rm{m}}}}{{{\rm{e}}}}{{{\rm{t}}}}{{{\rm{h}}}}{{{\rm{o}}}}{{{\rm{d}}}}}({{{{\rm{X}}}}}_{{{{\rm{f}}}}{{{\rm{e}}}}{{{\rm{a}}}}{{{\rm{t}}}}{{{\rm{u}}}}{{{\rm{r}}}}{{{\rm{e}}}}{{{\rm{s}}}}{{{\rm{e}}}}{{{\rm{l}}}}{{{\rm{e}}}}{{{\rm{c}}}}{{{\rm{t}}}}{{{\rm{i}}}}{{{\rm{o}}}}{{{\rm{n}}}}{{{\rm{m}}}}{{{\rm{e}}}}{{{\rm{t}}}}{{{\rm{h}}}}{{{\rm{o}}}}{{{\rm{d}}}}})+\\ {\beta }_{{{{\rm{m}}}}{{{\rm{i}}}}{{{\rm{c}}}}{{{\rm{r}}}}{{{\rm{o}}}}{{{\rm{b}}}}{{{\rm{i}}}}{{{\rm{o}}}}{{{\rm{m}}}}{{{\rm{e}}}}{{{\rm{f}}}}{{{\rm{e}}}}{{{\rm{a}}}}{{{\rm{t}}}}{{{\rm{u}}}}{{{\rm{r}}}}{{{\rm{e}}}}{{{\rm{t}}}}{{{\rm{y}}}}{{{\rm{p}}}}{{{\rm{e}}}}}({{{{\rm{X}}}}}_{{{{\rm{m}}}}{{{\rm{i}}}}{{{\rm{c}}}}{{{\rm{r}}}}{{{\rm{o}}}}{{{\rm{b}}}}{{{\rm{i}}}}{{{\rm{o}}}}{{{\rm{m}}}}{{{\rm{e}}}}{{{\rm{f}}}}{{{\rm{e}}}}{{{\rm{a}}}}{{{\rm{t}}}}{{{\rm{u}}}}{{{\rm{r}}}}{{{\rm{e}}}}{{{\rm{t}}}}{{{\rm{y}}}}{{{\rm{p}}}}{{{\rm{e}}}}})+\\ {\beta }_{{{{\rm{w}}}}{{{\rm{e}}}}{{{\rm{i}}}}{{{\rm{g}}}}{{{\rm{h}}}}{{{\rm{t}}}}{{{\rm{e}}}}{{{\rm{d}}}}}({{{{\rm{X}}}}}_{{{{\rm{w}}}}{{{\rm{e}}}}{{{\rm{i}}}}{{{\rm{g}}}}{{{\rm{h}}}}{{{\rm{t}}}}{{{\rm{e}}}}{{{\rm{d}}}}})+\\ {\beta }_{{{{\rm{s}}}}{{{\rm{a}}}}{{{\rm{m}}}}{{{\rm{p}}}}{{{\rm{l}}}}{{{\rm{e}}}}{{{\rm{n}}}}{{{\rm{u}}}}{{{\rm{m}}}}{{{\rm{b}}}}{{{\rm{e}}}}{{{\rm{r}}}}}({{{{\rm{X}}}}}_{{{{\rm{s}}}}{{{\rm{a}}}}{{{\rm{m}}}}{{{\rm{p}}}}{{{\rm{l}}}}{{{\rm{e}}}}{{{\rm{n}}}}{{{\rm{u}}}}{{{\rm{m}}}}{{{\rm{b}}}}{{{\rm{e}}}}{{{\rm{r}}}}})+\\ {\beta }_{{{{\rm{f}}}}{{{\rm{e}}}}{{{\rm{a}}}}{{{\rm{t}}}}{{{\rm{u}}}}{{{\rm{r}}}}{{{\rm{e}}}}{{{\rm{s}}}}}({{{{\rm{X}}}}}_{{{{\rm{f}}}}{{{\rm{e}}}}{{{\rm{a}}}}{{{\rm{t}}}}{{{\rm{u}}}}{{{\rm{r}}}}{{{\rm{e}}}}{{{\rm{s}}}}})$$

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.