Origin of Earth’s hydrogen and carbon constrained by their core-mantle partitioning and bulk Earth abundance

Abstract

Hydrogen and carbon concentrations in the Earth’s core are yet known. Here we determined their metal/silicate partition coefficients (D) simultaneously under typical conditions of core formation and found that D_H and D_C diminish in the presence of carbon and hydrogen, respectively, because of strong interactions between hydrogen and carbon in liquid metal, being markedly different from those separately examined in earlier experiments. With these partitioning data, we investigated the core and bulk Earth abundances of hydrogen and carbon based on core formation scenarios that are compatible with the bulk silicate Earth composition and the mass fraction and density of the core. The modelling results indicate that the Earth building blocks do not match enstatite chondrites in water abundance but require contributions by carbonaceous chondrites. The multi-stage core formation models combined with an Earth accretion scenario accounting for isotopic composition show 0.18–0.49 wt% H and 0.19–1.37 wt% C in the core, leading to 0.53–1.40 wt% H₂O (present as H in the core) and 0.07–0.44 wt% C in the bulk Earth. Our modelling also demonstrates that up to 53% and 72% of Earth’s water (hydrogen) and carbon, respectively, could have been derived from non-carbonaceous chondritic materials.

Introduction

Hydrogen and carbon are important volatile elements on our planet, and their sources^1,2 and the timing³ of the delivery to the growing Earth are of great interest. Since both hydrogen⁴ and carbon^5,6 are known to be strongly siderophile (iron-loving) under high pressure and temperature (P-T), the core is likely to be their largest reservoir. Indeed, the Earth’s outer core exhibits a large density deficit with respect to pure iron⁷, indicating the presence of substantial amounts of light impurity elements, but the core concentration of each light element has been controversial⁸. In addition to their bulk silicate Earth (BSE) abundances^9,10, understanding the hydrogen and carbon inventories of the core is essential to estimate their bulk Earth contents, which may suggest their origins.

The hydrogen and carbon contents in the core can be constrained by a combination of their metal/silicate partition coefficients under high P-T conditions of core formation and their BSE abundances, including the ocean water. The metal-silicate partitioning of hydrogen has been examined by experiments⁴ to 60 GPa and 4560 K as well as by theoretical calculations^11,12. The partitioning of carbon has been extensively studied below 25 GPa in large-volume presses^{13,14,15,16,17} and to 71 GPa in pressure and 5200 K in temperature by laser-heated diamond-anvil cell (DAC) techniques^5,6. However, these two earlier DAC works reported apparently inconsistent results, although experiments were conducted at similar P-T conditions.

Here, we examined the metal-silicate partitioning of hydrogen and carbon simultaneously in a DAC based on a combination of synchrotron X-ray diffraction (XRD) measurements at high pressure and the textural and compositional analyses on recovered samples by secondary ion mass spectrometry (SIMS) and field-emission-type electron probe microanalyzer (FE-EPMA). With these partitioning data, we modelled the Earth’s accretion and core formation processes that account for the BSE composition and the mass and density deficit of the core, which give core concentrations of hydrogen and carbon and accordingly their bulk Earth abundances. These results suggest that the core is a predominant reservoir for both hydrogen and carbon on Earth. We also found that non-carbonaceous chondritic materials could be an important source of the Earth’s water and carbon.

Results

Ten separate melting experiments were performed at 33–56 GPa and 3630–4760 K, corresponding to typical conditions of Earth’s core formation^18,19,20 under both hydrous and anhydrous conditions (Table 1). After melting at high pressures, all samples were recovered from a DAC and examined for melting texture and chemical composition on their cross sections at the centre of a heated area (Fig. 1). Quenched liquid metal was found at the central portion, being surrounded by silicate melt. The davemaoite (CaSiO₃-perovskite) and SiO₂ layers were present outside of the silicate melt pool, which is consistent with the XRD observations during melting (Fig. 2). The further outside, colder region was under subsolidus temperatures.

Fig. 1: Sample cross-section from run #1.

a Combined X-ray maps of Si (white), Ca (blue), and Fe (red), showing quenched liquid metal, silicate melt, CaSiO₃ davemaoite (Dvm,) and the SiO₂ phase. b Back-scattered electron (BSE) image. The SCAPS images of secondary ions intensity ratios of H/Si and C/Si. The H and C contents in silicate melt were determined from the regions of interest (ROIs, enclosed by black lines in (c, d)) in an area free from the lens-flare effects of the secondary ion optics (see Supplementary Fig. 16 and “Methods”) and metal blobs (see the BSE image in (b)). A quenched metal portion in (c) and (d) is from the X-ray map in (a). Note that a, c/d, and b are slightly different cross sections because of sputtering by the SIMS ion beam and repolishing with a focused ion beam in between. Scale bar, 10 µm.

Fig. 2: XRD patterns obtained in the high-pressure melting experiment.

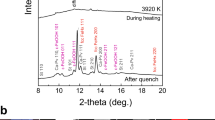
They were collected before (a), during (b) and after heating (c) to 3940 K at 42 GPa in run #1. During heating, XRD peaks were observed only from Dvm and CaCl₂-type SiO₂ (Ct), which were present outside of a silicate melt pool (see Fig. 1a), indicating the melting of both metal and silicate. After quenching temperature, the peaks from fcc FeH_x, ɛ-FeOOH, and (FeH_x)₇C₃ appeared. The amount of hydrogen in liquid metal was estimated from the phase proportion and hydrogen concentrations in these quench crystals. See text for details.

Table 1 Experimental conditions and results

Partitioning of hydrogen

The metal/silicate partition coefficients of hydrogen, ${D}_{{{{\rm{H}}}}}^{{{{\rm{metal}}}}/{{{\rm{silicate}}}}}$ were obtained as:

$${D}_{{{{\rm{H}}}}}^{{{{\rm{metal}}}}/{{{\rm{silicate}}}}}=\frac{{x^{\prime} }_{{{{\rm{H}}}}}^{{{{\rm{metal}}}}}}{{x}_{{{{\rm{H}}}}{{{{\rm{O}}}}}_{0.5}}^{{{{\rm{silicate}}}}}}$$

(1)

where ${x^{\prime} }_{{{{\rm{H}}}}}^{{{{\rm{metal}}}}}$ and ${x}_{{{{\rm{H}}}}{{{{\rm{O}}}}}_{0.5}}^{{{{\rm{silicate}}}}}$ represent the molar fractions of hydrogen in metal and silicate, respectively (see Eq. 10 for ${x^{\prime} }_{i}^{{{{\rm{metal}}}}}$ in “Methods”). The ${D}_{{{{\rm{H}}}}}$ values obtained in this study in the presence of carbon ranged from 0.7 to 26.1 (Table 1), notably lower than the ${D}_{{{{\rm{H}}}}}^{{{{\rm{metal}}}}/{{{\rm{silicate}}}}}$ = 22–46 measured in a carbon-poor system by previous DAC experiments⁴.

The metal-silicate partitioning of hydrogen can be expressed as a chemical reaction:

$${{{\rm{H}}}}{{{{\rm{O}}}}}_{0.5}^{{{{\rm{silicate\; melt}}}}}+\frac{1}{2}{{{{\rm{Fe}}}}}^{{{{\rm{metal}}}}}={{{{\rm{H}}}}}^{{{{\rm{metal}}}}}+\frac{1}{2}{{{{\rm{FeO}}}}}^{{{{\rm{silicate\; melt}}}}}$$

(2)

The exchange coefficient K_D for this reaction is parameterized as functions of P and T with regression constants a, b, c and d:

$${\log }_{10}{K}_{{{{\rm{D}}}}} ={\log }_{10}\frac{{{x}^{{\prime} }}_{{{{\rm{H}}}}}^{{{{\rm{metal}}}}}}{{x}_{{{{\rm{H}}}}{{{{\rm{O}}}}}_{0.5}}^{{{{\rm{silicate}}}}}}\cdot \sqrt{\frac{{x}_{{{{\rm{FeO}}}}}^{{{{\rm{silicate}}}}}}{{{x}^{{\prime} }}_{{{{\rm{Fe}}}}}^{{{{\rm{metal}}}}}}}={\log }_{10}\frac{{{x}^{{\prime} }}_{{{{\rm{H}}}}}^{{{{\rm{metal}}}}}}{{x}_{{{{\rm{H}}}}{{{{\rm{O}}}}}_{0.5}}^{{{{\rm{silicate}}}}}}\,+\,\frac{1}{4}\Delta {{{\rm{IW}}}}=\\ {\log }_{10}{D}_{{{{\rm{H}}}}}^{{{{\rm{metal}}}}/{{{\rm{silicate}}}}}+\frac{1}{4}\Delta {{{\rm{IW}}}}=a+\frac{b}{T}+c\cdot \frac{P}{T}+d\cdot {\log }_{10}\left(1-{{x}^{{\prime} }}_{{{{\rm{C}}}}}^{{{{\rm{metal}}}}}\right)$$

(3)

in which ${x^{\prime} }_{{{{\rm{C}}}}}^{{{{\rm{metal}}}}}$ is the molar fraction of carbon in liquid metal (Eq. 10), and $d\cdot {\log }_{10}\left(1-{x^{\prime} }_{{{{\rm{C}}}}}^{{{{\rm{metal}}}}}\right)$ approximates a non-ideal interaction between H and C^5,21. Following previous studies^4,22, oxygen fugacity fO₂ relative to the iron-wüstite (IW) buffer is approximated as $\Delta {{{\rm{IW}}}}\approx 2{\log }_{10}\left({x}_{{{{\rm{FeO}}}}}^{{{{\rm{silicate}}}}}/{x^{\prime} }_{{{{\rm{Fe}}}}}^{{{{\rm{metal}}}}}\right)$, which was obtained from the EPMA analyses. Fitting Eq. 3 to the present and earlier data⁴ yields a = 2.31(20), b = −1542(500), c = −38.9(78) and d = 6.69(30). Fig. 3a shows the negative pressure and positive temperature dependence of K_D for the partitioning of hydrogen after correcting for the effect of carbon, consistent with the results of Tagawa et al⁴. We note that carbon in liquid metal strongly reduces ${D}_{{{{\rm{H}}}}}^{{{{\rm{metal}}}}/{{{\rm{silicate}}}}}$ (Fig. 3b). All of the experimental data obtained in this study and Tagawa et al⁴. are well reproduced by Eq. 3 (Supplementary Fig. 1a).

Fig. 3: Partitioning of hydrogen.

a Pressure and temperature dependence of the exchange coefficient K_D for metal-silicate partitioning of hydrogen after correcting for the effect of carbon (Eq. 3). Blue (3000 K), purple (3500 K), orange (4000 K), and yellow lines (5000 K) show isotherms. b Reduction in metal/silicate partition coefficient D of hydrogen (molar basis) as a function of carbon concentration in liquid metal. Circles, this study; triangles, Tagawa et al⁴. Error bars represent one standard deviation.

Partitioning of carbon

Similarly, the metal/silicate partition coefficients for carbon ${D}_{{{{\rm{C}}}}}^{{{{\rm{metal}}}}/{{{\rm{silicate}}}}}$ were also calculated as:

$${D}_{{{{\rm{C}}}}}^{{{{\rm{metal}}}}/{{{\rm{silicate}}}}}=\frac{{x^{\prime} }_{{{{\rm{C}}}}}^{{{{\rm{metal}}}}}}{{x}_{{{{\rm{C}}}}}^{{{{\rm{silicate}}}}}}\,$$

(4)

The D_C ranged from 14 to 369 in the hydrogen (water)-free system and from 27 to 132 in the hydrogen (water)-bearing system (Table 1). We fitted the following equation to the present results combined with earlier DAC data^5,6 and low P-T data obtained for silicate melts with the ratio of nonbridging oxygens to tetrahedrally coordinated cations (nbo/t) less than 10 from multi-anvil and piston-cylinder experiments^13,14,15,17 that were performed in carbon-undersaturated systems:

$${\log }_{10}{D}_{{{{\rm{C}}}}}=a+b\cdot \Delta {{{\rm{IW}}}}+{{{\rm{c}}}}\cdot {nbo}/t+d\cdot {\log }_{10}\left(1-{x^{\prime} }_{{{{\rm{H}}}}}^{{{{\rm{metal}}}}}\right)$$

(5)

in which ΔIW represents oxygen fugacity relative to the iron-wüstite buffer. The fitting provides a = 1.51(30), b = −0.68(15), c = −0.33(7), and d = 1.76(77), showing the strong negative effects of oxygen fugacity, nbo/t, and hydrogen concentration in liquid metal on D_C (see Fig. 4a–c, respectively). Note that metal compositions were calculated as ${x^{\prime} }_{{{{\rm{i}}}}}^{{{{\rm{metal}}}}}$ also for the previous experimental data.

Fig. 4: Partitioning of carbon.

Partition coefficient D of carbon (molar basis) as a function of ΔIW (a) and nbo/t (b) obtained in hydrogen-free experiments and of hydrogen concentration in metal (c). See Eq. 5. Colour indicates temperature. Circles, this study; squares, Blanchard et al⁶. (closed) and Fischer et al⁵. (open); triangles, Fichtner et al¹⁷. (normal) and Dasgupta et al¹³. (inverted); crosses, Kuwahara et al^14,15. Error bars represent one standard deviation.

Considering the effects of oxygen fugacity and nbo/t, all of these earlier experimental data are well reproduced by Eq. 5 (Supplementary Fig. 1b). The P and T dependence of D_C is not explicit in Eq. 5 unlike previous DAC studies^5,6 (Supplementary Fig. 2). The low P-T data used together with the high P-T DAC data are key to clarifying such P and T effects; in contrast to earlier DAC studies^5,6, we did not employ data obtained in a graphite capsule, which causes carbon saturation in silicate melts, since saturation changes the partitioning behaviours^14,15. Li et al.¹⁶ also did not find the P and T effects on D_C when ΔIW < −1.5. In addition, it has been reported^14,16 that the solubilities of carbon in metallic liquid and silicate melt do not depend on pressure. Since the chemical potential of C in a carbon-saturated phase is identical to that in graphite/diamond, it suggests that the pressure dependence of chemical potentials of C is similar among these molten phases and graphite/diamond, and therefore the molar volumes of C in metallic liquid and silicate melt are close to each other, supporting the small pressure dependence of D_C (i.e., small volume change in the reaction).

Discussion

Single-stage core formation model

The single-stage core formation model is conceptually simple, assuming that the entire core and mantle reached chemical equilibrium under a certain P, T, and fO₂ condition. Such a condition has been estimated, based on the metal-silicate partitioning of moderately siderophile elements, to be 40 GPa and 3750 K (ref. ¹⁸), 50 GPa and 3500 K (ref. ¹⁹), or 54 GPa and 3350 K (ref. ²⁰) (Supplementary Table 1), and ΔIW = −2.3. The BSE water abundance may be 710 ppm²³, including 1.6 × 10²⁴g water in the crust, ocean, and atmosphere²⁴, while the higher BSE water contents of 1760 ppm and 1070 ppm H₂O have also been proposed^25,26. On the other hand, the carbon abundance in the BSE may be 120 ppm²⁷, 140 ppm²³ or ~160 ppm (or ~220 ppm)²⁸.

Based on the 710 ppm H₂O (ref. ²³) and 120 ppm C (ref. ²⁷) in the BSE, we can calculate core concentrations of hydrogen and carbon by using D_H and D_C at the conditions of core-mantle chemical equilibrium (core formation). Following the single-stage core formation model proposed by Wade and Wood¹⁸, Eqs. 3 and 5 showed 0.68 wt% H and 0.75 wt% C in the core with D_H = 92 and D_C = 67 (Fig. 5a, Supplementary Table 1), in which we employed nbo/t = 2.75 that is for a pyrolitic mantle composition²⁹, fixed the S content to be 2 wt% in the core from cosmochemical and geochemical constraints²⁷ and calculated the core abundances of Si and O using their metal-silicate partitioning data¹⁸. Also, similar calculations based on other core formation model¹⁹, including the metal/silicate partition coefficients of Si and O, found 0.45 wt% H and 1.15 wt% C in the core (D_H = 56 and D_C = 96) (Supplementary Table 1). The Fischer et al.'s²⁰ model provides 0.35 wt% H and 1.29 wt% C with D_H = 44 and D_C = 107.

Fig. 5: Modelling of single-stage core formation.

Hydrogen (water) and carbon concentrations in the core (a) and the bulk Earth (b) considering the P-T conditions of core metal segregation at 40 GPa and 3750 K¹⁸, 50 GPa and 3500 K¹⁹, and 54 GPa and 3350 K²⁰. Black circles, calculated using D_H and D_C simultaneously determined in this study; diamonds, D_H from Tagawa et al.⁴ and D_C from Blanchard et al.⁶; squares, D_H from Tagawa et al.⁴ and D_C from Fischer et al.⁵ Red and blue regions in b indicate H₂O and C concentrations in non-carbonaceous and carbonaceous chondrites, respectively. See Supplementary Table 8 for the H₂O and C contents in each type of chondrite.

These results suggest that the core is a primary reservoir for both hydrogen and carbon; >98% and >97% of their bulk Earth budgets may be present in the core, respectively. We also note that when we employ the separately-determined D_H (ref. ⁴) and D_C values^5,6 without considering the strong interaction between hydrogen and carbon, the C content in the core is calculated to be much higher⁶ or lower⁵ than described above, while H concentration is similar (Fig. 5a). Such core abundances indicate 1.10–2.08 wt% H₂O and 0.26–0.44 wt% C in the bulk Earth (Fig. 5b, Supplementary Table 1), which corresponds to Earth’s building blocks if we do not consider volatile loss during accretion.

Homogeneous accretion & multi-stage core formation model

The multi-stage core formation models may be more realistic scenarios in which the core grows stepwise during the Earth accretion³. Here we employ all of the nine multi-stage core formation models reported by Tagawa et al.⁴, where the Earth grows by 1000 steps upon accretion of impactors that are identical in size and composition. These models explain ~700 ppm H₂O in the BSE, including the ocean water and the mantle FeO, NiO and CoO contents based on their metal/silicate partition coefficients^3,19,20,30, as well as the Earth’s core mass fraction. In this study, we additionally examine the distributions of carbon with the newly determined D_H and D_C that consider the effect of their strong interactions (Eqs. 3 and 5).

We explored impactor H₂O and C concentrations, which lead to the amounts of residual water and carbon in silicate being both within the range of existing estimates of the present-day BSE concentrations of 710–1760 ppm H₂O (refs. ^23,24,25,26) and 120–220 ppm C (refs. ^23,27,28) at the end of accretion. The total difference in mantle concentrations of FeO, NiO and CoO (ref. ³¹) and core mass fraction between the modelling results and the target values is defined as:

$${\sigma }=\sqrt {1/4 \times \sum \left\{{\frac{({{{\rm{caluculated}}}}\; {{{\rm{value}}}})-({{{\rm{present}}}}\; {{{\rm{Earth}}}}\; {{{\rm{value}}}})}{({{{\rm{error}}}}\; {{{\rm{of}}}}\; {{{\rm{the}}}}\; {{{\rm{present}}}}\; {{{\rm{Earth}}}}\; {{{\rm{value}}}})}}\right\}^{2}}$$

(6)

We suppose that a model explains the core size and the BSE composition reasonably well when σ < 10. Each model (S1–S3, F1–F3 and R1–R3 models)⁴ gives the specific P-T evolution of metal-silicate chemical equilibrium, impactor size (=the Earth size divided by N × 1000), impactor bulk (silicate + core) composition (Supplementary Table 2) and exchange coefficients for Ni, Co, O and Si. Here we fixed Φ_Fe (metallic Fe/total Fe) = 0.987 and Φ_Si (metallic Si/total Si) = 0.034, unlike Tagawa et al⁴.’s simulations, by considering the core-mantle partitioning of O and Si in an enstatite-chondrite-like impactor³² at 1 bar and 2023 K (ref. ²⁹) using their partition coefficients³⁰.

We searched for the sets of P_final (the pressure of core metal segregation at the final step of accretion) and impactor water and carbon concentrations, which minimize the σ value (Eq. 6) while satisfying the residual 710–1760 ppm H₂O and 120–220 ppm C in the BSE. For each of the nine models, we found a σ minimum with specific P_final (Supplementary Fig. 3). With such P_final values, the present homogeneous multi-stage core formation models show that accreting identical impactors with 0.2–2.4 wt% H₂O and 0.2–1.0 wt% C accounts for the BSE composition (FeO, NiO, CoO, H₂O and C contents) and the Earth’s core size (Fig. 6a and Supplementary Fig. 4); typical examples of their evolutions during accretion are given in Supplementary Fig. 5. However, the total amount of light impurity elements in the core at the end of the Earth accretion (the calculated core concentrations of H, C, Si and O + assumed 2 wt% S, see Supplementary Fig. 5) are more than required to explain the present-day outer core density deficit³³ (Fig. 6a and Supplementary Fig. 4) even when the temperature at the inner core boundary (ICB) is relatively low (T_ICB = 4800 K) and the core liquid is saturated with Si + O under corresponding 3500 K at the core-mantle boundary³⁴ (note that low T_ICB and the SiO₂ crystallization from the liquid core leave relatively large room for hydrogen and carbon). It is therefore unlikely from the present modelling that the Earth’s building blocks included water and carbon from the beginning of accretion.

Fig. 6: Modelling of homogeneous accretion & multi-stage core formation (model S1).

The delivery of water and carbon to the Earth is considered from the beginning (a) and only after 50% accretion (b). The coloured region in the left panels indicates H₂O and C concentrations in impactors, explaining the BSE abundances of 710–1760 ppm H₂O and 120–220 ppm C in addition to the core mass fraction and the mantle FeO, Ni and Co contents (colour indicates the deviation from target values). Those in the central panels show the corresponding H and C contents in the core, which are compared with H and C concentrations required to explain the outer core density deficit when T_ICB = 5400 K (green curve) and 4800 K (right blue curve) (see text). The H₂O and C abundances in impactors (=Earth building blocks) are compared to those in non-carbonaceous (red region) and carbonaceous chondrites (blue region) in the right panels.

Next, we examined alternative scenarios in which water and carbon were delivered in a late stage of the Earth's accretion. Such a late delivery of volatiles has been considered for sulphur in a previous multi-stage core formation model^35,36,37. In the case of their delivery after 50% accretion (Supplementary Figs. 6–8), the calculated total amount of the core light elements (0.1–0.6 wt% H, 0.1–1.5 wt% C, Si and O contents and assumed S abundance) explains the present-day core density deficit when T_ICB is between 5400 K and 4800 K, taking the Si + O saturation and resulting SiO₂ crystallization upon core cooling into account³⁴ (Fig. 6b and Supplementary Fig. 7). These models require >1 wt% H₂O and <1 wt% C in the impactors during the latter half of the accretion in most models. Their typical evolutions are illustrated in Supplementary Fig. 8 for the S1 model showing relatively small σ values when the volatile-rich latter half impactors include 2.0 wt% H₂O and 0.4 wt% C (leading to 1.0 wt% H₂O and 0.2 wt% C in the bulk Earth) (Supplementary Table 3). This specific scenario finds 0.35 wt% H and 0.62 wt% C in the core, indicating that >95% of the bulk Earth budgets of both hydrogen and carbon may be present in the core.

Heterogeneous accretion & multi-stage core formation model

It is highly likely that the Earth was formed from a variety of different types of chondritic materials. Indeed, isotopic compositions, in particular Mo (ref. ³⁸), Ru (ref. ³⁹) and Zr isotopes⁴⁰, suggest that the Earth’s building blocks are close to enstatite (E)-chondrite-type materials but involve some carbonaceous chondrites (CCs) that are classified into CI, CM, CR, CO and CV (Supplementary Table 8). The recent isotopic mixing model by Dauphas et al. ⁴¹ proposed accretion scenarios to account for the Earth’s isotopic composition, showing the proportions and delivery timing of E-, CI-, and minor amounts of ordinary (O) chondrites (H, L, and LL) and other carbonaceous (CO + CV) chondrites. Their 4-stage model argued that water- and carbon-rich CC-type materials accreted to our planet mainly in the last 25% accretion, broadly consistent with our modelling described above. Here, the Dauphas et al.'s⁴¹ 4-stage accretion scenario was combined with our multi-stage core formation model (model S1⁴ in the previous section) such that the model is constrained not only by the BSE elemental composition and the core mass and density deficit but also by the isotopic composition. Furthermore, we also examined the effects of impactor size that changes the efficiency of chemical equilibrium between impactor metal and proto-Earth silicate^4,42 (by varying the number of steps for Earth accretion, N × 1000), differentiation of impactors before accreting to the Earth (by including volatile-free impactors with a frequency of 1-1/n) and volatile loss on Earth.

Considering the wide ranges of 1) the reported H₂O and C contents in E- and CI-chondrite-type materials^{2,43,44,45,46,47} (Fig. 7d, e, Supplementary Table 8, Supplementary Fig. 9), 2) N = 1–10 (Supplementary Fig. 10) and 3) n = 1–8 (Supplementary Fig. 11) along with 4) none or 25% carbon loss throughout the Earth accretion (water/hydrogen loss may have been minor)^48,49, we looked for the sets of these parameters that find σ < 10 through the search for P_final and 710–1760 ppm H₂O and 120–220 ppm C in the BSE. Consequently, these modellings show 0.18–0.49 wt% H and 0.19–1.37 wt% C in the core (Fig. 7a). Such core concentrations give 0.53–1.40 wt% H₂O (present as H in the core) and 0.07–0.44 wt% C in the bulk Earth (Fig. 7d). We note that these ranges of the core and bulk Earth H (H₂O) and C contents are similar to those obtained by the homogeneous accretion & multi-stage core formation modelling shown above that is based on the model S1 same as here and considers the delivery of water and carbon only after 50% accretion (Fig. 6b). In addition, in almost all cases, the parameter sets that satisfy the BSE composition and the Earth’s core size (σ < 10) provide the total amount of the core light elements accounting for the core density deficit with T_ICB = 4800–5400 K.

Fig. 7: Modelling of heterogeneous accretion & multi-stage core formation.

Water and carbon are delivered according to the 4-stage accretion scenario by Dauphas et al.⁴¹ that explains Earth’s isotopic composition. a–c Modelling results on core H and C concentrations (circles, n = 1; squares, 1 < n < 2; triangles, 2 < n < 3). Colours indicate difference from target values (σ) (a) and the fraction of NC-type materials as sources for Earth’s water (b) and carbon (c). d, e The bulk Earth H₂O (present as H in the core) and C abundances compared to those in each type of chondrite (Supplementary Table 8), including the Ryugu⁷¹ and Bennu⁷² samples. The dependence on n is indicated by colour. Closed and open symbols consider none and 25% loss of carbon during Earth accretion, respectively. Diamonds and squares show the variations in H₂O and C concentrations in E-/CI-type materials (varied in each model) and other types (fixed), respectively, employed in our modelling, while the reported ranges of the H₂O and C contents for NC and CC materials are indicated by boxes with broken and dotted lines, respectively.

The 0.19–1.37 wt% C in the core obtained in these simulations is higher than the core C concentrations of ~0.1–0.2 wt% reported by Blanchard et al.⁶ and Fischer et al.⁵, in which the effect of hydrogen on D_C was not taken into account. It is because the C abundance in the core is almost independent of the D_C in the Blanchard et al.'s⁶ model although they used a higher D_C. The D_C utilized in the modelling by Fischer et al.⁵ is the extrapolated one and lower than that applied in this study. Note that the present parameterization of D_C is consistent with the experimental data by Fischer et al.⁵ but employs more data including those by Blanchard et al.⁶ and this study. In addition, some recent simulations^48,49 included atmosphere as an additional reservoir, which is important in particular for C, but it reduces the calculated core H and C contents only by less than ~5% in the present modelling (Supplementary Fig. 12) since impactor metal reaches chemical equilibrium with a limited portion of an existing magma ocean⁴². Indeed, the Earth accretion and concurrent core formation must have been complicated processes, for which too few constraints are available so far. The present modelling of core composition employed the BSE isotopic composition and the core density deficit as additional constraints, neither of which has been used in earlier simulations. It is noted, however, that the possible ranges of the core H and C abundances demonstrated in this study are still dependent on model assumptions such as the limited efficiency⁴ of chemical equilibrium between impactor metal and proto-Earth silicate. This assumes that upon each impact, the timescale of the metal migration to the core is shorter than that of the compositional homogenization of the entire magma ocean⁴².

Origins of Earth’s water and carbon

All of these modellings show that the bulk Earth H₂O (incorporated as H in the core) abundance is higher than that of E-chondrites—in other words, E-chondrites alone cannot be the source of Earth’s water (Figs. 5b, 6b and 7d). Furthermore, the heterogeneous multi-stage core formation models show that 1 to 53% of Earth’s water may have derived from the non-carbonaceous (NC)-type materials (E- + O-chondrites) and the rest was from the CC-type ones that constitute 7% of the total Earth building blocks⁴¹ (Fig. 7b). Also, 2 to 72% of the Earth’s carbon could have originated from the NC-type materials with/without taking 25% loss during accretion into account^48,49 (Fig. 7c), strongly depending on carbon concentration in E-chondrites. We also note that 3–10% and 3–24% of the BSE H₂O and C budgets, respectively, were derived by the late veneer, the additional 0.5% accretion after the core formation⁴¹. It suggests that the majority of Earth’s hydrogen and carbon were involved in metal-silicate partitioning, which causes isotopic fractionation, leaving their isotopic ratios in the BSE different from those of the bulk Earth and Earth building blocks.

Methods

High-pressure melting experiments

Laser-heated DAC techniques were used to generate high P-T conditions (Table 1). We prepared five different glasses for silicate starting materials, which have mid-ocean ridge basalt (MORB) compositions with various amounts of H₂O; 1.0 wt% (w01), 0.15 wt% (w02), 0.6 wt% (w03), and none (n01 and n02) (Supplementary Table 4). A thin foil (~7 µm thick) of iron containing 4.0 wt% carbon, same as that employed previously⁵⁰, was sandwiched between layers of silicate glass. They were loaded into a 120 µm hole at the centre of a pre-indented rhenium gasket. Diamond anvils with a flat 300 µm culet were used. After loading, for experiments with anhydrous glass starting materials, we put the DAC into a vacuum oven at 400 K for >12 hours to remove moisture on the sample and subsequently compressed the sample in an argon atmosphere to avoid water adsorption. Under high pressure of interest, the sample was heated from both sides with a couple of 100 W single-mode Yb fibre lasers at BL10XU, SPring-8 synchrotron radiation source, with in-situ XRD measurements⁵¹. XRD patterns were collected before/during/after heating using a monochromatic X-ray beam with an energy of ~30 keV that was focused to a 6 µm area (full width of half maximum) on the sample position. Melting of a sample was confirmed by the disappearance of XRD peaks except weak ones that derived from silicate liquidus phases outside of a silicate melt pool (Fig. 2). Heating duration ranged from 4 to 60 seconds, which is long enough for each element to diffuse in liquid metal⁵² and silicate melt⁵³. Indeed, both metal and silicate were found to be homogeneous in composition in this study, except for heterogeneous distributions of small metallic blobs in the silicate melt pool (Fig. 1b). It has been demonstrated by earlier experiments using a multi-anvil press that molten metal and silicate melt reached chemical equilibrium in such a heating time scale⁵⁴. Considering the much smaller sample size and higher temperatures in the present DAC study than in the multi-anvil experiments, the time necessary for chemical equilibration should be shorter. Temperature was measured by a spectro-radiometric method⁵¹. Pressure was measured based on the Raman shift of a diamond anvil at 300 K after heating⁵⁵ and corrected for thermal pressure contributions that have been estimated to be +2.5 GPa per 1000 K (refs. ^4,56). The errors in pressure and temperature may be ±10% and ±5%, respectively⁵⁷.

XRD and EPMA analyses of liquid metal

The hydrogen contents in liquid iron were estimated from XRD data collected at high pressures and 300 K, since the iron sample loses hydrogen when it transforms into the body-centred cubic structure^4,58. The XRD patterns showed the appearance of face-centred-cubic (fcc) FeH_x and hydrogen-bearing (FeH_x)₇C₃ [or (FeH_x)₃C] formed from liquid metal upon quenching temperature (Fig. 2c). Their lattice volumes were larger than those of pure fcc Fe and Fe₇C₃ (or Fe₃C) at equivalent pressure and 300 K, respectively^59,60,61, which is attributed to the incorporation of hydrogen into their interstitial sites. Following Tagawa et al⁴., the hydrogen content x was calculated as:

$$x=\frac{{V}_{{{{{\rm{FeH}}}}}_{x}}-{V}_{{{{\rm{Fe}}}}}}{{\Delta V}_{{{{\rm{H}}}}\_{{{\rm{Fe}}}}}}{{{\rm{in}}}}\; {{{\rm{Fe}}}}{{{{\rm{H}}}}}_{x}$$

(7)

$${x}=\frac{{V}_{{\left({{{{\rm{FeH}}}}}_{x}\right)}_{7}{{{{\rm{C}}}}}_{3}}-{V}_{{{{{\rm{Fe}}}}}_{7}{{{{\rm{C}}}}}_{3}}}{{\Delta V}_{{{{\rm{H}}}}\_{{{\rm{Fe}}}}7{{{\rm{C}}}}3}}{{{\rm{in}}}}\; {({{{{\rm{Fe}}}}}{{{{\rm{H}}}}}_{x})}_{7}{{{{\rm{C}}}}}_{3}$$

(8)

$${x}=\frac{{V}_{{\left({{{{\rm{FeH}}}}}_{x}\right)}_{3}{{{\rm{C}}}}}-{V}_{{{{{\rm{Fe}}}}}_{3}{{{\rm{C}}}}}}{{\Delta V}_{{{{\rm{H}}}}\_{{{\rm{Fe}}}}3{{{\rm{C}}}}}}\,{{{\rm{i}}}}{{{\rm{n}}}}\; {({{{\rm{Fe}}}}{{{{\rm{H}}}}}_{x})}_{3}{{{\rm{C}}}}\,$$

(9)

where V_FeHx, V_(FeHx)7C3 and V_(FeHx)3C represent the observed lattice volume per Fe atom of each phase, and V_Fe, V_Fe7C3 and V_Fe3C are from their equations of state^59,60,61. ΔV_H represents the volume increase per hydrogen atom. We employed ΔV_{H_Fe} previously reported for fcc Fe⁶². ΔV_{H_Fe7C3} was determined by first-principles calculations in this study (see below for the first-principles calculations section, Supplementary Table 5 and Supplementary Fig. 13). Since hydrogen favours different interstitial sites depending on hydrogen concentration, we calculated x in (FeH_x)₇C₃ based on three different ΔV_{H_Fe7C3} applicable to each hydrogen concentration range, x < 0.14, 0.14< x < 0.29 and 0.29 < x < 0.57 (Supplementary Table 6). We also found that ΔV_H is similar between Fe and Fe₇C₃, in particular x = 0.22 and 0.45 observed in (FeH_x)₃C at 45–47 GPa and 300 K (Supplementary Table 6 and Supplementary Fig. 13), and therefore used ΔV_{H_Fe7C3} to calculate x in (FeH_x)₃C. In all runs, fcc FeH_x, ɛ-FeOOH and (FeH_x)₇C₃ [or (FeH_x)₃C] were found in XRD patterns collected from temperature-quenched liquid. Their hydrogen concentrations x were estimated to be 0.03–1.76, 0.21–0.30, and 0.22–0.45, respectively (Supplementary Table 6). We then calculated the total hydrogen concentration in liquid to be 0.33 to 0.98 wt% (Supplementary Table 7) based on the proportions of these crystals in quenched liquid, which were obtained by mass balance calculations using the FE-EPMA analyses (see below), considering the presence of silicon in the iron site. The incorporation of silicon into Fe increases its unit-cell volume to a minor extent⁶³. While 0.16–6.47 wt% Si may be present in these iron and iron carbides in the present experiments (Supplementary Table 7), the estimate of the hydrogen content x is reduced by 0.02 at 50 GPa even when 5.9 wt% Si is included⁶³.

The carbon contents in quenched metal liquids were obtained based on the electron microprobe analyses on the cross sections of recovered samples. After recovering samples at ambient conditions, sample cross sections at the centre of a laser-heated spot were prepared parallel to the compression/laser-heating axis with a focused ion beam (FIB, Versa 3D^TM, FEI). Textural and chemical characterizations were made with an FE-type scanning electron microscope (FE-SEM) and energy dispersive X-ray spectroscopy (EDS). Gold coating was made. We found 3.04–9.51 wt% C in quenched liquid metal along with other major elements with an FE-EPMA (JXA-8530F, JEOL) (Supplementary Table 7). At least five different points were measured for each phase. We employed an acceleration voltage of 12 kV, beam current of 15 nA, and LIF (Fe), TAP (Al, Na), TAPH (Mg), LDE1 (O), LDE2H (C), and PETJ (K, Ca, Si, Ti) as analyzing crystals. The calibration curve for C was obtained with Fe₃C, Fe-0.84 wt% C (JSS066-6, the Japan Iron and Steel Federation), and a rhenium gasket (assumed to be free of carbon) (Supplementary Fig. 14). Fe, Al₂O₃, MgO, Si, SiO₂, TiO₂, CaSiO₃, KTiOPO₄, and NaAlSi₃O₈ were used as standards for other elements. The X-ray counting time for peak/background was 20/10 seconds. The ZAF correction was applied. The major element compositions of silicate melt and the silicate starting materials were also obtained with an FE-EPMA (Supplementary Table 4).

SIMS measurements of silicate melt

We determined the hydrogen (water) and carbon contents in quenched silicate melts with SIMS equipped with a two-dimensional ion detector, stacked CMOS-type active pixel sensor (SCAPS) at the Hokkaido University^{4,64,65,66,67} (Fig. 1c, d). This system provides quantitative maps of secondary ions emitted from the sample surface because the CMOS sensor exhibits a good linear relationship between an output voltage and the number of secondary ions⁶⁶. Therefore, the abundance of each element from the intensity map can be quantified. The sample cross sections were coated with a ~70 nm thick Au layer by plasma sputtering to compensate for electrostatic charging on the sample surface. We used the Cs⁺ primary beam rastered across a 100 μm × 100 μm region on the sample. In order to prevent the effect of electrical charging, analyses were performed while applying electrons with an electron gun. A contrast aperture was set to be 100 μm in diameter, the exit slit was opened fully for 1H^- and 750 μm for others. Pressure during measurement was 2 × 10^-7 Pa. The SCAPS images of ¹H^-, ¹²C^-, and ²⁸Si^- secondary ions were collected. Accumulation time was 150, 100, and 10 seconds in each image, respectively. We employed five silicate glasses with known H₂O and C concentrations as standards (0.0 to 1.8 wt%, 0.0 to 389 ppm, respectively)⁶⁸ and prepared an additional silicate glass standard that contains 1.3 wt% C to fully cover the range of C concentration in silicate melt in the present experiments. Based on these standard glass analyses, we converted intensity ratios, ¹H^-/²⁸Si^- and ¹²C^-/²⁸Si^- into mass ratios. The intensity ratios from the secondary ion images are linearly correlated with the mass ratios of H/Si or C/Si of these standards (correlation coefficient R² = 0.997 and 1.000, respectively, as shown in Supplementary Fig. 15). Water (hydrogen) or carbon concentration in silicate melt was then obtained by multiplying the H/Si or C/Si ratio by the Si content acquired by FE-EPMA. While the silicate melt in run #1 included H₂O much more than 1.8 wt% in the standard glass, each parameter in Eq. 3 for D_H does not change beyond uncertainty when excluding the data from run #1.

Hydrogen distributions were homogeneous in quenched silicate melt (Supplementary Fig. 16), suggesting that hydrogen did not migrate from liquid metal to surrounding silicate upon quenching temperature. The ¹²C^- intensities from metal were higher by more than two orders of magnitude than those from silicate melt (Supplementary Fig. 16). The high C intensity from the metal leaked into the surrounding silicate melt due to the lens-flare or aberration effect. Therefore, the regions of interest (ROIs) in the silicate melts, from which we obtained their hydrogen and carbon abundances, were chosen from an area free from such flare effect from the metal based on the 2D map and line profile of the log₁₀(C) values (Supplementary Fig. 16). In addition, we avoided an area where small metallic blobs are present in the silicate melt. As shown in a back-scattered electron image (Fig. 1b), the outer part of a silicate melt layer is free from the metallic blobs. Following the arguments made in the earlier experiments on metal-silicate partitioning of carbon by Blanchard et al.⁶, we interpret that such blobs are not quench products but were present during melting. Indeed, the back-scattered electron image given in Fig. 1b does not show the Fe depletion in areas next to the blobs, which supports that they were not formed from silicate melt upon quenching. The SIMS analyses demonstrate that the amounts of H₂O widely ranged from 0.11 to 10.78 wt% in silicate melts (Supplementary Table 4). Their carbon contents were found to be 0.02–0.60 wt% and 0.008–0.44 wt% when using hydrous and anhydrous silicate starting materials, respectively.

Activities of elements in (H, C)-rich metal and oxygen fugacity

Liquid metals found in this study included carbon (and hydrogen in experiments using H₂O-bearing starting materials). The presence of hydrogen and carbon decreases the molar fraction of iron in metal (${x}_{{{{\rm{Fe}}}}}^{{{{\rm{metal}}}}}$), which apparently increases the oxygen fugacity relative to iron-wüstite (IW) buffer, $\Delta {{{\rm{IW}}}} \sim 2\,{\log }_{10}\left({x}_{{{{\rm{FeO}}}}}^{{{{\rm{silicate}}}}}/{x}_{{{{\rm{Fe}}}}}^{{{{\rm{metal}}}}}\right)$ and changes the exchange coefficient ${K}_{{{{\rm{D}}}}}^{{{{\rm{O}}}}}={x}_{{{{\rm{Fe}}}}}^{{{{\rm{metal}}}}}{x}_{{{{\rm{O}}}}}^{{{{\rm{metal}}}}}/{x}_{{{{\rm{FeO}}}}}^{{{{\rm{silicate}}}}}$ for the reaction FeO^silicate = Fe^metal + O^metal. According to Tagawa et al.⁴, the ${K}_{{{{\rm{D}}}}}^{{{{\rm{O}}}}}$ values calculated without considering the presence of hydrogen and carbon are consistent with those obtained in the (H, C)-free system. It suggests that both hydrogen and carbon do not have colligative properties in iron solvent since small H and C atoms are incorporated into liquid Fe interstitially. Therefore, the activity of element i in metal is approximated as;

$${x}_{i}^{{\prime} }=\frac{{N}_{i}}{{\sum }_{k\ne {{{\rm{H}}}},{{{\rm{C}}}}}{N}_{k}}\,$$

(10)

We obtained the mol-based D values from earlier experimental data with the same procedure.

First-principles calculations

First-principles calculations based on density functional theory were performed using the Quantum Espresso (QE) codes⁶⁹. Generalized-gradient approximation⁷⁰ was adopted, along with projector-augmented wave (PAW) pseudopotentials available on the QE website (energy cutoff of 90 Ry). In our calculations, Fe₇C₃ (20-atom cells, P6₃mc symmetry) with various site occupations of H were considered, including Wyckoff positions 2a, 2b, 6c, and 12 d. All considered structures are fully optimized (4×4×6 k-point mesh), and the results are fitted to the 3rd-order Birch–Murnaghan equation of state (Supplementary Table 5, Supplementary Fig. 13). For all considered structures, the ferromagnetic (FM) state is more favourable than the nonmagnetic (NM) state. As the H concentration increases, the favourable site occupations are 2a, 2a + 2b, and 2a + 6c for Fe₇C₃H, Fe₇C₃H₂, and Fe₇C₃H₄, respectively.