Quantum computation via Floquet tailored Rydberg interactions

Abstract

Rydberg atoms have stood out as a highly promising platform for realizing quantum computation. Floquet frequency modulation (FFM), in Rydberg atom systems, provides a unique tool for achieving precise quantum control and uncovering exotic physical phenomena. This work introduces a method to realize controlled arbitrary phase gates in Rydberg atoms by manipulating system dynamics using FFM. Notably, the need for laser addressing of individual atoms is eliminated, enhancing convenience for practical applications. Furthermore, this approach is integrated with soft quantum control strategies to enhance the fidelity and robustness of the resultant controlled-phase gates. Finally, as an example, this methodology is applied in Grover-Long algorithm to search target items with zero failure rate, demonstrating its substantial significance for future quantum information processing applications. This work leveraging Rydberg atoms and FFM may herald a new era of scalable and reliable quantum computing.

Introduction

Due to unique advantages and exotic dynamics, neutral atoms have emerged as one of the most promising and rapidly developing platforms in quantum computation and quantum many-body physics^{1,2,3,4,5,6,7,8}. When excited to Rydberg states, neutral atoms exhibit relatively long lifetimes and strong Rydberg-Rydberg interaction (RRI)^{9,10,11,12,13}, which can manifest as the form of dipole-dipole or van der Waals forces. This interaction gives rise to the Rydberg blockade mechanism, wherein the excitation of one atom to the Rydberg state prevents the excitation of neighboring atoms^{2,14,15,16,17,18,19,20}. This phenomenon has been extensively utilized for the implementation of quantum logic gates^{6,21,22,23,24,25,26,27,28,29} and holds significant promise for various applications in quantum computing, with ongoing experimental advancements^30,31,32. Furthermore, this feature allows quantum information to be encoded in the collective states of atomic ensembles, enabling the realization of mesoscopic quantum information processing and thus forming Rydberg superatoms^33,34,35. Beyond the Rydberg blockade mechanism, Rydberg anti-blockade (RAB)^{36,37,38,39,40,41,42} constitutes a critical dynamical process in neutral atomic systems, enabling the simultaneous excitation of multiple atoms to strongly interacting states. In particular, RAB permits a resonant two-photon transition between ground-state pairs and doubly excited Rydberg states in diatomic systems, thus playing a pivotal role in the realization of two-atom phase gates^43,44,45 and the preparation of steady-state entanglement^37,38,46. In addition to conventional Rydberg blockade and antiblockade effects, diverse dynamical regimes have been explored based on interacting Rydberg atoms. For example, the unconventional Rydberg pumping (URP) mechanisms has been developed⁴⁷ freezes the system dynamics even when the coupling between ground and Rydberg states is switched on. Moreover, the selective Rydberg pumping (SRP) represents another particularly intriguing dynamics in Rydberg atom systems⁴⁸. This mechanism enables selective resonance pumping of the two-atom ground state $\left\vert 11\right\rangle$ to a single-excited Rydberg state while effectively suppressing transitions from the other three ground states $\left\vert 00\right\rangle$, $\left\vert 01\right\rangle$, and $\left\vert 10\right\rangle$. Such state-selective control offers a powerful and reliable approach for precisely manipulating quantum system dynamics, significantly advancing our capability to engineer quantum states with high fidelity.

Alternatively, in the realm of coherent quantum dynamics control, periodic driving serves as a prevalent method for state manipulation^{49,50,51,52,53}. By applying Floquet frequency modulation (FFM), which involves periodic modulation of quantum systems at elevated frequencies, dynamic stability can be achieved^54,55,56. Furthermore, through the judicious selection of appropriate modulation amplitude and frequency, the Rabi coupling strength can be effectively regulated. This significantly enhances the dynamics of quantum systems, providing a broader array of choices for manipulating quantum systems. By periodically modulating the atom-field detuning, FFM provides a robust approach to realizing RAB dynamics, irrespective of the strength of the RRI. This technique significantly enhances RAB processes and enables the stabilization of long-lived Rydberg states with strong interactions, even for closely spaced atoms. The practical execution of quantum computation necessitates the efficient and resilient deployment of quantum logic gates^{57,58,59,60,61} to enable the completion of numerous quantum tasks. Nevertheless, most of existing dynamic protocols often fall short of meeting this demand.

In this work, we employ the FFM method to tailor Rydberg interaction for implementing quantum computation. The versatile applications of FFM in coherent quantum system control allow for the exploration of diverse quantum phenomena. Through the manipulation of frequency-modulation parameters of driving field, the system dynamics can be adeptly regulated to realize robust quantum gates. The integration of FFM with advanced quantum control of Rydberg atoms may open new avenues for efficient and robust quantum computation, paving the way for practical implementations of complex quantum algorithms and the exploration of novel quantum phenomena in coherently controlled systems, which is based on the following features of our present work on exploring exotic dynamics in Rydberg atoms for quantum computation. This potential stems from our exploration of exotic dynamics for Rydberg-atom quantum computation, holding the following key features.

Firstly, previous studies on periodic driving primarily focused on specific dynamic phenomena without providing a comprehensive analytical framework^50,54. In contrast, we derive an exact analytical solution, enabling universal realization of both RAB and URP regimes. Uniquely, while the referenced URP regime requires two driving fields⁴⁷, our protocol achieves the same effect with just one. More importantly, unlike traditional second-order RAB regimes^{44,62,63,64,65}, our scheme operates with undegraded dynamics, significantly enhancing the speed of running the system evolution. Secondly, compared with existing three-step Rydberg-blockade–based two-qubit gates and periodical-driving–induced two-qubit Rydberg gates that necessitate individual laser addressing^45,66, our approach accomplishes the gate task in a single step without requirement of individual addressing on atoms. Thirdly, we employ FFM to periodically modulate the atom-field detuning, thereby overcoming the constraints imposed by RAB on atomic separations. Simultaneously, owing to the intricate dynamics inherent in the Floquet system, various control parameter values can be chosen to implement the C-Phase gates, which provides a clear optimal choice for us both in terms of gate time and attainable fidelities. Finally, we integrate the constructed C-Phase gate with Gaussian soft quantum control optimization techniques^{67,68,69,70,71,72,73,74,75}, thereby improving the fidelity of the C-Phase gate and mitigating the occurrence of undesirable high-frequency oscillations during the evolution process. In addition, as an important example of application, we turn to apply our Floquet Rydberg-atom C-Phase gates for implementing Grover-Long search algorithm^{76,77,78,79,80,81,82,83,84,85}. By carrying out the phase rotation by an arbitrary angle, Grover-Long algorithm enables the target items search with high success rate to be realized effectively⁷⁸. Our approach facilitates multi-item searching with a unit success probability, eliminating the necessity for individual addressing and simplification of the quantum circuit offers a promising and feasible avenue for the practical implementation of the algorithm.

Results

Model and Hamiltonian

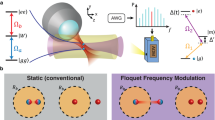
As illustrated in Fig. 1, we consider a scenario involving two neutral atoms interacting via RRI. Each atom is stimulated from the hyperfine ground state $\left\vert 1\right\rangle$ to the Rydberg excited state $\left\vert r\right\rangle$ with Rabi frequency denoted as Ω(t)e^iϕ(t) and detuning Δ(t). In the interaction picture with rotating-wave approximation (RWA), the evolution of the system is governed by the Hamiltonian (ℏ ≡ 1)

$$\hat{H}(t)=-\Delta (t)\sum \limits_{i=1}^{2}{\left\vert r\right\rangle }_{i}\left\langle r\right\vert +\left[\frac{\Omega (t)}{2}{e}^{i\phi (t)} \sum\limits_{i=1}^{2}{\left\vert 1\right\rangle }_{i}\left\langle r\right\vert +{{\rm{H.c.}}}\right]+V\left\vert rr\right\rangle \left\langle rr\right\vert ,$$

(1)

where i indexes the i-th atom, V represents the RRI strength of the Van der Waals type, and the laser detuning $\Delta (t)={\Delta }_{0}+\delta \sin ({\omega }_{0}t)$ undergoes sinusoidal FFM with the modulation frequency ω₀ and the modulation amplitude δ. The notation $\left\vert ab\right\rangle \equiv {\left\vert a\right\rangle }_{1}\otimes {\left\vert b\right\rangle }_{2}$ is employed throughout this study for conciseness. In implementing FFM, we can utilize a Rydberg excitation laser controlled by an acoustic-optic modulator (AOM) driven by an arbitrary waveform generator (AWG). Unlike conventional Floquet engineering techniques where FFM does not rely on periodic pulses but it directly alters the effective coupling between energy levels^86,87.

Fig. 1: The schematic illustration depicts the energy level configuration of two Rydberg atoms trapped in optical tweezers.

Each atom comprises two hyperfine ground states, denoted as $\left\vert 0\right\rangle$ and $\left\vert 1\right\rangle$, alongside a Rydberg excited state represented by $\left\vert r\right\rangle$. Simultaneously, both atoms undergo excitation from state $\left\vert 1\right\rangle$ to state $\left\vert r\right\rangle$ with Rabi frequency Ω(t)e^iϕ(t) and detuning Δ(t), while exhibiting Rydberg interactions between their respective $\left\vert r\right\rangle$ states.

Now we introduce the unitary operator, ${\hat{U}}(t)={\exp}\left[-if(t)\sum\nolimits_{i = 1}^{2}|r|_{i}\left\langle r\right| -iVt\left|rr\right\rangle \left\langle rr\right|\right]$ with $f(t)=-{\Delta }_{0}t+\delta /{\omega }_{0}\cos ({\omega }_{0}t)$, the Hamiltonian (1) is transformed into ${\hat{H}}^{{\prime} }(t)=i{\dot{\hat{U}}}^{{\dagger} }(t)\hat{U}(t)+{\hat{U}}^{{\dagger} }(t)\hat{H}\hat{U}(t)$, calculated as

$${\hat{H}}^{{\prime}}(t)=\frac{\Omega (t)}{2}{e}^{i[\phi (t)+f(t)]}\left[(\sqrt{2}\left\vert W\right\rangle \langle 11| +| 0r\rangle \langle 01| +| r0\rangle \left\langle 10\right\vert )+\sqrt{2}{e}^{iVt}\left\vert rr\right\rangle \left\langle W\right\vert \right]+{{\rm{H}}}.{{\rm{c}}}.,$$

(2)

in which the single-excitation intermediate state is denoted as $\left\vert W\right\rangle =(\left\vert 1r\right\rangle +\left\vert r1\right\rangle )/\sqrt{2}$. We define the modulation index α = δ/ω₀ and assume Δ₀ = 0 for simplicity. By employing the Jacobi-Anger expansion $\exp [\pm i\alpha \cos {\omega }_{0}t]=\mathop{\sum }_{m = -\infty }^{\infty }{J}_{m}(\alpha )\exp [\pm im({\omega }_{0}t+\pi /2)]$, the modified Hamiltonian ${\hat{H}}^{{\prime} }(t)$ can be expressed as

$${\hat{H}}^{{\prime} }(t)=\frac{\Omega (t)}{2}{e}^{i\phi (t)}\mathop{\sum }_{m=-\infty }^{\infty }{J}_{m}(\alpha ){e}^{im{\omega }_{0}t+im\frac{\pi }{2}}\left[\left(\left\vert 0r\right\rangle \left\langle 01\right\vert +\left\vert r0\right\rangle \left\langle 10\right\vert +\sqrt{2}\left\vert W\right\rangle \left\langle 11\right\vert \right)+\sqrt{2}{e}^{iVt}\left\vert rr\right\rangle \left\langle W\right\vert \right]+{{\rm{H.c.}}},$$

(3)

where J_m(α) represents the mth order Bessel function of the first kind. To simplify subsequent analyses, the Rabi frequencies between the states are individually rescaled to

$${\Omega }_{a}(t)=\Omega (t){e}^{i\phi (t)}\sum \limits_{m=-\infty }^{\infty }{J}_{m}(\alpha ){e}^{im{\omega }_{0}t+im\frac{\pi }{2}},$$

(4)

$${\Omega }_{b}(t)=\Omega (t){e}^{i\phi (t)}\sum \limits_{m=-\infty }^{\infty }{J}_{m}(\alpha ){e}^{i(m{\omega }_{0}+V)t+im\frac{\pi }{2}}.$$

(5)

By selecting a significantly high modulation frequency ω₀, the Rabi frequencies Ω_a(t) and Ω_b(t) are predominantly influenced by the resonance terms in Eq. (4). Specifically, the Rabi frequency Ω_a(t) is governed by J₀(α), whereas for Ω_b(t), we establish mω₀ = −V to satisfy the resonance criterion.

For a more intuitive analysis, we partition the system dynamics into distinct sectors, specifically involving the computational states $\left\vert 00\right\rangle$, $\left\vert 01\right\rangle$, $\left\vert 10\right\rangle$, and $\left\vert 11\right\rangle$. The state $\left\vert 00\right\rangle$ remains unchanged as $\left\vert 0\right\rangle$ is decoupled to the driving field. In the cases of the initial states $\left\vert 01\right\rangle$ and $\left\vert 10\right\rangle$, the dynamics can be described in the two-level systems, respectively, governed by

$$\begin{array}{rcl}{\hat{H}}_{01}(t)&=&\frac{{\Omega }_{a}(t)}{2}\left\vert 01\right\rangle \left\langle 0r\right\vert +{{\rm{H.c.}}},\\ {\hat{H}}_{10}(t)&=&\frac{{\Omega }_{a}(t)}{2}\left\vert 10\right\rangle \left\langle r0\right\vert +{{\rm{H.c.}}}\end{array}$$

(6)

For the initial state $\left\vert 11\right\rangle$, however, it is reduced into a three-level system with the Hamiltonian

$${\hat{H}}_{11}(t)=\frac{\sqrt{2}{\Omega }_{a}(t)}{2}\left\vert 11\right\rangle \left\langle W\right\vert +\frac{\sqrt{2}{\Omega }_{b}(t)}{2}\left\vert W\right\rangle \left\langle rr\right\vert +{{\rm{H.c.}}}$$

(7)

The quite difference between Hamiltonian expressions in the cases of initial states $\left\vert 01\right\rangle$ ($\left\vert 10\right\rangle$) and $\left\vert 11\right\rangle$ is the very essence to achieve nontrivial two-atom quantum gates.

C-Phase gate of two Rydberg atoms

In this section, we utilize the FFM scheme to construct a universal two-qubit C-Phase gate, capitalizing on its intricate dynamics. By varying the modulation index α and modulation frequency ω₀, we present the time-average population^50,54 of the doubly excited Rydberg state $\left\vert rr\right\rangle$ within 10 μs in Fig. 2a with the RRI strength of V = 20Ω. The results indicate that the FFM scheme can effectively manipulate the dynamic behavior of system according to the population behaviors of $\left\vert rr\right\rangle$. Notably, when the resonance condition ω₀ = V is satisfied, the population of the $\left\vert rr\right\rangle$ state is primarily modulated by J₀(α) and J₁(α). By selecting values of α at which either J₀(α) or J₁(α) vanishes, the population of $\left\vert rr\right\rangle$ state can be effectively suppressed. Moreover, the conventional RAB effect necessitates operating outside the atomic blockade radius, which restricts the interaction strength V to very small values^1,43. However, as illustrated in Fig. 2a, even for significantly large V, the doubly excited Rydberg state can still be realized by selecting the appropriate parameter α. This finding effectively overcomes the inherent limitations of the traditional RAB mechanism, particularly in terms of interaction strength and interatomic distance constraints.

Fig. 2: Schematic illustrating the impact of FFM on Rydberg anti-blockade dynamics and the transition dynamics of the four ground states.

a The time-average population of $\left\vert rr\right\rangle$ varies as a function of the modulation index α and the normalized modulation frequency ω₀/Ω. The red and green dashed curves correspond to J₀(α) = 0 and J₁(α) = 0, respectively. b Dynamics of transitions among the four ground states: the $\left\vert 00\right\rangle$ state remains unaltered, transitions of the $\left\vert 01\right\rangle$ and $\left\vert 10\right\rangle$ states exhibit Rabi oscillations with the same Rabi frequency Ω_a(t), while the $\left\vert 11\right\rangle$ state is excited to the $\left\vert rr\right\rangle$ state via the intermediate state $\left\vert W\right\rangle$ with equivalent Rabi frequencies of $\sqrt{2}{\Omega }_{a}(t)$ and $\sqrt{2}{\Omega }_{b}(t)$, respectively.

To construct the desired two-qubit C-Phase gate ${\hat{U}}_{CP}=$ diag (1, −e^iϑ, −e^iϑ, 1), we employ two sequential identical Rydberg global pulses with equal duration τ but a laser phase jump ϑ inserted between the two pulses. Here, we first analyze the case of a square pulse (SP) sequence. In this scenario, the duration of each pulse segment is denoted as τ = π/ΩJ₀(α), and the total gate time is correspondingly 2τ. The specific pulse sequence can be described as follows: when 0 < t ≤ τ, Ω(t) = Ω, and τ < t ≤ 2τ, Ω(t) = Ωe^iϑ. Utilizing the unitary operator ${\hat{U}}_{f}=\mathop{\sum}\nolimits_{f}{\exp}\left(-i\int_{0}^{2\tau }{\hat{H}}_{f}(t)dt\right)$, where f = 00, 01, 10, 11 and ${\hat{H}}_{00}(t)=0$, each pulse induces a transformation in the atomic states. An in-depth exploration into the evolution of the four computational basis states under the impact of ${\hat{U}}_{CP}$ is presented in Fig. 2(b). The state $\left\vert 00\right\rangle$ is unaffected by these pulses with ${\hat{U}}_{f}\left\vert 00\right\rangle =\left\vert 00\right\rangle$, while the states $\left\vert 01\right\rangle$ and $\left\vert 10\right\rangle$ return to themselves with an additional phase factor represented by ${\hat{U}}_{f}\left\vert 01\right\rangle (\left\vert 10\right\rangle )=-{e}^{i\vartheta }\left\vert 01\right\rangle (\left\vert 10\right\rangle )$ after a duration of 2τ. Lastly, concerning the evolution of the state $\left\vert 11\right\rangle$, our objective is to return it to the same state without accumulating any phase after the complete evolution. This is achieved by appropriately selecting the time-dependent functions ∣Ω_a(t)∣ and ∣Ω_b(t)∣. Thus, we define ∣Ω_b(t)∣ as N times ∣Ω_a(t)∣ and evaluate the time evolution operator ${\hat{U}}_{f}$ for the corresponding three-level system using Eq. (7). By applying the condition ${\hat{U}}_{f}\left\vert 11\right\rangle =\left\vert 11\right\rangle$, we can analyze the changes in population P₁₁ and phase Φ₁₁ of the state $\left\vert 11\right\rangle$ as N varies. It can be seen that when

$$N=(\sqrt{31}-\sqrt{7})n+\sqrt{7},\,n=0,1,2,\cdots$$

(8)

the population P₁₁ = 1 and the phase Φ₁₁ = 0 are satisfied, the numerical result shown in Fig. 3a also prove this, and the state $\left\vert 11\right\rangle$ undergoes self-evolution without accumulating any additional phase. In other words, we can choose various values of n for the realization of the universal C-Phase gate, which undoubtedly demonstrates the unique advantages of our FFM scheme, enriching the dynamics of the quantum system and offering diversified options for the construction of quantum gates. With increasing n, the population of the state $\left\vert 11\right\rangle$ remains close to 1 due to the significant disparity between ∣Ω_b(t)∣ and ∣Ω_a(t)∣. This intriguing behavior, similar to the URP mechanism⁴⁷, effectively freezes the evolution of a two-atom system featuring the same ground states. Therefore, our protocol offers a reliable approach for implementing the URP mechanism. By selecting a sufficiently large value of N, the URP mechanism can be achieved using just a single driving field.

Fig. 3: Schematic diagram of population and phase dynamics in the $\left\vert 11\right\rangle$ state and the evolution of the Bessel function.

a Diagram illustrating the variations in population and phase of $\left\vert 11\right\rangle$ as the ratio N of ∣Ω_b(t)∣ to ∣Ω_a(t)∣ is altered. b Evolution of the Bessel function of the first kind with respect to the modulation index α, denoting J₀ and J₁ as the zeroth and first order Bessel functions of the first kind, respectively.

To satisfy the resonance conditions detailed in Eq. (4), we assign ω₀ = V such that the coupling strength between the singly-excited state $\left\vert W\right\rangle$ and the doubly-excited state $\left\vert rr\right\rangle$ is primarily influenced by J₁(α), while the Rabi frequency between the state $\left\vert 11\right\rangle$ and state $\left\vert W\right\rangle$ is predominantly governed by J₀(α). This configuration ensures that ∣Ω_b(t)∣ = N∣Ω_a(t)∣ is equivalent to J₁(α) = NJ₀(α), enabling us to select a suitable modulation index α to attain the desired nontrivial two-qubit gate illustrated in Fig. 3b. The aforementioned FFM approach facilitates the realization of the two-qubit C-Phase gate: ${\hat{U}}_{CP}=$ diag (1, −e^iϑ, −e^iϑ, 1) in reference to the computational basis $\{\left\vert 00\right\rangle ,\left\vert 01\right\rangle ,\left\vert 10\right\rangle ,\left\vert 11\right\rangle \}$.

Parameter selection and numerical simulation

In this section, we employ feasible experimental parameters to conduct a numerical simulation for testing the performance of our FFM scheme. The excitation process from the ground state $\left\vert 1\right\rangle$ to the Rydberg state $\left\vert r\right\rangle$ can be achieved via a two-photon mechanism in ⁸⁷Rb atoms^6,7,88. Within the FFM scheme, to meet the condition V = ω₀ ≫ Ω, it is necessary to have Rydberg states characterized by sufficiently high principal quantum numbers or close interatomic separations to ensure a potent RRI strength. Hence, we consider energy levels as two hyperfine ground states $\vert 0\rangle =\vert 5{S}_{1/2},F=1,{m}_{F}=1\rangle$ and $\vert 1\rangle =\vert 5{S}_{1/2},F=2,{m}_{F}=2\rangle$⁸⁹, an intermediary state $\vert p\rangle =\vert 5{p}_{3/2}\rangle$ or $\vert p\rangle =\vert 6{p}_{3/2}\rangle$, and the Rydberg strongly-interacting state $\vert r\rangle =\vert 70{S}_{1/2}\rangle$ possessing an interaction coefficient of C₆/2π = 858.4 GHz μm⁶. For an accessible atomic temperature T_a = 10 μK, the lifetime τ_r of the Rydberg state $\vert r\rangle$ in ⁸⁷Rb atoms with a principal quantum number 70 is ~400 μs⁶. The strength of RRI is set as V = 2π × 70.18 MHz, considering an interatomic separation of d = 4.8 μm^88,90.

To study evolution of the two-atom system, we utilize the Lindblad master equation to assess the gate performance under dissipative effects, expressed as

$$\frac{\partial {\hat{\rho}} (t)}{\partial t}=-\frac{i}{\hslash }[{\hat{H}}{(t)},{\hat{\rho}} (t)]+{{{\mathcal{L}}}}_{r}[\hat{\rho }]$$

(9)

where ${\hat{\rho}} (t)$ represents the density matrix operator corresponding to the two-atom system, ${\hat{H}}(t)$ stands for the time-varying Hamiltonian of the system as depicted in Eq. (1), and the dissipation terms ${{{\mathcal{L}}}}_{r}[\hat{\rho }]$ account for the spontaneous decay originating from the strongly-interacting states, elucidated as

$${{{\mathcal{L}}}}_{r}[\hat{\rho}]=\mathop{\sum}\limits_{i=1,2}\mathop{\sum}\limits_{j=0,1}\left({\hat{L}}_{j}^{i}\hat{\rho }{\hat{L}}_{j}^{i{\dagger} }-\frac{1}{2}{\hat{L}}_{j}^{i{\dagger} }{\hat{L}}_{j}^{i}\hat{\rho }-\frac{1}{2}\hat{\rho }{\hat{L}}_{j}^{i{\dagger} }{\hat{L}}_{j}^{i}\right)$$

(10)

in which the Lindblad operators ${\hat{L}}_{j}^{i}=\sqrt{{\gamma }_{j}}{\vert j\rangle }_{i}\langle r\vert$ represent the jump operators characterizing the spontaneous emission of the atom from the Rydberg state $\left\vert r\right\rangle$ to a ground state $\left\vert j\right\rangle$, where γ_j represents the decay rate from $\left\vert r\right\rangle$ to the ground state $\left\vert j\right\rangle$. Here we assume γ₀ = γ₁ = 1/(2τ_r) with τ_r being the lifetime of the Rydberg state.

To demonstrate the efficacy and resilience of our proposed two-qubit C-Phase gate across diverse initial conditions, we evaluate the average fidelity⁹¹

$$\bar{F}(\xi ,\hat{U})=\frac{{\sum }_{k}{\mathrm{tr}}\,[\hat{U}{\hat{U}}_{k}^{{\dagger} }{\hat{U}}^{{\dagger} }\xi ({\hat{U}}_{k})]+{d}_{k}^{2}}{{d}_{k}^{2}({d}_{k}+1)},$$

(11)

in which $\hat{U}$ represents the perfect logic gate, ${\hat{U}}_{k}$ stands for the tensor of Pauli matrices $\hat{I}\hat{I},\hat{I}{\hat{\sigma }}_{x},\hat{I}{\hat{\sigma }}_{y},\hat{I}{\hat{\sigma }}_{z},...,{\hat{\sigma }}_{z}{\hat{\sigma }}_{z}$ for a two-qubit gate, d_k = 2^x, with x being the number of qubits in a quantum gate and in this case, d_k = 4. $\xi ({\hat{U}}_{k})$ denotes the trace-preserving quantum operation achieved by solving the master equation (9).

As illustrated by the cyan dashed line in Fig. 4a, the average fidelity of the C-Phase gate we have constructed varies with the Rabi frequency ranging from 2π × 1 MHz to 2π × 20 MHz when n = 0, which indicates that the Rydberg blockade condition Ω ≪ V should be satisfied to attain a relatively higher and stable gate fidelity. For subsequent analysis, we selected a time-independent Rabi frequency of 2π × 3.5 MHz. In Fig. 4b, we present the evolving average fidelity of the C-Phase gate with ϑ = π/2 for n = 0, 1, 2, 3 corresponding to the gate time T = 2π/∣Ω_a(t)∣, yielding final average fidelities of 0.9973, 0.9870, 0.9856, and 0.9647, respectively. It can be observed that for n = 0, the achieved gate fidelity is the highest with the shortest gate time. Conversely, for n = 1, 2 and 3, the gate time increases due to the decreasing values of selected J₀(α) and J₁(α), leading to a decline in the gate fidelity influenced by the non-resonant terms and dissipation of system.

Fig. 4: Schematic representation of gate fidelity fluctuations.

a The average fidelity of the constructed C-Phase gate fluctuates as the square pulse Rabi frequency Ω and the Gaussian pulse maximum amplitude Ω_g ranges from 2π × 1 MHz to 2π × 20 MHz when n = 0. b The evolution of the average gate fidelity of the implemented C-Phase gate over time, when n equals 0,1,2,3. The time-independent Rabi frequency Ω = 2π × 3.5 MHz, V = ω₀ = 2π × 70.18 MHz, and the gate duration being T = 2π/∣Ω_a(t)∣. c The temporal progression of the average gate fidelity for the C-Phase gate utilizing Gaussian soft quantum control when n = 0,1,2,3. The time-dependent Rabi frequency is given by Ω_g(t) with the maximum amplitude Ω_g = 2π × 8.1 MHz, ${T}_{g}=(-1+a)\pi /| {\Omega }_{g}(t)| {J}_{0}(\alpha )(4a-\sqrt{\pi })$ and a gate time of T = 8T_g. Additionally, V = ω₀ = 2π × 70.18 MHz.

Gaussian-pulse optimization

Observing from Fig. 4b and the cyan dashed line of Fig. 4a, we note that the fidelity evolution exhibits pronounced oscillations due to imperfect parameter settings aimed at mitigating the high-frequency oscillations. These substantial oscillations render the resultant C-Phase gate particularly susceptible to control errors. To address this issue, we leverage the technique of soft quantum control⁶⁷ to refine the parameters for better adherence to RWA conditions, thus damping the high-frequency oscillatory effects and reducing parameter uncertainties during the phase accumulation, ultimately enhancing the gate performance.

Under the implementation of soft quantum control, the time-independent SP with Rabi frequency Ω can be transformed into a time-evolving Gaussian pulse (GP), given by

$${\Omega }_{g}(t)=\left\{\begin{array}{ll}{\Omega }_{g}\left[{e}^{\frac{-{(t-2{T}_{g})}^{2}}{{T}_{g}^{2}}}-a\right]/(1-a),\quad &0 < t\le 4{T}_{g},\\ \quad &\\ {\Omega }_{g}\left[{e}^{\frac{-{(t-6{T}_{g})}^{2}}{{T}_{g}^{2}}}-b\right]/(1-b),\quad &4{T}_{g} < t\le T,\end{array}\right.$$

(12)

where Ω_g and T_g denote the maximum amplitude and width of GP, respectively. Furthermore, a = exp $[-{(2{T}_{g})}^{2}/{T}_{g}^{2}]$ and b = exp $[-{(T/2-6{T}_{g})}^{2}/{T}_{g}^{2}]$ causing the amplitude is zero at the start and end. Ensuring the pulse area remains constant, we deduce ${T}_{g}=(-1+a)\pi /| {\Omega }_{g}(t)| {J}_{0}(\alpha )(4a-\sqrt{\pi })$ by satisfying $\int_{0}^{4{T}_{g}}{\Omega }_{g}(t)dt=\pi$ and $\int_{4{T}_{g}}^{{t}_{g}}{\Omega }_{g}(t)dt=\pi$ with the gate time T = 8T_g. To highlight the distinctive superiority of the GP over the SP, the variation in gate fidelity with respect to the GP’s maximum amplitude under soft control is illustrated by the solid red line in Fig. 4a. The findings demonstrate that this approach noticeably enhances gate performance and facilitates a more gradual evolution of fidelity. Employing this GP configuration, we choose the maximum amplitude Ω_g = 2π × 8.1 MHz so that the optimized gate time is consistent with the SP and illustrate the average gate fidelity of the C-Phase gate for the cases n = 0, 1, 2, 3 in Fig. 4c. The results depict a substantial reduction in oscillations through Gaussian soft quantum control. Moreover, GP offers practical advantages over traditional SP in experimental scenarios⁷. Consequently, the combination of our approach with Gaussian soft control significantly enhances operational feasibility in experiments, showcasing promising and valuable applications.

Gate resilience

Subsequently, we delve into the robustness of the constructed C-Phase gates against parameter inaccuracies, with a particular focus on the impact of laser intensity on the fidelity of the C-Phase gate. To explore this scenario, we examine the effects of deviations in the Rabi frequency Ω, detuning Δ_0, and gate time T, encompassing both upward and downward deviations. To quantify these deviations, we introduce the deviation value δΩ, δΔ₀, and δT, yielding actual parameters

$$\Omega \to \Omega (1+{W}_{1}),\quad {\Delta }_{0}\to {\Delta }_{0}+{W}_{2},\quad T\to T(1+{W}_{3}).$$

(13)

Then, we analyze the influence of errors on the entanglement fidelity of an equivalent Bell state $\left\vert {\Psi }_{{{\rm{Bell}}}}\right\rangle =(\left\vert 00\right\rangle -i\left\vert 01\right\rangle -i\left\vert 10\right\rangle +\left\vert 11\right\rangle )/2$. The entanglement fidelity is defined by ${{\rm{tr}}}[\hat{\rho }(T)\left\vert {\Psi }_{{{\rm{Bell}}}}\right\rangle \left\langle {\Psi }_{{{\rm{Bell}}}}\right\vert ]$, where density operator $\hat{\rho }(T)$ at the final moment is obtained by solving the master equation with an initial two-atom product state $\left\vert {\psi }_{0}\right\rangle =(\left\vert 0\right\rangle +\left\vert 1\right\rangle )\otimes (\left\vert 0\right\rangle +\left\vert 1\right\rangle )/2$ when employing either SP or GP for the laser configuration, as illustrated in Fig. 5a–c. We observe that the entanglement fidelity exhibits a comparable level of performance degradation when subjected to the same relative error in either pulse strength or detuning parameters, regardless of whether a SP pulse or GP is employed. This phenomenon can be attributed to the fundamental dependence of quantum evolution on the effective pulse area. Specifically, an equivalent relative error in the pulse strength parameter across both scenarios results in identical alterations to the effective pulse area. Consequently, precise control over pulse strength and detuning emerges as a critical requirement for achieving high-fidelity C-Phase gate operations within the present gate implementation scheme. Alternatively, it is noteworthy that the robustness of C-Phase gates against pulse strength errors can be significantly enhanced through optimal control methodologies. These techniques introduce additional degrees of freedom into the Rydberg system^29,92,93,94, thereby potentially improving error tolerance. However, this enhanced robustness comes at the cost of increased implementation complexity, which may inadvertently introduce new sources of error into the system. Regarding the timing error in Fig. 5c, the entanglement fidelity demonstrates remarkable resilience when the GP is used. This robustness stems from the inherent property that moderate deviations in operation time do not significantly alter the pulse area. Only when the actual pulse duration falls substantially below the desired value, does the entanglement fidelity exhibit a marginal decrease. This behavior stands in stark contrast to the SP gate implementation, where the entanglement fidelity shows pronounced sensitivity to timing errors. Such sensitivity arises from the direct linear relationship between pulse duration errors and pulse area variations when the SP is used.

Fig. 5: Schematic representation of gate robustness characteristics.

The impact of errors in the a Rabi frequency Ω, b detuning Δ₀ and c gate time T on state fidelity is examined using square pulse and Gaussian pulse configurations. The relevant parameters remain consistent with V = ω₀ = 2π × 70.18 MHz, Ω = 2π × 3.5 MHz, and the time-dependent Rabi frequency Ω_g(t) as previously described. Each point denotes the average of 1001 results obtained by randomly picking 1001 disorders from [−W_k, W_k] with k = 1, 2, and 3 in (a), (b), and (c), respectively.

Regarding the error associated with the RRI strength V, our protocol faces a challenge similar to that of the conventional RAB gate schemes. Namely, the gate fidelity is sensitive to fluctuations in the RRI strength. In most Rydberg gate implementations, the atoms are assumed to be at fixed spatial positions, ensuring a constant RRI intensity. However, in practice, atoms exhibit finite temperature effects, and their residual thermal motion introduces positional uncertainty. As a result, precise control over the RRI strength becomes exceedingly difficult. We systematically investigate the impact of V variations on the entanglement fidelity, as illustrated in Fig. 6a, covering a relative error range δV/V ∈ [−0.2, 0.2]. The results indicate that the entanglement fidelity exhibits remarkable sensitivity to relative errors even when the absolute error range is limited in ~0.01 (see inset box). Additionally, we investigate the impact of modulation index α variation on the entanglement fidelity of our protocol. As shown in Fig. 6b, following a similar approach to equation (13), the actual parameter was derived through α → α(1 + W₄) under both SP and GP conditions. The results indicate that while significant fluctuations in the value of α diminish the fidelity advantage, the feasibility of our protocol can be ensured when the actual implementation maintains precise control over α limited with the relative error <0.05.

Fig. 6: Diagram showing the variation of entanglement fidelity.

a Schematic diagram illustrating the effect of Rydberg interaction strength V error on entanglement fidelity under square pulse and Gaussian pulse. b Diagram depicting the impact of modulation index α fluctuations on the robustness of our protocol, comparing square pulse and Gaussian pulse. c Impact of Doppler dephasing errors on entanglement fidelity at various temperatures for square pulse and Gaussian pulse. The associated parameters remain consistent with the aforementioned ones.

Furthermore, we simulate the dynamics of quantum systems with Doppler dephasing errors^95,96. The Rydberg atom, regardless of its temperature, is not at rest in the trap. Doppler dephasing caused by the random motion of imprisoned atoms is one of the most important sources of error in experiments, which will limit the performance of quantum gates. Due to the presence of the Doppler effect, the Rydberg excitation Rabi frequency changes to Ω(t) → Ω(t)e^iδt, where δ = k_effΔv denotes the Doppler shift with effective laser wavevector k_eff and atomic root-mean-square speed $\Delta v=\sqrt{{k}_{{{\rm{B}}}}{T}_{a}/m}$. In which k_B, T_a, and m represent the Boltzmann constant, atomic temperature, and atomic mass, respectively. For the two-photon transition process of Rb atoms, we choose laser wavelengths of λ₁ = 780 nm and λ₂ = 480 nm, respectively. Moreover, we replace the orthogonal lasers with the counterpropagating lasers to reduce the effect of Doppler dephasing, thus obtaining k_eff = 2π(1/λ₂ − 1/λ₁). The numerical results of the fidelity of the C-Phase gate we constructed are shown in Fig. 6c, and it should be noted that the temperature simulated here is much higher than the current experimental conditions, where the temperature of the atoms in the optical tweezers can be cooled to 5.2 μK⁹⁷. Even so, in the presence of a Doppler shift, the fidelity of the quantum gate can still reach more than 0.98 for cases of the SP and the GP. Besides, the usage of GP exhibits better performance in resilience against the Doppler dephasing, knowing from a smaller slope of the red entanglement fidelity line in Fig. 6c.

Finally, it is noted that the pronounced sensitivity to V variations suggests significant potential for applications in enhanced quantum metrology of external microwave fields (referring to ref. ⁹⁸), despite the negative effect on quantum gates. Based on the implementation of Hamiltonian in Eq. (7), to perform criticality-enhanced precision measurement of microwave electric fields by exploiting the extreme sensitivity of doubly-excited state $\left\vert rr\right\rangle$ population to deviations in RRI, the following approach can be executed. First, Ω_a = Ω_b= Ω is set to excite the ground state $\left\vert 11\right\rangle$ into Rydberg state $\left\vert rr\right\rangle$ through a two-atom Raman process with evolution duration π/Ω, enabling collective excitation in the RAB regime. Then the system is tuned near a non-equilibrium phase transition critical point by adjusting the probe laser detuning Δ_p and Rabi frequency Ω_p, where quantum fluctuations diverge and the optical transmission exhibits a steep, population-dependent spectral edge. At criticality, the interplay between RRI-induced shifts of $\left\vert rr\right\rangle$ and external microwave fields amplifies the sensitivity: Small microwave-induced Stark shifts Δ_mw perturb the critical detuning, causing significant changes in $\left\vert rr\right\rangle$ population and transmission signals. The Fisher information, derived from the maximal slope of transmission spectra, quantifies the metrological gain, revealing a giant enhancement over single-atom systems due to critical two-atom RAB correlations. By continuously probing the transmission near the critical point and analyzing differential photon-counting signals, even very weak microwave field amplitudes can be resolved, leveraging the divergent susceptibility and nonlinear dynamics of the interacting Rydberg atoms.

Application in the Grover-Long algorithm

Finally, we consider to apply the proposed C-Phase gates in implementing the multi-item quantum search algorithm. According to the Grover-Long algorithm^80,99, by replacing the phase inversion with phase rotation in oracle and diffusion operations, the desired target items can be searched with zero failure rate. The detailed circuit diagram is presented in Fig. 7a, together with the following steps.

Fig. 7: Diagram of the Grover-Long algorithm.

a The quantum circuit depicting the search algorithm for both one-item and two-item scenarios. b The fidelity evolution of the target state in the search algorithm for one-item and two-item over time, where the solid red line denotes the one-item and the dashed blue line represents the two-item.

(i) Starting with the initial state $\frac{1}{2}(\left\vert 00\right\rangle +\left\vert 01\right\rangle +\left\vert 10\right\rangle +\left\vert 11\right\rangle )$, the oracle operator is applied to mark the target items. The utilization of one-item search $\left\vert 11\right\rangle$ as a case study to elucidate the implementation procedure, the oracle operator is defined as U₁ = $\left\vert 00\right\rangle \left\langle 00\right\vert +\left\vert 01\right\rangle \left\langle 01\right\vert +\left\vert 10\right\rangle \left\langle 10\right\vert -\left\vert 11\right\rangle \left\langle 11\right\vert$, which is implemented by selecting ϑ = π/2 in C-Phase gate together with the single-qubit operator U = $\left\vert 0\right\rangle \left\langle 0\right\vert +i\left\vert 1\right\rangle \left\langle 1\right\vert$ applied to both qubits. For the two-item target state $(\left\vert 01\right\rangle +\left\vert 10\right\rangle )/\sqrt{2}$, the oracle operator is given by U₁ = $\left\vert 00\right\rangle \left\langle 00\right\vert +i\left\vert 01\right\rangle \left\langle 01\right\vert +i\left\vert 10\right\rangle \left\langle 10\right\vert +\left\vert 11\right\rangle \left\langle 11\right\vert$, which is realized by setting ϑ = −π/2 in C-Phase gate.

(ii) For the diffusion operator, the inverse Hadamard operation (H^†) is initially applied to each qubit. The operator U₂ is identical to U₁ in the case of the one-item search. However, for the two-item search, U₂ is defined as $\left\vert 00\right\rangle \left\langle 00\right\vert +\left\vert 01\right\rangle \left\langle 01\right\vert +\left\vert 10\right\rangle \left\langle 10\right\vert +i\left\vert 11\right\rangle \left\langle 11\right\vert$, which is implemented by setting ϑ = −5π/4 in C-Phase gate together with the single qubit operation U = $\left\vert 0\right\rangle \left\langle 0\right\vert +{e}^{i\pi /4}\left\vert 1\right\rangle \left\langle 1\right\vert$ applied to each qubit. Finally, the Hadamard operation is applied to each qubit to complete the diffusion process.

Following these steps, the one-item and two-item searches are successfully implemented, with the dynamical processes are illustrated in Fig. 7b. The achieved fidelities of 0.9975 for the one-item search and 0.9879 for the two-item search underscore the effectiveness of our scheme. Notably, the proposed approach simplifies the circuit design and eliminates the need for individual addressing in two-qubit operations, thereby significantly improving the accuracy and efficiency of the quantum search algorithm.

Discussion

We have introduced a strategy to realize a C-Phase gate utilizing Rydberg atoms with FFM techniques. This approach is implemented through the Floquet periodic modulation of the atom-field detuning. This method leverages the synergistic effect between periodic modulation and RRI strength, providing a versatile platform for quantum system manipulation through parameter optimization. Notably, it effectively circumvents the conventional limitation where interaction strength is strictly governed by interatomic distance in Rydberg systems. This capability is particularly advantageous for the development of quantum logic gates. With respect to the most recent experimental parameters concerning the alkali metal rubidium atom, the C-Phase gates devised by our proposed approach exhibit outstanding performances. Furthermore, our method can be integrated with the Gaussian soft quantum control to enhance the fidelity and robustness of the C-Phase gate. Ultimately, our C-Phase gates holds promise for search algorithms with high success rates, thereby significantly enhancing the efficacy of multi-qubit operations without the necessity for laser independent addressing. We envision that combining FFM with advanced quantum control of Rydberg atoms will unlock new opportunities for achieving efficient and fault-tolerant quantum computation, enabling the realization of sophisticated quantum algorithms and the discovery of unprecedented quantum phenomena in precisely engineered coherent systems.

Methods

Floquet frequency modulation

Utilizing the FFM method, we implement periodic modulation of the atom-field detuning, selecting optimal modulation parameters to govern the quantum system dynamics towards achieving high-fidelity and robust quantum gates. Through a sequence of procedures including the system Hamiltonian picture transformation and Jacobi-Anger expansion, we derive the equivalent Rabi frequency dominated by Bessel functions. By manipulating the modulation index appropriately, we steer the system’s evolution to realize the targeted controlled-phase gates.

Under the modulation of Floquet method, the Hamiltonian of the system transforms into

$$\frac{\hat{H}(t)}{\hslash }=-\Delta (t)\mathop{\sum}\limits_{i=1}^{2}{\hat{\sigma }}_{rr}^{i}+\frac{\Omega (t)}{2}{e}^{i\phi (t)}\mathop{\sum}\limits_{i=1}^{2}{\hat{\sigma }}_{x}^{i}+V{\hat{\sigma }}_{rr}{\hat{\sigma }}_{rr}$$

(14)

where ${\hat{\sigma }}_{ab}=\left\vert a\right\rangle \left\langle b\right\vert$ and a, b ∈ {r, 1}. Besides, ${\hat{\sigma }}_{x}={\hat{\sigma }}_{r1}+{\hat{\sigma }}_{1r}$.

Soft quantum control

When SP are employed, the fidelity evolution exhibits pronounced oscillations. To mitigate this issue, we employ soft quantum control techniques to optimize the parameters and convert the SPs into GPs. This transformation aims to align more effectively with the requirements of RWA, thereby diminishing the impact of control errors and ultimately enhancing the gate performance.

The optimized time-evolving GP form is presented in Eq. (15)

$${\Omega }_{g}(t)={\Omega }_{g}{e}^{\frac{-{(t-2{T}_{g})}^{2}}{{T}_{g}^{2}}},0 < t\le T$$

(15)

where Ω_g and T_g denote the maximum amplitude and width of GP, respectively.