Quantitative cancer-immunity cycle modeling for predicting disease progression in advanced metastatic colorectal cancer

Abstract

Patients with advanced metastatic colorectal cancer (mCRC) typically exhibit significant interindividual differences in treatment responses and face poor survival outcomes. To systematically analyze the heterogeneous tumor progression and recurrence observed in advanced mCRC patients, we developed a quantitative cancer-immunity cycle (QCIC) model. The QCIC model employs differential equations to capture the biological mechanisms underlying the cancer-immunity cycle and predicts tumor evolution dynamics under various treatment strategies through stochastic computational methods. We introduce the treatment response index (TRI) to quantify disease progression in virtual clinical trials and the death probability function (DPF) to estimate overall survival. Additionally, we investigate the impact of predictive biomarkers on survival prognosis in advanced mCRC patients, identifying tumor-infiltrating CD8+ cytotoxic T lymphocytes (CTLs) as key predictors of disease progression and the tumor-infiltrating CD4+ Th1/Treg ratio as a significant determinant of survival outcomes. This study presents an approach that bridges the gap between diverse clinical data sources and the generation of virtual patient cohorts, providing valuable insights into interindividual treatment variability and survival forecasting in mCRC patients.

Introduction

Colorectal cancer (CRC) is the third most prevalent malignant tumor globally and the second leading cause of cancer-related deaths, posing a significant health challenge¹. Metastatic colorectal cancer (mCRC), in particular, is associated with poor prognosis and presents considerable clinical challenges². Recent clinical trials have highlighted the efficacy of combination therapy involving the novel chemotherapeutic TAS-102 and bevacizumab in advanced mCRC patients, significantly improving survival rates³. This therapeutic approach has shown promising results and is expected to transform the treatment landscape for advanced mCRC. However, despite its favorable efficacy compared to standard treatments, discrepancies in response and persistent tumor recurrence remain significant obstacles in clinical practice⁴.

Tumor-immune interactions play a crucial role in cancer initiation and progression, underscoring the need to better understand these dynamics^5,6. The recently proposed cancer-immunity cycle concept provides a comprehensive framework that highlights the critical role of the immune system in eradicating tumor cells^7,8,9. By expanding beyond the localized tumor microenvironment, the cancer-immunity cycle offers a holistic perspective on immune responses across different body compartments^7,8,9, making it a valuable tool for quantitatively analyzing the prognosis of mCRC patients.

Mathematical modeling offers a powerful approach to unraveling the complex interactions between tumors and the immune system. Ordinary differential equations (ODEs) have been extensively used as the primary mathematical tool for modeling and analyzing tumor-immune interactions. In the 1990s, Kuznetsov et al.¹⁰ applied the foundational principles of the Lotka-Volterra model to tumor-immunity dynamics. Subsequently, Kirschner et al.¹¹ incorporated the interactions between IL-2, tumor cells, and effector cells into their model. Pillis et al.¹² expanded this framework by introducing NK cells, CD8+ T cells, and circulating lymphocytes, enabling an exploration of the effects of chemotherapy and immunotherapy on tumor progression. Robertson-Tessi et al.¹³ further advanced this field by developing a comprehensive mathematical model that included a negative feedback loop to account for immunosuppressive mechanisms. Additionally, numerous studies have developed ODE-based models to investigate various aspects of tumor-immune interactions, significantly advancing this field of research^{14,15,16,17,18,19,20}. While capturing all cell types and signaling molecules involved in tumor-immunity interactions is ambitious, it is critical to balance model complexity to avoid overlooking the intricate dynamics observed in experimental and clinical settings.

In recent years, significant advancements in tumor immunology have enabled the development of high-dimensional, complex models based on tumor immunity mechanisms. Concurrently, reaction-diffusion equations (RDEs) have been increasingly employed to describe molecular diffusion and intercellular interactions systematically. For instance, Lai and Friedman et al.^21,22,23 used RDE models to clarify the biological mechanisms driving interactions among tumor cells, immune cells, and cytokines, facilitating the study of combination therapy for tumors. These models have primarily focused on investigating the synergistic or antagonistic effects of different drugs in tumor therapy. Additionally, Kim et al.^24,25,26 leveraged RDE models to define adhesion processes, providing mathematical insights into various cell migration patterns. While RDE models excel at describing the spatiotemporal dynamics of tumor-immune interactions, they fall short in explaining the biological mechanisms across different compartments of the organism.

In multi-compartmental modeling, quantitative systems pharmacology (QSP) models have gained considerable attention. These models utilize ODEs to investigate tumor-immune interactions. Wang and Popel et al.^27,28,29,30 developed QSP models dividing the human body into four compartments: central, peripheral, tumor, and tumor-draining lymph nodes. These models integrate various immune cells, cytokines, and drug modules into their respective compartments, enabling realistic simulations of immune responses. Furthermore, QSP models provide valuable insights into the interindividual variability in treatment responses among patients receiving the same therapy. However, they lack a comprehensive quantitative description of the cancer-immunity cycle.

In this study, we propose a quantitative cancer-immunity cycle (QCIC) model, a multi-compartmental, multi-scale, multi-dimensional ODE framework, to elucidate the complex dynamics of tumor-immune interactions during disease progression and therapy. Integrating knowledge from immunology, oncology, clinical medicine, computational systems biology, and applied mathematics, the QCIC model offers a detailed mathematical description of cell fate decisions and tumor immunity mechanisms. This model aims to capture inter-individual treatment variation, thereby providing valuable insights into personalized therapeutic strategies. We introduce the treatment response index (TRI), based on changes in tumor volume before and after treatment, to evaluate short-term treatment efficacy. Additionally, we designed the death probability function (DPF) to quantitatively assess the risk of patient death associated with tumor growth. Finally, this study investigates the influence of predictive biomarkers on survival outcomes in advanced mCRC patients, identifying tumor-infiltrating CD8+ cytotoxic T lymphocytes (CTLs) as a key predictor of disease progression and the CD4+ Th1/Treg ratio as a significant determinant of survival prognosis.

Results

Quantitative cancer-immunity cycle model

In this study, we developed a mathematical model based on the cancer-immunity cycle theory, termed the QCIC model, to quantitatively describe the dynamic evolution of mCRC^7,8,9. The QCIC model was established to achieve the following objectives: (1) capture drug resistance and recurrence phenomena in mCRC patients undergoing clinical treatment, (2) elucidate inter-individual therapeutic variability among mCRC patients receiving identical treatment regimens, and (3) predict patient survival using predictive biomarkers derived from the QCIC model. A schematic of the research framework and the QCIC model is presented in Fig. 1.

Fig. 1: Illustration of the research framework for data-driven virtual patient generation and in silico clinical trials using the QCIC model.

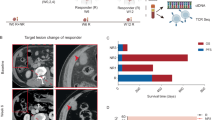
a Short-term efficacy indices for solid tumors derived from clinical trial reports. b Tumor-immune interaction mechanisms across multiple compartments. The TDLN compartment focuses on antigen presentation and cell differentiation, the PB compartment facilitates immune cell transport between tissues, the TME represents the complex interplay between tumor and immune cells, and the BT compartment serves as the primary site for immune cell production. c The PK/PD model. d Mathematical description of the seven main steps of the QCIC model. Step 1: Tumor cell antigens released via mechanisms including normal apoptosis (${\kappa }_{1}\overrightarrow{D}$), immune attack (${\kappa }_{2}\overrightarrow{I}$), and chemotherapy-induced killing (${\kappa }_{3}\overrightarrow{C}$). Step 2: Tumor antigen presentation is facilitated by activated dendritic cells. Step 3: T-cell priming and activation, the differentiation and proliferation are described by the Michaelis-Menten and Hill functions, respectively. Steps 4 and 5: Immune cell migration and chemotaxis. Step 6: Tumor cell heterogeneity that is represented by drug-sensitive (X₁), drug-resistant (X₂), and drug-pressure (X₃) tumor cell types. Step 7: Tumor-immune interactions that involve immune cell-mediated targeting and tumor-induced immunosuppression via the PD-1/PD-L1 pathway. e Generate virtual patients displaying clinical disease progression by adjusting tumor heterogeneity parameters. f Predicting inter-individual treatment differences in advanced mCRC patients through in silico clinical trials. g Prediction of survival rates for different mCRC patients based on QCIC model-derived predictive biomarkers. For detailed descriptions of mechanisms, symbol meanings, and dynamic equations, refer to Methods 4.2, Supplementary Text 1, and Supplementary Text 2.

Research framework

The framework of our study is outlined as follows. Firstly, we selected 10 representative mCRC clinical trials conducted between 2012 and 2023, all of which adhered to consistent management protocols and requirements^{31,32,33,34,35,36,37,38,39,40}. Clinical tumor efficacy evaluation indices were extracted from these trials, including complete response (CR), partial response (PR), stable disease (SD), progressive disease (PD), objective response rate (ORR), and disease control rate (DCR) (Fig. 1a). These indices were used to evaluate the QCIC model’s ability to predict treatment variability among mCRC patients.

Secondly, the QCIC model was constructed as a multi-compartmental ODE model based on tumor immunity mechanisms (Fig. 1b). This model comprises four compartments: tumor-draining lymph node (TDLN), peripheral blood (PB), tumor microenvironment (TME), and bone marrow and thymus (BT). In TDLN (compartment A), dendritic cells perform antigen presentation to initiate the tumor immune response⁴¹. Naive T cells differentiate into various subpopulations of effector T cells in response to antigen stimulation and the local cytokine environment^42,43. The PB (compartment B) functions as the main site for blood circulation, enabling cell migration between compartments⁴⁴. In the TME (compartment C), complex interactions occur between the immune system and tumor cells^45,46,47. Effector T cells and NK cells, which are key components of adaptive and innate immunity, respectively, effectively eliminate tumor cells. The BT (compartment D) continuously produces naive and immature immune cells to maintain immune system stability^48,49.

Our study primarily investigates the progression of mCRC in responses to chemotherapy (TAS-102) and anti-VEGF therapy (bevacizumab). To account for tumor cell heterogeneity, we assumed that tumors consist of three types of cells: drug-sensitive tumor cells (DSTC), drug-resistant tumor cells (DRTC), and drug-pressure tumor cells (DPTC). These cell types exhibit distinct progression dynamics and varying responses to treatment. Furthermore, chemotherapy can induce the transition of drug-sensitive and drug-resistant cells into drug-pressure cells⁵⁰. Drug-pressure tumor cells are defined as those that do not respond to chemotherapy.

Next, we integrated a pharmacokinetic (PK)/pharmacodynamic (PD) model into the QCIC model to elucidate the mechanism of drug action (Fig. 1c). In this model, drug concentrations in the central compartment represent those in tumor tissue and peripheral blood, while drug concentrations in the peripheral compartments correspond to other regions. This integration enabled the development of a QCIC model that effectively incorporates the mechanism of drug action. The mathematical formulation of the PK/PD model is given in Methods 4.3 and Supplementary Text 2.

Subsequently, the mathematical formulations of the QCIC model were established based on the cancer-immunity cycle illustrated in Fig. 1d. The biological mechanisms of each step are detailed as follows:

• (1) Cancer cell antigen release. In the TME, tumor-associated antigens released by necrotic tumor cells are captured and processed by dendritic cells, initiating systemic immune responses^7,8.

• (2) Cancer cell antigen presentation. Dendritic cells process antigens and present them as peptide-major histocompatibility complex (MHC) complexes^51,52.

• (3) T cell activation. Antigen-loaded dendritic cells migrate to TDLN via the lymphatic circulation, where they present antigenic peptides to naive T cells, promoting the production and proliferation of effector T cells⁴¹.

• (4) Trafficking of T cells to tumors. Effector T cells travel through the PB system to reach tumor tissue⁴⁴.

• (5) T cell infiltration into tumors. Effector T cells infiltrate the tumor via vascular permeability and chemokine-mediated signaling⁵³.

• (6) T cells recognize cancer cells. Effector T cells in the TME recognize and bind to cancer cells through their T cell receptors.

• (7) Killing of cancer cells. Effector T cells induce tumor cell death via direct contact or release of cytotoxic substances, such as granzyme, perforin, and interferon, thereby eliminating tumor lesions^7,8.

Finally, we identified the range of model parameter values based on their biological interpretations and generated a virtual patient cohort by adjusting the sampling frequency of model parameters (Fig. 1e). The treatment responses of these virtual patients closely matched those observed in real clinical trials, capturing individual variations in treatment outcomes among patients (Fig. 1f). Additionally, biomarker analyses were performed to assess the survival prognosis of advanced mCRC patients (Fig. 1g).

Mathematical formulation

The QCIC model describes the dynamic evolution of various tumor and immune cell populations. The formulation considers multiple processes influencing the behavior of cell type i: source (${{\mathcal{S}}}_{i}$), differentiation (${{\mathcal{D}}}_{i}$), proliferation (${{\mathcal{P}}}_{i}$), transition (${{\mathcal{T}}}_{i}$), migration (${{\mathcal{V}}}_{i}$), chemotaxis (${{\mathcal{X}}}_{i}$), killing (${{\mathcal{I}}}_{i}$), and apoptosis (${{\mathcal{A}}}_{i}$). Let [i]_n(t) denote the density of cell type i in compartment n at time t. The dynamics of [i]_n(t) are governed by the following equation:

$$\frac{{\rm{d}}{[i]}_{n}(t)}{{\rm{d}}t}={{\mathcal{S}}}_{i}+{{\mathcal{D}}}_{i}+{{\mathcal{P}}}_{i}+{{\mathcal{T}}}_{i}+{{\mathcal{V}}}_{i}+{{\mathcal{X}}}_{i}+{{\mathcal{I}}}_{i}+{{\mathcal{A}}}_{i}.$$

(1)

Below, we detail the mathematical representation of each process.

Cell source ${{\mathcal{S}}}_{i}$

The source term is defined as:

$${{\mathcal{S}}}_{i}={\theta }_{i}^{mn},$$

(2)

which represents the release of cell type i from compartment m to compartment n. This term models the continuous generation of naive or immature cells originating from the bone marrow or thymus.

Cell differentiation ${{\mathcal{D}}}_{i}$

Cell differentiation occurs in two contexts. First, naive T cells within the TDLN differentiate into various effector T cell types in response to activated dendritic cells and cytokines. This process is mathematically represented as a combination of the Michaelis-Menten and Hill functions^21,54,55:

$${{\mathcal{D}}}_{i}={\kappa }_{i}\left(1+\sum _{p}{\lambda }_{ip}\frac{{[p]}_{m}}{{K}_{p}+{[p]}_{m}}\right)\prod _{q}\frac{{K}_{iq}}{{K}_{iq}+{[q]}_{m}}\frac{{[D]}_{m}^{n}}{{K}_{D}^{n}+{[D]}_{m}^{n}}{[{i}_{0}]}_{m},$$

(3)

where κ_i is the differentiation rate of cell type i, λ_ip is the enhancement coefficient of cytokine p on the differentiation of cell type i, [p]_m and [q]_m are cytokine concentrations in compartment m, K_p and K_iq denote the half-saturation and inhibition constants, [D]_m is the density of activated DCs, K_D is the half-saturation constant of activated DCs, n Hill’s coefficient, and ${[{i}_{0}]}_{m}$ is the density of naive T cells in compartment m.

Secondly, in the TME, neutrophils and macrophages polarize into pro-tumor or anti-tumor phenotypes. Polarization is mathematically described as:

$${{\mathcal{D}}}_{i}={\psi }_{i}\left(1+\sum _{p}{\lambda }_{{i}_{0}p}\frac{{[p]}_{m}}{{K}_{p}+{[p]}_{m}}\right){[{i}_{0}]}_{m},$$

(4)

where ψ_i is the polarization rate, ${\lambda }_{{i}_{0}p}$ is the enhancement coefficient, and i₀ is the precursor of cell type i.

Cell proliferation ${{\mathcal{P}}}_{i}$

The cell proliferation term is modeled in three contexts. The proliferation of naive T cells in the TDLN adheres to the logistic equation as⁵⁴:

$${{\mathcal{P}}}_{i}={\beta }_{i}{[i]}_{m}\left(1-\frac{{[i]}_{m}}{{K}_{i}}\right),$$

(5)

where β_i represents the proliferation rate of naive T cells and K_i is the corresponding carrying capacity.

The proliferation of lymphocytes (e.g., T cells and NK cells) in the TDLN under cytokine influence is represented as:

$${{\mathcal{P}}}_{i}={\beta }_{i}\left(1+\sum _{p}{\lambda }_{ip}\frac{{[p]}_{m}}{{K}_{p}+{[p]}_{m}}\right)\prod _{q}\frac{{K}_{iq}}{{K}_{iq}+{[q]}_{m}}{[i]}_{m},$$

(6)

where β_i represents the proliferation rate, λ_ip denotes the enhancement coefficient, K_p is the half-saturation constant, and K_iq denotes the inhibition constant.

We assume that various tumor cell subpopulations compete for resources for their proliferation. The tumor cell proliferation is modeled using competitive logistic equations⁵⁶:

$${{\mathcal{P}}}_{i}={\beta }_{i}{[i]}_{m}\left(1-\frac{{\sum }_{j}{a}_{ij}{[j]}_{m}}{{K}_{i}}\right),$$

(7)

where K_i represents the carrying capacity of tumor cell type i, a_ij represents the competition coefficients for tumor cells.

Cell type transition ${{\mathcal{T}}}_{i}$

Cell type transitions can be driven by cytokines or drug pressures, resulting in cellular plasticity. Mathematically, cell type transition is represented as²¹:

$${{\mathcal{T}}}_{i}={\rho }_{ij}\sum _{p}\frac{{[p]}_{m}^{n}}{{K}_{p}^{n}+{[p]}_{m}^{n}}{[j]}_{m}\quad \,{\text{or}}\,\quad {{\mathcal{T}}}_{j}=-{\rho }_{ij}\sum _{p}\frac{{[p]}_{m}^{n}}{{K}_{p}^{n}+{[p]}_{m}^{n}}{[j]}_{m},$$

(8)

where ρ_ij represents the transition rate, [p]_m is the concentrations of cytokine or drug p in compartment m, K_p represents the half-saturation constant, n represents the Hill’s coefficient. Specifically, we select n = 1 for cytokines and n > 1 for drugs.

Cell migration ${{\mathcal{V}}}_{i}$

Cell migration between different compartments is modeled as^54,55:

$${{\mathcal{V}}}_{i}^{n}={{\mathcal{V}}}_{{\rm{input}}}^{n}-{{\mathcal{V}}}_{{\rm{output}}}^{n}=\sum _{m}{\upsilon }_{i}^{mn}\frac{{V}_{m}}{{V}_{n}}{[i]}_{m}-\sum _{l}{\upsilon }_{i}^{nl}{[i]}_{n},$$

(9)

where ${\upsilon }_{i}^{mn}$ and ${\upsilon }_{i}^{nl}$ are migration rates, and V_m and V_n are compartment volumes.

Cell chemotaxis ${{\mathcal{X}}}_{i}$

Chemotaxis under chemokine influence is represented as^27,28:

$${{\mathcal{X}}}_{i}^{n}=\sum _{p}{\chi }_{ip}^{mn}\frac{{[p]}_{n}}{{K}_{p}+{[p]}_{n}}{[i]}_{m}\quad or\quad {{\mathcal{X}}}_{i}^{m}=-\sum _{p}{\chi }_{ip}^{mn}\frac{{[p]}_{n}}{{K}_{p}+{[p]}_{n}}{[i]}_{m},$$

(10)

where ${\chi }_{ip}^{mn}$ is the chemotactic rate, and K_p is the chemokine’s half-saturation constant.

Cell killing ${{\mathcal{I}}}_{i}$

Immune killing of tumor cells is formulated as^18,21,22,23:

$${{\mathcal{I}}}_{i}=-\left(\sum _{j}{\eta }_{ij}{[j]}_{m}\right)\left(1-{\lambda }_{{P}_{L}}\frac{{[{P}_{L}]}_{m}}{{K}_{{P}_{L}}+{[{P}_{L}]}_{m}}\right){[i]}_{m},$$

(11)

where η_ij is the killing rate by tumor cells, and ${\lambda }_{{P}_{L}}$ represents the killing regulation coefficient by the PD-1/PD-L1 complex, ${K}_{{P}_{L}}$ represents the half-saturation constant, ${[{P}_{L}]}_{m}$ represents the concentration of PD-1/PD-L1 complex in the compartment m.

Cell apoptosis ${{\mathcal{A}}}_{i}$

Apoptosis is represented by four mechanisms. The natural apoptosis is described as^18,21,22,23:

$${{\mathcal{A}}}_{i}=-{d}_{i}{[i]}_{m},$$

(12)

where d_i is the apoptosis rate.

Self-limiting cell death induced by lymphocyte contact is expressed as:

$${{\mathcal{A}}}_{i}=-{d}_{i}\left(1+{\lambda }_{i}\frac{{[i]}_{m}}{{K}_{i}+{[i]}_{m}}\right){[i]}_{m},$$

(13)

where d_i is the apoptosis rate, λ_i represents the regulatory coefficient caused by the self-limiting, K_i is the half-saturation constant.

Moreover, tumor cells can induce programmed death of T cells and NK cells by PD-1/PD-L1. The effect is formulated as:

$${{\mathcal{A}}}_{i}=-{d}_{i}\left(1+{\lambda }_{i{P}_{L}}\frac{{[{P}_{L}]}_{m}}{{K}_{{P}_{L}}+{[{P}_{L}]}_{m}}\right){[i]}_{m},$$

(14)

where d_i is the apoptosis rate, ${\lambda }_{i{P}_{L}}$ represents the apoptosis regulation coefficient.

Finally, the chemotherapy-induced apoptosis is expressed as⁵⁷:

$${{\mathcal{A}}}_{i}=-{\sigma }_{i}\left(1-{e}^{-{\varepsilon }_{C}{[{C}_{{\rm{hem}}}]}_{m}}\right){[i]}_{m},$$

(15)

where σ_i is the killing rate by chemotherapy, ε_C represents the effective coefficient, ${[{C}_{{\rm{hem}}}]}_{m}$ denoes the concentration of the chemotherapy drug.

The equations above summarized the formulations governing the population dynamics of various cell types. To fully capture the cancer-immunity cycle, it is necessary to integrate these cell population dynamics with molecular-level dynamics of cytokines and chemokines. The dynamic changes in molecular concentrations typically involve both production and degradation processes. The behavior of a cytokine or chemokine p in compartment n can be described by the following equation:

$$\tau \frac{{\rm{d}}{[p]}_{n}(t)}{{\rm{d}}t}={{\mathcal{G}}}_{p}+{{\mathcal{H}}}_{p}$$

(16)

where ${{\mathcal{G}}}_{p}=\mathop{\sum }\nolimits_{i = 1}^{k}{\delta }_{pi}{[i]}_{n}$ and ${{\mathcal{H}}}_{p}=-{d}_{p}{[p]}_{n}$ represent the production and degradation of cytokine or chemokine p, respectively; τ ≪ 1 represents the fast time scale parameter. Here, k denotes the number of cell types capable of secreting cytokine or chemokine p, δ_pi is the secretion rate of cytokine or chemokine p by cell type i, and d_p is the degradation rate of cytokine or chemokine p. In the QCIC model, the molecular-level dynamics are assumed to occur on a faster timescale compared to the slower dynamic evolution at the cellular level.

In summary, we developed an ODE-based framework consisting of 95 variables, including 52 cell populations and 43 molecular concentrations, based on the construction principles of the QCIC model. This framework is designed to describe the dynamic processes of the tumor-immune response. Detailed dynamics involving tumor cells, immune cells, cytokines, and chemokines are presented in Supplementary Texts 1–4.

Parameter estimation

The QCIC model integrates kinetic parameters representing fundamental biological mechanisms, including cell differentiation, proliferation, transition, migration, chemotaxis, killing, apoptosis, and the secretion and degradation of cytokines. We estimated parameter ranges based on their underlying biological mechanisms. First, we defined biologically plausible ranges for each parameter. Next, parameters were randomly assigned within these ranges to ensure biological relevance. Finally, clinical data were used to fine-tune the parameters, ensuring that model predictions aligned with observed clinical outcomes. Essential parameters influencing cancer-immune responses were prioritized, and random sampling was employed to generate virtual patient cohorts. The parameter sampling distribution was adjusted to ensure consistency between the outcomes of in silico clinical trials and clinical trial data (see Methods 4.4 and Supplementary text 4–5).

Dynamic parameter estimation primarily relied on published literature to establish the order of magnitude for each parameter type. For example, the migration rates of cell type i between compartments (${\upsilon }_{i}^{mn}$) range from 10⁻³ to 10¹day^−1 54. Compartment volumes (V_m) typically from 10⁻² to 10¹ L⁵⁴. Cell proliferation rates (β_i) range from 10⁻¹ to 10⁻²day⁻¹, as indicated in mathematical modeling studies^21,23,54,56. Similarly, cytokine regulatory coefficients for cell proliferation, differentiation, and death (λ_ip) range from 0 to 1^54,58.

The carrying capacities of cells (K_i) range from 10⁷ to 10⁹cells ⋅ L^{−1 21,23,27,28,29,54,56}. The half-saturation constants for cytokines and chemokines (K_p) range from 10³ to 10⁷pg ⋅ L⁻¹, based on half-saturation estimation methods (Supplementary Text 3)^21,23,28. The half-saturation constant of cells (K_i) ranges from 10⁹ to 10¹¹ cells ⋅ L^−1 28. Cell differentiation rates (κ_i) and polarization rates (ψ_i) ranges from 10⁻² to 10⁻¹ day^−1 28,54. The cell phenotype transformation rate (ρ_ij) ranges from 10⁻³ to 10⁻¹day^{−1 21,28,59}. Cell chemotaxis rates (${\chi }_{ip}^{mn}$) range from 10⁻² to 10⁻¹day⁻¹, based on immunological experiments^{60,61,62,63,64,65,66,67,68,69,70,71}.

Cell apoptosis and cytokine degradation rates were estimated using half-life calculation methods (Supplementary Text 3). The cell apoptosis rate ranges from 10⁻³ to 10⁰ day^{−1[ 21,27,28,29,54,56,58}, while cytokine degradation rates range from 10⁻² to 10³ day^{−1[ 14,21,28}. The immune cell release rate (${\theta }_{i}^{mn}$) is between 10⁸ and 10¹⁰cells ⋅ L⁻¹ ⋅ day^−1 54. Cytokine and chemokine secretion rates (δ_pi) range from 10⁻¹⁰ to 10⁻²pg ⋅ cell⁻¹ ⋅ day^{−1 13,21,54}. The immune checkpoint expression rate (ϕ_i) is between 10⁻⁸ and 10⁻⁶ g ⋅ cell^−1[ 18. Competition coefficients (a_ij) between tumor subpopulations range from 1 to 6⁵⁶, and the immune cell-mediated tumor killing rate (η_ij) is between 10⁻¹² and 10⁻⁹L ⋅ cell⁻¹ ⋅ day^{−1[ 21,23}.

The parameter ranges and magnitudes are listed in Supplementary Table S3. Specific values and biological functions for each parameter type are detailed in Supplementary Tables S4–S20. For further details on parameter estimation, please refer to Supplementary Texts 3–5.

Prediction of short-term treatment efficacy

In clinical trials, the short-term treatment efficacy of drugs in patients with advanced mCRC is typically assessed using six indices: CR, PR, SD, PD, ORR, and DCR. ORR is defined as the sum of CR and PR, while DCR includes CR, PR, and SD. These evaluation metrics are defined based on changes in tumor status before and after treatment⁷². In this study, to evaluate the predictive performance of the proposed model, we analyzed data from 10 clinical trials involving a total of 2566 advanced mCRC patients (Fig. S1)^{31,32,33,34,35,36,37,38,39,40}. Given the poor prognosis of advanced mCRC patients who are ineligible for surgery, CR, PR, and ORR are rarely observed. Therefore, SD, PD, and DCR are the most relevant indices for evaluating short-term treatment efficacy.

To compare the model predictions with clinical data, we introduced a treatment response index (TRI) as a quantitative measure to assess short-term tumor treatment efficacy. The TRI is defined as (Methods 4.5)

$${\rm{TRI}}=\frac{{V}_{{T}_{{\rm{after}}}}-{V}_{{T}_{{\rm{before}}}}}{{V}_{{T}_{{\rm{before}}}}},$$

where ${V}_{{T}_{{\rm{before}}}}$ and ${V}_{{T}_{{\rm{after}}}}$ represent the pre-treatment (baseline) and post-treatment tumor volumes, respectively. The TRI quantifies the change in tumor volume relative to its baseline value after treatment. According to the Response Evaluation Criteria in Solid Tumors (RECIST) version 1.1⁷², patients are classified as PD if TRI≥0.2, DCR if TRI < 0.2, and SD if − 0.3 ≤ TRI < 0.2.

To validate the QCIC model’s predictive capability for short-term outcomes, we employed the model to generate 100 benchmark virtual patients and conducted in silico clinical trials. We classified each virtual patient based on model simulation and the TRI, from which we obtained the percentages of the six indices under each treatment strategy and compared them with clinical trial data. Model simulations showed that patients with advanced mCRC treated with placebo exhibited SD, PD, and DCR ratios of 15%, 85%, and 15%, respectively (Fig. 2a), closely matching the mean clinical trial data of 15.3%, 84.5%, and 15.5%. Similarly, for patients receiving TAS-102 chemotherapy, the model predicted SD, PD, and DCR ratios of 44%, 55%, and 45%, which closely aligned with the average clinical trial results of 44.4%, 54.3%, and 45.7%, respectively (Fig. 2b). Furthermore, for combination therapy with TAS-102 plus bevacizumab, the model predicted SD, PD, and DCR ratios of 61%, 36%, and 64%, which were consistent with the clinical trial averages of 58.9%, 37.2%, and 62.8%, respectively (Fig. 2c). Additional comparisons between model simulations and individual clinical trials are shown in Fig. S2, demonstrating consistency across all six indices. These results suggest that the QCIC model effectively generates virtual patient cohorts that reflect clinical indices used to evaluate short-term treatment efficacy.

Fig. 2: Validation of the QCIC model at the population level by comparing short-term treatment efficacy evaluation indices (SD, PD, and DCR) from model simulations and clinical data.

a Placebo group, data sourced from^31,32,33. b TAS-102 group, data sourced from^{32,33,34,35,36}. c TAS-102+bevacizumab group, data sourced from^{34,35,36,37,38}. The simulation data comes from 100 benchmark virtual patients using the QCIC model. Solid tumor progression was evaluated according to the simulations at week 8. The bar chart displays a comparison between model prediction and experimental data. Colored dots indicate various clinical data. Dashed lines are used to compare the difference between clinical trials and model simulation. The RECIST for clinical data were calculated using (18) in Methods 4.1, and the RECIST for simulation data were obtained through TRI in Methods 4.5.

To further investigate the QCIC model’s ability to predict cancer progression, we analyzed inter-individual treatment responses based on the benchmark virtual patients and visualized the outcomes at the initial follow-up (eighth week) using spider plots (left) and waterfall plots (right) in Fig. 3. Simulations revealed that the DCR ratio increased from 15% in patients treated with placebo to 45% in patients receiving TAS-102 chemotherapy (Fig. 3a, b), suggesting that 30% of patients may significantly benefit from the treatment. This result highlights the capacity of TAS-102 chemotherapy to reduce tumor burden in advanced mCRC patients. Furthermore, combination therapy with TAS-102 plus bevacizumab further increases the DCR rate to 64% (Fig. 3c), indicating that nearly 50% of patients may experience significant clinical benefits compared with placebo, and a 20% improvement compared with TAS-102 monotherapy. These model simulations underscore the added clinical benefits associated with combination therapy.

Fig. 3: The tumor dynamic evolution (left) and short-term efficacy (right) of benchmark virtual patients generated by the QCIC model.

Treatment response is evaluated based on RECIST V.1.1 in the placebo group (a), TAS-102 group (b), and TAS-102+bevacizumab group (c). Tumor volume changes were recorded every two treatment cycles (every eight weeks), consistent with medical imaging used to assess disease progression. In spider plots on the left, each thin line represents an individual virtual patient, while the thick line represents the average performance across the cohort. Red indicates PD patients, yellow indicates SD patients, and blue indicates CR/PR patients. In the waterfall plots on the right, each bar represents tumor volume change relative to the baseline for a virtual patient during the first imaging examination (eighth week). The left side of the blue dashed line represents the PD patient population, while the right side represents the DCR patient population.

Prediction of the overall survival

To assess the QCIC model’s ability to predict the long-term efficacy of drug therapy in advanced mCRC patients, we introduced a death probability function (DPF) based on tumor burden. In clinical practice, the causes of patient death are complex and multifaceted. In this study, we focused on the effect of tumors and assumed that the death probability is primarily determined by the number of dominant tumor cell types.

Let $\vec{X}=({X}_{1},{X}_{2},{X}_{3})$, where X_i represents the number of tumor cells of type i. The relative number of dominant tumor cells is denoted as $\chi (\vec{X})=\frac{{X}_{j}}{{K}_{j}}$, where j denotes the index of the dominant cell type, defined such that ${X}_{j}=\max \{{X}_{1},{X}_{2},{X}_{3}\}$, and K_j is the corresponding carrying capacity (Table S19). The DPF under the i-th treatment option (placebo, TAS-102, or TAS-102+bevacizumab) is defined as (Methods 4.6):

$${P}_{i}(\vec{X})=\frac{1}{1+\exp (-(\chi (\vec{X})-{\mu }_{i})/{\sigma }_{i})},$$

(17)

where μ_i and σ_i are shape parameters. The shape parameters for each treatment option are provided in Table S21 in Supplementary Text 5.

We used DPF along with tumor evolution data from the baseline virtual patients to evaluate the death risk in advanced mCRC patients. To describe the variability in treatment outcomes across different environments, we randomly selected shape parameters μ_i and σ_i from the ranges given in Table S21 and conducted 10 rounds of calculations. The median overall survivals (M-OS) were derived from these calculations. The results showed that the M-OS for advanced mCRC patients receiving placebo, TAS-102, and TAS-102+bevacizumab were 6.1 months vs. 6.01 months, 7.6 months vs. 7.52 months, and 10.1 months vs. 10.01 months, respectively, in model simulations and clinical trials (Fig. 4a). These findings demonstrate that the QCIC model can effectively predict long-term outcomes following drug therapy.

Fig. 4: Comparison of long-term efficacy evaluation indices in model simulations and clinical data.

a M-OS comparison between model simulations and clinical data. Different color dots represent results from various clinical trials, with dot size weighted by the number of patients. b Death frequencies at 3, 6, 9, and 12 months post-treatment obtained from model simulations and clinical trials. The thick solid line depicts model calculation results, while the dashed line represents clinical trial outcomes.

We also conducted the death frequency analysis among the patients. We compared the death frequencies at 3, 6, 9, and 12 months post-treatment between 10 rounds of random calculation and various clinical trials. The results demonstrated a significant reduction in death rates for patients in the TAS-102 chemotherapy group compared to the placebo group, particularly at 6 months, where the death rate decreased from 33.7% to 22.6% (Fig. 4b). Furthermore, combination therapy significantly reduced patient deaths within the initial 3 months, dropping from 14.2% to 4.7% (Fig. 4b). These findings highlight the effectiveness of TAS-102 in improving six-month survival rates for advanced mCRC patients compared to placebo. Meanwhile, TAS-102+bevacizumab further enhanced survival rates in the early treatment phase (within 3 months).

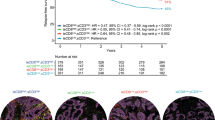
To track disease progression in advanced mCRC patients, we used Kaplan-Meier survival curves to depict overall survival under different treatment options, integrating both clinical data and simulation results (Fig. 5a–c). Figure 5d compares overall survival over time across the three treatment groups. Notably, TAS-102 chemotherapy extended the M-OS from 6.1 to 7.6 months, representing a 1.5-month improvement. Furthermore, the combination therapy of TAS-102 plus bevacizumab extended M-OS by an additional 2.5 months compared to TAS-102 monotherapy.

Fig. 5: Overall survival of advanced mCRC patients on the population scale.

a Placebo group. b TAS-102 group. c TAS-102+bevacizumab group. d Comparison of overall survival in advanced mCRC patients across various treatment options. The solid think lines in blue, red, and orange represent the survival curves predicted by the model for the placebo group, TAS-102 chemotherapy group, and TAS-102+bevacizumab group, respectively. The dashed lines represent survival curves from different clinical trials.

From a one-year overall survival perspective, the combination therapy of TAS-102 plus bevacizumab significantly improved patient survival rates, increasing one-year survival from 16% to nearly 40%–an enhancement of approximately 24% (Fig. 5d). TAS-102 monotherapy improved one-year survival by approximately 11%, while the addition of bevacizumab to TAS-102 therapy further boosted one-year survival by 13% (Fig. 5d).

Predictive biomarkers for mCRC based on the QCIC model

In the advanced stages of cancer development, adaptive immunity is primarily associated with the dynamic evolution of tumors, whereas innate immunity is often linked to factors such as myelosuppression, infection, and viral invasion. To investigate potential biomarkers for predicting progression in advanced mCRC patients, we analyzed the following four indices for virtual patients: the density of tumor-infiltrating CD4+ Th1 cells, the density of tumor-infiltrating CD8+ CTL cells, the tumor-infiltrating CD4+ Th1/Treg ratio, and the tumor-infiltrating CD8+ CTL/Treg ratio. We conducted 4000 random parameter samplings and computational simulations using the parameterized QCIC model, classifying the results into two groups: responders and non-responders. Responders were defined as patients achieving CR, PR, SD, while non-responders were defined as patients with PD. From the 4000 random simulations under different treatment regimens, we excluded instances of inevitable blow-up or decay phenomena in the high-dimensional system solutions and randomly selected 500 data points from each group to compare the distributions of various predictive biomarkers (Fig. 6). To further describe the differences in the distribution of predictive biomarkers between responders and non-responders, we performed a Student’s t-test on two independent data samples using the ttest2 function in MATLAB.

Fig. 6: Distribution of predictive biomarkers calculated by the QCIC model in responders (R) and non-responders (NR).

Distribution of tumor-infiltrating CD4+ Th1 cells (a), CD4+ Th1/Treg (b), CD8+ CTL cells (c), and CD8+ CTL/Treg (d) in responders and non-responders. The data are represented as box plots, where the line inside each box indicates the median and the upper and lower edges represent the upper and lower quartiles, respectively. The p-value of each comparison is less than 0.01 (t-test).

To further evaluate the predictive performance of these biomarkers, we constructed receiver operating characteristic (ROC) curves using machine learning binary classification models. Numerical simulation data from the initial clinical diagnosis (the eighth week) were used as the test set to assess the predictive ability of these biomarkers for short-term treatment outcomes. Among the four biomarkers, the density of tumor-infiltrating CD8+ CTL cells exhibited the highest area under the curve (AUC) in both TAS-102 monotherapy and combination therapy with bevacizumab, reaching 0.77 (Fig. 7a, b). Thus, the density of tumor-infiltrating CD8+ CTL cells emerges as a critical predictive biomarker for short-term treatment efficacy in advanced mCRC patients. Conversely, the tumor-infiltrating CD8+ CTL/Treg ratio demonstrated the poorest predictive performance (Fig. 7a, b).

Fig. 7: ROC analysis of predictive biomarkers in TAS-102 monotherapy and combination therapy with bevacizumab.

ROC analysis of individual biomarkers for TAS-102 (a) and TAS-102+Bevacizumab (b). ROC analysis of combined biomarkers for TAS-102 (c) and TAS-102+Bevacizumab (d). The response status (R vs NR) for each virtual patient was predicted by comparing the pretreatment levels of predictive biomarkers to their respective cut-off values. ROC receiver operating characteristic; AUC area under the curve.

Furthermore, we performed a comprehensive analysis of combined predictive biomarkers. The results showed that the combination of tumor-infiltrating CD4+ Th1 cell density and the CD4+ Th1/Treg ratio exhibited strong predictive power for short-term treatment efficacy, with an AUC of 0.92 for TAS-102 monotherapy and 0.91 for TAS-102 combined with bevacizumab (Fig. 7c, d). Similarly, combinations of tumor-infiltrating CD4+ Th1 cell density and the CD8+ CTL/Treg ratio, as well as CD8+ CTL cell density and the CD4+ Th1/Treg ratio, also demonstrated robust predictive performance, achieving AUC values of 0.85 for TAS-102 monotherapy and 0.86 for TAS-102 in combination with bevacizumab (Fig. 7c, d).

Survival prognosis based on predictive biomarkers of mCRC

To further explore the prognostic value of predictive biomarkers in advanced mCRC patients, we divided the benchmark virtual patients into two groups based on each predictive biomarker: high and low levels. In addition, 40 randomized simulations were conducted, and the mean survival curves, along with the 95% confidence interval, were calculated. The Kaplan-Meier survival curves are shown in Fig. 8.

Fig. 8: Prognostic analysis of predictive biomarkers in combination therapy with TAS-102 plus bevacizumab.

Overall survival analysis in patients with advanced mCRC based on four predictive biomarkers: the tumor-infiltrating CD8+ CTL/Treg ratio (a), the density of tumor-infiltrating CD4+ Th1 cells (b), the tumor-infiltrating CD4+ Th1/Treg ratio (c), and the density of tumor-infiltrating CD8+ CTL cells (d).

Our findings revealed that all four predictive biomarkers significantly influenced patient survival prognosis, though the extent of their impact varied. Notably, a lower tumor-infiltrating CD8+ CTL/Treg ratio was associated with better survival prognosis in the low-expression group, achieving a one-year overall survival rate of 13.1% (Fig. 8a). Among the biomarkers, the tumor-infiltrating CD4+ Th1/Treg ratio exhibited the most pronounced difference in survival outcomes between high- and low-level groups (Fig. 8c). Specifically, this biomarker demonstrated a substantial 79.5% difference in the one-year overall survival rate.

The density of tumor-infiltrating CD4+ Th1 and CD8+ CTL cells also strongly predicted one-year overall survival, with differences of 77.8% and 77.7%, respectively, though these were slightly less pronounced than the CD4+ Th1/Treg ratio (Fig. 8b, d). In summary, the tumor-infiltrating CD4+ Th1/Treg ratio emerged as the most remarkable clinical index for predicting survival prognosis in advanced mCRC patients, as demonstrated by the QCIC model.

Discussion

Mathematical modeling of tumor progression has emerged as a cornerstone of mathematical oncology and computational cancer biology, with numerous studies underscoring its importance^{11,12,13,14,15,16,17,73,74,75,76,77,78,79,80,81}. Various mathematical models, including reaction-diffusion equation, differential equation, differential-integral equation, and individual cell-based modeling, have been applied to study tumor evolution dynamics by quantifying the inter-regulatory relationships among tumor cells, immune cells, and cytokines in the tumor microenvironment^{21,22,23,59,82}. However, the systematic development of models that accurately describe treatment variability among patients–particularly those addressing disease heterogeneity during tumor treatment–remains in its infancy. Recent advancements in QSP models based on pharmacokinetic mechanisms have made significant strides in addressing inter-individual treatment differences and tumor recurrence in cancer patients^27,28,29,30. Nevertheless, the challenge of analyzing survival prognosis using predictive biomarkers derived from mathematical models persists, presenting an important direction for future research.

Patients with advanced mCRC exhibit substantial inter-individual heterogeneity in their responses to clinical treatments. A quantitative understanding of the interactions between tumor evolution and the host immune response is critical for capturing these differences. In this study, we developed the QCIC model–a multi-compartment, multi-scale, multi-dimensional mathematical framework–to quantitatively describe the primary biological processes underlying tumor-immune interactions (Fig. 1). The QCIC model integrates cellular-level biological mechanisms, such as regeneration, differentiation, proliferation, apoptosis, migration, and chemotaxis, with molecular-level processes, including antigen release, presentation, cytokine/chemokine secretion and degradation, and drug metabolism. By incorporating compartments representing key biological sites, such as the tumor microenvironment, peripheral blood, tumor-draining lymph nodes, bone marrow, and thymus, the model provides spatial and temporal dimensions to immune response behaviors. This design enables the model to capture the heterogeneity observed in patients’ clinical responses and offers a systematic approach to understanding tumor evolution and inter-individual treatment variability.

Our study demonstrated that the QCIC model accurately derived short-term clinical efficacy metrics consistent with clinical trials (Fig. 2) and effectively predicted the dynamic evolution of tumor burden in advanced mCRC patients (Fig. 3). The model also assessed long-term clinical outcomes, showing significant improvements in six-month survival rates with TAS-102 chemotherapy and a reduced risk of early mortality with TAS-102 plus bevacizumab combination therapy (Fig. 4). Importantly, the simulated M-OS closely matched clinical data, underscoring the model’s ability to capture both short- and long-term clinical outcomes in mCRC patients (Fig. 5). Furthermore, the analysis of predictive biomarkers derived from the QCIC model highlighted tumor-infiltrating CD8+ CTL cell density as a critical indicator of short-term treatment efficacy (Fig. 7). Prognostic analysis revealed that the tumor-infiltrating CD4+ Th1/Treg ratio serves as a key predictor of survival prognosis (Fig. 8). These findings demonstrate that the QCIC model bridges mathematical modeling and clinical prognosis, advancing existing frameworks toward clinical applications.

It is important to note that the QCIC model relies on patient-specific clinical data, including imaging assessments of solid tumor dynamics, to calibrate the key parameters reflecting tumor heterogeneity. This calibration enhances the model’s ability to provide valuable references for individualized treatment. By predicting tumor dynamics based on pre-treatment medical data, the model can guide timely adjustments to therapeutic strategies during clinical care. While this study focused on the efficacy of TAS-102+bevacizumab therapy, the QCIC model is adaptable to evaluating other drug combinations, provided sufficient clinical data are available. This adaptability holds promise for identifying optimal treatment options for individual patients.

The multi-compartmental QCIC model provides a comprehensive overview of the biological mechanisms underlying tumor-immune regulation, but it has notable limitations. Firstly, the system’s complexity increases the number of parameters, many of which require further experimental determination to obtain better estimations. Second, due to challenges in acquiring patient-specific data on tumor evolution, the QCIC model has not yet been employed to predict disease progression for individual patients. Third, some other important factors, such as nutrition, metabolism, and overall body functioning, should be integrated into the model. Furthermore, the current QCIC model does not integrate single-cell sequencing data or incorporate mechanisms related to immune checkpoint blockade therapy and the gut microbiome. These limitations are waiting for systematically addressed in future studies.

In recent years, accumulating evidence has shown that the dynamic responses within the tumor immune microenvironment (TiME) and the extra-tumor immune microenvironment (extra-TiME) exhibit complex nonlinear patterns during immunotherapy⁸³. Advances in single-cell sequencing technologies and statistical inference methods will enable the calibration of kinetic parameters for immune cells in the QCIC model using nonlinear immune evolution data. Additionally, training the QCIC model on such data will enhance its ability to capture the intricate dynamics of tumor-immune interactions and facilitate the extraction of clinically valuable immune linear scoring indicators.

The QCIC model is a mathematical framework constructed based on known mechanisms of action. According to the cancer treatment guidelines provided by the National Comprehensive Cancer Network (NCCN), the mechanisms of action of anti-tumor drugs can be incorporated into the QCIC model to evaluate the efficacy of various combination therapies in improving survival outcomes for mCRC patients. Immune checkpoint blockade represents a groundbreaking approach to cancer treatment, restoring T cell immune function to eliminate tumor cells. In previous research⁵⁹, we developed a mathematical model to study the competitive binding dynamics of PD-1 inhibitors, PD-1, and PD-L1, enabling further exploration of immune checkpoint inhibitors within the QCIC framework. An iterative QCIC model incorporating the mechanisms of action of immune checkpoint blockade will hold significant potential for leveraging the content of tumor-infiltrating immune cells to predict survival outcomes more accurately.

The microbiome, particularly within the intestinal tract, forms a complex ecosystem by interacting with tumor and immune cells in the colorectal cancer tumor microenvironment. The microbiome modulates immune cell activity through metabolic alterations, and both tumor and immune cells can present microbial antigens. A recent study¹⁸ developed a mathematical model to describe the interaction between the microbiome and the tumor immune system. Integrating microbiome mechanisms into the QCIC model is anticipated to open pioneering research directions in tumor-immune system modeling.

In this study, we introduce two quantities to evaluate the QCIC model’s performance in predicting short-term treatment effects and long-term survival: the TRI and DPF. In clinical practice, time-series data on tumor evolution can be used to further calibrate the distribution of tumor heterogeneity parameters. A calibrated QCIC model enables the rapid generation of virtual patients to simulate tumor evolution dynamics with inter-individual variability. TRI can then be inferred from these simulated data, providing predictions of short-term treatment outcomes at the population level. By incorporating patient survival data, the shape parameters of the DPF can be determined, offering more accurate survival prognosis predictions at the population level. However, the absence of comprehensive follow-up data and the variability in treatment dosing during clinical care pose significant challenges. Consequently, the model’s validity is currently limited to standard clinical trial conditions. Addressing these challenges requires integrating data on individual tumor evolution to enhance the model’s applicability to precision medicine.

The potential biases in the QCIC model represent a complex issue spanning three primary aspects: data bias, mechanism bias, and parameter bias. First, biases may arise from data used in model construction and training, including inadequate representativeness in clinical trials, errors in data collection, biases during data procession, and discrepancies in evaluation systems. Second, mechanism bias may occur due to the simplified or idealized assumptions made to describe complex biological interactions within the model. Third, parameter bias involves inaccuracies in parameter estimation, which can impair the model’s generalizability and performance when applied to new data.

In conclusion, integrating mathematical models, machine learning, and virtual experiments provides a powerful framework for addressing inter-individual variability in clinical treatment responses^29,84,85. Predictive biomarkers extracted from mathematical models offer valuable insights into cancer survival prognosis. Multidisciplinary studies, such as the one presented here, enhance our understanding of tumor evolution and therapeutic strategies, driving progress in solid tumor treatment. The findings and methodologies of this study establish a strong foundation for future research aimed at identifying optimal treatment combinations and improving the therapeutic options for solid tumors.

Methods

Clinical trials and data analysis

In this study, we selected 10 pivotal clinical trials conducted between 2012 and 2023, all of which employed consistent treatment regimens^{31,32,33,34,35,36,37,38,39,40}. Detailed information regarding these trials is presented in Fig. S1, Table S1, and Table S2. Patients in the monotherapy group received TAS-102 (35 mg/m²) orally twice daily on days 1–5 and days 8–12, with a 28-day cycle. In the combination therapy group, patients also received intravenous bevacizumab (5 mg/kg) on days 1 and 15. Data from 2566 clinical patients were meticulously integrated, comprising 507 patients in the TAS-102 plus bevacizumab group, 1486 in the TAS-102 group, and 573 in the control group. To ensure accuracy and utility, we excluded any unevaluated sections from the original dataset.

To integrate the results from multiple clinical trials, we employed the following equation:

$${Q}_{ij}=\mathop{\sum }\limits_{k=1}^{n}{\rho }_{jk}{Q}_{ijk},\,{\rho }_{jk}=\frac{{m}_{jk}}{{m}_{j}},$$

(18)

where Q_ij represents the weighted average of the i-th clinical indicator (e.g., CR, PR, SD, PD, ORR, and M-OS) under the j-th treatment strategy. In the equation (18), i, j, and k represent the indices for different clinical indicators, treatment strategies, and clinical trials, respectively; ${\rho }_{jk}=\frac{{m}_{jk}}{{m}_{j}}$ represents the weight coefficient of the k-th clinical trial under the j-th treatment strategy, where m_jk is the number of patients in the k-th clinical trial under the j-th treatment strategy, and m_j is the total number of patients under the j-th treatment strategy; Q_ijk is the percentage of patients following the i-th clinical indicator under the j-th treatment strategy in the k-th clinical trial. The values of m_jk, m_j, and Q_ijk are available as clinical trial data in Tables S1 and S2. The results of Q_ij are given in Table 1, which give the RECIST in Fig. 2 and Fig. S2.

Table 1 Data analysis based on 10 clinical trials

The biological mechanisms of tumor immunity

The human body’s tumor immune response can be divided into four compartments: TDLN, PB, TME, and BT (Fig. 9a). TDLN serve as pivotal secondary lymphoid organs in tumor immunity, facilitating lymphocyte proliferation, differentiation, and the activation of specific immune response⁴¹. Within these lymph nodes, antigen-presenting cells (APCs) stimulate naive T cells via peptide-MHC complexes on the cell surface, initiating a complex immune response process (Fig. 9a)^51,52. Dendritic cells, considered the most potent professional APCs, play a critical role in this process⁵¹. Naive CD4+ and CD8+ T cells differentiate into effector T cells with distinct biological functions under the influence of various cytokines (Fig. 9b)^42,43. PB acts as a conduit for immune cell migration between tissues, facilitating immune system communication and coordination (Fig. 9c)⁴⁴. TME consists of the milieu surrounding tumor cells, including tumor cells, immune cells, cytokines, and chemokines^45,47. Within this environment, tumor cells and immune cells interact dynamically, driving disease progression^45,46,47. Moreover, tumor cell death from natural apoptosis, immune attack, or chemotherapy accelerates the release of tumor-associated antigens, promoting dendritic cell activation and further stimulating the immune response^7,8. BT are primary lymphoid organs responsible for lymphocyte development before these cells participate in immune function within secondary lymphoid organs^48,49. Together, these processes form the biological mechanisms of tumor immunity, as depicted in Fig. 9. The dynamic evolution of the immune system under different treatment regimens is illustrated in Figs. S5 ~ S10.

Fig. 9: The biological mechanisms of tumor immunity.

a The tumor immune response is divided into four compartments: TDLN, PB, TME, and BT. Immune cells migrate between compartments via the body’s intrinsic circulatory mechanisms. Chemokines/chemokine receptors further regulate the migration patterns and localization of immune cells. b Differentiation of immune cells. Within the TDLN, tumor-associated antigens are presented by dendritic cells to naive CD4+ and CD8+ T cells, which differentiate into various effector T cells in response to cytokines. c Migration of immune cells between compartments. T_A, tumor-associated antigen; D₀, immature dendritic cell; D, activated dendritic cell; T_N4, naive CD4+ T cell; T_N8, naive CD8+ T cell; T₈, cytotoxic T lymphocyte cell; T₁, Th1 cell; T₂, Th2 cell; T₁₇, Th17 cell; T_reg, regulatory T cell; T_fh, follicular helper T cell; NK, natural killer cell; M, monocyte; M1, M1 macrophage; M2, M2 macrophage; N, neutrophil; N1, N1 neutrophil; N2, N2 neutrophil; M_MDSC, monocyte-derived myeloid-derived suppressor cell; G_MDSC, granulocyte-derived myeloid-derived suppressor cell; E_os, eosinophils; B_as, basophilic.

PK and PD models

To describe the dynamic evolution of drug metabolism, we used a two-compartment PK model^86,87. This model divides the body into a central and a peripheral compartment based on drug transport rates. The central compartment features rapid drug transport and elimination, while the peripheral compartment has slower drug distribution, requiring the drug to return to the central compartment for metabolism and excretion. In the QCIC model, we designated the TDLN and BT as peripheral compartments, akin to those in a two-compartment PK model. Conversely, PB and TME were designed as central compartments. Consequently, we postulated that the drug concentration in the tumor corresponds to that in the central compartment.

The PK model for TAS-102 and bevacizumab is expressed as

$$\frac{{\rm{d}}{[{\rm{Drug}}]}_{1}}{{\rm{d}}t}={k}_{21}^{{\rm{Drug}}}{[{\rm{Drug}}]}_{2}-{k}_{12}^{{\rm{Drug}}}{[{\rm{Drug}}]}_{1}-{k}_{10}^{{\rm{Drug}}}{[{\rm{Drug}}]}_{1}+J(t),$$

(19)

$$\frac{{\rm{d}}{[{\rm{Drug}}]}_{2}}{{\rm{d}}t}={k}_{12}^{{\rm{Drug}}}{[{\rm{Drug}}]}_{1}-{k}_{21}^{{\rm{Drug}}}{[{\rm{Drug}}]}_{2},$$

(20)

where [Drug]₁ and [Drug]₂ represent drug concentrations in the central and peripheral compartments, respectively, J(t) denotes the time course of drug uptake. The parameters ${k}_{12}^{{\rm{Drug}}}$ and ${k}_{21}^{{\rm{Drug}}}$ denote the drug distribution rates between the central and peripheral compartments, while ${k}_{10}^{{\rm{Drug}}}$ describes the drug clearance rate. Since the antitumor drug is administered at predetermined time points τ_i, i = 1, 2, ⋯, n, we use the Dirac delta function δ to describe the drug uptake:

$$J(t)=\mathop{\sum }\limits_{i=1}^{n}[{\rm{Drug}}]\cdot \delta (t-{\tau }_{i}),\,\delta (t-{\tau }_{i})=\left\{\begin{array}{ll}1,\,\quad &{\rm{if}}\,t={\tau }_{i}\\ 0,\,\quad &{\rm{if}}\,t\,\ne\, {\tau }_{i}\end{array}\right..$$

(21)

The PD model is a mathematical framework used to assess drug dosage and efficacy based on drug interactions⁸⁷. Patients with advanced mCRC often undergo multiple standard treatment regimens. Although commonly used anticancer drugs effectively control DSTCs, they fail to target DRTCs that emerge as a result of previous treatments. We hypothesize that the novel chemotherapeutic drug TAS-102 can inhibit both DSTCs and DRTCs^3,4.

Additionally, tumors may evade treatment and undergo plastic transformation through endogenous stress-relief pathways in response to chemotherapeutic pressure, leading to the emergence of new tumor subpopulations known as DPTCs^88,89. TAS-102 is ineffective against DPTCs. However, since bevacizumab is an anti-angiogenic agent, we hypothesize that it can inhibit the proliferation of all tumor cell subpopulations. The detailed dynamic equations are provided in Supplementary Text 2.

Virtual patient generation and in silico clinical trials

Virtual patient generation is a parameter sampling method in which each randomly generated set of parameters describes the physiological characteristics of a virtual patient⁹⁰. In silico clinical trials solve differential equations based on these generated parameter sets, enabling researchers to simulate individuals with specific physiological characteristics without requiring actual patient participation^27,28,29,30. To generate these virtual patient cohorts, certain parameters of the QCIC model are varied, while others remain constant (Fig. S4). We identified 21 parameters across 7 categories, including the carrying capacity of naive T cells, antigen activation rate, immune checkpoint expression rate, tumor proliferation rate, tumor carrying capacity, tumor apoptosis rate, and drug correlation coefficient, as key determinants of tumor heterogeneity (Supplementary Text 4 and 5, Table S20).

Given the characteristic diversity of shapes in the Beta distribution, we assumed that each of the 21 tumor heterogeneity parameters follows a Beta distribution within its respective sampling ranges. For each heterogeneity parameter p, we estimate its sampling range $[{p}_{\min },{p}_{\max }]$ and randomly assign a parameter value using the formula $p={p}_{\min }+({p}_{\max }-{p}_{\min })x$, where x ∈ (0, 1) is random variable that follows the Beta distribution with the following density function:

$$f(x;a,b)=\frac{{x}^{a-1}{(1-x)}^{b-1}}{B(a,b)},\quad B(a,b)=\frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}.$$

Here, a and b are shape parameters, which are determined by comparing model outputs with clinical data. Based on the range and shape parameters for each heterogeneity parameter (see Table S20), we randomly select parameter values according to the predefined Beta distribution. Each set of parameter values corresponds to a virtual patient. By simulating the model with these virtual patients, we can obtain the clinical outcomes.

The values and ranges of these parameters were derived from established mathematical models and clinical trials focusing on mCRC. The shape parameters of the Beta distribution were iteratively optimized and refined using system biology modeling experience, data from 10 selected clinical trials^{31,32,33,34,35,36,37,38,39,40}, and model output results.

During the execution of in silico virtual clinical trials, we employed the Runge-Kutta algorithm, implemented in MATLAB, to perform parallel computations of the differential equations under various parameter combinations. This allowed us to capture the temporal variations of system variables. By integrating deterministic models with random sampling techniques, we effectively captured inter-individual treatment differences in the clinical management of cancer patients. Fig. S4 illustrates the results of the global sensitivity analysis conducted on these tumor heterogeneity parameters.

Treatment response index

To validate the QCIC model’s effectiveness and applicability in predicting tumor progression and treatment response, we introduce the Treatment Response Index (TRI), defined as follows:

$${\rm{TRI}}=\frac{{V}_{{T}_{{\rm{after}}}}-{V}_{{T}_{{\rm{before}}}}}{{V}_{{T}_{{\rm{before}}}}},$$

(22)

where ${V}_{{T}_{{\rm{before}}}}$ and ${V}_{{T}_{{\rm{after}}}}$ represent the tumor volumes (V_T) before and after treatment, respectively. The TRI describes the relative change in tumor volume following treatment. The volume V_T is calculated based on the tumor cell density as:

$${V}_{T}=\frac{{v}_{{\rm{tumor}}}\times {[X]}_{C}\times {V}_{C}}{{V}_{e}},$$

(23)

where [X]_C represents the tumor cell density within the tumor microenvironment; v_tumor = 2.572 × 10⁻⁹ cm³/cell denotes the volume of a single tumor cell; V_C = 0.8L is the volume of the tumor microenvironment; and V_e = 0.37 represents the volume fraction of the intracellular space in the tumor^27,29.

To compare model simulation with clinical trials data, we adopted the RECIST v1.1 as the standard for evaluating tumor evolution⁷². Based on the RECIST v1.1 guidelines, patients with a 20% increase in tumor volume after treatment are classified as having progressive disease (PD), i.e., TRI ≥ 0.2. Patients with tumor volume changes ranging from a 20% increase to a 30% decrease are categorized as having stable disease (SD), corresponding to TRI ∈ [− 0.3, 0.2). Similarly, patients with an 80% tumor volume reduction are classified as having a complete response (CR), with TRI = − 0.8. Patients whose responses fall between SD and CR are defined as having a partial response (PR), with TRI ∈ [− 0.8, − 0.3). Thus, the model variables were converted into RECIST v1.1-based classifications, which are relevant to clinical diagnosis using the TRI.

Death probability function

In clinical medicine, the Kaplan-Meier survival curve is widely used to estimate the survival probabilities of cancer patients at the population level. The Kaplan-Meier survival function is defined as:

$$S(t)=\frac{\,{\rm{No.}}\, {\rm{survival}}\, {\rm{patient}}}{\rm{No.}} \,{\rm{total}}\, {\rm{patient}\,}\times 100 \% .$$

(24)

In mathematical oncology, the assessment of death for virtual patients is often performed by setting thresholds for total tumor cell count or tumor volume⁵⁹. However, due to patient variability and tumor heterogeneity, the likelihood of patient death can vary significantly. In our study, we assumed that the death probability of a patient is primarily determined by the number of dominant tumor cell types. Thus, we defined a death probability function (DPF) based on the tumor burden.

Let $\overrightarrow{X}=({X}_{1},{X}_{2},{X}_{3})$, where X_i represents the number of cells of type i. The relative number of dominant tumor cells is denoted as $\chi (\overrightarrow{X})=\frac{{X}_{j}}{{K}_{j}}$, where j is the index of the dominant cell type, defined such that ${X}_{j}=\max \{{X}_{1},{X}_{2},{X}_{3}\}$, and K_j is the corresponding carrying capacity (see Table S19). The PDF under the i-th treatment option (placebo, TAS-102, or TAS-102+bevacizumab) is defined as:

$${P}_{i}(\vec{X})=\frac{1}{1+\exp (-(\chi (\vec{X})-{\mu }_{i})/{\sigma }_{i})},$$

(25)

where μ_i and σ_i are shape parameters. The shape parameters for each treatment option are provided in Table S21 in Supplementary Text 5.

The death probability ${P}_{i}(\vec{X})\in [0,1]$ gives the likelihood of patient death based on the tumor burden $\vec{X}$ under the i-th treatment option. The death probability increases with the dominant tumor cell number. Specifically, the shape parameters μ_i and σ_i can be determined by setting the death probability for the i-th treatment as ${P}_{i}^{0}=\frac{1}{1+\exp (-(1-{\mu }_{i})/{\sigma }_{i})}$ when $\chi (\vec{X})=1$.

Following model simulation, the tumor burden $\vec{X}(t)$ dynamically varies with time. Consequently, the death probability ${P}_{i}(\vec{X}(t))$ also changes with time. In each model simulation, we generated a tumor burden time sequence $\vec{X}(t)$, and the data were stored for each day. Next, for each time t, we evaluated the survival status of the patient based on the probability ${P}_{i}(\vec{X}(t))$, i.e., the patient dies on the day t with probability ${P}_{{\rm{death}}}={P}_{i}(\vec{X}(t))$. To this end, we generated a random number p ∈ (0, 1), and the patient dies if $p\, <\, {P}_{i}(\vec{X}(t))$, or survives otherwise. Hence, starting from t = 0, we evaluated the survival status of each virtual patient until the patient died.

Quantitative and statistical analysis

To examine the impact of various parameters on model observations, we conducted a global sensitivity analysis using the Monte Carlo simulation method. We defined a sensitivity function as follows:

$$S=\frac{{V}_{T}(\tilde{\theta })-{V}_{T}(\theta )}{{V}_{T}(\theta )},$$

(26)

where θ represents the baseline parameter set, and $\tilde{\theta }$ represents the randomly sampled parameter set. The parameter sampling range was set to ±10% of the baseline parameters. We conducted 1000 random samplings and simulations to calculate the sensitivity function S at the time of the first clinical diagnosis (day 56). Additionally, the Pearson correlation coefficient (PCC) was used to assess the linear correlation between the randomly sampled parameter values and the sensitivity function S (Fig. S3).

Furthermore, we conducted global sensitivity analyses for the 21 tumor heterogeneity parameters in the value space, keeping all other parameters fixed. The random parameter values were divided into five equally spaced intervals, and the corresponding DCR and PD rates were calculated to observe how parameter changes affect treatment outcomes (Fig. S4).

For statistical analysis, we employed the Student’s t-test to assess the significance of differences in immune biomarkers between responders and non-responders. This test compares the means of two independent groups while considering data variability and sample size. Specifically, we implemented the test using MATLAB’s ttest2 function, which is designed for two-sample t-tests on independent data samples.