Protected area management has significant spillover effects on vegetation

Abstract

The Kunming–Montreal Global Biodiversity Framework calls for rapid global expansion of protected areas in response to ongoing biodiversity loss and ecosystem degradation¹. One of its strongest selling points is the benefits protected areas provide to adjacent human communities^2,3. However, little attention has been paid to how policy and management can support such benefits. Here, to address this gap, I explored influences on the effect sizes of vegetation spillovers from a candidate 12,513 Australian protected areas, defining spillovers as the difference in vegetation outside a protected area that occurs as a consequence of the existence of the protected area⁴. In 2020, 71% (2,189) out of the 3,063 protected areas for which full analysis was possible had a positive spillover effect of 0.1 or greater on at least 1 of 10 vegetation cover classes. Many protected area types were significant predictors of spillover magnitude. The covariance explained by protected area type with local and contextual variables was 14%, suggesting that internal management moderates adjacent locations. These findings highlight the potential to include spillover effects explicitly in global policy frameworks and suggest a pathway to an empirical basis for monitoring and accounting schemes that support biodiversity conservation and ecosystem service provision adjacent to protected areas.

Main

Under current global trends of loss and degradationof natural habitats, protected areas are critical for conserving biodiversity and maintaining the ecosystem goods and services that human societies depend on^5,6. Although we typically focus on what protected areas conserve, many of their benefits and costs occur beyond their boundaries^7,8. These spillover effects span social, ecological and economic spheres, and may include such critical benefits as water provisioning, pollination, pest control, forest regeneration, flood and storm protection, increased amenity and land prices, and revenue generation through tourism^4,9,10,11. Protected areas may also impose costs on adjacent human populations—for example, by increasing human–wildlife conflict¹², providing reservoirs for pathogens¹³ and restricting access to resources¹⁴.

Global conservation policies, such as the push for an increase in conserved land under the Kunming–Montreal Global Biodiversity Framework¹, recognize that protected areas bring local and regional benefits and costs. However, spillover effects are largely excluded from policy and legislation despite extensive evidence of their importance^6,9,10,15,16. Landscape planning has tended to divide landscapes into human-dominated or natural systems, although most ecosystem services are delivered locally at the interface between people and nature. People benefit directly from daily access to clean air and water, shade trees, flowers and fruits, and other ecosystem contributions^17,18. In both rural and urban environments, many of nature’s contributions to people are supported by adjacent protected areas¹⁹.

One of the barriers faced by landscape planners is that conservation science has focused more on ecosystems inside protected areas than those outside⁹. At present we cannot reliably predict the conditions under which beneficial spillovers from protected areas will occur. Even for relatively well-studied ecological spillovers, such as the movement of seeds from forests or fishes from marine protected areas, a lack of standardized methods and integrative conceptual frameworks together with a tendency to focus on single-variable outcomes (for example, forest/non-forest or fish biomass) means that the findings of the few meta-analyses of spillover effects across different locations^15,20 are difficult to apply to protected area planning²¹.

Bringing spillovers into the global policy debate will require broadening the spatial and temporal scales of spillover analyses and improving understanding of their causes. To address this need, I analysed ecological spillover effects from terrestrial protected areas using data on woody and herbaceous vegetation within and adjacent to 12,513 protected areas across the continent of Australia, excluding its small offshore islands, at the beginning and end of a 32-year time period (1988–2020). Vegetation spillovers are defined here as a type of ecological spillover through which vegetation outside a protected area remains or becomes more similar than expected to vegetation inside the protected area. My findings support the hypothesis that protected area management type influences vegetation spillovers to the surrounding landscape, suggesting potential for deliberate incorporation of spillover management in biodiversity conservation policy, planning and actions.

Continental patterns of vegetation cover

Spillover effects from protected areas are modulated by adjacent land cover and land use^22,23,24. Where human population density is very low, as in central Australia, ecological exchanges across protected area boundaries may be balanced; adjacent ecosystems are structurally and functionally intact, and no detectable spillover occurs. At the other extreme, organisms leaving a protected area may die if the surrounding landscape is hostile²⁵. Within this spectrum is a wide variety of situations over which the ecological or socioeconomic effects of protected areas may occur at different rates and magnitudes.

To provide context for the spillover analysis, I first used R software²⁶ to analyse natural vegetation cover information from a classified vegetation map^27,28 at 25 × 25 m resolution using 2,636,333 circular sampling polygons of diameter 150 m (for details, see Supplementary Information, Section 2 and Supplementary Fig. 1). Across the entire dataset, the most abundant natural woody vegetation class across Australia was 40–65% tree cover (class X28), and the most abundant natural herbaceous class was 15–40% cover (class X34). Mean values for all woody cover types except the most forested class (canopy >65%; class X27) have increased since 1988, whereas mean values for all herbaceous classes have decreased (Fig. 1). Owing to the geography of Australia, small proportional changes in area may still indicate a high percentage loss of a specific vegetation type. For example, despite its limited extent, loss of mature forest in Australia over the past 30 years has been proportionally extensive (and sufficient to endanger species of high conservation interest, such as koalas and sugar gliders)^29,30.

Fig. 1: Vegetation cover over time and relative to protected area boundaries.

a, Mean proportions of different natural vegetation classes as a percentage of total sampled area within 2,636,333 sampling polygons. This plot shows the proportions per sampling polygon of the ten different vegetation types considered in the analysis, in 1988 and 2020. Data are mean + s.d. (n = 2,636,333 independent sampling polygons, each of 150 m diameter). The full names for vegetation classes are given in Supplementary Table 2. On average, woody vegetation has increased through time across all classes except X27 (woody closed, canopy cover >65%) and herbaceous vegetation has decreased. b, Mean proportions of different vegetation types in protected and unprotected areas across all sampling polygons in the 2020 dataset. Data are mean + s.d. (n = 2,636,333 independent sampling polygons, each of 150 m diameter). Woody vegetation is disproportionally represented inside protected areas. For example, the mean percentage of forest (X27) in sampling polygons inside protected areas (9.32%) is just over nine times the mean in sampling polygons outside protected areas (1.03%), suggesting a critically important role for protected areas in the conservation of trees.

Across all sampling polygons, 31.4% of sampling polygons showed no net change in any vegetation type (n = 827,625 polygons). Although natural vegetation cover has thus been stable since 1988 across approximately one-third of the land area of Australia, some vegetation types are particularly dependent on protection for their persistence.

Hypothesis testing for spillovers

Clarity on how spillovers are defined and measured is critical for interpreting these results. ‘Spillover’ is used here to describe an effect of a protected area on adjacent vegetation. Spillover occurs if a protected area has more (positive spillover) or less (negative spillover) adjacent vegetation of a given type than expected, based on comparison of the observed data to a prediction from a carefully constructed counterfactual or null model. I have used a risk difference threshold of 0.1 or greater to determine whether any spillover occurs; nuances in conclusions relative to this threshold are explored later in the Article. Positive and negative are used throughout to describe the sign of the spillover effect and should not be confused with normatively ‘good’ or ‘bad’ conservation outcomes. Testing for spillovers involves comparisons between three different areas (Fig. 2).

Fig. 2: Testing spillover hypotheses using data from a single time step.

Top left, a hypothetical landscape consisting of a protected area (A), a potential spillover zone (B) and an area that is independent of protected area effects (C). Top right, comparisons that contrast samples from each of these areas can be used to support or refute hypotheses about the presence or absence of spillovers. The criteria assume that: (1) an ineffective protected area is one that does not make a difference to ecosystems within its boundaries; and (2) protected areas will produce spillovers only if PAs are effective (A makes a difference relative to C). I focus on hypothesis-separating diagnostic measures (the green ticks that are circled in red). The focal question is whether area A affects area B. To establish this, we need to also consider area C, which is free of the effects of A. We expect that positive or similar spillovers, in which vegetation in area B is more like that of the protected area than expected by chance, will lead to differences between samples in both A versus C and B versus C, and similarity between samples from A and B (that is, no effect of treatment A, or a weak effect, relative to area B). A lack of difference between A and B can also be consistent with other hypotheses, such as an ineffective or ‘unnecessary’ protected area that has no spillover. PA, protected area.

The most important comparison in establishing spillover presence or absence is the contrast between the spillover zone (group B) and the independent zone (group C) (Fig. 2). However, establishing the presence of a positive or negative spillover also requires understanding the similarities or differences between the protected area (group A) and the spillover zone (group B). Rigorous spillover confirmation thus requires that two criteria are met, rather than just a single criterion. If both are met, then the value from Contrast 2 quantifies the magnitude of the spillover effect.

Although this analysis uses data from 1988 and 2020, I present an analysis of landscape pattern rather than landscape change; thus, the two different years are analysed independently rather than using the difference between them. The primary reason for doing so was that protected area effects were relatively consistent between 1988 and 2020, supporting evidence from other research³¹ that implies that spillovers in Australian vegetation are outcomes of relatively long, slow processes.

Frequency and magnitude of spillovers

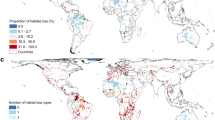
The Collaborative Australian Protected Areas Database (CAPAD)³² contains data for 14,205 terrestrial protected areas. Some are on remote offshore islands, and many are too small or too tightly clustered to analyse cleanly. A total of 12,513 protected areas (88% of the total; Fig. 3; for further details see Methods and Supplementary Information, section 8 and Supplementary Fig. 5) was thus considered. Sample sizes varied with vegetation types, but for 2020 a total of 7,512 protected areas (60% of candidate areas or 53% of all Australian protected areas) met the minimum sample size requirement for inclusion in reported analyses for at least one of the contrasts described in Fig. 2.

Fig. 3: Spillover effect sizes across Australia.

a, Variation in spillover effect sizes across Australia. The map shows the locations of protected areas and their effect size on the 0–5 km band, for positive effect sizes greater than 0.1. Each point marks the centroid of a protected area (shown behind in the same colour as the centroid; for smaller PAs, only the centroid is visible). Locations with higher positive spillovers are shown in red or dark blue. Smaller protected areas are clustered nearer to the coasts; no other obvious geographic pattern is immediately evident in spillover effect sizes. b, An example of spillover for an isolated protected area. Mount Armour Nature Refuge in Queensland (about 500 km west of Brisbane, Queensland, indicated approximately by the red star in the inset map of Australia) shows positive vegetation spillover (more forest than expected by chance) for class X27 in the 0–5 km band, relative to a counterfactual based on data from sampling polygons more than 50 km from the protected area boundary. Vegetation in class X27 is coloured green; all other land cover classes are coloured pale yellow. The pink circle is the centroid of the protected area, as depicted in panel a, and the protected area is drawn with a black boundary and cross-hatched fill. The pale blue buffer line indicates the edge of the 5 km spillover zone.

Most previous spillover analyses of terrestrial vegetation have analysed a single vegetation type, typically closed canopy forest. I instead considered a full range of different vegetation densities, initially analysing each vegetation type independently. As a result, positive effect sizes for one type of vegetation (more vegetation of that type in the spillover zone than expected based on the independent zone) were often balanced against negative effect sizes for another vegetation type (less of that vegetation type than expected). For example, as grasslands recover from over-grazing, herbaceous cover increases and may cross the 65% cover threshold from open to closed herbaceous cover (class X33 to class X32). This would lead to a net gain in class X32 and a net loss in class X33, yielding positive and negative effect sizes, respectively. If gains in class X32 were faster or more consistent adjacent to a protected area, meaningful differences might arise between the spillover zone and the independent zone. Unbalanced positive and negative spillovers imply either loss of natural land cover types or reclamation of pixels that were originally classified as non-natural or unvegetated, such as agricultural or peri-urban land.

Matching methods were used to correct for the potentially confounding influences of local biophysical conditions and protected area placement in spillover estimation, as described in Methods and Supplementary Information, section 8. Counterfactuals used only points for which the focal protected area was the nearest protected area, or that were more than 100 km from any protected area. I first evaluated aggregated data from the entire analysis for the year 2020, using only the first spillover band (0–5 km) to represent the spillover zone. These results (Table 1) consider all vegetation types and protected areas to show the numbers of meaningful outcomes (effect size >0.1) in each of the different contrasts, as summarized in Fig. 2.

Table 1 Aggregated results across all protected areas and vegetation types

These findings must be interpreted carefully in light of available sample sizes. Totals of 2,129 individual protected areas in 1988 and 2,189 protected areas in 2020 were confirmed as having both a non-meaningful effect size for Contrast 1 (comparison of the interior of the protected area to the spillover zone) and a meaningful effect size for Contrast 2 (comparison of the spillover zone to the independent zone) in any vegetation category (that is, both A = B and B ≠ C; Fig. 2). This total represents 17.5% of all candidate protected areas across Australia. However, generalization of this result is more accurately done in light of the actual number of protected areas included in both years in Contrast 1 (n = 3,063), Contrast 2 (n = 3,768), Contrast 3 (n = 6,068) and across all contrasts (n = 7,152). Thus, 71% (2,189 out of 3,063) of analysed protected areas in 2020 had a spillover effect over 0.1 on at least one vegetation type. This proportion was 1.5% lower for 1988, at 69.5%. Numbers and proportions of spillovers thus showed very little change across a 32-year period. In 2020, an additional 705 individual protected areas had spillover zones in the 0–5 km band with meaningful effects in Contrast 2, but could not be confirmed as showing spillovers owing to sample size issues in Contrast 1. Proportionally, around 501 (71% of 705) of these should also show meaningful spillovers.

Protected areas that were entirely excluded from the analysis for statistical reasons were either too small to support the sample size requirements for the analysis, were located in areas with very little surrounding natural vegetation (for example, urban parks), or were members of tightly grouped clusters of protected areas with small potential spillover zones. The distribution of terrestrial protected areas across Australia is clearly biased, with smaller protected areas clustered near the coasts (Fig. 3).

I used data within the 0–5 km distance band from protected area boundaries to examine trade-offs between protected area spillover effects. Comparison by vegetation category of the summed frequencies of positive and negative spillover effects of magnitude over 0.1 (using data in Table 1) gave a Pearson’s correlation of r = 0.71 (t = 2.9, P < 0.02, d.f. = 8), providing evidence of trade-offs between different vegetation types. Similarly, comparing vegetation types across all individual protected areas, in 2020 the spillover zones appear to facilitate shifts between open woodland (X28) and forest (X27) (r = −0.22, P < 0.001, n = 3,501), consistent with either reforestation or light deforestation adjacent to protected areas (further detail in Supplementary Information, Section 11 and Supplementary Fig. 8). There was little evidence for synergies between vegetation types, which would yield stronger positive correlations.

Management influence on spillovers

Spillover effects are driven by a variety of factors that can vary both inside and outside a protected area³³. A critical question for including spillovers in conservation planning and policy is whether management inside a protected area can make a difference to ecosystems and social-ecological systems outside its boundaries³⁴. Management activities are influenced by biophysical, social, political and economic variables^35,36. For example, using prescribed burns to thin woody vegetation in protected areas may depend on vegetation type, the economic capacity of management, available infrastructure for accessing and controlling fires, and the social acceptability of burning near private lands³⁷.

I used management attribute data for each protected area from the CAPAD dataset to test for an influence of management type on the effect size of protected area spillovers. To avoid the statistical effects of sample size inflation from locations that could not be tested for spillover effects, I used data for 2020 from the 3,441 protected areas that showed non-zero spillovers based on Contrast 2 and had full management information available. I again focused on the 0–5 km sampling band where spillover effects should be strongest. To avoid double-counting, while still comparing protected areas in different habitat types (for example, woodland and grassland), I used the largest observed spillover effect across the ten vegetation categories. I ran this analysis separately for positive and negative spillovers, using a square root transform on the absolute values to normalize the data prior to analysis and setting the value to zero in rows where there were either no positive or no negative spillovers.

I focused first on the International Union for Conservation of Nature (IUCN) categories. For positive spillovers, mean untransformed effect sizes and their s.d. by category were, in decreasing order, category V (2.46 ± 1.68), category II (2.35 ± 1.61), category IV (2.27 ± 1.84), category VI (2.12 ± 1.50), category III (1.89 ± 1.61), category Ib (1.79 ± 1.43) and category Ia (1.79 ± 1.64). For negative spillovers, the order of means by effect size magnitude were similar to those from positive spillovers: category IV (−1.67 ± 1.66), category V (−1.61 ± 1.48), category II (−1.53 ± 1.57), category Ib (−1.56 ± 1.43), category VI (−1.47 ± 1.43), category III (−1.36 ± 1.21) and category Ia (−1.35 ± 1.16). An ANOVA by IUCN protected area designation on the positive spillovers indicated a highly significant difference in effect sizes between IUCN management designations (F = 17.28, P < 2 × 10⁻¹⁶, d.f. = 6, n = 3,434). By contrast, treating the negative spillovers in the same manner gave a result that was only statistically significant to P < 0.1 (F = 1.88, P < 0.08, n = 3,434). Thus, management designation appears to strongly affect positive spillovers while only weakly affecting negative spillovers.

For positive spillovers, Tukey’s honest significant difference test gave significant differences between seven different contrasts in the IUCN categories (Fig. 4). With the larger mean effect first in each pair of comparisons, these were IV–Ia, II–Ia, IV–III, II–III (P < 0.001), IV–VI (P < 0.01), V–Ia and II–VI (P < 0.05). Differences in management designation between protected area types therefore had potentially important consequences for positive spillovers. Categories V, II and IV had the highest mean values and all featured prominently in significant differences from other categories. Category II contains strictly protected wilderness areas and categories IV and V contain protected habitat or species management areas and protected landscapes, respectively. Conversely, protected areas with the lowest identified spillover effects were in categories Ia (strict nature reserves) and III (natural monuments or features).

Fig. 4: Influence of management on spillovers.

Box plots of effect size according to IUCN protected area category (a) and Australian management type (b), showing median and s.d. of positive spillover effect sizes (Contrast 2: spillover zone versus independent zone) by management type for 3,510 protected areas (blue dots), both with two outliers excluded. Australian protected area types are shaded by IUCN category. In box plots, central horizontal lines are medians; edges delineate 25th and 75th percentiles; and whiskers extend to smallest and largest values within 1.5 times the interquartile range of the relevant percentile. Brackets above bars in a indicate pairs that exhibit a significant difference based on ANOVA and Tukey’s honest significant difference test; *P < 0.05, ***P < 0.001. III versus IV: P = 0.023; III versus V: P = 0.014; I1 versus V: P = 1.61 × 10⁻⁴; Ia versus VI: P = 3.64 × 10⁻⁶; Ia versus IV: P = 1.05 × 10⁻⁶; II versus III: P = 2.06 × 10⁻⁷; Ia versus II: P = 1.20 × 10⁻⁹. Sub-categories for CAPAD: ACCP, Conservation Covenant; CA, Conservation Area; CCA, Coordinated Conservation Area; CAZ1, CA Zone 1 National Park; CAZ3, CA Zone 3 State Conservation Area; COR, Coastal Reserve; CP, Conservation Park; CR, Conservation Reserve; FLR, Flora Reserve; FR, Forest Reserve; GR, Game Reserve; HA, Heritage Agreement; HIR, Historical Reserve; HR, Heritage Reserve; IPA, Indigenous Protected Area; KCR, Karst Conservation Reserve; MA, Management Area; NAP, Nature Park; NCA, Natural Catchment Area; NCR, Nature Conservation Reserve; NFR, Natural Features Reserve; NP, National Park; NPA, National Park Aboriginal; NPC, National Park (Commonwealth); NR, Nature Reserve; NRA, Nature Recreation Area; NREF, Nature Refuge; NRS, Addition - Gazettal in Progress; NS, National Park (Scientific); OCA, Other Conservation Area; PNR, Private Nature Reserve; PS, Private Sanctuary; RA, Reference Area; RCP, Recreation Park; REP, Regional Park; RNA, Remote and Natural Area; RR, Regional Reserve; RSR, Resource Reserve; S5G, 5(1)(g) Reserve; S5H, 5(1)(h) Reserve; SCA, State Conservation Area; SP, State Park; WP, Wilderness Park; WPA, Wilderness Protection Area. Unrepresented protected area types did not show measurable non-zero spillover effects.

These results highlight the many nuances that arise in understanding influences on spillover outcomes. The difference between category I and category II areas was surprising, but is consistent within the data as shown by the independently measured similarities between results for IUCN categories Ia and Ib. It may relate to the locations in which these areas are typically placed, if wilderness areas in category II are surrounded by other less human-impacted areas while category I areas more frequently act as islands of natural habitat where agriculture and ranching pressures are higher. The apparently high spillovers from class IV and V areas may reflect broader initiatives to manage landscapes at scale, potentially leading to higher levels of natural vegetation adjacent to their borders despite net habitat loss in the broader landscape.

The results might superficially be interpreted as implying that class VI protected areas offer lower ecological benefits to people beyond their boundaries, but it is important to note that many sustainable use areas in Australia are on Indigenous lands in sparsely populated areas. In light of known mechanisms and the contrasts presented in Fig. 2, the lower spillover effects from areas in class VI are more likely to indicate that these protected area types retain intact natural habitats on both sides of their boundaries and beyond, not a gradient of habitat loss extending from the boundary.

Analysis of positive spillovers using a more detailed breakdown of protected area types (Fig. 4) confirmed that protected area designation influences spillover effects (F = 7.82, P < 2 × 10⁻¹⁶, d.f. = 46). Post hoc Tukey’s test identified 54 statistically significant differences between different management classes (Supplementary Information, section 11.2, Supplementary Table 4). For negative spillovers, the management effect remained highly significant (F = 2.95, P < 1.5 × 10⁻¹⁰, d.f. = 46) but the Tukey’s test suggested that only four management classes were significantly different from each other (abbreviations defined in Fig. 4): RR versus ACCP (P < 0.048), NFR versus HA (P < 0.001), RR versus HA (P < 0.001) and RR versus NCR (P < 0.004). The sequence of untransformed mean negative effect sizes for these classes was RR (−2.5 ± 2.7), CC (−1.17 ± 1.0), NFR (−1.7 ± 1.5), HA (−1.2 ± 1.1) and NCR (−1.17 ± 1.2). RR featured in three of the four significant class differences with the more negative effect size. This management category is used primarily in Tasmania and South Australia as a tool to balance conservation with resource utilization, suggesting that the negative spillovers identified by this analysis do not reflect normatively positive conservation outcomes. However, the five management types in this dataset with both a substantial sample size and higher mean positive spillover effects were (in decreasing order) RA (4.6 ± 2.3), S5G (3.9 ± 2.4), WP (3.7 ± 1.4), RR (3.5 ± 2.4) and SP (3.2 ± 1.8). RR may thus be either: (1) supporting the replacement of one vegetation class by another, leading to high positive spillover in one vegetation type and high negative spillover in the category it replaces; or (2) sufficiently diverse that they function as effective conservation tools in some areas but not in others.

Considering the other management types highlighted by the positive spillover analysis, RAs are kept interference-free for use as monitoring baselines and seem more likely to be surrounded by intact ecosystems that buffer human impacts. S5G areas are specific to Western Australia; they are areas of land held by the Conservation and Parks Commission that are not in one of the other designated reserve types. WP areas are large, pristine areas with a strong protection status. However, both SR and RR areas may be used for a range of activities.

The protected area management types with reasonable sample sizes that were least likely to show positive spillovers were generic protected area (1.3 ± 0.96), CR (1.4 ± 1.4), REP (1.4 ± 0.7), S5H (1.5 ± 1.5) and NR (1.5 ± 1.5). These categories again show a mix of different management approaches and there is also considerable variance in their effect sizes, particularly within the larger samples (for example, NR areas have many outliers with effect sizes over 5). NR was the most sampled of this group and their relatively low overall mean spillover effect may be partially owing to being frequently located in areas where they are surrounded by less human-impacted habitats. Alternatively, many NR areas in Australia also target the conservation of indigenous marsupials, and these areas may be fenced for predator control and surrounded by firebreaks and roads.

This analysis provides, to my knowledge, the first evidence that protected area management affects the kind and magnitude of spillover effects across terrestrial Australian protected areas. It leaves many questions open for further research. More detailed comparison between results of the different contrasts outlined in Fig. 2, as well as exploration of the influences of local and regional policies on spillover effects, should yield a clearer and more nuanced explanation of why, where and when different management types support spillover effects. Despite these complexities, it is clear that management and use patterns inside protected areas can predictably affect the likelihood of spillover effects occurring on vegetation beyond their borders; and that further research on this theme may provide valuable tools and recommendations for increasing the net provision of ecosystem services outside protected area boundaries.

Having confirmed that differences in spillover effect sizes occur between management types, I used variance partitioning to compare management effects and habitat effects. The response variable for this analysis was spillover effect size as measured by Contrast 2 (that is, a matrix of data with 10 columns, corresponding to effect sizes from the 0–5 km spillover zone for all vegetation types relative to an area independent of protected area effects). It compared the explanatory power of protected area management types to explanatory matrices of data for local variables (rainfall, temperature, elevation, soils, elevation, slope, evapotranspiration and the count of pixels of each vegetation type occurring within the protected area), context-related variables (x and y coordinates of the protected area bounding box top left and bottom right, protected area extent, distance to nearest large town, distance to coast, distance to any road and distance to main road), and protected area gazettement date.

Gazettement date was subsequently dropped from the analysis owing to its low explanatory power (less than 1% of variance). The results showed that management and its indirect interactions with other variables can explain just over 16% of the variance in spillover effect size (Fig. 5). Although 65% of variance is unexplained, it was unexpected that a simple categorical measure of protected area type explains so much of the total variance, given probable differences within management types between districts, states and biomes. I interpret this result as suggesting that although protected area management may not be able to overcome local or regional constraints, it has an important influence on spillover magnitude within the envelope defined by those constraints.

Fig. 5: Proportional contributions of management.

The results of variance partitioning using absolute values of protected area spillover effect sizes as the response matrix and local, contextual and gradient-related variables as explanatory influences. The total proportions of variance explained uniquely by each variable independently were respectively 12% (local), 1% (context) and 2% (management). Inclusion of all covariance effects for each variable increased these proportions to 32% (local), 15% (context) and 16% (management). Together these variables explained 35% of the variance in spillover effects. Running the same analysis using all effect size data (Contrasts 1, 2 and 3) increased total explained variance to 45%, with cumulative totals being 43% (local), 17% (context) and 19% (management).

The results suggest that it is possible to make useful predictions about protected area vegetation spillover effect sizes from management information and a relatively small set of other readily measured variables. This finding is important because being able to estimate spillover likelihoods for an existing or potential set of protected areas would provide a quantitative tool for formally incorporating assumptions about spillover effects in conservation policy and planning, and for quantifying the associated uncertainties in potential outcomes.

To explore the predictability of vegetation spillovers, I used the 2020 data to develop a regression model to predict positive spillover magnitudes from all protected areas. I focused on positive spillovers (increases in vegetation of a given type) as being more predictable and potentially of higher conservation relevance. I used as the response variable the (square root-transformed) largest positive spillover effect across all vegetation types, including all 3,510 rows of data and using the variables included in the matrices described above. These variables included all of the continuous predictors, the additional contextual variables, and all management categories (noting that each management category is coded as a separate binary variable during regression). This analysis gave a significant overall regression model fit with an adjusted r² value of 0.26 (P < 2.2 × 10⁻¹⁶, F = 14.1, with degrees of freedom = 96 and 3,413; for more detail, see Supplementary Information, section 11.5 and Supplementary Table 6). This result is consistent with the results from variance partitioning.

After fitting, the model was used to predict positive spillover effects across the full sample of protected areas. Analysis of the results suggested that around 82 ± 0.26% of protected areas should produce a positive spillover effect over 0.1 within 5 km of their boundary. Repeating the regression analysis independently using different effect sizes across different distance bands relative to the protected area boundary offered a way to correct for the influence of differences in sample size from different sampling bands (Fig. 6). Calculations of benefits and costs to society from protected areas would need to consider how many protected areas are likely to provide beneficial spillovers, how large these benefits might be, and how far they might extend. These estimates thus provide potentially useful insights for decision-making at regional scales. Providing an effect size profile also offers a critical step towards the capacity to consider trade-offs—for example, contrasting the value of expanding existing protected areas with that of creating new protected areas.

Fig. 6: Spillover frequency at different effect sizes.

Numbers of protected areas with non-zero positive spillover effects (increases in any vegetation type relative to the counterfactual) of different sizes at different distance bands from their boundaries. Shading indicates 95% confidence intervals for each curve. The red vertical lines indicate the values of 0.2, 0.8 and 1.4 that have been proposed⁵⁵ as suitable values to distinguish between small, medium, large and very large effects, respectively. Noting that the residual standard error for these curves (uncertainty on the x axis) is 0.52, the number of protected areas that show a large spillover effect (effect size >0.8) decreases rapidly from the 0–5 km band, but even for the 45–50 km band, the number of protected areas that are estimated to exhibit spillovers is close to 20%. This figure provides, to my knowledge, the first large-sample estimate of distance-related decay in the magnitude of spillover effects, and thus of the magnitude of potential spillover benefits that might be expected from an average Australian protected area.

Discussion

I estimated that at least 71% of 3,063 measured Australian terrestrial protected areas consistently provided meaningful vegetation spillovers (effect size >0.1) in the 0–5 km band and predicted that the true proportion across 12,513 candidate protected areas was 82%. The number of protected areas exhibiting spillover effects declined with increasing distance from the protected area boundary; positive and negative spillover effects occurred together across different vegetation classes. Notably, the effect sizes of vegetation spillovers differed significantly between different protected area management types and could be predicted from a combination of readily measurable management, biophysical, vegetation and geographic gradient-related variables. Thus, this broad-scale statistical analysis strongly supports the findings of more mechanistic analyses^38,39, which suggest that with the addition of more specific and detailed information about protected area management practices, landscape arrangement, and location along spatial gradients relative to human activities, statistical models that can accurately predict vegetation spillover effect size from protected areas to adjacent lands are a plausible goal.

Although the findings strongly support the hypothesis that the type of a protected area makes a significant difference to its contributions to surrounding landscapes, understanding exactly how and why will need more intensive analyses of the nuances of different protected area types. For instance, a systematic review of spillover influences on (mainly) tropical forest cover data from 3,398 protected areas¹⁵ concluded that there was no effect of IUCN category on spillover magnitude. Further research is needed to understand whether the differences in our respective findings are due to differences in the nature of the included protected areas and countries, selection bias in previous studies for deforestation hotspots, or differing methods.

The results of this terrestrial analysis do not initially appear to strongly reflect what has been described for marine protected areas, where no-take and no-entry zones have been shown to offer the greatest benefits to adjacent fisheries and to have an important role in seascape connectivity^20,40,41. Nonetheless, there are some parallels: I found some evidence for the value of landscape management, and similar conclusions have also been reached for seascapes⁴⁰.

The scale of vegetation spillover effects that emerged from these data seems large, with some effects being detectable more than 45 km from the protected area boundary (although this is not without precedent²⁴). It is unclear what mechanism—whether ecological or socioeconomic—might produce spillovers at this scale. It might be explained by large farm sizes in rural Australia, low population density in the interior, and/or efforts to maintain vegetated corridors along riparian zones and between protected areas. Relatively few terrestrial locations in Australia are further than 150 km from any protected area (Supplementary Information, section 9 and Supplementary Fig. 6). Clarity on causality is critical for understanding spillovers^42,43, and this scale of effect might not apply to other continents. Finding an effect extending so far from protected area boundaries highlights the importance of careful calibration of spillover effect sizes in future analyses of spillovers. For example, in forest spillover studies it is common to assume a spillover zone of up to 10 km from the protected area boundary^44,45,46, and spillovers are often measured at much smaller distances^47,48,49. When estimating the potential costs and benefits of protected area spillovers, using a 0–10 km zone for analysis may lead to a significant underestimate of the impacted area.

Statistical prediction of spillover effects has potentially valuable applications in assessing where new protected areas might make the greatest contributions to their surrounding landscapes and in developing counterfactuals against which the management effectiveness of protected areas for spillovers can be evaluated⁵⁰. For example, comparison of actual protected area spillover effects to predicted effects could identify locations where management is over- or under-performing and the reasons why this occurs⁵¹. Consistent determination of the form, magnitude, timing and extent of spillovers will be crucial if spillovers are to be rigorously included in environmental accounting and land use planning and policy³. In the broader context of global goals for nature protection and the need to both reverse the decline of biodiversity and restore or reclaim natural areas, protected area spillovers will be vitally important for the resilience and ecological restoration of degraded landscapes and seascapes^52,53,54.

Defining the properties and underlying causes of spillover effects from protected areas is critical for both maximizing their benefits to society and protecting people from any associated costs. Quantifying spillover effects will also be central to any attempts to measure the full costs and benefits of protected areas to society³⁴. Failure to include spillovers in accounting exercises can lead to under-reporting of the benefits of protected areas, negatively impacting their social licence. Conversely, naive assumptions about likely spillover benefits and costs can inflate expectations and create other kinds of social and political problems for protected area creation and persistence. The proof of concept of spillover predictability presented here suggests that with more refinement, we can develop consistent policies that support protected area spillovers for regional social-ecological sustainability^14,34.

Methods

Data

All land cover and protected area datasets used in the analysis (see Supplementary Information, ‘Data sets’ and Supplementary Tables 1 and 2) are publicly available. I measured vegetation patterns using the Digital Earth Australia (DEA) 1:250,000 Land Cover Map (https://maps.dea.ga.gov.au)^27,28,56. The DEA Land Cover Map was created using the global standard of the Food and Agriculture Organization’s (FAO) Land Cover Classification System (LCCS) Taxonomy Version 2^57,58. The dataset combines quantitative reflectance data from the Landsat satellite and qualitative environmental descriptions to measure Australian vegetation cover and type at a grain of 25 × 25 m over the period 1988–2020. Although annual data are available, for this analysis I focused on the first and last years of the publicly available time series.

The DEA Land Cover Map distinguishes between cultivated and natural terrestrial vegetation, and between terrestrial and aquatic vegetation. I used the natural terrestrial vegetation data because of its higher value than cultivated land for biodiversity conservation. Natural vegetation in the DEA Land Cover Map describes areas that “have all or most of the characteristics of natural or semi-natural herbaceous or woody vegetation (based primarily on floristics, structure, function and dynamics)”^27,28,56. In Australia, natural or semi-natural vegetation may include areas that are grazed by domestic livestock to keep grassy areas open and reduce fire risk. Areas classified as naturally vegetated have a greater fraction of photosynthetic or non-photosynthetic vegetation than the bare soil fraction for at least two consecutive months. By contrast, vegetation classified as cultivated terrestrial vegetation occurs in areas “where management practices aimed at cultivation (including for grass production) are actively performed during the year being shown… [they] include crop planting and harvesting, fertilization and ploughing”⁵⁹.

A few details of the classification scheme are particularly relevant to interpretation of the findings of this analysis. Managed plantations and orchards are difficult to distinguish from natural vegetation and may be misclassified as described by the DEA Land Cover Map authors; and in some locations, in northern Australia in particular, variability in natural vegetation growth and fire management patterns can result in natural woodlands being misclassified as cultivated land. Similarly, in arid and semi-arid regions, natural terrestrial vegetation may transition into the natural surface class (naturally bare ground or rock) during dry periods. Finally, in urban areas, vegetated pixels are classified as natural only if the pixel is at least 30% vegetated. Although some years are singled out by DEA as being more likely to include classification errors (for example, 2010 as an unusually wet year and 2015 as an unusually dry year), the two years included in this analysis, 1988 and 2020, were both relatively ‘normal’⁵⁹. Although these details are unlikely to affect the overall conclusions drawn from this analysis, they may affect specific instances of findings about spillover effects. Note that to avoid confusion with other numeric information, X is used throughout the manuscript as a prefix to indicate a vegetation land cover class.

Data for potentially confounding variables (that is, variables that describe influences on vegetation cover other than protection) were assembled from a variety of sources. Variables were based initially on the findings of Joppa and Pfaff⁶⁰ and a list of established predictors described in related publications^15,61,62. The 14 biophysical variables for initial consideration included the following (described in more detail in the Supplementary Information and Supplementary Table 2): elevation, slope⁶³, BIO1 (annual mean temperature), BIO5 (maximum temperature in warmest month), BIO6 (minimum temperature in coldest month), BIO7 (temperature annual range), BIO9 (mean temperature of driest quarter), BIO12 (mean annual precipitation), BIO15 (precipitation seasonality (coefficient of variation))⁶⁴, SoilDES (soil depth in cm), Soil BDW0_5 and soil BDW5_15^65,66 (soil bulk density, measured using dry mass per volume, at depths of 0–5 cm and 5–15 cm), AET (actual evapotranspiration)⁶⁷, and agricultural capability⁶⁸. This list includes well-established influences on plant growth patterns, the climatic and soil variables identified by Bennett et al.⁶¹ as being most correlated with forest biomass, representative measures of the soil–plant interface, and a human perspective (agricultural potential) on the capacity of locations to support agriculture.

To correct for biases due to the placement of protected areas I also included four location-related measures: distance to town of >250,000 people, distance to coast, distance to major road, and distance to any road. I initially included human population density, but replaced this with ‘distance to town of >250,000 people’ because large areas of Australia have such low population densities that using actual human population density provided very little benefit in distinguishing between most locations and resulted a large number of missing data values that hindered statistical analyses. Note that although these variables will also correlate with land clearing processes, they are intended to correct for protected area position rather than to measure land clearing. Thus, the dates of the coverages used to generate these variables need only to align with the relatively slow process of protected area gazettement, rather than with any recent changes in land use or population expansion.

Extraction from these datasets to create attributes for each sampling polygon was undertaken in Google Earth Engine. The number of included covariates was constrained by the need to avoid overfitting in matching and regression analyses by maintaining a working ratio of at least five independent sampling points per predictor variable. I used variance partitioning and then principal components analysis to reduce the number of matching covariates (see Supplementary Information, section 7.4, for full details and related statistics). The first five principal components explained over 83% of the variance in the environmental data. The variance partitioning analysis indicated that these components explained ~18% of the variance in vegetation composition across all sampling polygons in both 1988 and 2020, with additional components explaining just over 1%.

Judging that the inclusion of additional components was not worth either the resulting loss of data from the larger analysis or (alternatively) the risks of overfitting regression models for protected areas where available sample sizes of sampling polygons were small, I ran the matching analysis using the first five principal components to correct for environmental confounding variables. Using principal components also has the added advantages that: (1) the components themselves were normally distributed, although slightly skewed in a few cases; and (2) the components were entirely uncorrelated with each other. Thus, the components fully meet textbook assumptions of regression analysis and related techniques.

Data on the management categories, gazettement dates, and other attributes of protected areas across Australia are provided in the CAPAD 2020 dataset. Some correction of minor errors in this dataset was required prior to use (details in Supplementary Information, section 1).

Data processing

A full set of data processing methods is provided in the Supplementary Information, sections 2–13. All coverages used in the analysis were reprojected into the Australian Albers (equal area) projection to ensure undistorted calculations of areas. The use of small, standardized sampling polygons in spillover analysis offers several advantages over most published alternatives (such as varying buffer or control area with protected area size^69,70 and large polygons⁷¹, or aggregation of pixels within distance bands^62,72) by offering a fine-resolution but highly standardized unit of analysis that can be easily aggregated or disaggregated without creating additional issues of autocorrelation, overlapping areas, or differences in area between data that are compared. Analyses that use single pixel values (for example, forest/non-forest) inevitably have to use counts or proportions of forested pixels for statistical analysis. Besides the problems created by different pixel trajectories over time, aggregation of pixels means that there are often different numbers of pixels per distance band from a protected area in such analyses because the areas of bands of a standard width increase with distance from the protected area boundary. The use of sampling polygons avoids these issues while also offering the advantage that their distance to the nearest protected area boundary is calculated as a continuous variable, meaning that re-analysis across multiple scales is simple. They also have the potential for use in a more advanced matching analysis approach that would use a continuous treatment variable (rather than the current standard of treatment/no treatment) if/when appropriate statistical tools for large-sample analysis of continuous treatments have been developed.

To create sampling points, I first used the ‘random points in polygons’ command in QGIS (not to be confused with the ‘inside polygons’ command) with the option of 50 points per polygon and a minimum spacing of 300 m to generate random points inside each of the CAPAD polygons. This generated 235,332 points inside protected areas (PAs; the ‘treatment’ sample). I used gBuffer in the R package rgeos⁷³ to add a 50 m buffer around each point, creating a set of circles of 50 m radius as the treatment sampling units for analysis. With a 50 m radius, each sampling polygon has an area of 7,854 m² (0.78 Ha).

I went through several iterations of running analyses and then creating more sampling polygons and adding them to the dataset to support greater inclusivity of protected areas. The first step included approximately 481,000 sampling points outside PAs and >300 m apart. I buffered these using gBuffer and merged the inside-PA and outside-PA data layers to create a single file with 716,171 50m-radius sampling polygons, of which approximately 1/3 were inside PAs and the rest were outside. I added a third set of points to the analysis by creating a 55 km merged buffer around all protected areas and using ‘random points in polygons’ in QGIS, with a minimum separation of 300 m, to add another 400,000 points distributed randomly inside these potential spillover zones. After converting these points to sampling polygons I used a spatial join with the existing sampling layer to identify and then remove all new polygons that were within 200 m of an existing sampling point. Finally, deciding that the sample size was still not sufficient, I relaxed the between-sampling polygon boundary constraint to 50 m and added another ~1.5 million sampling polygons, bringing the total up to 2,636,333 after removing overlapping or adjacent polygons. Due to the file sizes involved, later additions were run separately through the same processing steps as the other sampling points to add attributes and then merged with them prior to running the matching analysis.

Attributes from CAPAD were added to the sampling polygon coverage using a spatial join, which also added the distance of each sampling point to its closest PA. This distance was set to zero for points inside a PA. I imported the resulting file as a feature collection asset into Google Earth Engine and used a custom script to extract the number of pixels of each Land Cover class in the DEA vegetation map into a table for each image (year) in the dataset, from 1988–2020 (see Supplementary Information for all scripts). The overlay approach was inclusive of any overlap, rather than just using pixel centroids, meaning that values from 16 different 25 × 25 m land cover pixels were captured in each sampling polygon.

Land cover change characterization

To set the stage for the spillover analysis, I generated some simple visualizations and statistical tests exploring the amount and proportion of each vegetation type in 1988 and 2020 across all sampling polygons. The descriptive analysis is presented using a bar chart with error bars indicating a standard deviation from the mean. I used paired t-tests in base R to determine whether there was a higher average area of vegetation of different classes inside protected areas than outside.

Under natural conditions at least two vegetation types would usually change together (for example, closed canopy changes to open woodland, or vice-versa, leading to shifts in two vegetation cover types rather than one). Locations in which only one vegetation class changed will generally have entered a non-vegetated or non-natural cover type (for example, agriculture, built environment, bare soil, or water). I briefly explored uncorrected patterns by plotting histograms of the distance of each sampling polygon from the protected area boundary, for all polygons and by vegetation type (see Supplementary Information and Supplementary Fig. 2). This preliminary analysis showed that sampling points (and hence, the land mass of Australia) were lognormally distributed relative to protected area boundaries, with relatively few points further than about 150 km from any protected area.

Statistical analysis of spillover effects

All code used in these analyses is provided in the Supplementary Information, sections 2–13 and the associated code archive on Figshare. I used the Pawsey supercomputer (Setonix) to run matching analysis individually on each combination of PA × distance zones × land cover types × geographic contrast × year (see Supplementary Information, section 8). Statistical analysis for spillovers involves comparing a treatment (the PA) to a control or untreated location (areas outside PAs that are independent of spillovers from other PAs). Marginal effect sizes (treatment relative to control) were calculated individually for each PA and its surrounding zones. This two-step process involved (step 1) using propensity score matching in the R package MatchIt⁷⁴ to produce a balanced dataset; and then (step 2) estimating the magnitude of the treatment effect. Step 1 used generalized full matching with an underlying logistic regression model fitted to the binary (treatment/control) data. Note that this procedure produces an output that is continuous, not binary. In step 2, I followed the steps recommended by Greifer⁷⁵ and Chatton, et al.⁷⁶, using avg_comparisons (including the original covariates in the fitted model for the outcome) in the R package marginaleffects⁷⁵ to run a g-computation procedure with a cluster-robust standard error estimator to account for pair membership. This procedure estimates the risk difference (RD) as a measure of effect size for the ‘average effect of treatment for those who receive treatment’ (ATT). It uses the results from step 1 and includes the same covariates, but because it uses the continuous outputs from step 1 it is underpinned by a Gaussian distribution rather than the original logistic link. The output from step 2 was a set of statistics for each PA including the estimated RD for the treatment, its probability, and associated standard errors and confidence intervals.

I used effect size rather than the significance of the regression model to determine whether and where spillovers occurred. Risk difference, as a measure of absolute rather than relative effect, is considered one of the best measures for assessing the effectiveness of interventions⁷⁷. In this context it describes the degree to which the existence of a PA increases (positive values) or decreases (negative values) vegetation cover of the type under consideration, relative to the counterfactual. For example, for a comparison of the high forest canopy land cover type inside and outside a given PA, an RD value of 0.1 would indicate that a 10% risk increase (improvement in adjacent forest canopy cover) can be ascribed to the PA. RD is usually reported with a SE and confidence interval, but these could not feasibly be reported in the main manuscript for each PA due to the volume of protected areas in the analysis. They are given for each PA in the on-line version of the data. Effect sizes are generally classified as low, medium, or high; where threshold values must be selected for analytical reasons, effect sizes large enough to be of interest to the analyst are termed meaningful rather than significant. I used a threshold value of 0.1 for meaningful where decisions about the inclusion or exclusion of effects was necessary, and demonstrate the implications of varying the choice of threshold value in Fig. 6.

The number of individual attempts to estimate effect sizes across different parameter combinations (10 vegetation types × 10 distances × 12,500 PAs × 2 years × 2 full between-zone contrasts and one contrast (inside-PA versus independent from PA) that did not include all distance bands) made it unfeasible to individually check group balance for each PA after weighting. To check that the matching approach was effective, I saved the standardized mean difference (SMD) for each protected area for both the original dataset and the matched dataset generated by the matchit routine in the MatchIt package. The code is written in such a way that matching attempts that do not yield valid statistics will generate NA (not available) values in the output table that exclude those estimates from consideration. The mean SMD for the matched dataset across all protected areas was less than 0.01 for all six environmental variables used in the regression analysis, indicating that outputs from propensity score matching were suitably balanced, and lower than the control SMD for all variables. Histograms showing the shift in SMD before and after matching (that is, a large-sample version of the love plot) are provided in Supplementary Information, section 12 and Supplementary Fig. 11.

Individual PAs were dropped from a specific analysis if sample sizes were too small, and/or if the model failed to adequately converge for any reason. There were three main reasons why these situations arose: (1) one or more vegetation categories were either absent from the sampled location, or their abundance was too low in the area to support valid statistical comparisons; (2) the PA was too small to permit multiple sampling polygons in its interior; or (3) in areas with dense coverage of PAs, the sampling regime did not yield sufficiently many independent points at a given distance from a given PA to provide an adequate sample size for spillover analysis. Exact numbers of PAs included in each set of tests were therefore variable. Importantly, no subjective decisions were made about the inclusion or exclusion of PAs beyond the sampling and model-fitting criteria described briefly above and in considerable detail in the Supplementary Information, section 8.

After obtaining estimates of effect sizes for individual PAs as described above, I explored their relationships as described in the main text using standard statistical techniques in the software program R. I used the aov and TukeyHSD commands in base R to run the ANOVA and Tukey’s honest significant difference test to explore the relative contributions of different protected area management types to effect sizes. Variance partitioning, which offers an approach for comparing matrices of predictor variables to a matrix of response variables, was implemented using the vegan package⁷⁸. The advantage of variance partitioning over most alternative statistical approaches is that it allows the user to work with an entire matrix of response variables (which in my case was the full set of vegetation responses, across all categories, in the 0–5 km band) instead of losing information by reducing matrices to a single metric such as diversity or largest effect size. Finally, I used lm in base R to run the a multiple regression described in the main text and apply the model that was generated for each individual distance threshold to make predictions about the full dataset of all protected areas.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.