Introduction

Motivation

A Virtual Power Plant (VPP) is a coordinating framework and an integrated unit of resources, storage systems, and various energy management programs1. Generally, utilization of renewable energy sources (RESs) such as wind turbines (WTs), photovoltaics (PVs), and bio-waste units (BUs) in VPPs is proposed by various organizations to reduce environmental pollutants. WT and PV generate electrical energy respectively from wind collision with the turbine and solar radiation to the panel2. BU also uses environmental waste for energy production3. The power generated by these RESs is uncertain, so the day-ahead and real-time operation results for a VPP with a RES may differ4. This situation is recognized under conditions of flexibility shortage, and following that, generation-consumption unbalance may occur in real-time mode4. To deal with the mentioned issue, the use of flexible resources (resources capable of controlling active power), including storage systems, demand response programs (DRPs), and RESs in VPPs is necessary for system flexibility management4. Mobile storage devices like electric vehicles (EVs) and DRP are more accessible than mobile storage and RESs because they are in the hands of energy customers. Because to use RESs and stationary storage, it is necessary to incur installation and construction costs. However, EVs and DRP can be utilized with various incentive solutions for the goals of the Distribution System Operator (DSO) such as flexibility. In addition to this issue, various resources and storage devices are capable of controlling their active and reactive power at the same time5. So, a VPP can have a role in the Power Management System (PMS) in the distribution system. In this situation, a VPP can play the role of a reactive power source in the distribution system, following which, by establishing optimal performance for the VPP, it can enhance various technical and economic metrics of the distribution system.

Background study

A vast amount of research has been presented to investigate the operation of VPPs within the distribution system. To attain optimal operation of technical VPPs in a rearrangeable network, the formulation of an optimization problem is utilized in Ref.6 to handle the potential contingency issue in the system’s lines. The objective of this endeavor is to achieve optimal performance. Combined heat and power (CHP), renewable distributed generators (DGs), and dispatchable DGs are some of the carriers that are incorporated into the VPP, which is a sophisticated energy system that incorporates other carriers. The thermal and electrical storage systems, in addition to loads, are included in this category. To effectively plan and manage a VPP that is comprised of charging stations for EVs, stationary batteries, and renewable energy sources, it is recommended in Ref.7 that an Energy Management System (EMS) be used. Through the utilization of a two-stage stochastic formulation, the model can optimize the bidding procedure in the Day-Ahead Market (DAM). In this formulation, the uncertainties that have an impact on the estimation of the amount of energy that will be required for the following day are taken into consideration. In Ref.8, carbon trading and green certificate trading methods are incorporated into the optimal dispatch model of a VPP that incorporates WTs, PVs, gas turbines, and energy storage devices. The objective of the VPP optimization process is to provide the highest possible net profit while considering both economic and emission variables. VPP’s involvement in carbon trading and green certificate trading is used to develop three different schemes, compare and evaluate them, and investigate their effectiveness. The Ref.9 presents an effective strategy for maximizing the economic dispatch of a VPP. Taking into consideration the potential of energy storage systems (ESS) in EVs and data centers, the technique operates. In a test model of a data center facility, the optimization is carried out with the assistance of an advanced EMS. The problem is evaluated to maximize revenue for VPP, taking into consideration the pricing of the market as well as the hazards that are linked with distributed energy resources. The energy management of a VPP that includes a demand response program, energy storage technology, and a wind farm (WF) is the topic of discussion in the study10. The approach that has been deployed functions at the level of electricity transmission and takes into consideration the relationships between VPPs in day-ahead energy and reserve markets.

The proposed approach in Ref.11 is a bi-level coordinated dispatch method that utilizes VPPs, consisting of battery storage devices and dispatchable EVs. This technique aims to boost the robustness of the electrical energy and gas systems. The Monte Carlo simulation technique was employed to replicate the unpredictable and sequential nature of cascade failures resulting from severe weather events affecting power and gas systems. Additionally, VPPs use the direct control mode to deploy battery storage resources. Because of the cost-conscious nature of EVs, the relationship between VPPs and EV owners is likened to a Stackelberg game. The objective of this game is to determine the optimal pricing and timetable for discharging. This enables the reduction of dispatch costs while simultaneously optimizing the resilience and revenues of EV owners. In Ref.12, a proposition is made regarding the utilization of a method to visually represent, measure, and effectively employ the collective operational adaptability of a set of units. The developed technique depends on five parameters that are linked to active and reactive power. These measures aid the VPP’s operator in decision-making when faced with uncertain circumstances. The authors propose a leasing method for coal-fired units, as outlined in Ref.13, which relies on the integration of carbon credits and prices. This technique would grant the privilege to employ coal-fired units for VPPs. Subsequently, a range of demand response solutions are implemented to manage the adjustable loads of different customers, finally generating specific controlled resources for the VPP. Furthermore, to provide optimal decision-making by the VPP operator, a cost model is built that accurately represents the state of capacity degradation of the energy storage system. Reference14 investigates the challenges related to achieving complementary synergy between various power sources and micro-grids. Currently, there is a strong emphasis on enlarging the capacity of the power system for regulation, which is a crucial aspect. The study also considers various resources to create micro-grids with different features. These resources encompass both household and industrial loads, which serve as typical instances of demand-side resources. These resources possess unique power and energy attributes within the market for demand-side regulation. Literature15 provides an analysis of the management and operational challenges that arise when implementing distributed PV and ESS for residential, commercial, and industrial users. When it comes to combining distributed energy resources (DERs), VPP aggregators in many locations face the dilemma of choosing between two separate pricing strategies. This is an overlooked component in several currently accessible studies. The presentation in Ref.16 focuses on a bi-level power management approach for an active distribution network (ADN) that includes a VPP. The suggested technique coordinates the VPP operator (VPPO) and the distribution system operator. The VPP encompasses RES, ESS, and EV parking lots that are synchronized with the VPPO.

Reference17 outlines the operation of a Distribution Network that couples a VPP and Electric Springs. In fact, this system participates simultaneously in energy and reactive service markets. The prime aim of the proposed scheme is to maximize the predicted profits of systems in the mentioned markets. The constraints in the problem formulation are the AC optimal power flow equations, flexibility limits in the network, and the operating model of VPPs. Reference18 proposes a network state-based power scenario reduction strategy for renewable energy generation, where typical scenarios are selected by the state of the grid voltage. The proposed day-ahead scheduling model is a mixed-integer, nonlinear, large-scale, stochastic optimization problem with high dimensional random variables, which is difficult to solve directly by traditional centralized method. Reference19 contributes with a VPP operating model considering a full AC Optimal Power Flow while integrating different paths for the use of green hydrogen, such as supplying hydrogen to a Combined Heat and Power (CHP), industry, and local hydrogen consumers. In Ref.20, an interaction-based VPP operation methodology using distribution system constraints is proposed for DSO voltage management, assuming that the VPP primarily participates in the wholesale energy market. The research background includes an overview of the studies, which is presented in Table 1, the last portion of the document.

Table 1 The categorization of current research studies.
Full size table

Research gaps

According to the previous review and Table 1, some research gaps related to VPPs operation in the distribution network include the following.

  • Generally, in most research, the energy management or active power of VPPs in the power system has been considered. However, it should be noted that resources and storage devices that are in the VPP can also play a role in controlling reactive power. For example, in Refs.21,22, EVs control their active and reactive power with their charger. Also, RESs such as wind and solar systems are connected to the network by power electronic devices. These devices can also play a role in controlling reactive power. However, in only a small fraction of studies like16, the control or management of reactive power of VPPs in the power system has been considered. Note that reactive power management of the network can be effective in improving operational indices and voltage security16,21.

  • Most research attempts to boost the economic and operational metrics of the power system by VPPs have been considered. However, a network has various technical and economic metrics that are not correlated to each other. For instance, boosting the economic situation will require high power injection by local resources into the power system. But in this situation, a suitable situation for the operational index like voltage profile is not achieved. In addition to this, in the distribution network, the voltage is very sensitive to the power demand of the network. So much so that there is a high voltage drop at the end of the feeder buses of this network. Therefore, in this situation, estimating the voltage security index in the distribution network by local resources is of special importance. However, this issue has been discussed in fewer studies.

  • Power fluctuations in RESs arise from the inherent uncertainty in the power they generate. This results in VPPs with a RES having limited flexibility. This lack of flexibility can cause generation-consumption unbalance during real-time operation. To address this challenge, flexible sources are utilized alongside the RES. A flexible resource is an element used for controlling its active power. In most research, stationary storage like a battery has been used as a flexible resource. But note that EVs and demand response are also flexible resources that are more accessible. However, this issue has been discussed in fewer studies, so in Refs.9,11,16 EVs were utilized as a flexible resource.

  • Energy management of VPP in the distribution system is part of operational problems. In these problems, the execution steps are small thus making the solving part a time-consuming task. To reduce computational time, one solution is to simplify the problem. However, scenario-based stochastic optimization (SBSO) has mostly been employed to model uncertain parameters. In this method, quite a few scenarios are needed to access a trustable solution, so the volume of the problem in this method is not low. To address this issue, methods are needed that have a low number of scenarios. One of these techniques is the unscented transformation (UT) method, which is a stochastic optimization with a minimum number of scenarios than their counterpart methods. However, the use of this technique has been focused in fewer studies.

Contributions

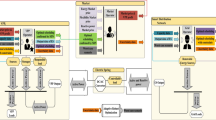
To deal with the mentioned gaps, simultaneous management of active and reactive power of renewable VPPs with EV parking lots (EVPL) and price-based load response (PBDR) is utilized in the present study, which is based on the economic, operational, and voltage security objectives of the DSO, as Fig. 1 depicts. The approach minimizes the weighted sum of expected energy cost functions, expected energy losses, and voltage security index. This problem is subject to AC power flow (AC-PF) constraints, operational and voltage security limitations of the Smart Distribution Network (SDN), operational model of RESs, EVPL, and PBDR in the form of VPP. RESs in the VPP include WT, PV, and BU. BU, by consuming environmental waste, produces gas and then uses this gas to generate electrical energy3. Therefore, it has a significant effect on reducing environmental pollutants. EVPL and PBDR are utilized in the VPP as a flexibility resource. By controlling the active power of these elements, the VPP is expected to experience desirable flexibility conditions. In the proposed scheme, load, energy price, renewable power, and EV parameters are uncertain. In the suggested approach, to deal with the last sturdy gap, the UT technique is adopted. Subsequently, to find an optimal or compromised solution, the fuzzy decision-making method is employed. In the end, by making a comparison between the background studies and the suggested approach, the following novelties are obtained for the proposed scheme:

  • Simultaneous active-reactive power management of flexible-renewable VPPs in the SDN to boost the economic, operational, and security indices of the distribution system simultaneously.

  • Investigation of the impact of the optimal performance of renewable VPPs with EV parking and price-based load response on the voltage security index of the distribution network.

  • Use of more accessible flexibility resources (elements that are in the hands of customers and do not require the installation of a new element) such as parking of electric vehicles and price-based load response alongside RESs in the form of VPP.

  • Use of the UT technique for simultaneous modeling of uncertainties of load, renewable power, EVPL, and energy price to simplify the problem.

  • Use of bio-waste in the VPP to reduce environmental pollutants by consuming environmental waste and examining its optimal performance in enhancing the economic and technical metrics of the distribution system.

Figure 1
figure 1

Active and reactive power management framework of renewable VPPs in the distribution network according to the economic and technical objectives of DSO.

Full size image

Paper organization

In the subsequent sections, we delve into the details of our study. “Modelling of the suggested approach” section presents the mathematical modeling of renewable VPP operation, incorporating EVPL and PBDR in the SDN. The uncertainty modeling is presented in “Modelling of uncertainties based on the UT method” section. “Numerical results and discussion” section reports the numerical findings derived from different cases. Lastly, “Conclusions” section provides a summary of the general conclusions drawn from this study.

Modelling of the suggested approach

The mathematical model of energy management of SDN in the presence of renewable VPPs with EVPL and PBDR is presented here following the economic, operational, and voltage security objectives. This scheme minimizes the weighted sum of operational costs, energy losses, and voltage security index, while it is subject to AC optimal power flow (AC-OPF), and the operational model of VPPs. The details of the proposed scheme formulation are explained below.

Objective function

Equation (1) gives the objective function and minimizes the weighted sum of the expected cost of energy purchased from the upstream network (first term), SDN energy losses (second term), and voltage security index (third term). The cost of SDN’s energy purchased from the upstream network per operating hour equals the product of the active power on the distribution substation located at the reference bus and the energy price21,22. The network energy losses, like the second term of Eq. (1), equal the sum of the active power of the distribution post and VPPs minus the active power of passive consumers in the network. Here, the worst security index (WSI) has been adopted21. In this method, the weak bus in SDN is first identified. The weak bus has the lowest voltage amplitude. Then, WSI is found for the weak bus. This quantity varies in the range of 0 to 1. Zero value shows voltage collapse conditions, and unity represents the no-load conditions of the network (the network with the minimum voltage drop). Therefore, the WSI should be maximized. Since the objective function is expressed as a minimum expression, the third term of Eq. (1) includes a negative coefficient21.

$$\min \,\,\,\,\,\,\,\,\omega_{EC} .\overbrace {{\sum\limits_{t,w} {\rho_{w} \gamma_{t,w} P_{S\,b = s,t,w} } }}^{{\text{Energy Cost}}} + \omega_{EL} .\overbrace {{\sum\limits_{b,t,w} {\rho_{w} \left( {P_{S\,b,t,w} + \sum\limits_{v} {\left( {A_{V\,v,b} P_{V\,v,t,w} } \right)} - P_{C\,b,t,w} } \right)} }}^{{\text{Energy loss}}} - \omega_{VS} .\overbrace {{\sum\limits_{t,w} {\rho_{w} WSI_{t,w} } }}^{{\text{Voltage Security Index}}}.$$
(1)

In Eq. (1), the parameters ωEC, ωEL, and ωVS represent the weight coefficients of the energy cost, energy loss, and voltage security functions, respectively. These coefficients have a value between zero and one, and their sum must always be equal to 123. Therefore, by changing the values of these weight coefficients, it is expected that the mentioned functions’ outputs are different, the plot of which in a 3-dimensional reference frame denotes the Pareto front of the suggested approach23. Next, a fuzzy decision-making technique24 is utilized to access an optimal or compromise point. The details of this technique for the suggested problem are as follows24:

  • Step 1 Find the minimum (Fmin) and maximum (Fmax) value of the energy cost, energy loss, and voltage security functions for three case studies ωEC = 1, ωEL = 1, and ωVS = 1.

  • Step 2 Select a random value for the weight coefficients so that their sum equals 1 (ωEC + ωEL + ωVS = 1)..

  • Step 3 Calculate the linear membership function for the energy cost, energy loss, and voltage security functions:

    • If the value of a function (F) is less than Fmin, the linear membership function value for this function is 1.

    • If the value of a function is between Fmin and Fmax, the linear membership function value for the mentioned function equals the difference of the function value to Fmax divided by the difference of Fmin and Fmax ((F − Fmax)/(Fmin − Fmax)).

    • If the function value is greater than Fmax, then the linear membership function value is zero.

  • Step 4 Determine the minimum value between the linear membership function of energy cost, energy loss, and voltage security (this amount is denoted by φ).

  • Step 5 Upon reaching the maximum number of specified members of the Pareto front, step 6 is executed. Otherwise, repeat steps 2 and 3.

  • Step 6 Select a solution or compromise point corresponding to a point from the Pareto front that has the maximum value of φ.

Constraints of SDN

The constraints of the SDN are presented in Eqs. (2)–(13). Constraints (2)–(7) describe the AC power flow model in the SDN5,6,7,8,9,10,11,12,13,14,15,16. These equations respectively express the active-reactive power balance on the buses, the active and reactive power on the distribution lines, and the voltage phase angle and magnitude at the reference bus. In this section, the desired voltage magnitude is equal to 1 p.u. The operational constraints of the SDN are stated in constraints (8)–(11)16,21,22. The maximum apparent power passing through the distribution lines and posts is modeled respectively in Eqs. (8) and (9). These constraints are also known as line and substation capacity constraints. Equation (10) presents the voltage magnitude constraint for the buses. The lower boundary leads to the prevention of SDN’s shutdown in severe voltage drop conditions. Its upper limit prevents insulation damage of SDN equipment due to high overvoltage21. Constraint (11) models the power factor limitation of the distribution posts. The power factor is equal to the ratio of active to apparent power. In the present study, the minimum power factor is set at 0.922. The voltage security model corresponding to the WSI is stated in Eqs. (12) and (13)21. In constraint (12), the WSI for the weak bus (p) is calculated21. WSI constraint is presented in Eq. (13). In this paper, the minimum value of WSI is considered to be 0.821.

$$P_{S\,b.,t,w} + \sum\limits_{v} {A_{V\,v,b} P_{V\,v,t,w} } + \sum\limits_{r} {A_{L\,b,r} P_{L\,b,r,t,w} } = \,P_{C\,b,t,w} \,\,\forall b,t,w,$$
(2)
$$Q_{S\,b.,t,w} + \sum\limits_{v} {A_{V\,v,b} Q_{V\,v,t,w} } + \sum\limits_{r} {A_{L\,b,r} Q_{L\,b,r,t,w} } = \,Q_{C\,b,t,w} \,\,\forall b,t,w,$$
(3)
$$P_{L\,b,r,t,w} = g_{L\,b,r} \left( {V_{b,t,w} } \right)^{2} - V_{b,t,w} V_{r,t,w} \left\{ {g_{L\,b,r} \cos \left( {\alpha_{b,t,w} - \alpha_{r,t,w} } \right) + b_{L\,b,r} \sin \left( {\alpha_{b,t,w} - \alpha_{r,t,w} } \right)} \right\}\,\,\,\,\forall b,r,t,w,$$
(4)
$$Q_{L\,b,r,t,w} = - b_{L\,b,r} \left( {V_{b,t,w} } \right)^{2} + V_{b,t,w} V_{r,t,w} \left\{ {b_{L\,b,r} \cos \left( {\alpha_{b,t,w} - \alpha_{r,t,w} } \right) - g_{L\,b,r} \sin \left( {\alpha_{b,t,w} - \alpha_{r,t,w} } \right)} \right\}\,\,\,\,\forall b,r,t,w,$$
(5)
$$\alpha_{b,t,w} = 0\quad \forall \;b = s,t,w,$$
(6)
$$V_{b,t,w} = 1\quad \forall \;b = s,t,w,$$
(7)
$$\sqrt {\left( {P_{L\,b,r,t,w} } \right)^{2} + \left( {Q_{L\,b,r,t,w} } \right)^{2} } \le \overline{S}_{L\,b,r} \quad \forall b,r,t,w,$$
(8)
$$\sqrt {\left( {P_{S\,b,t,w} } \right)^{2} + \left( {Q_{S\,b,t,w} } \right)^{2} } \le \overline{S}_{S\,b} \quad \forall b,t,w,$$
(9)
$$\underline{V}_{b} \le V_{b,t,w} \le \overline{V}_{b} \quad \forall b,t,w,$$
(10)
$$\overbrace {{\frac{{P_{S\,b,t,w} }}{{\sqrt {\left( {P_{S\,b,t,w} } \right)^{2} + \left( {Q_{S\,b,t,w} } \right)^{2} } }}}}^{{{\text{Power}}\,{\text{Factor}}}} \ge 0.9\quad \forall b,t,w,$$
(11)
$$WSI_{t,w} = \left( {V_{p - 1,t,w} } \right)^{4} - 4\left( {V_{p - 1,t,w} } \right)^{2} \left( {R_{L\,p - 1,p\,} P_{L\,p - 1,p,t,w} + X_{L\,p - 1,p\,} Q_{L\,p - 1,p,t,w} } \right) - 4\left( {X_{L\,p - 1,p\,} P_{L\,p - 1,p,t,w} - R_{L\,p - 1,p\,} Q_{L\,p - 1,p,t,w} } \right)^{2} \quad \forall t,w,$$
(12)
$$WSI_{t,w} \ge 0.8\quad \forall t,w.$$
(13)

Renewable VPP constraints

The operation model of renewable VPPs with EVPL and PBDR is presented in constraints (14)–(25). In constraints (14) and (15), the active and reactive power of VPPs from the SDN perspective is calculated. The active power of VPP is equal to the sum of the active power of RESs (wind, solar, and bio-waste), PBDR, and EVs in discharge mode minus the sum of the active power of EVs in charge mode and passive load. The reactive power of VPP is equal to the sum of the reactive power of RESs and EV chargers minus the reactive power of the passive load. In constraints (16)–(18), the apparent power capacity limitation of controllable PVs, WTs, and BUs is presented. These constraints also represent the capability curve of RESs. The operation model of PBDR is stated in constraints (19) and (20)25. The active power control limitation of consumers participating in the DRP is consistent with constraint (19). In constraint (20), it is also ensured that all the energy consumed by the consumer participating in PBDR is supplied from SDN during the operation horizon. Active power variations of PBDRs depend on the price signal so that the minimum energy cost based on Eq. (1) is achieved. In this DR model, in hours when the energy price is low (corresponding to off-peak hours), consumers increase their energy consumption in these hours. However, in the case of high energy prices (corresponding to peak hours), these consumers reduce their energy consumption25. In constraints (21)–(25), the operation model of EV parking is stated21,22,26. In constraint (21), the energy storage in the EV batteries is calculated. This quantity is the sum of energy stored in the previous hour, the primary energy of the EVs that are connected to the VPP recently, and the energy stored as a result of EVs operating in charge mode minus the energy discharged by EVs in discharge mode and the energy consumed by EVs26. The limitation of the charge and discharge rate of EV batteries is modeled in constraints (22) and (23). Equation (24) ensures that the charging and discharging operation of EVs does not occur simultaneously. Finally, the apparent power limitation or capability curve of EV chargers is stated in Eq. (25). In this equation, the limitation of active and reactive power controllable by EV chargers is stated21,22. CR and DR in each hour are the sum of the charge and discharge rate of the connection of EVs to the VPP. EA in each hour equals the primary energy of EVs newly linked to the VPP in that period. ED is also for the energy consumed by EVs leaving the VPP.

$$P_{V\,v,t,w} = P_{PV\,v,t,w} + P_{WT\,v,t,w} + P_{BU\,v,t,w} + P_{DR\,v,t,w} + \left( {P_{DCH\,v,t,w} - P_{CH\,v,t,w} } \right) - P_{C\,v,t,w} \,\,\,\,\,\,\forall v,t,w,$$
(14)
$$Q_{V\,v,t,w} = Q_{PV\,v,t,w} + Q_{WT\,v,t,w} + Q_{BU\,v,t,w} + Q_{EV\,v,t,w} - Q_{C\,v,t,w} \,\,\,\,\,\,\forall v,t,w,$$
(15)
$$\sqrt {\left( {P_{PV\,v,t,w} } \right)^{2} + \left( {Q_{PV\,v,t,w} } \right)^{2} } \le \overline{S}_{PV\,v} \quad \forall v,t,w,$$
(16)
$$\sqrt {\left( {P_{WT\,v,t,w} } \right)^{2} + \left( {Q_{WT\,v,t,w} } \right)^{2} } \le \overline{S}_{WT\,v} \quad \forall v,t,w,$$
(17)
$$\sqrt {\left( {P_{BU\,v,t,w} } \right)^{2} + \left( {Q_{BU\,v,t,w} } \right)^{2} } \le \overline{S}_{BU\,v} \quad \forall v,t,w,$$
(18)
$$- \sigma_{v} P_{C\,v,t,w} \le P_{DR\,v,t,w} \le \sigma_{v} P_{C\,v,t,w} \,\,\,\,\,\,\forall v,t,w,$$
(19)
$$\sum\limits_{v,w} {P_{DR\,v,t,w} = 0} \,\,\,\,\,\,\forall v,w,$$
(20)
$$E_{EV\,v,t,w} = E_{EV\,v,t - 1,w} + E_{A\,v,t,w} - E_{D\,v,t,w} + \eta_{CH} P_{CH\,v,t,w} - \frac{1}{{\eta_{DCH} }}P_{DCH\,v,t,w} \,\,\,\,\,\,\,\,\,\,\,\,\forall v,t,w,$$
(21)
$$0 \le P_{CH\,v,t,w} \le CR_{v,t,w} \,\,\,\,\,\,\,\,\,\,\,\,\forall v,t,w,$$
(22)
$$0 \le P_{DCH\,v,t,w} \le DR_{v,t,w} \,\,\,\,\,\,\,\,\,\,\,\,\forall v,t,w,$$
(23)
$$P_{CH\,v,t,w} P_{DCH\,v,t,w} = 0\,\,\,\,\,\,\,\,\,\,\,\,\forall v,t,w,$$
(24)
$$\sqrt {\left( {P_{DCH\,v,t,w} - P_{CH\,v,t,w} } \right)^{2} + \left( {Q_{EV\,v,t,w} } \right)^{2} } \le \overline{S}_{EV\,v} \quad \forall v,t,w.$$
(25)

In this article, as shown in Fig. 1, VPP is an aggregator and coordinator of resources, storage systems, and response loads managed by DSO. Based on this definition of VPP, its operation model will be in the form of relations (14)–(25). It is noteworthy that in this article, the optimal operation of VPP on the improvement of technical and economic indicators in the distribution network has been investigated. Therefore, VPP's goals, such as obtaining financial benefits, were not considered in this article. But there is no limit to the implementation of this issue, and VPP's objectives can be added to the objective function (1).

Modelling of uncertainties based on the UT method

Uncertain parameters of the problem (1)–(25) include the amount of load, PC and QC; renewable power generation, PWT, PPV, and PBU; energy price, γ, charge and discharge rate of EVs, CR and DR, and initial and consumption energy of EVs, EA and ED. The proposed problem is an operation problem with a small execution step; so, the problem needs to be simplified and the computation burden is lessened27. To achieve this goal, the volume of the problem should be decreased. To this end, the UT-based stochastic optimization27 has been adopted here so that uncertainties can be properly modeled. The method with the minimum number of scenarios can derive a trustable optimal solution. So, for b uncertainty parameters, it requires 2n + 1 scenarios. In the suggested approach, n = 10, so the number of scenarios is equal to 21.

The formulation of the problem is denoted as y = f(z). Here, y ∈ Rr is an uncertain output vector with r elements and the z ∈ Rn represents the vector of uncertain inputs. Also, μz and σz are the mean and covariance of z. Symmetric and asymmetric elements of σz are used to calculate the variance and covariance of uncertain parameters. Also, the UT method is applied to determine the mean and covariance of outputs, which are μy and σy27. The steps of the formulation of the problem are summarized here:

  • Step 1 Take 2n + 1 samples (zs) from the input data:

    $$z_{0} = \mu_{z} ,$$
    (26)
    $$z_{s} = \mu_{z} + \sqrt {\frac{b}{{1 - W^{0} }}\sigma_{z} } \,\,\,\,\,\,\,\forall s = 1,2,...,n,$$
    (27)
    $$z_{s} = \mu_{z} - \sqrt {\frac{b}{{1 - W^{0} }}\sigma_{z} } \,\,\,\,\,\,\,\forall s = 1,2,...,n,$$
    (28)

    here, W0 shows the weight of μz (mean).

  • Step 2 Evaluate the weighting factor of individual sample points:

    $$W^{0} = W^{0} ,$$
    (29)
    $$W_{s} = \frac{{1 - W^{0} }}{2n}\,\,\,\,\,\,\,\forall s = 1,2,...,n,$$
    (30)
    $$W_{s + b} = \frac{{1 - W^{0} }}{2n}\,\,\,\,\,\,\,\forall s + n = n + 1,n + 2,...,2n,$$
    (31)
    $$\sum\limits_{s = 1}^{n} {W_{s} } = 1.$$
    (32)

  • Step 3 Take 2n + 1 samples from the nonlinear function to achieve output samples using Eq. (33).

    $$y_{s} = f(z_{s} ).$$
    (33)

  • Step 4 Evaluate σy and μy of the output variable θ.

    $$\mu_{y} = \sum\limits_{s = 1}^{n} {W_{s} \theta_{s} } ,$$
    (34)
    $$\sigma_{y} = \sum\limits_{s = 1}^{n} {W_{s} \left( {\theta_{s} - \mu_{y} } \right)} - \left( {\theta_{s} - \mu_{y} } \right)^{T} .$$
    (35)

In the proposed scheme, uncertainty parameters are PC, QC, PWT, PPV, PBU; γ, CR, DR, EA, and ED. The total number of uncertainty parameters (n) is 10. According to the UT method, the total number of scenario samples is 2n + 1, therefore, it is equal to 21 for the proposed problem. In each scenario, a specific value is selected for each uncertainty parameter including load, renewable sources, and EVs based on the UT technique, (26)–(33), and the mean and standard deviation value of these uncertainties. In other words, the UT method considers the simultaneous modeling of all uncertainties in this section.

The proposed scheme includes a mathematical model28,29,30,31,32. This model is based on the optimization formulation33,34,35,36,37. It includes the objective function that is in terms of min or max38,39,40,41,42,43. The optimization problem includes the different constraints44,45,46,47. Constraints are equality or inequality48,49,50,51,52. To apply the optimization model on the distribution network, the network needs smart devices53,54,55,56. Smart systems include Telecommunication devices and intelligent algorithms57,58,59,60.

Numerical results and discussion

Case study

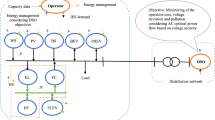
The suggested scheme, consistent with the formulation (1)–(25) and uncertainty modeling based on UT, (26)–(33), is applied in this section to the 69-bus IEEE SDN as illustrated in Fig. 261. The network has a base power of 1 MVA. The base voltage is 12.66 kV. The minimum and maximum permissible voltage magnitude are respectively 0.9 and 1.05 per unit62,63,64,65,66. The data of the distribution lines, such as resistance, reactance, conductance, susceptance, and capacity for the mentioned network are provided in Ref.61. This network has one distribution post that is connected to bus 1. The bus is considered as the reference bus. The capacity of the distribution post is also considered to be 5 MVA. The peak load data for different buses are stated in Ref.61. The load at different hours equals the multiplication of the peak load and load factor67,68,69,70,71,72. The expected daily curve of the load factor, consistent with the data of Isfahan, Iran, is plotted in Fig. 3. The energy price is based on the time of use (TOU), which for low-load (peak-load) hours, 1:00–7:00 (17:00–22:00), is 16 $/MWh (30$/MWh). The energy price in the mid-load range, 8:00–16:00 and 23:00–00:00, is 24$/MWh21. The mentioned network, as shown in Fig. 2, has 8 flexible-renewable VPPs. The location of these VPPs is shown in Fig. 2. Their data are based on Table 2. The power generated by a RES for different periods can be found by multiplying its capacity and the power generation rate of this resource. The expected daily curve of the power generation rate of WT, PV, and BU, based on the data of Isfahan, Iran, is plotted in Fig. 3. The number of EVs in each VPP is stated in Table 2. The specifications of each EV, such as battery capacity, vehicle type, charge and discharge rate, and charger capacity are stated in Refs.21,22. The efficiency of charging and discharging the EV battery is respectively considered to be 93% and 92%26. The initial and consumed energy of each EV is respectively equal to 20% and 80% of the EV battery capacity. The number of EVs present at each hour will be a multiplication of the number of EVs and the penetration rate of EVs. Figure 3 illustrates the expected daily curve of the EV penetration rate22. The peak load in each VPP equals 150% of the peak load at the VPP connection location.

Figure 2
figure 2

IEEE 69 bus SDN61 with flexi-renewable VPPs.

Full size image
Figure 3
figure 3

Daily curve of load factor, generation power rate of RESs, and EV penetration rate.

Full size image
Table 2 Data of RESs, EVPL, and PBDR in VPPs.
Full size table

Numerical results

The findings of the suggested plan, consistent with the data from the previous section, are presented. The simulation is performed in the GAMS optimization software environment, and the IPOPT algorithm72 is utilized in this software to solve the problem. This algorithm is suitable for solving non-linear problems, and it has a toolbox in the mentioned software. Therefore, this algorithm calculates the optimal values of the objective function, (1), considering constraints (2)–(25). The following part provides a complete report on the findings.

Evaluation of the compromise solution between economic, operational, and DSO security objectives

Table 3 tabulates the Pareto front for the suggested plan, where 0, 0.25, 0.33, 0.5, 0.75, and 1 are the values considered for different weight coefficients. Accordingly, the minimum values of energy cost, energy losses, and voltage security index (total WSI based on Eq. (1)) are respectively equal to 1422.6 $, 1.354 MWh, and 19.8 p.u. The maximum values of these functions are respectively equal to 2943.5 $, 3.023 MWh, and 23.1 p.u. Therefore, the range of variations (the difference between maximum and minimum values) are respectively equal to 1520.9 $, 1.669 MWh, and 3.3 p.u. The minimum values of energy cost and energy losses are obtained respectively for ωEC = 1 and ωEL = 1. The maximum value of total WSI is obtained for ωVS = 1. In Eq. (1), the coefficient of the voltage security index is negative, because WSI should be maximized. Therefore, at ωVS = 1, the best (maximum) value of the voltage security index is obtained. The maximum values of energy cost and energy losses are obtained respectively under conditions ωEL = 1 and ωEC = 1. The minimum value of total WSI is also obtained at ωEC = 1. Based on Table 3, the ascending and descending trends of objective functions are not the same. With the decrease in energy cost, energy losses become higher. The reason is that VPPs should inject high active and reactive power into the network to minimize energy costs. However, in such conditions, the power in the direction of VPP may increase towards the reference bus, which corresponds to an increase in the current flowing on the distribution lines and ultimately an increase in energy losses. The findings for the compromised solution between energy cost, energy losses, and voltage security are reported in Table 4. To extract a more accurate solution, the number of members of the Pareto front for Table 4 was increased. In such a way that the step of changes of each weight coefficient was considered equal to 0.01. According to Table 4, for modeling uncertainties with UT, the optimal values of energy cost, energy losses, and voltage security at the compromise point are respectively equal to 1862.1 $, 1.902 MWh, and 22.4 p.u. At this point, the energy cost is about 28.9% (1520.9 ÷ (1422.6–1862.1)) away from its minimum value (1422.6 $). This value for energy losses and voltage security is respectively about 32.8% and 21.2%. In other words, fuzzy decision-making has been able to obtain an optimal value for different objective functions in such a way that they are a little away from their best value (minimum value equal to energy cost and energy losses, and maximum value for voltage security).

Table 3 Pareto front of the suggested grid-connected VPP operation.
Full size table
Table 4 Compromise point of the suggested approach based on different uncertainty models and solvers.
Full size table

In Table 4, the results for modeling uncertainties with the UT and SBSO methods are presented. The SBSO combines the roulette wheel mechanism and the Kantorovich method73. The former initially produces quite a few scenarios (in this section, 2000 scenarios). In each of the scenarios, the values of uncertainty parameters are specified using their mean and standard deviation. The probability of each uncertainty parameter in each scenario is found by utilizing the normal probability function. The probability of each generated scenario is the multiplication of the probabilities of uncertainties. Subsequently, the Kantorovich method was adopted to reduce the number of scenarios to select a specific number of generated scenarios with the minimum distance from each other. Then, these scenarios are applied to the problem. The complete details of this method are explained in Ref.73. In Table 4, the results for 30, 60, 90, and 120 scenarios obtained from the Kantorovich method are stated. As per Table 4, the mentioned objective functions for a high number of scenarios in SBSO (more than 90 scenarios) are close to the results obtained in the UT method. But UT has obtained the mentioned solution for 21 scenarios based on “Modelling of uncertainties based on the UT method” section. This has resulted in UT obtaining a reliable solution in a much lower computational time than SBSO. For a low number of scenarios for SBSO, the distance of results to UT is greater. In this situation, based on Table 4, a more desirable situation for the objective functions compared to UT or a high number of scenarios in SBSO has been obtained. This desirable situation is because some of the important scenarios that have a significant impact on the problem have not been considered, and this is a limitation. Therefore, a reliable solution for SBSO is obtained for a high number of scenarios. The UT has a low number of scenarios, therefore, its computing time is much less than SBSO with several different scenarios. In SBSO, the computing time increases with the increasing of scenarios number. Because in this situation, the volume of the problem increases. Since for the number of scenarios more than 90, SBSO obtains a reliable solution, therefore, the suitable number of scenarios for SBSO is equal to 90, because compared to scenarios more than 90, it has less computing time.

In Table 4, numerical results are presented for different solvers such as IPOPT, CONOPT, BARON, KNITRO, LGO, and MINOS72. These algorithms in GAMS software have toolboxes and they are useful for solving non-linear problems. According to Table 4, among the mentioned algorithms, IPOPT has been able to obtain the most optimal solution in a lower computing time. So that it has the lowest amount of energy cost and energy loss and the highest amount of voltage security index. Its convergence time is equal to 472 s, but the calculation time in other algorithms is more than 600 s. Therefore, IPOPT is the most suitable solution algorithm for the proposed plan. Therefore, only the numerical results for IPOPT were expressed for SBSO.

Examination of the performance of renewable VPPs with PBDR and EVPL

In Figs. 4 and 5, the expected daily active and reactive power curves for RESs, EVPL, PBDR, and VPPs for the compromise point are presented, respectively. As per Figs. 3 and 4a, the trend of changes in the active power output of the RES is analogous to the daily power generation rate curve of this source, but they are numerically different. Based on this, it is seen that the highest level of power generated from all RESs is obtained in the hours of 8:00–18:00. But at other hours, the level of power generated by renewable wind, solar, and bio-waste resources is less. In Fig. 4b, consumers involved in PBDR raise energy demand in low-load (1:00–7:00) and mid-load (8:00–16:00 and 23:00–24:00) hours. Energy consumption in off-peak periods is more than mid-load hours. Based on “Case study” section, the energy price in the mid-load range is higher than in the low-load range. In peak-load hours (17:00–22:00), these consumers reduce their energy consumption. These hours correspond to high energy prices. This mode of operation of consumers in PBDR corresponds to the price signal and its goal is to reduce energy cost based on Eq. (1). EVs, based on Fig. 4b, receive high energy during off-peak periods (1:00–7:00) from VPP. This energy equals the energy consumption EVs need for future trips. They, because the energy price in these hours is low, obtain their required energy consumption in the low-load range to reduce energy costs. EVs also perform charging operations in the hours of 12:00–16:00. This operation is for storing energy in the EV batteries that can be injected into the VPP or network during peak-load hours. In other words, with the mode of operation of EVs, it is expected that their charging cost and ultimately the network energy cost will be reduced. Finally, the expected daily active power curve of VPPs from the network’s point of view is shown in Fig. 4c. This power is calculated by Eq. (14). According to Fig. 4c, VPPs inject a high level of active power into the network during 8:00–18:00. Because in these hours, RESs produce high energy. VPPs are also in the role of an electricity producer in peak-load hours. Because in these hours, EVPL and PBDR, along with RESs, wind, solar, and bio-waste, act as an electricity producer. But at other operating hours, the level of active power of VPPs is low, in such a way that VPPs are in the consumer mode in the low-load range. Because in these hours, EVPL and PBDR are in the consumer mode.

Figure 4
figure 4

Expected daily active power curve of, (a) RESs, (b) flexibility sources, (c) VPP.

Full size image
Figure 5
figure 5

Expected daily reactive power curve of (a) RESs, (b) flexibility sources, (c) VPP.

Full size image

Based on Fig. 5, it is observed that RESs and EVPLs inject reactive power into VPPs in the hours of 1:00–7:00 and 19:00–24:00, and at other hours they do not produce reactive power according to Fig. 5a,b. In the hours of 1:00–7:00, VPPs are in consumer mode according to Fig. 4. Therefore, to compensate for voltage drop and improve operational conditions (reducing energy losses) and voltage security in these conditions, RESs and EVPL inject reactive power into VPPs. In the hours of 19:00–24:00, the level of load consumption in the network is high. Therefore, various resources in VPP produce reactive power to boost the economic, operation, and voltage security metrics during these hours. Figure 5c shows the expected daily reactive power curve of VPPs. This power is calculated by Eq. (15). Accordingly, VPPs are in the mode of producing reactive power during 1:00–7:00 and 19:00–24:00. Because in these hours, RESs and EVPL produce reactive power according to Fig. 5. But at other hours, VPPs are in the mode of consuming reactive power. Because in these hours, based on Fig. 4, VPPs inject larger amounts of active power into the network. Therefore, in such conditions, an excess voltage may be created in the network. To address this issue, VPPs are in the mode of consuming reactive power to prevent severe voltage deviation.

Examination of the economic, security, and operational status of the SDN

In Table 5, the value of economic (energy cost), security (weak bus and minimum WSI value), and operation indices (energy losses, maximum voltage drop, maximum over-voltage, and peak load carrying capability (PLCC)) for various case studies are reported:

  • Case I: Load flow study (network without VPPs).

  • Case II: VPP including only RESs.

  • Case III: Case II + PBDR.

  • Case IV: Case II + EVPL.

  • Case V: Case III + EVPL without considering reactive power management by VPPs.

  • Case VI: Case III + EVPL considering reactive power management by VPPs.

Table 5 Economic, operation, and security situation of SDN considering various cases.
Full size table

PLCC refers to the network’s ability to handle a certain peak load, considering the daily load factor curve according to Fig. 3. As Table 5 expresses, the highest energy cost, energy losses, and voltage drop occur in Case I, where the minimum values of WSI, excess voltage, and PLCC exist. This condition originates because the entire network load is fed from different buses from the upstream network, and there are no local sources in the network. In Mode II, with the presence of RESs in VPPs, the situation of the mentioned indices improves, except for excess voltage. Compared to Case I, energy cost, energy losses, and voltage drop decrease by approximately 25%, 36.4%, and 44.6% respectively. WSI and PLCC increased by approximately 8.9% and 33.7% respectively. The maximum excess voltage increases to 0.034 p.u., but this value is smaller than its allowable boundary of 0.05 p.u. (1–1.05). In Case III, when PBDR are present along with RESs in the form of VPP, more desirable conditions for different indices compared to Cases I and II are obtained. In such a way that energy losses, energy cost, maximum voltage drop, WSI, and PLCC improve by approximately 40%, 44.2%, 46.7%, 19.5%, and 44.3% respectively than in Case I. In this condition, the maximum excess voltage decreases by about 35.3% compared to Case II. In Case IV, with the presence of EVPL along with RESs in VPP, a more desirable situation is obtained than in Case I, but in comparison with Cases II and III, the network situation is weaker. In this case study, compared to Case I, WSI, PLCC, energy losses and cost, and maximum voltage drop improve by approximately 17.7%, 29.7%, 32.5%, 23.6%, and 46.7% respectively. The maximum excess voltage also decreases by about 29.4% in Case IV compared to Case II. In Case V, EVPL and PBDR are placed in VPP along with RESs, but reactive power management by EVPL and RESs in VPP is eliminated. In this case, more desirable conditions for the network are obtained compared to Cases I to IV. However, the best economic, operational, and security situation of the network in Case VI is obtained compared to other case studies. Case VI is similar to Case V, with the difference that reactive power management of VPP is also considered. In Case VI, energy cost, energy loss, and maximum voltage drop decrease by approximately 43%, 47.9%, and 48.9% than in Case I. WSI and PLCC in this condition increase by approximately 26.9% and 51.4% respectively. In this condition, the maximum excess voltage decreases by about 61.8% compared to Case II.

Conclusions

This article presented an economic exploitation constrained by voltage security for a Smart Distribution Network, by focusing on the simultaneous active-reactive power management of a renewable VPP equipped with EV parking and price-responsive load. The suggested approach minimized the weighted sum of expected energy cost and energy losses minus the voltage security index. It was also subject to optimal AC power flow equations, voltage security constraints, and the operation model of resources, mobile storage, and energy consumption management program as a VPP. Subsequently, a fuzzy decision-making technique was adopted to extract a compromised solution between economic, operational, and voltage security objectives for the distribution system operator. The approach is subject to uncertainties of load, renewable power, energy price, and aggregation parameters of electric vehicles. In this article, the Unscented transformation method was incorporated so that uncertain parameters are perfectly modeled. Findings have shown that the fuzzy decision-making found values for economic, operational, and voltage security objective functions at a compromised point. The values had a small distance from their best value (minimum/maximum value of losses and energy cost/voltage security). This distance for energy loss, energy cost, and voltage security is approximately 32.8%, 28.9%, and 21.2%, respectively. The Unscented transformation method, compared to scenario-based stochastic optimization, was able to reach a trustable solution with the minimum possible number of scenarios and computational time. With the optimal simultaneous active-reactive power management of electric vehicles, load responsiveness, and RESs as a virtual power plant, the economic status, operation, and voltage security of the SDN have improved by approximately 43%, 47–62%, and 26.9% respectively, compared to power flow studies. Note that only PBDR can improve the economic, operation, and voltage security indices of the distribution network by about 44%, 35–47%, and 19.5%, respectively, compared to the power flow model.

Based on the numerical results, it was observed that the virtual power plants with their optimal performance in the distribution network can improve the economic and technical status of this network. Therefore, they can benefit from this in different markets. This topic was not included in the proposed plan; however, it was considered as future work.