Introduction

In recent years, with the rapid development of artificial intelligence technology, products such as robots, drones, and autonomous vehicles have been widely applied in human life1. These applications require scene perception based on depth information, making accurate depth estimation crucial. Depth estimation, a core technology for autonomous systems to perceive the environment and estimate their states, provides fundamental depth information for research on visual odometry, autonomous driving, robot localization, and 3D reconstruction2,3,4. By utilizing depth estimation for 3D reconstruction, more accurate information such as terrain height can be obtained, which is essential for areas such as environmental monitoring, urban planning, and natural disaster early warning and is crucial in various robotic systems and applications5. Existing depth sensors such as RGB-D cameras, LiDAR, and structured light sensors can provide accurate depth information6; however, these sensors have high hardware costs, large volumes, and high power consumption. Stereo cameras can obtain depth information through stereo matching methods7; however, such methods involve high computational complexity and demanding performance from computing units. Additionally, when temporal or spatial errors exist between two cameras in practical applications, the accumulation of errors may accelerate, further increasing algorithm requirements. In contrast, monocular depth estimation, which estimates depth maps from single RGB images, is a cost-effective and easy-to-deploy method. It does not have high hardware requirements and can obtain depth information solely from images. Therefore, methods based on single-image depth recovery have been widely studied.

Early research relied on depth cues such as image defocus, focus and defocus, and shadows to extract depth information from monocular images. However, such methods often have specific image requirements and may not be applicable to all scenes. With the development of machine learning, Saxena et al.8 utilized features to construct conditional random fields (CRFs) and Markov random fields (MRFs) to model depth information, considering global and long-range information, transforming the problem into a learning problem under a random field. However, traditional machine learning typically requires manual design and feature selection, making capture complex nonlinear relationships in data and achieving good generalizability is challenging in complex environments. In recent years, Eigen et al.9 used convolutional neural networks (CNNs) to perform monocular depth estimation tasks, estimating global coarse and local fine depth maps in two stages, realizing monocular depth estimation networks based on deep learning and achieving good results. Therefore, an increasing number of monocular depth estimation methods based on deep learning have been proposed.

In deep learning, monocular depth estimation methods can be divided into supervised and self-supervised learning methods based on whether real depth information is required during training. Supervised learning methods typically achieve high accuracy but require efficient training using large sets of images annotated with depth labels. This significantly increases the difficulty and cost of collecting large-scale, accurate, and dense ground-truth depth data. In contrast, self-supervised learning methods can avoid using large labelled datasets, effectively reducing costs and workload, thus attracting widespread attention in monocular depth estimation. Garg et al.10 regarded depth estimation as a novel view synthesis problem. They derived supervisory signals from the reprojection of images from different views based on the geometric relationships between consecutive frames to replace supervised losses based on depth labels, achieving unsupervised monocular depth estimation. Godard et al.11,12 proposed the Monodepth2 network. They introduced left-right disparity consistency and minimum reprojection losses to improve prediction accuracy, alleviate occlusion issues, and filter out moving objects with the same velocity as the camera using automasking. Many studies have applied transformer models13 in monocular depth estimation and achieved promising results. For instance, Zhao et al.14 introduced the monovision transformer as an encoder to model the global context based on Monodepth2. They progressively fused it with a convolutional decoder, enhancing the prediction accuracy by incorporating the transformer into the CNN. However, transformers are generally slower than CNNs due to their large number of parameters and quadratic complexity of multihead attention calculations, making them unsuitable for real-time tasks, especially for mobile robots and embedded devices. Diana et al.15 designed a lightweight network called FastDepth to meet real-time depth estimation requirements, which uses depth-separable convolutions throughout the network and network pruning to reduce inference time. However, such lightweight models sacrifice depth estimation accuracy to improve inference speed and cannot effectively balance speed and accuracy.

This paper adopts a combination of convolution and transformer structures as feature extractors for images and improves upon both CNNs and transformers to ensure both accuracy and improved inference speed. Shallow convolutional networks are employed, utilizing depth-separable convolutions16 to increase the receptive field of shallow networks. Stacking atrous convolution residual (ACR) modules achieves a shallow convolutional network with a larger receptive field. Additionally, an improved self-attention mechanism and feedforward network within a transformer are integrated to facilitate global context interaction. In the transformer component, a Multi-Dconv head transposed attention (MDTA) module is introduced to apply self-attention across feature dimensions, computing interchannel covariance to reduce computational complexity. The MDTA module emphasizes the spatial global context and leverages the complementary advantages of convolutional operations. It ensures global relationships are modelled between pixels and computes attention maps based on covariance. In the feedforward network section, inspired by Zamir et al.17, a two-step gated feedforward network (TSGFN) mechanism is proposed to suppress less informative features, focus on finer image features, and output high-quality feature maps.

Research methodology

Integration of Atrous convolution residual modules and an enhanced transformer for a monocular depth estimation network

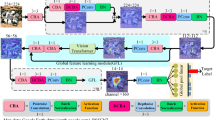
The model in this paper consists of an encoder and a decoder, adopting the classic encoder-decoder structure, as illustrated in Fig. 1. In the encoder, convolution and transformer fusion are utilized to extract image features and multiscale features are aggregated in the encoding layer through four stages.

The input image is passed through the Conv-stem convolution module in the first stage. This module consists of two convolutional layers with kernel sizes of 3 × 3 and a stride of 2. The image undergoes two convolutions for downsampling and local feature extraction, resulting in feature maps with a size of \({W \mathord{\left/ {\vphantom {W 2}} \right. \kern-0pt} 2} \times {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0pt} 2} \times C\). To compensate for the loss of spatial information caused by changes in feature scale, this paper uses ResNet18 for initial feature extraction from the input image. The extracted features are then passed through Pose Net to output the camera’s rotation matrix (R) and translation vector (t) for estimating the camera’s pose. Finally, the extracted results are concatenated with an average pooling module, enabling the network to acquire more spatial information from the original image, providing a better understanding of the context and positional information of the target. Subsequently, downsampling is performed on the feature maps using a 3 × 3 convolution with a stride of 2, resulting in feature maps with a size of \({H \mathord{\left/ {\vphantom {H 4}} \right. \kern-0pt} 4} \times {W \mathord{\left/ {\vphantom {W 4}} \right. \kern-0pt} 4} \times C\). From stage two to stage four, ACR modules and local-global transpose self-attention modules are utilized in each stage to extract features of different scales. These features are concatenated with the output of the pooling module and fed into the next stage. Finally, feature maps with dimensions of \({H \mathord{\left/ {\vphantom {H 8}} \right. \kern-0pt} 8} \times {W \mathord{\left/ {\vphantom {W 8}} \right. \kern-0pt} 8} \times C\) and \({H \mathord{\left/ {\vphantom {H {16}}} \right. \kern-0pt} {16}} \times {W \mathord{\left/ {\vphantom {W {16}}} \right. \kern-0pt} {16}} \times C\) are output. In the decoder, only one convolutional layer is used to fuse features, further reducing the overall computational burden of the depth estimation network. Finally, the inverse depth maps at different resolutions are output by connecting them with bilinear upsampling and prediction heads.

Fig. 1
figure 1

Overall structure of the self-supervised monocular depth estimation network.

Full size image

Atrous convolution residual module

The encoding layer adopts a shallow CNN network for training to effectively reduce the model size and training parameter count. However, shallow CNNs have certain limitations in terms of the receptive field. The proposed ACR module is introduced to improve local feature extraction. This module utilizes depth separable instead of traditional convolutions to extract image features. Depth-separable convolution consists of depthwise convolution and pointwise convolution. The depthwise convolution extracts features along the channel dimension, while the pointwise convolution combines features along the spatial dimension. The feature extraction ability of the model improves by increasing the number of feature channels through linear modules, introducing nonlinear transformations, reducing computational costs, and capturing image information. This fully leverages the advantages of depth-separable convolution, as depicted in Fig. 2, which illustrates the ACR module.

Fig. 2
figure 2

The model of ACR.

Full size image

Several ACR modules with different dilation rates are inserted into different stages, and the ACR modules are looped according to the stages to achieve multiscale fusion and aggregation of the local context.

The feature X with dimension .\(H \times W \times C\). is used as the input, and the output of the ACR module is as follows:

$$\hat {X}=X+Linear(Gelu(BN(Dconv(Linear(X)))))$$
(1)

where \(Linear\) denotes a linear transformation, expanding feature channels, \(Dconv\) represents a 3 × 3 depthwise separable convolution with a dilation rate of d, \(BN\) denotes a batch normalization layer, \(Gelu\) denotes an activation function, and finally, the output is obtained by restoring the dimension through a fully connected layer.

Using a shallow CNN network and increasing the receptive field can better capture the global information in the image; however, it may lead to the inability to effectively capture the local fine structures in the image, which may result in the loss or neglect of detailed features. To further optimize the model performance, this paper introduces the strategy of pooling cascading18. This module is constructed by an average pooling module and 1 × 1 convolution, which cascades multiscale image features after each downsampling. The pooling module helps to maintain critical information while reducing dimensionality and enhances the perception of features at different scales through multiscale fusion. By introducing the pooling cascading strategy, this paper captures local features in the image more meticulously while maintaining global information, thus further improving the model performance.

Local-global transposed transformer block

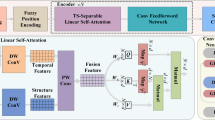
Due to the quadratic relationship between the computational complexity of self-attention and the input resolution, existing vision transformers face challenges when directly applied to visual tasks with high resolutions, such as depth estimation. This paper proposes the MDTA module to alleviate this issue, which significantly reduces the computational burden of spatial self-attention using transposed self-attention, improving the shortcomings of the original transformer architecture. The MDTA module employs a self-attention mechanism applied across channels and calculates cross-channel covariances to generate attention maps encoding the global context, thus reducing model complexity in terms of computational dimensions. As another crucial component within MDTA, a depthwise separable convolution module is introduced after the linear layer, emphasizing the local context before computing feature covariances to generate global attention maps. This helps transformer models capture relationships between input data spatial dimensions, enabling better handling of contextual information in language sequences and improving model performance. Figure 3 illustrates the specific structure of the MDTA module.

Given an input feature with dimension \(H \times W \times C\), it is expanded by \(N \times C\) into an image sequence, where \(H \times W\) represents the image resolution, denotes the total number of pixels in the input space, and C indicates the number of image channels. Through fully connected layers and 3 × 3 depthwise separable convolutions, the spatial context is encoded channelwise, resulting in a query matrix \({\mathbf{Q}}=W_{d}^{Q}W_{L}^{Q}{\mathbf{X}}\), a key matrix \({\mathbf{K}}=W_{d}^{K}W_{L}^{K}{\mathbf{X}}\) and a value matrix \({\mathbf{V}}=W_{d}^{V}W_{L}^{V}{\mathbf{X}}\), each with dimensions \(N \times C\), where \(W_{L}^{{( \cdot )}}\) denotes the fully connected layers, and \(W_{{\text{d}}}^{{( \cdot )}}\) represents the 3 × 3 depthwise separable convolutions. Therefore, the self-attention mechanism can be expressed as:

$${\mathbf{\hat {X}}}=Attention({\mathbf{Q}},{\mathbf{K}},{\mathbf{V}})+{\mathbf{X}}$$
(2)
$$Attention({\mathbf{Q}},{\mathbf{K}},{\mathbf{V}})={\mathbf{V}} \cdot Softmax\left( {{{\mathbf{K}}^T} \cdot {\mathbf{Q}}} \right)$$
(3)

where \({\mathbf{X}}\) and \({\mathbf{\hat {X}}}\) represent the input and output feature maps, respectively. Compared to the original self-attention mechanism, this paper reduces the computational complexity from \(\mathcal{O}\left( {h/{N^2}+Nd} \right)\) to \(\mathcal{O}\left( {{{{d^2}} \mathord{\left/ {\vphantom {{{d^2}} h}} \right. \kern-0pt} h}+Nd} \right)\), d is the vector dimension and h is the number of attention heads.

Fig. 3
figure 3

Local-global transposed transformer block.

Full size image

Additionally, this paper proposes a TSGFN to achieve better contextual interactions. Similar to MDTA, the TSGFN introduces depthwise separable convolutions to encode information from spatially adjacent pixel positions. The schematic structure of the TSGFN module is illustrated in Fig. 3. In contrast to a regular multilayer perceptron (MLP) feedforward network, where the MLP updates the activation function using only the current feature and treats each feature independently, the TSGFN controls the information flow through corresponding hierarchical levels in the pipeline. This allows each level to focus on fine details complementary to other levels, updating the current feature in two steps, and facilitating better contextual interactions across the entire text.

The input feature map is expanded through a fully connected layer to increase the number of feature channels. Then, image features are extracted using a 3 × 3 depthwise separable convolution to obtain \({\mathbf{X}}\). The feature map is updated in two steps. First, the features are split into two parts, \({{\mathbf{X}}_{\mathbf{f}}}\) and \({{\mathbf{X}}_{\mathbf{b}}}\), based on the feature channels. Part \({{\mathbf{X}}_{\mathbf{f}}}\) is multiplied by \({{\mathbf{X}}_{\mathbf{b}}}\) after passing through the Gaussian error linear unit (GELU) activation function, resulting in \({\mathbf{\tilde {X}}}\) after the first-step update. Then, the updated result \({\mathbf{\tilde {X}}}\) is passed through a fully connected layer. Using the same approach, the latter half \({{\mathbf{X}}_{\mathbf{b}}}\) of the original input feature map is used to update the former half \({{\mathbf{\tilde {X}}}_{\mathbf{b}}}\) of the current feature in the second step. Finally, the image features are restored to their original dimension and output as \({\mathbf{\hat {X}}}\). The TSGFN can be formulated as follows:

$${\mathbf{X}}=DWConv(Linear({\mathbf{X}}))$$
(4)
$${\mathbf{\tilde {X}}}=Linear(X\left[ {Gelu({{\mathbf{X}}_{\mathbf{b}}}) \odot {{\mathbf{X}}_{\mathbf{f}}},{{\mathbf{X}}_{\mathbf{b}}}} \right])$$
(5)
$${\mathbf{\hat {X}}}=Linear({\mathbf{X}}\left[ {{{{\mathbf{\tilde {X}}}}_{\mathbf{f}}},Gelu({{\mathbf{X}}_{\mathbf{f}}}) \odot {{{\mathbf{\tilde {X}}}}_{\mathbf{b}}}} \right])$$
(6)

where \(\odot\) represents elementwise matrix multiplication, and \(Gelu\) denotes an activation function. Compared to the MLP, the TSGFN module utilizes feature map segmentation and elementwise multiplication operations to model contextual information through interactions between feature channels. Elementwise multiplication can selectively emphasize or suppress feature responses between different channels, enabling the capture of richer feature representations.

Loss function

This paper utilizes the difference between the source and predicted images as the signal for supervising model training. Therefore, a loss function is designed based on the difference between the two, constraining network training through optical reprojection and edge-aware smoothness loss. By utilizing the intrinsic camera function K and the predicted pose P between two adjacent views, a reconstruction target image \(\hat {I}\) is obtained as a function \(\pi\) of the intrinsic function, pose, source image \({I_s}\) and depth \({D_t}\). The loss signal \({\mathcal{L}_{ss}}\) is calculated as a function \(\mathcal{F}\) of inputs \(\hat {I}\) and I:

$${\mathcal{L}_{ss}}\left( {\hat {I},I} \right)=\mathcal{F}\left( {\pi \left( {{I_s},P,{D_t},K} \right),I} \right)$$
(7)

The function \(\mathcal{F}\) is typically obtained as a weighted sum between the structural similarity item and the intensity difference item, calculated as the sum of the pixelwise structural similarity (SSIM) and the L1 loss between \(\hat {I}\) and I:

$$\mathcal{F}\left( {\hat {I},I} \right)=\frac{\alpha }{2}\left( {1 - SSIM\left( {\hat {I},I} \right)} \right)+(1 - \alpha )\left\| {\hat {I} - I} \right\|$$
(8)

where \(\alpha\) is typically set to 0.85. The minimum luminance loss is computed to handle out-of-view pixels in the source image and occluded objects:

$${\mathcal{L}}\left( p \right) = \mathop {\min }\limits_{{i \in [1, - 1]}} {\mathcal{F}}\left( {\widehat{{I_{i} }}(p),I(p)} \right)$$
(9)

Smoothness loss and edge-aware smoothness loss are used to improve the inverse depth map d:

$${\mathcal{L}_{smooth~}}=\left| {{\partial _x}d_{t}^{*}} \right|{e^{ - \left| {{\partial _x}{I_t}} \right|}}+\left| {{\partial _x}d_{t}^{ * }} \right|{e^{ - \left| {{\partial _y}{I_t}} \right|}}$$
(10)

Finally, both the view reconstruction loss \({\mathcal{L}_{ss}}\) and the smoothness loss \({\mathcal{L}_{smooth~}}\) are computed from the output at each scale \({\text{S}} \in \left\{ {{\text{1,}}\tfrac{{\text{1}}}{{\text{2}}}{\text{,}}\tfrac{{\text{1}}}{{\text{4}}}} \right\}\) to achieve full resolution and then averaged to train the network as \({\mathcal{L}_{tot}}\):

$${\mathcal{L}}_{{tot}} = \frac{1}{3}\sum\limits_{{s = 1}}^{3} {\left( {\mu{\mathcal{L}}_{{ss}} + \lambda {\mathcal{L}}_{{smooth}} } \right)}$$
(11)

where \({\mathcal{L}_{ss}}\) ensures the similarity between the generated depth map and the original image by measuring the difference between the output result and the original features. \({\mathcal{L}_{smooth~}}\) is used to further smooth the image, preventing the impact of excessive detail noise and irregularities, thereby improving the signal-to-noise ratio. The weights \(\mu ,\lambda \in\)[0,1] adjust the balance between the reconstruction loss and the smoothing loss in different models. These two types of losses have the same effect on street scene images, so the weight factors are set to 0.5.

Experimental dataset and evaluation metrics

This section evaluates the algorithm’s accuracy on the KITTI dataset19 and its generalizability on the Make 3D dataset8 to validate the effectiveness of the proposed method and its generalizability across different scenarios. Simultaneously, ablation experiments are conducted on various components proposed in this paper to verify the contributions of each module to the overall network.

Experimental dataset and parameter configurations

The KITTI dataset comprises 61 road scenes for autonomous driving and robotics research, captured using devices mounted on vehicles equipped with LiDAR sensors. This paper employs image segmentation as in Eigen et al.9 to train and evaluate the proposed method, where there are 39,180 images for training, 4424 for validation, and 697 for testing. All images used the same camera intelligence, with the camera principal point set to the image centre and the focal length set to the average of all focal lengths in KITTI. During testing, the predicted depths are constrained to the range of [0, 80] metres.

The Make 3D dataset is a monocular depth estimation dataset consisting of 534 pairs of RGB-D images, with 400 pairs used for training and 134 pairs used for testing. Towards the end of this paper, the model trained on the KITTI dataset is evaluated on 134 test images to assess the generalizability of the algorithm across various outdoor scenes.

The model in this paper is implemented on the PyTorch deep learning platform, utilizing Adam as the model optimizer, setting the number of epochs to 30, the batch size to 12, and the input image resolution to 640 × 192. The initial learning rate is set to 0.0001, with a 10x decay after the first 15 epochs, and the weight decay is set to 0.0001. Initializing the network with parameters trained on the ImageNet dataset enables rapid convergence. The experiments were conducted on an NVIDIA RTX6000 GPU with 24 GB of memory, and the training lasted for 18 h, achieving the highest accuracy on the network at the 29th epoch.

Evaluation metrics

The training results on the KITTI dataset are quantitatively analysed using the evaluation metrics proposed by Eigen et al.9 to validate the effectiveness of the model proposed in this paper. The primary accuracy metrics are as follows:

Absolute relative error:

$$Abs\text{Re} l = \frac{1}{N}\sum\limits_{{y \in N}} {\frac{{\left| {y - y^{*} } \right|}}{{y^{*} }}}$$
(12)

Squared relative error:

$$Sq\text{Re} l = \frac{1}{N}\sum\limits_{{y \in N}} {\frac{{(y - y^{*} )^{2} }}{{y^{*} }}}$$
(13)

Root mean square error:

$$RMSE = \sqrt {\frac{1}{N}\sum\limits_{{y \in N}} {(y - y^{*} )^{2} } }$$
(14)

Log root mean square error:

$$RMSE_{{\log }} = \sqrt {\frac{1}{N}\sum\limits_{{y \in N}} {(\log \,y - \log \,y^{*} )^{2} } }$$
(15)

where y represents the depth predicted by the depth network, \({y^ * }\) represents the ground-truth depth, and N denotes the total number of pixels with available ground-truth depth.

Experimental results and comparative analysis

Experimental results on the KITTI dataset

The model is evaluated on the KITTI dataset and compared with mainstream algorithms to validate the effectiveness of the algorithm proposed in this paper. The comparative experimental results are shown in Table 1. The first four metrics are errors, the middle three metrics indicate the model accuracy at different thresholds, and the last metric represents the model parameter count, which is one of the indicators for evaluating how lightweight the model is.

Comparing the algorithms in Table 1, it is evident that the algorithm proposed in this paper has the least parameter count (3.0 M). Compared to Monodepth2 with a ResNet-18 backbone, the RMSE decreases by 7%, the accuracy improves by 16% on the < 1.25 metric, and the parameter count decreases by 79%. Compared to the lightweight FastDepth network, which has a faster inference speed, the proposed algorithm performs better across all the metrics. Compared to recent lightweight networks such as R-MSFM6, Lite-HR-Depth, and Lite-Mono, the proposed algorithm falls only slightly behind Lite-Mono in the Sq Rel error metric but outperforms in accuracy and other error metrics. Compared to the latest MonoFormer, the proposed algorithm performs better in all the metrics except for Abs Rel while reducing the model parameter count by 87%. In summary, the algorithm proposed in this paper can control the model parameter count within a low range while ensuring network accuracy without producing significantly greater errors.

Table 1 Depth accuracy and error of different methods on the KITTI dataset.
Full size table
Fig. 4
figure 4

Visualization results on the KITTI dataset.

Full size image

Several lightweight algorithms are subjected to visual analysis to evaluate the advantages of the algorithm proposed in this paper. Figure 4 illustrates the visualization results on the KITTI dataset, showing the clearer boundary information extraction capability of the proposed algorithm compared to other lightweight networks. In the fourth experiment group, Monodepth2 exhibits blurred boundary extraction for road signs, failing to define their boundaries clearly, whereas our algorithm is able to extract the boundaries of road signs more accurately, showing superior boundary clarity. In the fifth experiment group, other algorithms failed to identify distant signs, while the proposed algorithm identified both signs relatively well, demonstrating better performance in recognizing distant objects with higher accuracy. Moreover, in the sixth experiment group, other algorithms confused the boundary information of the ground landmarks, while the proposed algorithm provided more accurate boundary information for each separately. This is attributed to the ability of the proposed algorithm to capture both local geometry and global semantic information in the environment through the local-global transposed transformer module, controlling the flow of effective information. This experiment demonstrates that the proposed algorithm can provide more accurate depth information for small but important objects in autonomous driving scenarios, such as signs, traffic lights, and barriers, thus exhibiting superior monocular depth estimation performance with significant implications for autonomous driving and related areas.

Generalization validation results on the make 3D dataset

In this paper, generalization experiments are conducted on the Make 3D dataset to evaluate the ability of the model to generalize to different real-world scenarios. Initially trained on the KITTI dataset using input images with a resolution of, the model is directly evaluated on the Make 3D dataset without any modifications following the evaluation method provided in Monodepth2. Figure 5 presents the visualization results of various algorithms on the Make 3D dataset. Despite no further training on this dataset, the proposed algorithm maintains relatively accurate depth extraction precision, with good detail features observed at the boundaries of some objects. Table 2 compares the generalization results between the proposed algorithm and other depth estimation algorithms. The experimental results indicate that compared to Monodepth2, the proposed algorithm achieves a decrease of 0.5 in RMSE and a decrease of 0.295 compared to R-MSFM6. Additionally, the proposed algorithm exhibits the lowest errors across all other error metrics. A quantitative and qualitative analysis of experimental results shows that the proposed algorithm can perform well on different outdoor datasets, demonstrating its strong generalizability.

Fig. 5
figure 5

Visualization results on the make 3D dataset.

Full size image
Table 2 Evaluation results on the make 3D dataset.
Full size table

Model complexity evaluation

In this paper, experiments were conducted on a Raspberry Pi 3 Model B, an edge device Syncbotic SBC-T800, and an Nvidia Titan X. The test images used were from the KITTI dataset with a resolution of 640 × 192. The model speed and complexity were evaluated based on parameters, frames per second (FPS), and floating point operations (FLOPs). Figure 6 illustrates the inference speed of different algorithms on three different devices. The algorithms positioned towards the top-right corner exhibit higher efficiency and accuracy, highlighting the advantages of the proposed algorithm. None of the algorithms achieved real-time depth estimation due to the lower configuration and absence of GPU deployment on the Raspberry Pi 3 Model B. However, when deployed on the edge device SBC-T800 without a GPU, the proposed algorithm achieved real-time performance. Furthermore, it maintained high inference speed on more advanced GPUs while demonstrating good performance in terms of estimation accuracy and error metrics.

Table 3 presents the quantitative analysis results of the complexity and inference speed of the proposed algorithm compared to those of other algorithms. The proposed algorithm significantly outperforms FastDepth, which is based on a lightweight CNN architecture and exhibits higher real-time performance, in depth estimation accuracy and RMSE metrics. While FastDepth achieves higher real-time performance through pruning, the proposed algorithm maintains superior accuracy. Monodepth2 and the proposed algorithm share similar real-time performance; however, Monodepth2 has twice the number of FLOPs and 5.1 times the number of parameters of the proposed algorithm, indicating higher model complexity. Despite its smaller parameter count, R-MSFM6 has the slowest inference speed in all experiments, lacking real-time performance, especially on edge devices. Compared to Lite-Mono, which shares a similar CNN-Transformer fusion architecture, the proposed algorithm achieves fewer parameters through depth-separable convolutions and exhibits higher accuracy and stronger inference capabilities by improving the transformer component.

In summary, the proposed algorithm achieves high accuracy while maintaining lower model complexity and faster inference speed. It is deployable on edge devices and meets real-time requirements.

Fig. 6
figure 6

The running speed of algorithms on different devices.

Full size image
Table 3 Model complexity and speed evaluation of different methods.
Full size table

Ablation experiments

Ablation experiments were conducted on each module proposed in this paper to understand better the effect of the proposed modules on network performance. All experiments were conducted on the KITTI dataset, with the image resolution set to 640 × 192. The experimental results are shown in Table 4.

Depth-separable convolution: In this paper, depth-separable convolutions are employed in the encoding layers to extract features. In the ablation experiment, the dilation rate was set to 1, and the subsequent pointwise convolution was removed to convert it into a regular convolution. The visualized result for Model A is shown in Fig. 7. The network parameter count decreased by 0.165 M, and the inference speed of the model decreased by 3 FPS. This ablation experiment resulted in the largest decrease in accuracy. The reason lies in the significance of the ACR module in expanding the receptive field of shallow networks, which is crucial for improving local feature extraction. Image features cannot be effectively extracted by relying only on shallow CNNs, leading to a decrease in model accuracy.

Transformer Module: In the ablation experiment results, when the transformer module was removed, the model’s parameter count decreased by 0.206 M, and the inference speed increased by 5 FPS. However, model accuracy significantly decreased. Additionally, the model’s ability to extract object boundaries also decreased, as shown in Model B in Fig. 7. The LGTF module provides global context information interaction for the entire network, improving the inherent locality of feature extraction in CNN networks. When removed, the model relies solely on shallow networks for global information extraction, which has limitations in capturing global information, leading to a decrease in model accuracy.

TSGFN Module: To further verify the role of the two-step gated feedforward network module in the transformer, an ablation experiment was conducted by replacing this module with a MLP feedforward neural network. After the replacement, the parameter count and inference speed remained largely unchanged; however, there was a slight decrease in model accuracy. This module in the transformer controls the feature responses between different channels, selectively emphasizing or suppressing image features. When this part of the module is replaced, the flow of information in the network is not affected by the gating mechanism, leading to uncontrolled noise information in the network, resulting in increased model error.

Table 4 Ablation experiment results.
Full size table
Fig. 7
figure 7

Visualization results of the ablation experiment.

Full size image

Conclusion

The inference speed and estimation accuracy of monocular depth estimation networks are crucial metrics for evaluating algorithms. However, there must be a balance between inference speed and estimation accuracy. A lightweight self-supervised monocular depth estimation method is proposed by integrating an improved transformer to address the issues of large model parameters and low computational efficiency in existing monocular depth estimation networks. This paper validates the effectiveness of the proposed method on two outdoor datasets, namely, the KITTI and Make 3D datasets, and conducts model complexity and real-time verification on three types of devices. The experimental results demonstrate that the proposed method has a model parameter count of only 3.0 M. On the KITTI dataset, it achieves an accuracy of 89.1% on the < 1.25 metric and performs optimally on the Make 3D dataset, indicating good generalizability. Visualization results from both datasets illustrate the ability of the network to effectively extract boundary information of objects such as signs and obstacles in the scene. With an inference speed of 87 FPS on the Nvidia Titan X, real-world experiments on edge devices confirm that the proposed algorithm can be deployed on edge devices, meeting real-time requirements. Compared to other lightweight networks, this proposed network achieves a better balance between accuracy and network inference speed. Through experiments, it was demonstrated that the proposed algorithm can maintain high accuracy while improving computational efficiency, realizing a lightweight self-supervised monocular depth estimation approach.