Enhancing HVDC transmission line fault detection using disjoint bagging and bayesian optimization with artificial neural networks and scientometric insights

Abstract

DC grid fault protection techniques have previously faced challenges such as fixed thresholds, insensitivity to high-resistance faults, and dependency on specific threshold settings. These limitations can lead to elevated fault currents in the grid, particularly affecting multi-modular converters (MMCs) vulnerability to large fault current transients. This paper proposes a novel approach that combines the disjoint-based Bootstrap Aggregating (Bagging) technique and Bayesian optimization (BO) for fault detection in DC grids. Disjoint partitions reduce variance and enhance Ensemble Artificial Neural Network (EANN) performance, while BO optimizes EANN architecture. The proposed approach uses multiple transient periods instead of a fixed time to train the model. Transient periods are segmented into multiple 1 ms intervals, and each interval trains a separate neural network. In this way, a robust local relay is created that does not require high-speed communication systems. Additionally, a discrete wavelet transform (DWT) is applied to select detailed coefficients of the transient fault current, measured at the DC line’s sending terminal for fault protection. EANN is trained in comprehensive offline data that considers noise impact. Simulation results demonstrate the scheme’s ability to detect faults as high as 400 Ω accurately. This makes it a robust, reliable, and effective solution for fault detection on high-voltage direct current (HVDC) transmission lines. Lastly, this research provides the first-ever scientometric analysis of HVDC transmission line fault protection using neural network algorithms, highlighting major research themes and trends. The scientometric analysis was based on a dataset of 136 available research articles from the Scopus database from the last ten years. Therefore, this research provides valuable insights into the use of ANN for HVDC transmission line fault protection.

Introduction

With the increasing adoption of MMC-based MTDC (modular multilevel convert-er-based multiterminal DC) grids, ensuring the reliability of MMCs (Modular Multilevel Converters) becomes crucial for the safe and reliable operation of the power system. For smooth operation of the converter, fault detection must be a prerequisite for a fault-tolerant process that must be quick and reliable to guarantee the uninterrupted service of the converter. Hence, fault detection in MMC-based MTDC systems poses significant challenges, primarily due to multiple sub-modules (SMs) within the converter. The fault detection process becomes even more critical because each SM can become a source of failure, necessitating effective fault detection methods to enhance system reliability and mitigate the risk of power system failures^1,2.

Several fault detection methods have been implemented for MTDC (Multiterminal DC) systems^3,4. However, the robustness of these protection strategies is often compromised by the reliance on manual thresholds associated with traditional techniques. In recent years, the emergence of the artificial intelligence (AI) approach has provided significant advantages over conventional methods. A significant reduction in engineering and development time could be achieved by eliminating the need for mathematical modeling in AI algorithms. ANNs are very efficient in self-learning and have an adaptive ability in pattern recognition to discern classes in composite problems⁵. A detailed and accurate mathematical model of each system under a fault scenario must be established to develop a formal relaying method. However, compared with the conventional techniques, ANNs use their innate capability to recognize patterns, allowing them to model non-linear interactions between input and output without requiring knowledge of the internal process^6,7,8. ANNs require simulated training data instead of deterministic and detailed system and fault models. The operating time is remarkably quick and reliable because it only contains a collection of simple, interconnected processing units^9,10,11.

Artificial intelligence techniques have proven to be highly effective in addressing non-linear problems and finding applications in various fields, particularly pattern recognition^12,13. Among these techniques, ANNs have gained prominence as “Universal Approximators” and have been extensively utilized across multiple engineering disciplines^14,15. In⁹, the author proposed neural network (NN)-based resilient DC fault protection, in which discrete wavelet transform (DWT) is employed to obtain characteristic patterns from faulty signals and applied at the input of ANN. However, the proposed method requires a large amount of offline data for ANN training, potentially causing time and computational costs^16,17. Furthermore, the effectiveness depends on fault location estimation accuracy, and the DC fault protection scheme may also be affected by grid topology and noise. NN-based fault detection and diagnosis approaches are presented in¹⁸ by extracting several features from the Clarke transformation. It is crucial to note, however, that the relative performance of hyperparameter optimization (HPO) algorithms might vary greatly depending on the performance goal. Furthermore, the appropriate value of the parameter epoch E is determined by the performance aim. It is also worth mentioning that the proposed approach is only evaluated on six deep neural networks (DNN) benchmarks in the study, and its performance on other benchmarks or real-world applications may differ.

Additionally, in¹⁹, ANNs were employed to identify fault conditions in high voltage direct current (HVDC) networks solely based on voltage recordings from the rectification unit. The method’s effectiveness may be affected by the hyperparameters used and the initial conditions. To converge to the ideal solution, the method may require a significant number of function evaluations, which could be computationally expensive. Lastly, the approach has not been tested for noisy or stochastic objective functions.

One of the complex tasks in the neural network is optimizing the hyperparameters for optimal performance. However, in past studies, most researchers choose hyperparameters manually or by hit and trial without employing any optimization algorithm. Therefore, in this research, Bayesian optimization (BO) is employed to fine-tune the hyperparameters of artificial neural networks (ANNs). BO is particularly well-suited for optimizing hyper-parameters^18,20, and it is also used in cloud infrastructure, maximum power point tracking, and power amplifier efficiency optimization^19,21.

In the context of electromagnetic interference (EMI) and similar applications, BO combined with deep neural networks (DNNs) offers advantages over time-consuming optimization methods like genetic algorithms (GA) and particle swarm optimization (PSO)²². ANNs are preferred over other intelligence methods because of their ability to self-learn and work effectively for complicated non-linear problems. However, recent research has been focusing on hybridizing multiple approaches with ANNs to address the challenges of noise, bias, and variance inherent to ANN models. This research presents a novel hybrid technique, BO-based multilayer bootstrap aggregating with ANN to identify the faults in the DC transmission line with the application of DWT. By combining these different methodologies, the proposed hybrid technique aims to enhance the accuracy and robustness of fault identification in DC transmission lines. It leverages the wavelet transform to extract relevant features from the signals, uses BO to optimize the parameters of the ANN model, and employs Bagging to aggregate the predictions of multiple ANN models trained on different subsets of the data.

Furthermore, to train the ANN, most of the previously discussed ANN techniques used a fixed threshold or a single time window with a specific duration ranging from 1 ms to 10 ms. These techniques can only identify one particular fault pattern or segment; they cannot recognize faults within various fault segments. In this research, the relay is designed to detect any data segment as ANN is trained by including the multiple segments of a transient period.

Simulation and evaluation are two complementary stages in our approach. Fault scenarios are first simulated using PSCAD/EMTDC, generating detailed and accurate data regarding the system’s behavior under various fault conditions. This includes transient voltage and current responses. This data is then exported to MATLAB, where a fault detection algorithm is implemented, involving feature extraction using DWT, algorithm implementation with an ANN), optimization through BO and performance evaluation based on metrics such as detection accuracy, false positive rate, false negative rate, and detection time. Although PSCAD/EMTDC and MATLAB are separate tools, they can be integrated using a co-simulation interface, allowing real-time data exchange between the two environments. Fault scenario simulations run in PSCAD/EMTDC generate data exported in a compatible format (e.g., CSV, MAT files) to MATLAB for processing. MATLAB fault detection results, including detection time and accuracy, inform the setup of tripping conditions in PSCAD/EMTDC. Specifically, a control signal is generated in MATLAB based on the detection results. It is exported and then used to trigger the hybrid Direct Current Circuit Breaker (DCCB) model in PSCAD/EMTDC. With co-simulation, MATLAB’s robust machine learning and data analysis capabilities are combined with PSCAD/EMTDC’s powerful simulation environment. This ensures a comprehensive evaluation of the proposed approach with the following contributions:

• a. Fast and robust relays do not get slow despite considering the multiple segments of a transient period in the ANN training because of the short time window of 1 ms.

• b. The proposed method can identify any data segment compared to other conventional & AI techniques because the ANN is trained for the various segments of the transient period.

• c. Compared with other AI algorithms, if ANN cannot identify the high impedance fault in a 1 ms period due to external factors, it will not rely on the backup protection method as other methodologies rely upon. Rather, it will detect the fault in the second (1–2 ms) segment.

• d. The proposed method is more reliable as ANN is trained for the numerous segments of the transient duration considering three-time windows (0–1, 1–2, 2–3) ms.

• e. Multiple time windows serve as a self-healing fast relay that does not depend on backup protection. The proposed self-healing algorithm improves breaker longevity by reducing thermal and electrical stress on hybrid DCCBs.

• f. The proposed scheme can accurately detect the fault with a 400 Ω fault impedance.

• g. Furthermore, a first-ever scientometric analysis of HVDC transmission line fault protection using neural network algorithms has been conducted. Recent trends in the literature, as identified through a focused scientometric analysis, reveal a growing emphasis on AI-driven solutions, particularly neural networks, for fault detection. However, existing research predominantly focuses on conventional ANN architectures with limited optimization, highlighting a significant gap in the application of advanced techniques such as Bayesian optimization and ensemble methods.

• h. Bayesian optimization is applied to optimize the hyperparameters of ANNs, as the performance greatly depends on the optimal value of hyperparameters.

• i. Moreover, in scientometric analysis, co-authorship analysis underscores the need for global collaboration in HVDC fault detection, with China leading the way, but broader AI integration is needed. Our research offers a scalable solution adaptable to diverse grid configurations.

To the authors’ knowledge, this is the first time ensemble artificial neural networks (EANNs) and bootstrapping combination has been used in the HVDC fault protection domain. HVDC systems, crucial elements of contemporary power grids, must be stable and reliable, and fault detection and identification play a significant part. The bootstrapping technique generates numerous subsets of the original dataset, enabling the training of various ANNs, also known as bootstrap models. These models capture various fault patterns and increase the system’s overall robustness. By combining the predictions from these bootstrap models, the ensemble of ANNs uses its collective experience and knowledge. Our findings show the usefulness of the proposed strategy in obtaining higher fault detection and identification accuracy compared to conventional methods after extensive experimentation. This novel use of the bootstrapping method in an EANN framework opens up a fresh and promising path for developing HVDC fault diagnosis.

The remainder of the paper is organized as follows: a review of scientometric analysis is presented in section II. In section III, MMC based MTDC topology utilized in the study is discussed. In sections IV and V, signal analysis and artificial neural network based on bootstrap aggregating and ensemble of artificial neural network are presented, respectively. Moreover, sections VI and VII cover BO-based ANN and its training. Simulation results are presented, followed by future work and conclusions. Figure 1 shows the overall graphical representation of the present work.

Fig. 1

The graphical representation of the present work.

Review of scientometric analysis

This study applies a scientometric analysis approach toward understanding research in applying AI algorithms, i.e., neural networks, in studying HVDC transmission faults. A detailed examination was conducted using the (visualization of similarities) VOS viewer tool. This tool is used for constructing and visualizing bibliometric networks. It creates maps based on network data, enabling the analysis of citation networks, co-authorship networks, and keyword co-occurrence networks, thus yielding useful insights into the contribution of publication trends to the subject²³. The Scopus database was used as the major source for publications. From 2014 to 2023, the search covered 136 documents only. This detailed analysis improves our awareness of the research landscape and directs future research. After a series of trials, the following Boolean search was performed to acquire a complete collection of publications using appropriate keywords. By applying following filters, the search yielded a targeted collection of research articles that form the basis of the scientometric analysis presented in this paper.

Filters: “TITLE-ABS-KEY ( ( (“high voltage direct current” OR “HVDC”) AND (“neural network”) AND (“fault”) ) ) AND PUBYEAR > 2013 AND PUBYEAR < 2024 AND ( LIMIT-TO ( SUBJAREA, “ENGI”) OR LIMIT-TO ( SUBJAREA, “ENER”) OR LIMIT-TO ( SUBJAREA, “COMP”) OR LIMIT-TO ( SUBJAREA, “MATH”) OR LIMIT-TO ( SUBJAREA, “MATE”) OR LIMIT-TO ( SUBJAREA, “DECI”) ) AND ( LIMIT-TO ( DOCTYPE, “ar”) OR LIMIT-TO ( DOCTYPE, “cp”) OR LIMIT-TO ( DOCTYPE, “cr”) )”

Author keyword analysis

An in-depth author’s keyword co-occurrence study is presented in this section, which aims to shed light on the use of neural networks for HVDC fault identification, classification, diagnosis, and related domains. As a result of this study, useful insights are obtained into the landscape of this subject by examining the clustering information derived from the analysis, which includes fault localization, fault diagnosis, HVDC system reliability, fault detection, and neural network simulation studies.

The size of each node in the keyword co-occurrence analysis represents the number of occurrences of the related term. Larger nodes imply a greater frequency of recurrence of the keyword, offering a visual depiction of its importance. The connections between nodes represent the relationship between the examined terms. The distance between terms appears to be smaller when they are closely connected. Furthermore, the thickness of the lines linking the nodes suggests that these terms are featured in several papers within the dataset.

Fig. 2

Author keyword co-occurrence Map.

Also, author keywords are used as units of analysis in the keyword co-occurrence analysis, which reveals the intellectual structure and content of the research materials²⁴. A minimum occurrence criterion of five was established through trials and tests to ensure correct clustering results in the visibility of the neural network in application in HVDC fault identification, classification, diagnosis, and related and related domains using VOS viewer software. As a result, only 73 out of 739 keywords meet this criterion. The generated maps of the keyword co-occurrence in Fig. 2 reveal the structure of the researched themes. Notably, the study shows that “HVDC” is the most frequently mentioned term, indicated by its prominence-sized node, with 22 occurrences. It has the strongest link strength (52) with other terms, suggesting its importance in the domain. Fault Location, fault diagnosis, fault detection, and artificial neural networks are the top five prominent terms.

Based on the clustering information, five distinct clusters, represented by different colors reflecting the specific research focuses, are observed. The fault location cluster (green) investigates artificial neural network techniques and methods related to pinpointing the location and protection of faults within the HVDC system. The fault diagnosis cluster (blue) delves into the methodologies for diagnosing and identifying faults in HVDC systems, particularly the HVDC converters, utilize convolutional, backpropagation (BP), and radial basis function (RBF) based neural networks, respectively. The HVDC system reliability cluster (red) explores aspects of the overall reliability and performance of HVDC systems employing artificial neural networks. The fault detection cluster (yellow) centers around detecting faults occurring within HVDC systems using various neural network types and other AI algorithms. Finally, the neural network simulation studies cluster (purple) involves studies that employ neural networks for simulating HVDC fault analysis scenarios that employ neural networks for simulating HVDC fault analysis scenarios.

The scientometric analysis of the keyword co-occurrence map provides significant insights into the HVDC fault analysis research landscape. In Fig. 3, the analysis delves into the interconnections between the term “HVDC transmission line” and other correlated terms. The results obtained from this examination reveal intriguing patterns within the network, comprising multiple nodes. Notably, the HVDC transmission line appears only 4 times, with an average publication year of 2017.67 from 2013 to 2022. It is interesting to observe that HVDC transmission line has only 8 links with other keywords, including fault detection (link strength: 1), fault classification (link strength: 1), fault location (link strength: 1), artificial neural network (link strength: 1), wavelet transform (link strength: 1) and genetic algorithm (link strength: 1). Because there are no major nodes or clusters indicating fault investigations in HVDC transmission lines, the keyword co-occurrence map shows a research gap in this domain, as evident by Fig. 3. This omission emphasizes the importance of the need for additional study and investigation to solve the difficulties and opportunities connected with faults in HVDC transmission lines. Future research concentrating on this essential feature will considerably increase fault analysis and the dependability of HVDC transmission lines, particularly using AI techniques such as artificial neural networks.

Fig. 3

Zoom map highlighting the interconnection between the HVDC transmission line term and other correlated terms.

Fig. 4

Map of co-authorship among countries (Lack of coordination between developed and under developed countries).

Co-authorship analysis among countries

The data on co-authorship across countries demonstrate various collaboration patterns regarding research production, citation impact, and total link strength; as depicted in Fig. 4, China has a strong research production and citation effect, with 59 documents and 386 citations, with a total link strength of 12. India has a moderate research production and citation impact, with 21 documents and 96 citations, with a total link strength of 6. Brazil has a smaller research output but a significant citation effect, with 11 documents, 104 citations and a total link strength of 6. The United Kingdom has a good research production and citation impact, with 11 documents, 229 citations and a total link strength of 12. Iran has a decent research production and citation impact, with 5 documents and 34 citations, but no major co-authorship links, with a total link strength of 0. Egypt has a smaller research output with 5 documents and 94 citations but a significant citation impact and a total link strength of 4. Canada has a limited research output and citation impact, with 4 documents and 10 citations, but a total link strength of 4, showing some collaborative links. Tunisia, South Korea, and Pakistan have lower research production and citation impacts, with relatively low levels of total link strength, suggesting a minimal contribution compared to other countries.

Conclusion of scientometric analysis

Considering the Paris agreement between 196 countries to increase the renewable energy share, HVDC transmission lines play a crucial role in the integration and efficient use of renewable energy sources. HVDC technology can reduce transmission losses by 30–50% compared to AC lines, as demonstrated by the Xiangjiaba-Shanghai HVDC line in China, which spans over 2,000 km with a transmission capacity of 6,400 MW and an efficiency of around 97%. Despite these advantages, including reduced carbon footprint and cost efficiency, the co-authorship analysis reveals limited involvement in HVDC transmission line fault research using neural networks, particularly among countries like India, Iran, Egypt, Brazil, and Pakistan. These nations, already significantly affected by global warming, would benefit from focusing more on HVDC technology to improve their renewable energy transmission infrastructure, especially in protecting HVDC transmission lines.

Considering the HVDC transmission line dynamics under which they operate, plus the AI-driven fault detection landscape, neural networks are at the forefront to provide robust and swift fault detection techniques. Therefore, according to the “AUTHOR KEYWORD ANALYSIS,” traditional methods have been replaced by advanced AI techniques such as ANN. At the same time, the “CO-AUTHORSHIP ANALYSIS AMONG COUNTRIES” reveals existing collaboration networks and the potential for international cooperation. The scientometric analysis, therefore, suggests that countries like India, Iran, Egypt, Brazil, and Pakistan should develop stronger interlinks among themselves and with developed nations like China, the USA, and the UK in HVDC transmission technology. This collaboration could enhance their focus on increasing the renewable energy share and improving the resilience of their energy infrastructure.

Moreover, while doing literature and scientometric surveys, we observed that most neural network-based techniques develop complex ANN architecture without any prior knowledge of hyperparameters. However, considering the complex hyperparameter space of ML models requires a probabilistic modelling approach based on BO to navigate towards promising regions of hyperparameter search space. The research also addresses a critical gap in existing AI fault detection methodologies, where most techniques offer primary fault detection but fail to consider relay failures, relying instead on backup protection that could affect a larger area than necessary.

Fig. 5

Configuration of MMC-based DC grid.

Table 1 MMC-based DC grid parameters.

AdoptedMMC-MTDC topology

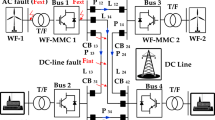
The PSCAD/EMTDC software is utilized to develop a four-terminal Modular Multilevel Converter (MMC)-based Multiterminal DC (MTDC) system, utilizing a grid test system as the basis²⁵. The parameters for the MMC-based DC grid are tabulated in Table 1. The chosen configuration for the MMC-based DC grid is a half-bridge sub-module. To resemble the real-life Zhang-Bei project, which aims to transmit electricity from renewable energy sources such as wind, solar, and hydroelectricity to Beijing through underground cables instead of overhead lines (OHL), a distributed configuration mode was employed for the DC reactor, as illustrated in Fig. 5. This configuration accurately represents the physical setup of the Zhang-Bei project, ensuring the simulation captures its unique characteristics and operational dynamics.

The MTDC system contains two off-shore wind farms (OWFs) connected to converters (1 & 2) that carry the electrical power to the on-shore converter (3 & 4) interconnected with the AC mainland. Each DC line has direct current circuit breakers (DCCBs) installed at both ends. The two separate AC voltage sources modeled the off-shore AC grid. The configuration is a symmetrical monopole with a DC link voltage of ± 320 kV. During the DC fault, the DC current increases in the HVDC grids, and the voltage suddenly decreases. In this case, U_F and I_F represent the parametric values of under-voltage and overcurrent to distinguish between external and interior fault types. While distinguishing, external faults (F_ext) and internal faults (F_int) are the worst cases to classify. F_int is used to simplify the categorization analysis for the provided MMC-HVDC configuration. DC voltage rapidly decreases from pre-fault levels to zero at the fault point. Mathematically, this sudden voltage change is represented as (1) developed in²⁶:

$${U_{F,\operatorname{int} }}=\frac{{{Z_c}/2}}{{{R_f}+{Z_c}/2}}( - {U_0})$$

(1)

• (1) Shows the voltage difference divided by the cable and the fault resistance (R_f). Here, the factor (1/2) indicates that the fault resistance is in series with the cable impedance (Z_c). Meanwhile, a similar kind of relation can be found during the external fault as well represented by (2):

  $${U_{F,ext}}=\frac{{{Z_c}}}{{sL+{Z_c}}}( - {U_0})$$

  (2)

• (2) Indicates that voltage is now distributed between the cable and the inductor ‘sL’. It demonstrates that the difference in (1) and (2) is due to the poles induced by the inductor ‘L’. A series inductor filters out high frequencies, and in like manner, fault resistance provides overall damping of the U_{F, int}. As an example, Z_c represents the overall properties of the impedance.

  Fig. 6

  

  The slope of DC voltage under internal and external fault, (b) Variation of dV/dt under internal and external fault events.

Figure 6a depicts the graphical representation. It can be seen that DC line voltage has a sharper slope under internal faults than under external faults. The gradient of F_ext under bolted fault is likewise smaller than that of the maximum internal fault impedance under consideration, as shown in Fig. 6b. As a result, the voltage change rate (dV_dc/ dT) can be used as an ANN input to discriminate internal from external faults. The DC line voltage has a high-frequency component under internal fault that varies with the fault location due to the current limiting inductor’s boundary effect and contains small high-frequency components under external fault. Therefore, such fault information is useful for detecting internal and external faults. The frequency domain DC line current characteristic is affected by fault resistance and location. The discrete wavelet (DWT), the digitally implementable CWT equivalent, is used to extract the transient DC features in the suggested fault diagnostic technique. The Daubechies mother wavelet was chosen for this study due to its superior ability to capture transient features in the fault signals, which are critical for accurate fault detection^7,8,11,27. Unlike the Haar wavelet, which is less smooth, the Daubechies wavelet provides a better balance between time and frequency localization²⁸. Additionally, the Daubechies wavelet family is known for its orthogonality and compact support. It is particularly suitable for analyzing non-stationary signals with abrupt changes, such as those encountered in fault conditions²⁹. While Coiflet and Symmlet wavelets also offer good properties, the Daubechies wavelet has been extensively validated in similar applications, providing a reliable basis for its selection in this study³⁰.

Signal analysis

The wavelet transform is an effective signal-processing algorithm that detects abnormal operating conditions. It achieves this by decomposing power signals into different frequency ranges using a series of low-pass and high-pass filters. This decomposition provides a time-frequency multi-resolution analysis, enabling the identification of abrupt variations in electrical parameters such as voltage, phase, current, and frequency. In this specific analysis for fault detection, the Daubechies 4 (db-4) wavelet is utilized as the mother wavelet basis function. The db-4 wavelet was chosen for its optimal balance between computational efficiency and its effectiveness in capturing transient characteristics of fault signals. Extensive testing showed that db-4 provided the best trade-off between accuracy and computational resources compared to higher-order Daubechies wavelets like db-5, db-6, and db-7.

The signal is divided into approximate “a” and detail “d” coefficients, which represent the low-frequency and high-frequency bands, respectively. This decomposition process is illustrated in Fig. 7. Examining these coefficient sets makes it possible to gain valuable insights into the presence of faults or abnormalities.

Fig. 7

Wavelet decomposition tree.

To obtain a discrete version of the Wavelet Transform (WT) for an input signal f(t), which is discretized, where the variable “n” represents the sample number in the series. The scaling parameter is represented as $\:s={a}^{j}$, where ‘a’ is a constant and ‘j’ is an integer that determines the scale of the wavelet. Similarly, the translation parameter ‘u’ is discretized as $\:u=k{u}_{o}{a}^{j}$, where ‘k’ is a constant and ‘u’ is an integer representing the position of the wavelet. With the discretized parameters, the Discrete Wavelet Transform (DWT) of the sampled input sequence, f(n), can be defined as in (3):

$$DWT_{\psi }^{f}(j,k)=\frac{1}{{\sqrt {{a^j}} }}\sum\limits_{{n= - \infty }}^{N} {f(n)\psi (\frac{{n - k{u_0}{a^j}}}{{{a^j}}})}$$

(3)

In 1(3), k, j, a, and u_o are integer numbers with a > 1 and u_o≠ 0. The time domain signal f(t) can be written in terms of scaling, Φ(t), and wavelet, Ψ(t), functions as in (4):

$$f(t) = \sum\limits_{{k = - \infty }}^{\infty } {aN(k)\Phi N,k(t) + \sum\limits_{{j = 1}}^{N} {( {\sum\limits_{{k = - \infty }}^{\infty } {dj(k)\psi j,t(t)} } )} }$$

(4)

In (4), dj is the detail coefficient at various resolution levels, and aN is the last approximation coefficient at level N.

The second norm, also known as “the norm,” of the detail coefficients dj(k) extracted from various frequency bands, is utilized as the input data vector for a classifier. The calculation of the decomposed signal’s norm is expressed by (5):

$$normdj=\sqrt {\sum\limits_{{i=1}}^{n} {|dji{|^2}} }$$

(5)

where ‘j’ indicates the level of decomposition, with the maximum level denoted as ‘N’ and ‘dj’ represents the detail coefficient consisting of ‘n’ elements at level ‘j’. The proposed feature vector, denoted as ‘x’ can be mathematically expressed as in (6) and (7):

$$x={[{x_1} \ldots {x_j} \ldots {x_N}]^T}$$

(6)

$$x=[||{d_1}|| \ldots ||{d_j}|| \ldots ||{d_N}]$$

(7)

Artificial neural network

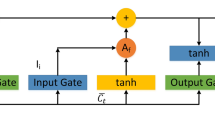
ANN is inspired by human biological programming and models how the human brain works³¹. Like the human brain, ANN learns patterns from data through training experiences. During training, ANN generates numerous individual units, known as neurons, interconnected through weighted links, forming layered structures. Typically, ANN consists of input, output, and hidden layers, as shown in Fig. 8. The inputs determine the neurons in the input layer, whereas the output response determines the neurons in the output layer. The architecture layout defines the ANN’s accurate response³². The core of this architecture is shaped by adjustable parameters (such as weights and bias) and hyperparameters, which must be set before training. During training, the weighted total of the inputs determines the neuron activity. The transfer function transmits the activation signal to generate a single neuron output. The transfer function introduces non-linearity into the network. During training, the inter-unit connections are optimized until the prediction error decreases and the network reaches the targeted accuracy level. New input information can be generated to forecast performance after a network has been trained and tested.

Fig. 8

ANN structure of the proposed technique.

Four 1 ms input vectors are designed for the ANN input: three vectors represent the transient DC current, while the fourth vector represents dv/dt. The vectors (x1, x2, x3) correspond to internal DC line faults throughout the transient period, and x4 denotes dv/dt. Regarding external faults, ANN is trained using one segment of DC voltage as the effect of external faults diminishes with higher fault impedance, making them easier to differentiate from internal faults. On the other hand, for internal faults, three segments of transient fault current are utilized for ANN training since the prominence of DC fault current decreases under high fault impedance, making it challenging to detect solely from the first segment. Therefore, multiple 1 ms window length segments are selected to identify high impedance faults accurately.

Representing the input vector as X = (x1, x2, x3, x4)^T, the output vector as O = (o1, o2)^T, and the hidden layer output as H = (h1, h2, h3, … h32)^T, the signal generation of ANN can be indicated by (8) and (9):

$${h_j}=f(\sum\nolimits_{{i=1}}^{7} {{w_{ij}}.{x_i}+{b_i})} ,j=123, \ldots 32$$

(8)

$${O_k}=f(\sum\nolimits_{{i=1}}^{{32}} {{w_{jk}}.{b_j}+{\theta _k}),k=1,2}$$

(9)

Here, b_j(j = 1,2,3,…,32) and w_ij(i = 1,2,3,4; j = 1,2,3,…,32) denotes the bias and weight from the input layer to the hidden layer, respectively. θ_k(k = 1,2) and w_jk(j = 1,2,3,…,32; k = 1,2) denotes the bias and weight from the hidden layer to the output layer. Here, ‘f’ indicates the activation function, where the assign function is used to shrink the training error, as in (10).

$$f(x)=\frac{2}{{1+{e^{( - 2x)}}}} - 1$$

(10)

All AI models have a set of hyperparameters defined before the training, and its optimal value fits the training data with the AI model. These parameters formulate the AI structure, including learning rate, hidden layers, search space, the number of neurons, etc., that differ from the AI internal parameters such as bias and weight. The hyperparameters are determined through BO in this research, which gives efficient performance to the validation dataset.

Bootstrap aggregating

Bootstrap Aggregating, commonly known as bagging, was initially introduced by Breiman³³ to improve the stability and accuracy of predictions by combining the results of multiple individual models³⁴. Therefore, bootstrapping helps minimize variance by reducing over-fitting and improving the precision of machine learning algorithms. During the training process, each model learns from a slightly different perspective due to the variations in the training data^35,36. Once all the models are trained, predictions are made by aggregating the outputs of the individual models. Figure 9 shows several common bootstrap aggregating (bagging) techniques, including disjoint partition, small bags, small bags with no replication, and disjoint bags.

Consider the hypothetical dataset as shown in Fig. 9a. The disjoint partition, Fig. 9b method, divides the data into smaller subsets so that each element is selected only once, ensuring that the union of these subsets must be equal to the hypothetical dataset. On the other hand, in the case of small bags Fig. 9c, a tiny number of elements are repeated when creating small bag subsets. Because repetition happens when producing small bag subsets individually, the union of small bag subsets may not necessarily be identical to the original hypothetical dataset. Lastly, disjoint bag training is conducted similarly to disjoint partition; however, in this case, each bootstrap sample is formed independently by randomly selecting elements with replacements from the hypothetical dataset. As a result, some data points may appear in multiple samples, and others may not, as seen in Fig. 9e. By randomly distributing the data, bagging reduces variance and improves neural networks’ capacity for generalization. As a result, increasing the number of Bootstraps and training the ANN leads to increased accuracy.

Fig. 9

Bootstrap aggregating techniques (a) hypothetical training data set. (b) Disjoint partition. (c) Small bags. (d) small bags without replication. (e) Disjoint bags.

Fig. 10

Ensemble artificial neural network.

Ensemble artificial neural network

Ensemble Artificial Neural Network (EANN) is a computational framework that combines multiple individual artificial neural networks (ANNs) to improve the performance and robustness of predictions or classifications, as shown in Fig. 10^37,38. The primary concept behind an EANN is to create multiple ANNs and then integrate their output to generate a final prediction³⁹. As a result, EANN mixes various outputs, as demonstrated in Fig. 11, which ensures a decrease in error and an increase in accuracy and reliability for an HVDC fault scheme.

The EANN in this study has been developed employing disjoint partition bootstrapping by training various neural network models on unique, non-overlapping subsets of data, thus reducing variance in EANN models^40,41. This diversity among the training sets means that each network learns different patterns and features from the data. When the outputs of these diverse networks are aggregated, the ensemble model benefits from a broader range of insights. This helps average out individual errors and biases. As a result, the overall variance of the model is reduced, leading to more stable and accurate predictions⁴². This reduction in variance is particularly significant in fault detection tasks, where the ability to generalize across different fault scenarios is crucial for reliable performance⁴³.

In conclusion, disjoint-based bootstrap aggregating improves the performance of the EANN by reducing variance, preventing overfitting, and increasing model robustness. By training multiple neural networks on different, non-overlapping subsets of the data, the method ensures diversity among the individual models. Aggregating the outputs of these diverse networks helps to average out errors, mitigate individual biases, and enhance overall prediction accuracy and reliability. This makes the EANN more effective for complex fault diagnosis and classification applications such as fault detection in HVDC systems.

Lastly, Bayesian optimization is used to optimize the performance of each distinct neural network within the EANN by fine-tuning its hyperparameters⁴⁴. This iterative approach adapts the ensemble to the unique fault identification challenge, improving accuracy and detection capabilities.

To the authors’ knowledge, this approach has not been implemented in the literature for HVDC fault identification and classification. Each subset is a training set for a different neural network in this approach, ensuring that learning patterns are diverse. The EANN aggregates predictions from various separate models during fault detection, allowing for more robust and accurate fault classification.

Bayesian optimization based artificial neural network

Bayesian optimization-based artificial neural networks (ANNs) use Bayesian optimization techniques to optimize the hyperparameters of an ANN model^45,46. In conventional ANN training, hyperparameters such as learning rate, number of layers, and number of neurons must be manually set, which can be challenging and time-consuming. Bayesian optimization offers an automated approach to search and find the optimal hyperparameters for the ANN.

• A) Formulation of the objective function

  The objective function of the proposed model is to improve the performance of ANN models. As a result, an optimized intelligent model will be able to detect DC faults. Bayesian optimization tries to optimize a scalar objective function f (x) for ‘x’ in a constrained domain. BO formulates a solution of a black-box function as expressed by (11):

  $${x^*}={\arg _{x\varepsilon X}}\hbox{min} f(x)$$

  (11)

Table 2 Bayesian algorithm.

It carries out this duty by building a series of function evaluations (x₁,., x_T) so that the optimum of a function is determined in the fewest iterations possible. BO is well suited to withstand stochastic noise in function evaluations and optimization over a continuous domain with less than twenty dimensions⁴⁷. The objective function is substituted, and the uncertainty in the substitute is measured using the Gaussian process⁴⁸. The next step is to define the Acquisition function using the surrogate and suggest the subsequent sample. The Bayesian algorithm is described in detail in Table 2. We have the 30th iteration for BO. Plus, the best model is selected by the model selection process. In this process, different settings of hyperparameters generate different models, and the objective function is based on the mean square error that helps to select the best model.

Gaussian process

BO develops a Gaussian process (GP) through estimate to reason about f. A random variable that is regularly distributed may be linked at any location along the continuous input space thanks to this flexible distribution. As a result, the new observation’s predictive distribution, which likewise has a Gaussian distribution, is derived⁴⁹. The mean and variance are provided by (12) and (13):

$$\sigma ^{2} (x^{\prime } ) = k(x^{\prime } ,x^{\prime } ) - k(x^{\prime } ,X)K(X,X)^{{ - 1}} k(x^{\prime } ,X)^{T}$$

(12)

$$\mu (x^{\prime } ) = k(x^{\prime } ,X)K(X,X)^{{ - 1}} y$$

(13)

where K(U, J) is a covariance matrix whose element (i, j) is calculated as ki, j = k(xi, xj) with xi Є U and xj Є V, where U and V are particular domains during training.

Acquisition function

The acquisition function a(x), a less expensive function from the surrogate model, is constructed to discover the following point to be evaluated because the original function f(x) is difficult to estimate. As a result, the acquisition function is maximized in place of the original function to choose the following point: $\:{x}_{t+1}={arg}{max}_{x\in\:X}{a}_{t}\left(x\right)$. In this auxiliary optimization issue, conventional mathematical methods can efficiently optimize the acquisition function⁴⁴. The acquisition functions covertly balance the exploitation of currently promising regions with the investigation of search space.

• B) Selection of minimum and maximum values for design variables (Search Space).

In this study, the hyperparameters search space for the ensemble ANN network is based on the selection of hyperparameters. We have selected hyperparameters such as learning rate with a search range from 0.00001 to 1.0, neurons per layer with a range of 10 to 1000, and activation functions with options ReLU, Sigmoid, Tanh. The selection of optimized parameters will help to generalize well and prevent overfitting. Guidelines for search space can be found in²⁰.

We have incorporated the expected improvement per second and acquisition function a(x) based on detailed analysis and reading; detailed information can be found in²⁰. This function was chosen because it allows exploration and exploitation to be balanced. Exploration means finding new areas, while exploitation means focusing on the promising ones. In a few iterations, this pathway helps to find the right parameters with a minimal amount of computational work.

Consequently, a refined surrogate model and a comprehensive exploration of the search space over 30 iterations increase the probability of finding the optimal points. Note that a proper selection of iterations also reduces computational complexity²⁰.

Fig. 11

Flowchart of Bayesian optimization-based ANN.

ANN training with bayesian optimization

This section outlines the training and application of bootstrapping and Bayesian optimization on an ensemble artificial neural network (EANN). The novel approach not only improves the ANN performance as well as enhances its efficiency. Figure 11 shows the procedures for the Bayesian algorithm-based EANN.

The step (1) in any ANN application is to define the relevant problem. In this study, the challenge of HVDC transmission line fault detection is addressed by ANN. For this purpose, relevant input features, i.e., current and voltage, output targets, i.e., fault types, are identified. Also, constraints and objectives are set to aim for maximum accuracy and minimize false positives/negatives. After the problem definition, step (2) is to initialize the population. Each individual in the population may be regarded as a set of hyperparameters for the ANN. The hyperparameters are obtained using the hyper-parameter selection mode, in which the datasets for training and testing for various simulation modeling are collected by adjusting fault location and impedance.

Table 3 Internal fault scenarios for training data.

Table 4 External DC bus and AC Fault Scenarios for Training Data.

ANN training datasets are obtained under various fault circumstances with variable fault lengths, fault impedances, and fault types. Furthermore, while the MTDC system is in a steady-state operation, external faults such as external DC line faults are tested. As a result, thorough training data sets for many simulations are generated, as shown in Tables 3 and 4. In PSCAD/EMTDC, three types of faults, Pole to Pole (PTP), Pole to ground (PTG), and Negative pole to ground (NPT), are performed to train the ANN for the system depicted in Fig. 5.

After successful population initialization, step (3) of the proposed algorithm performs disjoint bootstrapping. For this, a subset of the original population, i.e., the original training dataset, is divided randomly into multiple disjoint subsets, also called bootstrap samples. These disjoint data sets are fed to numerous ANN networks collaborating to make predictions. This group of collective ANN networks is called ensemble ANN (EANN).

Step (4) of the proposed algorithm involves each ANN network in the population, to be evaluated via training and testing. The training dataset determines the best hyperparameters for selecting ANN in the BO-based AI model. In step (5), BO chooses the optimum ANN hyperparameters that result in the lowest mean squared error (MSE), and ANN is trained on the given training data. Thus, the AI model of BO evolves in each cycle till the desired result is achieved. After training the ANN model, it is assessed for the testing dataset, which is different from the one utilized for training.

The hyper-parameter values are tuned for the EANN model learned on each disjoint bootstrap sample using Bayesian optimization. The following are the steps for Bayesian optimization:

• a) Determine the search space by defining the search ranges or distributions for the hyperparameters that need to be optimized, for example, learning rate, number of layers, number of neurons per layer, activation functions, etc.

• b) Select an acquisition function that maintains a balance between exploration and exploitation.

• c) Begin the Bayesian optimization process by randomly sampling an initial set of hyperparameter settings or using a predefined startup technique.

• d) Evaluate each configuration’s fitness by training and testing an appropriate ANN model on the disjoint bootstrap sample.

• e) The Bayesian model is updated with the evaluated data points to learn the underlying surrogate model. Gaussian processes and tree-based models are common surrogate models.

• f) Selection of the next hyperparameter configuration to be examined using the acquisition function. This configuration compromises exploration and exploitation (sampling from places with high predicted performance).

• g) Stages (d) to (f) are repeated. The evaluation, update, and selection stages should be repeated until the optimization budget (number of evaluations or time) is depleted or a termination requirement is reached.

After the BO application, step (6) involves replacing the original individuals in the population with the optimized individuals for each disjoint bootstrap sample. This ensures that the population evolves based on the hyperparameters that perform the best. Lastly, step (7) deals with population evolution. Evolutionary mechanisms may also be used for selection, crossover, mutation, genetic algorithms, differential evolution, and other evolutionary processes. The fitness ratings from the Bayesian optimization stage are vital to steer the evolutionary process.

Subsequently, after the completion of population evolution, steps (1) to (7) are repeated for a specific number of generations or until convergence is achieved, enabling the selection of the best individuals at the end of the evolutionary process and optimizing the individual ANN models.

Lastly, the best individual(s)’ performance is evaluated on a different validation or a test set. However, it is important that this test set had not been employed during the optimization process. This way, an overall evaluation of the generalization performance of the optimized ANN model is obtained. By combining disjoint bootstrapping and Bayesian optimization, hyperparameter space can be effectively explored to optimize the performance of the EANN models.

ANN is trained using optimal hyperparameters specified by BO. The ideal value for these parameters is determined by minimizing the objective function. As a result, BO presents an ANN model that has been rapidly and quickly trained for the given dataset collected under various fault circumstances expressed by (14):

$$MSE=\frac{1}{n}\sum\nolimits_{{i=1}}^{n} {({y_n} - y_{n}^{*}} )$$

(14)

where n denotes the data size, y_n represents the actual output, and y_n* indicates the predicted output.

Fig. 12

The best validation performance is (a) ANN with random hyperparameters and (b) the proposed technique.

Choosing the correct number of neurons in the hidden layer is one of the most difficult aspects of creating a neural network. The hidden layer is responsible for the internal computation of the data and the link between the input data and the output response. The suggested technique determines neurons in the hidden layer using Bayesian optimization for optimal ANN performance. The best number of neurons and learning rate were 32 and 0.01 with Tanh, respectively, with an MSE of 0.0128. As a result, BO chooses the optimal AI model based on the validation dataset’s error rate.

As shown in Fig. 12, the best validation performance (mean squared error between expected and actual output) with the predefined number of neurons calculated by the proposed technique outperforms ANN with random hyperparameters. The proposed technique for dealing with high-impedance faults in a power system employs a trained algorithm capable of detecting the fault by varying the thresholds of the specified relay. If the fault impedance is low, the algorithm employs a short time window and the relay’s initial threshold, allowing for a quick reaction. However, when the fault impedance is high, the algorithm switches to the 2nd or 3rd threshold, which has faster-rising rates and can identify faults at the DC line’s far end. This approach enables a more effective and reliable method of identifying and responding to high-impedance faults without requiring supplementary backup protection.

Test results of BO-based ANN

The relay is specifically built to train the numerous transient period segments. It can predict whether a data segment is faulty or healthy. Previous studies only considered a fixed threshold for fault detection or a certain data length for the transient duration to train the relay. To extract the special spectral characteristic under fault situations, the data length must be specific to ensure reliability. Still, the relay operation becomes slow due to the considerable data length. For dependability and to obtain a quick reaction, the relay in the proposed method is built to train the data segments that make up the transient period while considering a window length of 1 ms, as stated in Fig. 13.

Fig. 13

Relay Logic of the suggested algorithm.

Fig. 14

The protection system of the proposed scheme has a fault at Link-12, in series with CB₁₂.

Figure 14 illustrates the relay design’s overall protection scheme. The sampling circuit uses current transducers (CT) to collect the analog signals sent to the A/D trans converter’s input. The digital signal will then be processed by the signal processing unit, using real-time WT to extract the spectral properties of the sampled signal with a 1 ms window length.

As a result, ANN input vectors are obtained after signal processing. The functioning of the DCCB is determined based on the relay output after the well-trained Bayesian optimization-based ANN algorithm has output the results after receiving the ANN input vector. Lastly, the proposed relay logic for the BO-based ANN protection scheme is depicted in Fig. 15.

Fig. 15

The protection system of the proposed scheme.

Performance evaluation

The training procedure for the proposed technique consists of two steps: offline training and online fault detection. The computationally intensive processes involved in Disjoint Bagging and Bayesian Optimization—such as training multiple models and fine-tuning hyperparameters—are carried out offline. This means that the complexity associated with these tasks does not directly affect the online implementation of the model. Moreover, a single hidden layer is used to carry out the complex task while maintaining the balance between the computational efficiency and complexity of neural networks. Once the ANNs are trained and optimized, three new fault scenarios (PTP, PTG, and NPT) are executed to test the efficiency of the suggested technique utilizing data that differs from the training data. Tables 5 and 6 indicate the range of parameters for the new fault scenarios.

After offline training, the relay can be used for online fault protection. Therefore, offline training time is not a significant concern. According to the proposed scheme’s architecture, ANN can manage fault impedance up to 200 Ω under the first threshold, 300 Ω under the second threshold, and up to 400 Ω in the successive thresholds. It is crucial to handle high impedance faults with this diversity of fluctuating fault impedance under various segments to maintain a quick and dependable response. Earlier, the primary protection had trouble detecting faults in the high impedance category due to the reduced peak value of the transient fault current. Longer data length signals are needed, which slows down the relay’s quick response. As a result, the backup protection cannot identify higher impedance defects, isolating the majority of the damaged area and certain healthy portions.

Table 5 Internal fault scenarios for testing data.

Table 6 Internal fault scenarios for testing data.

Table 7 ANN results for the new test sample (Internal faults and external faults).

Evaluation under varying fault impedance and fault location

Table 7 present the detection capabilities of the proposed protection scheme for three fault types: PTP, PTG, and NPT. The scheme successfully detects all three fault types across various fault conditions. It can be seen from Table 7 that the relay detects all the faults accurately. Due to the traveling wave feature and the shorter window length, faults on DC lines are always detected by the first threshold of the specified relay when the fault impedance is less than 200 Ω, even those occurring at the far end. However, the 2nd segment of the planned relay detects the problem when the fault impedance is greater than 200 Ω. With high impedance faults, the growing value of the DC fault current is less influenced in the 2nd millisecond of fault, especially when the faults occur at the farthest end. The second section can detect up to 300 Ω fault impedance.

Similarly, as the third threshold can detect faults up to 400 Ω, a fault bigger than 300 Ω fault impedance is identified in the 3rd segment of the proposed relay. Each segment of the input data with a length of 1 ms can be accurately detected using the suggested procedures. Due to the time required for the traveling wave to reach the local terminal, the fault detection in the subsequent section is delayed by one millisecond. Nonetheless, this delay is negligible and considered insignificant for DC applications.

Figure 16 presents the overall ANN classification results for the 1st segment. The over-all classification accuracy is 99.4% for a 1ms time window. Figure 17 shows that accuracy improves as the time window length increases despite the increase in fault resistances from 10 Ω to 285 Ω. There is an increase of 0.19%. Meanwhile, 0.34% was observed for the 3rd threshold, with fault resistances increasing from 10 Ω to 485 Ω, as illustrated in Fig. 18.

Fig. 16

Overall 1st segment classification results for the New Test Sample (Internal Faults and External Faults).

Fig. 17

Overall 2nd, segment classification results for the New Test Sample (Internal Faults and External Faults).

Fig. 18

Overall 3rd segment classification results for the New Test Sample (Internal Faults and External Faults).

Results

The study assessed the effectiveness of an H-DCCB model for artificial neural network-based multiple-time window segment relay protection. The goal was to detect and isolate faults within milliseconds, preventing system downtime. Ten hybrid-DCCBs designed in⁵⁰ were integrated into the test system, adapting to the MTDC grid requirements. The H-DCCB’s self-protection mechanism was disabled to subject them to maximum fault stress during the designated time window. The experiments involved three fault scenarios on DC link-14, with fault resistance and distance from Bus-4 adjusted according to the time window segment. Specifically, we set the fault resistance to 35 Ω at a distance of 15 km for a duration of 1 ms, 60 Ω at 25 km for 2 ms, and 85 Ω at 35 km for 3 ms.

According to the proposed ANN-based protection scheme, fault detection decisions are made approximately 1–2 milliseconds after the occurrence of the fault. This rapid detection is facilitated by segmenting transient periods into multiple 1 ms intervals, enabling efficient fault condition analysis. Furthermore, the protection scheme is capable of detecting and managing faults with a maximum fault resistance of up to 400 Ω. These features collectively ensure that the protection system is both fast and reliable, maintaining the HVDC transmission line’s stability and safety.

Fig. 19

H-DCCB test results for scenario 1: fault resistance 35 Ω.

Scenario: 1

The first scenario introduced a low impedance fault with a 35 Ω resistance from MMC 1 at 1.5 s. A pre-fault current of 1.8 kA was attainted for all three scenarios. The relay unit detected the increase and sent a trip command within 1 ms. However, the breaker experienced an additional delay of 0.1 ms due to internal delays associated with the H-DCCB, limiting the peak fault current to 6.8 kA, well below its rated 16 kA current interruption capability, as shown in Fig. 19a⁵⁰. As a result, the main breaker IGBT valves attained a peak temperature of 44.8 °C, as depicted in Fig. 19c.

Scenario: 2

To address potential failure while minimizing grid disturbance, the second segment aimed to achieve a balanced approach. A fault impedance value of 60 Ω was chosen for this scenario. Figure 19 demonstrates a total relay delay of 2 ms, with an additional 0.1 ms delay attributed to the breaker after the fault occurred at t = 1.5 s. The breaker initiated the tripping sequence when the DC fault current reached 4 kA. Notably, the electrical and temperature experienced in this scenario were lower compared to the first scenario, as depicted in Fig. 20.

Fig. 20

H-DCCB test results for scenario 2: fault resistance 60 Ω.

Scenario: 3

Finally, the third segment of the experiment employed a 3 ms time window and, similar to the previous segment, an additional 0.1 ms delay for sending a trip signal to the breaker. This extended time frame allowed for detecting high-impedance faults, as the DC fault current is less conspicuous in such cases. It is important to note that high-impedance faults typically exhibit lower transient fault current peaks. Hence, the relay unit must continuously monitor the abnormal rise in fault current over an extended period to prevent thermal stress on the IGBT valves. Figure 21 shows that the breaker’s electrical and thermal parameters remained well below the maximum rated limits during these high-impedance fault scenarios.

Overall, the novel time window-based ANN protection strategy efficiently trips the H-DCCB to neutralize and isolate the faulty segment so that the rated fault current stays within three times the pre-fault current range in the respective time window. This not only reduces the electrical and thermal stresses on the breaker components but may also reduce the H-DCCB sizing and eliminate the need for any dedicated backup protection.

Fig. 21

H-DCCB test results for case 3: fault resistance 85 Ω.

Furthermore, to validate the effectiveness of the proposed protection scheme, no trip signals should be issued for the neighboring DC-links. This was verified by monitoring the currents of lines L12, L34, and L14 during a 35 Ω fault inception at 100 km from MMC-3 on L13, as depicted in Fig. 22. The results confirmed that the ANN protection scheme was not activated, and none of the DC circuit breakers (dc-CBs) on the healthy lines were tripped. Consequently, the current was restored to its steady-state value at t = 1.508 s.

Evaluation under noisy event

The performance of the proposed technique was evaluated by introducing white Gaussian noise to the DC fault current during various noisy situations. Figure 23 demonstrates the outcomes. To validate the scheme’s reliability, Table 8 indicates that the proposed method does not malfunction under noisy situations and detects all three fault types: PTP, PTG, and NPT precisely. The Artificial Neural Network (ANN) was utilized to detect the fault under noisy conditions, and the results indicate that the method is effective even at 20 db of noise.

According to Fig. 24, the overall classification results for each segment ranged from 25 db to 45 db noise. According to the results, the classification rates of each segment gradually decrease as the noise intensity increases. Greater uncertainty will appear as the noise intensifies. Despite strong noise corruption, segment accuracy reaches 99.17% from 25 db to 45 db noise. Hence, the suggested method performs well and can reliably detect problems in noisy environments without malfunctioning.

Fig. 22

Currents in DC link 12, 34, and 14 during an external fault in DC link 13.

Fig. 23

Effect of 20db noise on the original signal.

Table 8 ANN results under the different noisy events.

Fig. 24

Effect of 25-45db noise on the classification results for the New Test Sample.

Comparison with existing methods

The comparison between the proposed BO-based ANN algorithm and existing ANN methods is illustrated in Table 9, highlighting several key advantages. The proposed approach is comprehensive, adaptable to shorter data lengths, and operates independently of new infrastructure or communication linkages. Notably, the table shows that our solution achieves fault detection in less than 1.25 ms using the primary segment, which is significantly faster than other methods. This swift response is achieved through a non-complex ANN architecture that efficiently detects DC faults while avoiding issues such as overfitting, underfitting, or computational inefficiency. Therefore, the proposed algorithm can be used with any of them, overcoming drawbacks and improving the reliability and robustness of MMC-MTDC protection systems.

Further, a significant challenge in artificial intelligence is the need for large datasets and the authenticity of the data, which is addressed in the paper by using disjoint bagging to reduce overfitting, thus reducing the reliance on an excessively large dataset⁵¹. Additionally, BO is used to fine-tune hyperparameters efficiently, and this approach reduces the need for massive datasets by efficiently navigating the hyperparameter space^52,53. Moreover, the proposed model is further enhanced by training an ANN with noisy data so that it can perform reliably even when the training data is not perfect. A number of these issues are not properly addressed in existing ANNs.

Many existing AI techniques overlook the impact of stress on DCCBs, a critical factor that can affect the longevity and reliability of these expensive components. Our proposed technique addresses this gap by enhancing system reliability and extending breaker lifespan, thereby offering a more cost-effective solution for maintaining HVDC system integrity.

Table 9 Comparison between proposed and existing Protection schemes.

Future work

Future work will focus on empirical validation involving external faults in neighboring links to further substantiate the scheme’s effectiveness and robustness. This will include comprehensive simulations and hardware-in-loop testing to ensure the protection scheme’s reliability across a broader range of fault conditions. Additionally, future research will explore the implications of not requiring high-speed communication links in practical HVDC systems to provide a comprehensive understanding of the system’s overall impact and benefits.

Conclusion

Our work advances the technical capabilities of HVDC fault detection and aligns with the identified research trends in the field. The supplementary scientometric analysis provides a broader context, emphasizing the relevance and timeliness of adopting advanced AI techniques in power systems. Taking this analysis into account, the following contribution has been made.

• 1) This research paper presents a novel high-speed communication-less AI-based DC fault protection scheme for meshed DC grids, considering multiple segments during the transient period.

• 2) The Artificial Neural Network (ANN) hyperparameters are tuned using BO, thereby improving the ANN’s performance. The disjoint partition bootstrap aggregating method trains multiple ANN models and selects the best output.

• 3) In the proposed scheme, the ANN is designed to train on three segments of the transient fault current, each with a window length of 1 ms, covering the entire 3 ms transient period. This enables accurate identification of fault signal patterns, effectively detecting faults up to 400 Ω.

• 4) Using a smaller window size (1 ms) ensures that the ANN training process remains efficient with faster response. Moreover, one simple ANN with a non-complex structure enables it to be implemented in any given hardware without any high computational burden.

• 5) A low level of thermal and electrical stress on hybrid DCCBs demonstrates the overall effectiveness of the proposed algorithm, which increases breaker longevity.

A comprehensive training dataset is created using a simulation model to train the ANN for various fault locations, with fault impedance being altered. Subsequently, the proposed technique is evaluated using a comprehensive testing dataset that includes different fault locations and impedances distinct from the training dataset. The simulation results verify that the suggested technique accurately identifies internal and external faults, exhibiting robustness, reliability, and efficiency. Lastly, the reliability and effectiveness of the HVDC system in fault prevention are enhanced through hybrid-DCCBs and multiple time window segment relay protection strategy, achieving millisecond fault identification and isolation.