Hybrid salp swarm maximum power point tracking algorithm for photovoltaic systems in highly fluctuating environmental conditions

Abstract

The maximum power delivered by a photovoltaic system is greatly influenced by atmospheric conditions such as irradiation and temperature and by surrounding objects like trees, raindrops, tall buildings, animal droppings, and clouds. The partial shading caused by these surrounding objects and the rapidly changing atmospheric parameters make maximum power point tracking (MPPT) challenging. This paper proposes a hybrid MPPT algorithm that combines the benefits of the salp swarm algorithm (SSA) and hill climbing (HC) techniques. As long as the rate of change of irradiance does not exceed a specific limit, the HC mode is applied to track the global maximum power point (GMPP). Once a high rate of change in irradiation is detected, the SSA mode is activated. Moreover, the proposed algorithm employs the concept of boundary conditions to handle fast and slow fluctuating irradiance patterns. A comprehensive comparative evaluation of the proposed hybrid SSA-HC with state-of-the-art MPPT algorithms has been undertaken. Four distinct cases have been examined, including irradiance conditions with varying rates of change and partial shading conditions. The proposed hybrid SSA-HC algorithm has been validated and tested using a developed hardware setup, simulated in MATLAB for solar photovoltaic (PV) systems, and compared with standard SSA and HC. The performance of the tracking capability of this proposed hybrid technique at both steady-state and dynamic conditions under rapid and gradual irradiance changes demonstrates its superiority over recent state-of-the-art algorithms.

Introduction

Research, exploitation and utilization of renewable resources at a larger scale are essential to long term and sustainable supply of energy. Solar photovoltaic (PV) is expected to be among the most prominent renewable energy due to its ease of installation, minimal maintenance requirement and widespread availability. The benefits and advantages of this form of renewable energy often referred to as as green energy includes its ability to address environmental concerns. However, despite its advantages, there are notable disadvantages such as the low conversion efficiency of the PV modules and higher initial installation costs compared to those of fossil fuel systems. One effective way to enhance the efficiency of PV arrays is through maximum power point tracking (MPPT). Improving the MPPT algorithm, which is primarily implemented through software, is an economical method to increase the output power of PV systems MPPT ensures that the operating point on the P-V characteristic curve always stays at the maximum power point (MPP). The fundamental principle of MPPT involves measuring the input voltage and current of the PV array to calculate the output power. The process begins by sensing the voltage and current, followed by calculating instantaneous power. The MPPT algorithm then determines the duty cycle for the converter to match the power at the MPP position which represents the peak on the P-V curve.

Recent studies have explored advanced methodologies to address efficiency and stability challenges in renewable energy systems. Techniques such as infrared small target detection and hybrid power system reliability models¹ provide valuable insights for optimizing energy system performance under diverse environmental conditions. Multi-power supply optimization strategies² and impedance measurement techniques for grid-connected converters^3,4 have been pivotal in improving the robustness of PV systems. Innovative cooling mechanisms, such as air-water combination systems⁵, and cost optimization strategies in smart grid communication⁶ further illustrate the diverse approaches to enhancing system functionality and efficiency.

The P-V curve characteristic consists of two parts.

• 1. Uniform conditions: Environmental conditions and solar irradiance occur uniformly for all modules. Changes in the module will occur uniformly if temperature, insolation and any environmental changes occur.

• 2. Partial shading: Non-uniform environmental conditions and solar irradiance for all modules. This phenomenon occurs due to the shadow of other objects such as trees, towers, tall buildings and clouds, etc. Under these conditions, the PV characteristic curve exhibits multiple peaks. The global maximum power point (GMPP) is the highest peak while the local maximum power point (LMPP) are all the remaining peaks. The MPPT algorithm searches for the GMPP among these peaks. Environmental conditions vary significantly across seasons. For instance, in winter and summer, changes in solar irradiance and temperature are gradual but unpredictable. During the rainy season, rapid and fluctuating changes in atmospheric conditions occur, exacerbated by the active movement of dust particles during stormy or hot periods. Similarly, in winter, snow and fog significantly alter environmental conditions. These irregularities result in shading effects on PV panel surfaces caused by dust particles, snow, raindrops, clouds, fog, and shadows from external objects. With high fluctuating atmospheric environmental conditions, highly nonlinear conditions become a major problem of MPPT, in which the solution is high time-bounded. These varying environmental conditions require a superior MPPT algorithm and able to solve time-bounded nonlinear problems quickly to reduce power loss and extract the optimal energy consumption of PV panels. Previous literature review showed that MPPT algorithm based on conventional methods has been used to track GMPP such as perturb and observe (P&O)^7,8,9, incremental conductance (InCond)^10,11,12, Extremum Seeking Control (ESC)¹³. This conventional method only succeeds in tracking GMPP in uniform shaded conditions. Under partial shading conditions, intelligent control techniques namely Fuzzy Logic (FL)^{14,15,16,17,18} and Artificial Neural Network (ANN)^{19,20,21,22,23} are introduced for MPPT to operate more effectively. However, the data required for intelligent control techniques such as FL and ANN are large and this results in an excessive storage burden on the processor. Therefore, metaheuristic methods have been proposed by the researchers to improve the efficiency of the MPPT algorithm. Based on easy implementation and simple structure, particle swarm optimization (PSO)²⁴ is evaluated under partial shading conditions to track GMPP. The tracking process by a classical PSO is to produce several iterations with a high magnitude before convergence occurs. Iterations with high magnitude occur due to low velocities converging slowly and high-velocity update particles deviating from the path. The disadvantages of classical PSO that cause a lot of power loss on PV modules, the basic structure of classical PSO is modified by some researchers to form deterministic PSO (DPSO)²⁵. The DPSO method slightly improves the performance but still leaves an efficiency gap due to the local mode using the conventional method (InCond). The next proposed improvement technique is a combination of P&O and PSO. On this combined technique, the local peak (LMPP) uses the P&O searching procedure until moves to the global peak (GMPP) by using the PSO. The disadvantage of this technique is that its initial tracking dependency on P&O makes it unsuitable for fast search mode. This hybrid method (ACOPO) uses ant colony optimization (ACO) for global peak (GMPP) search while local peaks (LMPP) search by P&O. The disadvantage of the hybrid ACOPO algorithm is that the GMPP search is based on an iteratively variable probability distribution with the sequences of random decisions. In addition, when dynamic change conditions, the shifting of searches by P&O from local peaks to global peaks results in slow GMPP tracking. In^{26,27,28,29,30} proposes a hybrid method to overcome the disadvantages of conventional MPPT algorithm tracking under partial shading conditions. This hybrid method is able to find GMPP but in terms of hardware, the complexity of the proposed algorithm creates unnecessary delays due to the computational burden on the processor control unit. Therefore, researchers have proposed a few new MPPT techniques such as^31,32,33,34 and flower pollination algorithm (FPA)³⁵. However, previous literature reviews of MPPT techniques^36,37,38,39 show that none have the ability to resolve environmental changes that occur rapidly and slowly simultaneously. In this work, a technique of combining metaheuristic algorithms with conventional algorithms is proposed to reduce the number of iterations, excessive search delay, avoid deviating from GMPP. This new technique is known as the hybrid SSA-HC MPPT algorithm. Therefore, the advantage of the proposed hybrid SSA-HC algorithm in this paper is that it can find GMPP under fast and slow fluctuating atmospheric conditions. Through simulation, this hybrid method is compared with the popular recent MPPT techniques (HC⁴⁰, GWO⁴¹, BOA⁴², PSO⁴³, GOA⁴⁴, standard SSA⁴⁵). The superiority of the hybrid SSA-HC algorithm in tracking MPP contributes to a minimum time duration with a small number of search particles in addition to fast and accurate tracking. The main attributes of the technique conceptualizing a combination of bio-inspired salp swarm and hill climbing are required for high speed convergence, robustness, fast tracking, GMPP detection accuracy, least random oscillation and high power efficiency. Based on a review of existing algorithm^5,46,47 shortfalls, a new combination technique of metaheuristic and conventional (hybrid SSA-HC) is utilized to control the MPPT problem for PV system. The mobility of the transition between SSA and HC during exploration and exploitation while searching target enables the power extraction process to occur quickly, minimum oscillations and avoid divergence from actual power locus. The controllability and effectiveness characteristics of hybrid SSA-HC are summarized as follows:

• 1. Oscillations at the initial of tracking and steady-state are eliminated which saves power loss convergence in a short time.

• 2. The hybrid SSA-HC implementation is simple and only requires 1 parameter to be tuned i.e. C₁ to balance the exploitation and exploration of the optimization process.

• 3. Able to handle MPPT at less sampling time than the existing MPPT algorithm.

• 4. The implementation of hybrid SSA-HC in the optimization of composite, unimodal and multimodal mathematical problems is highly effective.

• 5. Based on the intelligence and drift of bio-inspired swarm concept and dynamic perturbation step size of conventional HC help the hybrid SSA-HC avoid traps on the LMPP as well as not diverge from its tracking locus.

PV array under uniform and partial shading conditions

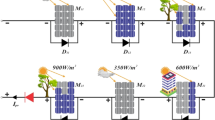
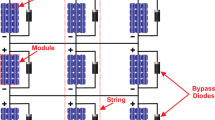
The complete solar PV system for this study is shown in Fig. 1. The buck-boost converter is an interposed device to supply the output of the PV panel to the load. The software code embedded through the buck-boost converter is using the hybrid SSA-HC MPPT algorithm. A uniformly shaded PV array on all modules resulting from uniform environmental conditions will generate a P-V curve consisting of a single peak. All PV array modules generate a P-V curve and an equal amount of power at this condition. However, under real environmental conditions, all PV array modules receive non-uniform solar irradiance due to the shadows of tall buildings, trees, or clouds. Therefore, the resulting P–V curve at these varying environmental conditions is multiple peaks. Figures 2 and 3 show the uniformly and partially shaded PV array and the varying % of irradiation on each PV module. Figure 2 shows the 100% of irradiation direct sunlight interaction to a PV module at an irradiation condition of 1000 W/m², 500 W/m², 800 W/m² and 600 W/m². Then followed the pattern A-E condition where the % of solar irradiation is between 80%, 70%, 60%, 50% and 20% on a few PV modules due to the obstacle. The effect of high obstacle shadow on the PV module generates a low percentage of irradiation, vice versa as in Fig. 3. Based on Figs. 3 and 5 types of shading patterns (A – E) on the PV array. The condition of an uncertain percentage of solar irradiation creates a problem in MPPT which is a non-linear problem. Therefore, atmospheric conditions that fluctuate rapidly and slowly require a time-bound MPPT solution. In practice, some modules from the PV array receive irradiance directly and some are under partial shading. The current generated by the partially shaded module is less than that of the module that receives direct irradiance. The module connection configuration in the PV array is in series and a voltage drop occurs at each parallel resistance of the module when current passes through it. The effect of this voltage drop reduces the maximum output power of the PV module and creates a hotspot. This reduction in output power in each PV module can be overcome through a bypass diode. These bypass diodes are installed in parallel with the PV module to bypass the current on all modules.

Fig. 1

The block diagram for the proposed hybrid SSA-HC MPPT algorithm.

Fig. 2

PV configuration of uniform irradiance.

Fig. 3

Partial shading PV array configuration.

Fig. 4

A salps chain.

Hybrid SSA-HC MPPT algorithm and application

The hybrid SSA-HC MPPT algorithm is a combination of salp swarm algorithm (SSA) and hill climbing (HC) optimization. The purpose of combining metaheuristic (SSA) and conventional (HC) techniques is to solve rapidly and slowly changing atmospheric conditions. The advantage of SSA is to enhance the ability of the algorithm under rapid irradiance changes and HC for irradiance changes occur slowly. The performance of the proposed combination of the two techniques (SSA-HC) enhances the tracking capability of MPP during fluctuations (rapidly and slowly) of irradiance by reducing the number of iterations, minimum the computational burden and avoiding the algorithm deviating from its tracking direction. The SSA algorithm is introduced by Seyedali Mirjalili in 2017⁴⁸. This algorithm is based on the concept of salp chain foraging and coordinated changes to find the best location for food sources. The concept of salp chain behaviour is illustrated in Fig. 4. In the model of the salps chain, the salp leader initiates a food source search movement and is followed by the salps follower. With food sources replaced with global optimum, salp leader start with the concept of finding the global optimum and are chased by salps follower whose initial population of salps herd is random. Movement the salp leader towards the global optimum and automatically guide the salps chain move towards it. The main purpose of this hybrid algorithm is to find the MPP when fluctuations of irradiance occur rapidly and slowly for PV systems. The hybrid SSA-HC algorithm is a combination of the advantages of the proposed SSA and the improvements of HC to find the MPP. The advantage of the proposed SSA algorithm is that it can track the MPP fast and accurately when irradiance changes occur suddenly and also during partial shading conditions. While the advantage of the modified HC is to prevent the MPP tracking direction from deviating from its tracking locus when the irradiance change occurs gradually. Therefore, the combination of these two techniques (SSA-HC) can reduce high iterations during sudden step change of the irradiance and successfully global tracking solution during irradiance changes slowly while reducing significant power loss. Integrated between the proposed SSA with modified HC to form the hybrid SSA-HC algorithm to enhance MPP tracking capability, as well as reduce the iteration number, computational burden and search particle number. The basic process of the hybrid SSA-HC is, the proposed SSA algorithm introduces the concept of duty cycle boundaries to direct the tracking area towards the probable GMPP region. The advantage of the duty cycle boundary (DCB) concept is that it can reduce the MPP tracking iterations during rapid fluctuation of irradiance. While the improvement of HC is based on the concept of boundary perturbation condition technique to decide the best position of the MPP to avoid deviating from the actual power under the slow irradiance fluctuation. The MPP tracking process for PV systems is online and hardware-based. Therefore, a superior and simple MPPT optimization method is essential to reduce large iterations, computational burden and power losses. Therefore, the hybrid SSA-HC algorithm is the best solution for rapid and slow fluctuating atmospheric change conditions.

Fig. 5

The combined variation of the advantages of the SSA and HC algorithms during rapid and slow irradiance change.

Salp swarm algorithm (SSA)

The bio-inspired optimizer is one branch of the metaheuristic algorithm which is a potential algorithm known as SSA. The SSA algorithm is inspired based on the behavior of the salps chain or a swarm of salps navigating the deep ocean in search of food sources. The SSA implementation structure is uncomplicated and can be used to optimize designs or mathematical functions that are difficult to express analytically. A swarm of salps (salps chain) is shown in Fig. 4, where i represents the position of the salps, d_i^k is the personal position of the salps chain and F is the symbol of food source. The symbol F is replaced as global best (Gbest) in the implementation of the MPPT technique which on each iteration during the MPP tracking process is updated. The working principle of the SSA method can be divided into two groups: salp leader and salps follower. The salp leader equation for the tracking update process is proposed as follows:

$$d_{i}^{k}=F+{C_1}((ub - lb){C_2}+lb{\text{) }}{C_{\text{3}}}<0$$

(1)

$$d_{i}^{k}=F - {C_1}((ub - lb){C_2}+lb{\text{) }}{C_{\text{3}}} \geqslant 0$$

(2)

In the MPP tracking process by the SSA algorithm, the coefficient ${C_1}$ parameter is important to balance exploitation and exploration can be written as:

$${C_1}=2{e^{ - {{\left( {\frac{{4l}}{L}} \right)}^2}}}$$

(3)

where l is the constant value of the current iteration number and L is the constant value of the maximum iteration number to achieve the MPPT process in the PV system. Random vectors for parameters ${C_2}$, ${C_3}$ are generated uniformly in the range 0 to 1.

The equation of the salps follower can be written as follows:

$$d_{i}^{k}=\frac{1}{2}\left( {d_{{i - 1}}^{k}+d_{i}^{k}} \right)$$

(4)

The parameters for the salps follower equation in (4) show that $d_{i}^{k}$ represents the number of salps follower population for which ith salps positions and kth represent number iterations in the search space dimension.

Hill climbing (HC)

The fundamental theory of hill climb (HC) MPPT is similar to perturb and observe (P&O) MPPT although it involves different operating methods. The direct duty cycle (D) perturbation method is implemented in HC compared to the reference voltage/current perturbation method for P&O. The objective function is the main key in the MPPT method. The HC method uses the condition that P (n) > P (n-1) is the objective function in its application. Based on the functional point perturbation technique is used to find the global maximum power point (GMPP). Then based on the concept of the objective function, power changes before and after perturbation are detected in the PV system. The HC method is often used as the basic reference for comparison with any new MPPT method. The HC method is a simple structure, easy implementation and the fundamental method that is always used. The working principle of HC is based on voltage and current sensing to calculate or generate the power (P) of PV arrays. Then, the main idea of HC work perturbation is based on the change of power by providing perturbation in the duty cycle according to the following concept:

$$D_{new}{\text{=}}D_{old}{\text{ + \varvec{\Delta}}}D{\text{ (if }}P{\text{> }}P_{old}{\text{)}}$$

(5)

$$D_{new}{\text{=}}D_{old} - {\text{\varvec{\Delta}}}D{\text{ (if }}P{\text{ < }}P_{old}{\text{)}}$$

(6)

The ∆D is the step size and is an important parameter in determining the duration of the perturbation cycle. When ∆D is large, the speed of convergence is fast and the oscillation at a steady state is high. When ∆D is small, the MPP tracking process is at a slow duration and the oscillation at a steady state is small.

Hybridizing and application of SSA-HC algorithm

The proposed hybrid SSA-HC algorithm is to enhance an MPP tracking solution under rapid and slow fluctuating environmental conditions. The main idea of this hybrid algorithm takes advantage of the proposed SSA when the irradiance changes rapidly in addition to partial shading. While the advantage of HC is that can track the MPP when the irradiance change slowly is utilized in this hybrid algorithm. Figure 5 shows an illustration of the proposed hybrid SSA-HC concept. The complete flowchart for this proposed hybrid technique is shown in Fig. 6. The hybrid algorithm pushes the disadvantage of HC and pulls the advantage of the proposed SSA during sudden step change of irradiance (rapidly) under partial shading as shown in Fig. 5 (t = 0 to t = 5 s). At the time t = 5 s to t = 12 s in Fig. 5, this hybrid algorithm pushes the disadvantage of the proposed SSA and pulls the advantage of the HC when the irradiance detected change occurs slowly (gradually). In this proposed hybrid algorithm, first, the proposed SSA algorithm will act when the detected irradiance changes occur rapidly (large changes in power). The direct duty cycle control strategy is utilized in the proposed SSA for fast and smooth tracking GMPP. The initial value of the duty cycle (D) to enhance comprehensive MPP tracking is 3. This selected value is a reasonable compromise and suitable for use in this study. Second, the initial duty cycle sent to the DC-DC buck-boost converter yields output power that will be stored and read by the algorithm. Thirdly, setting the maximum output power as an objective function for the algorithm to evaluate the fitness function. Updates the salp leader position equation based on the global best (GBest) position identified through the fitness function to enhance the efficiency of the MPPT application. To ensure effective detection, another modification to the SSA algorithm is proposed.

Fig. 6

The flowchart of proposed hybrid SSA-HC.

The proposed modification is for determination of the correct boundary limit i.e. by introducing duty cycle boundary (DCB). The upper and lower boundary limits are defined as duty cycles (D_U, D_L). Utilizing this boundary limit technique leads to a faster tracking time. In addition, the optimization process can be reduced by limiting the maximum area that can be explored which can avoid a large amount of power being wasted. The determination of D_U and D_L values is based on the concept of voltage-current range (VCR) where the range of MPP values could be located. Figure 7 proves the proposed SSA tracking mechanism is more superior and efficient by utilizing the DCB concept compared to other MPPT algorithms. Whereas Fig. 8 shows an illustration of the duty cycle (D) movement for the proposed SSA. Modifications to the salp leader Eqs. (7) & (8) based on the DCB concept contribute to fast tracking and high convergence speed compared to other MPPT algorithms.

Fig. 7

The proposed SSA MPP tracking speed mechanism.

Fig. 8

Illustration of the duty cycle comparison (D) between the proposed SSA and the standard during the MPP tracking process.

Modification of the salp leader position equation as follows:

$$d_{i}^{k}=GBest+{C_1}(({D_U} - {D_L}){C_2}+{D_L}{\text{) }}{C_{\text{3}}}>0.5$$

(7)

$$d_{i}^{k}=GBest - {C_1}(({D_U} - {D_L}){C_2}+{D_L}{\text{) }}{C_{\text{3}}} \leqslant 0.5$$

(8)

An illustration of the number of duty cycle (D) tracking iterations of the proposed SSA is shown in Fig. 8. After GBest is identified in the first iteration, then update the salp leader Eqs. (7) and (8) and move towards (Gbest) in the same direction. Then followed by the salps follower Eq. (9). With the proposed SSA using the direct GBest technique, the particle salp exploration moves straight forwards into the potential target by a skipped non-potential region. Compared to standard SSA algorithm that uses conventional techniques and contributes to large iteration, long tracking time and slow convergence speed as shown in Figs. 7 and 8. The base ${C_3}$ is set at a value of 0.5 and is then followed by the salps follower equation:

$$d_{i}^{k}=\frac{1}{2}\left( {d_{{i - 1}}^{k}+d_{i}^{k}} \right)$$

(9)

The improvement on the ${C_1}$ coefficient which is an important parameter in balancing the exploitation and exploration of the proposed SSA algorithm is written as:

$${C_1}=2.5{e^{ - {{\left( {\frac{{4.5l}}{L}} \right)}^2}}}$$

(10)

A slight modification to the coefficient ${C_1}$ (Eq. (10)) plays an important role in speeding up the process of balancing the exploration and exploitation capabilities of the proposed SSA algorithm. Figure 7shows that the standard SSA duty cycle requires 10 iterations to reach the global peak (GMPP) compared to the proposed SSA based on the standard SSA principle in⁴⁵. The tracking illustration of the proposed SSA algorithm is shown systematically in Figs. 7 and 8. Based on the VCR and DCB concepts, the proposed SSA algorithm can skip unnecessary regions during the GMPP tracking process which contributes to a simple optimization process and avoids energy waste. Thus, it is clear in Fig. 7 that the proposed SSA outperforms the other MPPT and standard SSA algorithms in terms of effectiveness and efficiency on the MPPT controller of PV systems.

When the detected irradiance conditions change slowly (gradually), the HC algorithm is employed to find the GMPP on the P-V curve. The modification of the HC during GMPP tracking under very slow irradiance changes is to ensure that steady state oscillation conditions and deviation from the GMPP tracking direction are minimized. Slight modification to the HC is implemented through an intelligent check i.e. based on boundary perturbation condition technique. This technique consists of adaptive perturbative step size and eliminating the loss of tracking MPP. An adaptive perturbative step size technique is utilized to reduce the perturbation size to a minimum value to solve the high oscillation problem. The oscillation is detected based on the concept of the power increasing or decreasing by five consecutive ɸ. When the summation of five ɸ is less than 5 it indicates that the MPP is converged in the steady state as in Eq. (11). Whereas when the summation of five ɸ is more than 5 based on Eq. (12), it indicates that the MPP is not converged in the steady state.

$$\Delta D \cdots ~\frac{{\Delta P}}{P}<\Delta \Phi\left( {{\text{MPP converged to steady state}}} \right)\,\left( {{\text{duty cycle perturbation size is maintain }}\left( {{\text{2}}\% } \right)} \right)$$

(11)

$$\begin{array}{*{20}{c}} {\Delta D=\Delta D - \phi } \\ {\phi =9{e^{ - 3}}} \end{array} \cdots \frac{{\Delta P}}{P}>\Delta \Phi \left( {{\text{MPP not converged to steady state}}} \right)\Delta \Phi =5 \cdots {\text{Gradient slope value of the }}P - V{\text{curve}})$$

(12)

When the oscillation is detected, the initial perturbation size of the duty cycle (D) set at a value of 2% is reduced $\phi =9{e^{ - 3}}$ based on the Eq. (12). Therefore, it is crucial to maintain the oscillation at a very small value to avoid power loss.

For the technique of eliminating the possibility of a loss of MPP tracking direction, Eqs. (13) & (14) show the HC modification mechanism to avoid the possibility of a loss of tracking direction. Based on the boundary technique utilized in Eq. (13), the duty cycle perturbation ∆D is maintained at a minimum value when the value of the irradiance gradient (∆P/P) is smaller than the threshold value $\left( {\Delta {T_r}} \right)$. With this Eq. (13) it can be assumed that the MPP tracking is still in its locus.

$$\begin{array}{*{20}{c}}\Delta D \\ ({{\text{duty cycle perturbation size is maintain}}({\text{2}}\%))}\end{array}\qquad\qquad\qquad \frac{\Delta P}{P} < \Delta {T_{r}}$$

(13)

$$\begin{array}{*{20}{c}} {\Delta D=\Delta D+\phi } \\ {\phi =8{e^{ - 3}}} \end{array} \cdots \frac{{\Delta P}}{P}>\Delta {T_r}$$

(14)

Whereas when the irradiance gradient (∆P/P) value is greater than the threshold $\left( {\Delta {T_r}} \right)$ value, the duty cycle perturbation ∆D value is added to the value of $\phi =8{e^{ - 3}}$ (Eq. (14)). Based on Eq. (14) shows that the MPP tracking deviates from the MPP direction. The threshold $\left( {\Delta {T_r}} \right)$value based on⁴⁹ is 10 W. Therefore, utilizing the boundary concept for adaptive perturbative step size and eliminating the loss of tracking MPP can reduce oscillations and deviations from the MPP operating point as well as avoid energy wastage.

Advantages of hybrid SSA-HC MPPT algorithm

In general, the advantages of hybrid SSA-HC under diversified optimization problems are highlighted as follows:

1) It requires only one tuning parameter (${C_1}$) for the exploitation and exploration phases.

2) The proposed algorithm is based on the concept of duty cycle boundary to narrow down the.

search area towards the probable GMPP area.

3) This integration technique forms a skipping mechanism to avoid scanning several unnecessary.

sections of the P-V curve which contributes to minimum and accurate iterations.

4) The boundary of the duty cycle enables the hybrid SSA-HC particles to move at almost zero.

iteration cycle oscillations and remain near the tracking locus.

5) The proposed hybrid algorithm has a simple implementation and straightforward control.

structure without the require any extra to the component hardware; requiring only several.

additional to the line of software codes embedded into the MPPT controller program.

6) It is based on a systematic model enabling fast particle position updating which contributes to.

accurate tracking and power convergence efficiency of more than 95%.

7) The effectiveness of the proposed hybrid SSA-HC can act on suddenly and slowly fluctuating.

irradiance conditions.

Simulation results and discussion

In this section, 4 different operating case are discussed. These operating cases are selected for the comprehensive formulation of the hybrid SSA-HC performance compared to HC, GWO, BOA, PSO, GOA and standard SSA. In case 1, the irradiance is a sudden step change for uniform. Case 2 is a sudden step change of the irradiance for partial shading conditions. Whereas in case 3 and 4 are sudden step and gradual change of irradiance at sampling time 0.02 s and 0.03 s. The result of hybrid SSA-HC is analyzed in terms of steady-state oscillations, tracking time, power convergence and actual MPP tracking efficiency compared to other metaheuristic and conventional algorithms. The performance analysis of hybrid SSA-HC, other metaheuristics and conventional algorithms are presented in detail in case 1, 2, 3 and 4. Table 1 summarizes the parameter tuning for the standard SSA-, GOA-, PSO-, BOA-, GWO- and HC MPPT algorithm.

Table 1 Parameter tuning for other metaheuristic and conventional MPPT algorithms.

Case 1: sudden step change of the uniform conditions

In case 1, the irradiance changes uniformly over time. The irradiance level changes rapidly for every 2 s as an illustration in Fig. 9. The comparison of the duty cycle tracking of the hybrid SSA-HC with the standard SSA, GOA, PSO, BOA, GWO and HC are shown in Fig. 10. At time intervals between 0 s and 2 s, the duty cycle efficiency achieved by the hybrid SSA-HC to track MPP is the highest with 239.6 W compared to 239.5 W (standard SSA), 239.3 W (GOA), 239.1 W (PSO), 239.1 W (BOA), 239.3 W (GWO) and 237 W (HC) are shown in Table 2. The duty cycle convergence efficiency of the proposed hybrid SSA-HC achieves the highest value of 96.68% compared to other MPPT algorithms as summarized in Table 2.

Fig. 9

Illustration of MPP search mechanism under uniform irradiance.

Fig. 10

Tracking profile duty cycle comparison of hybrid SSA-HC, standard SSA, GOA, PSO, BOA, GWO and HC.

At the time interval between t = 2 s to t = 4 s (Fig. 10), the hybrid SSA-HC algorithm achieved the highest power efficiency (120.4 W) compared to 120.2 W (standard SSA), 120.3 W (GOA), 120.2 W (PSO), 120.2 W (BOA), 120.2 W (GWO) and 119.5 W (HC), respectively. The power convergence efficiency achieved by the proposed hybrid algorithm is 96.64% as shown in Table 2. During the MPP tracking operating region between t = 4 s to t = 6 s as shown in Fig. 10, the hybrid SSA-HC showed better performance with the power efficiency is 192.6 W compared to the standard SSA, GOA, PSO, BOA, GWO and HC achieves of 192.6 W, 192.2 W, 192.1 W, 192.1 W, 192.2 W and 191.4 W, respectively. Based on Fig. 10, the proposed hybrid algorithm can track MPP effectively and settles at MPP about 50% faster than standard SSA, GOA, PSO, BOA, GWO and HC. The proposed hybrid SSA-HC algorithm can reduce overshoot and undesired oscillations which can help save power loss (Fig. 10). High random oscillations significantly by standard SSA, GOA, PSO, BOA and GWO at time interval t = 1 s to t = 2 s (1000 W/m²), t = 2 s to t = 4 s (500 W/m²) and t = 4 s to t = 6 s (800 W/m²) is observed in Fig. 10. While HC successfully tracked the MPP but produced oscillations and could not settle down at the MPP due to continuous perturbation. Thus, at case 1 evaluation, the hybrid SSA-HC algorithm is successfully minimized undesired oscillations of standard SSA, GOA, PSO, BOA, GWO and HC causing power loss and reduced efficiency. Figure 11 is a bar chart showing the tracking efficiency of each algorithm such as hybrid SSA-HC, standard SSA, PSO, GOA, GWO, BOA and HC. In addition, this proposed hybrid algorithm is able to balance the tracking time and efficiency with high convergence speed, fast tracking, and high efficiency for PV systems.

Fig. 11

Bar charts comparative of the tracking efficiency using Hybrid SSA-HC, Standard SSA, PSO, GOA, GWO, BOA and HC.

Table 2 Tracking performance under dynamic sudden step change uniform conditions.

Case 2: sudden step change of the partial shading conditions

The P-V curve for partial shading consists of multiple peaks (Fig. 12) which can be classified into global MPP (GMPP) and local MPP (LMPP). The multiple peaks of the P-V curve for partial shading complicate tracking by conventional algorithms (HC) to distinguish between GMPP and LMPP. This tendency results in a significantly decreased controller efficiency. The P-V curve of partial shading in Fig. 12 represents pattern A, pattern B and pattern C. Pattern A shows 1 GMPP (177 W) and 1 LMPP exist on the P-V curve. Followed by the P-V curve for pattern B consist of 1 GMPP (136.5 W) and 2 LMPP. While the P-V curve for pattern C shows 1 GMPP (114.5 W) followed by 2 LMPP as shown in Fig. 12.

Fig. 12

Illustration of GMPP search mechanism under partial shading.

The hybrid SSA-HC successfully detected GMPP with excellence compared to other competing MPPT algorithms. A detailed comparison of duty cycle tracking by hybrid SSA-HC compared to standard SSA, GOA, PSO, BOA, GWO and HC are shown in Fig. 13. Based on Table 3, the maximum power achieved by hybrid SSA-HC, standard SSA, GOA, PSO, BOA, GWO and HC is 136.3 W, 135.5 W, 136.2 W, 136.1 W, 135.1 W, 136 W and 110.3 W at time interval t = 0 s to t = 2 s, respectively. The highest tracking efficiency achieved by hybrid SSA-HC is 97.54% followed by GOA (95.56%), PSO (94.27%), standard SSA (91.63%), GWO (92.70%) and BOA (90.78%), respectively. While HC achieved the lowest tracking efficiency of 63.45% due to being stuck on LMPP as shown in Fig. 13. At the time interval between t = 2 s to t = 4 s (Fig. 13), the hybrid SSA-HC achieved the highest tracking efficiency of 95.59% (114.3 W) followed by the standard SSA 80.33% (114 W), PSO 90.72% (114 W), GOA 96.67% ( 136.2 W), BOA 89.32% (112.6 W), respectively. While GWO and HC tracking are stuck at LMPP with low efficiency, 79.56% (95.56 W-high oscillation) and 47.43% (55.01 W), respectively.

Fig. 13

Tracking profile duty cycle comparison of hybrid SSA-HC, standard SSA, GOA, PSO, BOA, GWO and HC.

Hybrid SSA-HC successfully tracks 176.9 W between time interval t = 4 s to t = 6 s followed by GOA (176.5 W), PSO (176.5 W), GWO (176.4 W), BOA (176.4 W), standard SSA (176.1 W), and HC (111.3 W-stuck at LMPP) as shown in Fig. 13, respectively. The power tracking efficiency by hybrid SSA-HC is the highest at 96.85% followed by GOA (94.63%), PSO (93.42%), BOA (93.03%), GWO (93.34%), standard SSA (87.73%) and HC (60.17%) as shown in Table 3, respectively. The average tracking and settling time by hybrid SSA-HC is less than 500 ms compared to standard SSA, GOA, PSO, BOA and GWO which exceeded 1000 ms as shown in Fig. 13. While the tracking time by the HC is neglected as it is trapped at LMPP and deviates far from the GMPP. Therefore, based on Fig. 13, it shows that the duty cycle updating by hybrid SSA-HC is more orderly, has fewer iterations, is faster and removes undesired oscillations by other MPPT algorithms. Figure 14 is a bar chart representing the tracking efficiency of Table 3 for Hybrid SSA-HC, standard SSA, PSO, GOA, GWO, BOA and HC.

Fig. 14

Bar charts comparative of the tracking efficiency using Hybrid SSA-HC, standard SSA, PSO, GOA, GWO, BOA and HC.

Table 3 Tracking performance under dynamic sudden step change PSC.

Case 3: sudden step and gradual change of the irradiance at sampling time 0.03 s

At case 3, another evaluation of sudden step and gradual change of irradiance as shown in Fig. 15. In this evaluation, the proposed hybrid SSA-HC is compared with GOA, PSO, GWO, BOA and HC at a sampling time of 0.03 s. Figure 16 shows a comparison of power convergence and a detailed analysis of the power tracking during sudden step change of the irradiance at time of 0 s to 2 s. The hybrid SSA-HC algorithm shows minimal oscillation and reduces undesired perturbation at GOA, PSO, GWO and BOA. This hybrid algorithm based on a systematic random selection of tracking particles can break the LMPP trap that occurs in HC.

Fig. 15

Illustration of actual power search mechanism under sudden step and gradual change.

Fig. 16

Tracking profile duty cycle comparison of hybrid SSA-HC, GOA, PSO, BOA, GWO and HC.

Based on the results in Fig. 16 at time t = 0 s to t = 2 s, the hybrid SSA-HC successfully locates GMPP (152.6 W) on pattern D with an average tracking time of less than 500 ms compared to GOA, PSO, GWO, BOA and HC with an average tracking time exceeding 1000 ms. During time between t = 2 s to t = 4 s under pattern E, the power curve obtained by the hybrid SSA-HC is 96.78 W by successfully eliminating random searches by GOA, PSO, GWO and BOA. While HC is trapped at LMPP. Hybrid SSA-HC tracking time is fast i.e. less than 500 ms compared to GOA, PSO, GWO and BOA with tracking time exceeding 1000 ms. Whereas during the time interval between t = 4 s to t = 5 s (Fig. 16), the hybrid SSA-HC successfully extracts the power of 120.4 W at 500 W irradiance. In this case, the hybrid SSA-HC algorithm can improve the random search with high oscillation by GOA, PSO, GWO, BOA and HC with a tracking time of less than 500 ms as shown in Fig. 16. During the time between t = 5 s to t = 12 s as shown in Fig. 16, the irradiance change is gradually from 500 W/m² to 800 W/m² and to 600 W/m². The tracking performance of the hybrid SSA-HC when the irradiance increases gradually from 500 W/m² to 800 W/m² ( t = 5 s to t = 8 s) with the gradient of 100 W/m²/s is able to track the power locus almost perfectly with tracking efficiency and power at point A is 99.70% (182 W). During the interval time t = 8 s to t = 9 s, the hybrid SSA-HC successfully track the power efficiency is 192.6 W (99.95%) as shown in Fig. 16; Table 4. Whereas when the irradiance decreases gradually from 800 W/m² to 600 W/m² ( t = 9 s to t = 11 s) with the gradient of 100 W/m²/s, the hybrid SSA-HC successfully tracks the GMPP (176.2 W) with tracking efficiency is 99.59% as shown in Fig. 16; Table 4. For the GOA, PSO and BOA as shown in Fig. 16; Table 4, the tracking direction is deviated far from the actual locus of power as the irradiance increase and decreases gradually (t = 5 s to t = 12 s). While the GWO also loses tracking direction with the high steady state oscillations. However, the HC successfully reached the top of the ramp but with a high steady state oscillation. Thus, based on Fig. 16, the tracking by GOA, PSO, BOA, GWO and HC showed that the reduction in the output power is significant during the gradual irradiance change. Table 4; Fig. 17 concludes that the tracking efficiency of the hybrid SSA-HC during sudden step and gradual change of irradiance is superior compared to GOA, PSO, BOA, GWO and HC at sampling time 0.03 s.

Fig. 17

Bar charts comparative of the tracking efficiency using Hybrid SSA-HC, PSO, GOA, GWO, BOA and HC at st 0.03s.

Table 4 Tracking performance under dynamic sudden step and gradual change at St = 0.03 s.

Case 4: sudden step and gradual change of the irradiance at sampling time 0.02 s

In this case 4, the evaluation pattern and type are similar to case 3 but the sampling time is set at 0.02 s. Hybrid SSA-HC performance is compared with GOA, PSO, BOA, GWO and HC. Figure 18 shows the power comparison of hybrid SSA-HC and other MPPT algorithms. The evaluation at case 4 as in Fig. 18 is for the comparison of the behavior of the implemented algorithm at sampling time 0.02 s. The maximum power successfully achieved by hybrid SSA-HC is the same in case 3 above which is 152.5 W in the time interval between t = 0 s to t = 2 s. During this time interval, the hybrid SSA-HC tracking time is less than 0.2 s with the least number of iterations as shown in Fig. 18. While the tracking time for GOA, PSO, BOA and GWO exceeded 0.5 s with high and undesired particle search direction and HC trapped at the LMPP with oscillation at a steady state.

Fig. 18

Tracking profile duty cycle comparison of hybrid SSA-HC, GWO, PSO, GOA, BOA and HC.

The GMPP tracking time at the time interval t = 2 s to t = 4 s taken by the hybrid SSA-HC is less than 0.2 s. As shown in Fig. 18, the comparison results show that the hybrid SSA-HC has a minimum settling time. GOA, PSO and BOA take more than 1s for GMPP tracking. Whereas GWO is unable to settle at the searched maximum power with high oscillation at steady state and HC is trapped on LMPP as shown in Fig. 18. During the time interval between t = 4 s to t = 5 s, the GMPP tracking achieved by the hybrid SSA-HC is 120.4 W with the calculated fast tracking time of 4.15 s. For GWO and PSO, random search has a significantly high oscillation and diverges away from the actual direction of GMPP (Fig. 18). While BOA and GOA have settling times of 4.5 s and 4.3 s, respectively. Based on the Fig. 18 (4 –5 s) shows the GOA diverge from its tracking locus. HC converges to the GMPP but produces non-settled oscillations at the GMPP due to continuous perturbation and observation (Fig. 18). At the comprehensive range of irradiance gradual change i.e. from 500 W/m² to 800 W/m² between the time interval t = 5 s to t = 8 s and 800 W/m² to 600 W/m² at the time interval t = 9 s to t = 12 s as shown in Fig. 18. The comparative performance between hybrid SSA-HC, GOA, PSO, BOA, GWO and HC in this range is presented in Table 5; Fig. 19.

Fig. 19

Bar charts comparative of the tracking efficiency using Hybrid SSA-HC, PSO, GOA, GWO, BOA and HC at st 0.02s.

During the gradual increases of irradiance change (gradient of 25 W/m²/s), the tracking of the actual GMPP by the hybrid SSA-HC is almost perfect as shown in Fig. 18 (5 –8 s). On the other hand, the GMPP search by HC exhibits large steady-state oscillations due to the large perturbation size. While GOA and BOA visible significant loss of tracking direction as shown in Fig. 18 (5–8 s). For PSO and GWO unable to cope during gradual increases of irradiance change with the loss of tracking direction with significant high oscillations at time interval t = 5 s to t = 8 s. At irradiance of 800 W/m² conditions between the time interval t = 8 s to t = 9 s, the peak of the ramp could not be tracked by GOA, BOA, PSO and GWO (Fig. 18). During this time interval, the loss of tracking direction by GOA, BOA, PSO and GWO is significant with PSO and GWO producing very high oscillations. While the HC is almost perfect to track ramps but with high oscillation capability at steady conditions.

Table 5 Tracking performance under dynamic sudden step and gradual change at St = 0.02 s.

On the contrary, hybrid SSA-HC shows superior tracking with high efficiency in Fig. 18 (8 –9 s). In the irradiance change gradually decreases region (with a gradient of ∆G/∆t < 100 W/m²/s) as shown in Fig. 18 (9 –12 s). The hybrid SSA-HC tracking performance is very consistent with high efficiency. On the other hand, loss of tracking direction at the actual power frequently occurred in GOA, BOA, PSO, GWO and HC which showed significantly decreased efficiency in Fig. 18 (9 –12 s). On the evaluation of case 4, it can be concluded that the hybrid SSA-HC shows high tracking efficiency despite operating at a short sampling time of 0.02 s as shown in Fig. 19 with 1 for condition 0–2 s, 2 (2–4 s), 3 (4–5 s), 4 (gradually increases 5–8 s), 5 (8–9 s) and 6 for gradually decreases (9–12 s). As observed in Fig. 18; Table 5, the efficiencies of GOA, PSO, BOA, GWO and HC decreased significantly during the irradiance change suddenly and gradually effect of sampling time is set to 0.02 s which contributed to the significant power loss.

Experimental validation

Experimental validation is conducted to prove the efficiency and accuracy of the proposed hybrid SSA-HC algorithm as shown in Fig. 20. The commercial PV array simulator by Chroma ATE Inc. (Model: 62050 H–600 S) is employed to emulate the real characteristics of the P-V and I-V curves of PV arrays. The 500 W DC-DC buck-boost converter is deployed as the interposed between the PV simulator and the load. The specifications of the experimental components are similar to the specifications of the simulation parameters. For power switching mode, devices such as MOSFET and fast recovery diodes are utilized. The proposed hybrid technique is implemented on a Texas Instruments TMS320F28335 DSP controller. Programming for rapid software development processes is developed in the MATLAB/Simulink embedded coding platform integrated with Code Composer Studio (CCS). The serial connection configuration of four PV modules (MSX-60 by SOLAREX) is considered for the experimental work as similar to the simulation setup. The four PV array (MSX-60) connection has the following specifications: maximum power (Pmax) = 239.40 W, voltage at MPP (Vmpp) = 68.4 V, current at MPP (Impp) = 3.5 A, short circuit current (Isc) = 3.8 A and open circuit voltage (Voc) = 87.2 V. The comparative performance between hybrid SSA-HC, standard SSA and HC are presented in Figs. 21, 22 and 23. The practical performance of HC for sudden step and ramp of 100 W/m²/s is shown in Fig. 21. The power responses (in hardware) can be observed slow tracking of HC during sudden step change and high oscillations of steady state at the operating point for this conventional algorithm.

Fig. 20

The experimental setup.

Fig. 21

Tracking MPP responses of Hill Climbing algorithm during sudden step change and gradual change of irradiance.

Fig. 22

Tracking MPP responses of standard SSA algorithm during sudden step change and gradual change of irradiance.

Fig. 23

Tracking MPP responses of proposed hybrid SSA-HC algorithm during sudden step and gradual change of irradiance.

In the practical performance of the standard SSA i.e. Figure 22, during the interval period of a sudden step change of irradiance, the power tracking by the standard SSA is slow. During a gradual change of irradiance with the ramp of 100 W/m²/s, the tracked power diverges significantly from the dotted line of the actual power locus as observed in Fig. 22. It should be understood that the direction of GMPP tracking by the standard SSA diverging far from the actual GMPP is an uncontrollable phenomenon. This occurs because of the change in direction of the perturbation as the irradiance period increases slowly. Thus, based on Fig. 22, the large significant power divergence locus by the standard SSA caused the MPPT control efficiency to drop to 83.03%.

On the other hand, Fig. 23 shows the performance of hybrid SSA-HC tracking when implemented practically. The hybrid SSA-HC showed perfect locus tracking i.e. fast tracking during sudden step and gradual change of irradiance as shown in Fig. 23. During the gradual irradiance change, modification of HC is performed by the proposed algorithm to ensure that the operating point is reached near the GMPP. Proposing this hybrid technique can negligible the power deviation that occurs and the control MPPT efficiency can be maintained above 99% which is 99.63%, almost similar to the simulation.

Based on the boundary technique implemented, the experimental results prove that this hybrid technique successfully guides the operating point in the actual locus track and successfully overcomes significant power divergence.

Suggestions for future work

The contributions of this work in enhancing the MPPT’s efficiency are far from complete. There is still much room for improvement and development in MPPT for PV systems. The following are some suggestions for future research:

• a) Improve the bio-inspired SSA by using a simple sorting technique to improve the tracking and convergence time. A simple sorting technique can reduce a highly undesirable condition because abrupt changes in the duty cycle increase the transient delay between the perturbation and the measured voltage and current used to estimate PV power.

• b) The hybrid SSA-HC MPPT algorithm has been tested in various environments, including uniform, partial shading, rapid and slow fluctuations. Furthermore, it is suggested that the European EN 50,530 dynamic efficiency test is implemented to confirm its effectiveness further.

• c) The performance of hybrid SSA-HC can be studied in terms of its implementation on a PV system connected to the power grid via inverter. Depending on the constraints in that research area, hybrid SSA-HC can be further enhanced to inspire its use in commercial appliances.

Conclusion

In this study, a novel MPPT technique called hybrid SSA-HC is proposed for highly rapidly and slowly fluctuating atmospheric conditions under uniform and partial shading conditions. The hybrid SSA-HC is a combination of SSA and HC algorithms. In this hybrid technique, SSA acts when atmospheric conditions fluctuate rapidly and HC acts when atmospheric conditions fluctuate slowly. With the dependence of MPPT control operations on atmospheric conditions, the problem of MPPT is to become time-bound nonlinear due to changes in atmospheric conditions that fluctuate rapidly and slowly. Therefore the proposed hybrid SSA-HC algorithm is the best option for fast and accurate GMPP search. The benefit of the hybrid SSA-HC technique is to increase the efficiency of MPPT by reducing the standard nature of metaheuristic and conventional as well as increasing the convergence speed of GMPP. In addition, this hybrid technique reduces the number of iterations. The computational burden as well as avoids stagnation problems with the selection of the correct optimal particle position. The performance of hybrid SSA-HC is compared with several popular and recent algorithms (GOA, PSO, BOA, GWO and HC) under uniform and partial shading in dynamic fluctuating conditions. The results of simulation and experiment of hybrid SSA-HC at rapid and slow fluctuation conditions under uniform and partial conditions show the superiority of hybrid SSA-HC over all existing algorithms. It can be concluded that the hybrid SSA-HC shows an accurate and good dynamic change response under a short sampling time (0.02 s and 0.03s) compared to state of art algorithms. In addition, this hybrid technique can increase reliability and robustness. The advantage of this technique is that it is free from the undesired initial condition as well as easy to implement on MPPT control in various environmental conditions.