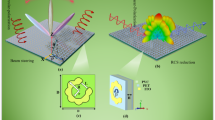
Abstract
Intelligent reflecting surfaces (IRS) are valuable tools for enhancing the intelligence of the propagation environment. They have the ability to direct EM Waves to a specific user through beamforming. A significant number of passive elements are integrated into metasurfaces, allowing for their incorporation onto various surfaces such as walls and buildings. In certain situations, metasurfaces may need to be installed on surfaces that are not flat, such as surfaces with curves or surfaces with two sides. Line of sight and non line of sight rays are radiated toward IRS and both components must be considered in channel modeling. In this work, a unit cell with three polarization modes, consisting of absorption, reflection, and a 1-bit phase shift, is designed and investigated. The unit cell in the nonplanar metasurface is composed of two vertical surfaces. A mathematical model is used to analyze two vertically-faced metasurfaces. The results include S parameter values and full structure radiation pattern in simulation and measurement. It is demonstrated that both absorption reflection mode and phase shift mode are achieved within a specific frequency band. The simulations demonstrate that an appropriate absorption level, reaching − 10 dB, is achieved in absorption mode. In reflection mode, a 180-degree phase shift is achieved within the same frequency band. Reports on the radiation pattern of two vertically faced structures indicate that there is no quantized beam when there is a one-bit phase shift. Channel modeling and signal to noise ratio of the designed metasurface in wireless network is represented in comparison with planar metasurface with the same cell number.
Similar content being viewed by others
Introduction
Reconfigurable Intelligent Surfaces have gained significant interest due to their ability to control electromagnetic waves in wireless propagation environments. This is particularly relevant in the context of 5G and 6G wireless networks, where the small wavelength of millimeter waves makes them susceptible to attenuation and scattering by small objects. As a result, intelligent surfaces play a crucial role in allowing the propagated waves to bypass obstacles and efficiently focus on the desired user. With RIS, the propagation environment can be controlled alongside the transmitter and receiver.The reconfigurable feature of the metasurface allows for dynamic beam steering and signal to noise ratio maximization in MIMO channel of wireless network1. Beamforming using RIS enables precise beam direction and coverage control for users. The Multiple Input Multiple Output (MIMO) technique improves network capacity and tackles challenging propagation environments. The beamforming technique in massive MIMO was initially introduced in the 4G Network2. Numerous studies have explored the use of hybrid beamforming in the context of massive MIMO and have been classified accordingly3. The number of antenna elements in the Massive MIMO method can increase implementation costs and complexity. This is due to the presence of an RF chain block for each antenna element. The RIS concept involves the use of passive elements instead of active antenna elements for the implementation of massive MIMO.
By applying appropiate phase shift it is possible to maximize signal to noise ratio1,the noise consists of thermal noise and interference caused by other users. Many papers worked on joint beamforming optimization of base station weighting and irs cell status such as1 worked on single user and multiuser beamforming optimization4 worked on double irs beamforming.
Phase shift is a crucial component of beamforming. Using a phase gradient on a metasurface, it becomes possible to break conventional Snell’s law and precisely steer the reflected ray to the desired angle. In conventional Snell’s law, the absence of a phase gradient results in the reflected wave angle being the same as the incident wave angle. Most metasurfaces utilize a discrete phase shift. For example, pin diodes5, MEMS switches6, mechanical adjustments2, and changes in chemical potential7 can be used to tune metasurface and reflect array unit cells to make phase shifts of 1 bit or 2 bits. This allows for dynamic changes in the phase state of each unit cell. The general concepts of IRS were introduced in8. Metasurfaces are crucial in improving the signal-to-noise ratio in user positions within 5G cellular networks. This is achieved by carefully adjusting the state of each cell, leading to optimal performance9. Each cell state expresses the cell phase shift and the cell attenuation derived by a designed unit cell. For example, previous studies10,11 have utilized different techniques, such as using pin diodes connected to the ground plane in a shunt connection.12 Employed current reversal techniques, and13 focused on developing a dual-polarized, two-bit reflect array unit cell that utilizes eight-pin diodes. The interfaces and design of the unit cell are crucial factors, surpassing the significance of lumped elements. A resonator is utilized at millimeter-wave frequencies to minimize the impact of pin diode fluctuations on phase shift, as demonstrated in14. One disadvantage of the 1-bit metasurface is the generation of a quantized beam, which is absent in the 2-bit metasurface. One possible solution to this issue is incorporating an offset phase into the metasurface to suppress the unwanted beam15.
In most applications, additional functions are often required alongside phase shifting. These functions may include a transmission-to-reflection switch using a pin diode16, integrated circuit17, moving dielectric slab2, and changing the chemical potential in a graphene-based metasurface18. In addition to transmission and reflection, absorption function is added to the metasurface in reference19. Single-polarized works typically use one or two diodes5,20, while dual-polarized works require multiple pin diodes in each metasurface cell13 for symmetrical structure. Most symmetrical structures exhibit four-angle shapes, such as cross12 or ring21. The symmetrical structure can also be achieved by using an equilateral triangle structure, which is not affected by polarization22. The mentioned metasurface designs were confined to planar metasurfaces. There will be a need to study metasurfaces in two vertically-faced, cylindrical, or spherical shapes. The study of wave behavior over curvilinear metasurface is demonstrated in23 by analytical approach.
This paper introduces a metasurface with a 3-mode function that includes absorption, reflection, and phase shift. The metasurface operates in dual polarization by utilizing a symmetrical structure with three-pin diodes positioned symmetrically for each layer. The bottom layer is responsible for controlling absorption and reflection, while the top layer is responsible for controlling phase shift. The simulation results for the unit cell and full structure design at 26.8 GHz are provided in the next part. The simulation results demonstrate two metasurface sheets that are vertically faced and applicable in wireless networks. These designs utilize the designed unit cell to demonstrate the superior performance of the quantized beam in a 1-bit structure positioned between two vertical planes. This works novelty is described in below points.
-
Beamsteering and channel modeling of two vertically metasurface is investigated and optimization results of maximized SNR are presented.
-
Three operating mode unit cell is proposed in millimetere wave frequency applicable in 5G and 6G wireless network.
-
The unit cell scheme is 3 angle symmetrical structure instead of 4 angle symmetrical structure to minimize number of pin diodes.
Design and principle
In this section, we will discuss the design and theoretical issues of the unit cell, as well as the theoretical analysis of the two-faced metasurface. Two steps are involved in estimating the MIMO channel in a wireless network24. During the initial stage of channel estimation, it is necessary to switch off the RIS to estimate the direct channel between the base station and the user. In the second stage, each cell is switched on to estimate the channel for each cell. RIS-Assisted Communication considers two propagation paths: the RIS path and the direct path. The RIS unit cells must operate in both absorption and phase shift modes. This paper presents the design of a RIS operating in three different modes. The primary principle of line-of-sight beamforming metasurface is to change the reflecting angle through phase change. The generalized form of Snell’s law, as shown in Eq. (1), demonstrates how the direction of the reflected wave is changed by the phase gradient of the metasurface structure.
The phase condition of each cell is determined by the difference between the induced phase by the incident wave and the required phase to steer the beam to the desired angle.The continuous phase of each unit cell is calculated using Eq. (2). The calculated phase is quantized to its closest value of 0 or 180° according to Eq. (3) in the 1-bit meta surface. The calculated phase in a 2-bit metasurface is quantized to the nearest value of 0, 90, 180, or 270°.
where:
\({\varphi _r}\left( {{x_n},{y_m}} \right) = - jksin\left( {{\theta _r}} \right) [{x_n}\cos \left( {{\varphi _r}} \right) + {y_n}\sin \left( {{\varphi _r}} \right) ]\)
and
\({\varphi _i}\left( {{x_n},{y_m}} \right) = - jksin\left( {{\theta _i}} \right) [{x_n}\cos \left( {{\varphi _i}} \right) + {y_n}\sin \left( {{\varphi _i}} \right) ]\)
Where \(\theta\) is wave elevation angle and \(\phi\) is wave azimuth angle radiation pattern synthesize by metasurface can be approximated by using reflect array patch antenna equation shown in Eqs. (4) and (5):
Where
in (5) the \(\alpha _mn\) mn is reflection attenuation caused by the cell number mn and \(\alpha _1bit\) is quantized phase shift of the cell number mn when the metasurface is controlled by 1 bit phase shift mechanism
Two vertically faced array
In certain wireless communication scenarios, it is necessary to utilize two vertical faces of a metasurface for beamforming, as using just one face is not enough to cover the desired area. The concept of a two-faced metasurface is illustrated in Fig. 1a. Two metasurfaces are embedded on two vertical faces. The faces can potentially serve as walls for a building.
Equations (6) and (7) show the array factor of two linear arrays positioned vertically, as shown in Fig. 1b.
The extension of Eqs. (6) and (7) for 2D planar Array is given as (8), (9).
where \(\theta\) represents the beam elevation angle, \(\phi\) is the beam azimuth angle, and \(\phi _{mn}\) is the phase shift of elements m and n. d represents the spacing of two adjacent elements, as shown in Fig. 1b. Equations (7) and (9) show the phase shift required for the 1D and 2D linear array. Equation (8) is used to calculate the induced phase caused by the incident wave that arrives at angle \(\theta _i\) based on Eq. (10).
The phase required for each meta surface element to steer the beam towards the desired direction \(\theta _r\) is provided in Eq. (11).
where m is the index of meta surface element. The phase shift required to steer the incident angle \(\theta _i\) to reflection angle \(\theta _r\) is given in Eq. (12).
For a 1-bit metasurface, the phase shift calculated in Eq. (12) must be quantized according to Eq. (13).
3 mode unit cell design
Figure 2. shows the main geometry and functions of the reconfigurable unit cell operating in three modes. Figure 2b,c show the lower layer controls absorption and reflection, while the top layer controls the phase shift. The layer beneath the ground plane is a DC control layer that does not have any impact on the other layer functions. Table 1 displays the upper and lower pin diode states during the operation of these three modes. Due to their rapid switching capability, millimeter wave pin diodes (MACOM-000907) are utilized for switching absorption mode to reflection mode in the lower layer and achieving a 180-degree phase difference in the top layer when the lower layer is in reflection mode. The MACOM-000907 pin diode has an equivalent circuit of \(L=0.05nH\) and \(R=4.2\Omega\) in the on state, and \(L= 0.05nH\) and \(C= 42fF\) in the off state as shown in Fig. 4b.25.
Since the unit cell is polarization-independent, it is necessary for the unit cell structure to be symmetric. In most studies, a quad-angle structure is utilized to achieve polarization independence. However, in this study, a three-angle structure is introduced in order to minimize the number of pin diodes and reduce costs. Three diodes are positioned symmetrically, as shown in Fig. 2a. The detailed geometry is shown in Fig. 3 while Fig. 3e shows expanded view of the designed unit cell, alongside the parameter values provided in Table 2.
Lower layer design
The suggested design configuration in21 includes a split ring absorber. The design of a reconfigurable absorber split ring is shown in Fig. 3d, while the corresponding equivalent circuit is depicted in Fig. 4a and parameters regarding to layer Substrate thickness were given in Fig. 3a. When the upper layer is in forward bias, it becomes transparent to the incident wave. By placing pin diodes in the gaps, switching from absorption mode to reflection mode is achieved by electronically changing the resonance frequency of the split ring. The resonance frequency is obtained from Eqs. (14) and (15).
where L and C represent the equivalent capacitance and inductance of the split ring. By changing \({C_{total}}\), the resonance frequency is changed, and the absorption mode is transferred to another frequency. The split ring gap is modeled as a capacitor, while the ring and other parts are modeled as inductors. Applying DC voltage to the pin diode parallel circuit changes the gap capacitor and has an impact on the resonant frequency. Figure 3d shows the design geometry of the split ring in the lower layer. Another gap is utilized for the purpose of isolating DC bias between the anode and cathode sides of pin diodes. The fr4 substrate is commonly used for lower layer design in high-loss scenarios, particularly at millimeter wave frequencies. It has a loss tangent of \(\sigma\)= 0.032 and \(\epsilon\) = 4.15 at 22–28 GHz, and the copper thickness is 35 \(\upmu\)m. Figure 5 illustrates the impact of substrate thickness on resonance frequency in absorption mode. As the thickness increases, the absorption frequency decreases. A thickness of 1.35 mm for fr4 is selected for the h2 parameter because it resonates at 26.8 GHz. The smaller values of h2 result in a reduced reflection loss at the absorption frequency. The anode side of the pin diode is connected to the control layer of the metasurface. The cathode side of the pin diode is connected to the ground using vias with a diameter of 0.2mm. The central part of the design connects the DC control layer to the phase shift layer. in(15) \(C_{var}\) denotes dynamic capacitance caused by the gap between central patch and beginning part of delay line on phase control layer. By applying pin diode the capacitance will be changed as the pin diodes change from forward bias to reverse bias.
Schematic of the unit cell. (a) Side view. (b) Top part of the upper layer. (c) Bottom part of the upper layer. (d) Bottom layer. (e) Expanded view of unit cell structure consist of DC bias feeding layer structure for phase shift layer and absorption reflection control layer. The positions of (b–d) are illustrated in (a).
(a) Equivalent circuit of the designed unit cell. The bottom layer is split ring with coil and capacitor equivalent circuit, while the top layer is patch and three delay lines act transparently when the top layer pin diode are in forward bias mode. (b) Equivalent circuit of Macom -0000907 pin diode used.
Upper layer design
The upper layer is responsible for controlling phase shift. The main patch connection to three external parts is controlled through the use of biasing pin diodes. The additional component includes a delay line that is connected to the ground through vias. The substrate used in the upper layer is RT duroid 5880, with a \(\epsilon _r=2.2\) and a dielectric loss tangent of \(\sigma\)= 0.009. Vias behave similarly to short circuits at low frequencies, while having a coil-like function at high frequencies. Phase shifting is implemented by the delay line, and via connects it to ground. The schematics of the upper layer are depicted in Fig. 3b and its lower part is depicted in Fig. 3c, while the corresponding parameter values can be found in Table 2. Figure 6 illustrates the impact of variations in the Rad variable from Table 2 on phase shifting. As shown in Fig. 2b and c, an air gap is present between the phase shift control layer and the reflection absorption control layer. This gap allows for the placement of lower-layer pin diodes.
Illustration of the changes in phase shift in relation to the variations in the radial size of the delay line (represented by the ‘rad’ variable in Fig. 3b). It is observed that a radial size of 65° facilitates a 180-degree phase shift, in addition to a minimal phase shift difference in both x and y polarizations.
Simulation results
Simulation and results In some cases, IRS can be embedded on non-planar surfaces to bypass obstacles in wireless propagation environments, as discussed in the previous section. This section presents the simulation results of the unit cell and the full structure design of a planar metasurface and two vertically facing metasurfaces. The full structure results are shown for two vertically faced metasurfaces with a size of 14*14. The absorption frequency for a normal split ring is 32 GHz, while adding an inner ring and vias decreases the absorption frequency to 26.8 GHz. The absorption and phase shift results of the designed unit cell are shown in Fig. 7 for both x and y polarizations. It is important to note that the polarization conversion of the unit cell remains consistently below 19.7 dB across all frequencies, as shown in Fig. 7a.
Figure 7a shows that a S parameter below − 10 dB is achieved in the frequency band of 26.5–27 GHz. Figure 7b demonstrates a significant phase shift of 184° in reflection mode across a wide range of frequencies, specifically 26.5–27 GHz.As discussed in the previous section, utilizing two vertical faces can be beneficial when the coverage area is located near a corner of a wall or building. This allows for beamforming to involve both faces. The designed unit cell is utilized in the full structure design. The geometry of the full structure design is shown in Fig. 8a,b. It is important to mention that the beamforming target should be located within − 45 to + 45 of the array broadside in order to involve both faces of the metasurface in two-faced metasurface beamforming. If the beamforming target is outside the − 45 to +45 range, only one of the two vertically facing metasurfaces is used for beamforming, while the target is in the dead zone of the other face.
Schematics of the full-structure metasurface: (a) Planar, and (b) Two vertically-faced metasurfaces. (c) Feeding network of metasurface located in DC part in part 4 of Fig. 3.
The phase shift configuration of two vertically faced metasurfaces is shown in Fig. 9a–c for three reflection angles when the incident wave is coming from the broadside. It is observed that the quantization beam does not exist in the two-faced metasurface, even with a one-bit phase shift. A quantized beam is generated in a planar metasurface when there is a similarity between the phase shifts of 0 and 180°, as well as − 180 and 0°, when the inducted phase is equal in all cells. In the case of a two-faced metasurface, the equality of these two phase states is disrupted because of the varying phase shift induced on the unit cells. This can be seen in Eq. (16), which is another representation of Eq. (12).
Figure 9 shows the radiation pattern of both the full structure simulation and the analytical model for a one-bit metasurface in a vertically faced geometry at 26 GHz. This frequency band effectively resulting in a desirable radiation pattern. The radiation pattern results are illustrated for both full wave simulation showed in Fig. 9g–i and MATLAB simulation showed in Fig. 9d–f.
The unit cell phase states are demonstrated for 2 vertical faces for (a) 15° reflection direction; (b) 30° reflection direction; (c) 45° reflection direction. The incident wave originates from the broadside and is demonstrated in red arrows. The analytical model of the radiation pattern obtained in MATLAB simulation (2D radiation pattern) (d) 15°; (e) 30°; (f) 45°. Radiation pattern of two vertically-faced metasurfaces at 26 GHz obtained in full wave simulation (3D radiation pattern). With desired reflection direction of (g) 15°; (h) 30°; (i) 45°.
An analytical model is shown in Fig. 9d–f, showcasing two vertically faced metasurfaces consisting of 2*14*14 passive elements. It explores reflection angles of 15, 30, and 45°, as described by Eqs. (6) and (7) from the previous section. The incident wave is assumed to approach from the broadside. The results are provided for azimuth angles ranging from − 45 to 225°. These angles correspond to the area in front of the metasurface, similar to the range of 0 to 180° for a planar metasurface. The main beam direction in Fig. 9g–i are shown as red vertical lines in Fig. 9d–f to compare main beam direction in ideal matlab simulation and full wave simulation. In practical massive MIMO systems, the number of passive elements embedded on a giant surface is significantly large, resulting in a narrow beam.
Simulation and fabrication result of phase shift part
As described in previous sections phase control part and absorption reflection control part operated in different layers. By appropiate design of upper layer it is possible to achieve phase shift function even ground plane is replaced with the absorption reflection layer. In this section the design of patch and delay line similar to section II is presented. In unit cell design simulation, full structure design and simulation and fabrication results. Figure 10 shows schematics of unit cell and design parameters their value given in Table 3 for similar parameters introduced in Fig. 3 the parameters ae only for the phase shift layer depicted in Fig. 3b. The substrate is made of ro4003 with 3.55 of dielectric constant and 0.0027 of loss tangent with h1=1.6mm of thickness. Similar to Fig. 8 schematics of phase shift part full structure is shown in Fig. 11 for single planar metasurface and two vertically faced metasurface. Each planar surface contains 26*26 unit cells. PCB tracks in 0.2 mm width are used instead of pin diodes. The unit cells which are in forward state there is PCB track between central patch and starting point of delay line the same place as pin diodes shown in Fig. 10. The unit cells which are in reverse state there have no track. Individual planar surfaces are used for each beam steering condition since this technique is not reconfigurable. Figure 12 shows fabricated metasurface and test setup. Two single planar surfaces are used for 15° of beam steering. Other PCBs with different unit cell states are used for other beam condition. Four PCBs as single planar are used for each unit cell condition as shown in Fig. 13a,b. Figure 13c,d show simulated and measured radiation pattern and red vertical line shows Ideal beam steering direction.
The unit cell phase states are demonstrated for 2 vertical faces for (a) PCB1 and PCB2 for 15° reflection direction; (b) PCB3 and PCB4 for 30° reflection direction; The incident wave originates from the broadside and is demonstrated in red arrows and reflected wave is demonstrated in green arrows. Radiation pattern of two vertically-faced metasurfaces at 25.7 GHz obtained in full wave simulation and measurement results. With desired reflection direction of (c) 15°; (d) 30°;
Channel modeling
The radiation pattern and beam steering model are typically employed in line-of-sight (LOS) communication. However, in wireless communication, it is crucial to also consider non-line-of-sight (NLOS) components. In this context, the Multiple Input Multiple Output (MIMO) channel modeling tool is essential (17). Presents the common channel model for MIMO communication, demonstrating that the MIMO channel in wireless communication includes both LOS and NLOS channel matrices. In this work, the factor k is taken to be 2.
where none line of sight component is modeled as rayleigh distribution. By using IRS, it is possible to alter the propagation environment. As shown in (18), there are two propagation paths from BTS to user: the direct path from BTS to user and the IRS path.
where \(\phi\) is a diagonal matrix, with each of its diagonal elements depicting the status of each cell as either forward bias or reverse bias. \(H_1\) is the channel matrix between the BTS and IRS, and \(H_2\) is the channel matrix of the propagation path between the IRS and users. The optimal weighting for base station antenna elements is obtained using the Maximum Ratio Transmission (MRT) method by assigning the conjugate value of the propagation environment channel matrix, as shown in (19).
As the array factor of the two vertically faced arrays was stated in (8), for a plane wave incident EM signal, the line-of-sight component of \(H_1\) and \(H_2\) is calculated by determining the distance between element i of the base station and element j of the IRS, as well as the distance between element j of the IRS and the user. The geometry of \(r_{ij}\) and R is shown in Fig. 14, and the distance values are calculated using (20) and (21). The IRS is located within a 44-meter distance of the base station array antenna.
wWere \(r_ij\) is distance between element i of base station and element j of IRS and R is the distance between element j of IRS and user.
by having distances line of sight component of Channel between base station and IRS and channel between IRS and users is calculated by (23) and (23)
Feeding lines for each face of the two-faced metasurface are shown in Fig. 8c and illustrated in Table 4. Each row has four biasing lines, with two of them beginning from the left side and two from the right side. The first three elements on each side have their own feeding source, while the next four elements of each row are fed by the same source, thereby having the same bias voltage and cell state. This limitation must be considered in the optimization process, as each cell is not fed individually; clusters of metasurface elements share the same cell state. Table 4 shows the unit cells of each row which have a common feeding source.
The GA optimization method is used in the calculation of unit cell states. GA Algorithm is searched based optimization method inspired by genetics and natural selection is used to find optimal and near optimal solution for complicated problems. In the first stage of genetic algorithm initial population of candidate solutions are represented and then evolved over generation. For finding optimal phase states in two vertically faced metasurface the GA algorithm is used as described in follows.
In the first stage Phase distribution of unit cell are calculated supposing that the channel between BTS and IRS and channel between IRS and the user is line of sight channel. The calculated phase is used as initial population for GA Algorithm. In the next stage, some random cells are chosen to be mutated. If the cell is in forward bias state, it will be changed to reverse bias state. If the cell is in reverse bias state it will be converted to forward bias state. Different sets of results are evaluated and the best fitted results are chosen to go to the next stage. This process is continued to reach the optimal result.
The optimization goal is to minimize transmitted power to achieve the desired SNR at the user’s location, as mentioned in (24) and (25). The initial population includes cell states in line-of-sight propagation according to (12) and (13). After GA optimization is implemented for choosing IRS element states, the required power emitted by the base station antenna of the two vertically faced metasurfaces is shown in Fig. 15 for different horizontal distances. The y-axis represents the power required to achieve 15 dB of SNR when the noise power is 3 femtowatts at the user location. The result is compared with a planar metasurface of the same element size of \(28 \times 14\) in the same location and the case without IRS. The IRS is optimized to achieve maximum SNR when the user is located at a 10-meter horizontal spacing of D. As shown in Fig. 15, the minimum power is required to achieve the desired SNR at \(D = 10\) m. When the user’s location exceeds 22 meters, only one of the surfaces works while the user is not in the covering zone of the other.
Conclusion
In wireless communication, metasurfaces need to be embedded on various surfaces and should not be affected by polarization. This paper investigates the two vertically faced metasurfaces using three-mode polarization-free unit cells. The symmetrical geometry of the unit cell is achieved through a combination of a 3-angle structure and pin diodes. The simulation results demonstrate that there is absorption occurring in the frequency range of 26.5-27 GHz in absorption mode, while in reflection mode, there is a phase shift of 180° within the same frequency band. The full structure simulation on a planar surface and two vertically faced surfaces is conducted and measurement results for two vertically faced metasurface are presented. The results demonstrate that effective beam steering and minimum required base station power are achieved through the appropriate distribution of phase shifts in metasurface unit cells.
Data availability
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Wu, Q. & Zhang, R. Beamforming optimization for wireless network aided by intelligent reflecting surface with discrete phase shifts. IEEE Trans. Commun. 68, 1838–1851. https://doi.org/10.1109/TCOMM.2019.2958916 (2019).
Kitayama, D. et al. Transparent dynamic metasurface for a visually unaffected reconfigurable intelligent surface: controlling transmission/reflection and making a window into an rf lens. Opt. Express 29, 29292–29307. https://doi.org/10.1364/OE.435648 (2021).
Ahmed, I. et al. A survey on hybrid beamforming techniques in 5g: Architecture and system model perspectives. IEEE Commun. Surveys Tutorials 20, 3060–3097. https://doi.org/10.1364/OE.435648 (2018).
Zheng, B., You, C. & Zhang, R. Double-irs assisted multi-user mimo: Cooperative passive beamforming design. IEEE Trans. Wireless Commun. 20, 4513–4526. https://doi.org/10.1109/TWC.2021.3059945 (2021).
Huang, C. et al. Dynamical beam manipulation based on 2-bit digitally-controlled coding metasurface. Sci. Rep. 60, 42302. https://doi.org/10.1109/TWC.2021.3059945 (2017).
Bayraktar, O., Civi, O. A. & Akin, T. Beam switching reflectarray monolithically integrated with rf mems switches. IEEE Trans. Antennas Propag. 60, 854–862. https://doi.org/10.1109/TAP.2011.2173099 (2011).
Farzin, P., Nooramin, A. S. & Soleimani, M. Reprogrammable reflection-transmission integrated coding metasurface for real-time terahertz wavefront manipulations in full-space. Sci. Rep. 14, 11156 (2024).
Wu, Q. & Zhang, R. Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network. IEEE Commun. Mag. 58, 106–112. https://doi.org/10.1109/MCOM.001.1900107 (2019).
Di, B. et al. Hybrid beamforming for reconfigurable intelligent surface based multi-user communications: Achievable rates with limited discrete phase shifts. IEEE J. Sel. Areas Commun. 38, 1809–1822. https://doi.org/10.1109/JSAC.2020.3000813 (2020).
Tran, N. M. et al. A novel coding metasurface for wireless power transfer applications. Energies 12, 4488. https://doi.org/10.3390/en12234488 (2019).
Yang, H. et al. A 1-bit reconfigurable reflectarray antenna: design, optimization, and experiment. IEEE Trans. Antennas Propag.
Dai, L. et al. Reconfigurable intelligent surface-based wireless communications: Antenna design, prototyping, and experimental results. IEEE Access 8, 45913–45923. https://doi.org/10.1109/ACCESS.2020.2977772 (2020).
Pereira, R. et al. Dual linearly-polarized unit-cells with nearly 2-bit resolution for reflectarray applications in x-band. IEEE Trans. Antennas Propag. 60, 6042–6048. https://doi.org/10.1109/TAP.2012.2213051 (2012).
PGros, J.-B., Popov, V., Odit, M. A., Lenets, V. & Lerosey, G. A reconfigurable intelligent surface at mmwave based on a binary phase tunable metasurface. IEEE Open J. Commun. Soc. 2, 1055–1064. https://doi.org/10.1109/OJCOMS.2021.3076271 (2021).
Wu, Q. et al. Single-layer 1-bit prephased single-beam metasurface using true-time delayed unit cells. IEEE Antennas Wirel. Propag. Lett. 21, 1095–1099. https://doi.org/10.1109/LAWP.2022.3157903 (2022).
Hu, Q. et al. An intelligent programmable omni-metasurface. Laser Photon. Rev. 16, 2100718. https://doi.org/10.1002/lpor.202100718 (2022).
Ma, Q. et al. Highly integrated programmable metasurface for multifunctions in reflections and transmissions. APL Mater. 10, 2100718. https://doi.org/10.1063/5.0093424 (2022).
Farzin, P. & Soleimani, M. Graphene-based metasurface for real-time control of three electromagnetic wave modes and polarization state. Diam. Relat. Mater. 139, 110279. https://doi.org/10.1016/j.diamond.2023.110279 (2023).
Song, X. et al. Switchable metasurface for nearly perfect reflection, transmission, and absorption using pin diodes. Opt. Express 29, 110279. https://doi.org/10.1364/OE.436261 (2023).
Yoo, M. & Lim, S. Active metasurface for controlling reflection and absorption properties. Appl. Phys. Express 7, 112204. https://doi.org/10.7567/APEX.7.112204 (2014).
Jeong, H., Le, D. H., Lim, D., Phon, R. & Lim, S. Reconfigurable metasurfaces for frequency selective absorption. Adv. Opt. Mater. 8, 1902182. https://doi.org/10.1002/adom.201902182 (2020).
Hasan, R. M., Baqir, M. A., Hameed, M., Naqvi, S. A. & Ali, M. M. Triangular metallic ring-shaped broadband polarization-insensitive and wide-angle metamaterial absorber for visible regime. JOSA A 39, 136–142. https://doi.org/10.1364/JOSAA.444523 (2022).
La Spada, L., Spooner, C., Haq, S. & Hao, Y. Curvilinear metasurfaces for surface wave manipulation. Sci. Rep. 9, 3107. https://doi.org/10.1038/s41598-018-36451-8 (2019).
Nadeem, Q.-U.-A., Kammoun, A., Chaaban, A., Debbah, M. & Alouini, M.-S. Intelligent reflecting surface assisted wireless communication: Modeling and channel estimation. 9, 3107. https://doi.org/10.1038/s41598-018-36451-8. arXiv:1906.02360 (2019).
Yang, F. et al. Two-dimensional beam steering based on compact programmable coding metasurface. Appl. Sci. 12, 11780. https://doi.org/10.3390/app122211780 (2022).
Author information
Authors and Affiliations
Contributions
H.S. and M.J. conceived of the presented idea. H.S., M.j., and M.S. developed the theory and performed the computations.H.S. and M.S. verified the analytical methods. M.S. encouraged M.J. to investigate the subject andsupervised the findings of this work. All authors discussed the results and contributed to the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Jahangiri, M., Soleimani, H. & Soleimani, M. Beam steering by two vertically faced metasurfaces using polarization free unit cells with three operating modes. Sci Rep 15, 394 (2025). https://doi.org/10.1038/s41598-024-84601-y
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-024-84601-y