Modelling of queuing systems using blockchain based on Markov process for smart healthcare systems

Abstract

Queueing theory employs mathematical analysis to establish effectiveness metrics. Optimization models are then formulated using significant and efficient measures, such as data, to ascertain system efficiency and requirements. Each queuing system represents a discrete event system problem, and simulating these systems aids in addressing challenges and conducting practical performance analysis. Blockchain offers various benefits, including redistribution, accessibility, durability, reliability, constancy, anonymity, auditability, and data security. Its applications span across cryptocurrencies, financial services, reputation management, the 'Internet of Things’, the sharing economy, and social and community services. Notably, foundational theory is increasingly pertinent in the blockchain field. For instance, performance analysis and optimization of blockchain systems rely on mathematical models like Markov processes and queueing theory. In smart healthcare, blockchain technology enhances disease diagnosis, patient care, and overall quality of life. Due to the substantial patient data stored on blockchain in smart healthcare architectures, queueing models are indispensable for efficient data processing. This paper leverages Markov chains to establish queueing theory for blockchain systems and assess the performance of smart healthcare architecture. A "Markovian-batch-service" queueing framework is devised for this purpose, modeling input and processing parameters essential for reliable queuing network simulations.

Introduction

With an ever-growing population, it is imperative to immediately and effectively ensure the well-being of the community. It necessitates the development of smart technologies and devices that continuously monitor a person’s health while also dispensing timely advice and care. Electronic Medical Record is the term used to describe how smart healthcare reports the data transmitted by smart health equipment¹. Professionals in the medical field then review this data to help with diagnosis and treatment. Both patients and hospitals can save money and time with this ‘digital’ record-keeping and analysis². Blockchain can allow for the protected and controlled movement of sensitive data between patients, doctors, and other healthcare professionals. As a result, it can improve data sharing and encourage system-to-system communication. Additionally, it illustrated a suggested framework for how blockchain might offer a crucial foundation for healthcare organizations to allow more precise diagnosis and treatment through potentially secure data sharing, including from remote locations. After observing a symptom, a patient seeks medical attention. Healthcare professionals can access the blockchain to access his medical records and learn about his recent treatment status. Doctors may order, carry out, and analyze diagnostic tests for patients using the same blockchain platform³. The patient could potentially avoid redundant testing, making it more cost-effective for him. The efficient processing of this enormous number with the least amount of waiting time is necessary for blockchain to operate at its best. Thus, the creation of blockchain queues is required. It is necessary to build a queueing model to forecast queue lengths and waiting times and make analytical decisions⁴.

The paper is organized as follows. After the brief introduction about Modelling of Queuing Systems in "Introduction" and "Literature review" sections describes the Method for Inverse Transformation. "Markov chain" section explores Markov Chain. "A blockchain technology" section deals with Literature Review of Blockchain in Healthcare. "Proposed blockchain queue model description" section discusses about Proposed Blockchain Model followed by Working Standards for Healthcare using Blockchain in "Working standards for healthcare using blockchain technology" section. Finally, in "Results and discussions" section we discuss about the Results and limitations to proposed work followed by conclusion and future work in "Conclusion and future work" section.

For a system to be ordered, queueing theory is very important. The mathematical analysis of waiting times and queue length is known as queuing theory⁵. In a queue, there are "customers," "objects," or "information." When resources are scarce, queue formation is necessary. Figure 1 shows the queuing system. There are three sections in the queue:

Fig. 1

Queuing system.

• Arrival Process: Each user and client in the line is listed, along with the time of their arrival.

• The service process explains how consumers access services and depart from the system.

• Queue: The queue is filled with the actual number of users.

With the aid of simulation tools, the characteristics and behavior of each network were represented using queueing models. It is feasible to assess the effects of each change on the system design and gain a better understanding of the anticipated “performance” of the actual system using simulation. Markov chains’ future states depend only on their current probability, which makes them discrete state-space stochastic processes with an intriguing property. Computer simulation describes a technique that uses a computer to dynamically display the system’s structure and behaviors to assess, forecast, and give information for decision-making.

Single-server queue

In real life, single-server queues might be the most common form of queuing. In several situations, such as commerce (such as a sales clerk), industry (such as a manufacturing line), and transportation, one can find a line with a single server (such as queues). Therefore, it is quite useful to be able to simulate and analyze the behaviour of a single server queue. The statistical distributions for "inter-arrival" intervals and “service periods” both follow the exponential distribution since “arrivals” and “service” are both “Poisson” processes. The single server represented by (M/M/1) has an endlessly long queue and an unlimited calling population.

Due to the mathematical nature of the exponential distribution, several fairly simple correlations can be found for a range of performance indicators, given the “arrival rate” and “service rate”⁶. This is advantageous since a lot of queuing circumstances may be roughly modeled by an M/M/1 queuing model. To simulate the behavior of a "single-server" queueing system with an “infinite” number of clients and FCFS queuing discipline, the (M/M/1) model was developed. We’ll change the "inter-arrival" and "inter-service" times to see how they affect the other variables. Estimates will be made for all relevant performance measurements⁷.

Figure 2 depicts the model layout, and Fig. 3 displays the transition diagram (using Markov representation) for “Single-Server-Queuing-Model”.

Fig. 2

Single-server-queuing-model.

Fig. 3

Transition diagram single-server-queuing-model.

Poisson-distribution

The Poisson distribution, which depicts the likelihood of all events occurring during the specified time frame, is a probability distribution⁸.

Presumptions

• The sum of all occurrences of an event in the interval is m, where m = 0,1,2––

• Each thing happens on its own.

• The frequency of events occurring is constant.

• There is a little pause between each event and its counterpart.

The Poisson distribution of m variables is defined in terms of these presumptions.

Illustration

Let’s say that an event occurs on average once.

The number of occurrences of an event in the interval (m) = {0, 1, 2…}.

As a result, the likelihood that m events will occur during the specified interval is

$${\text{P }}\left( {{\text{m }}\hbox{``}{\text{interval}}\hbox{''}} \right){\text{ }} = {\text{ e}}^{{ - \lambda }} \frac{{\lambda ^{{\text{m}}} }}{{{\text{m}}!}}$$

(1)

λ: average frequency of occurrence of an event. The Euler number e is 2.71828. m: 0, 1, 2…, m!: factorial of m.

Exponential distribution

In a Poisson process, the interval of time between event occurrences has an exponential distribution.

The formula is:

$${\text{P}}\left( {{\text{ti}}} \right) = {\text{ e}}^{{ - \upmu {\text{ti}}}}$$

(2)

µ: average service rate (ti >  = 0), ti: time spent performing service, Probability of service time > ti = P(ti).

Multi-server queue

Additionally, it is known as a multi-server queue. Customers can access services from any server shown in Fig. 4. The first server that becomes available will be given to the customers once they have waited in line^9,10. Customers arrive on many server systems with a Poisson distribution and an ‘A’ arrival rate. The customer may access any of the k systems that are arranged in parallel. The service-time is distributed ‘exponentially’. Regarding ‘arrival rate’ and ‘service rate’, each of the k servers is separate from the others.

Fig. 4

Multi-server-queuing-model.

In a system with multiple servers, there are two circumstances:

• There will be no queue formation (q − k) and all clients will be serviced at once if (k = q). The servers might not do anything.

  $$\left[ {{{\upmu k }} = {\text{ k}}{\upmu }} \right]$$

  (3)

This equation applies when there are fewer customers than servers or an equal number of customers and servers. Each server has an individual service rate μ, so with k servers in operation, the total service rate becomes μk = kμ.

k = 0, 1, 2,…, q = number of servers; k = number of customers.

• All of the servers are considered busy if (k >  = q). There will be a maximum number of clients in line (k − q).

  $$\left[ {{\upmu k} = {{\text{q}\upmu }}} \right]$$

  (4)

This equation applies when the number of customers exceeds the number of available servers. Even though more customers are waiting, the total service rate does not increase because all servers are already fully utilized. Therefore, the service rate remains μk = qμ, where q is the number of servers.

In the "M/M/k" sequence, the "arrival" and "departure" are shown in Fig. 4. More than two servers are used in the M/M/k system to serve customers.

Literature review

A thorough description of the blockchain network’s structure may be found in¹¹. Additionally, a thorough analysis was done of each node’s self-organizing mechanisms in the blockchain backbone network. In response to concerns about “access control” and the handling of "sensitive data,"¹² developed a blockchain-based data-sharing system. This method completely utilizes the independence and stability of the blockchain.

Identification-related technological problems and limitations can be solved by the blockchain, as¹³ shows. They provided a succinct summary of the blockchain’s potential for expansion into both new and ongoing industrial initiatives. The researchers proved that “blockchain technology” is workable for application in the business sector after examining the “challenges” and market restrictions that it has to go beyond. According to¹⁴, a “batch” service-queuing system with two separate “service phases” can accurately simulate block establishment and mining operations.

Numerous studies have also examined the use of blockchain technology in conjunction with a queuing paradigm. In order to describe the latency encountered in Bitcoin transactions, a methodical framework including of both machine learning and the queuing theory approach was made available¹⁵. The architecture created a connection between transaction delays and the intervals between each pair of block validations. A blockchain simulation model was created¹⁶ using queuing theory. To confirm their blockchain model, they next simulated two months’ worth of transactions using real data from “bitcoin” and "ethereum.".

A method for estimating queue waiting times was proposed by¹⁷ using only the historical log data generated by the batch task scheduler. It is advised to use a hidden Markov model, particularly for predicting line wait times. The steps in the list below are as follows: first, outliers are removed before using a statistics-based parametric approach for outlier detection; second, the hidden state parameters are derived using the historical job log and the observed queue waiting for the time sequence; and third, the predicted parameters at time (t) are used to calculate the queue waiting interval at time t + 1. These findings show that the proposed technique increases prediction accuracy when compared to more well-established prediction algorithms.

A “hidden Markov” model (HMM) was presented by Neuts¹⁸ to simulate such queuing procedures in environments with probing vehicles. The observed pattern of probe vehicles is an observation in this model, while the length of the queue during each cycle represents a hidden state. Using an "HMM," they suggested two different methods for estimating the queue length. They created a method for calculating the HMM quality metrics using previous data from probing vehicles. The suggested queue length ("cycle-by-cycle") estimating approaches outperform the currently employed methods, according to validation data.

In-depth analysis of the trends and the benefits of applying blockchain technology to the Internet of Things and healthcare is done in¹⁹. Moreover, it is noted that although blockchain has several benefits for the healthcare industry, authors choose to use it mostly for data handling and medication supply chain management. By providing patients more control over their own data, this helps to empower them and prevent the sale of fake medications.

Through a thorough assessment of the literature, Villarreal et al.²⁰ provides a thorough analysis of the architectural approaches used to improve security and interoperability in blockchain-based health management systems. Based on the results, a number of situations were found in which these methods can be used successfully. These scenarios also included information about the settings, difficulties, and architectural considerations of each scenario, with an emphasis on interoperability and security. Then, a high-level architectural framework was suggested and verified by means of an experiment that covered the whole process of developing a language appropriate to a given domain by employing the model-driven engineering technique customized for particular smart contracts.

A comprehensive analysis of current efforts to use blockchain-based solutions is examined in²¹. This study presents a methodical approach for classifying and evaluating various systems. The authors carefully positioned each of the more than 40 systems and solutions in the study by defining their scope and placing them in accordance with the previously described categories pertaining to interactions, functional components, obstacles, and advantages.

This study focuses on analyzing blockchain-related studies in the medical field, as reported in²². Healthcare stakeholders have criticized the traditional approach for exchanging health record data because of its centralizing tendencies and vulnerability to data exchange disruptions and breakdowns. Access control, data integrity, consistency, and provenance are the main problems of distributed ledger technology that require improvement. Ethereum and Hyperledger are the two most common blockchain frameworks and platforms used here.

A method for inverse transformation

This method is relevant only in situations where the cumulative density function can be reversed computationally. Let’s say we want to create stochastic variates using a probability density function (pdf). Be the cumulative density function, F(y), we observe that the region [0,1] is where F(y) is defined. To create the following straightforward stochastic variate generator, we investigate this characteristic of the cumulative density function²³.

First, we create a random number, n, and set it to be equal to F(y). As a result, F(y) = n. Then, by inverting F, the quantity y is determined. To put it another way, y = F − 1(n), where F-1(n) denotes the inverse transformation of F²⁴.

Exponential distribution sampling

To create variables from a uniform distribution, we employ the inverse transformation technique. The exponential distribution’s probability density function is described as follows:

$${\text{f}}\left( {\text{y}} \right) \, = {\text{ be}} - {\text{by }},\;{\text{b }} > \, 0,\;{\text{y }} > \, 0.$$

(5)

The cumulative density function is defined in²³:

$${\text{F}}\left( {\text{y}} \right) = \int\limits_{0}^{{\text{y}}} {{\text{f}}({\text{t}}){\text{dt}}} = \int\limits_{0}^{{\text{y}}} {{\text{be}}^{{ - {\text{bt}}}} {\text{t}}\;{\text{dt}}} = 1 - {\text{e}}^{{ - {\text{by}}}}$$

(6)

The following expressions provide the expectation and variance.

$${\text{E}}\left( {\text{Y}} \right) \, = \int\limits_{{\text{n}}}^{0} {{\text{bet}}^{{{\text{bt}}}} } {\text{dt}}\;{\text{dt}} = 1/{\text{b}}$$

(7)

The following is the inverse transformation approach for producing random variables²⁴.

$$[{\text{N}} = {\text{ F}}\left( {\text{y}} \right) = \, \left( {\left( {{1} - {\text{ e}}^{{{-}{\text{by}}}} } \right)} \right)$$

(8)

$$\left( {\left( {{1} - {\text{n}} = {\text{ e}}^{{{-}{\text{by}}}} } \right)} \right)$$

(9)

$$\left( {{\text{y}} = \, \left( { - {1}/{\text{b}}} \right){\text{ log }}\left( {{1} - {\text{n}}} \right) \, = \, - {\text{E }}\left( {\text{y}} \right){\text{ log }}\left( {{1} - {\text{n}}} \right)} \right)$$

(10)

$$\left( {{\text{y}} = \, \left( { - {1}/{\text{b}}} \right){\text{ log }}\left( {\text{n}} \right)} \right)$$

(11)

Markov chain

“Discrete-Markov” represents a “Markov” process having parameters (“time” and “state”). Since time is an infinite and continuous variable, any two numbers that are close neighbors can be divided indefinitely²⁵. The Markov chain’s state is finite, and its time parameter is discontinuous at this time.

When one state is listed, the subsequent state has no connection to the preceding state and is only tied to the present state²⁶.

Consider a "discrete-time" process such as Yi, i = [0, 1, 2,….] The process X’s "state-space" in this case is value. The set X is “finite” or "countable." The set of all possible states, which includes the Markov chain, is referred to as state space²⁷. The finite-dimensional distributions for the procedure are shown below:

$${\text{P}}\left\{ {{\text{Y}}^{0} = {\text{m}}_{0} , \ldots \ldots ,{\text{Y}}^{{\text{i}}} = {\text{n}}} \right\},~\;{\text{m}}_{0} , \ldots ..,{\text{ n }}{\sf C}\!\!\!\!\raise.8pt\hbox{=} {\text{ X}},\;{\text{i}} > = 0,$$

(12)

A probability distribution unique to the set X, the process’s state space, and the value Yi € X, the process’s state at the time i are used to calculate the likelihood of each event in the process²⁸. Therefore, if the “finite” dimensional distributions of two random processes are the same, then their distributions are the same.

$$`P{\text{'}}\left\{ {{\text{Y}}^{i + 1} = {\text{ n}} {\text{Y}}^{0} , \, \ldots .,{\text{ Y}}^{i} } \right\} \, = \, `P{\text{'}}\left\{ {{\text{ Y}}^{{i + 1}{}} = \, \left. {{\text{n}} } \right|{\text{Y}}^{i} } \right\}$$

(13)

For each m, n € X and i >  = 0, the “stochastic” method based on countable-set X and Y = {Yⁱ: i >  = 0} is a “Markov” chain.

$$P\left\{ {{\text{Y}}^{i + 1} = \left. {\text{n}} \right| {\text{Y}}^{i} = {\text{ m}}} \right\} = P_{{{\text{mn}}}}$$

(14)

where P_mn represents the likelihood that a Markov chain will transition from state m to state n.

$$P_{mn} > = 0\sum\limits_{{^{{{\text{i}} = 0}} }}^{\infty } {P_{mn} = {1},{\text{ n }} = 0;{1};.} .$$

(15)

• (i) The state Yi + 1 is independent of the preceding state at any time according to the Markov property. The present state, or Y0,…, Yi + 1, is necessary for the future state to exist and is independent of the prior state.

• (ii) Due to the characteristics of the Markov chain, the process is time-homogeneous, meaning the time parameter does not affect the transition probabilities. If the transition probabilities were time-dependent functions, the Markov chain for P(Yi) would no longer be time-homogeneous.

A matrix called P_mn contains the transition probability.

$$P = \left[ {\begin{array}{*{20}c} {P_{0} } & {P_{1} } & \cdots \\ {P_{2} } & {P_{3} } & \cdots \\ \cdots & \cdots & \cdots \\ \end{array} } \right]$$

(16)

The transition probability matrix is the name of this procedure.

When examining the structure of stochastic processes, one of the most challenging problems is how to describe the distribution of finite-dimensional stochastic processes²⁹. The initial probability distribution of Y⁰ and the transition probability of Yⁱ together determine the distribution of Yⁱ in limited dimensions.

We may get the following formula by assuming that P_mn is the “transition”—probability and beginning prob. Markov chain Yⁱ and that m = P, Y⁰ = m for all m⁰,., m_i € X and i >  = 0.

$$\left\{ {{\text{Y}}^{0} = {\text{ m}}_{0} ,..,\;{\text{Y}}^{i} = {\text{m}}_{{\text{i}}} } \right\} \, = \, \beta_{m0} Pm_{0} m_{1} \ldots .{\text{ P}}m_{i - 1} n_{i}$$

(17)

The likelihood of the process taking i steps to move from state m to state n is known as P_mn. Specifically, P¹_ij = P_ij

$$P^{i} = PP \ldots P_{i}$$

(18)

The transition graph, which may be used to represent a Markov chain state transition, is depicted in Fig. 5. Additionally, a transition probability is provided for each edge in the graph. The transition graph can be used to teach the terms “reachable” and "connected."

Fig. 5

Graph of Markov chain.

A Markov chain having six states (A, B, C, D, E, and F) is depicted in Fig. 5. Transition probabilities are shown by the arrows connecting the states. Moving from B to E, for example, has a probability of 0.4, but moving from B to C has a probability of 0.6. B (0.7) and E (0.6) self-loops indicate the likelihood of remaining in the same state. The diagram, which is frequently used in stochastic processes such as queueing systems or decision models, represents a probabilistic system in which entities change states according to the provided probabilities.

A blockchain technology

Blockchains are decentralized electronic ledgers that often operate independently of a bank, corporation, or government and are very safe, impervious to manipulation, and decentralized. A group of users can enter transactions into a shared ledger that is unchangeable once it is entered, as long as the blockchain network remains operational³⁰. 2008 saw the development of contemporary "crypto-currencies" through the fusion of many computing and technology concepts, including the blockchain idea. These digital currencies are secured by cryptographic techniques rather than by a centralized database or authority.

This technology became well-known in 2009 with the launch of the Bitcoin network, the first of several modern cryptocurrencies. The transfer of digital data, which functions as electronic money, takes place in a distributed system similar to Bitcoin and other similar systems. Because this transfer is openly documented on the Bitcoin blockchain, anyone connected to the network can independently verify the transaction’s legality²⁹. Information can be digitally signed by users with Bitcoin, transferring ownership to another user. The Bitcoin blockchain is independently managed and updated by a distributed group of individuals. Because of cryptographic procedures, the blockchain is immune to later attempts to change the ledger (changing blocks or fabricating transactions). “Bitcoin” and “Ethereum” are the only two cryptocurrency platforms made possible by blockchain technology. For this reason, blockchain technology is often associated with Bitcoin or even companies that deal with cryptocurrencies in general³¹.

There are more uses for “technology” than merely the fields in which it is now being researched. On the other hand, a simple description of each part can help one grasp the more complex overall system. A decentralized digital record with cryptographically signed blocks of transactions is what is commonly referred to as a blockchain. Each block is cryptographically linked to the previous one after validation and a consensus decision, making tampering evident. Tamper resistance arises from the difficulty of altering older blocks while new ones are constructed. The ledger is replicated across the network, and predetermined standards automatically resolve inconsistencies.

A basic blockchain paradigm is shown in Fig. 6, where each block has block data and a block header. The hash of the data in the current block, a timestamp, a nonce, and the hash of the preceding block are all included in the block header. These hashes are used to consecutively link blocks, guaranteeing data security and integrity over time.

Fig. 6

Generic chain of blocks.

Need of blockchain in healthcare

The field of healthcare is advancing at a very quick speed. There is currently a rising need for first-rate medical facilities that use state-of-the-art technology. Blockchain has the potential to completely transform the healthcare industry. Additionally, a patient-centric approach is becoming more prevalent in the healthcare industry, with a focus on two essential components: always having access to the right healthcare resources and easily accessible services. Healthcare firms may now provide the best possible patient care and facilities thanks to blockchain technology. The exchange of health information is another time-consuming and repetitive activity in the healthcare sector that adds significantly to business costs. By using blockchain technology, this problem can be quickly resolved³².

Through the use of blockchain technology, people can participate actively in health research projects. Furthermore, better research and data sharing on public health would enhance healthcare for different populations. Traditionally, the whole healthcare system and its affiliated institutions have been governed by a single, centralized database. Up until now, data security, data sharing, and interoperability in population health management have been the most urgent problems. Blockchain solves this particular problem well. When used correctly, this technology offers real-time updates and access while improving security, data interchange, interoperability, and data integrity. Furthermore, data protection is a major problem, especially with regard to wearable technology and personalized treatment³³.

Safety concerns arise because patients and healthcare providers need a safe and convenient way to capture, transmit, and consult data over networks. Thus, these problems are addressed by the application of blockchain technology³⁴. Blockchain guarantees total transparency throughout the prescription process, from manufacturing to drug availability in pharmacies. In order to efficiently schedule procurements and avoid disruptions and shortages in clinics, pharmacies, and other healthcare institutions for specific pharmaceuticals, IoT and blockchain can be used to monitor traffic, shipping routes, and speed³⁵. Adoption of blockchain-based digital systems guarantees that logistics data is unchangeable, fostering confidence and prohibiting diverse drug procurement parties from altering records, payments, and medications without authorization. By removing obstacles to multi-level authentication, this system can improve patient outcomes while remaining cost-effective³⁶.

Blockchain’s ability to maintain an immutable, decentralized, and transparent record of all patient data makes it well-suited for security applications. Moreover, while blockchain is publicly visible, it also offers privacy by concealing individuals’ identities behind intricate and secure algorithms, safeguarding the confidentiality of medical data³⁷. Thanks to its decentralized structure, patients, physicians, and healthcare providers can rapidly and securely share the same information.

Security challenges in blockchain for healthcare

Blockchain technology has a lot to offer the healthcare industry in terms of data quality, transparency, and effective medical record administration. Nevertheless, a number of security issues still exist, endangering its uptake and dependability. With the backing of recent research, this essay examines these issues and offers solutions.

Sybil attacks

In order to disrupt the network, malicious actors generate many false identities. Because identity authentication is frequently less stringent in permissionless blockchains, this kind of attack poses a serious risk. For instance, Sybil attacks have the ability to skew consensus processes, which hinders decision-making and undermines network confidence.

51% attack

When a malicious entity gains control of more than half of a blockchain network’s processing capacity, they can alter transaction histories and prevent new blocks from being added.

Because of their lower computational limits, research indicates that smaller blockchain networks are especially susceptible to this attack³⁸.

Smart contract vulnerabilities

It is possible to take advantage of smart contract shortcomings which could result in financial losses or illegal access to data. As highlighted in³⁹, there is a chance that improperly inspected smart contracts could reveal private patient information, especially in healthcare institutions.

Data breach and privacy issues

Despite the immutability of data provided by blockchain, patient privacy may be jeopardized if metadata is exposed or if off-chain storage is vulnerable. According to studies, the danger of data breaches is greatly increased when insufficient encryption or reliance on unsafe cloud storage is used⁴⁰.

Man-in-the-middle (MITM) attacks

Unprotected lines of communication between blockchain nodes and healthcare IoT devices may lead to data tampering. MITM attacks have the ability to introduce fabricated medical data into the system, which could result in inaccurate and perhaps hazardous treatments⁴¹.

Mitigation strategies for healthcare blockchain

Identity management

To counter Sybil attacks, make sure that Decentralized Identifiers (DIDs) have strong identity verification procedures in place⁴². Multi-signature authentication improves security by ensuring that only authorized parties are able to complete transactions.

Consensus mechanism

The Byzantine Fault Tolerance (BFT) boosts defenses against 51% of attacks, particularly in consortium and private blockchains⁴³. Equitable Allocation of Resources: Put laws into place to restrict mining concentration and lessen the dangers of computing power monopolies.

Secure smart contracts

The formal Verification prior to deployment, find and fix smart contract flaws using mathematical analysis. Regular Audits should be done to make sure that defined security criteria are being followed, conduct ongoing security audits³⁹.

Privacy and data encryption

Secure data processing is made possible by homomorphic encryption and zero-knowledge proofs, which preserve secrecy and privacy. Sensitive patient data is encrypted and safeguarded off-chain in hybrid storage, which only stores metadata on-chain⁴⁰.

Protecting communication channels

End-to-end encryption (E2EE) secures and maintains the secrecy of data transferred between devices and blockchain nodes. Blockchain-Based Communication Protocols provide safe and compatible frameworks for the Internet of Things in healthcare, improving the security of communications⁴¹. Although blockchain usage in healthcare has enormous potential, its inherent security issues must be resolved. Strong identity management, cutting-edge encryption methods, safe consensus processes, and careful observation can all help to reduce risks and maintain confidence. To create a safe and effective blockchain-based healthcare environment, ongoing research and development will be essential.

Constant network monitoring using AI and ML techniques

Use AI and ML techniques to identify possible threats and anomalous patterns. Implementing real-time alert systems will allow for prompt reactions to security threats that have been recognized⁴².

Proposed blockchain queue model description

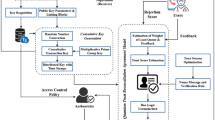
In this section, we have devised a blockchain queuing system in conjunction with a Markov process. A queueing model is imperative for all stages of a smart healthcare system. To effectively utilize this feature, it is essential to incorporate the appropriate queueing models. Assuming the blockchain system functions as intended, we can conceptualize the system as a blockchain queue. Figure 8 demonstrates the proposed blockchain queue model with a Markov chain. In healthcare, users (doctors, patients) send medical data following a "Markovian-arrival process" (MkAP) while entering the blockchain_system, which encompasses the steps of “block_generation” and “blockchain_building”. In this part, we define six stages: Defining roles and permissions, the "Markovian arrival process", the “block_generation process”, blockchain logging, the "blockchain _building process and smart contracts." Additionally, we introduce an intriguing blockchain queue based on real blockchain history.

Roles and permissions

In order to establish a safe and effective blockchain queuing system for the healthcare industry, responsibilities and permissions must be established first. The following describes the roles and the permissions that go with them:

Patient

They have the ability to access their own billing information and medical reports. A user’s login and password are used to verify access.

Doctor

Doctors are able to see and edit patient details.To protect data privacy and stop unwanted modifications, administrative access has been restricted.

Administrator

The administrator possesses extensive permissions to oversee all documents. Maintaining overall system health, ensuring regulatory compliance, and supervising system operations are among the responsibilities.

Markovian-arrival-process (MkAP)

The blockchain receives transactions using a "Markovian-arrival process." A continuous-time Markov process of the "GI/M/1 type" is established in a section on Markov processes of that type. It uses a geometric solution to express the stationary-probability-vector and specifies a sufficient stability condition for the blockchain.

An Markov process of G1/M1/Type

For the blockchain queuing system depicted in Fig. 7¹¹, we establish a continuous-time “Markov” process [GI/M/1] type in this section. The stationary probability-vector for this system and a stable condition for the system are then produced using the (matrix-geometric) solution⁴⁴.

Fig. 7

Markov process to its states.

“X (t)” and “Y (t)” represent, respectively, the block and queue transaction counts at time t. The queuing system at a time [t] may then be considered to be (X (t), Y (t)). Note that for various situations of (“X (t)”, “Y (t)”), X = [0, 1,…, b] and Y = [0, 1, 2,…]

$$\begin{aligned} \mu = & (\{ (((`{\text{i}},{\text{ j}}{\text{'}}): - `{\text{i}}{\text{'}} = \left[ {0,{1},...,{\text{b}}} \right], `{\text{j}}{\text{'}} = [0,{ 1},{ 2},...])\} ) \\ & = (\{ [(0,0),{(1}, \, 0{)},...,{\text{(b}}, \, 0{)};{(}0,{ 1)},{(1},{ 1)},...,({\text{b}},{ 1}); \, . \, . \, . \, ]) \\ & \quad ([(0,{\text{ b}}),({1},{\text{ b}}),...,({\text{b}},{\text{ b}});(0,{\text{ b }} + { 1}),({1},{\text{ b }} + { 1}),...,({\text{b}},{\text{ b }} + { 1}) \, ; \, . \, . \, .]\} ). \\ \end{aligned}$$

(19)

I (t) shall equal X (t) and Y (t). Consequently, (‘I (t)’: ‘(t >  = 0)’) is “continuous-time” {‘GI/M/1’} on the state-space. The Fig. 7 depicts Markov process ‘I (t)’: (t >  = 0) state transition relation; as a result, its “infinitesimal” generator is provided by

$$P = \left( {\begin{array}{*{20}c} {B_{0 } } & {A_{0} } & {} \\ {B_{{{1} }} } & {A_{{1}} } & {A_{0} } \\ {B_{2} } & {A_{{1}} } & {A_{0} } \\ \ldots & \ldots & \ldots \\ \ldots & \ldots & \ldots \\ {B_{B} } & {A_{{1}} } & {A_{0} } \\ {A_{{\text{B}}} } & {A_{{1}} } & {A_{0} } \\ {A_{{\text{B}}} } & {A_{{1}} } & {A_{0} } \\ \ldots & \ldots & \ldots \\ \ldots & \ldots & \ldots \\ \end{array} } \right)$$

where A₀ = λ_I,

$$A_{{1}} = \left( {\begin{array}{*{20}c} { - (\lambda + \eta_{2} )} & {} & {} & {} & {} \\ {\eta_{1} } & { - (\lambda + \eta_{1} )} & {} & {} & {} \\ \ldots & {} & \ldots & {} & {} \\ \ldots & {} & {} & \ldots & {} \\ {\eta_{1} } & {} & {} & {} & { - (\lambda + \eta_{1} )} \\ \end{array} } \right),A_{b} = \left( {\begin{array}{*{20}c} 0 & \ldots & 0 & {\eta_{2} } \\ \end{array} } \right)$$

(20)

and

$$B_{0} = ~\left( {\begin{array}{*{20}l} {\hbox{``} - \lambda \hbox{''}} & {} & {} \\ {\hbox{``}\eta _{1} - {\text{ }}(\lambda + \eta _{1} )\hbox{''}} & {} & {} \\ \ldots & \ldots & {} \\ {\eta _{1} } & {} & { - {\text{ }}(\lambda + \eta _{1} )} \\ \end{array} } \right)$$

(21)

$$B_{{1}} = \left( {\begin{array}{*{20}l} 0 & {\eta_{2} } & 0 & {...} & 0 \\ \end{array} } \right),\;B_{{1}} = \left( {\begin{array}{*{20}l} 0 & 0 & {\eta_{2} } & {...} & 0 \\ \end{array} } \right), \ldots \ldots ,B_{{\text{b}}} = \left( {\begin{array}{*{20}l} 0 & {...} & {...} & 0 & {\eta_{2} } \\ \end{array} } \right)$$

(22)

In this part, we’ll discuss the mean drift approach’s application to the system stability requirement.

$$A = {\text{ }}\left[ {A_{0} + A_{{\text{1}}} + A_{{\text{b}}} } \right] = \left( {\begin{array}{*{20}l} {\hbox{``} - \eta _{2} \hbox{''}} & {} & {} & {} & {\eta _{2} } \\ {\hbox{``}\eta _{1} \hbox{''}} & { - \eta _{1} } & {} & {} & {} \\ \ldots & {} & \ldots & {} & {} \\ {\hbox{``}\eta _{1} } & {} & {} & { - \eta _{1} } & {} \\ {\hbox{``}\eta _{1} } & {} & {} & {} & { - \eta _{1} } \\ \end{array} } \right)$$

(23)

Indisputable irreducibility, aperiodicity, and positive recurrence characterise the Markov process A with finite states⁴⁵. In this instance, its stationary probability vector is denoted by the notation Λ = (Λ₀, Λ₁,…, Λ_b). A = 0 and e = 1 are the only solutions to the linear equations, “column vector” is e. It is easy to confirm that

$$\Lambda = \frac{\eta 1}{{\eta 1 + \eta 2}},0, \ldots ,0,\frac{\eta 2}{{\eta 1 + \eta 2}}$$

(24)

The Markov process P is positive continuous under the following theorem’s necessary and sufficient conditions.

Block generation process

When data flows reach the block generation phase, they enter a queuing system. The system employs a first-come, first-served queuing criterion to select data. Recently generated blocks are linked to create a blockchain, and a new block is generated during this phase using a cryptographic hash algorithm.

Blockchain logging

The blockchain component uses the following characteristics to guarantee reliable data monitoring and auditing:

Data access logs

A blockchain ledger records every instance of data access. Logs contain the timestamp, the type of access, and the identity of the person who accessed the data.

Immutability

Because of the intrinsic immutability of blockchain technology, access records cannot be changed, resulting in a trustworthy and impenetrable audit trail that guarantees total accountability and transparency.

Blockchain building process

In addition to a list of transactions, a block also contains metadata such as timestamps for previous and most recent blocks and a nonce field. Considering the historical context of the blockchain, it becomes evident that the two phases (block generation and blockchain development) can be easily understood. The time required at this stage depends on network consensus and the network delay present during the consensus process, as the freshly created blockchain also employs its consensus method. The term “blockchain time” here refers to the time needed to construct a blockchain.

Using this method, we can calculate the “mean” wait time, mean idle time, delay, throughput, and channel utilization for all data streams within a blockchain. Figure 8 represents the blockchain system consisting of six phases: (Roles and Permissions), ("Markovian-arrival-process" MkAP), (Blockchain generation process), (Blockchain Logging), (Blockchain building process) and (Smart Contracts).

Fig. 8

A blockchain queuing system using Marckov chain.

Annotation 1: A non-Poisson form of transaction receiving is possible with the blockchain system (for example, a "Markov arrival process," a "renewal process," or a non-homogeneous “Poisson process”). Service wait times might not always shorten, though. The study of blockchain queues with "renewal arrival techniques" or with "generic service time" distribution is still an interesting open question in the field of research.

Annotation 2: The maximum block size, “blockchain” security, and other factors are crucial in the blockchain system. We may employ “decision models” and “game queueing” models based on certain of them in the research of blockchain systems. It will be important and useful to advance blockchain technology in several prospective applications, so it is important to analyze these fundamental components.

Smart contracts

Smart contracts add automation to the system to improve accuracy and efficiency:

Automated tasks

Transaction approvals

These require no human involvement and validate eligibility (such as insurance coverage).

Invoice generation

This feature computes charges using preset pricing models and automatically creates invoices based on treatment data.

Trigger mechanisms

Certain operations, such processing payments upon patient approval or validating and submitting insurance claims, can be started by smart contracts.

Medical data is entered into the system by a user, such as a patient or healthcare professional in Fig. 8. This information may consist of insurance claims, billing details, or patient medical records. A probabilistic approach called the Markovian Arrival handle (MkAP), which optimizes block generation and scheduling, is used to handle data from the queue. The data is grouped into a block by the system in order to be added to the blockchain. Every block contains the Transaction Number, Nonce: A distinct value used in block validation Date and time of creation: The precise moment the block was made A cryptographic connection to the previous block in the chain is known as the hash of the previous block. The integrity of the blockchain is ensured in the suggested model by including a hash of the preceding block in every block. If a hash mismatch for all blocks after a single block is altered then it renders the chain invalid. Data tampering is prevented and immutability is guaranteed by this approach. It is computationally prohibitive for an attacker to try to change data in a single block because they would have to change all following blocks. A nonce—a number that is used only once—is also included in every block to aid with mining and validation procedures like Proof of Work (PoW). The probability of fraudulent block production is decreased by the substantial computational difficulty introduced by the nonce. This function reduces the possibility of Sybil attacks by making sure that adding a new block efficiently uses a significant amount of processing power preventing malicious actors.

Adding a timestamp to every block improves security by accurately documenting the addition of data to the blockchain. By verifying the sequence and timestamp of every block, this method aids in the detection and prevention of replay attacks. User medical records and other incoming data go through a queue before being processed and published to the blockchain. This queuing method lowers the possibility of data injection attacks by acting as a buffer to confirm and authenticate the integrity of the input. To keep transaction patterns unexpected, the stochastic arrival of data and transactions is modeled using the Markovian Arrival Process (MkAP). MkAP defends against timing attacks and improves system security by blocking recognizable patterns. Lastly, because the blockchain is decentralized and replicates across several nodes, it safeguards against single points of failure.

The blockchain ledger, a decentralized and unchangeable record, is updated with the freshly formed block. An unbreakable data chain is created by securely connecting each block to the one before it using cryptographic hashes. Critical tasks are automated using smart contracts, including Transaction Approval and invoice generation. By eliminating the need for manual intervention, these procedures improve reliability as well as effectiveness. The cornerstone of the blockchain is a Genesis Block. The chain is expanded by adding subsequent blocks, such Blocks 1 and Z. Cryptographic hashes are used to link each block, guaranteeing security and continuity. Admin oversees the system, controls users, and makes sure rules are followed.

This design ensures high availability and strong security by making the system resistant to Distributed Denial of Service (DDoS) attacks and individual node breaches.

Working standards for healthcare using blockchain technology

Every time a patient visits a physician for a checkup, there’s a chance that, following a diagnosis, the physician will advise the patient to undergo some useless testing. Additionally, a patient may be willing to switch doctors and wish to begin treatment with any other physician. All reports, lab results, and medications with appropriate invoices must be kept on file on the blockchain in the event that a patient or doctor needs to know how much a patient spent on a specific treatment, as shown in Fig. 9.

Fig. 9

Healthcare using blockchain.

No person may change medication charges or treatment invoices without the patient’s consent, even when all records are maintained on the block chain. If a patient has a variety of tests or medications during their treatment, the billing or record-keeping for each report and meeting needs to be updated on the block chain. In order to update the records following the surveillance review, in the event that medicines and lab tests generate substantial expenditures for the treatment. If all of the patient’s activities are recorded inside the block chain, it will be unable to make any more modifications to the bill once it has been created and added. Two separate cases were covered in the text below.

Case 1: Patient report tracing from the system

Let us envision an example where a number of patients obtain blockchain-based assistance with their medical records. Reports are automatically created, logged, and arranged appropriately. Three components make up every block on the blockchain: data, a distinct hash, and the hash of the block before it. Depending on its intended use, several types of data are stored on blockchains. For example, the unique hash functions as a fingerprint to identify a block and its contents in a patient record blockchain that holds patient information. A block’s hash is produced at creation and is updated whenever its content changes. In Fig. 10, a transaction block is shown to demonstrate this. Hence, in order to identify any alterations, the block hashes are essential.

Fig. 10

Transaction block.

To demonstrate this within the healthcare industry, let’s look at a set of three blocks, as shown in Fig. 11. The entity name, block hash, and hash of the previous block make up each block. Every relevant piece of information is documented on the blockchain whenever a patient sees a physician. The block’s hash will change if this data or report counts change. Block 3 and any subsequent blocks will become invalid as a result of the block’s hash changing since they will no longer be able to refer to a valid prior hash. Because changing one block changes all the others, it is necessary for an attacker to change each block in the chain in order to successfully tamper with the blockchain. This means that unless these differences are found, it is almost hard for a tampered block to be approved by others.

Fig. 11

Blockchain creation in healthcare.

Case 2: Securing patient invoices distributed within a medical facility

While transferring the patient invoices, there can be another instance. There could be compromised data if malicious activity modifies the patient billing. Any reputable third-party authority is usually used to carry out this process. Nevertheless, there are additional costs associated with this process. However, all of these problems can be easily handled with blockchain solutions. Blockchain safeguards patient bills against fraudulent activity and is faster. Blockchain will add a block from the first chain using the Markovian method once the bill is ready. The user will add a new block with its new hash and old hash to the chain in the following phase, which will mark the conclusion of the final block chain as provided.

Results and discussions

Initially, a Matlab simulator was used to verify the security of the proposed blockchain-based framework before giving the simulation tests. As previously stated, an analysis of the suggested framework’s internal operation has been done in this study. While ensuring the security of both the network and the application at the same time is a difficult problem, we have presented a trusted security architecture that guarantees both high levels of trust between nodes and the provision of legitimate network services to users. A 400 m × 400 m network area is established, and 250 nodes are installed, as shown in Table 1. Moreover, 802.11 is the MAC layer protocol in use.

Table 1 MatLab Simulation parameters.

The system’s behavior throughout the model’s implementation phase is measured or estimated using the performance evaluation procedure. Each constructed or generated reliable model is useful for predicting performance during the stages of planning, designing, or operation. Performance modeling is the process of simulating a system with a model and then manipulating the model to learn more about the behavior and performance of the real world. Correct and trustworthy measurements are the most crucial and essential technique for performance evaluation. It is frequently utilized to ensure that the proposed model does not deviate from the performance tolerances and conforms to the planned requirements.

To apply and validate the models and acquire parametric values for the results, measurements are used in analytical and simulation modeling. In our work, we use the blockchain-based queuing model with the Markov Chain. The arrival procedure adheres to the Poisson distribution. An exponential distribution is used to describe the service time. Throughput, delay, and channel utilization are the three components of data transmission that are modeled here. Additionally, we determined the system’s average waiting time and average idle time.

Performance measures

Several performance measures are taken to illustrate the effectiveness of the aforesaid blockchain-based queueing healthcare system using Markov process. It is listed as follows:-

Arrival-rate (λ)

What controls how "users/customers" enter a queue is their "arrival rate." Customers might arrive at various times in both groups and alone.

Service-rate (µ)

The Service Rate determines the resources required to begin the service as well as how long it will take to complete. The quantity of resources available and whether servers are set up in parallel or in series are also taken into account when determining the service rate.

Mean-waiting-time

The waiting time is the length of time customers must wait in line before obtaining services (W).

Mean idle time

In queuing systems, idle time occurs whenever a server is not providing clients with a service. A server that is in this status is known as a free server. A free server is typically thought to be ready and prepared to begin providing service anytime a demand arrives.

Single server queue

Table 2 depicts the several Cases and parameters to be used for Single-Server-Queue Performance Evaluation.

Table 2 Single server queue performance evaluation.

Case 1: Arrival rate (λ) = 0.9 Service rate (μ) = 0.6

See Fig. 12

Fig. 12

Arrival distribution, service distribution, mean waiting time and mean idle time for case 1.

Case 2: Arrival rate (λ) = 0.9 Service rate (μ) = 0.4

See Fig. 13

Fig. 13

Arrival distribution, service distribution, mean waiting time and mean idle time for case 2.

Case 3: Arrival rate (λ) = 0.7 Service rate (μ) = 0.6

See Fig. 14

Fig. 14

Arrival distribution, service distribution, mean waiting time and mean idle time for case 3.

Case 4: Arrival rate (λ) = 0.5 Service rate (μ) = 0.6

See Fig. 15

Fig. 15

Arrival distribution, service distribution, mean waiting time and mean idle time for case 4.

Case 5: Arrival rate (λ) = 0.1 Service rate (μ) = 0.6

See Fig. 16

Fig. 16

Arrival distribution, service distribution, mean waiting time and mean idle time for case 5.

Figures 12, 13, 14, 15, 16 shows the various parameters used for Single-Server-Queue performance evaluation. The different cases ranging from 1 to 5 were taken which tests the single server queue on different arrival rates and service rates, thereby calculating their Mean Waiting Time and Mean Idle Time.

Since λ > μ, the server in Fig. 12 has a high workload, resulting in long mean waiting times (310 units) and little idle time (0.0025 units). This situation shows a strained blockchain node processing a large number of transaction requests, which could lead to congestion and transaction delays.

Figure 13 shows that the system becomes overloaded when the service rate is further decreased. Idle time is almost negligible (0.005 units), and the mean waiting time peaks at 650 units. Processing issues may result from this crucial blockchain node being overloaded with transaction intakes.

Figure 14 shows how the workload is balanced when the arrival rate gets closer to the service rate. The average waiting time decreases to 110 units, while idle time marginally rises to 0.008 units. This is an example of an ideal blockchain node that efficiently handles modest transaction loads.

In Fig. 15, waiting time decreases considerably (by 11 units) and idle time rises to 0.33 units when the service rate exceeds the arrival rate. This situation demonstrates a blockchain node that is moderately loaded and has enough capacity to process incoming transactions.

Figure 16 illustrates how a low arrival rate leads to significant idle time (9 units) and very little waiting time (0.28 units). This situation reflects an underutilized blockchain node that is frequently dormant and awaiting transaction information.

Case 1: Service Rate (μ) = 0.6, Arrival Rate (λ) = 0.9

A single-server queue with a higher arrival rate than service rate is examined in Fig. 12. Given that the server is slower than the incoming rate, there may be longer wait times. The server will operate almost continuously with few idle periods as a result of the increasing load.

Case 2: Service Rate (μ) = 0.4, Arrival Rate (λ) = 0.9

Figure 13 illustrates how the server becomes overloaded with inbound requests due to the reduced service rate. The mean waiting time will rise dramatically as the server tries to keep up, with an even worse service rate than in Case 1. Idle time is almost nonexistent because the server is always being used by queries. Cases 1 and 2 illustrate how high arrival rates that exceed service rates result in longer wait times and shorter idle periods, imitating the situations where transaction backlogs arise as seen in Figs. 12 and 13.

Case 3: Arrival Rate (λ) = 0.7, Service Rate (μ) = 0.6

As seen in Fig. 14, the arrival rate is now approaching the service rate, which eases the server’s workload. As a result of the system’s improved ability to balance incoming workloads and processing capacity, waiting times are shorter than in Case 1. Anticipate a little bit extra idle time as there may not always be a request waiting on the server. Because Case 3 shows arrival rates close to service rates, performance is balanced and appropriate for the average blockchain transaction loads in Fig. 14.

Case 4: Arrival Rate (λ) = 0.5, Service Rate (μ) = 0.6

The server will spend more time idle as Fig. 15 illustrates that the service rate is higher than the arrival rate. Because fewer requests are received and duties are completed swiftly, waiting periods are reduced. Because the server is frequently waiting for requests, idle time grows.

Case 5: Arrival Rate (λ) = 0.1, Service Rate (μ) = 0.6

Figure 16 illustrates how a system where the server is primarily idle is created by a very low arrival rate and a greater service rate. There is very little waiting time because arrivals are rare. There will be long stretches of inactivity on the server. Figures 15, 16, and Case 4,5 illustrate how underutilized nodes in the blockchain network are indicated by reduced arrival rates relative to service rates, high idle times, and little delays.

Multi-server queue

Table 3 depicts the parameters to be used for Multi-Server-Queue Performance Evaluation.

Table 3 Multi server queue performance evaluation.

Figure 17 shows the various parameters used for Multi-Server-Queue performance evaluation. Multi-Server Queue was evaluated on different service rates, thereby calculating their Mean Waiting Time and Mean Idle Time.

Fig. 17

Arrival distribution, service rate, mean waiting time and mean idle time for four servers.

This Fig. 17 evaluates the performance of a multi-server queue under different service rates. Arrival Rate (λ) = 0.9 for all servers, with service rates varying from μ1 = 0.9 to μ4 = 0.4. The waiting time increases as the service rate of the servers decreases, with the slowest server having the highest waiting time. Idle times vary inversely with the service rate, where faster servers are less idle, and slower ones have more idle periods. When servers are set up properly, multi-server configurations can improve speed in a blockchain network by distributing workload. This is seen in Fig. 17.

Parameters used for performance evaluation

Here are a few fundamental performance metrics for the proposed model in comparison to the existing approaches. The proposed model undergoes evaluation by considering several performance criteria in contrast to the existing methods. The experimental assessment of both the proposed and existing approaches has been carried out effectively, yielding numerous outcomes across various parameters.

Delay

Network delays include sending delays, transmission delays, processing delays, and queue delays.

$$\left[ {{\text{Delay }} = T{\text{send }} + T{\text{txn}} + T{\text{processing }} + T{\text{queue}}} \right]$$

(25)

where Tprocessing denotes the processing delay and Tsend the `block-sending-delay`. The transmission delay Ttxn is the time it takes a block to reach the next-node; Tqueue is the data flow’s `queuing-waiting-delay`.

In Fig. 18, the focus is on comparing the queuing and processing delays between two models in the context of a Blockchain Queuing System Using Markov Chain for Smart Healthcare. The transmission and propagation delays are considered constant across both models. The primary difference arises in how the data is queued and processed within the two frameworks: The existing blockchain-based electronic healthcare paradigm shows better performance (lower delay) when the system’s runtime is less than one minute⁴⁶. The proposed blockchain queuing model with Markov Chain excels as runtime and throughput increase due to the integration of Markov Chain theory.

Fig. 18

Comparison of delay through MM1 and MMk queuing model.

The Markov Chain improves the queuing mechanism by optimizing the data flow within the blockchain network. This enhancement leads to reduced queuing delay compared to the existing system. As the processing capacity of the system increases with runtime and throughput, the proposed model processes data more efficiently than the traditional model. The proposed model ensures that delays are minimized over time. The blockchain system achieves higher throughput and faster data processing, which is crucial for real-time healthcare applications where timely data transmission and processing are critical. The graph likely demonstrates that the proposed blockchain queuing system with Markov Chain outperforms the existing system in terms of delay reduction, particularly in scenarios with higher operating times and data throughput. This performance gain makes it highly suitable for smart healthcare systems that require efficient and rapid data handling.

Throughput

Throughput measures how well a system can handle problems, requests, and transactions in a certain amount of time. It also serves as a key indicator for concurrency in the system. To describe it in this context, we use TPS (transactions per second).

The following is the formula:

$${\text{T}}_{{{\text{sec}}\Delta {\text{T}}}} = \frac{{{\text{T}}_{{{\text{Sec}}\;\Delta {\text{T}}}} }}{{\text{T}}}$$

(26)

T is the amount of time between when the transaction was issued and when the block was confirmed, “TSum” (ΔT) is the total number of transactions that were included in the block. The FCFS queuing paradigm operates under the principle of "come first, be served first," hence managing data flow based on priority is not required. Markov theory is used in the proposed queuing model, which over time increases queuing efficiency and reduces data flow wait times⁴⁷. As a result, the model’s throughput can be increased.

In Fig. 19, throughput (measured in transactions per second, TPS) is analyzed for a Blockchain Queuing System Using Markov Chain in the context of smart healthcare. The comparison highlights the efficiency of the proposed model under varying loads. The proposed Markov Chain-based queuing model demonstrates higher throughput compared to the existing blockchain system. As transaction loads increase, the efficiency of the proposed system improves, showcasing its ability to process more transactions per second without significant delays.

Fig. 19

Comparison of throughput through MM1 and MMk queuing model.

The MMk queuing model is integral to the proposed system. It distributes the workload across multiple servers within a multi-node blockchain network. This distribution reduces bottlenecks, ensuring that higher transaction volumes are handled efficiently. The proposed system’s architecture, powered by Markov Chain theory and the MMk model, supports scalability by effectively managing increased transaction loads. The multi-node blockchain network leverages parallel processing, allowing the system to maintain a high throughput even during peak demands, which is critical for real-time smart healthcare applications.

The Markov Chain model optimizes the queuing and processing mechanisms, ensuring transactions are completed quickly and efficiently. Compared to the existing model, the proposed system demonstrates a superior ability to scale and adapt, making it suitable for handling the complex and high-volume data requirements of smart healthcare systems.

The graph likely illustrates that the proposed Markov Chain-based blockchain system achieves significantly higher throughput than the traditional model, particularly under increasing transaction loads. This improvement demonstrates the system’s potential to enhance the efficiency of smart healthcare applications by supporting real-time, high-volume transaction processing in a scalable and reliable manner.

Channel utilization

When a channel is sending data, channel utilization is the ratio between time T_job to the total time T_all, i.e.

$$\eta {\text{channel }} = \frac{{T{\text{job}}}}{{T_{all} }}$$

(27)

In Fig. 20 channel utilization is analyzed, focusing on the efficiency of resource use in a Blockchain Queuing System Using Markov Chain for smart healthcare applications. The proposed blockchain queuing model with Markov Chain achieves a higher channel utilization rate (over 80%) compared to the existing blockchain model, which has a channel utilization of only 55%. This significant improvement highlights the ability of the proposed system to utilize available bandwidth and resources more effectively⁴⁷. The MMk model optimizes the distribution of tasks among multiple servers, reducing idle time and improving resource allocation.

Fig. 20

Comparison of channel utilization through MM1 and MMk queuing model.

By minimizing inefficiencies, the proposed model ensures that the blockchain nodes operate closer to their full capacity, leading to higher throughput and reduced data wait times. Higher channel utilization reflects better system performance, meaning more data can be processed in less time. Improved resource utilization directly reduces the delays in data processing and queuing. The system satisfies the demanding performance requirements of smart healthcare applications, where timely data processing is critical.

Higher channel utilization ensures that critical healthcare data, such as patient records and real-time health monitoring data, is processed with minimal delays. The proposed model demonstrates its scalability and reliability in handling the complex and high-volume transactions typical of smart healthcare systems. Figure 20 illustrates how the proposed blockchain queuing model with Markov Chain significantly improves channel utilization compared to the existing model. By leveraging the MMk queuing system and optimizing resource allocation, the proposed model achieves over 80% channel utilization, reflecting lower idle capacity, higher node efficiency, and overall better performance for smart healthcare blockchain applications.

Evaluating scalability across varying load conditions and network sizes

We have used a simulation technique to assess the scalability of the proposed architecture, which includes developing various scenarios with differing number of transactions (i.e., requests for patient data) and growing the network to include additional clinics, hospitals, and patients. Measured metrics include load balancing across nodes, throughput, transaction latency and success rate.

$${\text{Latency}} = {\text{Transmission}}\;{\text{Time }} + {\text{ Propagation}}\;{\text{Time }} + {\text{ Processing}}\;{\text{Time }} + {\text{ Queuing}}\;{\text{Delay}}$$

(28)

The resulting graph illustrates how three important performance metrics—latency, throughput, and success rate—are affected by network growth. Every statistic is examined as the overall number of nodes (patients, clinics, and hospitals) rises, offering information about the system’s scalability and effectiveness.

Figure 21 shows that latency increases as the number of nodes in the network increases because more transactions are created as the network grows, lengthening queues and lengthening waiting periods. Higher workloads cause the processing time at each node to increase and the communication overhead across dispersed nodes (patients, clinics, and hospitals) to expand.

Fig. 21

Scalability comparison of performance metrics—latency, throughput, and success rate across varying load conditions.

As the number of nodes increases, throughput slightly declines. Resource contention results from the system having to manage a greater number of transactions and coordinate across dispersed components when there are more nodes.

As the network expands, the transaction success rate somewhat drops. Failures may result from overloaded nodes’ inability to complete certain transactions within reasonable time frames.

To overcome this problem we have used load balancing in scalability of proposed model using H_FAC (Hybrid Firefly and Cuckoo Search Technique)⁴⁸.

The Fig. 21 compares the performance metrics—latency, throughput, and success rate—as the network expands with and without load balancing. In a healthcare network, these metrics show how a distributed system manages growing numbers of nodes (patients, clinics, and hospitals). Latency rises with the number of nodes because more transactions lead the system to become more congested. Overloading each node results in delay in processing and response times. The implementation of load balancing results in an equal distribution of the load among the nodes. This lowers latency by reducing congestion. Because resources are employed more effectively and response times are faster in the load-balanced scenario, the latency is continuously decreased.

As the network grows, the latency with load balancing improves by 20%, demonstrating how well load distribution works to cut down on delays. Distributing queries among several nodes lowers latency and avoids bottleneck-induced delays.

The throughput of the network is excellent at first, but it steadily drops as additional nodes are added. This is because unequal load distribution reduces system efficiency, giving certain nodes bottlenecks and underutilizing others. Even when there are more nodes in the system, load balancing allows it to process more transactions per second. This is so that no node is overloaded and the system as a whole can process more transactions. This is made possible by the traffic being dispersed evenly.

Implementing load balancing improves system efficiency by increasing throughput by 10%, enabling the system to process more transactions per second. The system can manage more transactions by effectively utilizing all of its resources, which results in an increase in throughput.

Because more nodes and traffic result in more failures (such as timeouts or overloaded servers), the success rate decreases as the system grows. Dropped or unsuccessful transactions may result from inability of node to manage the traffic. By distributing the load uniformly, load balancing reduces overloads and failures. As a result, a greater proportion of transactions are successfully completed as the system grows, increasing the success rate by 2%.

As the network expands, load balancing lowers the chance of unsuccessful transactions by increasing the success rate. As the load is better managed, the chance of transaction failures decreases and the success rate increases.

The graph in Fig. 21 illustrate how congestion and overloads can cause the system’s performance to deteriorate as the number of nodes (patients, clinics, and hospitals) increases. Nonetheless, load balancing enhances every important metric.

Limitations of current research

One of the key limitations of the proposed framework is its scalability. Although the design aims to establish a high level of trust among nodes, the challenges associated with scaling block chain networks cannot be overlooked. The study did not thoroughly investigate how the framework performs under conditions of increased demand or within larger network configurations. Additionally, the performance evaluation did not take into account temporal dynamics—specifically, the fluctuations in network conditions that may occur over time. Such variations can be considered highlighting the necessity for a more comprehensive analysis that considers these evolving factors.

Conclusion and future work

In the pursuit of delivering timely and efficient healthcare services, healthcare professionals engage in the continuous collection, documentation, and assessment of extensive patient data. To streamline decision-making processes, our research adopts the blockchain queue model. In this research, we employ a Markov chain to establish a queueing theory specifically tailored to blockchain systems. We thoroughly evaluate various performance indicators within the healthcare system, supporting the assertion that our model has the potential to facilitate the creation of an effective smart healthcare system. Within the context of the "multi-service" and "multi-channel model" integrated with blockchain, queuing theory plays a pivotal role. Notably, we focus on metrics such as the average waiting time and average idle time. In our performance assessment, we employ metrics including throughput, delay, and channel utilization. Our research consistently demonstrates superior performance across all three of these pivotal metrics when compared to existing approaches. Consequently, our model enhances the efficiency of healthcare systems incorporating blockchain applications. One of the major challenges in this research was analyzing the multiple channel model in blockchain systems where transactions are processed during the block-generation and blockchain-building operations. In the future, this problem can be solved and system efficiency can be increased by implementing the priority service discipline. Even though third parties are not involved in blockchain technology and it is extremely safe, numerous attacks like the Sybil attack have grown to be a serious issue. Private blockchains can be utilized in the healthcare industry in the future so that every user may be authenticated by the network administrator using distinct IDs and no security risks arise.