Image guided construction of a common coordinate framework for spatial transcriptome data

Lais, Peter; Mishra, Shawn; Xiong, Kun; Shi, Huanan; Atwal, Gurinder Singh; Bai, Yu

doi:10.1038/s41598-025-01862-x

Download PDF

Article
Open access
Published: 24 May 2025

Image guided construction of a common coordinate framework for spatial transcriptome data

Peter Lais²,
Shawn Mishra¹,
Kun Xiong¹,
Huanan Shi¹,
Gurinder Singh Atwal³ &
…
Yu Bai¹

Scientific Reports volume 15, Article number: 18074 (2025) Cite this article

3181 Accesses
3 Citations
Metrics details

Subjects

Abstract

Spatial transcriptomics is a powerful technology for high-resolution mapping of gene expression in tissue samples, enabling a molecular level understanding of tissue architecture. The acquisition entails dissecting and profiling micron-thick tissue slices, with multiple slices often needed for a comprehensive study. However, the lack of a common coordinate framework (CCF) among slices, due to slicing and displacement variations, can hinder data analysis, making data comparison and integration challenging, and potentially compromising analysis accuracy. Here we present a deep learning algorithm STaCker that unifies the coordinates of transcriptomic slices via an image registration process. STaCker derives a composite image representation by integrating tissue image and gene expression that are transformed to be resilient to noise and batch effects. STaCker overcomes the training data scarcity by training exclusively on diverse synthetic data. Its performance on various benchmarking datasets shows a significant increase in spatial concordance in aligned slices, surpassing existing methods. STaCker also successfully harmonizes multiple real spatial transcriptome datasets acquired from various platforms. These results indicate that STaCker is a valuable computational tool for constructing a CCF with spatial transcriptome data.

STAIG: Spatial transcriptomics analysis via image-aided graph contrastive learning for domain exploration and alignment-free integration

Article Open access 27 January 2025

Systematic comparison of sequencing-based spatial transcriptomic methods

Article Open access 04 July 2024

Mapping the topography of spatial gene expression with interpretable deep learning

Article 23 January 2025

Introduction

Spatial transcriptomics is a cutting-edge OMICS technology that enables characterizing transcriptome-wide gene expressions at spatially resolved locations in a tissue Section^1,2. The data acquisition involves dissecting a thin slice (5–20 µm) from a tissue block for subsequent molecular analysis. Multiple slices are often profiled to ensure data reliability. However, each slice is analyzed separately due to variations in cutting and displacement or by sample attrition. Integrating multiple slices into a common coordinate framework (CCF) is critical to enhance resolution, detect spatial patterns, and build a three-dimensional perspective of the tissue microenvironment from two-dimensional profiles.

Despite the importance of the CCF, existing methods are limited. Most require manual interventions or user-defined landmarks^3,4,5,6, leading to potential user biases and low throughput. Landmark-free automated approaches such as PASTE and GPSA^7,8 align slices mainly upon transcriptome profile similarities. However, gene expression at a given location (aka, ‘spot’) is often obtained from a single or a few cells with low transcript detection rates (~ 5%), yielding high noise in the expression readout. In addition, these transcriptome profiles can also vary due to non-spatial confounding factors such as cell state changes and batch variations, making it challenging to accurately determine spatial relationships across multiple slices using gene expression alone.

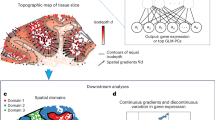
In this work, we approached this challenge by combining gene expression with the microscopy data of the tissue slice acquired simultaneously with the transcriptome in many platforms⁹. Our method, STaCker (Spatial Transcriptomics Common coordinate builder), formulates the CCF construction as an image registration task. In image registration (more commonly known as imaging alignment), each spatial transcriptome slice is treated as an image, and the registration process aligns correspondences between these images, thereby aligning the spatial transcriptome slices. STaCker offers an automated, end-to-end solution that eliminates the need for predefined landmarks. Unlike previous approaches that relied on local image patches to assess spatial proximity⁸, our approach utilizes the whole image to extract both local and long-range information for alignment. Additionally, instead of solely relying on tissue images¹⁰, we converted transcriptome data into a contour map and overlaid it onto the tissue image. The contour map emphasizes the spatial arrangement of clusters of tissue spots or cells. It enables us to concentrate on aligning regions or neighborhoods with similar cell compositions, rather than achieving an exact cell-level alignment. This precise alignment is not meaningful, as the cells captured in each slice are unlikely to be the same.

We chose elastic models to register the derived composite image representations. Unlike rigid methods, elastic registration allows for local deformations such as stretches and contractions to better match the shape and structure of the objects in the images^11,12,13. This contrasts with rigid registration methods, which only allow for translations and rotations¹⁴. Elastic registration is often used in medical imaging to align images acquired at different time points or from different modalities^12,15, and it has also been applied to the alignment of microscopic images^16,17. Recently, deep learning-based elastic registration methods, using convolutional neural networks (CNNs) to align images based on latent similarity embeddings, have gained popularity for their robustness and accuracy^18,19. We adopted the CNN framework in the development of STaCker.

Many deep learning algorithms learn how to properly perform tasks using acquired “training” data. Despite some success, this approach often suffers from a lack of sufficient training data; moreover, test cases containing features that are not present within the training data often cause model performance to suffer. A unique feature of STaCker is its exclusive use of synthetic data for training. Training on synthetic data is especially beneficial for spatial transcriptome slice alignment, because available datasets are limited due to the nascent nature of the field and the high cost. Deep neural networks trained with synthetic images have been reported to be as effective or even more robust in some cases^20,21. Synthetic data allows control over data variability like color, contrast or rotation, aiding training a robust network. It can be easily augmented to improve model generalization and reduce overfitting. More importantly, a model trained with synthetic data is not platform-specific, bolstering its overall applicability and generalization.

In the following sections, we present STaCker, a deep convolutional neural network-based model that integrates tissue imaging with gene expression data to learn feature representations and perform alignment. STaCker is an automated end-to-end approach without the need for predefined landmarks. The performance of STaCker is assessed using simulated datasets with known ground truth as well as multiple real spatial transcriptome datasets and is compared with that of multiple existing methods. STaCker effectively unified the spatial coordinates of deformed slices in various tissue types, surpassing existing methods. These outcomes demonstrate that STaCker is a valuable computational tool for establishing a CCF with spatial transcriptome data.

Results

Overview of the workflow of STaCker

STaCker is a deep learning algorithm designed to register a “moving” spatial transcriptome slice to a “reference” counterpart. In this work, we use the terms “reference”, “moving” and “moved” to denote the fixed slice, the slice that needs to be aligned, and the slice after alignment, respectively. The workflow involves several steps: processing tissue images, overlaying transcriptome information on each image, applying an image registration module to generate a deformation field, and using this field to align the moving spatial slice to the reference (Fig. 1, see also Methods).

The image data associated with each spatial transcriptome slice underwent a series of pre-processing steps before input into the alignment module (Fig. 1a, top panel, see Methods for more details). These steps include color correction, non-tissue background masking, cropping, and resizing. Gene expression data from each slice was processed to create an image-like input (Fig. 1a, bottom panel; Methods). Transcriptome profiles were normalized, transformed, and integrated via a mutual nearest neighbor algorithm²² to minimize batch biases. Dimension reduction and clustering were used to identify groups of tissue spots or cells with similar gene expressions. The location of these clusters signified the spatial variation in molecular contents, providing valuable information about the tissue structure. A contour map derived from cluster boundaries was overlaid on the processed tissue image, which was input to the image registration module.

As shown in Fig. 1b and detailed in Methods, the image registration module comprised an ingestion module, an encoder–decoder block, and a field composition module. The ingestion module employed a Siamese structure to receive the fixed reference image and the moving image. The encoder–decoder block implemented a U-Net backbone with skip connections at each level. The final layer of the decoder is connected to the field composition module to produce the deformation field for alignment. While we primarily used the U-Net backbone in this study, it is essential to note that STaCker is not limited to this architecture. Other network models, such as visual transformers, capable of mapping features from imaging data to a deformation field, can also be utilized.

The deep neural network model was trained using synthetic data (Fig. 2 and Methods). Each training instance consisted of four images: a colored reference image ($\widehat{r}$), a segmentation mask image (label map) associated with the reference image (${l}_{r}$), a colored moving image ($\widehat{m}$), and a label map associated with the moving image (${l}_{m}$). The label maps were created first, using Simplex noise distributions with customizable frequencies and amplitudes (Methods). Simplex noise is widely applied in generating natural appearing textures, including organ surfaces^23,24. It has also proven effective in synthesizing segmented microscopic medical images to augment training data for deep learning²⁵. Afterward, the colored reference and moving images were produced using the respective label maps as templates (Methods).

The network model was trained using a loss function based on the Dice score between reference and moved label maps, along with a regularization term to discourage abrupt deformations (Eqs. (1) and (2), Methods). The Dice score assesses the agreement of class labels instead of pixel-wise intensities that reflect fine-grained details like individual cell positions present in tissue. It emphasizes aligning cell regions rather than achieving precise cell-level alignment.

Once trained, STaCker can be utilized to align spatial transcriptome data. It takes as inputs the transcriptome-integrated tissue images from both the reference and moving spatial transcriptome slices. The model produces a deformation field that defines the adjustments for each spot in the moving slice to align with the reference slice, along with the aligned coordinates and image after applying these adjustments (see “Alignment of spatial slices section” in Methods for additional details).

Synthetic data training enables accurate image registration

We first assessed the performance of STaCker’s image registration module trained upon synthetic data, focusing exclusively on image registration tasks without involving transcriptome data, as a quality control measure. Two tasks were considered. First, we generated a new multi-color image not included in the training set and warped it either by adding Simplex noises of varying amplitudes (Fig. 3a) or by random manual deformations. The manual warping was performed by the Warp Transform tool in GIMP²⁶ with a brush size of 25% of the largest dimension of the image to drag around arbitrary regions in random directions. The manual distortions represented independent warps that the module did not encounter during training. The distortion levels were quantified using normalized cross correlation (NCC, Eq. (3)), a metric that measures the similarity between the warped and the unwarped images. For comparison, we included the results from the affine alignment, as well as the nonlinear transformations using two well-established image registration tools: ANTs²⁷ and WSIreg^28,29. ANTs, together with the Elastix algorithm that underlies WSIreg, are esteemed for their high quality and are frequently used as benchmarks for assessing other methods in the field^30,31,32,33. After the image registration, STaCker significantly improved the NCC scores (two-sided student t-test p-values < 0.001, Fig. 3a) in all warped cases, consistently outperforming ANTs, WSIreg and the affine alignment by a large margin.

In the second task, we considered an actual tissue H&E staining image. A coronal slice of mouse hindbrain obtained from Allen Brain Institute³⁴ was used as the reference image. We applied Simplex noise warping and manual warping to create a set of moving images (Fig. 3b). Like the results in Fig. 3a, STaCker outcompeted ANTs and WSIreg in all test cases. Note that ANTs sometimes introduced wavy edges around the pyramus and medulla regions. In contrast, these apparent artifacts were absent in STaCker. The NCC score presented for STaCker and ANTs is an average of ten executions. Consistent results were observed with ten times more runs (Supplementary Fig. 1), confirming the stability of their registration and consequently the validity of the conclusion. The result demonstrates that the image module of STaCker can effectively register real tissue images, despite training solely on synthetic images.

When applied to spatial transcriptome data, no modifications are required in the image module. The data are transformed into images (Fig. 1a) and can be directly input to the image module. The resulting deformation field is then used to update the spot or cell coordinates on the slices. The detailed procedure for applying STaCker to spatial transcriptome data is outlined in the “Alignment of spatial slices” section within the Methods.

STaCker accurately aligns digitally warped spatial transcriptome slices

Upon the validation of the image registration module, we proceeded to evaluate STaCker’s ability to align spatial transcriptome slices. We chose a sagittal dissection of mouse brain profiled using Visium^35,36 and digitally warped it to various degrees (Fig. 4). The level of distortion is quantified using the NCC and mean square error (MSE, Eq. (4)) scores associated with the applied Simplex noise warping. The undistorted slice and each distorted slice formed a pair of reference and moving inputs for the model, respectively. The advantage of digital warping is that the ground truth is known. The spatial transcriptome of the sagittal dissection was from 3248 in-tissue spots that passed quality control.

Figure 4 summarizes the alignment of the digitally warped moving slices to the reference slice performed by STaCker, STUtility, PASTE, and GPSA^7,8,10,14, all can provide landmark-free alignment. All programs were run with author-published parameters for Visium data (see Execution of programs section in Methods). As the warping distortions increased, the MSEs between the pre-alignment moving slices and the reference slices also increased (0.0089, 0.0308 and 0.0690, Fig. 4). In each case, STaCker effectively reduced the MSE by ~ 2.7–25 fold (0.00036, 0.0064 and 0.0259, respectively), accompanying its good matching between the post-alignment (red crosses) and the reference coordinates (gray dots). The residual discordance in the post-alignment of STaCker increased slightly with larger initial distortions. This phenomenon is expected as STaCker employs a regularized loss function. Nevertheless, even in the most discordant case (Fig. 4, bottom row), STaCker placed the majority (81% on average) of the spots associated with the highest MSEs (top 10%) nearest to a spot in the reference slice that has the matching class label, indicating these spots were correctly located in the expected regions for their class labels (Supplementary Fig. 2). Thus, although STaCker might not perfectly align these most dislocated spots, it managed to assign them biologically correct locations.

STUtility, PASTE and GPSA were executed using the published parameter settings for Visium slices. They all performed less well than STaCker with substantially higher post-alignment MSEs in all cases (Fig. 4b). As STUtility employs merely rigid transformations, it may not be able to correct non-linear deformations, which could explain its suboptimal performance. Including STUtility results here offers a reference point for linear rigid alignment. Our discussion will concentrate on the alignment outcomes of programs that manage non-linear deformations. In this test, PASTE failed to improve the MSE values compared to the pre-alignment, except for a mild ~ 11% reduction in the case of the low-degree distortion (post-alignment MSE = 0.00793). GPSA yielded the worst MSEs among the tested programs. Additionally, the aligned tissue spots by GPAS appear to aggregate upon convergence (see also Supplementary Fig. 3a and c). This result persisted when running GPSA with different choices of parameters (Supplementary Fig. 3c). We speculated that GPSA may suffer a low sensitivity to transcriptomically differentiate the neighbor spots given the limited number of genes (10 by default) it handles. Increasing the number of genes to 100 did not resolve the aggregation (Supplementary Fig. 3b and c). Attempts of more genes led to a memory shortage issue that rendered GPSA computationally impractical and thus it was not pursued further.

We also tested another tool STalign that can perform non-linear alignment¹⁰. However, STalign’s default values of the parameters did not work well in our tests (Supplementary Fig. 4). There are no published parameter sets by authors that are applicable to align a pair of H&E images³⁷. Since STalign depends on user visual evaluation for parameter selection, it becomes challenging to demonstrate the absence of bias if we, as the individuals conducting the comparison, are also responsible for tuning the results. Consequently, results from the parameters we tuned are unsuitable for this benchmarking task. Thus, we excluded STalign from this and the following tests on aligning H&E images to each other. Although we cannot quantitatively assess STalign’s performance in aligning Visium datasets, it is important to highlight that the responsibility of tuning more than a dozen parameters falls on the user and relies primarily on visual judgments, which is a notable limitation of STalign. Navigating through the combinations of these parameters for alignment via visual inspection is tedious and leads to subjective outputs. Therefore, for ease of use and to achieve objective results, programs that do not require visual tuning or landmark selections during usage, such as STaCker, may be preferred.

To confirm that the above observations are not isolated instances, we conducted a benchmarking alignment in human lymph nodes³⁸ in a similar manner (Supplementary Fig. 5). The tissue texture in the human lymph nodes is noticeably different from the mouse brain (Fig. 4 and Supplementary Fig. 5, leftmost columns). STaCker and the other programs were applied to align each moving slice to the reference slice, following the same procedure as described earlier and in Methods. Compared to PASTE and GPSA, STaCker delivered the lowest MSEs (rightmost columns in Supplementary Fig. 5, 0.00025, 0.0014 and 0.016, respectively) and the highest consistency between the post-alignment coordinates and the reference coordinates (Supplementary Fig. 5, grey dots and red crosses). The result suggests that STaCker retains its leading performance in an independent dataset.

STaCker outperforms in the de novo alignment of slices

STaCker allows users to align multiple slices from repeated experiments by defining one of the slices as the reference for aligning the remaining, referred to as the “fixed-template” mode alignment. Alternatively, STaCker offers a “de novo” option where slices are aligned to each other without a single fixed reference. To evaluate STaCker’s performance in de novo alignment, we used a section from the previously discussed mouse sagittal posterior brain slice and digitally warped it four times independently to create a set of slices for alignment (Fig. 5). The section contains 115 tissue spots. STaCker was run in the “de novo” mode (see also Methods), PASTE in its “center-alignment” mode, and the four slices were passed to GPSA as four “views”. STUtility does not offer de novo alignment. To overcome this inconvenience, we iterated through all the slices, using one as a reference to align the rest. The average of any quantitative measure over these iterations was then used for downstream evaluation.

Before alignment, the mean MSE over all pairs of slices is 0.103 (Fig. 5, the panel of unaligned coordinates). After de novo alignment, STaCker reduced the mean pairwise MSE to 0.041, followed by PASTE (0.098) and STUtility (0.119), then GPSA (0.601). The four sets of post-alignment coordinates of the spots by STaCker were most mutually consistent as well (Fig. 5, the panel of STaCker aligned coordinates). Note that in STaCker’s de novo mode, none of the slices retained their original spot coordinates. Instead, they converged towards each other as expected in de novo alignment.

The four slices aligned by other programs remained considerably discordant. The spots aligned by GPSA aggregated and largely dislocated from their original positions (Fig. 5, the panel of GPSA aligned coordinates). On average, only 0.4% of the spots in a slice retained the exact same neighboring spots (defined as those within 150 microns of a given spot) after the alignment, indicating that GPSA did not maintain the integrity of the spatial relationships among the spots. In contrast, STaCker preserved the spatial neighborhood well (over 97% of spots retained their neighbors). In general, the results of the programs echo their performance in aligning a single moving slice to a reference, which is expected as the same underlying algorithms are used for either the pairwise or the de novo alignment in each program.

STaCker harmonizes real-world spatial transcriptomes from serial dissections and biological replicates

STaCker’s robust performance in the previous benchmarking encouraged us to apply it to spatial transcriptome slices with real deformations. We considered two common scenarios: serial tissue dissections from the same biological donor (Fig. 6) and tissue slices acquired from independent biological replicates (Fig. 7). Figure 6 displays four serial dissections of the dorsolateral prefrontal cortex (DLPFC) of an adult human brain, profiled using Visium³⁹. These slices show a mild but noticeable discoordination (Fig. 6a). For instance, the top portion of slice 1 at site 2 is severed, and the shapes of slices at site 1 and site 2 differ. STaCker, PASTE and GSPA were executed upon convergence using their respective de novo alignment modes with default or recommended parameters for Visium data. For programs that lack a de novo option (e.g. STUtility), we performed a series of alignments using each slice as the reference, as described previously (Fig. 5). Each alignment was evaluated individually, and the average evaluation metrics were used to assess their performance.

The dorsolateral prefrontal cortex is known to have six well-established layers of grey matter (L1–L6) surrounding the white matter. The tissue spots were annotated with these layers based on their transcriptome profiles (Fig. 6b)⁴⁰. Our framework assumes that similar biological regions should exhibit similar molecular content. Therefore, aligning the slices with respect to these tissue domains is desirable. After alignment, the spatial concordance across the slices was evaluated based on these domains. In Fig. 6b, the profiled spots (circles) in each of the four slices are colored according to their respective tissue domains. Prior to alignment, most cortex layers were intertwined with neighboring regions, making it difficult to define each layer clearly (Fig. 6b, unaligned). After the alignment, STaCker produced a well-layered structure with minimal protrusion and overlapping between the domains. Notably, STaCker was the only program that partially restored the severed portion of slice 1 at site 2, correctly aligning it with the L1 layer from the other slices. In addition to visual evaluation, we utilized O’Neill’s entropy-based spatial coherence score (SCS, Eq. (5), (6))⁷ and the mean pairwise adjusted rand index (MPARI, Eq. (7))^41,42 to quantify the clarity of the cortex domains across the slices (Fig. 6c and d). STaCker substantially improved both the SCS and the MPARI (SCS = 750.7, MPARI = 0.93) compared to the unaligned (SCS = 558.2, MPARI = 0.56). This was followed by PASTE (SCS = 610.6, MPARI = 0.75). Rigid transformations alone, employed by STUtility, did not improve either metric (SCS = 316.8, MPARI = 0.55). GPSA was excluded from these quantitative assessments due to severe unrealistic distortions in the aligned slices, which rendered the discussion of spatial relationships among the tissue spots meaningless.

One of the primary objectives of coordinate consolidation is to improve the detection of spatial gene patterns, thereby deepening our understanding of the molecular environment and tissue changes. For benchmarking purposes, we examined a set of genes enriched in each of the cortex layers, such as FABP7, AQP4 (L1), HPCAL1, ENC1 (L2), CARTPT (L3), RORB (L4), PCP4 (L5), and KRT17 (L6). These genes are expected to exhibit non-random spatial patterns, which can be compared between pre- and post-alignments and across different programs. For example, in L1 region, the expression of AQP4 (Fig. 6e) is broadly dispersed around the top portion of the unaligned slices but becomes concentrated and well-defined along the outer layer after STaCker alignment. Similar improvements are seen with PCP4 and KRT17 (Fig. 6e) and other genes (Supplementary Fig. 6). Compared to STaCker, other programs produced less distinct and more smeared patterns. To quantify the spatial prominence of these gene expression patterns, we calculated Moran’s I spatial autocorrelation scores⁴³ (Fig. 6f). STaCker shows the most improvements in the autocorrelation scores, followed by PASTE and STUtility. These results demonstrate a leading performance of STaCker regarding the enhancement of spatial gene pattern detection.

The second dataset comprised four biological replicates of the mouse olfactory bulb slices published earlier¹. Unlike serial dissections from the same tissue block, which often have similar shapes, orientations, and molecular contents, independently acquired spatial transcriptome slices from different subjects are prone to variations. In this dataset¹, we observed minor to large discrepancies in the slice orientation and shape, with occasional tears (Fig. 7a). Additionally, there were non-negligible batch effects in the transcriptome profiles (Supplementary Fig. 7a). The tissue spots from both slices were classified into three clusters based on their transcriptome profile (see Input transcriptome data pre-processing section in Methods). These clusters correspond to the granule cell (orange dots), mitral cell (cyan dots) and glomerular (red dots) layers of the mouse olfactory bulb, respectively (Fig. 7a and b). Due to the lack of a de novo option in STUtility, a series of alignments was executed using every slice as the reference, and the average performances were considered for the evaluation.

Upon visual inspection, the three layers are not depictable before the alignment. While all programs except GPSA enhanced the clarity of the tissue domains, STaCker’s output exhibited the least entanglement among the spots from different layers. Consistently, its SCS (Fig. 7c) and MPARI values (Fig. 7d) are the highest, indicating the alignment is most organized and consistent across the slices. STUtility did not fully correct the orientation of slice 1 via its rigid transformations, although it did improve the overall coherence over the slices. GPSA was excluded from further quantitative evaluations as it failed to create a useful alignment. It also had the lowest sample-wise batch mixing entropy post-alignment among all the programs tested, suggesting it is susceptible to sample-to-sample variation in the transcriptome data (Supplementary Fig. 7b). STaCker remains resilient to batch variations, as its alignment yielded a leading sample-to-sample mixing entropy. This is expected as STaCker did not directly rely on gene expressions of individual cells or spots but on their classifications, which were more robust to random noise. It also employed tissue images as an orthogonal modality to reduce the bias from transcriptome alone. We further examined the spatial autocorrelations of representative marker genes Spon1, Uchl1 and Nrxn3 associated with the glomerular, mitral cell and granule cell layers, respectively (Fig. 7e). After alignment, STaCker delivered the most elevations in Moran’s I scores (Fig. 7f), illustrating its capability to harmonize biological replicates at the molecular level.

It is important to note that real data applications lack ground truth. We designed our evaluation metrics (e.g. SCS, MPARI, Moran’s I correlation) for real-world data based on the assumption that similar biological regions should have similar molecular content, as defined by transcriptome data. Nonetheless, not all programs (e.g. STUtility) utilize transcriptome data from the spatial slices. They rely on different data modalities (e.g. image) and may be subjected to evaluation bias under our framework. Given the diverse data types utilized by different programs, it is inevitable to choose an evaluation with a certain bias. Since gene expression provides high-dimensional molecular level information, it is often more sensitive than tissue morphology in reflecting biological changes. Thus, these evaluations remain our choice.

STaCker achieves high quality alignments for in situ hybridization (ISH)-based spatial transcriptome

Another major spatial transcriptome platform is in situ hybridization (ISH)-based, such as MERFISH and Xenium^44,45. These platforms are data-intensive, often surveying hundreds of thousands of cells in one slice. The large number of cells presents a substantial computational challenge to programs (e.g. PASTE, GPSA) that align coordinates based on mutual similarity among individual cells¹⁰. However, ISH-based profiling acquires images of nucleus or cell body staining, such as DAPI (4′,6-diamidino-2-phenylindole) labeling, allowing for the convenient application of image-guided registration offered by STaCker. Importantly, there is no significant added computational overhead when applying the deformation field derived from image registration to hundreds of thousands of coordinates.

We applied STaCker and other alignment programs to three mouse brain slices profiled via MERFISH (Fig. 8a)⁴⁶. We included STalign in this test because STalign’s tutorial provided parameters for aligning two MERFISH slides. All programs were executed under their published parameter settings associated with the input data type (see Execution of programs section in Methods). A total of 253,676 cells were collected in this dataset. PASTE and GPSA were unable to execute efficiently to align the full collection of cells. Therefore, their alignments were quantified and evaluated using 10% randomly subsampled cells (Supplementary Fig. 10). For single-cell resolution data, we define a tissue domain as an area or a neighborhood of similar cell type compositions, also referred to as a niche. The cell types were first identified and then merged into niches using Seurat (Methods). Figure 8b and Supplementary Fig. 10a illustrate the three brain slices color-coded by niches before and after alignment. Visually, STaCker and STalign achieved more coherent tissue domains across the slices with and without subsampling, as evidenced by their leading SCS and MPARI scores (Fig. 8c and Supplementary Fig. 10b). The main distinction between STaCker and STalign lies in the alignments around the hippocampus region (CA1–CA3 and dentate gyrus), where STalign appears to result in less concordance across the slices (Fig. 8b and Supplementary Fig. 10a). GPSA produced aggregated coordinates, as observed in other test cases in this study.

Figure 8d displays examples of genes with varying spatial patterns, such as Htr1a (hippocampus CA1 region), Drd1 (caudoputamen), Efemp1 (pia mater) and Gpr101 (hypothalamus and amygdala) in slices aligned by STaCker and other programs, compared to unaligned slices. The spatial patterns of these genes are depicted most clearly following STaCker’s alignment, with clean and sharp boundaries of gene-enriched areas. For instance, the hippocampus CA1 domain is neatly highlighted by the expression of Htr1a, with no visible misalignment across the slices. Efemp1 expression concentrates in a delicate thin layer surrounding the brain (pia mater), as well as around ventricles and fiber tract, elucidating fine variations of molecular content that were undetectable before alignment.

For each gene, we further examined the spatial consistency of its expression across every pair of slices using a cosine similarity-based gene coherence score (Methods) and Moran’s I spatial correlation¹⁰. As stated earlier, our goal is not to align individual cells but rather the domains or neighborhoods containing a similar composition of cells, which is more biologically meaningful. Thus, the Gene Coherence Score and Moran’s I correlation were evaluated over pseudo-spots (Methods)¹⁰. To determine the size of the pseudo-spots, we analyzed gene expressions from pseudo-spots of various sizes (50 μm, 100 μm, 200 μm, and 500 μm, as shown in Supplementary Fig. 8). We found that larger pseudo-spots (100 μm or more) struggled to effectively depict differences among STaCker and other programs in registering fine spatial structures, such as the CA1 and pia mater regions highlighted by genes Htr1a and Efemp1, respectively. Therefore, we selected a pseudo-spot size of 50 μm × 50 μm. This size also aligns with the commonly achieved spatial resolution in the field, making it a sensible choice for conducting our benchmarking to ensure the results are relevant for users.

Figure 8e illustrates Moran’s I scores (left panel) and gene coherence scores (right panel) of the gene expression over all pairs of slices. STaCker and STalign show strong performance, achieving significantly higher scores compared to the rigid alignment method STUtility (two-sided student t-test p-value < = 5.4e-14). This finding applies to all genes displaying non-trivial spatial patterns (i.e. genes with a Moran’s I p-value < = 0.01) when compared to STUtility outcomes (Fig. 8f), and remains valid when using larger pseudo-spot sizes (Supplementary Fig. 9). In the comparison between STaCker and STalign, the Gene Coherence Scores for Htr1a and Efemp1 are notably higher with STaCker, consistent with visual assessments of their spatial patterns post-alignment (Fig. 8d). In STalign, Htr1a expression shows less overlap across slices (Fig. 8d, first row), reflecting previously noted registration challenges in the hippocampus area (Fig. 8b). STalign exhibits less consistency in Efemp1 expression along peripheral regions (Fig. 8d, third row). Among the genes with non-trivial spatial distribution, the majority show a significantly higher Moran’s I correlation or Gene Coherence Score with STaCker (Fig. 8g orange dots), while few or none favor STalign (Fig. 8g blue dots). The results suggest that while both methods are effective, the alignment achieved by STaCker is more spatially coherent. In terms of user experience, here STalign was executed using the parameters that the authors specifically tuned for the MERFISH dataset. Generally, STalign requires iterative user adjustments based on a visual assessment of the alignment, which can be time-consuming and prone to individual bias. Conversely, STaCker offers automated alignment without needing user adjustments based on visual impressions, providing better efficiency and objectivity.

In the subsampled data, STaCker also achieved greater enhancements in cross-slice spatial coherence of tissue domains and gene expressions compared to the other programs (Supplementary Fig. 10). Consistent with the observations in Fig. 8, STalign exhibited less coherence around the hippocampus (Supplementary Fig. 10a) and overall lower quantitative alignment assessments (Supplementary Fig. 10b–e). Note that ISH-based platforms typically profile only a few hundred genes, making it challenging to differentiate a cell from similar ones based solely on these gene expressions. In this test, both PASTE and GPSA alignments were less effective than STaCker, as evidenced by visual inspection of the domain clarity (Supplementary Fig. 10a) and quantitative measurements (Supplementary Fig. 10b–d). Varying the pseudo-spot size did not change this conclusion (Supplementary Fig. 11). These findings underscore the benefits of effectively utilizing the imaging modality, as exemplified by STaCker, in both sequencing- and ISH-based spatial profiling, which encompasses most spatial transcriptome applications. More importantly, employing image registration adapts effortlessly to high-resolution spatial transcriptome data (~ 10⁵ cells per slice), whereas methods like PASTE and GPSA face significant computational hurdles in these scenarios.

STaCker integrates well the spatial profiling data from different platforms

We have demonstrated STaCker’s successful application to both NGS-based and ISH-based data, allowing the integration of spatial transcriptomes across different platforms. For this task, we selected two independently published datasets of mouse brain hemispheres, profiled by Visium and Xenium, respectively^47,48. Both slices are in coronal orientation but show visible differences in size and shape, particularly in the hippocampal area, likely due to biological and dissection variabilities (Fig. 9a). This represents a realistic application scenario. Only STaCker, STUtility and STalign that are capable of cross-platform alignment were considered for this test. STaCker was executed in de novo mode to prevent bias towards either platform. STUtility and STalign that lack a de novo option were conducted using each slice as the reference, and the average performances from these executions were used for evaluation. All programs were run with author-published parameters for the input data type (see Execution of programs section in Methods).

Figure 9b presents an overlay of the coordinates from the Visium (red circles) and Xenium (blue crosses) slices, allowing for a qualitative assessment of the consistency in slice size and shape following integration. The Visium and Xenium coordinates from STaCker and STalign show a decent overlap. On the other hand, rigid corrections by STUtility made minimal adjustments to the unaligned coordinates.

As the spatial resolutions in the two slices differ by an order of magnitude (a few microns for Xenium and a few tens of microns for Visium), it becomes challenging to precisely define tissue domain boundaries consistently across both platforms, which complicates the comparison of their consistency between the slices using metrics such as SCS and MPARI. For quantitative evaluation, we therefore focused on gene expression coherence across the slices. After all, molecular level consistency underlies domain level coherence. To assess the spatial autocorrelation of a gene, cells in the Xenium data were merged into 55-micron × 55-micron pseudo-spots to align with the resolution of Visium. For the Gene Coherence Score, another type of pseudo-spots was created by aggregating cells within a radius of 22.5 microns (i.e. 55 microns in diameter) around the centroid of each Visium spot, ensuring that matching spatial locations were sampled when comparing the expression correlations between the Visium and Xenium slices. There were 344 genes overlapping between the two platforms. The spatial expression of several representative genes is shown in Fig. 9c, highlighting various subregions in the hemisphere. After STaCker’s alignment, well-mixed red (Visium) and blue (Xenium) spots were observed for each gene, suggesting high spatial concordance. STalign and STUtility resulted in less coherent alignments, as seen with genes like Aldh1a2 along the brain meninge, Fibcd1 in the hippocampus CA1 region, and Prox1 in the dentate gyrus. Consistently, the Moran’s I scores and the gene coherence scores were highest in STaCker for these genes (Fig. 9d). We extended the comparisons to include all genes with a non-random spatial pattern (genes with Moran’s I p-value < = 0.01). Figure 9e illustrates the distribution of Moran’s I scores and Gene Coherence Scores across all non-random genes. For both metrics, the mean distribution by STaCker is significantly higher than that of STUtility (two-sided Student’s t-test p-value ≤ 2e-3) and STalign (two-sided Student’s t-test p-value ≤ 6e-5). Moreover, more genes exhibit a significantly higher Moran’s I correlation or Gene Coherence Score when aligned with STaCker (Fig. 9f, orange dots), while few genes achieve higher scores with STalign (Fig. 9f, blue dots). These results suggest the leading capability of STaCker in integrating different platforms.

Discussion

Constructing a unified coordinate system across multiple spatial transcriptome slices is an important but unmet need for data comparison, integration, and interpretation. A common approach involves aligning tissue spots or cells based on the similarity of their gene expression profiles within a permitted range of translocation. Nevertheless, this process is complicated by the inherent noise in gene expression at the single-cell or near single-cell resolution, as well as biological or technical batch effects that can significantly alter expression.

STaCker addresses these challenges by approaching the construction of a common coordinate as an image registration problem. Unlike previous methods that relied on image patches associated with each spot to determine the spot-to-spot similarity and spatial proximity⁸, STaCker convolutes the image features across the entire slice, capturing more comprehensive contextual information and global features to aid alignment.

STaCker also transforms the transcriptome data into a contour map, which is then superimposed onto the tissue image. The contour map captures the spatial organization of spot or cell clusters, defined by dimensionally reduced gene expressions, making it more resilient to data noise and batch effects. The molecular level transcriptomic readout offers supplementary information to the tissue image, especially in areas where the image may lack sensitivity to changes in the tissue microenvironment due to limited resolution or unaltered morphology.

Moreover, utilizing image registration scales seamlessly with high resolution spatial transcriptome data, which typically consists of hundreds of thousands or more coordinates per slice. In contrast, non-image-based methods (e.g. PASTE, GPSA) face substantial computational burden under these circumstances, making them impractical, as demonstrated in our benchmarking. Using image as a universal input permits integration across different profiling platforms, despite variations in spatial resolutions or gene quantifications, enabling broader application. Among the image-based methods, since STalign relies on users’ visual preferences for parameter selection, we concentrated our quantitative comparisons on datasets with applicable landmark-free parameter settings published by the authors of STalign. In these scenarios, STaCker demonstrates its advantage by producing more genes with higher spatial autocorrelation and cross-slice coherence in expression. Moreover, considering usability, it is important to recognize that the task of fine-tuning more than a dozen parameters according to personal visual discretion is prone to user biases. Consequently, for obtaining objective outcomes, software such as STaCker, which avoids the need for visual adjustments or landmark selection, might be preferable.

STaCker’s image registration module was trained using synthetic images of arbitrary colors and shapes, aiming to build a model that is robust to different microscopic features. This approach has proven successful, as STaCker performed well with data from various platforms. The use of synthetic images also helps address the challenge of limited data for training a deep neural network. During training, STaCker tailored its objective to spatial transcriptome data. The loss function prioritized consistency between images based on tissue domain labels rather than pixel-wise details. This is because we do not expect to profile identical cells across slices. Consequently, STaCker may ignore aligning some subtle differences in an area if the region is deemed coherent across slices based on the tissue image and gene expressions. We believe the output in such scenarios remains biologically meaningful because the cells or spots within these areas are considered indistinguishable given the available data, implying no further spatial adjustment is needed. If subregions can be identified with higher resolution images or more sensitive transcriptome data, STaCker can adapt to these enhancements without altering its framework.

In the current work, the primary application of STaCker is to unify the spatial transcriptome coordinates among multiple replicates or several consecutively dissected slices. It can be applied in two modes, either aligning to a user-defined reference or mutually among the inquired slices themselves. Our benchmarking showed that STaCker can effectively improve the deformations. Nevertheless, the larger the distortions the less extent STaCker can restore due to applied regularizations. On the other hand, its conservative behavior may be desired in practice to avoid overcorrection.

Our results demonstrate the effectiveness of the image-guided strategy in creating a common coordinate framework for spatial transcriptome slices. This work also provides a useful foundation for future improvements. For example, we plan to enable STaCker to handle full megapixel resolution images acquired in spatial transcriptome measurements, preserving more subtle changes in the tissue microenvironment. Multi-scale training and workflows to enhance parallelization and scalability may be considered for this purpose. STaCker’s current image registration module is trained to match the global shape of the tissues. It would be useful to expand the model to support partial alignments by incorporating strategies such as homography estimation⁴⁹. Another intriguing direction would be to generate image-like input solely from transcriptome data through suitable feature extractions. This could broaden STaCker’s applicability to platforms that do not acquire microscopic images (e.g. Slide-Seq). More importantly, it is critical to differentiate slice distortions from true structural changes to ensure that spatial profiling across different biological states can be unified and compared. We anticipate that better digestion of rich morphology features, along with fine-tuned regularizations, will help address these challenges and further broaden the application of STaCker.

Methods

Input image data pre-processing

The image associated with a spatial transcriptome slice was preprocessed using Python package histomicstk⁵⁰. For histology staining images, we applied the Reinhard color normalization algorithm if noticeable color deviations or variations existed. The non-tissue background of each image was masked using saliency.tissue_detection module. If it was challenging to identify non-tissue background pixels using the colored image, an intensity threshold was applied to the grayscale version of the image, followed by the restoration of the color in the identified tissue foreground. Each color channel was subsequently scaled to be within [0,1]. The image was cropped to remove undesired background sections and resized to a given resolution for input into the model.

Input transcriptome data pre-processing

The gene expression data from a spatial transcriptome slice profiled was converted into an image-like input as follows (Fig. 1a, bottom panel). For each slice, the transcriptome profiles of all spots (or cells) were collected into a count matrix. The columns of the count matrix represented the spot or cell IDs, and the rows represented genes. The count matrix was normalized to have an equivalent total number of counts per column, followed by variance stabilizing transformations (SCTransform) using R package Seurat²². After processing each slice, the transcriptome data from all slices were integrated to minimize batch biases using Seurat function IntegrateData, followed by Principal Component Analysis for a dimensionality reduction. The top principal components (PCs) were used to perform Leiden clustering to identify clusters of the tissue spots or cells (e.g. number of PCs = 30, resolution = 0.1–0.3). The clusters were visually inspected and further merged based on transcriptome similarity and spatial proximity to focus on the major domains in the tissue.

After identifying the clusters, the pixel at the center of each spot or cell was given the corresponding cluster label of that particular spot or cell. The labels for the remaining pixels were estimated using a Voronoi partition created from these central pixels. We then extracted the boundaries between different cluster regions, creating a contour map that represented the spatial organization of the tissue spots or cells based on the transcriptome. Pixels on the contour map were assigned an intensity of 1 along the boundaries in each color channel. This contour map was then overlaid on the previously processed tissue image, specifically at the pixels underlying the contour lines, with a blending ratio of 0.3:0.7. Pixels not on the boundaries retained their original intensities in the tissue image. These composite images were then fed into the image registration module. Users have the flexibility to bypass the inclusion of the transcriptome-derived contour map when its utility is considered limited, such as when the transcriptome data quality is poor, or when the transcriptome provides little or no extra information about the spatial organization of cells.

For MERFISH data, we utilized cell-level gene expressions and the coordinates of cell centroids provided by the standard vendor pipeline⁴⁶. The cells were normalized, transformed, and clustered based on their gene expressions following the guidelines provided by Seurat⁵¹, using the top 30 principal components at a resolution of 0.3. The clusters were further consolidated into niches using the “BuildNicheAssay” function in Seurat (niches.k = 10, neighbors.k = 50). A niche, defined as a region with consistent cell type compositions, offers a more suitable representation of tissue domains than individual cells. Consequently, the contour map was generated at the resolution of niches for downstream alignment of ISH-based spatial profiling data. When evaluating the alignment in MERFISH data, we focus on biologically meaningful pseudo-spots rather than individual cells. These pseudo-spots represent neighborhoods containing specific cell compositions. They were generated using a mesh grid of 200-micron by 200-micron squares over the tissue of interest. The expressions from all cells within each square were pooled per gene to define the transcriptome of a pseudo-spot.

To align the Visium and Xenium data, cells in the Xenium slice were first consolidated into pseudo-spots of 55-micron by 55-micron to better match the Visium spots, using the same procedure as applied to the MERFISH data above. These pseudo-spots were also used for calculating Moran’s I scores in this test case. Next, the Visium spots and the Xenium pseudo-spots were co-clustered using Seurat with the top 15 principal components and a resolution of 0.1 over the shared 344 genes. The resulting clusters were used to generate contour maps for the composite image inputs.

Deep neural network architecture

As depicted in Fig. 1b, the registration model was composed of an ingestion module, an encoder–decoder block, and a field composition module. The ingestion module uses a Siamese structure to receive the fixed reference image and the moving image to be aligned. The encoder–decoder block is embodied in a U-Net backbone⁵², consisting of four levels of contractions and four levels of expansions with skip connections included at every level. The final layer of the decoder is connected to the field composition module to output the deformation field for alignment, as well as its inverse for downstream convenience. Note that the model is not limited to a U-Net architecture. Other network models that can extract and map features from imaging data to a deformation field can be used.

Model training using synthetic images

The model was trained using synthetic training data of varying features. In that way, the alignment model can apply to different image acquisition protocols (e.g. various histology or fluorescence microscopy staining techniques). Additionally, using synthetic training data can help address the issue of limited training data availability, which is common in deep neural network training. In contrast to existing technologies, our approach to image synthesis and training is uniquely devised to suit the task of aligning spatial transcriptome slices (Fig. 2). Each instance of a training data record contains a quartet of synthetic images: a colored reference image ($\widehat{r}$), a segmentation mask image (referred to as the label map in this work) associated with the reference image (${l}_{r}$), a colored moving image to be aligned with the reference image ($\widehat{m}$), and a label map associated with the moving image (${l}_{m}$). Pixels in the label map are classified into a finite number of distinct classes, with each pixel being assigned a specific class label. Although those classes are abstract regarding the training data, they can reflect spatially segregated regions of tissue microenvironment and/or cell compositions in the context of a tissue slice.

More specifically, for a particular quartet of synthetic images of dimension $(H,W)$, where $H$ denotes the image height and $W$ denotes the image width, the reference and moving label maps were first generated. This process began with generating a multi-layer noise distribution $\mathcal{N}$ of shape $(N,H,W)$, where $N$ denotes the number of layers and is customizable. Each layer ${n}_{i} | i\in \left\{\text{0,1},\dots ,N-1\right\}$ corresponded to a class label ${c}_{i}$. Each layer ${n}_{i}$ was a single channel image of smooth textures created using random seeded two-dimensional Simplex noise (OpenSimplex version 0.4.2)⁵³ with the maximum amplitude of 0.5 and a frequency uniformly sampled from [5/512, 15/512]. Every layer ${n}_{i}$ of the distribution $\mathcal{N}$ was then individually warped by a Simplex noise ${\mathcal{S}}_{b,i}$ of the same shape $(H, W)$. When generating the warping noise, we applied random seeding with a frequency between 15/512 and 25/512 and a maximum amplitude sampled log-uniformly from 10.24 to 102.4. The translocations defined by ${\mathcal{S}}_{b,i}$ indicate for each pixel of the warped layer $i$ which pixel intensity from the original layer $i$ to take. This step formed the warped noise distribution $\widehat{\mathcal{N}}$, also of shape $(N,H,W)$.

Next, $\widehat{\mathcal{N}}$ was condensed along the dimension $N$ to form a “base” label map $l$ of shape $(H, W)$ whose elements consist of the class labels ${c}_{0}, {c}_{1}, \dots , {c}_{N-1}$. In other words, any arbitrary element of $l$ at a position $(row, col)$ was defined by finding the solution to $l\left(row, col\right)\equiv {c}_{i}=\text{arg}\underset{i}{\text{max}}\widehat{\mathcal{N}}\left(i, row, col\right) | i\in \left\{\text{0,1},\dots ,N-1\right\}$ (Fig. 2). An additional copy of $l$ was made, and each copy was warped further by an additional separate Simplex noise ${\mathcal{S}}_{s,r}$ and ${\mathcal{S}}_{s,m}$ parameterized with a frequency sampled from [95/512, 105/512] and a maximum amplitude sampled from [10.24, 102.4]. This formed a “reference” label map ${l}_{r}$ and a “moving” label map ${l}_{m}$, respectively, each of which looks similar in appearance but exhibits noticeable differences (Fig. 2).

We then converted the label maps ${l}_{r}$ and ${l}_{m}$ [shape $(H, W)$] into reference and moving images $r$ and $m$ [shape $(H, W, 3)$], respectively. To do this, we randomly selected an RGB color for each class ${c}_{i}$ that appeared within the label maps and assigned that color to all pixels belonging to class ${c}_{i}$ in images $r$ and $m$. Both images were then subjected to Gaussian blurring and an intensity bias field to introduce variations in image sharpness and illumination that might appear in realistic microscopic images. This culminated in colored reference and moving images $r$ and $m$, respectively.

The network model was trained concerning a loss function based on a similarity metric of a pair of reference and moving label maps and a deformation vector field to align the moving image to the reference image (Fig. 1b):

$$L\left({m}^{\prime},r\right)=-Dice\left({l}_{{m}^{\prime}}, {l}_{r}\right)+{\lambda }_{reg}\nabla \overline{u}$$

(1)

where $r$ and ${l}_{r}$ represent a training reference image and the reference label map associated with that image, respectively. ${m}^{\prime}$ and ${l}_{{m}^{\prime}}$ represent, respectively, a moved image and the moved label map associated with that image, after applying the inferred deformation field by the model. ${\lambda }_{reg}$ =0.1 is a regularization factor, and $\nabla \overline{u}$ is the gradient of the inferred deformation vector field. In Eq. (1), the regularization term ${\lambda }_{reg}\nabla \overline{u}$ discourages abrupt large deformations. The Dice score $Dice\left({l}_{{m}^{\prime}}, {l}_{r}\right)$ is a similarity metric that assesses agreement of the pixel-wise class labels between the reference label map and moved label map, instead of the pixel-wise color and intensity agreement between the reference image and the moved image.

$$Dice\left({l}_{{m}^{\prime}}, {l}_{r}\right)=\frac{2{\sum }_{i=1}^{C}|{l}_{m}^{i}\cap {l}_{r}^{i}|}{{\sum }_{i=1}^{C}\left|{l}_{m}^{i}\right|+{\sum }_{i=1}^{C}|{l}_{r}^{i}|}$$

(2)

where $C$ is the number of classes, $|{l}_{m}^{i}|$ and ${|l}_{r}^{i}|$ denote the number of pixels assigned class $i$ in ${l}_{m}$ and ${l}_{r}$, respectively. $|{l}_{m}^{i}\cap {l}_{r}^{i}|$ represents the number of pixels that are simultaneously assigned class $i$ in both maps. This design of the loss function suits the fact that the tissue slices to be aligned are not expected to be identical regarding fine grain details, such as the position of individual cells. Instead, the preferred matching is regarding the regions of cells. The training was conducted using 65,536 synthetic images with mini-batches of 32 images and the Adam optimizer. This batch size hyperparameter was chosen as it is commonly recommended for U-Net^54,55. The hyperparameter learning rate began at a standard value of 1e^-4 for U-Net^56,57,58, and was dynamically adjusted by the Adam optimizer to decrease exponentially whenever the loss reached a plateau. In each epoch, 32 independent synthetically generated images were used for validation testing. Convergence was achieved within 300 epochs. The same trained model was applied to all datasets in this study.

Alignment of spatial slices

The trained STaCker model can align the coordinates of spots/cells in a moving slice to a reference slice. The procedure is outlined as follows. The input is a set of transcriptome-incorporated images, each corresponding to the reference and moving spatial transcriptome slices. These images are prepared as described in the sections of “Input image data pre-processing” and “Input transcriptome data pre-processing”. Each image is stored as a 3-dimensional array, where the dimensions correspond to the height, width, and the number of color channels of the image. The standard outputs from STaCker include a deformation field, a registered image, and the aligned coordinates of the tissue spots or cells. The deformation field is formatted as a numerical matrix, containing a displacement vector for each pixel in the moving slice. This vector specifies the magnitude and direction of movement needed to align the moving slice with the reference slice. STaCker uses the deformation field to generate the aligned tissue spot or cell coordinates, providing these outputs for user convenience.

For input images that exceed the neural network’s default input size (256 × 256 pixels), STaCker employs a tessellation strategy to handle them. It generates a uniform tiling along the width and the height of the reference (or the moving) image, with each tile image fitting the default size of 256 × 256 pixels. Each tile partially (default 25%) overlaps spatially with every other adjacent tile image. The matching pairs of moving and reference tile images are supplied to the registration model and yield N_T tile deformation fields, where N_T denotes the total number of tiles in the reference image which is equivalent to that of the moving image. Each of the N_T tile deformation fields and every one of its adjacent tile deformation fields share a defined common region. STaCker joins the N_T tile deformation fields to form a full-size deformation field by calculating a weighted average of the tile deformation fields overlapping at each pixel within the common region. The weight is inversely proportional to the distance between the center of a tile and the specific pixel.

STaCker can align a group of slices either in a “fixed-template” mode or a “de novo” mode. In the fixed-template mode, one of the slices is set as the fixed reference, and the remaining slices are aligned to it, using the same process of aligning a pair of slices as described earlier. On the other hand, the “de novo” mode harmonizes the slices without a fixed reference. It first adjusts the scale, position, and orientation of the slices in a coarse-grained manner, wherein one user-specified slice is taken as the reference, and the rest are affine-aligned to it. Subsequently, for each slice ${s}_{i}$ among the $S$ total slices, STaCker performs a pairwise alignment by applying the trained registration model on ${s}_{i}$ using each of the $(S-1)$ remaining slices ${s}_{j}\left(j\ne i\right)$ as fixed references. The resulting $(S-1)$ sets of aligned coordinates of ${s}_{i}$, together with the unaligned coordinates of ${s}_{i}$ (which can be considered as the result from the alignment against itself), are averaged and output as the final post-alignment coordinates of the slice ${s}_{i}$. Note the de novo mode itself is not iterative, as the post-alignment coordinates of a slice is not used as the reference when aligning other slices.

Users have the flexibility to run STaCker multiple times if the moving slice has a significant displacement. This can be done until the spatially transformed coordinates of the spots/cells stabilize or a user-specified number of iterations is achieved (e.g., 3 iterations). All the STaCker results presented in this study were obtained from a single iteration, which yielded favorable results compared to other tested methods (see Results). While additional iterations may not generally be required, we provide this option for added flexibility.

Execution of programs

For all non-linear image registrations, ANTs was executed with type_of_transform = ’SyN’ while keeping all quantitative parameters at their default settings. WSIreg was applied using reg_params = [“rigid”, “affine”, “nl”] and thru_modality = None. STaCker operates without requiring user-defined quantitative parameters and was executed using its default settings.

For spatial transcriptome alignment, STUtility and STaCker function without user-specified quantitative parameters and were applied as-is across all test datasets. PASTE employed its default quantitative parameters (-a 0.1 -c kl -p 15 -l n -i 1 -t 0.001 -w None -s None)⁵⁹, which are suitable for both Visium and cellular resolution ISH platforms as noted by the authors⁷. GPSA also utilized the parameter set established by the authors for Visium slices (m_X_per_view = 200, m_G = 200, N_GENES = 10), and for the cellular resolution data (m_X_per_view = 100, m_G = 100, N_GENES = data-determined number of spatially variable genes)⁶⁰.

STalign was executed using the landmark-free parameter settings listed below. As noted in the text accompanying Fig. 4, the authors’ tutorial does not provide instructions for aligning pairs of H&E images. Therefore, we had to exclude STalign from test cases involving the alignment of H&E image pairs. To ensure comprehensive benchmarking, we evaluated the default performance of STalign in this scenario, as shown in Supplementary Fig. 4. In this figure, we aligned the H&E images by using STalign.LDDMM with default values⁶¹ as follows: a = 500, p = 2.0, expand = 2.0, nt = 3, diffeo_start = 0, epL = 2e-8, epT = 23–1, epV = 50, niter = 2000, sigmaM = 1.0, sigmaA = 5.0, sigmaB = 2.0, sigmaR = 5e5, sigmaP = 2e1. The parameters muA and muB, denoting the colors of non-tissue regions to be excluded from alignment as defined by the authors, were set to torch.tensor([0,0,0]), i.e. black in our context. For the MERFISH dataset, we used the same parameter settings published by the authors for this data⁶². Specifically, we rasterized the reference MERFISH data with STalign.rasterize with dx = 30 and blur = 1.5. The alignment was then performed using STalign.LDDMM with niter = 10,000, epV = 50, and other parameters remaining at their default values. For aligning an H&E image to a Xenium slice and vice versa, we utilized the parameters exemplified by authors in analogous scenarios^63,64. The non-default parameters for Visium-to-Xenium alignment included epV = 10, niter = 2000, muA = torch.tensor([0,0,0]), and muB = torch.tensor([1, 1, 1]). Based on the instructions by the authors’ tutorial, we set values of sigma, sigmaB, and sigmaM to 0.153, the standard deviation of the intensity of the pixel in the rasterized and normalized Xenium image. For Xenium-to-Visium alignment, the non-default parameters were epL = 5e-11, epT = 5e-4, epV = 5e1, niter = 200, and sigmaP = 2e-1, with sigma, sigmaB, and sigmaM set to 0.12, reflecting the standard deviation of pixel intensity in the normalized H&E target image.

Quantitative evaluation of the alignment

The normalized cross correlation (NCC) is a measure of the consistency of pixel-wise intensity distributions between a pair of images. The NCC between two images R and M, is calculated as follows:

$$NCC\left(R, M\right)=\frac{{\sum }_{x,y}(R\left(x,y\right)-{\mu }_{R})(M\left(x,y\right)-{\mu }_{M})}{\sqrt{{\sum }_{x,y}{(R\left(x,y\right)-{\mu }_{R})}^{2}{\sum }_{x,y}{(M\left(x,y\right)-{\mu }_{M})}^{2}}}$$

(3)

Here $R\left(x,y\right)$ and $M\left(x,y\right)$ are the pixel intensities of images $R$ and $M$ at coordinates $\left(x,y\right)$, respectively. ${\mu }_{R}$ and ${\mu }_{M}$ are the mean intensities of images $R$ and $M$. Note the formula is simplified to suit our application, where both images consistently possess identical dimensions and expect full overlap.

Mean squared error (MSE) is used to assess the quality of aligned spatial transcriptome slices in the benchmarking datasets. MSE quantifies the discordance between two sets of 2-dimensional spatial coordinates of tissue spots, typically a query and a reference set. Before calculating the MSE, we translocate and scale the reference coordinates to be between 0 and 10 along both x and y axes and apply the same translocation and scaling parameters to the query coordinates. This normalization process eliminates the influence stemming from the size of the spatial transcriptome slices on the MSE values, making it easier to cross-reference results from different benchmarking datasets. MSE is defined as the following:

$$MSE\left(S, T\right)=\frac{1}{N}{\sum }_{i=1}^{N}{[({S}_{x}^{i}-{T}_{x}^{i})}^{2}+{({S}_{y}^{i}-{T}_{y}^{i})}^{2}]$$

(4)

where $N$ is the total number of spots, (${S}_{x}^{i}$, ${S}_{y}^{i}$) and (${T}_{x}^{i}$, ${T}_{y}^{i}$) are the normalized coordinates of spot $i$ in spatial slices $S$ and $T$, respectively.

We utilized the spatial coherence score (SCS) as defined in previous publications⁷. The SCS is calculated as follows:

$$SCS={(E}_{observed}-<{E}_{permutated}>)/{\sigma }_{{E}_{permutated}}$$

(5)

where ${E}_{observed}$ and ${E}_{permutated}$ are the O’ Neill’s entropy associated with the actual spatial arrangement of cells or spots and their randomly permuted configurations, respectively. The entropy is defined as:

$$E=-{\sum }_{i\in C}{\sum }_{j\in C}{p}_{ij}log{p}_{ij}$$

(6)

Here, ${p}_{ij}$ standards for the probability of class $i$ and $j$ being the nearest neighbors. The notation $<{E}_{permutated}>$ represents the arithmetic mean of ${E}_{permutated}$ over 1000 permutations, while ${\sigma }_{{E}_{permutated}}$ denotes the corresponding standard deviation. During each permutation, the class labels of the cells or spots were randomly shuffled, and the resulting ${E}_{permutated}$ was computed according to Eq. (6).

The Mean Pairwise Adjusted Rand Index (MPARI) is defined as follows:

$$MPARI={<ARI({{C}_{j},C}_{j|i}^{*}, k)>}_{i,j\in S, i\ne j}$$

(7)

where ${C}_{j}$ represents the true class label of spots in slice $j$, ${C}_{j|i}^{*}$ denotes the inferred class labels of spots in slice $j$. Each inferred label is based on the $k$ nearest neighbors in slice $i$ and determined by the majority vote of their labels. $ARI$ is the adjusted rand index score⁴¹. Slice $i$, $j$ belong to the set of slices $S$.

Given cosine similarity measures the consistency of the spatial expression patterns of a gene between two slices, the gene coherence score (GCS) is defined as the mean cosine similarity of a gene over every pair of slices:

$$GCS={<{\sum }_{l}{x}_{l}^{i}{x}_{l}^{j}/(\sqrt{{\sum }_{l}{{(x}_{l}^{i})}^{2}}\sqrt{{\sum }_{l}{{(x}_{l}^{j})}^{2}})>}_{i,j\in S,i\ne j}$$

(8)

For any given gene, ${x}_{l}^{i}$ and ${x}_{l}^{j}$ represent the expression of the gene at the spatial location $l$ in slice $i$ and slice $j$, respectively. Slices $i$ and $j$ belong to the set of slices $S$.

Data availability

Code availability

The source code of STaCker is deposited at GitHub https://github.com/regeneron-mpds/stacker.

References

Ståhl, P. L. et al. Visualization and analysis of gene expression in tissue sections by spatial transcriptomics. Science 353(6294), 78–82 (2016).
Article ADS PubMed Google Scholar
Moses, L. & Pachter, L. Museum of spatial transcriptomics. Nat. Methods 19(5), 534–546 (2022).
Article PubMed CAS Google Scholar
Ortiz, C. et al. Molecular atlas of the adult mouse brain. Sci. Adv. 6(26), eabb3446 (2020).
Article ADS PubMed PubMed Central CAS Google Scholar
Maniatis, S. et al. Spatiotemporal dynamics of molecular pathology in amyotrophic lateral sclerosis. Science 364(6435), 89–93 (2019).
Article ADS PubMed CAS Google Scholar
Andersson, A. et al., A Landmark-based common coordinate framework for spatial transcriptomics data. bioRxiv, (2021).
Preibisch, S., Karaiskos, N. & Rajewsky, N. Image-based representation of massive spatial transcriptomics datasets. bioRxiv, (2022).
Zeira, R. et al. Alignment and integration of spatial transcriptomics data. Nat. Methods 19(5), 567 (2022).
Article ADS PubMed PubMed Central CAS Google Scholar
Jones, A. et al. Alignment of spatial genomics data using deep Gaussian processes. Nat. Methods 20(9), 1379 (2023).
Article PubMed PubMed Central CAS Google Scholar
Toyama, S. et al. Application of spatial transcriptomics analysis using the Visium system for the mouse nasal cavity after intranasal vaccination. Front. Immunol. 14, 1209945 (2023).
Article PubMed PubMed Central CAS Google Scholar
Clifton, K. et al. STalign: Alignment of spatial transcriptomics data using diffeomorphic metric mapping. Nat. Commun. 14(1), 8123 (2023).
Article ADS PubMed PubMed Central CAS Google Scholar
Zitová, B. & Flusser, J. Image registration methods: A survey. Image Vis. Comput. 21(11), 977 (2003).
Article Google Scholar
Oliveira, F. P. M. & Tavares, J. M. R. S. Medical image registration: A review. Comput. Methods Biomech. Biomed. Eng. 17(2), 73 (2014).
Article Google Scholar
Haskins, G. et al. Deep learning in medical image registration: A survey. Mach. Vis. Appl. 31(1), 8 (2020).
Article Google Scholar
Bergenstråhle, J. et al. Seamless integration of image and molecular analysis for spatial transcriptomics workflows. BMC Genomics 21(1), 1–7 (2020).
Article Google Scholar
Andrade, N., Faria, F. A. & Cappabianco, F. A. M. A practical review on medical image registration: From rigid to deep learning based approaches | IEEE Conference Publication | IEEE Xplore. In 2018 31st SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI) (2018).
Rueckert, D. et al. Nonrigid registration using free-form deformations: Application to breast MR images. IEEE Trans. Med. Imaging 18(8), 712 (1999).
Article PubMed CAS Google Scholar
Sokooti, H. et al. Nonrigid image registration using multi-scale 3D convolutional neural. In Medical Image Computing and Computer Assisted Intervention − MICCAI 2017 (2017).
Fu, Y. et al. Deep learning in medical image registration: A review. Phys. Med. Biol. 65(20), 20TR01 (2020).
Article PubMed PubMed Central Google Scholar
Yu, H. et al. Convolutional neural networks for medical image analysis: State-of-the-art, comparisons, improvement and perspectives. Neurocomputing 444, 92 (2021).
Article Google Scholar
Hoffmann, M. et al. SynthMorph: Learning contrast-invariant registration without acquired images. IEEE Trans. Med. Imaging 41(3), 543 (2022).
Article PubMed PubMed Central Google Scholar
Kim, Y.-W. et al. How transferable are video representations based on synthetic data?. Adv. Neural. Inf. Process. Syst. 35, 35710–35723 (2022).
Google Scholar
Stuart, T. et al. Comprehensive integration of single-cell data. Cell 177(7), 1888 (2019).
Article PubMed PubMed Central CAS Google Scholar
Archer, T. Procedurally generating terrain. In 44th Annual Midwest Instruction and Computing Symposium Duluth, 378–393 (2011).
Xuemei, L., Huan, L. & Hui, Y. Generation of organ texture with Perlin noise | IEEE Conference Publication | IEEE Xplore. In 2010 International Conference on E-Health Networking Digital Ecosystems and Technologies (EDT) (2010).
Bae, H.-J. et al. A perlin noise-based augmentation strategy for deep learning with small data samples of HRCT images. Sci. Rep. 8(1), 17687 (2018).
Article ADS PubMed PubMed Central CAS Google Scholar
Whitt, P. Beginning photo retouching and restoration using GIMP.
Avants, B., Tustison, N. J. & Song, G. Advanced normalization tools: V1.0. Insight J. (2009).
Patterson, N. H. Multi-modal whole slide image registration (wsireg). https://github.com/NHPatterson/wsireg (2022).
Klein, S. et al. elastix: A toolbox for intensity-based medical image registration. IEEE Trans. Med. Imaging 29(1), 196 (2010).
Article PubMed Google Scholar
Ou, Y. et al. Comparative evaluation of registration algorithms in different brain databases with varying difficulty: Results and insights - PubMed. IEEE Trans. Med. Imaging 33(10), 2039 (2014).
Article PubMed PubMed Central Google Scholar
Nazib, A., Fookes, C. & Perrin, D. A comparative analysis of registration tools: Traditional vs deep learning approach on high resolution tissue cleared data (2018).
Borovec, J., Munoz-Barrutia, A., & Kybic, J. Benchmarking of image registration methods for differently stained histological slides | IEEE Conference Publication | IEEE Xplore. In 2018 25th IEEE International Conference on Image Processing (ICIP) (2018).
Ljimani, A. et al. Analysis of different image-registration algorithms for Fourier decomposition MRI in functional lung imaging. Acta Radiol. 62(7), 875 (2021).
Article PubMed Google Scholar
Mouse hindbrain coronal slice in Allen Brain Atlas. http://api.brain-map.org/api/v2/image_download/102118006.
Spatial transcriptome of mouse brain sagittal-posterior serial section 1 by 10x Genomics Visium platform. https://www.10xgenomics.com/resources/datasets/mouse-brain-serial-section-1-sagittal-posterior-1-standard-1-1-0.
Spatial transcriptome of mouse brain sagittal-posterior serial section 2 by 10x Genomics Visium platform. https://www.10xgenomics.com/resources/datasets/mouse-brain-serial-section-2-sagittal-posterior-1-standard-1-0-0.
Kalen Clifton, M. A. et al. STalign Tutorials. https://jef.works/STalign/tutorials.html (2023).
Spatial transcriptome profiling of human lymph node by 10x Genomics Visium platform. https://www.10xgenomics.com/resources/datasets/human-lymph-node-1-standard-1-1-0.
Visium data of human dorsolateral prefrontal cortex. https://github.com/LieberInstitute/HumanPilot.
Maynard, K. R. et al. Transcriptome-scale spatial gene expression in the human dorsolateral prefrontal cortex. bioRxiv, (2020).
Hubert, L. et al. Comparing partitions. J. Classif. 2(1), 193–218 (1985).
Article Google Scholar
Pedregosa, F. et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830 (2011).
MathSciNet Google Scholar
Gittleman, J. L. & Kot, M. Adaptation: Statistics and a null model for estimating phylogenetic effects. Syst. Biol. 39(3), 227 (1990).
Google Scholar
Chen, K. H. et al. Spatially resolved, highly multiplexed RNA profiling in single cells. Science 348(6233), aaa6090 (2015).
Article PubMed PubMed Central Google Scholar
Janesick, A. et al. High resolution mapping of the tumor microenvironment using integrated single-cell, spatial and in situ analysis. Nat. Commun. 14(1), 8353 (2023).
Article ADS PubMed PubMed Central CAS Google Scholar
MERFISH spatial transcriptome of mouse brain. https://info.vizgen.com/mouse-brain-data.
Visium spatial transcriptome of mouse hemisphere coronal dissection. https://www.10xgenomics.com/datasets/mouse-brain-section-coronal-1-standard.
Xenium in situ spatial transcriptome of mouse hemisphere coronal dissection. https://cf.10xgenomics.com/samples/xenium/1.4.0/Xenium_V1_FFPE_wildtype_5_7_months/Xenium_V1_FFPE_wildtype_5_7_months_outs.zip.
DeTone, D., Malisiewicz, T., & Rabinovich, A. Deep Image Homography Estimation. https://arxiv.org/abs/1606.03798 (2016).
Gutman, D. A. et al. The digital slide archive: A software platform for management, integration and analysis of histology for cancer research. Cancer Res. 77(21), e75–e78 (2017).
Article PubMed PubMed Central CAS Google Scholar
Analysis of Image-based Spatial Data in Seurat. https://satijalab.org/seurat/articles/seurat5_spatial_vignette_2 (2023).
Ronneberger, O., Fischer, P. & Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Lecture Notes in Computer Science (2015).
Svensson, A. OpenSimplex. https://github.com/lmas/opensimplex (2022).
Pereira, Y. d. S. et al. Analysis of U-net neural network training parameters for tomographic images segmentation.
Kandel, I. & Castelli, M. The effect of batch size on the generalizability of the convolutional neural networks on a histopathology dataset. ICT Express 6(4), 312 (2020).
Article Google Scholar
Jain, P. K. et al. Attention-based UNet deep learning model for plaque segmentation in carotid ultrasound for stroke risk stratification: An artificial intelligence paradigm. J. Cardiovasc. Dev. Dis. 9, 326 (2022).
PubMed PubMed Central Google Scholar
Moustafa, M. S. S. et al. Hyperspectral change detection based on modification of UNet neural networks. J. Appl. Remote Sens. 15(2), 028505 (2021).
Article ADS Google Scholar
Liu, F. & Wang, L. UNet-based model for crack detection integrating visual explanations. Construct. Build. Mater. 322, 136265 (2022).
Article Google Scholar
Zeira, R. et al. PASTE github depository. https://github.com/raphael-group/paste (2022).
Jones, A. et al. GPSA github repository. https://github.com/andrewcharlesjones/spatial-alignment (2023).
Clifton, K. et al. STalign github repository. https://github.com/JEFworks-Lab/STalign (2023).
Clifton, K. et al. https://jef.works/STalign/notebooks/merfish-merfish-alignment.html (2023).
Clifton, K. et al. https://jef.works/STalign/notebooks/merfish-visium-alignment-with-point-annotator.html (2023).
Clifton, K. et al. https://jef.works/STalign/notebooks/xenium-heimage-alignment.html (2023).

Download references

Acknowledgements

We thank John Sikorski for sourcing and managing GPU cloud computing resources. We also thank Wen Fury for the helpful discussions during the method development and evaluation.

Author information

Authors and Affiliations

Regeneron Pharmaceuticals, Inc., Tarrytown, NY, 10591, USA
Shawn Mishra, Kun Xiong, Huanan Shi & Yu Bai
New York University Grossman School of Medicine, New York, NY, 10016, USA
Peter Lais
Flagship Pioneering, Cambridge, MA, 02142, USA
Gurinder Singh Atwal

Authors

Peter Lais
View author publications
Search author on:PubMed Google Scholar
Shawn Mishra
View author publications
Search author on:PubMed Google Scholar
Kun Xiong
View author publications
Search author on:PubMed Google Scholar
Huanan Shi
View author publications
Search author on:PubMed Google Scholar
Gurinder Singh Atwal
View author publications
Search author on:PubMed Google Scholar
Yu Bai
View author publications
Search author on:PubMed Google Scholar

Contributions

Y.B., S.M., and G.A. designed the research. P.L., S.M., and Y.B. developed the algorithm. P.L., Y.B., K.X., and H.S. conducted the data analysis. Y.B., P.L., and S.M. wrote the manuscript.

Corresponding author

Correspondence to Yu Bai.

Ethics declarations

Competing interests

P.L., S.M., Y.B., and G.A. have filed a patent application relating to the STaCker computational framework. Y.B., S.M., K.X., H.S. are employees of Regeneron Pharmaceuticals. Additionally, Y.B., S.M., K.X., H.S., and G.A. hold shares in Regeneron Pharmaceuticals. The manuscript’s subject matter does not have any relationship to any products or services provided by Regeneron Pharmaceuticals.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Supplementary Information.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Lais, P., Mishra, S., Xiong, K. et al. Image guided construction of a common coordinate framework for spatial transcriptome data. Sci Rep 15, 18074 (2025). https://doi.org/10.1038/s41598-025-01862-x

Download citation

Received: 05 December 2024
Accepted: 08 May 2025
Published: 24 May 2025
Version of record: 24 May 2025
DOI: https://doi.org/10.1038/s41598-025-01862-x