Combined CNN-BiLSTM-Att tourism flow prediction based on VMD-MWPE decomposition reconstruction

Abstract

Predicting tourist flow is crucial for making effective management decisions at scenic spots. To further improve the accuracy of scenic passenger flow prediction, the current study proposed a data preprocessing approach that combines variational modal decomposition (VMD) with multiscale weighted permutation entropy (MWPE). Additionally, a tourist flow prediction method was introduced, utilizing a combination of bi-layer convolution, bidirectional long short-term memory, and an attention mechanism (CNN-BiLSTM-Att). First, the historical passenger flow data was decomposed into multiple intrinsic modal functions using VMD. Second, the IMF subsequence was measured using the MWPE metric, leading to the construction of a new feature matrix. Finally, the CNN-BiLSTM prediction model, incorporating an attention mechanism and optimized using a genetic algorithm, was applied to generate the final prediction results. Using Lushan Scenic Area (China) as a case study, our experimental results demonstrate that the proposed model significantly outperforms benchmark approaches including XGBoost, LSTM and CNN-BiLSTM. The comparative analysis reveals consistent improvements across all evaluation metrics: achieving a minimum 7.46% reduction in the MAPE, at least 7.2% decrease in BRMSE, and a minimum 1.74% enhancement in the R². These statistically significant improvements validate the model’s superior predictive capability for tourist flow forecasting. The demonstrated performance, combined with its methodological robustness, suggests strong practical applicability and promising potential for implementation across similar tourism management contexts.

Introduction

With the harmonious development of the social environment and substantial improvements in living standards, the tourism industry has demonstrated remarkable vitality. However, determining how to operate and manage tourist attractions more effectively to ensure the rational allocation of resources and enhance the quality of the tourist experience remains an urgent challenge¹. Scenic area passenger flow prediction is an important part of tourism planning and management. Accurate prediction of scenic area passenger flow for scenic area management, tourist services, safety, and security have an important role for the government and related tourism enterprises in promoting the sustainable development of tourism, which has important significance².

Currently, the main academic methods for passenger flow prediction include traditional statistical methods, such as the autoregressive integrated moving average (ARIMA)model³ and decision tree⁴, as well as deep learning algorithm models such as support vector machine (SVM)⁵ and deep neural network (DNN)⁶. While Kumar and Hariharan⁷ employed grid search optimization to tune the hyper-parameters of their ARIMA model for traffic prediction, it should be noted that the ARIMA framework is fundamentally limited to modeling stationary or linear time-series data.

This methodological constraint leads to significantly degraded predictive performance when applied to nonlinear phenomena such as passenger flow patterns, which typically exhibit complex temporal dependencies, seasonality variations, and abrupt fluctuations characteristic of tourism demand dynamics. Passenger flow exhibits stochastic and nonlinear characteristics, highlighting the limitation of traditional statistical methods, such as ARIMA, which struggle to provide accurate fits for such data. In contrast, deep learning algorithms have gained attention and application due to their strong learning ability and high accuracy. Compared with traditional statistical models, deep learning models are better suited for handling nonlinear problems⁸. For instance, in a prior study⁹, SVM model were applied to monitor visitor flow at scenic spots. However, SVMs are more sensitive to noise and outliers and are overly dependent on the quality of the dataset. Reference¹⁰ used a deep neural network to predict the passenger flow of urban tourism, effectively addressing the problem of SVM’s sensitivity to noise and outliers while achieving a certain level of prediction accuracy. Deep neural network (DNN) limited in modeling time-series data, particularly in capturing long-term dependencies, thereby constraining their accuracy in tourism flow prediction. Further methodological improvements are needed to enhance predictive performance. Given the inherent limitations of individual models, researchers have increasingly focused on hybrid approaches that combine complementary strengths to improve passenger flow prediction accuracy. Reference¹¹ used the LSTM model with a spatiotemporal correlation method to predict tourist flow data, effectively mitigating SVM’s sensitivity to noise and outliers. Consequently, scholars increasingly focus on combined models that leverage the strengths of different models to improve passenger flow prediction. References^12,13,14 employed CNN to extract the corresponding spatial features, followed by the LSTM network to predict scenic passenger flow. This combined approach achieved better prediction results than using a single model. As a unidirectional recurrent neural network, LSTM fails to fully capture bidirectional temporal dependencies within input sequences, consequently compromising its accuracy in tourist flow prediction. Reference¹⁵ proposed a CNN-BiLSTM prediction model to overcome the limitations of LSTM by incorporating bidirectional processing, achieving better prediction results than CNN-LSTM. In tourist flow prediction, conventional models often overlook critical variables such as extreme weather conditions, holiday effects, and traffic restrictions, consequently compromising prediction accuracy. The integration of attention mechanisms can effectively address this limitation by dynamically weighting these influential factors to enhance model performance. Reference¹⁶ used the attention mechanism to improve the gated recursive unit model, enabling it to automatically learn and selectively focus on the important information in the inputs, thereby improving the model’s performance and generalization. Building on this approach, the current study proposed a CNN-BiLSTM model with an attention mechanism to improve the accuracy of scenic passenger flow prediction.

High-quality input data significantly enhances the accuracy of tourist flow prediction in scenic areas. Researchers typically combine feature selection with tourist flow decomposition to preprocess model inputs¹⁷. For feature selection, while Linear Discriminant Analysis (LDA) has been applied to tourist flow data screening¹⁸, its linearity assumption proves inadequate for handling the nonlinear and non-stationary characteristics inherent in tourism-related features (e.g., temperature, weather conditions). This limitation necessitates more appropriate feature selection methodologies to improve prediction accuracy. The research approach adopted by scholars such as Reina^19,20, which employs spatial clustering to extract relevant features, demonstrates both methodological novelty and theoretical robustness. The approach proposed by Reina et al. enables the extraction of key features such as tourism congestion indices and weather-related variables, offering significant learning and referential value. In terms of tourism flow decomposition, commonly used decomposition methods include wavelet decomposition (WD)²¹, empirical modal decomposition (EMD)²², and variational modal decomposition (VMD)²³. Reference²⁴ employed wavelet transform (WT) to decompose historical tourist flow data, demonstrating its capability to reveal distinct temporal components while simultaneously capturing both localized details and global trends. However, WT exhibits high sensitivity to noise interference, which may introduce substantial errors during signal decomposition and reconstruction processes, consequently compromising the accuracy of subsequent predictive models. Reference²⁵ used EMD to decompose traffic flow data into multiple intrinsic modal functions (IMFs), effectively addressing noise interference and improving prediction accuracy. However, EMD is prone to mode aliasing, which can lead to incorrect IMF components. To address this issue, References^26,27 employed VMD to decompose time series signals, significantly reducing the issue of modal aliasing and achieving higher prediction accuracy compared to EMD. However, the decomposition of data into too many subsequences with VMD can substantially increase computational cost. To reduce the computational cost, Zhao et al. used permutation entropy (PE) to aggregate the subsequences after decomposition for prediction²⁸. However, PE is a single-scale measure of the complexity of information and suffers from metric imprecision, leading to a higher reduction in prediction accuracy after merging. The multi-scale weighted alignment entropy introduces different scales of alignment entropy. Through the way of adding the average of the comprehensive consideration of the signal characteristics at different scales, it can more comprehensively describe the complexity of the time series signal. Prediction after aggregation in this way has little effect on prediction accuracy²⁹. Building upon this foundation, our study employs a VMD-MPWE approach for preprocessing the raw tourist flow data. For instance, features including weather conditions, temperature readings, humidity levels, and vehicle restriction status are systematically selected, and subsequently, the components derived through the VMD-MPWE methodology are integrated with these screened features to constitute the input dataset, whereupon the final tourist flow predictions are generated via model prediction and reconstruction. This approach effectively enhances prediction accuracy while simultaneously reducing computational complexity.

To summarize, in terms of tourism flow prediction: in the existing literature, some of them do not deal with the volatility and non-stationarity of the data, which has a greater impact on the prediction accuracy; some of them use single-model prediction, but the combination of models is more advantageous; and some of them do not use the attention mechanism, while adding the attention mechanism can focus on the key information and enhance the model adaptability, which is conducive to further improving the prediction accuracy. Consequently, to address some defective issues in the existing literature and to improve the accuracy of prediction, this paper proposes a combined CNN-BiLSTM-Att tourist flow prediction method based on VMD-MWPE decomposition and reconstruction. To address the volatility and the non-stationarity of scenic spot passenger flow data, the VMD algorithm was applied to decompose the data into multiple IMFs, thereby reducing its volatility and non-stationarity. Subsequently, the MWPE was introduced to aggregate the IMF into several new subsequences. These subsequences were then combined with additional features, such as weather data, to form a new matrix, which serves as an input for the CNN-BiLSTM-Att model. This model predicted the values of each subsequence, and these predictions were superimposed to produce the final prediction results.

The main contributions of the current study were as follows:

• (1) A novel decomposition and reconstruction method was proposed. The VMD algorithm was employed to decompose historical scenic passenger flow data, reducing its volatility and non-stationarity. Additionally, MWPE was used to describe the complexity of the data across multiple scales, enabling more precise aggregation of each component.

• (2) New prediction models were introduced for tourism flow. The CNN-BiLSTM model with an attention mechanism was used to predict scenic spot passenger flow, effectively improving prediction accuracy.

• (3) A new method for tourism flow prediction was proposed. This method combines VMD-MWPE with CNN-BiLSTM-Att for tourism flow prediction, an approach rarely explored in this field. It provides a new idea for future research by other scholars.

The current study is structured as follows: Section "Relevant methods" describes the relevant methods proposed in the current study. Section "Tourism flow forecasting model framework and process" introduces the framework for scenic spot passenger flow prediction. Section "Empirical analyses" evaluates the effectiveness of the proposed method using passenger flow data from Mount Lushan, with a comparative analysis against benchmark models. Section "Conclusion" summarizes the current study and outlines future research directions.

Relevant methods

Variational modal decomposition

Tourism flow represents a type of nonlinear and non-smooth data, making direct prediction ineffective, therefore necessitating the application of data decomposition techniques to reduce its non-smooth characteristics, thereby enhancing prediction accuracy. Moreover, VMD decomposition serves as a novel technique for decomposing nonlinear signals through multiresolution analysis, accomplished by formulating a constrained variational problem, enabling signal frequency band separation and data non-smoothness reduction³⁰. The mathematical principle underlying the VMD algorithm for decomposing tourism flow data operates as follows.

• (1) Constructing variational problems

The VMD algorithm decomposes an input signal (historical tourist flow data) into subsequences ${u}_{k}\left(t\right),$ each with different center frequencies and finite bandwidth. The decomposition was performed by solving a variational problem, with the constrained variational model expressed in the following equation:

$$\left\{\begin{array}{c}\underset{\left\{{f}_{k}\right\} \left\{{\omega }_{k}\right\}}{\text{min}}\left\{\sum_{k = 1}^{k}{\Vert {\partial }_{t}\left[\left(\delta \left(t\right) + \frac{j}{\pi t}\right)\cdot {u}_{k}\left(t\right)\right]{e}^{j{\omega }_{k}t}\Vert }_{2}^{2}\right\}\\ s.t. \sum_{k = 1}^{k}{u}_{k}\left(t\right)= f(t)\end{array}\right.$$

(1)

Here, $\omega$ denotes the center frequency. $\left\{{\omega }_{k}\right\}$ represents the center frequency of the k-th signal component of the modal function, $\left\{{u}_{k}\right\}$ denotes the individual modes, ${u}_{k}(t)$ is the kth order frequency-modulated signal, $\delta \left(t\right)$ is the unit pulse function, and $f\left(t\right)$ is the input signal: historical tourist flow data, j is the imaginary unit, t represents the time variable, ${\partial }_{t}$ denotes the partial derivative with respect to time t. ${\Vert \cdot \Vert }_{2}^{2}$ represents the L2 norm, and k indicates the number of modal components.

• (2) Solving variational problems

The signal is reconstructed using the penalty factor $\alpha ,$ the Lagrange multiplier operator $\tau$, and the quadratic penalty factor. $\tau \left(t\right)$ is responsible for the tight constraints of the condition, and the Lagrange augmentation (L) is computed as illustrated in Eq. (2).

$$L\left(\left\{{u}_{k}\right\},\left\{{\omega }_{k}\right\},\tau \right)=\alpha \sum_{k}\Vert {\partial }_{t}\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)\cdot {u}_{k}\left(t\right)\right]{{e}^{-j{\omega }_{t}t}\Vert }^{2}+\Vert s\left(t\right)-\sum_{k}{u}_{k}{\left(t\right)\Vert }^{2}+\langle \tau \left(t\right),s\left(t\right)-\sum_{k}{u}_{k}\left(t\right)\rangle$$

(2)

Here, $\left\{{u}_{k}\right\}$ and $\left\{{\omega }_{k}\right\}$ represent the modal components and their corresponding center frequencies, ${\widehat{u}}_{k}^{n+1}\left(\omega \right)$, $\widehat{s}\left(\omega \right)$, $\widehat{\tau }\left(\omega \right)$ are the Fourier transforms corresponding to ${\widehat{u}}_{k}^{n}\left(t\right)$, $\widehat{s}\left(t\right)$, and $\widehat{\tau }\left(t\right)$, respectively. j represents the imaginary unit; ${u}_{k}\left(t\right)$ denotes the k-th modal component obtained from decomposing the historical tourist flow data f(t); s(t) serves as an auxiliary representation of the original signal for constraint purposes.

The alternating direction multiplier method was used to iteratively update and search for the “saddle point” of Eq. (2). The optimal solution of Eq. (1) is solved as follows:

Step 1: Initialize ${\widehat{u}}_{k}^{1}$, ${\widehat{\omega }}_{k}^{1}$, ${\widehat{\lambda }}_{k}^{1}$, n;

Step 2: Loop n = n + 1;

Step 3: Update ${u}_{k}$, $k \epsilon \{1, 2,\cdots , K\}$; update ${\omega }_{k}$; update $\lambda$ for all ω > 0, as presented in Eqs. (3)–(5).

$${\widehat{u}}_{k}^{n + 1}\left(\omega \right)=\frac{\widehat{s}\left(\omega \right)-\sum_{i \ne k}{\widehat{u}}_{i}\left(\omega \right)+\frac{\widehat{\lambda }\left(\omega \right)}{2}}{1 + 2\alpha {\left(\omega -{ \omega }_{k}\right)}^{2}}$$

(3)

$${\omega }_{k}^{n + 1}=\frac{{\int }_{0}^{\infty }\omega \left|{v}_{k}^{n + 1}\right.{\left.\left(\omega \right)\right|}^{2}d\omega }{{\int }_{0}^{\infty }\left|{v}_{k}^{n + 1}\right.{\left.\left(\omega \right)\right|}^{2}d\omega }$$

(4)

$${\widehat{\lambda }}^{n + 1}\left(\omega \right)={\widehat{\lambda }}^{n}\left(\omega \right)+\tau \left(\widehat{s}\left(\omega \right)-\sum_{k}{\widehat{u}}_{k}^{n+1}\left(\omega \right)\right)$$

(5)

where $\omega$ denotes the frequency-domain variable, $\widehat{\lambda }\left(\omega \right)$ represents the Lagrangian multiplier; ${v}_{k}^{n+1}$ indicates the k-th sub-signal in the frequency domain at the (n + 1)-th iteration.

Step 4: Repeat Steps 2 and 3 until Eq. (6) is satisfied, indicating that the iteration should stop and that K components of IMF have been obtained.

$$\sum_{k}\frac{||{\widehat{u}}_{k}^{n+1}-{{\widehat{u}}_{k}^{n}\Vert }_{2}^{2}}{||{{\widehat{u}}_{k}^{n}\Vert }_{2}^{2}}<\varepsilon$$

(6)

where $\varepsilon$ denotes the preset threshold value.

In addition, VMD is very sensitive to the number of decomposition layers. When the number of VMD decomposition layers is too small, useful information in the original signal is lost. When the number of decomposition layers is too high, it increases the computational resource consumption, time cost, and risk of overfitting. As a result, to select the appropriate number of decomposition layers, the center frequency method is used to determine the K value of the VMD. The number of decomposition layers was determined to be 6 using the center-frequency method when using the VMD to decompose the historical tourist flow. After decomposition, six IMF components with different center frequencies will be obtained.

Multiscale weighted permutation entropy

Following VMD decomposition of tourist flow data, six distinct components are obtained. Given the potential for increasing data volumes in future applications, predictive modeling using all six components would incur substantial computational costs. To mitigate this computational challenge, the multi-scale weighted permutation entropy (MWPE) method is employed to quantify the complexity of each component, followed by recombination of components based on entropy value similarity. The mathematical foundations underlying the MWPE algorithm are presented below.

• (1) The original time series $X = \left\{x\left(i\right), i = 1, 2,\cdots , N\right\}$ is subjected to phase space reconstruction as in Eq. (7).

  $${X}_{i}^{(m)}=\left\{{X}_{i}^{(m)},{X}_{i + \tau }^{(m)},\cdots ,{X}_{i + (m - 1)\tau }^{(m)}\right\}$$

  (7)

  Here, m signifies the embedding dimension, and $\tau$ represents the delay time.

• (2) Calculate the weights of each subsequence as in Eqs. (8) and (9).

  $${w}_{i}= \frac{1}{m}\sum_{k = 1}^{m}{({x}_{i - \left(k - 1\right)\tau }-{\overline{X} }_{k}^{(m)})}^{2}$$

  (8)
  $$\overline{X}_{k}^{\left( m \right)} = \frac{1}{m}\mathop \sum \limits_{k = 1}^{m} x_{{i - \left( {k - 1} \right)\tau }} ,\quad \quad k = 1,2, \cdots m.$$

  (9)

  where ${w}_{i}$ denotes the ith weight; ${\overline{X} }_{k}^{(m)}$ denotes the mean value of the sequence

• (3) Calculate the probability of each permutation occurring.

  The feature information of each subsequence ${X}_{i}^{(m)}$ is represented by the weighted permutation entropy and ${\pi }_{k}$, with the probability of occurrence of each permutation ${P}_{m}({\pi }_{k})$ given in Eq. (10).

  $${P}_{w}({\pi }_{k})=\frac{\sum \{{w}_{i}|1\le i\le N-\left(m-1\right)\tau ,i\epsilon {Z}^{+},N({X}_{i}^{(m)})\}}{\sum {w}_{i}}$$

  (10)

  Here, ${w}_{i}$ denotes the i-th weight, $N({X}_{i}^{(m)})$ represents the permutation pattern ${\pi }_{k}$ of ${X}_{i}^{(m)}$.

• (4) Calculate the value of weighted arrangement entropy as illustrated in Eq. (11).

  $$WPE\left(X,m,\tau \right)=-\frac{1}{lnm!}\sum_{k=1}^{K}{P}_{w}({\pi }_{k})ln{P}_{w}({\pi }_{k})$$

  (11)

• (5) Coarse granulation

  The original time series $X=\left\{x(i),i=\text{1,2},\cdots ,N\right\}$ is coarsely granulated to obtain the sequence ${y}_{j}^{(s)}$, as presented in Eq. (12).

  $${y}_{j}^{(s)}=\frac{1}{s}\sum_{i=\left(j-1\right)s+1}^{js}{x}_{i}, j=\text{1,2},\cdots ,[\raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$S$}\right.].$$

  (12)

  Here, s is the scale factor, and [N/S] is rounded down.

  The MWPE coarse granulation process is shown in Fig. 1.

  As Fig. 1 displays, MWPE measures the complexity of the model from multiple scales, and the evaluation will be more comprehensive and precise than single-scale entropy, such as permutation entropy and sample entropy.

• (6) Calculate the alignment entropy of each coarse-grained sequence as presented in Eq. (13).

  $$MWPE\left(X,m,\tau ,s\right)=WPE({y}^{\left(s\right)},m,\tau )$$

  (13)

Fig. 1

Schematic diagram of MWPE coarse granulation process.

Dual convolutional neural network

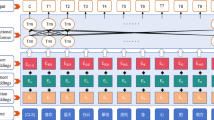
CNN scan passenger flow time-series data by sliding through a convolutional kernel, which effectively captures multi-scale temporal features (e.g., daily variations, weekly periodicities) using multilayer convolution and pooling operations³¹. For instance, scenic area passenger flow is influenced by multiple determinants (e.g., seasonal patterns, holiday effects, weekday/weekend variations), and these features are captured by the CNN to provide more comprehensive feature inputs for subsequent BiLSTM processing of long-term temporal dependencies. A two-layer CNN structure is used in the article, as displayed in Fig. 2: the structure contains two convolutional layers: two pooling layers and a fully connected layer. The role of the convolutional layer is to extract many different types of features by using several different convolutional kernels. The role of the pooling layer is that pooling operations reduce the dimensionality of the data, reduce the amount of computation in subsequent layers, and can make the model more robust to small changes in the input data. The role of the fully connected layer is to integrate the features extracted by the previous layers and make the final decision as per the requirement. In this network model, a 3 × 3 convolutional kernel was used in the convolutional layer, MaxPooling(MP) was applied in the pooling layer, and the Rectified Linear Unit (ReLU) function was chosen as the activation function.

Fig. 2

Convolutional neural network architecture consisting of two layers.

The convolution operation expression is presented in Eq. (14) as follows:

$${y}_{l}\left(i\right)=\sum_{{l}^{\prime}}\sum_{{i}^{\prime}}{K}_{{l}^{\prime}}\left({i}^{\prime}\right){X}_{{l}^{\prime}}\left(i+{i}^{\prime}\right)+{b}_{l}$$

(14)

Here, ${y}_{l}\left(i\right)$ is the output of the lth layer, ${K}_{{l}^{\prime}}\left({i}^{\prime}\right)$ denotes the weight of the convolution kernel in the l' layer, ${X}_{{l}^{\prime}}\left(i+{i}^{\prime}\right)$ represents the input of the l layer, and ${b}_{l}$ signifies the deviation of the convolution kernel in the lth layer.

The ReLU function is used in neural networks to introduce nonlinear, helping the network capture complex patterns in the input data. The expression for the ReLU function is given in Eq. (15):

$$f\left(x\right)=\text{max}(0,x)$$

(15)

In CNN network architecture, a pooling layer is added after the convolutional layer to reduce the computational burden. Two common pooling operations are average pooling and MP. In the current study, maximum pooling was used to help reduce feature dimensions and improve computational efficiency, as expressed in Eq. (16):

$$\text{max}\_\text{pool}({x}_{l})={\text{max}}_{i}({x}_{l-1})$$

(16)

where ${x}_{l}$ is the neuron activation value in one channel of layer $l$.

Bi-directional long short-term memory networks with attentional mechanisms

In tourism flow forecasting, the BiLSTM-Attention mechanism substantially enhances the model’s capacity to learn intricate temporal patterns and boost prediction precision for critical periods (e.g., holidays, special events) via bidirectional sequence modeling and adaptive attention weighting³². For instance, when forecasting summer tourist flows in Mount Lushan Scenic Area, BiLSTM effectively captures the long-term trend characteristics including 'student vacation periods in early July’ and 'peak summer visitation in mid-August’. The Attention mechanism adaptively enhances short-term critical periods including “weekend peaks” and "extreme heat days" to prevent the dominant seasonal trend from obscuring localized variations. The prediction accuracy is enhanced through the synergistic integration of BiLSTM and Attention mechanisms. The fundamental mathematical principles underlying BiLSTM-Attention are as follows:

The BiLSTM comprises two directional LSTM networks operating in opposing orientations (the LSTM structure is depicted in Fig. 3), enabling simultaneous processing of both historical and prospective temporal information, thereby augmenting the model’s temporal pattern learning capacity.

Fig. 3

Structure of a single long short-term memory network (LSTM).

In BiLSTM, the input at each time point is passed simultaneously to both the forward and reverse layers, each producing an output according to LSTM’s computational rules. These two outputs are then combined to form the final output. The unfolded structure of BiLSTM is illustrated in Fig. 4.

Fig. 4

Schematic diagram of the network construction of the Bi-directional long short-term memory network (BiLSTM).

The update process of the BiLSTM network is illustrated in Eqs. (17)–(19):

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{h_{t} }} = {\text{LSTM}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{X_{t} }} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{h_{{\left( {t - 1} \right)}} }} } \right)$$

(17)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftharpoonup}$}}{{h_{t} }} = {\text{LSTM}}\left( {\overline{{X_{t} }} ~,~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftharpoonup}$}}{{h_{{\left( {t - 1} \right)}} }} } \right)$$

(18)

$$Y_{t} = W_{y} \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{h_{t} }} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftharpoonup}$}}{{h_{t} }} } \right]$$

(19)

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{X_{t} }}$ denotes the forward input; $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftharpoonup}$}}{{X_{t} }}$ denotes the reverse input, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{h_{t} }}$ represents the output of the forward layer, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftharpoonup}$}}{{h_{t} }}$ denotes the output of the reverse layer, ${Y}_{t}$ represents the combined output of the two layers, ${W}_{y}$ denotes the weight of the output layer, ${b}_{y}$ is the bias of the output layer, and [;] represents the operation used to join elements together.

Although BiLSTM performs well in modeling time series data, it does not distinguish the importance of features at different time steps. Long sequences of data may result in the loss of early information. Attention mechanisms, inspired by human cognitive processes, allow the model to focus on important areas while minimizing attention to secondary information. By incorporating an attention mechanism, neural networks can enhance their computational power by focusing on critical information, thereby optimizing the allocation of computational resources to the most important factors. The steps for calculating the Attention layer are as follows:

Step 1: Calculate the attention score. Use the output of the BiLSTM layer as the input to the Attention layer. First, define a query vector q, whose dimension is usually the same as the BiLSTM hidden state dimension. By computing the correlation score between the query vector q and the hidden state ${h}_{t}$ of the BiLSTM at each time step, calculated as in Eq. (20):

$${e}_{t}=q\cdot {h}_{t}$$

(20)

where ${e}_{t}$ denotes the attention score, and q denotes the query vector.

Step 2: Calculate the attention weights: the obtained attention score e_t is normalized, the attention weights are obtained by Softmax function, and the weights are calculated as Eq. (21):

$${a}_{t}=\frac{{e}^{{e}_{t}}}{\sum_{i=1}^{sl}{e}^{{e}_{i}}}$$

(21)

where ${a}_{t}$ denotes the weight, and $sl$ denotes the sequence length.

These weights indicate the degree of importance of the information at each time step for the prediction task and $\sum_{t=1}^{sl}{a}_{t}=1$.

Step 3: Generate Context Vector: use the computed attention weight ${a}_{t}$ to weight and sum the hidden state ${h}_{t}$ of BiLSTM to get the context vector $c=\sum_{t=1}^{sl}{a}_{t}{h}_{t}$.

Building upon these theoretical foundations, adaptive weight allocation is implemented across varying operational contexts, where the attention mechanism automatically assigns higher weights to temporally significant periods such as holidays. For instance, when encountering extreme weather conditions (e.g., three consecutive days of heavy rainfall), the attention mechanism intensifies its focus on the corresponding precipitation periods by assigning substantially higher weights; similarly, when processing scenic area traffic restriction inputs indicating reduced visitor numbers, if the restrictions persist into the following day, the mechanism will allocate significantly greater weights to these time steps compared to others.

Therefore, a BiLSTM with an attention mechanism was introduced. This process reallocates weights to different features, enabling the model to focus on key features and important information. It also facilitates more efficient use of historical information, allowing the model to generate more accurate outputs at each time step.

Tourism flow forecasting model framework and process

CNN-BiLSTM-Att model

The results from using a single model to predict time series data are unsatisfactory. To improve prediction accuracy, the current study proposed a combined CNN-BiLSTM model with an attention mechanism. This model consists of a CNN layer, an attention layer, and a BiLSTM layer. The attention mechanism is introduced to address the different importance of time-series data features. Because the existing model cannot integrate both local features and global feature information effectively, the current study combines CNN and BiLSTM to extract different dimensional features. The structure of the model is illustrated in Fig. 5.

Fig. 5

Network structure of the CNN-BiLSTM-Att model.

As illustrated in Fig. 5, the model’s input features comprise meteorological conditions (temperature, precipitation), along with the decomposed tourist flow components (PF1, PF2). The model first extracts multidimensional features from the input data using a convolutional layer. A subsequent maximum pooling layer further reduces the feature dimensions and simplifies network computation. Then, a second convolutional layer with 128 filters and another maximum pooling layer further enhances feature extraction using similar pooling strategies. A Time⁃ Distributed layer is embedded in the network to prepare the data for the subsequent BiLSTM. The BiLSTM layer combines two LSTM layers with 128 cells each, processing data in opposite directions to capture long-term dependencies. In addition, a customized attention mechanism allows the model to focus on key-time step information. Ultimately, following processing through the Fully Connected and Dropout layers, the model produces predicted values for each tourist flow component via a final single-neuron Fully Connected output layer, with the aggregate prediction derived through summation of all component forecasts.

Description of the overall framework for tourism flow prediction

The overall framework of the current study illustrated in Fig. 6 comprises four main parts: data preprocessing, model construction, prediction, and evaluation of prediction effectiveness.

• (1) Data preprocessing

Fig. 6

Block diagram of tourism flow prediction.

Data preprocessing includes several steps: data cleaning, data windowing, data decomposition aggregation reconstruction, and normalization. Data cleaning involves removing outliers and handling missing data to ensure the data’s quality. Data windowing transforms the raw time series data into a consistent format, using the data from the last cell within each window as the target variable. Data decomposition, aggregation, and reconstruction are performed using VMD decomposition, followed by aggregation based on the MWPE of each subsequence. Normalization maps the data to the range of (0, 1), reducing the weight bias across different features and preventing some features from interfering with the model’s results. Additionally, 1901visitor flow records from Jiuzhaigou, China, were utilized for validation^33,34.

• (2) Model construction and forecasting

This involves constructing the deep learning model (CNN-BiLSTM-Att) with other baseline models. The processed input data are composed into an input matrix, which is fed into the CNN-BiLSTM-Att model to generate the predicted results.

• (3) Parameter optimization

Parameter optimization involves using genetic algorithms to optimize parameters such as the learning rate and the hidden layer dimension of BiLSTM³⁵. Debugging is performed through repeated training and prediction cycles to optimize the model’s prediction accuracy.

• (4) Assessment of forecasting effects

The prediction effectiveness evaluation session is used to test the effectiveness of the CNN-BiLSTM-Att model against other deep learning models for scenic passenger flow prediction. This section includes an assessment based on the fitted curve and error metrics (MAE, MAPE, RMSE, and R²).

Tourist flow forecasting process

The process of the tourist flow forecasting method proposed in this paper is presented in Fig. 7.

Fig. 7

Flowchart of the proposed tourist flow forecasting method.

First, the initial scenic spot flow data are collected and processed, including data cleaning, window splitting, data decomposition aggregation, and normalization. Then, all normalized data are fed into the GA-optimized prediction model of CNN-BiLSTM-Att, the prediction results are obtained by training prediction, and finally the prediction results are evaluated and analyzed.

Empirical analyses

Description of experimental data

In the current study, the feasibility and effectiveness of a hybrid CNN-BiLSTM-Att prediction method based on VMD-MWPE were investigated, using the world-famous Mount Lu as an arithmetic example. The experiment analyzed a dataset of 588 entries from the Lushan Scenic Area, China, from January 1, 2023, to August 10, 2024. The dataset is partitioned into training (70%), validation (15%), and test (15%) sets following standard machine learning practice. Given the limited sample size of the collected dataset, the model exhibits heightened susceptibility to overfitting. Consequently, the following preventative measures were implemented during the experimental phase:

• 1. Data Enhancement (Window Warping + Gaussian Noise);

• 2. Structured Dropout: use SpatialDropout1D to prevent BiLSTM overfitting;

• 3. Bayesian Early Stop: force termination when the standard deviation of val_loss fluctuation for 5 consecutive epochs is < 0.005;

In addition, given the extended data collection period, the initial dataset was cleaned to address issues, such as missing values, duplicates, and anomalies of the data, ensuring high data quality.

Performance evaluation criteria

In this study, four metrics are used to assess the predictive effect and performance of the proposed model¹⁸. The error metrics are mean absolute error (MAE), mean absolute percentage error (MAPE), standardized root mean square error (BRMSE), and coefficient of determination (R²). The mathematical expressions are shown in Eqs. (22)–(25):

$$MAE=\frac{1}{N}\sum_{i=1}^{N}\left|{V}_{i}^{t}-{V}_{i}^{f}\right|$$

(22)

$$MAPE=\frac{1}{N}\sum_{i=1}^{N}\left|\frac{{V}_{i}^{t}-{V}_{i}^{f}}{{V}_{i}^{t}}\right|\times 100\%$$

(23)

$$BRMSE=\frac{1}{{S}_{max}-{S}_{min}}\sqrt{\frac{1}{N}\sum_{i=1}^{N}{({V}_{i}^{t}-{V}_{i}^{f})}^{2}}$$

(24)

$${R}^{2}=1-\frac{\sum_{i=1}^{N}{({V}_{i}^{t}-{V}_{i}^{f})}^{2}}{\sum_{i=1}^{N}{({V}_{i}^{t}-\overline{{V }_{i}^{t}})}^{2}}$$

(25)

where ${V}_{i}^{t}$ denotes the true value, ${V}_{i}^{f}$ denotes the predicted value, $\overline{{V }_{i}^{t}}$ denotes the mean of the true value, and N represents the sample size. The smaller values of MAE, MAPE, and BRMSE denote a better model. The value of ${R}^{2}$ ranges from 0 to 1, and as the value approaches 1, it denotes better model interpretability and goodness-of-fit.

Analysis of VMD-MWPE decomposition and polymerization

To address the challenge of prediction inaccuracy caused by non-stationary tourist flow patterns, this study employs VMD-MWPE to preprocess the raw data, thereby generating optimized input features for the CNN-BiLSTM-Attention hybrid model and ultimately enhancing forecasting precision. Using the center frequency method, the number of decomposition layers was determined to be six. Figure 8 illustrates the waveforms of the components resulting from the VMD decomposition.

Fig. 8

Component waveform after VMD decomposition.

To optimize computational efficiency, the multi-scale permutation entropy (MPE) method is employed to quantitatively assess the complexity of each decomposed component. For comprehensive validation of MWPE’s superior performance, comparative analyses were conducted against conventional entropy measures including permutation entropy (PE), sample entropy (SE), and fuzzy entropy (FE). This study employs MWPE to quantify the information entropy of each decomposed component, followed by entropy-based subsequence merging that consolidates the original six subsequences into two representative sequences, thereby achieving significant computational efficiency gains. The remaining components undergo an identical merging procedure, as visually demonstrated in Fig. 9.

Fig. 9

Histogram of entropy value.

The merged components were sequentially fed into the prediction model to generate 7-day forecasts, with corresponding prediction errors and goodness-of-fit metrics detailed in Table 1.

Table 1 Performance comparison of entropy-based decomposition methods for tourist flow prediction.

Based on the experimental results presented in Table 1, the proposed MWPE method demonstrates superior computational efficiency, achieving the shortest model prediction time. Furthermore, it yields the most accurate predictions with a MAPE of 3.03% and BRMSE of 3.12%, representing the lowest error rates among all compared methods, while simultaneously attaining the highest R² value of 0.96. These results clearly indicate that MWPE outperforms conventional entropy-based methods (PE, SE, FE) in terms of both computational performance and prediction accuracy.

To comprehensively evaluate the efficacy of the proposed VMD-MWPE decomposition-aggregation framework, we conducted comparative analyses with three established decomposition techniques: wavelet transform (WT), empirical mode decomposition (EMD), and ensemble empirical mode decomposition (EEMD). Table 2 presents the corresponding prediction errors for both 3-day and 7-day forecasting horizons.

Table 2 Comparison of the effect of different decomposition algorithms.

Table 2 presents that the MAE, MAPE, and BRMSE values of VMD-MWPE are the smallest, and its R² is the highest. This indicates that the prediction performance after processing the data with the VMD-MWPE method significantly surpasses that of the WT, EMD, and EEMD methods. Accordingly, it proves the effectiveness of the VMD-MWPE method proposed in the current study.

Comparative analysis of CNN-BiLSTM-Att with other methods

Following data preprocessing, the refined input features are fed into the CNN-BiLSTM-Attention hybrid model to generate final tourist flow predictions. These results are subsequently benchmarked against predictions from comparative models (XGBoost, LSTM, CNN-LSTM) through comprehensive statistical analysis.

• (1) Comparative analysis of the proposed model with other models

To ensure rigorous comparability across all models, the tourist flow dataset underwent preprocessing through the VMD-MWPE decomposition framework prior to model input. The predictive performance of the proposed CNN-BiLSTM-Attention model was systematically compared against six benchmark algorithms: ARIMA, SVM, Decision Tree (DT), Random Forest (RF), Deep Neural Network (DNN), LSTM, eXtreme Gradient Boosting (XGBoost), BiLSTM, CNN-LSTM, and CNN-BiLSTM, with particular focus on their respective prediction error metrics. The results are presented in Table 3.

Table 3 Prediction errors of tourist flow by different models at mount Lu.

As evidenced by the comparative results in Table 3, the BiLSTM model demonstrates superior predictive performance among the four individual benchmark models (DNN, LSTM, XGBoost, and BiLSTM), achieving optimal metrics for the 15-day forecasting horizon: 8.68% MAPE, 9.13% BRMSE, and 0.847 R². During regular non-holiday periods, the predictive accuracy of individual models may satisfy basic operational requirements for scenic area management. However, during peak travel seasons when tourist volumes experience significant surges, management stakeholders increasingly prioritize higher prediction precision to facilitate optimal advance planning and resource allocation.

The CNN-BiLSTM-Attention model demonstrates exceptional predictive performance across multiple time horizons, achieving:

For 3-day predictions: MAPE (2.73%), BRMSE (2.71%), and R² (0.988).

For 7-day predictions: MAPE (3.03%), BRMSE (3.12%), and R² (0.979).

For 15-day predictions: MAPE (6.33%), BRMSE (6.82%), and R² (0.875).

These results reveal two key findings:

A consistent pattern of gradually declining accuracy with extended prediction horizons across all models. The CNN-BiLSTM-Attention model exhibits superior resilience to this degradation, maintaining significantly better performance in long-term forecasting compared to benchmark approaches.

The CNN-BiLSTM-Attention model demonstrates consistent accuracy improvements across all forecasting horizons compared to the baseline CNN-BiLSTM model. Specifically, the attention-enhanced model achieves:

For 3-day predictions: 7.46% reduction in MAPE; 7.20% reduction in BRMSE.

For 7-day predictions: 7.62% decrease in MAPE; 8.51% decrease in BRMSE.

For 15-day predictions: 8.92% lower MAPE; 10.76% lower BRMSE.

These substantial and progressively increasing improvements across all time horizons clearly demonstrate the effectiveness of the attention mechanism in enhancing tourist flow prediction accuracy. The performance gains are particularly notable for longer-term forecasts (15-day), where the attention mechanism provides over 10% reduction in BRMSE.

To better demonstrate the comparative advantages of the proposed CNN-BiLSTM-Attention framework, Fig. 10 visually summarizes the 15-day prediction error metrics across all evaluated models.

Fig. 10

Error indicators of different models for forecasting. Tourist flow graphs.

As comprehensively demonstrated by the quantitative results in Table 3 and visual evidence in Fig. 8, the proposed CNN-BiLSTM-Attention model achieves dual optimization of both minimal prediction errors and maximal goodness-of-fit. These findings establish that our model outperforms: (1) individual baseline models including DNN and LSTM, and (2) existing hybrid approaches such as CNN-LSTM and CNN-BiLSTM.

To further reflect the superiority of the proposed model, the tourist flow prediction of different models was compared with the actual passenger flow. The predicted and actual patronage values are presented in Fig. 11.

Fig. 11

Comparison of predicted and true values of the model.

Figure 11 demonstrates that the predicted values of the proposed method align most closely with the true values. The next better result was observed with the CNN-BiLSTM model, while the DNN model revealed the worst prediction. This proved the stability and superiority of the proposed CNN-BiLSTM-Att model. In addition, scenic spot managers can optimize the management of the scenic spot according to the prediction results, such as on the 8th, 9th, and 15th days, increase the service staff and tourism facilities in the scenic spot; on the 2nd–4th days, and on the 10th–13th days, reduce the service staff and tourism facilities in the scenic spot, and so on.

Fig. 12

Probability intervals for tourism flow forecasting.

To further validate the superior performance of the proposed method, approximately 2,000 data records from Jiuzhaigou were utilized for experimental verification. A comparative analysis of prediction performance across different models is presented in Table 4.

• (2) Interval forecasting of tourist flow

Table 4 Prediction error comparison of tourist flow by different models in Jiuzhaigou.

The above deterministic forecasting methods cannot effectively capture the trends in future scenic spot flow, nor do they address the uncertainty of the predicted results. Therefore, interval prediction of tourist attractions flow provides a better scientific basis for scenic spot managers to make decisions and optimize resource allocation. Taking the passenger flow of the Lushan Scenic Area as an example, the probability density function was established using the absolute error, and the A-D test was applied, as demonstrated in Fig. 12. As illustrated in Fig. 12, at a 95% confidence level, the error bounds are (− 6853, 5086) and at an 85% confidence level, the error bounds are (− 3389, 3156). This demonstrates that the method proposed in the current study offers excellent prediction accuracy and robustness.

Discussion and analysis

The tourism flow forecasting proposed in this research has a wide range of applications.

In tourism management, tourism managers can make arrangements and decisions based on the results of tourism flow forecasting, and some application scenarios are as follows:

Adjustment of human resources: According to the results of the predicted number of tourists, increase the service personnel in the scenic area, such as tour guides, security personnel, cleaning personnel, etc., during the peak period, such as the 8th, 9th, and 15th days in Figs. 9 and 10. The tour guides can provide explanation services for more tourists and enhance the experience of tourists. The security personnel can maintain the order of the scenic area and ensure the safety of tourists. The cleaning personnel can ensure the tidiness of the scenic area environment.

Physical resource deployment: Reduce the number of tourist facilities, such as sightseeing buses, cable cars, and other means of transportation operated during the trough, e.g., days 2–4 and days 10–13 in Figs. 9 and 10. Increase the number of sightseeing buses, cable cars, and other modes of transportation operating at peak times, such as days 8, 9, and 15 in Figs. 9 and 10. Catering and accommodation facilities also need to be adjusted according to the forecast. If a large number of tourists are forecast to stay overnight, hotels in scenic spots can prepare enough rooms in advance, and restaurants can prepare sufficient ingredients.

Supervision of service quality: During peak tourist periods, such as days 8, 9, and 15 in Figs. 9 and 10, supervision and inspection of each service point in the scenic area will be strengthened to ensure that the quality of service does not deteriorate.

Marketing planning: If the tourism forecast shows that the number of tourists is low during a certain period, such as days 2–4 and 10–13 in Figs. 9 and 10, targeted promotional activities can be carried out. For example, discounted tickets and packages (including scenic spot tickets, amusement ride tickets, food and beverage vouchers, etc.) can be introduced to attract more tourists.

Sustainable development of tourism: Through high-precision forecasting, scenic spots are able to make advance adjustments to ticket reservations, traffic arrangements, and staffing. This helps prevent ecological damage such as garbage accumulation and vegetation trampling that may result from overloaded operations. Moreover, diversion measures, like staggering entry times, can be implemented. These efforts not only enhance visitor satisfaction but also increase the likelihood of repeat visits. Local governments can leverage the prediction model to optimize regional tourism development plans, with particular focus on aspects such as transportation infrastructure and hotel approvals. By using this model, they can also anticipate abnormal fluctuations in passenger flow and assist scenic spots in formulating contingency plans. Through these measures, the sustainable development of the tourism industry is effectively ensured.

In other application domains, the CNN-BiLSTM-Att prediction approach, which is predicated on VMD-MWPE decomposition and aggregation, holds significant potential. It can be adopted and extended to the realm of time series forecasting, including but not limited to applications like traffic flow prediction and wind power prediction. This methodology offers a novel and effective means to address complex predictive challenges in these diverse fields. For instance, when applied to traffic flow prediction, relevant departments can optimize public transportation schedules based on precise traffic forecasts. They can proactively increase the frequencies of subways and buses, thereby enhancing commuting efficiency. In the domain of new energy power generation, the accurate predictions yielded by the method described in this paper offer several benefits. It can optimize the coordinated operation of thermal power, wind power, and photovoltaic power, minimizing wind and solar curtailment. Additionally, it enables the prediction of peak loads, guiding users to stagger their electricity consumption during peak periods and alleviating the stress on the power grid.

Conclusion

Accurate prediction of tourist flow is crucial for resource management and personnel allocation in the scenic area, playing a significant role in achieving sustainable development. In this paper, the proposed CNN-BiLSTM-Attractive Area Passenger Traffic Combination Prediction Model, which is built upon VMD-MWPE decomposition and reconstruction, is compared with benchmark models like XGBoost and LSTM. The results reveal remarkable improvements in prediction accuracy. Specifically, the MAPE is reduced by a minimum of 7.46%, the BRMSE is decreased by at least 7.2%, and the R² as a fit metric is enhanced by a minimum of 1.74%. These findings unequivocally demonstrate the excellent prediction performance of the proposed model, endowing it with robust theoretical underpinnings and practical significance.

• (1) Due to the fluctuating and non-stationary characteristics of scenic spot passenger flow, accurate predictions based solely on historical passenger flow data were challenging. In the current study, we proposed the VMD-MWPE decomposition and aggregation method, which effectively improved the prediction accuracy of scenic passenger flow. This method of handling data provides a strong theoretical basis when guiding other time series analyses.

• (2) The prediction performance of single models, such as DNN and LSTM, as well as common combination models, such as CNN-LSTM, did not meet expectations. In the current study, we proposed a CNN-BiLSTM prediction model with an attention mechanism to further improve the prediction accuracy. The CNN-BiLSTM-Att model predicts the highest accuracy and the smallest error when compared with CNN-LSTM, CNN-BiLSTM, and other models, demonstrating its effectiveness for passenger flow prediction. Simultaneously, the model has a greater reference value for traffic flow, wind and light forecasting, and comprehensive energy load forecasting.

• (3) The current study presents a scenic spot flow forecasting method that offers valuable guidance to tourist attraction managers. Accurate forecasts provided direct support for unified management, rational source scheduling, and tourist diversion. This is of significant importance to scenic spots, especially popular ones, and even the entire tourism industry.

In the future, there are two main areas of research:

• (1) To study the impact of the age structure of tourists on the flow of tourists to facilitate tourism managers in developing better programs to promote the sale of tourism products and improve conduct. The tentative plan is to categorize people into four age stages: under 18, 18–25, 25–60, and over 60, and combine them with a new predictive model, the hotter than hot Transformer technology, for predictive analytics.

• (2) Using the Internet, collect information on scenic spots in several different regions to validate the prediction method, which makes the researched method have stronger generalization and robustness.