Denoising research of shearer picks load signal based on MPE-VMD algorithm

Abstract

For the problem of noise in the load acquisition signal of shearer picks, which will affect the extraction and analysis of critical features of the load signal, a denoising algorithm based on MPE-VMD is proposed in this paper. The Blocks, Bumps, and Doppler signals containing noise are selected as the test signals according to the characteristics of the shearer picks load signals. The test signal is denoised using the method of this paper, the VMD algorithm, the WT algorithm, and the EMD algorithm, respectively. The comparison results show that the MPE-VMD algorithm proposed in this paper has the best denoising effect, followed by WT, then VMD, and EMD has the worst denoising effect. Finally, the method in this paper is applied to the denoising of the acquired picks load signals, and good results are achieved.

Introduction

As the core component in the coal cutting and rock breaking process of shearer, the performance and efficiency of the pick are directly related to the effectiveness of the entire coal mining operation.Therefore, the precise calculation of the pick’s cutting force and the in-depth study of the pick’s cutting mechanism have long been both a hotspot and a challenge in the field of shearer technology.Numerous scholars, both domestically and internationally, have devoted themselves to this field, aiming to explore more accurate and efficient theoretical models and experimental methods.

In terms of theory, Evans¹, a British scholar, was the first to propose a coal rock cutting theoretical model, whose model was mainly based on the tensile strength of coal rock to construct the mathematical expression of the cutting force of the picks. Goktan² refined based on Evans’s theoretical model by considering the effect of friction between the picks and coal rock and modified the cutting force formula of picks proposed by Evans. Roxborough³ conducted many pick cutting experiments for coal rock specimens with different compressive strengths and tensile strengths and modified the Evans theoretical model based on the experimental results. Nishimatsu⁴, a Japanese scholar, proposed a theoretical model of shearer knife-type picks cutting coal rock based on the Mohr-Coulomb strength theory. The Soviet scholar Belon⁵ proposed that a stress concentration phenomenon occurs in the contact area between the pick tip and coal rock during the cutting process, resulting in the coal rock being squeezed into a dense core. Because of this phenomenon, a dense core theory was proposed to derive a semi-empirical formula for the cutting force of the picks. Niu Dongmin⁶ considered the influence of the physical characteristics of coal rock bedding and jointing on the cutting force of picks and developed a mathematical model of the cutting resistance of picks based on the theoretical model of fracture mechanics.

Regarding experiments, Liu⁷ independently built a shearer spiral drum test bench, measured the cutting resistance of picks under different pick diameters, coal wall hardness, and drum speeds and analyzed the influence law of the above-mentioned factors on the cutting resistance of picks. Chunsheng Liu⁸ established a mathematical model for the lateral force of conical picks, analyzed the correlation between pick inclination angle and cutting load spectrum, and verified the accuracy of the theoretical model through experiments. Chunhua Wang⁹ observed the coal-breaking process of different pick shapes through a homemade cutting test bench and derived the empirical relationship between the pick taper and the rock-breaking effect. Xuefeng Li¹⁰ used PFC3D material software to simulate the rock-breaking process of picks and measure the cutting resistance of picks, and the simulation results were verified by shearer cutting experiments. Xuluo Chen¹¹ established a wireless transmission system based on zigbee wireless technology and labview virtual technology to obtain the load of shearer picks.

For denoising, Pierre Comon¹² proposed the independent component analysis method. Zhaohua Wu¹³ proposed an ensemble empirical mode decomposition (EEMD) with a strong denoising effect for signal data with additional white noise. Mika¹⁴ used principal component analysis for the extraction of non-linear features of image signals and, thus, for data reconstruction and denoising of images. Zibulevsky¹⁵ applied the sparse decomposition method to the blind source separation problem and concluded through the study that the method outperforms the conventional methods in decomposing the original signal as well as denoising. Orris¹⁶ used the phase-matching method to denoise the signal, and for low signal-to-noise ratio signals, almost distortion-free signals can be obtained by processing. Ghael¹⁷ designed a new wavelet denoising algorithm that used wavelet shrinkage estimation as a design wavelet domain Wiener filter to improve the denoising effect by a factor of 2 compared to the conventional wavelet al.gorithm.

In summary, despite significant progress in the study of the pick’s cutting mechanism and experimental validation, the denoising of shearer picks load signals remains a pressing issue that needs to be addressed. The quality of the denoising directly affects the accuracy of cutting force calculations and the depth of cutting mechanism research. Therefore, based on a thorough review of previous research, this paper proposes a new denoising algorithm—MPE-VMD—for shearer picks load signals. To evaluate the denoising performance of this algorithm, this paper uses five parameters—root mean square error (RMSE), signal-to-noise ratio (SNR), square ($R^{{2}}$), peak signal-to-noise ratio (PSNR), and correlation coefficient (cc)—as evaluation metrics.By comparing with traditional denoising algorithms such as WT, VMD, and EMD, this paper demonstrates that the MPE-VMD algorithm has significant advantages in denoising shearer picks load signals.This research not only provides more accurate data to support the in-depth study of the pick cutting mechanism but also lays a solid foundation for the further development and optimization of shearer technology.

Shearer picks load testing experiment

Experimental plan

In order to realize the real-time monitoring of the picks stress state during the cutting process of shearer, the experiment of cutting the coal wall was conducted in the “National Research and Development (Experimental) Center of Energy Coal Mining Machinery and Equipment” of China Coal Equipment Zhangjiakou Coal Machinery Plant. The strain sensor was installed on the picks. The sensor installation positions are shown in Fig. 1. The drum selected for the experiment has three spiral blades, each containing seven picks. A total of nine test picks, equipped with sensors, are installed. Two test picks are installed on each spiral blade, with one test pick placed between every two normal picks on the same blade. Three test picks are installed on the end disc.

Fig. 1

Sensor layout scheme.

The schematic diagram of the test system is shown in Fig. 2. The testing system is mainly composed of four parts: DH1210 strain sensor, wireless strain acquisition module, wireless communication master receiving module, and PC. The test equipment specifications and parameters are shown in Table 1. The test system works on the following principle: The DH1210 strain sensor installed inside the picks converts the stress signal of the picks into a voltage signal, which is transmitted to the wireless strain acquisition module via a cable and then to the wireless gateway via wireless transmission. Finally, the PC reads the voltage signal value from the wireless gateway. The voltage signal value is converted into stress value by the calibration formula, and the picks stress state is displayed in real-time.

Fig. 2

Schematic diagram of the test system.

Table 1 Sensor and test equipment parameters.

The experimental site is shown in Fig. 3. The experimental conditions are the height of the coal wall is 3 m, the hardness of the coal wall is $f = 3$,the shearer model is MG500/1130WD type drum shearer, the drum diameter is 1.8 m, the drum speed is 32r/min, the traction speed is 3 m/min, the total length of the coal mining face is 70 m. The cutting process of the shearer is divided into three stages: no load, slant-cutting, and straight-ahead regular cutting.

Fig. 3

Experimental site.

• (a) No-load working condition of shearer.

The no-load condition means the shearer does not conduct cutting operations and only travels in the traction direction. The schematic diagram of the no-load working condition of the shearer is shown in Fig. 4. Three traction speed conversions are also completed in the experiment, and the specific steps for implementation are as follows:

The shearer starts operating from the far left and travels to the right at a 4 m/min traction speed.

When the shearer travels to the 18th hydraulic support (the right drum reaches the 18th hydraulic support), the traction speed changes to 6 m/min and continues to travel to the right.

When the shearer travels to the 28th hydraulic support (the right drum reaches the 28th hydraulic support), the traction speed changes to 8 m/min and continues to travel to the right to the far-right end.

Fig. 4

Schematic diagram of shearer straight ahead no-load working condition.

• (b) Slant-cutting working condition of shearer.

Slant-cutting working condition means that the shearer travels on the S-bend and cuts the coal wall. The schematic diagram of the slant-cutting working condition of the shearer is shown in Fig. 5. In order to form a contrast with the straight-ahead no-load, three times speed adjustments are also performed in the experiment, which is implemented as follows:

The S-bend is set between the 25th and the 16th hydraulic support. The traction speed is set to 1.5 m/min. The shearer continues cutting to the left after traveling from the 25th hydraulic support to the 16th hydraulic support.

When the shearer travels to the 12th hydraulic support, the traction speed changes to 3 m/min and continues cutting to the 8th hydraulic support.

The traction speed of the shearer is changed to 5 m/min from the 8th hydraulic support and cutting is stopped at the far-left end of the coal wall.

Fig. 5

Schematic diagram of shearer S-bend cutting working condition.

• (c) Straight-ahead regular cutting of shearer.

Shearer straight-ahead regular cutting working condition means that the coal mining machine travels straight ahead along the traction direction and cuts the coal wall. The schematic diagram of the straight-ahead regular cutting working condition of the shearer is shown in Fig. 6. Three cutting speeds are performed during the experiment, which is implemented as follows:

Firstly, the coal wall with bevels will be cut flush, stopping at the 30th hydraulic support from approximately the far-left end.

The shearer returns to the 28th hydraulic support and starts cutting to the right, setting the traction speed to 1.5 m/min and cutting the coal wall until the 32nd hydraulic support stops.

Fig. 6

Schematic diagram of shearer straight-ahead cutting working condition.

Experimental results

In the shearer cutting experiment, a total of nine test picks were used.The numbering of these test picks is shown in Table 2. Strain sensors installed on the picks were used to collect the cutting resistance of the picks under various working conditions in real-time, with a sampling frequency of 200 Hz. Data were selected from three experimental conditions: the no-load condition, the slant-cutting condition, and the straight-ahead regular cutting condition. Each dataset consists of 1000 sampling points, forming the time history curves for the no-load condition, straight-ahead regular cutting condition, and slant-cutting condition, as shown in Figs. 7, 8, and 9.

Table 2 Pick number table.

Fig. 7

Time history curve of the cutting resistance of the test pick under no-load condition.

Fig. 8

Time history curve of the cutting resistance of the test pick under straight-ahead regular cutting condition.

Fig. 9

Time history curve of the cutting resistance of the test pick under slant-cutting condition.

For Figs. 7, 8 and 9, the processed data of cutting resistance for different test picks under various conditions is shown in Table 3. Analysis of Table 3 reveals the following: under the no-load condition, for the nine test picks, the maximum values range from 43.17 N to 59.55 N, the average values range from 17.22 N to 17.96 N, and the standard deviation ranges from 7.11 N to 8.157 N. Under the straight-ahead regular cutting condition, for the nine test picks, the maximum values range from 3530.0 N to 5826.0 N, the average values range from 807.0 N to 1221.0 N, and the standard deviation ranges from 462.3 N to 759.4 N. Under the slant-cutting condition, for the nine test picks, the maximum values range from 1939.0 N to 2232.0 N, the average values range from 501.7 N to 743.4 N, and the standard deviation ranges from 389.0 N to 486.8 N.

Table 3 Test pick data statistics.

To comprehensively analyze the force state of the test picks under different working conditions and eliminate errors caused by the installation positions of the test picks, each test pick’s data was processed by spatial and temporal synchronization, summing, and then averaging, which is :

$$\begin{array}{*{20}c} {\hat{F}(t) = \frac{{\sum\limits_{i = 1}^{n} {F_{i} (t - \tau_{i} )} }}{n}} & {n = 9} \\ \end{array}$$

(1)

where $n$ is the number of test picks; $\hat{F}(t)$ is the equivalent force of the test pick at time $t$ after processing; $F_{i} (t + \tau_{i} )$ is the force of the $i$-th test pick at time $t + \tau_{i}$. Where $\tau_{i}$ denotes the time required for the $i$-th pick to rotate clockwise to the same position as the first test pick, using the first test pick as a reference. $\tau_{i} = \frac{{\varpi_{i} }}{\omega }$, where $\varpi_{i}$ represents the angular difference between the $i$-th test pick and the 1st test pick, and $\omega$ is the drum angular velocity.

The experimental data for each test pick under the no-load condition, slant-cutting condition, and straight-ahead regular cutting condition of the shearer were selected. For each working condition, 6000 sampling points were collected for each test pick. These data were processed using Eq. (1) to construct the time history curves of the equivalent pick load under different working conditions, as shown in Fig. 10.

Fig. 10

Time history curve of the equivalent pick load.

Analysis of Fig. 10 shows that under the slant-cutting and straight-ahead regular cutting conditions, the equivalent cutting load of the test picks exhibits a certain degree of periodicity. However, under the no-load condition, the obtained load data is disordered, weakly periodic, and much smaller than the pick loads under straight-ahead regular cutting and slant-cutting conditions. Therefore, this part of the load data is noise caused by factors such as the vibration of the shearer body, internal transmission mechanisms, and hydraulic system operation.

Firstly, mathematical and statistical analysis of the no-load noise data is performed, which means that the mean value $\mu_{x}$, standard deviation $\sigma_{x}$, skew coefficient $\gamma_{1}$, and kurtosis coefficient $\gamma_{2}$ of the no-load noise data are calculated. The calculation formulas are as follows:

$$\left\{ {\begin{array}{*{20}c} {\mu_{x} = E[X]} \\ {\sigma_{x} = \sqrt {E[(X - \mu_{x} )^{2} ]} } \\ {\gamma_{1} = \frac{{E[(X - \mu_{x} )^{3} ]}}{{\sigma_{x}^{3} }}} \\ {\gamma_{2} = \frac{{E[(X - \mu_{x} )^{4} ]}}{{\sigma_{x}^{4} }}} \\ \end{array} } \right.$$

(2)

where $X$ is the no-load noise data.

The mean value $\mu_{x} = 17.8{8}$, standard deviation $\sigma_{x} = 7.{79}$, skew coefficient $\gamma_{1} = 1.2{6}$, and kurtosis coefficient $\gamma_{2} = 4.6{6}$ of the no-load noise data can be calculated. The probability density histogram of the no-load noise data and the probability density curve are plotted as shown in Fig. 11.

Fig. 11

No-load noise probability density diagram.

Based on the shape of the no-load noise probability density curve in Fig. 11 and the magnitude of the skew coefficient $\gamma_{1}$ and kurtosis coefficient $\gamma_{2}$,the no-load noise data may obey the gamma distribution, and its probability density function expression is:

$$G(\alpha ,\beta ) = \frac{{\beta^{\alpha } }}{\Gamma (\alpha )}x^{\alpha - 1} e^{ - \beta x} ,x > 0$$

(3)

where $\Gamma (\alpha )$ is the gamma function. Using the parameter estimation with a 95% degree of confidence, the parameters with a gamma distribution of the no-load noise data are obtained as $\alpha = {6}{{.08}}$ and $\beta = 2.9{4}$. The method of Kolmogorov–Smirnov hypothesis testing is used to verify that the no-load noise signal obeys the gamma distribution, which is $G({6}{{.08}},2.9{4})$.

Improved VMD algorithm

Traditional VMD algorithm

VMD was proposed by Konstantin Dragomiretskiy and Dominique Zosso¹⁸ in 2014. The algorithm is based on Wiener filtering, Hilbert transform, and hybrid frequency, adaptively decomposing the signal into a series of pattern components with sparse characteristics.

The purpose of VMD is to decompose the signal $x(t)$ to be analyzed into a mode signal $u_{k} (t)$ with a specific sparsity, the mode signal $u_{k} (t)$ can be expressed as:

$$u_{k} (t) = A_{k} (t)\cos (\phi_{k} (t))$$

(4)

where $A_{k} (t)$ is the non-negative envelope and $\phi_{k} (t)$ is the phase.

The analytical signal for each mode signal $u_{k} (t)$ is calculated using the Hilbert transform as:

$$\xi_{k} = (\delta (t) + \frac{j}{\pi t}) \cdot u_{k} (t)$$

(5)

The spectrum of each mode signal is modulated to the corresponding fundamental frequency band, which is:

$$\overline{\xi }_{k} = \left[ {(\delta (t) + \frac{j}{\pi t}) \cdot u_{k} (t)} \right]e^{{ - j\omega_{k} t}}$$

(6 )

The bandwidth of each mode signal is estimated, and the sum of all estimated bandwidths is minimized, and the corresponding variational equation is:

$$\left\{ {\begin{array}{*{20}c} {\mathop {\min }\limits_{{\{ u_{k} (t),\omega_{k} \} }} \left\{ {\sum\limits_{k} {\left\| {\partial_{t} (\overline{\xi }_{k} (t))} \right\|_{2}^{2} } } \right\}} \\ {{\text{s}}{\text{.t}}{. }\sum\limits_{k} {u_{k} (t) = x(t)} } \\ \end{array} } \right.$$

(7)

where $u_{k} (t) = \{ u_{1} (t), \cdots ,u_{K} (t)\}$, and $\omega_{k} = \{ \omega_{1} , \cdots ,\omega_{K} \}$.

By introducing a quadratic penalty factor $\alpha$ and a Lagrange multiplier $\lambda$, Eq. (8) is transformed into the unconstrained variational equation.

$$\begin{gathered} L(\{ u_{k} (t)\} ,\{ \omega_{k} \} ,\lambda ) = \alpha \sum\limits_{k} {\left\| {[\delta (t) + \frac{j}{\pi t}u_{k} (t)]e^{{ - j\omega_{k} t}} } \right\|}_{2}^{2} + \left\| {x(t) - \sum\limits_{k} {u_{k} (t)} } \right\|_{2}^{2} \hfill \\ + \left\langle {\lambda (t),x(t) - \sum\limits_{k} {u_{k} (t)} } \right\rangle \hfill \\ \end{gathered}$$

(8)

The alternating direction multiplicative optimization algorithm can be used to solve the minimum value problem of Eq. (8).

$$\left\{ {\begin{array}{*{20}c} {u_{k}^{n + 1} (t) \leftarrow \arg \min L(\{ u_{i < k}^{n + 1} \} ,\{ u_{i \ge k}^{n} \} ,\{ \omega_{i}^{n} \} ,\lambda^{n} )} \\ {\omega_{k}^{n + 1} \leftarrow \arg \min L(\{ u_{i}^{n + 1} \} ,\{ \omega_{i < k}^{n + 1} \} ,\{ \omega_{i \ge k}^{n} \} ,\lambda^{n} )} \\ {\lambda^{n + 1} \leftarrow \lambda^{n} + \gamma (x(t) - \sum\limits_{k} {u_{k}^{n + 1} (t)} )} \\ \end{array} } \right.$$

(9)

where $\gamma$ is the noise margin.

Improved VMD algorithm

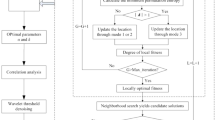
Since the number of decomposition layers $K$ and the quadratic penalty factor $\alpha$ of the VMD algorithm significantly influence the denoising results. In this paper, the multi-scale permutation entropy (MPE) will be used as the judging criterion for the decomposition effect of the VMD algorithm, and the Levenberg-Marguardt algorithm will be used to find the optimal number of decomposition layers $K$ and the quadratic penalty factor $\alpha$ for a given range.

The signal $x(t)$ is coarse-grained and re-segmented to construct a multi-timescale series, and then each coarse-grained time series is calculated, which is:

$$y_{j}^{(s)} = \frac{1}{s}\sum\limits_{i = (j - 1)s + 1}^{js} {x_{i} } ,j = 1,2,...,[N/s]$$

(10)

where $s$ is the scale factor, $N$ is the length of the original signal, and $[N/s]$ denotes the rounding of $N{\text{/s}}$.

The phase space reconstruction is performed for the coarse-grained series $y^{(s)}$, and the matrix $Y^{(s)}$ is obtained as:

$$Y_{j}^{{^{{({\text{s}})}} }} = \left[ {\begin{array}{*{20}c} {x^{(s)} (1)} & {x^{(s)} (1 + \tau )} & \cdots & {x^{(s)} (1 + (d - 1)\tau )} \\ {x^{(s)} (2)} & {x^{(s)} (2 + \tau )} & \cdots & {x^{(s)} (2 + (d - 1)\tau )} \\ {x^{(s)} (j)} & {x^{(s)} (j + \tau )} & \cdots & {x^{(s)} (j + (d - 1)\tau )} \\ \vdots & \vdots & \ddots & \vdots \\ {x^{(s)} (K)} & {x^{(s)} (K + \tau )} & \cdots & {x^{(s)} (K + (d - 1)\tau )} \\ \end{array} } \right]$$

(11)

where $d$ is the embedding dimension, which can be calculated using the false nearest neighbors algorithm (FNN). $\tau$ is the delay time, which can be calculated using the average mutual information (AMI). $K$ is the number of reconstructed components in the reconstructed space, $K = N - (d - 1)\tau$.

Every row in matrix $Y_{j}^{(s)}$ is the reconstruction component, and there are $K$ reconstruction components. For each reconstructed component, re-arranged in ascending order, each row in $Y_{j}^{(s)}$ yields a set of symbolic series, which is:

$$s(v) = \{ j_{1} ,j_{2} ,j_{3} \cdots ,j_{d} \}$$

(12)

where the number of $s(v)$ is the same as the number of reconstructed series $d!$.

Permutation entropy $H_{P}$ at different scales:

$$H_{P} (d) = - \sum\limits_{v = 1}^{V} {P_{v} \ln } P_{v}$$

(13)

where $P_{v}$ is the appearance probability of the $v$ th serial number.

The Levenberg-Marguardt algorithm is one of the most effective methods for solving optimization problems, with the advantages of global convergence, fast convergence, and high accuracy, and can perform a dynamic search for an optimal number of decomposition layers $K$ and quadratic penalty factor $\alpha$ of the VMD algorithm.

Algorithm: MPE-VMD algorithm.

where $\eta$ is the damping factor,$\theta$ is the amplification factor,$\varepsilon$ is the allowance error and $I_{{{\text{max}}}}$ is the maximum number of iterations.

Evaluation indexes

The evaluation of the denoising effect can generally be discriminated by five indexes: root mean square error (RMSE), signal-to-noise ratio (SNR), square ($R^{{2}}$), peak signal-to-noise ratio (PSNR), and correlation coefficient (cc).

RMSE is an indicator used to measure the error between the denoised signal and the reference signal, reflecting the average magnitude of the error. It is simple, intuitive, and easy to implement. RMSE reflects the absolute error between the signal and the denoised signal, with smaller values indicating better denoising performance. This is expressed in Eq. (14a).

SNR is used to measure the energy ratio of the signal relative to the noise, typically expressed in decibels (dB). It directly measures the relative relationship between the signal and the noise. SNR reflects the ratio of signal strength to noise strength, with larger values indicating better signal quality. This is expressed in Eq. (14b).

$R^{{2}}$ is an indicator used to measure the degree of signal fitting, reflecting the linear correlation between the reference signal and the denoised signal. It assesses the overall fitting effect between the signal and the reference signal. The value of $R^{{2}}$ ranges from [0, 1] (and may be negative in some cases), with values closer to 1 indicating a better fit. This is expressed in Eq. (14c).

PSNR is an extension of SNR that incorporates the peak amplitude of the signal for evaluation. It is commonly used to assess images or signals with a fixed dynamic range and is easy to interpret. PSNR is typically used for signals with a fixed dynamic range, such as images or audio. Larger values indicate better denoising performance, and it is expressed in Eq. (14d).

CC reflects the linear correlation between two signals and is sensitive to linear dependencies. The value of CC ranges from [− 1, 1], and when the value is close to 1, it indicates a high correlation in shape between the signal and the denoised signal. This is expressed in Eq. (14e).

$$S_{RMSE} = \sqrt {\frac{{1}}{n}\sum\limits_{i = 1}^{n} {\left[ {x_{d} (i) - x_{o} (i)} \right]^{2} } }$$

(14a)

$$S_{{{\text{SNR}}}} = {\text{10log}}_{{{10}}} \frac{{\sum\limits_{i = 1}^{n} {x_{o}^{{2}} (i)} }}{{\sum\limits_{i = 1}^{n} {\left[ {x_{d} (i) - x_{o} (i)} \right]^{2} } }}$$

(14b)

$$S_{{R^{{2}} }} = {1 - }\frac{{\sum\limits_{i = 1}^{n} {[x_{d} (i) - x_{o} (i)]^{2} } }}{{\sum\limits_{i = 1}^{n} {[x_{o} (i) - \overline{{x_{o} (i)}} ]^{2} } }}$$

(14c)

$$S_{{{\text{PSNR}}}} = {\text{10log}}_{{{10}}} \frac{{\sum\limits_{i = 1}^{n} {\max^{2} } }}{{\sum\limits_{i = 1}^{n} {\left[ {x_{d} (i) - x_{o} (i)} \right]^{2} } }}$$

(14d)

$$S_{{{\text{cc}}}} = \frac{{\left\{ {\sum\limits_{i = 1}^{n} {\left[ {x_{d} (i) - \overline{{x_{d} (i)}} } \right] \cdot \left[ {x_{d} (i) - \overline{{x_{d} (i)}} } \right]} } \right\}^{2} }}{{\sum\limits_{i = 1}^{n} {\left[ {x_{d} (i) - \overline{{x_{d} (i)}} } \right]^{2} \cdot \sum\limits_{i = 1}^{n} {\left[ {x_{o} (i) - \overline{{x_{o} (i)}} } \right]^{2} } } }}$$

(14e)

where $x_{o} (i)$ is the original signal, $x_{d} (i)$ is the denoised signal, $\overline{{x_{o} (i)}}$ is the mean value of the original signal, and $\overline{{x_{d} (i)}}$ is the mean value of the denoised signal.

Simulation

In order to test the denoising effect of the multi-scale permutation entropy-based variational modal decomposition algorithm (MPE-VMD) proposed in this paper, three signals with similar characteristics to the picks load signals are selected as test signals. Since the load signals of regular cutting and slant-cutting have certain periodicity and mutability, the Blocks signal, Bumps signal, and Doppler signal are selected as the test signals. The Blocks signal consists of a series of stepwise segmented constants, with sudden jumps between segments, displaying distinct discontinuities. This behavior is analogous to the sudden load changes caused by varying cutting conditions during shearer cutting experiments. Therefore, the Blocks signal is selected as a test signal. The Bumps signal is composed of multiple local peaks, each with varying shapes, positions, and widths, presenting multiple irregular spike-like changes. This signal resembles the real-world load fluctuations encountered by underground shearers when encountering hard rock or interbedded gangue. Thus, the Bumps signal is chosen for testing. The Doppler signal is a non-stationary periodic signal that varies over time, with its frequency and amplitude undergoing complex dynamic changes. Its complex dynamic behavior is similar to the load signals collected during memory cutting operations in underground coal mining, particularly when encountering faults or interbedded gangue, with simultaneous adjustments to drum rotation and traction speed. Therefore, the Doppler signal is used as a representative test signal. These three signals simulate different characteristics of signals: the Blocks signal simulates the abrupt change characteristics of a signal, the Bumps signal simulates the local detail characteristics, and the Doppler signal simulates the complex frequency variation characteristics. Together, they comprehensively examine the ability of denoising algorithms to balance preserving the key features of the signal and suppressing noise, thus providing a thorough evaluation of the algorithm’s performance. The images of these three signals are shown in Fig. 12. The noise signal obeying the gamma distribution $G({6}{{.08}},2.9{4})$ is added to the test signal, and the test signal containing noise is obtained as shown in Fig. 13.

Fig. 12

Original signal.

Fig. 13

Signal with noise.

In order to compare the denoising ability of MPE-VMD proposed in this paper horizontally, the blocks, bumps, and doppler signals containing noise are now denoised by EMD, WT, VMD, and MPE-VMD algorithms, respectively, and the denoising effect plots are obtained as shown in Figs. 14, 15, 16 and 17.

Fig. 14

EMD.

Fig. 15

WT.

Fig. 16

VMD.

Fig. 17

MPE-VMD.

The analysis of Figs. 14, 15, 16 and 17 shows that in the denoising effect of blocks signal, the signal has noticeable distortion after denoising using the EMD algorithm, the signal has a large peak and jitter after denoising using the WT algorithm, and it is relatively better using VMD algorithm and MPE-VMD algorithm. On the denoising effect of the bumps signal, the signal still has certain distortion after denoising by the EMD algorithm, the bottom of the signal has certain fluctuation after denoising by the VMD algorithm, and the denoising effect of the WT algorithm and MPE-VMD algorithm is promising. On the denoising effect of the doppler signal, the VMD algorithm has some fluctuation in the early stage of the signal after denoising, and there is a big difference with the original signal. The other three algorithms have achieved good results. In general, the MPE-VMD algorithm has the best denoising effect.

In order to achieve a more intuitive representation and quantitative analysis of the denoising effect of the test signal, signal-to-noise ratio (SNR), peak signal-to-noise ratio (PSNR), square ($R^{{2}}$), root mean square error (RMSE), and correlation coefficient (CC), which are five parameters, are used to evaluate the denoising effect. In addition, the computational time required by each algorithm was considered. The evaluation of the denoising effect for the four algorithms is shown in Table 4, and a radar plot is drawn based on the evaluation indexes as shown in Fig. 18.

Table 4 Evaluation table of denoising effect.

Fig. 18

Radar plot of denoising indexes.

The analysis in Table 4 shows that when denoising the block signal containing noise, the five indexes of SNR, PSNR, $R^{{2}}$, RMSE, and CC of the MPE-VMD algorithm are optimal, which are 36.00 dB, 42.45 dB, 0.9988, 20.61, and 0.9997, respectively. The five indexes of SNR, PSNR, $R^{{2}}$, RMSE, and CC of the EMD algorithm are the worst, which are 10.19 dB, 16.28 dB, 0.5259, 402.5, and 0.5268, respectively. When denoising the bumps signal containing noise, the four indexes of SNR, PSNR, $R^{{2}}$, and RMSE of the MPE-VMD algorithm are the best, which are 37.10 dB, 45.56 dB, 0.9997, and 18.16, respectively, and the CC index of the WT algorithm is the best, which is 0.9991. The five indexes of SNR, PSNR, $R^{{2}}$, RMSE, and CC of the EMD algorithm are the worst, which are 17.15 dB, 25.57 dB, 0.9706, 180.5, and 0.9719, respectively. When denoising the doppler signal containing noise, the four indexes of SNR, PSNR, $R^{{2}}$, and RMSE of the MPE-VMD algorithm are the best, which are 37.10 dB, 41.55 dB, 0.9993, and 18.17, respectively, and the CC index of WT algorithm is the best, which is 0.9996. The five indexes of SNR, PSNR, $R^{{2}}$, RMSE, and CC of the EMD algorithm are the worst, which are 19.618 dB, 23.98 dB, 0.9608, 136, and 0.9672, respectively. In terms of denoising time efficiency, the WT algorithm is the fastest, while the proposed MPE-VMD algorithm takes the longest. However, all processing times are under 0.5 s for 6000 noisy signal data points, which is acceptable for practical applications.

The combined effect of the denoising ability of different algorithms can be more intuitively obtained from the analysis of Fig. 18. In the radar plot, the area enclosed by the five index points of different denoising algorithms is the comprehensive performance of the denoising ability. The larger the enclosed area, the stronger the denoising ability is. The denoising ability for the block signal containing noise is MPE-VMD, VMD, WT, and EMD in descending order. The denoising ability for bumps signal containing noise is MPE-VMD, WT, VMD, and EMD in descending order. The denoising ability for doppler signal containing noise is MPE-VMD, WT, VMD, and EMD in descending order. Comparing the comprehensive ability of the four denoising algorithms, which are MPE-VMD, WT, VMD, and EMD, the MPE-VMD algorithm proposed in this paper has the best denoising effect, followed by WT, and then VMD and EMD have the worst denoising effect.

Practical application

Algorithm implementation

The proposed MPE-VMD algorithm is applied to denoise the pick load signals under two operating conditions—straight-ahead regular cutting and slant-cutting—as shown in Fig. 10. The resulting time course curve of picks load after denoising are presented in Fig. 19, and the statistical parameters before and after denoising are summarized in Table 5.

Fig. 19

Time course curve of picks load after denoising.

Table 5 Statistical analysis before and after denoising.

As shown in Fig. 19, the denoised signals appear smoother with reduced jitter, indicating that most of the noise has been effectively removed while preserving the original peak features. The closely spaced peaks correspond to coal breaking by the picks, while the flat regions represent idle cutting states. Compared to the raw data, the denoised signal more accurately reflects the true characteristics of the load. According to Table 5, the mean values remain nearly unchanged after denoising under both straight-ahead regular cutting and slant-cutting conditions, while the peak values and standard deviations are notably reduced.

Robustness validation

To further verify the practical applicability of the proposed algorithm, robustness testing was conducted using three common types of faulty signals: signal interruption, external noise, and abrupt signal mutation. These fault types were introduced under two operating conditions—straight-ahead regular cutting and slant-cutting entry—as shown in Fig. 10. The resulting load signals under these fault conditions are illustrated in Figs. 20 and 21. The proposed MPE-VMD algorithm was then applied to denoise these signals, with the resulting denoised load signals presented in Figs. 22 and 23.

Fig. 20

Load signal with faults under straight-ahead regular cutting conditions.

Fig. 21

Load signal with faults under slant-cutting conditions.

Fig. 22

Denoised load signal with faults under straight-ahead regular cutting conditions.

Fig. 23

Denoised load signal with faults under slant-cutting conditions.

A comparative analysis of Figs. 22 and 23 with Figs. 20 and 21 reveals the following observations: for load signals with signal interruption faults, both the denoised straight-ahead regular cutting and slant-cutting signals successfully retain the fault-related discontinuities; for signals with external noise, the denoised signals under both operating conditions effectively eliminate most of the external noise components; and for signals with abrupt signal mutations, the denoised signals still exhibit some residual transients, but the amplitudes of these abrupt changes are significantly reduced.To further quantify the analysis results, the signal in Fig. 19 was used as the original signal. The corresponding signals in Figs. 22 and 23 were compared against it using five evaluation metrics: signal-to-noise ratio (SNR), peak signal-to-noise ratio (PSNR), square ($R^{{2}}$), root mean square error (RMSE), and correlation coefficient (CC). The evaluation results are summarized in Table 6.

Table 6 Quantitative evaluation of denoising performance.

As shown in Table 6, the signal-to-noise ratio (SNR) ranges from 8.058 to 25.514 dB, with the highest SNR observed for the slant-cutting signal containing abrupt signal mutation faults, and the lowest for the straight-ahead regular cutting signal with signal interruption faults. The peak signal-to-noise ratio (PSNR) ranges from 16.079 to 34.877 dB, with the highest PSNR for the straight-ahead regular signal containing abrupt signal mutation faults and the lowest for the slant-cutting signal with signal interruption faults. The square($R^{{2}}$) spans from 0.375 to 0.991, reaching its maximum for the slant-cutting signal with abrupt signal mutation faults and its minimum for the straight-ahead regular cutting signal with signal interruption faults. The root mean square error (RMSE) falls between 42.947 and 505.477, with the lowest RMSE for the slant-cutting signal with abrupt signal mutation faults and the highest for the straight-ahead regular cutting signal with signal interruption faults. The correlation coefficient (CC) ranges from 0.593 to 0.991, with the slant-cutting signal containing abrupt signal mutation faults having the highest CC and the straight-ahead regular cutting signal with signal interruption faults the lowest. Overall, these five metrics (SNR, PSNR, $R^{{2}}$, RMSE, and CC) indicate that the proposed algorithm demonstrates strong robustness against abrupt signal mutation and external noise faults, while its performance against signal interruption faults is relatively weaker in comparison.

Application and deployment scheme

To further facilitate practical engineering applications, a deployment scheme for load signal acquisition, data analysis, and denoising processing in underground environments was developed, as illustrated in Fig. 24. The DH1210 strain sensor, embedded inside the cutting pick, converts the stress signals into voltage signals, which are transmitted via cables to a wireless strain acquisition module. The signals are then sent through the Beenet wireless protocol to a wireless gateway, which connects to the underground industrial Ethernet via a mining switch. From there, the signals are transmitted to an aboveground industrial PC (IPC) through the ring network. The IPC, equipped with data acquisition and analysis software developed on the MATLAB platform, performs denoising and visualization of the acquired load signals.

Fig. 24

Deployment scheme.

Conclusions

In order to more accurately analyze the cutting load signal characteristics of shearer picks, an MPE-VMD denoising algorithm is proposed in this paper. Based on the characteristics of the collected load signals of the picks under regular cutting conditions and slant-cutting conditions, blocks, bumps, and doppler are selected as the test signals, respectively. The statistical parameters and distribution characteristics of the no-load picks load signal are extracted and introduced into the test signal as a noise signal. The MPE-VMD algorithm proposed in this paper and WT, VMD, and EMD algorithms are used to denoise the test signals, respectively, and the five parameters of signal-to-noise ratio (SNR), peak signal-to-noise ratio (PSNR), square ($R^{{2}}$), root mean square error (RMSE), and correlation coefficient (CC) are used as evaluation indexes. From the comparison of the comprehensive denoising ability of the four denoising algorithms, which are MPE-VMD, WT, VMD, and EMD, the MPE-VMD algorithm proposed in this paper has the best denoising effect, followed by the WT algorithm, then the VMD algorithm, and the EMD algorithm has the worst denoising effect. Finally, the method of this paper is applied to the actual picks signal denoising process, and the denoising result reduces the noise in the signal while retaining the same mutation characteristics of the original signal, thus verifying the practicality and feasibility of this method.