Introduction

Time series forecasting plays a crucial role in many applications such as energy consumption planning1, traffic flow analysis2, financial risk assessment3 and cloud resource allocation4. Time series data recorded from the real world usually exhibit diverse and unsteady characteristics due to the complex transient conditions experienced during their evolution5. This phenomenon reflects the complexity and diversity of time series data in real-world applications and poses challenges for their analysis and modeling (i.e., distributional shifts induced by time series non-stationarity)6.

A recent approach to solve the above distributional bias problem is to utilize plug-and-play normalization methods, Kim et al7 proposed a method called reversible instance normalization (RevIN), RevIN consists of two distinct steps, normalization and unnormalization. The former normalizes the input to fix its distribution based on the mean and variance, while the latter returns the output to the original distribution. To alleviate the challenges posed by non-stationarity in time-series data, Liu et al8 proposed SAN (Slice-Level Adaptive Normalization), a flexible normalization and denormalization scheme that removes non-stationarity and independently models variations in the statistical properties of the original time-series data through local time slices, thus achieving prediction performance improvement on a wide range of benchmark prediction models The prediction performance improvement is realized on a variety of benchmark prediction models. To address the challenges posed by complex non-uniform distributions and pattern drift in real time-series data, Sun et al9 proposed the TFPS (Time-Frequency Pattern Specific) architecture, which utilizes pattern-specific expert modules in combination with bi-domain encoders and subspace clustering techniques to dynamically identify and model unique patterns in data segments, which This results in significantly improved prediction accuracy.Fan et al10 systematically summarized the distribution drift problem in temporal prediction and classified it into distribution changes within the input space (recall window) and output space (prediction window) (internal space drift) and distribution differences between the input and output spaces (cross-space drift). Meanwhile, Dish-TS, a generalized neural architecture, is proposed to effectively mitigate the effects of distributional drift by learning and adjusting the distributions in the input and output spaces respectively through a dual-coefficient network (Dual-CONET). All of these methods normalize the input time series to a uniform distribution, explicitly removing non-smoothness to reduce the differences in data distribution.

However, non-stationarity is an inherent property of real-world time series, and also good guidance for discovering temporal dependencies for forecasting.In experiments, it has been found that direct smoothing of time-series data causes ordinary transformer models to lose the ability to capture the important event-based temporal dependencies in the data. That is, the data loses important non-stationarity properties during the smoothing process, causing the model to fail to correctly capture eventful changes in the data and limiting the model’s forecasting ability, a problem known as over-stationarization. It is precisely these important non-stationarity properties that should be the focus of the attention mechanism, such as drastic changes in traffic flow due to traffic accidents, abnormal sensor readings due to sudden equipment failures, and meteorological data variations due to sudden rainstorms. However, designing highly complex and nonlinear deep model structures for better learning of non-stationarity features to solve the problem of unpredictable event-based changes will lead to severe overfitting (validation loss increases significantly and training loss still decreases sharply). Therefore, how to reduce the time series non-stationarity to improve predictability while avoiding the problem of model overfitting is a key issue to further improve the prediction performance.

Fig. 1
figure 1

Examples of forecasts of energy consumption and illustrations of their daily averages (MeanByDay). We also plot the mean of the input sequence and the mean of the horizon sequence in the figure.

Full size image

In this paper, a sample of predictions is plotted in Fig. 1 to better illustrate our observations. Despite the temporal correlation, the mean values of the input sequences are significantly different from the mean values of the field-of-view window (from 35.79 to 48.3), suggesting that there may be a generalized distributional shift. Furthermore, this distributional bias can change rapidly at finer-grained slice levels, and this rapid change violates the underlying assumptions of existing normalization methods (which typically assume that the distribution of the input data is relatively stable). As a result, the use of inappropriate normalization methods not only destroys the intrinsic pattern of the input series, but also leads to bias in the final prediction results.

In this paper, we explore the impact of non-stationarity in time series forecasting and propose NSPLformers as a general framework. The framework consists of two interdependent modules and a two-stream asymptotic learning architecture: Series Stationarization for improving the predictability of non-stationarity time series; and De-stationary Attention for mitigating the over-stationarization problem. Specifically, Series Stationarization employs a simple but effective normalization strategy that unifies the statistical properties of each time series without additional parameters, while De-stationary Attention approximates the attention mechanism of the original data and compensates for the inherent non-stationarity of the original time series. The architecture of Dual Data Stream Progressive Learning utilizes the concept of de-redundancy to propose a progressive learning approach aimed at systematically acquiring the components of the supervised signals to improve the performance of time series (TS) prediction. And an auxiliary output stream is introduced in each Block to form a highway that gradually guides to the final prediction. The subsequent Block outputs of this output stream will subtract the previously learned results layer by layer, enabling the model to gradually learn the residual parts of the supervised signal. The dual data stream design further facilitates the implicit layer-by-layer decomposition of the input and output streams, enhancing the model’s flexibility, interpretability, and resistance to overfitting.

The contribution of this paper is threefold:

  • The predictive ability of non-stationary sequences is crucial in actual predictions. Through detailed analysis, it was found that the current stationarisation method leads to over-stationarisation, thereby limiting the predictive ability of Transformers;

  • We propose a low-cost non-stationary progressive learning Transformer, which includes sequence smoothing to improve sequence predictability, de-smoothing attention mechanisms, and progressive learning modules. We simplify the attention mechanism calculation using low-rank approximation methods to reduce complexity and reintroduce the non-stationarity of the original sequence to avoid over-stationarization issues;

  • This paper constructs a dual data stream design that promotes implicit gradual decomposition of input and output streams based on incremental learning through auxiliary output streams and improved information aggregation mechanisms, thereby giving the model greater flexibility, interpretability, and resistance to overfitting, effectively resolving the dilemma between sequence predictability and model capability.

Related work

In recent years, due to the powerful nonlinear fitting capabilities of deep learning11, time series prediction models have been applied to various fields such as medicine12,13,14 , petroleum exploration15, industrial production16,17, classification detection1819, and many others. However, time series (TS) from the real world often exhibit various non-stationary characteristics due to their evolution under complex transient conditions5. The characteristics of non-stationary time series are reflected in the continuous changes in their statistical properties and joint distributions20, making accurate prediction extremely challenging.21 As a result, numerous scholars have conducted research on the prediction of non-stationary time series.

Transformer-based time series forecaster

Recently, deep learning models have achieved remarkable success in time series prediction, in order to capture the long-term coupling of inputs and outputs over a long period of time, Zhou et al designed a transformer-based Informer for long-series time series forecasting (LSTF), which overcomes the limitations of the traditional Transformer by introducing the ProbSparse self-attention mechanism, self-attention distillation and generative decoder, which overcomes the limitations of quadratic time complexity, high memory consumption, and encoder-decoder architecture of traditional Transformer.22.WU et al aimed to solve the long time series prediction problem by proposing a novel decomposition architecture with autocorrelation mechanism, which enables the model to have the capability of progressive decomposition of complex time series, correlation discovery and representation aggregation at the subsequence level level23. Liu et al proposed a novel neural network architecture called SCINet to efficiently model and predict time series through recursive downsampling, convolution, and interactive operations24. Nie et al proposed an efficient design of a multivariate time series prediction and self-supervised representation learning model based on the Transformer, the model is based on two key components:(i) segmentation of time series into sub-series level patches; and (ii) channel independence, which achieves retention of local semantic information, quadratic reduction in computation and memory usage of the attention graph and the ability of the model to focus on longer histories25. Zhang et al. proposed a Crossformer named Transformer base model, which effectively captures cross-time dependencies and cross-dimensional dependencies in multivariate time series (MTS) by introducing Dimension-Segment-Wise (DSW) embedding and Two-Stage Attention (TSA) layer, and establishes a Hierarchical Encoder-Decoder (HED) architecture to utilize different scales of information, experimental results show that Crossformer significantly outperforms previous state-of-the-art approaches on six real-world datasets26. Considering the limitations of point-by-point representations in terms of local semantics, liu et al.27 proposed a model named iTransformer to efficiently capture cross-variate correlations in multivariate time series and learn nonlinear representations by inverting the functionality of the attention mechanism and feedforward network in Transformer. These models aim to extract diverse and informative patterns from historical observations to improve the accuracy of time series forecasting. In order to improve the accuracy of real-world time series forecasting, the key challenge is twofold, on the one hand, the fact that data from numerous real-world data series data exhibit exhibit dynamic and evolving patterns, a phenomenon known as non-stationary. This property usually leads to training and testing This property usually leads to inconsistent distributions between the training set, the testing set, and the future unseen data set. Thus, the non-stationary property in time-series data requires the development of robust predictive models that can cope with the variation of such data distributions over time, and failure to address this challenge often leads to reduced representational power and impaired model generalization. On the other hand, there is the phenomenon of overfitting when deep models learn high-dimensional non-stationary features of emergent events, which usually manifests itself as feature redundancy, poor interpretability and weak generalisation.

Redundancy-reduced progressive learning

A new training strategy based on progressive learning was proposed by Zhou et al. By equipping each low-precision convolutional layer with an auxiliary full-precision convolutional layer based on the low-precision network structure. At the same time, a decay method is introduced to gradually reduce the output of the added full-precision convolutional layer, thus keeping the topology the same as the original low-precision convolutional layer, and realising the progressive learning strategy28. A stepwise approach for learning independent hierarchical representations and realizing the learning of representations from high-level to low-level in the VAE framework. The effectiveness of the approach in decoupling representation learning is confirmed by quantitative and qualitative evaluations on a benchmark dataset and is the first attempt to progressively extend the VAE capacity to learn hierarchical representations for improved decoupling29. Zhao et al proposed a three-stage learning framework for retrieval by gradually learning complex knowledge of mixed-modal queries and introduced a self-supervised adaptive weighting strategy30. The above methods attempt sequence decomposition applied to the input sequence to enhance the predictability of the time series and reduce the impact of algorithmic complexity on the model. However, the mainstream time series prediction algorithms are susceptible to severe overfitting when the original sequence has strong non-stationarity. In this paper, the proposed method mitigates the overfitting problem by implicitly decomposing the supervised signals by learning each time-varying pattern through progressive bootstrapping.

NSPLformer

As mentioned earlier, stationary is an important component of time series predictability. Previous research efforts have focused on “direct smoothing” to reduce the non-smoothness of the series in order to obtain better predictability. However, non-stationarity is an inherent property of real-world time series, and the design of “direct smoothing” will lead to over-stationarization of the model, and the design of complex deep models to learn unprocessed non-stationary features will lead to severe overfitting of the model. To solve the above dilemma, this paper proposes NSPLformer (Non-stationary Progressively Learning Transformer). The model involves: Series Stationarization to attenuate the time series non-stationarity, De-stationary Attention mechanism to recombine the non-stationary features of the original series, and a design of the dual data stream model structure to suppress overfitting. As Fig. 2, with the support of these designs, the model can improve time series data predictability while maintaining model capability.

Series stationarization

The statistical properties (e.g., mean and standard deviation) of non-stationary time series change during the inference process, which makes it difficult for the deep model to perform effective generalized prediction. Therefore, in this paper, in terms of dealing with the non-stationarity of the original time series, the normalization module is designed to firstly deal with the non-stationary series caused by different data distributions, and finally the inverse normalization module restores the model output to the original statistical characteristics.Here are the details.

Fig. 2
figure 2

NSPLformer normalizes and denormalizes the input series by smoothing and adjusts the time-dependent weights using the de-smoothing attention mechanism to better handle non-smooth time series.

Full size image

Normalization moudule Existing normalization methods for non-stationary time series prediction are to normalize the input series to remove non-stationary factors and restore them to the output series by denormalization. As Fig. 3 the method in this paper differs from it in that by slicing the input sequence into multiple non-overlapping slices and performing a local normalization operation on each slice, it is able to effectively remove the non-stationary factors while preserving the intrinsic pattern of each slice.

Fig. 3
figure 3

This section proposes a model-independent symmetric normalization module that removes and recovers non-stationary factors from time series data from a slicing perspective.

Full size image

This local processing is more advantageous than the global normalization method, especially when dealing with complex non-stationary time series. Eventually, the normalized slices are recombined into a new input sequence by an inverse normalization step. The input \(x^i\) is first split into M non-overlapping slices \(\{x_j^i\}_{j=1}^{M}\), where the mean and standard deviation of each slice \(x_j^i\) can be expressed as:

$$\begin{aligned} \mu _j^i = \frac{1}{T} \sum _{t=1}^T x_{j,t}^i,(\sigma _j^i)^2 = \frac{1}{T} \sum _{t=1}^T (x_{j,t}^i - \mu _j^i)^2 \end{aligned}$$
(1)

Where \(\mu _j^i,\sigma _j^i\in \mathbb {R}^{C \times 1}\) and \(x_{j,t}^i\) is the value of slice \(x_j^i\) at t-th time step.The normalized input sequence \(\bar{x}_j^i = \frac{x_j^i - \mu _i}{\sigma _i}\) can be expressed as:

$$\begin{aligned} \bar{x}_j^i =\frac{1}{\sigma _j^i + \epsilon }\cdot (x_j^i - \mu _j^i)^2 \end{aligned}$$
(2)

Where \(\cdot\) is the element-wise product and \(\epsilon\) is a small constant.Finally, a new input sequence with non-stationary factors removed is formed by recombining the slices and used as input to the prediction model.

De-normalization module In order to recover the characteristics of the original sequence, we apply a denormalization process to the model output \(\textbf{Y}' = [Y'_1, Y'_2, \ldots , Y'_O] ^T \in \mathbb {R}^ {O \times C} \) using the statistical parameters \(\mu _j^i\) and \(\sigma _j^i\) of the original sequence.In contrast to normalization, De-normalization is performed on a per-slice basis. For the predictive model output \(\textbf{Y}'\), which is split into K non-overlapping slices \(\{\bar{y}_j^i\}_{j=1}^K\), the statistically based inverse normalization of any slice can be expressed as

$$\begin{aligned} \hat{y}_j^i = \bar{y}_j^i \cdot (\sigma _j^i + \epsilon ) + \mu _j^i \end{aligned}$$
(3)

Finally, all slices are restored in chronological order. By leveraging the model’s translational and scaling equivariance, the normalization and de-normalization modules ensure that the model maintains high prediction stability and accuracy, even when the mean or amplitude of the input sequence changes. This robustness is crucial for reliable performance under varying input conditions.

De-stationary attention

In time series forecasting, although the statistical features can be recovered to the corresponding forecasts by inverse normalization, etc., the non-stationary nature of the original series cannot be fully recovered by simple inverse normalisation. Specifically, Series Stationarization can generate similar normalised inputs \(x^{\prime }\) based on different time series \(x_1\) and \(x_2\), and the basic model will get the same attention when processing these normalised inputs, thus failing to capture the temporal dependencies associated with the non-stationary. This phenomenon is particularly relevant in the case of attention computation. This phenomenon is particularly noticeable in the attention computation process. In addition, non-stationary time series tend to lose their intrinsic structure during stationarization and fragmentation, where these segments are forced to have the same mean and variance after back-normalisation, and are therefore closer to similar distributions than to the true distribution of the original data before normalisation. This results in models that are more likely to produce outputs that are over stationarization and lack variation, which contradicts the natural non-stationary nature of the original time series.

To address the problem of over-stationaryization caused by sequence normalisation, we propose a new De-stationary Attention Mechanism . The mechanism aims to approximate the attention distribution obtained when no normalisation is performed, thus enabling the identification and capture of specific temporal dependencies from raw non-stationary data, reducing the prediction error due to over-stationarization.

Analysis of the plain model As mentioned earlier, the over-stationarization problem stems from the disappearance of the inherent non-stationarity information in the original time series, which leads to the underlying model’s inability to capture eventful temporal dependencies for prediction. Therefore, we attempt to approximate the learned attention from the original non-stationary time series. The known self-attention mechanism31 is as follows:

$$\begin{aligned} \textrm{Attn}(Q, K, V) = \textrm{Softmax}\left( \frac{QK^T}{\sqrt{d_k}}\right) V \end{aligned}$$
(4)

Where \(Q, K, V \in \mathbb {R}^{S \times d_k}\) are the Queries, Keys, and Values of length S, respectively, all of dimension \(d_k\), and the \(\textrm{Softmax}(\cdot )\) operation is performed on a row-by-row basis. To simplify the analysis, it is assumed that the embedding layer and the feed-forward layer f have a linear nature and their operations are completely independent of each time point. That is, each \(q_i\) in \(Q = [q_1, q_2, \dots , q_S]^T\) can be expressed as \(q_i = f(x_i)\),where the input time series \(x = [x_1, x_2, \dots , x_S]^T.\)

Since it is common practice to stabilize each time series variable to avoid the over-dominance of scale by a particular variable, we assume that each variable of the time series x has the same variance. This simplification reduces the original vector of standard deviations \(\sigma _x \in \mathbb {R}^{C \times 1}\) to a scalar. After passing through the normalization module, the model receives a smoothed input of:

$$\begin{aligned} x' = \frac{x - 1 \mu _x^T}{\sigma _x} \end{aligned}$$
(5)

Where \(1 \in \mathbb {R}^{S \times 1}\) is a vector of all ones. Based on the above assumption of linear nature, it can be shown that the attention layer will receive the query vector \(Q'\) as:

$$\begin{aligned} Q' = [f(x'_1), \dots , f(x'_S)]^T = \frac{Q - 1 \mu _Q^T}{\sigma _x} \end{aligned}$$
(6)

where \(\mu _Q \in \mathbb {R}^{d_k \times 1}\) is the mean value of the query vector Q along the time dimension. Similarly, Key and Value are converted to \(K^{\prime }\) and \(V^{\prime }\) . The attention mechanism based on \(Q^{\prime }\) and \(K^{\prime }\) after stationarized is:

$$\begin{aligned} Q' K'^T = \frac{1}{\sigma _x^2} \left( QK^T - 1 \mu _Q^T K - K \mu _Q 1^T + 1 \mu _Q^T K \mu _Q 1^T \right) \end{aligned}$$
(7)
$$\begin{aligned} \textrm{Softmax}\left( \frac{QK^T}{\sqrt{d_k}}\right) = \textrm{Softmax}\left( \frac{\sigma _x^2 Q' K'^T + 1 (\mu _Q^T K)^T + (Q \mu _K) 1^T - 1 (\mu _Q^T \mu _K) 1^T}{\sqrt{d_k}}\right) \end{aligned}$$
(8)

where \(Q_{\mu K} \in \mathbb {R}^{S \times 1}\) and \(\mu _Q^T\mu _K \in \mathbb {R}\),These quantities are iteratively applied to each column and element of \(\sigma _x^2 Q^{\prime } K^{\prime T} \in R^{S \times S}\) during the computation. Using the translation invariance of the Softmax function, the computation of the attention mechanism can be simplified as follows:

$$\begin{aligned} \textrm{Softmax}\left( \frac{QK^T}{\sqrt{d_k}} \right) = \textrm{softmax}\left( \frac{\sigma _x^2 Q' K'^T + 1 \mu _Q^T K^T}{\sqrt{d_k}} \right) \end{aligned}$$
(9)

This section derives a direct expression for the attentional mechanism \(\textrm{Softmax}(QK^T/\sqrt{d_k})\) learnt from the original sequence x. In addition to \(Q^{\prime }\) and \(K^{\prime }\) in the stationarized time series \(x^{\prime }\), non-stationary information needs to be introduced, which is eliminated during the sequence stationarization process. Therefore, in order to recover the original non-stationary time series features, the lost non-stationary information needs to be reintroduced inside the depth model.

De-stationary Attention In order to restore the original attention to the non-stationary series, we try to introduce unappreciatednon-stationary information into its computation. Defining the approximate scaling scalar \(\tau = \sigma _x^2 \in \mathbb {R}^+\) and the displacement vector \(\Delta = K \mu _Q \in \mathbb {R}^{S \times 1}\) as the de-smoothing factors, this section try to learn the non-stationary factors directly from the non-stationary x, Q and K statistics by a simple but effective multilayer perceptron. Since we can only find limited non-stationary information from the known \(Q^{\prime },K^{\prime }\), a reasonable source for compensating non-stationarity at one time can only be the original sequence. Therefore, in this paper, we use a multilayer perceptron to map the input sequences into a high-dimensional space to learn the non-smooth factors \(\tau\) and \(\Delta\) from \(\sigma _x^2\),\({\sigma _j^i}^2\),x,\(\bar{x}_j^i\) respectively.And the De-stationary Attention is calculated as follows.

$$\begin{aligned} \begin{aligned} \log \tau= \text {MLP}\left( \sigma _x^2, (\sigma _j^i)^2, x, \overline{x}_j^i \right) \\ \Delta= \text {MLP}\left( \mu _x, \mu _j^i, x, \overline{x}_j^i \right) \\ \text {De-stationary}(Q', K', V', \tau , \Delta )= \text {Softmax}\left( \frac{\tau Q' {K'}^T + 1 \Delta ^T}{\sqrt{d_k}} \right) V' \end{aligned} \end{aligned}$$
(10)

The de-stationary factors \(\tau\) and \(\Delta\) are shared across all de-stationary attention layers. The de-stationary attention mechanism learns the temporal dependencies from the stationarized sequences \(Q^{\prime }\), \(K^{\prime }\) and the statistical properties of the original sequences \(\sigma _x^2\) ,\({\sigma _j^i}^2\),x,\(\bar{x}_j^i\) and multiplies them by the stationarized value \(V^{\prime }\) . Thus, it is able to exploit the predictability of the stationarized series while maintaining the time dependence inherent in the original series.

De-stationary attention is low rank

In this section, the non-stationary attention mechanism is optimised in terms of linear time and memory complexity. In this section, two linear projection matrices \(E,F \in \mathbb {R}^{n \times K}\) are added in the computation of key and value to reduce the computational cost of computing the context mapping matrix P based on the stochastic projection method. First, the original \(n \times d\) dimensional key and value layer is projected to the \(k \times d\) dimensional projected key and value layer, and then an \(n \times k\) dimensional context mapping matrix \(\bar{p}\) is computed using the scaled dot product attention mechanism.

$$\begin{aligned} \text {De-stationary}(Q', EK', FV', \tau , \Delta ) = \text {Softmax}\left( \underbrace{\frac{\tau Q' (EK')^T + 1 \Delta ^T}{\sqrt{d_k}}}_{P: n \times k} \right) \cdot \underbrace{FV'}_{k \times d} \end{aligned}$$
(11)

Finally, only O(nk) time and space complexity is required to compute the context embedding using \(\tilde{P} \cdot (FV^{\prime })\). Thus, choosing a very small projection dimension k such that \(k \ll n\), then the method can significantly reduce memory and computational cost consumption. The following theorem shows that when \(k = O(d / \epsilon ^2)\) (independent of n), one can use a linear non-stationary attention mechanism to approximate \(\tilde{P} \cdot V^{\prime }\) with an error of \(\epsilon\).

Theorem 1

(Linear De-stationary Attention) For any \(Q, K, V \in \mathbb {R}^{n \times d}\), if \(k = \min \{\theta (9d \log (d) / \epsilon ^2), 5\theta (\log (n) / \epsilon ^2)\}\), then there exists matrices \(E, F \in \mathbb {R}^{n \times k}\) such that, for any row vector w of matrix \(Q (K)^T / \sqrt{d_k}\), we have: \(w \cdot \left( \frac{Q (K)^T}{\sqrt{d_k}} \right) \cdot FV' \cdot P_{n \times k}\)

$$\begin{aligned} \Pr \left( \Vert \text {softmax}(w E^T) F V' - \text {softmax}(w) V' \Vert \le \epsilon \Vert \text {softmax}(w) \Vert \Vert V '\Vert \right) > 1 - o(1) \end{aligned}$$
(12)

where \(E = \delta R\) and \(F = e^{-\delta } R\), R is an \(n \times k\) matrix whose elements are independently distributed from the normal distribution N(0, 1/k) and \(\delta\) is is a small constant. By applying the results of the above formula to each row vector of matrix A and each column vector of matrix \(V'\), it can be proven that for any row vector \(A_i\) of matrix A, the error between the transformed result and the original result is controlled within an acceptable range with high probability, thereby verifying the effectiveness and stability of the model in processing high-dimensional data.

$$\begin{aligned} \Pr \left( \left\| \exp (A_i E^T) F V - \exp (A_i) V \right\| \le \epsilon \left\| \exp (A_i) V \right\| \right) > 1 - o(1) \end{aligned}$$
(13)

By setting \(k = \dfrac{5 \log (nd)}{\epsilon ^2 - \epsilon ^3}\), the above procedure shows that for a given approximation error \(\epsilon > 0\), the approximation error condition we wish to obtain will almost certainly hold for a set value of k, suggesting that we can control the approximation error by choosing an appropriate value of k for the model in this paper. This suggests that the model in this paper can control the approximation error with an appropriate choice of k-value, and significant improvements in training and inference speed are observed. For more details, please refer to the appendix.

Progressively learning block

Time series forecasting models are prone to severe overfitting when dealing with time series data due to the non-stationarity of the time series, the time series evolves under complex transient conditions. This is manifested by the fact that during the training process, the training loss still decreases dramatically, but the validation loss still increases significantly. In this section, a progressive learning module is designed to systematically acquire the components of a supervised signal by decomposing the supervised signal and learning different parts of the time series sequentially. The module adopts a dual data stream and subtraction mechanism, where the module generates a prediction result and subtracts it from the prediction results of the subsequent layers to generate a residual data stream, through which the module is able to reduce the prediction error layer by layer in this decreasing way. At the same time, the module builds a ‘high-speed channel’ for the prediction results to go directly to the next module, which gradually learns the residual streams and output streams of the stacked blocks, and gradually approaches the real labels, thus improving the model performance and effectively avoiding overfitting.

When the attention mechanism deals with time series where different attributes are independent of each other, the attention mechanism still tries to learn the relationship between these attributes, increasing the complexity of the model and the number of parameters, resulting in a large amount of redundant information and leading to model overfitting. To mitigate this problem, this section implements a correction metric by subtracting the attention output from the input. This ensures that attention can be effectively utilised to its inherent advantage, thus improving overall performance. This process can be expressed as:

$$\begin{aligned} \begin{aligned}&\tilde{X}_{l,1} = De - \text {stationary}\left( X_{l,1}\right) \\&R_{l,1} = X_{l,1} - \delta \tilde{X}_{l,1} \end{aligned} \end{aligned}$$
(14)

Where,\(\hat{X}_{l,1}\) represents the input signal processed by the Attention mechanism (Attention) in the \(l\text {th layer}\),\(R_{l,1}\) denotes the remainder of the input \(X_{l,1}\) after block processing, and \(\delta\)is the Dirac function.\(\delta\) is used to eliminate the Attention layer when an unfavourable influence is applied. Similarly, the input signal processed by the feedforward layer will be ubtracted from the input and can be expressed as:

$$\begin{aligned} \begin{aligned}&\tilde{X}_{l,2} = \text {FeedForward}\left( R_{l,1}\right) \\&R_{l,2} = X_{l,2} - \delta \tilde{X}_{l,2} \end{aligned} \end{aligned}$$
(15)

The feedforward layer consists of two identity mappings with an activation function inserted between them, which specialises in non-linear transformations of the temporal aspect. This feature is particularly important when dealing with multivariate time series data with strong independence between features. Specifically, the current block contains two parallel data streams: the output \(\tilde{X}_l\) processed by the neural modules, and the residual \(\tilde{R}_l\) obtained by subtracting \(\tilde{X}_l\) from the input, which is processed by a gate mechanism and then directed to the next block or projected to the output space. The two data streams are processed through the gate mechanism and are then directed to the next block or projected to the output space.

Drawing inspiration from RNNs32, this section adopts an approach that can autonomously regulate the transfer of information, similar to the control mechanisms inherent to cells in RNNs. Thus, we introduce a gate mechanism at the end of each block to control the transmission of the two data streams.

For residual stream, the gate mechanism can be expressed as:

$$\begin{aligned} X_{l+1} = \sigma \left( \theta _1(R_{l,2}) \right) \cdot \theta _2(R_{l,2}) \end{aligned}$$
(16)

where \(\sigma\) is the sigmoid function and \(\theta _1\) and \(\theta _2\) are learnable neurons with different parameters. Similarly, for the intermediate output stream \(\tilde{X}_l\),the gate mechanism can be expressed as:

$$\begin{aligned} o_{i+1} = \sigma \left( \theta _3 \left( [\hat{X}_{l,1}, \hat{X}_{l,2}] \right) \cdot \theta _4 \left( [\hat{X}_{l,1}, \hat{X}_{l,2}] \right) \right) \end{aligned}$$
(17)

Where [] denotes concatenation. \(o_(l+1)\) enables the module to better utilise the output of the non-stationary attention mechanism and the output of the feedforward layer. The gating mechanism can introduce signal morphing in both data streams, effectively adjusting the amount of information output from the current block. It enables the model to selectively enhance or attenuate the influence of specific phases, thus adequately mitigating the overfitting effects of independent attributes and redundant information on the model and enhancing its modeling capabilities. Compared with other time series prediction models, the model proposed in this paper is able to complete the screening and amplification of information, learn the residual and output signals in an incremental learning manner, and gradually approximate the supervised.

Overall architecture

The overall architecture uses stacked Progressively learning blocks combined with non-stationary attention mechanisms, parallel data flow structures, gating mechanisms and Normalisation module De-normalization module.Comparing with the standard Transfomer model31, the model proposed in this paper designs the non-stationary attention mechanism for the non-stationary nature of the original series in order to improve the prediction ability of non-stationary time series. Comparing with the variants of Transformer33,22, this paper varies the terms within \(Softmax(\cdot )\) with a de-stationary factor \(\tau\), \(\delta\) to reintegrate the non-stationary information. In terms of time series forecast decomposition, the architecture proposed in this paper differs from Prophet34, N-BEATS35, Autoformer23, FEDformer36 and Nonstationary Transformers37 in the sense that the above methods apply decomposition to the input series to enhance predictability, reduce computational complexity or ameliorate the adverse effects of non-stationarity. However, these popular methods are susceptible to significant overfitting when applied to non-stationary TS. The method proposed in this paper employs a Progressively learning approach to supervise the learning of each time-varying pattern, achieved by implicitly decomposing the supervised signals, to effectively address the overfitting problem due to the independence of the original sequence features or non-stationarity.

Experiment

NSPLformer has been comprehensively evaluated on widely-use real-world datasets, covering various mainstream time series forecasting applications including energy, transportation, electricity, weather, and exchange.

All experiments were implemented in PyTorch and conducted on a single NVIDIA P100 16GB GPU. We utilised ADAM with initial learning rates of \(\{10^{-3}, 5 \times 10^{-4}, 10^{-4}\}\) and L2 loss for model optimisation. The batch size was set to 128, and the number of training epochs was fixed at 10. For all models, this paper tested performance under four prediction lengths \(T \in \{96, 192, 336, 720\}\), with a lookback window \(L = 96\). The dataset was split into training, validation, and test sets in a 7:2:1 ratio, with early stopping used to prevent overfitting, and a random seed of 2025.

Datasets

As shown in Table 1, here are the descriptions of the datasets: (1)Electricity38 records the hourly electricity consumption of 321 clients from 2012 to 2014. (2)ETT22 contains the time series of oil de-stationary factors and power load collected by electricity transformers from July 2016 to July 2018. ETTm1 /ETTm2 are recorded every 15 minutes, and ETTh1/ETTh2 are recorded every hour. (3)Exchange39 collects the panel data of daily exchange rates from 8 countries from 1990 to 2016. (4)40 contains hourly road occupancy rates measured by 862 sensors on San Francisco Bay area freeways from January 2015 to December 2016. (5)41 includes meteorological time series with 21 weather indicators collected every 10 minutes from the Weather Station of the Max Planck Biogeochemistry Institute in 2020.(6)Solar documents the solar power generation of 137 photovoltaic (PV) facilities in the year 2006, with data collected at 10-minute intervals.

This paper employs the Augmented Dickey-Fuller (ADF) test statistic as an indicator to quantitatively measure the degree of stationarity.

Table 1 Summary of datasets. Smaller ADF test statistic indicates a more stationary dataset.
Full size table

Baselines

Due to the inferior performance of traditional models (such as ARIMA) compared to the latest Transformer-based models, this paper selects a range of state-of-the-art (SOTA) Transformer-based models as comparative benchmarks for analysis. These include iTransformer27 , PatchTST25, TimesNet42, FEDformer36, Autoformer23 and Informer22.

Main results

The model presented in this paper maintains state-of-the-art performance across all base-line and prediction lengths. Notably, the non-stationary asymptotic learning model outperforms other deep models on datasets with high non-stationarity. As shown in Table 3,the best results are highlighted in red and bold, and the second best results are highlighted in purple and underlined. iTransformer and PatchTST stand out as the most recent models recognised for their superior average performance. Compared to these, the paper proposed models show average performance improvements of 1.5% and 4.5% respectively, achieving significant performance gains. Achieved performance in multiple dimensional comparisons across the 8 datasets is most excellent/sub-optimal, with each individual metric showing performance improvements. For example, under the input-prediction-720 setting, the paper proposed model reduces the MSE on the Electricity dataset by 15.7% (0.255\(\longrightarrow\)0.215) and 11.9% (0.244\(\longrightarrow\)0.235) compared to iTransformer and PatchTST, respectively. Similarly, in traffic flow, the MSE is reduced from 1.6% (0.433\(\longrightarrow\)0.426) and 16.8% (0.512\(\longrightarrow\)0.426).The experimental results indicate that the proposed NSPLformer exhibits superior predictive performance across datasets with varying horizons (Table 2).

Table 2 Comparison of different models across various datasets and lengths.
Full size table

Framework generality

This paper applies the framework proposed in this paper to four mainstream Transformers and reports the performance improvement of each model. As shown Table 3, the approach in this paper continuously improves the predictive power of different models. Overall, it achieves an average improvement of 50.74% on Transformer, 59.77% on Informer, and 19.28% on Autoformer, making each of them outperform the previous state-of-the-art. At the same time, the model validates non-stationary Progressively learning Transformer as an effective and stable framework for a wide range of Transformer-based models, and enhances their non-smooth predictability and interpretability to achieve advanced performance.

Table 3 Perform boosting by applying the proposed framework to Transformer and its variants. We report the average MSE/MAE (illustrated in Table 2) and the relative MSE reduction rate (Promotion) for all the predicted lengths in our framework.
Full size table

Quality evaluation

In order to explore the role of each module in our proposed framework, we compared the prediction results of ETTm2 obtained by three models,vanilla Transformer, the one with a non-stationary attention mechanism and the non-stationary progressive learning model proposed in this paper. In Fig. 4 it is found that these two modules enhance the non-stationary prediction ability of Transformer from different perspectives. Not only aligning the statistical properties between each series of inputs facilitates Transformer’s massive generalisation to out-of-distribution data, but also the attention shows the inherent non-stationary of the real world time series.

To explore the role of each module in our proposed framework, we compare the prediction results of the three models on the ETTm2 dataset, and the experimental results are shown in Fig. 4, which indicate that the two modules, the Series Stationarization module and the Attention Mechanism for recombining non-stationary information, respectively, enhance the non-stationary prediction ability of Transformer from different perspectives. The Series Stationarization module significantly improves Transformer’s generalisation ability when dealing with out-of-distribution data by aligning the statistical attributes of each series input. However, as shown in Fig. 4b , relying on Series stationary alone for training leads to an over-stationarization problem, making the deep model more inclined to output unvolatile series with significantly high stationary and ignoring non-stationary properties of real-world data. By introducing a non-stationary attention mechanism and progressively learning module, the model focuses on the inherent non-stationarity of real-world time series. It is useful to accurately predict detailed sequence variations, which is crucial in real-world time series forecasting.

Fig. 4
figure 4

Visualization of ETTm2 predictions given by different models.

Full size image

Over-stationarization problem

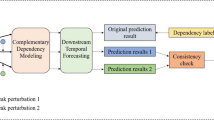
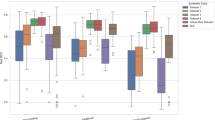
In order to statistically validate the over-stationarisation problem, we trained the Transformer model using the aforementioned methods and ranked all the predicted time series in chronological order, and subsequently compared their degree of stationarity with the ground truth (see Fig. 5). The results show that models relying only on stationarization methods tend to output time series with an unusually high degree of stationarity, i.e., the forecasts are too stationary and do not accurately reflect the characteristics of the actual data. In contrast, the model incorporating De-stationary Attention predicts stationarity that is very close to the true value, with relative stationary ranging from 97% to 102%. Furthermore, as the stationarity of the time series increases, the severity of the over-stationary problem also increases. This huge discrepancy in stationary can explain the poor performance of the Transformer model using only the stationary method. At the same time, it also verifies that the de-stationary attention, as an internal renovation mechanism, demonstrates a significant effect in mitigating the over-stationarization problem.

Fig. 5
figure 5

Relative stationarity defined as the ratio of the ADF test statistic between the model prediction and ground truth. From left to right, the dataset becomes progressively less stationary (i.e., the dataset becomes increasingly non-stationary). Models using only stationary methods (left) tend to output overly-stationarization time series, while our method (right) provides predictions that are much closer to the smoothness of the actual values.

Full size image

Ablation study

In order to validate the effectiveness of the model components proposed in this paper, comprehensive ablation studies including component replacement and component removal experiments were conducted as shown in Fig. 6. In the experiments, the symbols ‘+’ and ‘-’ are used to denote addition or subtraction operations during the aggregation of input or output streams. The results of the study show that the use of subtractive operation (-X) significantly improves the average performance of the model than additive operation (+X) when only the input streams are used. For example, on the Electricity dataset, the prediction error was reduced from 0.181 to 0.173, a reduction of 4.4%. In addition, introducing high-speed output streams into the model and changing the aggregation method of the output streams from addition (+Y) to subtraction (-Y), and integrating the gating mechanism (G) into the model is expected to further improve the prediction performance. For example, on the Traffic dataset, the prediction error is reduced from 0.420 to 0.410, a reduction of 2.4%. In summary, the advantages of integrating these components can significantly improve the overall performance of the model for different time series prediction tasks.

Fig. 6
figure 6

Ablation studies for each component of NSPLformer. all results are averages of all predicted lengths. The variables X and Y denote the input and output streams, while the symbols ‘+’ and ‘-’ denote the addition or subtraction operations used for stream aggregation. The letter ‘G’ denotes the gating mechanism added to the output of each block.

Full size image

In order to validate the broad applicability of NSPLformer as a versatile architecture, this study replaced its original attention mechanisms to observe the change in model performance when novel attention mechanisms were introduced. Specifically, NSPLformer was chosen as the base model and its original attention mechanisms were replaced with the following four novel attention mechanisms: Prob-Attention22, Period-Attention43, Flow-Attention44, and Auto-Correlation23. The experiments were conducted on the Traffic, Electricity and Weather datasets, and the evaluation metrics were Mean Squared Error (MSE). The results of the experiments are shown in Fig. 7, indicating significant changes in model performance when using these novel attention mechanisms. Specifically, Prob-Attention shows superior performance: the average MSE on the Electricity dataset decreases from 0.264 to 0.173, a decrease of 34.5%; the average MSE on the Weather dataset decreases from 0.631 to 0.264, a decrease of 58.2%, which is significantly better than that of the original Full- Attention. period-Attention and Flow-Attention also show good performance on these datasets. However, the performance improvement of Auto-Correlation fails to meet expectations, mainly due to the difficulty of its intrinsic autocorrelation mechanism to capture the subtle change patterns characterised by dramatic fluctuations in attributes. This study provides new insights and approaches for the application of NSPLformer in time series forecasting tasks. The findings highlight the potential of integrating advanced attention mechanisms to further enhance model performance and adapt to complex forecasting scenarios.

Fig. 7
figure 7

Ablation studies of NSPLformer using various Attention. All results are averaged across all prediction lengths. The tick labels of the X-axis are the abbreviation of Attention types.

Full size image

Complexity and memory usage comparison analysis

The linear low-rank approximation of the non-stationary attention mechanism significantly reduces computational complexity by decomposing high-dimensional matrices into low-rank factors, thereby reducing the computational complexity of self-attention from \(O(n^2 \cdot d)\) to \(O(n \cdot k \cdot d)\), where k is much smaller than n. Thus, the complexity is approximately \(O(n \cdot d)\). This method has advantages over other mainstream models, as shown in Table 4.

Compared to iTransformer, which has a time complexity of \(O(n^2 \cdot d)\), the low-rank approximation effectively reduces complexity, enabling more efficient processing of long sequences. PatchTST achieves a complexity of \(O((N/P)^2 \cdot d)\) (where P is the patch length) by dividing the input sequence into local blocks (patches), improving parallelism while maintaining a certain level of modelling capability.Compared to PatchTST, which has a complexity of \(O((N/P)^2 \cdot d)\), NSPLformer further simplifies attention calculations at different scales. Although TimesNet achieves lower complexity \(O(n^2 \cdot d)\) through a convolutional structure, the linear low-rank approximation retains the advantage of the attention mechanism in capturing global dependencies.For FEDformer with a complexity of \(O(n \log n)\), low-rank decomposition can be applied to frequency-domain attention, thereby optimising computations in both the time and frequency domains.In summary, the linear low-rank approximation of non-stationary attention mechanisms not only improves computational efficiency but also retains adaptability to non-stationary data and the ability to capture global dependencies, making it particularly suitable for complex sequence modelling tasks.

Table 4 Complexity analysis comparison table.
Full size table

The Fig. 8 shows a performance comparison between NSPLformer and the baseline model when processing the Traffic dataset (862 variables), focusing on prediction accuracy (MSE), training efficiency (ms/iter), and memory usage (GB).

NSPLformer demonstrates significant advantages in memory optimisation:Memory usage: NSPLformer’s memory consumption is 3.79 GB, significantly lower than other models (TimesNet: 11.3 GB, FEDformer: 4.86 GB, PatchTST: 8.58 GB), highlighting its lightweight design characteristics.Performance balance: While maintaining low memory usage, NSPLformer’s MSE value (0.42) outperforms PatchTST (0.51) and FEDformer (0.61), and is close to iTransformer (0.43), indicating that its prediction accuracy has not significantly decreased due to resource savings.Training Efficiency: NSPLformer’s training time is 192 ms/iter, which is at an intermediate level, balancing computational efficiency with model performance.

Fig. 8
figure 8

Traffic dataset multi-model computational efficiency comparison analysis.

Full size image

Conclusion and future work

This paper proposes NSPLformer to address the issues of non-stationarity and severe overfitting faced by deep models in time series prediction. These two issues interact, exacerbating overfitting due to non-stationarity in the original data, which further obscures the non-stationary characteristics in the data. To address this issue, we adopt a segmented stationarity method and introduce an attention mechanism to reintegrate non-stationary information, while proposing a subtraction-based information aggregation framework. Unlike traditional methods, which typically mitigate overfitting by suppressing non-stationarity, often leading to excessive smoothing of the data, our approach directly learns non-stationary features from the original sequence, thereby improving the stationarity of the sequence. Specifically, we design a progressive learning-based architecture that processes dual data streams through implicit and stepwise decomposition. In this architecture, the input stream is progressively decomposed through subtraction operations in multiple residual blocks. This decomposition mechanism enables the model to better understand and represent the structure of the input sequence, effectively capturing differences and patterns in the data. Meanwhile, the output stream gradually improves prediction accuracy at each stage by learning the residuals of the supervision signal layer by layer. By focusing on reducing prediction error, the model’s data predictability and predictive capability are significantly enhanced. In experiments, NSPLformer demonstrates outstanding versatility and performance across eight mainstream analysis tasks, achieving an average performance improvement of 5.3% compared to mainstream models. In the future, we will further explore large-scale pre-training, lightweight, and real-time deployment methods for time series, as well as their applications in industries such as healthcare and finance.