Introduction

Long non-coding RNAs (lncRNAs) are one class of non-protein-coding RNA transcripts surpassing 200 nucleotides in length. lncRNAs serve pivotal regulators in cellular processes1,2. lncRNAs are taken as competitive endogenous RNAs involved in microRNAs, and regulate gene expression indirectly by competitively binding with target gene mRNAs3,4,5,6. Furthermore, lncRNAs exhibit distinct functions in cancers, including gene expression regulation and cell cycle progression, which can cause cancer or tumour metastasis7,8. For example, PCA3 could be a promising biomarker for detecting early prostate cancer9, and GAS5 severely affects cognitive dysfunction and multiple pathologies related to Alzheimer’s disease (AD) as an endogenous sponge10.

Inference of new lncRNA-disease associations (LDAs) is necessary to find potential biomarkers for complex diseases. However, traditional laboratory techniques are limited to high time consuming, expensive cost and intensive labor11,12. Consequently, efficient computational algorithms are essential to decipher their associations. Current LDA prediction are mainly falling into two classes: similarity-based and machine learning-based.

Similarity-based methods assume that lncRNAs with similar biological functions have higher chance of being associated with diseases sharing phenotypes. Similarly, diseases exhibiting analogous phenotypic features are more likely to be linked with lncRNAs with analogous functionality. As a result, computing similarity scores for lncRNAs and diseases is crucial to similarity-based predictions. These similarities, including lncRNA expression similarity13,14, function similarity11,15, cosine similarity16, Gaussian Association Profile Kernel (GAPK) similarity, and heterogeneous information network17 were used to construct lncRNA-lncRNA network. Moreover, disease semantic similarity based on ontology or MeSH descriptor, cosine similarity, and GAPK similarity were utilized to build disease-disease network.

Through fusing multiple similarities, similarity-based methods could enrich lncRNA and disease representations and reduce the effects of missing values in similarity matrices on predictions. RWSF-BLP18 incorporated multiple similarity matrices and devised a bidirectional label propagation algorithm for predictions. DeepMNE19 employed kernel neighborhood information for similarity measurement and developed a network fusion method to leverage multiple source information. SSMF-BLNP20 identified potential associations based on selective similarity matrix fusion. OM-MGRMF21 fully utilized the optimized measurement methods and multi-graph regularization matrix factorization.

Machine learning-based methods have been increasingly prevalent in bioinformatics including LDA prediction22,23. They are classified as traditional machine learning-based predictions and deep learning-based predictions. Traditional algorithms extract noncoding RNA-disease feature representations and learn the optimal classifiers for predictions. These classifiers mainly include Laplacian regularized least squares24, matrix completion25, random forest26,27, matrix factorization21,28,29,30,31,32,33, collaborative filtering34, Node2vec-based neural collaborative filtering35, and boosting models11,36,37. Deep learning-based algorithms have been broadly used in LDA prediction due to their powerful representation learning ability38,39,40, such as stacked denoising auto-encoder41, deep belief network42, attention mechanism43,44, generative adversarial network45, deep neural network46, and Convolution Neural Network (CNN)47.

Particularly, Graph Neural Networks (GNNs) have achieved widespread application due to their optimal performance in handling graph-structured data38,48,49,50, for example, RNA-disease association identification51,52,53. They can provide deep representations for each lncRNA-disease pair (LDP) and have exhibited exceptional potentials in LDA identification. GNN-based LDA prediction methods mainly include Graph Convolutional Network (GCN)45,54,55,56, Graph Attention Network (GAT)57,58, Graph Auto Encoder (GAE)15,59, Graph Transformer60, and Graph Contrastive Learning16,58.

Although existing studies have relatively efficiently inferred LDAs, machine learning-based methods focused on training a better classifier but failed to fully learn LDP features. Furthermore, deep learning-based methods learned LDP latent representations, but neglected the neighborhood information in graph-based structural data. GNN can enhance the node representations by effectively aggregating the neighborhood information in a graph.

Here, we propose a hybrid representation learning framework, named LDA-GMCB, by leveraging Graph embedding module, Multi-head self-attention mechanism with CNN layer, and the gradient Boosting algorithm with histogram for predicting LDAs. Extensive experiments were performed under the testing scenarios, which includes 5-fold cross validation and cold start. The outcomes confirmed the performance of LDA-GMCB when forecasting LDAs. This work has the following three main distributions:

  • A graph embedding module that incorporates GCN and GAT is proposed to learn the graph embeddings of lncRNAs and diseases simultaneously.

  • A multi-head self-attention (MSA) mechanism with CNN layer (MSA-CNN) is devised to learn and aggregate the node representations with different importance for lncRNAs and diseases.

  • A gradient boosting model with histogram (HGBoost) is fully used to classify unknown LDPs.

Results

Data sources

Here, we used LDA data from lncRNADisease61 and MNDR62, which comprehensively records a large number of LDAs, as data sources to train the model and perform predictions. Based on the two databases, we deleted lncRNAs without sequences and diseases without MeSH. As a result, we screened 605 experimentally confirmed associations involved to 82 lncRNAs and 157 diseases in lncRNADisease v2.0, 1,529 associations involved to 190 diseases and 89 lncRNAs in MNDR, and 1,956 associations between 365 lncRNAs and 189 diseases in lncRNADisease v3.0. The detailed information about the datasets is shown in Table 1.

Table 1 The information of LDA datasets.
Full size table

Experimental settings

We utilized 5-fold cross-validation (CV) to optimize the model by adjusting its configuration and tuning its parameters. During training, known LDAs were taken as positive samples, and the equal number of unconfirmed LDPs were randomly screened as negative samples. Parameters in LDA-GMCB and comparison methods were shown in Table 2. Their performance was assessed using Area Under the ROC Curve (AUC), Area Under the Precision-Recall (PR) Curve (AUPR), F1-score, Accuracy, Recall, and Precision. To verity the robustness and dependability of predictions, all experiments have been repeatedly executed 20 times.

Table 2 Parameter settings.
Full size table

Baselines

We compared LDA-GMCB with five popular LDA inference methods, i.e., SDLDA63, LDNFSGB64, IPCARF26, LDA-VGHB11, and GEnDDn15.

SDLDA63: SDLDA63 first described each LDP based on their linear and nonlinear representations learned by SVD and fully connected neural network, and used a multi-layer perceptron (MLP) to conduct predictions.

LDNFSGB64: LDNFSGB64 described each LDP based on their global and local features learned from their similarity information, and reduced their feature dimension using an autoencoder, finally performed predictions through the gradient boosting algorithm.

IPCARF26: IPCARF26 extracted LDP features using incremental principal component analysis and deciphered their associations via random forest.

LDA-VGHB11: LDA-VGHB11 extracted LDP features by combining SVD and variational GAE, and then inferred new relationships using heterogeneous Newton boosting machine.

GEnDDn15: GEnDDn15 learned LDP features through non-negative matrix factorization and graph attention autoencoder and classified LDPs based on dual-net neural architecture and deep neural network.

Comparison of LDA-GMCB with five baselines

To assess the LDA-GMCB performance, we compared it with five baselines, i.e., SDLDA, LDNFSGB, IPCARF, LDA-VGHB, and GEnDDn. The five baselines also randomly selected negative associations as many as positive ones from unknown LDPs. Their performance is shown in Table 3. Figure 1 illustrates their ROC and PR curves.

Table 3 Performance of LDA-GMCB and five baselines on lncRNADisease v2.0, MNDR, and lncRNADisease v3.0. The best performance is denoted as bold.
Full size table
Fig. 1
figure 1

The ROC and PR curves of LDA-GMCB and five baselines on lncRNADisease v2.0, MNDR, and lncRNADisease v3.0.

Full size image

On lncRNADisease v2.0, LDA-GMCB gained the best AUC and AUPR, outperforming the second-highest method, GEnDDn, by 1.67% in AUC, and 1.47% in AUPR, respectively. On MNDR, LDA-GMCB gained the best AUC and AUPR, surpassing GEnDDn by 2.57% in AUC, and 0.41% in AUPR, respectively. On the above two datasets, although LDA-GMCB computed slight lower precision, accuracy, and F1-score, it computed better AUC and AUPR, which are more important measurements. More importantly, on lncRNADisease v3.0, LDA-GMCB computed the highest performance, exceeding GEnDDn by 2.46% in precision, 0.39% in recall, 1.58% in accuracy, 1.45% F1-score, 1.41% in AUC, and 1.13% in AUPR, respectively.

In Fig. 1, the ROC curve from LDA-GMCB consistently stay above five baselines’ curves across almost all points, indicating that it achieved a better trade-off between true positives and false positives. Furthermore, the PR curve from LDA-GMCB exhibited an advantage compared to five baselines, particularly in the range of high recall, indicating its ability to maintain high precision even when recall increased. This characteristic made LDA-GMCB especially suitable for applications where maximizing true positives while minimizing false positives is critical.

Cold-start study

Despite considerable advancements in predicting LDAs in recent years, many approaches depend significantly on pre-existing data and are limited to the so-called ‘cold start’ issue when identifying relationships for new lncRNAs or rare diseases. Therefore, we further tested whether LDA-GMCB was effective in deciphering associations for new lncRNAs or rare diseases by simulating a cold-start scenario. Based on five-fold CV strategy, we randomly masked 20% of lncRNAs or diseases and removed their heterogeneous association information during training.

During cold-start scenarios, the masked lncRNAs (or diseases) may have pre-computed sequence (or semantic) features, but have no known associations. Therefore, all lncRNAs and diseases participated in constructing lncRNA-lncRNA similarity network and disease-disease similarity network, respectively. When dividing the training and testing sets, we masked the rows (or columns) in Y and removed the corresponding association information. For masked lncRNA/disease nodes, their initial node embeddings were still retained, and their node embeddings can be updated by aggregating similar neighbor node information through the GCN/GAT layer. Finally, HGBoost was used to implement predictions.

Table 4 and Fig. 2 elucidate prediction accuracy of LDA-GMCB under cold start scenario for lncRNAs, that is, randomly masking 20% of lncRNAs. Under this setting, LDA-GMCB gained the best performance, followed by LDA-VGHB (i.e., the second-best method) on the two databases. Particularly, it computed the optimal AUCs of 0.9303 and 0.9693, outperforming 4.89% and 1.52% than LDA-VGHB, respectively, and the best AUPRs of 0.9169 and 0.9724, better 2.20% and 1.07% than LDA-VGHB, respectively. As a result, LDA-GMCB captured potential diseases linking with a new lncRNA more accurately.

Table 4 Performance comparison under cold-start for lncRNAs. The best performance is denoted as bold.
Full size table
Fig. 2
figure 2

The LDA identification performance under cold start scenarios.

Full size image

Table 5 and Fig. 2 illustrate the performance of LDA-GMCB under cold start scenario for diseases, that is, randomly masking 20% of diseases. Under this setting, LDA-GMCB obviously surpassed other four algorithms on the two databases. For instance, it gained the highest AUCs of 0.9610 and 0.9831, better 1.94% and 0.90% than LDA-VGHB, and the best AUPRs of 0.9591 and 0.9809, outperforming 1.62% and 0.81% in comparison to LDA-VGHB, respectively. As a result, LDA-GMCB effectively deciphered possible relationships for an unknown disease.

Table 5 Performance comparison of cold-start for disease. The best performance is denoted as bold.
Full size table

Robustness analysis

To evaluate the robustness of LDA-GMCB, we repeated 5-fold CV for 20 rounds and listed the average results of AUC and AUPR obtained by LDA-GMCB in Table 3, where LDA-GMCB still computed the best performance on lncRNADisease v2.0 and MNDR. As shown in Fig. 2, the box plots of both the summary statistics and the distributions of AUC and AUPR after 20 rounds demonstrated its promising performance in terms of robustness.

Moreover, we conducted statistical hypothesis tests to demonstrate the significant difference between LDA-GMCB and LDA-VGHB and GEnDDn based on AUC and AUPR. Since LDA-VGHB and GEnDDn are two new LDA prediction models and significantly outperformed the other three baselines, we only implemented robustness analysis between LDA-GMCB and the two baselines. Specifically, we performed the T-test and Wilcoxon rank-sum test by comparing LDA-GMCB with the two baselines in terms of AUC and AUPR. The results are shown in Table 6. LDA-GMCB significantly outperformed the baselines at a confidence level of 95% (P-value< 0.05). This again indicated the superior advantage of LDA-GMCB in LDA prediction.

Table 6 The T-test and Wilcoxon rank-sum test results obtained by comparing LDA-GMCB with LDA-VGHB and GEnDDn.
Full size table

Performance of LDA-GMCB with four popular classifiers

To determine the effectiveness of HGBoost on LDP classification, we tested the performance of four classifiers when deciphering potential associations, such as MLP, SVM, random forest (RF), and XGBoost. MLP, SVM, RF and HGBoost were run using scikit-learn toolkit and XGBoost were implemented based on the open source library. All five classifiers were tested 20 times under 5-fold CV on lncRNADisease v2.0, MNDR, and lncRNADisease v3.0, respectively.

As shown in Table 7, HGBoost gained the best outcomes. The average AUCs for HGBoost were 0.9464, 0.9734, and 0.9657, and the average AUPRs were 0.9506, 0.9779, and 0.9605, respectively. Figure 3 characterized their ridgeline plot. The outcomes elucidated that HGBoost was significantly better than other classifiers, indicating that HGBoost was more suitable for LDP classification than other algorithms. Therefore, LDA-GMCB took HGBoost as its classification model.

Table 7 Performance of LDA-GMCB using different classifiers on lncRNADisease v2.0, MNDR, and lncRNADisease v3.0. The best performance is denoted as bold.
Full size table
Fig. 3
figure 3

The performance comparison of HGBoost and other four classifiers.

Full size image

Ablation study

The LDA-GMCB model incorporated linear and nonlinear representation learning to decipher potential LDAs. To decipher whether the combination of linear and nonlinear features assists in predictions, we implemented ablation analysis by removing each individual part in our model. Table 8 and Fig. 4 list the LDA-GMCB performance under 5-fold CV when only using linear representations through low-rank SVD, nonlinear representations through graph representation learning, or their combination, respectively. The outcomes indicated that their combination boosted LDA prediction in comparison with two individual methods in most cases.

Table 8 Ablation experiments results of three different feature extraction approaches. The best performance is denoted as bold.
Full size table
Fig. 4
figure 4

The performance of LDA-GMCB under three distinct feature extraction approaches.

Full size image

Sensitivity analysis of parameters

LDA-GMCB used SVD for LDP linear feature learning and HGBoost for LDP classification. To evaluate the effects of rank in SVD and depth in HGBoost on predictions, we conducted parameter sensitivity analysis. As shown in Table 9, we set rank for SVD to 5, 8, and 16 on lncRNADisease v2.0 and MNDR. When rank for SVD was 5, LDA-GMCB computed better performance on the two datasets in most conditions. Thus, rank for SVD was finally set to 5.

Table 9 Performance across different SVD ranks for lncRNADisease v2.0, MNDR, and lncRNADisease v3.0. The best performance is denoted as bold.
Full size table

As shown in Table 10, we set depth for HGBoost to 3, 4, 5, 6, 8, and 10 on the three datasets. When depth for HGBoost was 6, LDA-GMCB computed the best values for the six measurements. Thus, depth for HGBoost was finally set to 6.

Table 10 Performance across different depths for HGBoost on lncRNADisease v2.0, MNDR, lncRNADisease v3.0. The best performance is denoted as bold.
Full size table

Case study

Numerous investigations have suggested that alterations in lncRNA expression levels are strongly linked to the development of various diseases. To validate the dependability of LDA-GMCB in forecasting LDAs in actual cases, we performed case studies on two neurological diseases for identifying their possible lncRNAs: AD65 and Parkinson’s Disease (PD)66.

We began with using the entire set of relationships in lncRNADisease v2.0 and MNDR as our training dataset for predictions. Subsequently, we prioritized lncRNAs linked to AD and PD according to their association strength predicted by LDA-GMCB and inferred the top 10 lncRNAs. The findings are listed in Tables 11 and 12 and Fig. 5. The experimental results demonstrated that half of prospective associations identified by LDA-GMCB could be corroborated by publicly available databases, i.e., lncRNADisease v3.067 and RNADisease v4.068. Moreover, many associations proven by related researches have been successfully predicted. DGCR5-AD and HIF1A-AS1-PD were inferred to be associated LDPs. The outcomes fully corroborated the effectiveness and dependability of LDA-GMCB in predicting actual LDAs.

Table 11 The top 10 lncRNAs predicted by LDA-GMCB for AD and PD on lncRNADisease v2.0.
Full size table
Table 12 The top 10 lncRNAs predicted by LDA-GMCB for AD and PD on MNDR.
Full size table
Fig. 5
figure 5

The top 10 lncRNAs predicted by LDA-GMCB for AD and PD on lncRNADisease v2.0 and MNDR.

Full size image

Discussion and conclusions

Dysregulated expression of lncRNAs can change expression profiles of corresponding target genes that they regulate and further potentially triggers the occurrence and development of specific diseases. Hence, discovering potential LDAs is highly significant to the diagnosis and therapy of diseases especially cancers. Computational techniques, as a supplement to laboratory techniques, have been accumulated to decipher their relationships.

Herein, we exploited a hybrid representation framework, LDA-GMCB, for decoding underlying relationships for LDPs. LDA-GMCB first learned the LDP graph representations by integrating GCN, GAT, and GCN. Subsequently, it proposed an MSA mechanism with CNN to aggregate the node representations with different importance for lncRNAs and diseases. After that, it used a low-rank SVD for extracting linear features of LDPs. Finally, it developed an HGBoost model to classify unknown LDPs based on the learned features.

To assess the LDA-GMCB performance, we conducted extensive experiments. First, LDA-GMCB was compared with five baselines under 5-fold CV, that is, SDLDA, LDNFSGB, IPCARF, LDA-VGHB, and GEnDDn. It gained the best performance and a better trade-off between true positives and false positives. Next, LDA-GMCB was compared with the five baselines under cold start scenarios for lncRNAs and diseases. It efficiently deciphered potential associations for a new lncRNA or disease. Subsequently, HGBoost was compared with four classical classifiers, that is, MLP, SVM, RF, and XGBoost. HGBoost outperformed the above four classifiers, elucidating its better LDP classification ability. Moreover, we also decoded the performance of LDA-GMCB with low-rank SVD, graph representation learning, or their combination. LDA-GMCB with their combination was better than one with individual feature learning ways. Finally, we predicted possible lncRNAs for AD and PD using LDA-GMCB and found that DGCR5 and HIF1A-AS1 could have relationships with them, respectively.

LDA-GMCB efficiently deciphered new relationships for all LDPs. It has the following four advantages. First, LDA-GMCB constructed a graph embedding module and effectively captured graph representations of lncRNAs and diseases by leveraging GCN and GAT. The model exhibited good robustness when learning discriminative features for lncRNAs and diseases. Subsequently, MSA mechanism with CNN was adopted to learn node representations with distinct importance for lncRNAs and diseases. The MAS mechanism efficiently balanced the expressiveness, computational ability, and generalization performance of our proposed LDA-GMCB model due to its better multi-perspective and multi-granular structure. Moreover, it used a low-rank SVD to extract LDP linear features. Finally, LDA-GMCB devised a histogram-based optimization algorithm, HGBoost, for LDP classification. HGBoost fully utilized binning statistical analysis and the approximation strategy and thus obviously alleviated the computational burden.

Although LDA-GMCB better deciphered associations for LDPs, its performance may be further improved by aggregating more information. Thus, in the future, we could concentrate on three key fields. First, it is efficient to leverage more biological association data and design multi-source data integration model75 for predictions. Moreover, accurately screening negative LDAs from LDPs can assist in LDA prediction. Matrix operation-based negative sample selection38 could screen relatively reliable negative LDAs and further improve prediction. Finally, graph learning strategies, ensemble frameworks, and attention mechanisms17,40,49,50 offer valuable insights into LDA prediction. We will integrate them to LDA prediction framework.

In conclusion, we devised a deep learning model, LDA-GMCB, for LDA prediction by leveraging graph embedding technique with GCN and GAT, MSA mechanism with CNN, a low-rank SVD, and HGBoost. We hope that our work can help potential biomarker discovery of complex diseases.

Methods

Problem formulation

Considering two sets composed of m lncRNAs and n diseases, let \(\varvec{Y} \in R^{m \times n}\) represents a set of all possible LDPs. For each LDP \((l_i,d_j )\), \(\varvec{Y}( l_i,d_j ) = 1\) denotes a verified linkage between lncRNA \(l_{i}\) and disease \(d_{j}\), \(\varvec{Y}( l_i,d_j ) = 0\), otherwise. We aim to train a model for predictions.

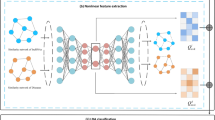
Pipeline of LDA-GMCB

As shown in Fig. 6, LDA-GMCB mainly includes four stages: (a) Nonlinear feature learning based on graph representation learning with graph embedding and MSA-CNN. (b) Linear feature learning based on low-rank SVD. (c) Feature fusing based on concatenation operation. (d) LDP classification based on HGBoost.

Fig. 6
figure 6

The illustration of LDA-GMCB.

Full size image

Nonlinear feature extraction with graph representation learning

To learn LDP nonlinear representations, we combine their biological similarity and graph representation learning. First, disease similarity and lncRNA similarity are computed. A graph representation learning module is proposed to learn deep latent nonlinear representations of lncRNAs and diseases by leveraging graph embedding module and MSA-CNN, respectively. As shown in Fig. 6, each graph embedding module contains one GCN layer, one GAT layer, and one GCN layer. The MSA-CNN module learns node representations with different importance by integrating the outputs from different graph convolutional layers.

Disease semantic similarity

To build disease similarity network, we employ MeSH descriptors to evaluate semantic similarities between different diseases. A directed acyclic graph (DAG), where node and edge denote the MeSH descriptor of a disease and relationship between two diseases, respectively, is applied to depict relationships between various diseases. Consequently, the semantic similarity between \(d_i\) and \(d_j\) is measured by Eq. (1):

$$\begin{aligned} \textrm{DSSM}(d_i,d_j)=\frac{\sum _{x\in {N}_{d_i}\cap {N}_{d_j}}({S}_{d_i}({x})+{S}_{d_j}({x}))}{\sum _{{x}\in {N}_{d_i}}{S}_{d_i}({x})+\sum _{{x}\in {N}_{d_j}}{S}_{d_j}({x})} \end{aligned}$$
(1)

where \({N}_{d_i}\) contains \(d_i\) and its ancestral diseases in DAG(\(d_i\)). \({S}_{d_j}(x)\) is semantic contribution of x to \(d_i\) by Eq. (2):

$$\begin{aligned} {\left\{ \begin{array}{ll} S_{d_{i}}(x)=\max \left\{ (\Delta +\gamma _x)*S_{d_{i}}(x^{\prime })|x^{\prime }\in \text {children of } d_{i}\right\} & \text { if }~x\ne d_{i} \\ S_{d_{i}}(d_{i})=1 & \text { otherwise} \end{array}\right. } \end{aligned}$$
(2)

where \(\Delta\) represent semantic contribution factor corresponding to x and \(x^{\prime }\), and \(\gamma\) represents information content (IC) contribution factor involving to x and other diseases. \(\Delta\) was set to 0.5. For the disease x, its \(\gamma _x\) value change with the continuously updated version of MeSH.

lncRNA functional similarity

Since functionally similar lncRNAs tend to link with phenotypically similar diseases, functional similarity between \(l_i\) and \(l_j\) can be assessed via disease semantic similarity by Eq. (3):

$$\begin{aligned} \textrm{LFSM}(l_{i},l_{j})=\frac{\sum _{1\le {q}\le |D_{i}|}DS(d_{q},D_{j})+\sum _{1\le r\le |D_{j}|}DS(d_{r},D_{i})}{|D_{i}|+|D_{j}|}\quad \quad \end{aligned}$$
(3)

here

$$\begin{aligned} \textrm{DS}({d}_q,{D}_j)=\max _{1\le {t}\le |{D}_j|}(\textrm{DSSM}({d}_q,{d}_t)) \end{aligned}$$
(4)

where \(D_i\) denotes a set of diseases linking with \(l_i\), and \(\textrm{DS}(d_{r},D_{i})\) denotes the semantic similarity between \(d_r\) and \(D_i\).

Disease and lncRNA GAPK similarity

Since some diseases have no DAGs and thus have no MeSH descriptors, their semantic similarity can’t be measured. As a result, we utilize the topological structure of LDA network and use GAPK to measure their similarity. Given an association profile \(\textrm{AP}_{d_i}\) of \(d_i\), GAPK similarity between \(d_i\) and \(d_j\) is measured by Eq. (5):

$$\begin{aligned} \textrm{DGSM}(d_i,d_j)=\exp (-\mu ||\textrm{AP}(d_i)-\textrm{AP}(d_j)||^2) \end{aligned}$$
(5)
$$\begin{aligned} \mu =\frac{1}{\frac{1}{{n}}\sum _{{i=1}}^{{n}}||\textrm{AP}(c_{i})||^{2}} \end{aligned}$$
(6)

where \(\mu\) is used to control the kernel bandwidth. Similarly, GAPK similarity between \(l_i\) and \(l_j\) is measured by Eq. (7):

$$\begin{aligned} \textrm{LGSM}(l_i,l_j)=\exp (-\mu ||\textrm{AP}(l_i)-\textrm{AP}(l_j)||^2) \end{aligned}$$
(7)
$$\begin{aligned} \mu =\frac{1}{\frac{1}{{N_{l}}}\sum _{{i=1}}^{{N_{l}}}||\textrm{AP}(l_{i})||^{2}} \end{aligned}$$
(8)

where \(\textrm{AP}_{l_i}\) denotes the GAPK vector of \(l_i\) corresponding to the i-th row in \(\varvec{Y}\).

Similarity matrix fusion

To thoroughly measure similarity from biological characteristics and topological structures, we leverage functional similarity and GAPK similarity for lncRNAs, and semantic similarity and GAPK similarity for diseases by Eq.(9):

$$\begin{aligned} {\left\{ \begin{array}{ll} & L_{ij} = ({\textrm{LFSM}(l_i,l_j)+\textrm{LGSM}(l_i,l_j)})/{2} \\ & D_{ij}= ({\textrm{DSSM}(d_i,d_j)+\textrm{DGSM}(d_i,d_j)})/{2} \end{array}\right. } \end{aligned}$$
(9)

Graph embedding module

Graph embedding techniques effectively incorporate graph-based topological information and can precisely capture relationships between nodes based on neighborhood aggregation mechanisms. Graph embedding methods exhibit powerful robustness in learning discriminative node features, even these nodes have sparse or noise-contaminated features22. Here, we employ GCN to gain representations of lncRNAs and diseases, respectively. Given lncRNA similarity network \(G_l\) composed of \(N_l\) lncRNAs, and corresponding adjacency matrix \(\varvec{L} \in \mathbb {R}^{N_l \times N_l}\) (i.e., similarity network) and input lncRNA representations \(\varvec{H} \in \mathbb {R}^{N_l \times F_l}\) with \(F_l\)-dimensional feature, the output lncRNA representations \(\varvec{H}^{\textrm{new}}\) are denoted by a GCN layer by Eq. (10):

$$\begin{aligned} \varvec{H}^{\textrm{new}}=\textrm{GCN}(\varvec{L},\varvec{H}) \end{aligned}$$
(10)
$$\begin{aligned} \textrm{GCN}\left( \varvec{L},\varvec{H}\right) =\sigma \left( \varvec{A}^{-\frac{1}{2}}\widetilde{\varvec{L}}\varvec{A}^{-\frac{1}{2}}\varvec{HW}\right) \end{aligned}$$
(11)

where \(\widetilde{\varvec{L}}=\varvec{I}+\varvec{L}\), \(\varvec{A}=\sum _j\widetilde{\varvec{L}}_{i,j}\), \(\varvec{W} \in \mathbb {R}^{F_l \times F_l}\), and \(\sigma\) are the degree matrix, the trainable weight matrix, and the ReLU activation function, respectively.

GAT can set different weights for adjacent nodes based on their importance through the MSA mechanisms. Hence, we introduce a GAT layer between two GCN layers to help the following GCN layer to learn more informative features for lncRNAs and diseases. For lncRNAs, the output node representations \(\varvec{H}^{\textrm{new}}\) in the GAT layer are denoted by Eq. (12):

$$\begin{aligned} \varvec{H}^{\textrm{new}}=\textrm{GAT}(\varvec{L},\varvec{H}) \end{aligned}$$
(12)
$$\begin{aligned} \vec {\varvec{H}}_{i}^\textrm{new}=\sigma \left( \frac{1}{K}\sum _{k=1}^K\sum _{j\ne i}\phi _{ij}^k{\varvec{W}}_k\vec {\varvec{H}}_i\right) \end{aligned}$$
(13)

where \(\vec {\varvec{H}}_{i}^\textrm{new}\), K, \(\varvec{W}_k\), and \(\vec {\varvec{H}}_i\) denote the representations of \(l_i\) in \(\varvec{H}^{\textrm{new}}\), the number of attention mechanisms, the weight matrix corresponding to the k-th attention mechanism, the input representations of \(l_i\). \(\phi _{it}^k\) is the k-th attention coefficient between \(l_i\) and \(l_t\) and is computed by Eq. (14):

$$\begin{aligned} \phi _{{ij}}^{{k}}=\frac{\exp (LeakyReLU(a_{{k}}^{\top }[\varvec{W}_{{k}}\vec {\varvec{H}}_{i}||\varvec{W}_{k}\vec {\varvec{H}}_{j}||B_{k}\varvec{L}_{ij}]))}{\sum _{{t\ne i}}\exp (LeakyReLU(a_{{k}}^{\top }[\varvec{W}_{{k}}\vec {\varvec{H}}_{i}||\varvec{W}_{k}\vec {\varvec{H}}_{t}||B_{k}\varvec{L}_{it}]))} \end{aligned}$$
(14)

where \(a_k \in \mathbb {R}^{2F_l + 1}\) is a learnable parameter with initial value of random number. It denotes the weight vector corresponding to the k-th attention mechanism. || denotes the concatenation operation. \(B_k\) denotes the learnable weight of edge \(\varvec{L}_{ij}\). And LeakyReLU is an activation function with \(LeakyReLU(x)=max(0.01x,x)\). \([\varvec{W}_{{k}}\vec {\varvec{H}}_{i}||\varvec{W}_{k}\vec {\varvec{H}}_{j}||B_{k}\varvec{L}_{ij}]\) maps node pair features and edge features to the same space, enabling the attention mechanism to simultaneously capture semantic similarity (\(\varvec{W}_k\varvec{H}_i\) and \(\varvec{W}_k\varvec{H}_j\)) of nodes and association strength (\(\varvec{B}_k\varvec{L}_{ij}\)) between nodes.

Graph embedding modules for lncRNAs and diseases can learn their feature representations from corresponding similarity networks through GCN and GAT layers, respectively. Given lncRNA similarity matrix \(G_l\), its adjacency matrix \(\varvec{L}\), the input \(F_l\)-dimensional features \({\varvec{H}}_{l}^{(0)} \in \mathbb {R}^{N_l \times N_l}\) in \(G_l\), GCN and GAT are used alternately to learn the graph representations of lncRNAs in different node levels by Eq. (15):

$$\begin{aligned} {\left\{ \begin{array}{ll} & \varvec{H}_{l}^{(1)}= \textrm{GCN}(\varvec{L}, \varvec{H}_{l}^{(0)}) \\ & \varvec{H}_{l}^{(2)}= \textrm{GAT}(\varvec{L}, \varvec{H}_{l}^{(1)})\\ & \varvec{H}_{l}^{(3)}= \textrm{GCN}(\varvec{L}, \varvec{H}_{l}^{(2)}) \end{array}\right. } \end{aligned}$$
(15)

Similarly, given the adjacency matrix \(\varvec{D}\) and initial features \({\varvec{H}}_{d}^{(0)} \in \mathbb {R}^{N_d \times N_d}\) in disease similarity network \(G_d\), we employ GCN and GAT to capture multi-level node representations \(\varvec{H}_{d}^{(1)}\), \(\varvec{H}_{d}^{(2)}\) and \(\varvec{H}_{d}^{(3)}\) of diseases by Eq. (16):

$$\begin{aligned} {\left\{ \begin{array}{ll} & \varvec{H}_{d}^{(1)}= \textrm{GCN}(\varvec{D}, \varvec{H}_{d}^{(0)}) \\ & \varvec{H}_{d}^{(2)}= \textrm{GAT}(\varvec{D}, \varvec{H}_{d}^{(1)})\\ & \varvec{H}_{d}^{(3)}= \textrm{GCN}(\varvec{D}, \varvec{H}_{d}^{(2)}) \end{array}\right. } \end{aligned}$$
(16)

To boost their feature representations, we concatenate \(\varvec{H}^{(1)}\) and \(\varvec{H}^{(3)}\) of lncRNAs and diseases, respectively:

$$\begin{aligned} {\left\{ \begin{array}{ll} & \varvec{H}_{l}= \textrm{Concat}(\varvec{H}_{l}^{(1)},\varvec{H}_{l}^{(3)}) \\ & \varvec{H}_{d}= \textrm{Concat}(\varvec{H}_{d}^{(1)},\varvec{H}_{d}^{(3)}) \end{array}\right. } \end{aligned}$$
(17)

MSA mechanism

The MSA mechanism can model complex relational patterns from multiple perspectives across different subspace projections through parallelized computation. Its multi-perspective and multi-granular structure high-level balances model expressiveness, computational ability, and cross-task generalization performance48. Since node information from different layers exhibits different contributions to predictions, we employ the MSA mechanism to learn node representations with distinct importance through an MSA mechanism \(\text {MSA}(\cdot )\) and 1D CNN \(\text {CNN}(\cdot )\) by Eq. (18):

$$\begin{aligned} {\left\{ \begin{array}{ll} & \varvec{Z}_{l}= \textrm{CNN}(\textrm{MSA}(\varvec{H}_{l})) \\ & \varvec{Z}_{d}= \textrm{CNN}(\textrm{MSA}(\varvec{H}_{d})) \end{array}\right. } \end{aligned}$$
(18)

Training

Based on the representations of lncRNAs \(\varvec{Z}_{l}\) and disease \(\varvec{Z}_{d}\), association matrix \(\varvec{R}\) between lncRNAs and diseases is computed by Eq. (19):

$$\begin{aligned} \varvec{R}={\varvec{Z}_{l}}^{\top } \varvec{Z}_{d} \end{aligned}$$
(19)

The higher \(\varvec{R}_{ij}\) denotes greater association possibility between lncRNA \(l_i\) and disease \(d_j\). The binary cross-entropy is taken as the loss function to assess the difference between predictions \(\varvec{R}\) and original matrix \(\varvec{Y}\) when training the nonlinear representation learning model. Here, we can obtain the nonlinear representations \(\varvec{Z}_{l}\) and \(\varvec{Z}_{d}\) of lncRNAs and diseases based on the minimization of loss function. After MSA-CNN operation, the obtained \(\varvec{Z}_1\) and \(\varvec{Z}_d\) have stable data distribution. Therefore, \(\varvec{Z}_1\) and \(\varvec{Z}_d\) need not normalization operation. Moreover, dot-product is the most common and universal measurement method. Compared with other similarity methods, dot-product operation can directly reflect the strength of association between lncRNA and disease representation vectors. Meanwhile, dot product operation has low computational complexity and is suitable for scaling to large datasets. Thus, we use the dot-product operation for leveraging lncRNA and disease representations.

Linear feature extraction

Recommendation system76 has demonstrated the powerful linear feature learning ability in various supervised learning tasks. Low-rank SVD is an efficient approximation method. It maps a high-dimensional matrix to a lower-dimensional subspace through random projection and exact decomposition. Here, we use a low-rank SVD algorithm to extract linear representations of lncRNAs and diseases.

Given \(\varvec{Y}\), we first generate a randomized Gaussian matrix \(\Omega \in \mathbb {R}^{n \times (q + k)}\) based on the given rank (q) and oversampling parameter k. Next, we obtain a more stable projection matrix \(\varvec{P}\) through power iteration. Finally, we compute an orthogonal basis matrix \(\varvec{Q} \in \mathbb {R}^{m \times (q + k)}\) based on QR decomposition by Eq. (20):

$$\begin{aligned} \varvec{P}= \varvec{QR},\qquad \varvec{Q}^{\top }\varvec{Q}=\varvec{I} \end{aligned}$$
(20)

According to the orthogonal basis matrix \(\varvec{Q}\) and original LDA matrix \(\varvec{Y}\), we construct a reduced matrix \({\varvec{B}}=\varvec{Q}^\top \varvec{Y}\) and perform full SVD on \({\varvec{B}}\) by Eq. (21):

$$\begin{aligned} {\varvec{B}} = \tilde{ \varvec{U}} \Sigma \varvec{V}^{\top } \end{aligned}$$
(21)

Finally, the low-rank approximation of \(\varvec{Y}\) is represented by Eq. (22):

$$\begin{aligned} \hat{\varvec{Y}}= \varvec{U} \Sigma \varvec{V}^{\top }, \varvec{U} = \varvec{Q} \tilde{ \varvec{U}} \end{aligned}$$
(22)

where \(\varvec{U} \in \mathbb {R}^{m \times q}\) and \(\varvec{V} \in \mathbb {R}^{n \times q}\) denote the linear embeddings of lncRNAs and diseases, respectively, and \(\Sigma \in \mathbb {R}^{q \times q}\) is a diagonal matrix containing singular values.

LDA prediction

Through graph representation learning and low-rank SVD, we learn nonlinear and linear features of lncRNAs and diseases, and concatenate them to gain final hybrid feature matrices \(\varvec{X}_{l}\) and \(\varvec{X}_{d}\) for predictions. Consequently, the final descriptor of an LDP \((l_i,d_j)\) is represented as Eq. (23):

$$\begin{aligned} {z}_{ij}=[\varvec{X}_{l}({i}),\varvec{X}_{d}({j})] \end{aligned}$$
(23)

where \(\varvec{X}_{l}({i})\) denotes the i-th row in \(\varvec{X}_{l}\) and \(\varvec{X}_{d}({j})\) denotes the j-th row in \(\varvec{X}_{d}\).

HGBoost is a powerful scalable ensemble learning model by leveraging gradient boosting with histogram-based optimization algorithm. During each iteration, HGBoost conducts binning statistic analysis on feature values to build histograms, approximates the information gain for potential splits, and further selects optimal thresholds for node splitting. Through the approximation strategy, HGBoost alleviates the computational burden when sorting features and accelerates training speed by parallel searching splitting nodes across multiple features. For an LDP \({z}_{ij}\) and its true label \(y_t\), HGBoost defines its loss function to predict its label \(\hat{y}_t\) by Eq. (24):

$$\begin{aligned} \mathscr {L}(y, \hat{y}_t) = -\frac{1}{N_{ld}} \sum _{t=1}^{N_{ld}} \left[ y_t \ln (\hat{y}_t) + (1 - y_t) \ln (1 - \hat{y}_t) \right] \end{aligned}$$
(24)

where \(N_{ld}\) is the number of LDPs.