Small signal modelling and analysis of quasi Z-source direct matrix converter for wind energy conversion system

Abstract

To enhance the voltage gain and regulate the output voltage under various loading and wind speeds, the Quasi Z-Source Direct Matrix Converter (QZSDMC) is proposed for PMG-based Direct Drive Wind Energy Conversion Systems (DDWECS). At first, using state space analysis, the small signal model of the QSDMC in space domain has been attained, and the transfer function of QZSDMC has been further calculated and analyzed. The stability analysis of the QZSDMC was conducted and proved that the system remains stable for all ranges of output power without using filter. The proposed QZSDMC based DDWECS with Improved Space Vector Pulse Width Modulation (ISVPWM) Control Scheme was simulated using Matlab and compared with existing methods. The simulation results are validated with 1 kW, 415 V, 50 Hz experimental setup with FPGA Processor. The outcomes are examined using the following metrics: switching stress, boost factor, total harmonic distortion, and efficiency.

Introduction

In the variable speed WECS, power converters play a major role since they act as an intermediary between the generator and the load¹. Many literatures have proposed about the various topologies of power converters for Variable Speed Direct Drive Permanent Magnet Generators². A simple low cost power converter configuration made up of a AC-DC converter, a boost/buck converter and an inverter was proposed in³. Back to back power converter with two level are also presented in^4,5. Using a traditional rectifier and a Z-Source inverter, a two-stage conversion was first introduced in⁶. Next, Neutral Point Converter (NPC) which is connected back to back with three level has also been discussed by⁷. An integrated diode rectifier power converter, a 3-level boost converter and a clamped Neutral Point inverter that connects the output of generator to grid was presented at⁸. Currently, the employment of Matrix Converter for PMSG based WECS connected with the grid has gained more attention as presented by at^9,10,11.

Since traditional ac-dc-ac power converters provide three stages of power conversion, it increases system size, expense, loss and reduces system reliability and performance^12,13,14. A bridge rectifier with diode is employed to rectify the PMG voltage at the output in the three-stage conversion of power¹⁵. To attain the required output, the dc chopper is then utilized to control the voltage in the capacitor that is supplied to the inverter. Some of the limitations of Voltage Source Inverters (VSI) are bulky, increase in losses, rich current harmonics, higher output Total Harmonic Distortion (THD), and requires output LC filter and unidirectional power handling capability. This system’s total efficiency is reduced since it employs three stages of power conversion.

The conceptual and theoretical restrictions of conventional VSI and CSI has proposed an Z-Source Power Converter that affords a novel power conversion idea¹⁶. It has many advantages such as increasing or decreasing the voltage, higher efficiency and higher reliability¹⁷. Using a special impedance network, the Z-source inverter links the inverter’s focal circuit to the input supply via a rectifier¹⁸.

The primary function of this paper is to predict the most efficient power converter with a suitable PWM control technique for Variable Speed PMG based direct drive WECS¹⁹. For its compactness, Matrix Converter (MC) was an outstanding competitor among conventional converters, which does not need any dc link and provides direct ac to ac conversion that facilitates maximum wind power extraction^20,21. But the voltage transfer ratio of Matrix Converter was restricted to 0.866²².

Z-Source Direct Matrix Converter (ZSDMC), which connects an Impedance-Source circuit to the Direct Matrix Converter, was developed to get around this problem²³. Although ZSDMC offers buck boost ability with fewer LC components, the Z-Source network of ZSDMC has an intrinsic phase shift which ends in imprecise control and increased switching stresses, increasing the system’s loss. The maximum voltage transfer ratio is 1.15^24,25,26. Additionally, it generates irregular input current, necessitating the need of a sizable filter circuit to decrease the current harmonics at the input.

²⁷.

The paper introduces a direct drive wind energy conversion system (DDWECS) built around a Quasi Z source matrix converter (QZSMC) to enhance the voltage transfer ratio. PWM techniques are now the most crucial control methods, which includes many types of boost control methods²⁸. However, conventional CBPWM for QZSMC, has higher switching stresses, higher losses, higher THD, and lower efficiency. A unique Improved Space Vector Pulse Width Modulation Scheme (ISVPWM) for QZSMC based DDWECS has been suggested in order to overcome the limitations of standard CBPWM^29,30. It is possible to raise the quasi Z source network’s duty ratio by altering the shoot through dispersal in space vector modulation^31,32. Furthermore, control, modeling and utilization of QZSDMC to WECS, have not yet been discussed³³. Hence, this paper objects to focus on modeling, control and evaluating QZSDMC’s stability for interfacing PMG-WECS and load. The small signal model and its transfer function have been developed for both QZSDMC, to confirm the stability of the system.

To clearly highlight the advancements over existing works, the following novel contributions of the proposed Quasi Z-Source Direct Matrix Converter (QZSDMC) and its PWM techniques are summarized:

• Enhanced Voltage Gain: The proposed QZSDMC achieves a voltage gain of 1.15, surpassing traditional converters, which are typically limited to a maximum of 1.1.

• Improved PWM Scheme: The introduction of the Improved Space Vector PWM (ISVPWM) scheme significantly reduces switching losses and Total Harmonic Distortion (THD) compared to conventional Carrier-Based PWM (CBPWM).

• Reduced Switching Stresses: The ISVPWM-based QZSDMC demonstrates a 12% reduction in voltage stress and lower current stress (1 A), improving efficiency and extending converter lifespan.

• Optimized Shoot-Through Control: A novel shoot-through control strategy is implemented, optimizing the duty ratio to enhance the voltage boosting capability without compromising stability.

Additionally, this paper is arranged as explained: In Sect. 2, the working modes of QZSDMC have been explained and the small signal model of QZSDMC in space domain has been attained. The transfer function of proposed QZSDMC has been derived and the effect of inductive and capacitive elements and the shoot through state on the transient response of proposed converter has been analysed. The QZSDMC is used in Sect. 3 as an interface between the separate load and PMG-WECS, and the controller is made to produce the required output. In Sects. 4 and 5 of this paper, the performance of the suggested QZSDMC with ISVPWM control technique was compared with the CBPWM strategy.

Quasi Z-source direct matrix converter

Topology

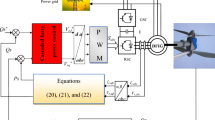
QZSDMC topology has four parts specifically input filter, QZS network, DMC and three phase load as given in Fig. 1^34,35.

The QZS network consists of six inductors (Lx1,Lx2,Ly1,Ly2,Lz1,Lz2) and six capacitors (Cx1,Cx2,Cy1,Cy2,Cz1,Cz2) along with three additional bidirectional switches (S1,S2,S3). These additional switches can be operated by a single gate signal since they share the same switching status as S0. The special network with impedance source permits the proposed circuit to run in the buck- boost mode as well as offering the innovative features that other conventional converters cannot achieve³⁶.

The operating concept of envisaged QZSDMC topology can be separated into Shoot through State (ST) and Active or Non shoot through state (NST)³⁷. At the time of Shoot through State (ST), the switch S0 is turned OFF and the output of QZSDMC such as x’, y’ and z’ has been shorted for enhancing the voltage. Whereas in the course of Non Shoot through State (NST), the switch S0 is switched on in order to carry out regular switching operation of Direct Matrix Converter³⁸. Since the system is symmetrical, the inductance L of all the inductors (Lx1 to Lz2) and also, the capacitance C of all the capacitors (Cx1 to Cz2 ) of the QZS network are same³⁹. Let the total time period for full complete switching cycle is T, the time period for Zero State is T0 and the Time period for Active State is T1 and hence, T = T0 + T1. The shoot through time period’s duty ratio can be given by D = T0/T1.

Fig. 1

Topology of voltage fed QZSDMC.

Small signal model

The suggested small signal modeling and investigation continues through the supposition that while supplied by variable voltage and frequency sinusoidal voltage source, the QZSDMC is feeding an RL load^40,41,42. In the QZS network, the switch S0 is closed during active state. Let the state variables (inductor currents, capacitor voltages in the QZS network and output current vector) can be defined based on space vector as Eqs. (1),

$${\text{x}}({\text{t}})=\left[ {\begin{array}{*{20}{c}} {{{\text{i}}_{{\text{L}}1}}({\text{t}})}&{{{\text{i}}_{{\text{L}}2}}({\text{t}})}&{{v_{{\text{C}}1}}({\text{t}})}&{{{\text{v}}_{{\text{C}}2}}({\text{t}})}&{{{\text{i}}_{\text{L}}}({\text{t}})} \end{array}} \right]$$

(1)

Let’s specify the input voltage vector of QZS network as V_iq, input variable. Assuming,

$$\begin{gathered} {C_1}={C_{x1}}={C_{y1}}={C_{z1}} \hfill \\ {C_2}={C_{x2}}={C_{y2}}={C_{z2}} \hfill \\ {L_1}={L_{x1}}={L_{y1}}={L_{z1}} \hfill \\ {L_2}={L_{x2}}={L_{y2}}={L_{z2}} \hfill \\ \end{gathered}$$

(2)

Furthermore, assume that R_L and L_L gives the resistance and inductance of the RL load, respectively.

State-space representation during shoot-through state

By turning on all of the switches for one, two, or three phase legs, a shoot-through state can be reached. At shoot through state, the differential equation can be given in the state space form as given by Eq. (3)

$$\:K\stackrel{.}{x}={A}_{1} \cdot x+{B}_{1} \cdot u$$

(3)

From the equal model of shoot through state, the state space form in Eq. (3) can be derived as shown in Eq. (4) to (8),

$$\:{L}_{1}\frac{d{i}_{L1}\left(t\right)}{dt}={V}_{C1}\left(t\right)$$

(4)

$$\:{L}_{2}\frac{d{i}_{L2}\left(t\right)}{dt}={V}_{C2}\left(t\right)$$

(5)

$$\:{C}_{1}\frac{d{V}_{C1}\left(t\right)}{dt}=-{i}_{L1}\left(t\right)$$

(6)

$$\:{C}_{2}\frac{d{V}_{C2}\left(t\right)}{dt}=-{i}_{L2}\left(t\right)$$

(7)

$$\:{L}_{L}\frac{d{i}_{L}\left(t\right)}{dt}=-{R}_{L}{i}_{L}\left(t\right)$$

(8)

From Eq. (4) to (8), state space equations for shoot through duty period is given by Eqs. (9),

$$\left[ {\begin{array}{*{20}c} {L_{1} } & 0 & 0 & 0 & 0 \\ 0 & {L_{2} } & 0 & 0 & 0 \\ 0 & 0 & {C_{1} } & 0 & 0 \\ 0 & 0 & 0 & {C_{2} } & 0 \\ 0 & 0 & 0 & 0 & {L_{L} } \\ \end{array} } \right]\frac{d}{{dt}}\left[ {\begin{array}{*{20}c} {i_{{L1}} \left( t \right)} \\ {i_{{L2}} \left( t \right)} \\ {v_{{C1}} \left( t \right)} \\ {v_{{C2}} \left( t \right)} \\ {i_{L} \left( t \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ { - 1} & 0 & 0 & 0 & 0 \\ 0 & { - 1} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {0R_{L} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {i_{{L1}} \left( t \right)} \\ {i_{{L2}} \left( t \right)} \\ {v_{{C1}} \left( t \right)} \\ {v_{{C2}} \left( t \right)} \\ {i_{L} \left( t \right)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right] \cdot Viq\left( t \right)$$

(9)

Where

$$\:K=\left[\begin{array}{ccccc}{L}_{1}&\:0&\:0&\:0&\:0\\\:0&\:{L}_{2}&\:0&\:0&\:0\\\:0&\:0&\:{C}_{1}&\:0&\:0\\\:0&\:0&\:0&\:{C}_{2}&\:0\\\:0&\:0&\:0&\:0&\:{L}_{L}\end{array}\right],\:A1=\left[\begin{array}{ccccc}0&\:0&\:1&\:0&\:0\\\:0&\:0&\:0&\:1&\:0\\\:\text{-1}&\:0&\:0&\:0&\:0\\\:0&\:\text{-1}&\:0&\:0&\:0\\\:0&\:0&\:0&\:0&\:\text{-}{{\text{R}}_{L}}_{\:}\end{array}\right],\:B1=\left[\begin{array}{c}0\\\:1\\\:0\\\:0\\\:0\end{array}\right]$$

(10)

State space representation during non-shoot through state

Similarly, the state space representation of QZSDMC during active state can be given as in Eqs. (11),

$$K\dot{x} = A_{2} \cdot x + B_{2} \cdot u$$

(11)

The following Eqs. (12) to (16) can be obtained from the equivalent circuit of active state,

$$\:{L}_{1}\frac{d{i}_{L1}\left(t\right)}{dt}=-{V}_{C2}\left(t\right)$$

(12)

$$\:{L}_{2}\frac{d{i}_{L2}\left(t\right)}{dt}=-{V}_{C1}\left(t\right)+{V}_{iq}$$

(13)

$$\:{C}_{1}\frac{d{V}_{C1}\left(t\right)}{dt}=-{i}_{L2}\left(t\right)+{i}_{L}$$

(14)

$$\:{C}_{2}\frac{d{V}_{C2}\left(t\right)}{dt}=-{i}_{L1}\left(t\right)+{i}_{L}$$

(15)

$$\:{L}_{L}\frac{d{i}_{L}\left(t\right)}{dt}=-{V}_{C1}\left(t\right)-{V}_{C2}\left(t\right)+{R}_{L}{i}_{L}\left(t\right)$$

(16)

From Eqs. (12) to (16), the state space equations during non-shoot through state in matrix form can be written as Eqs. (17),

$$\left[ {\begin{array}{*{20}c} {L_{1} } & 0 & 0 & 0 & 0 \\ 0 & {L_{2} } & 0 & 0 & 0 \\ 0 & 0 & {C_{1} } & 0 & 0 \\ 0 & 0 & 0 & {C_{2} } & 0 \\ 0 & 0 & 0 & 0 & {L_{L} } \\ \end{array} } \right]\frac{d}{{dt}}\left[ {\begin{array}{*{20}c} {i_{{L1}} \left( t \right)} \\ {i_{{L2}} \left( t \right)} \\ {v_{{C1}} \left( t \right)} \\ {v_{{C2}} \left( t \right)} \\ {i_{L} \left( t \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & { - 1} & 0 \\ 0 & 0 & { - 1} & 0 & 0 \\ 0 & { - 1} & 0 & 0 & 1 \\ { - 1} & 0 & 0 & {C_{2} } & 1 \\ 0 & 0 & { - 1} & { - 1} & { - R_{L} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {i_{{L1}} \left( t \right)} \\ {i_{{L2}} \left( t \right)} \\ {v_{{C1}} \left( t \right)} \\ {v_{{C2}} \left( t \right)} \\ {i_{L} \left( t \right)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]v_{{iq}} \left( t \right)$$

(17)

Where

$$\:K=\left[\begin{array}{ccccc}{L}_{1}&\:0&\:0&\:0&\:0\\\:0&\:{L}_{2}&\:0&\:0&\:0\\\:0&\:0&\:{C}_{1}&\:0&\:0\\\:0&\:0&\:0&\:{C}_{2}&\:0\\\:0&\:0&\:0&\:0&\:{L}_{L}\end{array}\right],\:A2=\left[\begin{array}{ccccc}0&\:0&\:0&\:-1&\:0\\\:0&\:0&\:\text{-1}&\:0&\:0\\\:0&\:\text{-1}&\:0&\:0&\:1\\\:\text{-1}&\:0&\:0&\:0&\:1\\\:0&\:0&\:\text{-1}&\:\text{-1}&\:\text{-}{{\text{R}}_{L}}_{\:}\end{array}\right],\:B2=\left[\begin{array}{c}0\\\:1\\\:0\\\:0\\\:0\end{array}\right]$$

(18)

Equation (3) can be resolved to identify the equilibrium of the state vector. The equilibrium values of state variable is given by Eq. (19) to (21)

$$\:0=AX+BU$$

(19)

$$\:0=CX+EU$$

(20)

$$\:0=\left(D{A}_{1}+{D}^{{\prime\:}}{A}_{2}\right)X+\left(D{B}_{1}+{D}^{{\prime\:}}{B}_{2}\right)U,$$

(21)

Where,

$$\:A=D{A}_{1}+{D}^{{\prime\:}}{A}_{2}$$

$$\:B=D{B}_{1}+{D}^{{\prime\:}}{B}_{2}$$

$$\:C=D{C}_{1}+{D}^{{\prime\:}}{C}_{2}$$

$$\:E=D{E}_{1}+{D}^{{\prime\:}}{E}_{2}$$

Assume

$${\text{L}}={{\text{L}}_1}={{\text{L}}_2}\;{\text{and}}\;{\text{C}}={{\text{C}}_1}={{\text{C}}_2}.$$

(22)

By resolving Eq. (17), the converter steady state equation can be given by Equations (23) to (24),

$$\:{i}_{L1}={i}_{L2}=\frac{1-D}{1-2D}{I}_{L}$$

(23)

$$\:{V}_{C1}=\frac{1-D}{1-2D}{V}_{iq}$$

(24)

$$\:{V}_{C2}=\frac{D}{1-2D}{V}_{iq}$$

(25)

Let V_im be the output voltage vector of QZSDMC.

V_im=0 in shoot through state.

Whereas,

$${V_{im}}={V_{C1}}+{V_{C2}}\,\,\, \text{in\,non-shoot\,through\,state}$$

(26)

From (26) considering (24) and (25), we get, Eq. (27)

$$\:{V}_{im}=\frac{1}{1-2D}{V}_{iq}$$

(27)

From Eq. (19), it is concluded that QZSDMC can achieve an ideal unlimited boost factor.

The small signal association among the state variables can be achieved by relating small signal perturbations $\:{\widehat{v}}_{i1}\left(t\right)$ to input voltage and to the shoot through duty ratio of S₀ given by Eqs. (28),

$$\:{v}_{i1}\left(t\right)={V}_{i1}+{\widehat{v}}_{i1}\left(t\right),\:d\left(t\right)=D+\widehat{d}\left(t\right)$$

(28)

The perturbations results in small signal differences in the state variable.

Let

$${\text{x}}={\text{X}}+{\text{x}}$$

(29)

Merging equations of mode 1 and mode 2, we get small signal state Eqs. (30),

$$\:K\widehat{\dot{X}}=\left(D\cdot\:{A}_{1}+D{\prime\:}\cdot\:{A}_{2}\right)\cdot\:\widehat{X}+\left(D{B}_{1}+D{\prime\:}{B}_{2}\right)\cdot\:U+({A}_{1}-{A}_{2})X+({B}_{1}+{B}_{2})U$$

(30)

Solving above equations, the Laplace transform of small signal Equations in space domain can be derived and is given by Equations (31) to (33),

$$\:sL{\stackrel{\wedge\:}{i}}_{L1}\left(s\right)=D{\stackrel{\wedge\:}{V}}_{C1}\left(s\right)-D{\prime\:}{\stackrel{\wedge\:}{V}}_{C2}\left(s\right)+({V}_{C1}+{V}_{C2})\stackrel{\wedge\:}{d(s})$$

(31)

$$\:sL{\stackrel{\wedge\:}{i}}_{L2}\left(s\right)=-D{\prime\:}{\stackrel{\wedge\:}{V}}_{C1}\left(s\right)+D{\stackrel{\wedge\:}{V}}_{C2}\left(s\right)+({V}_{C1}+{V}_{C2})\stackrel{\wedge\:}{d(s})+{\stackrel{\wedge\:}{V}}_{iq}$$

(32)

$$\:sC{\stackrel{\wedge\:}{V}}_{C1}\left(s\right)=-D{\stackrel{\wedge\:}{i}}_{L1}\left(s\right)+D{\prime\:}{\stackrel{\wedge\:}{i}}_{L2}\left(s\right)-D{\prime\:}\stackrel{\wedge\:}{{i}_{L}}\left(s\right)+(-{i}_{L1}-{i}_{L2}+{I}_{L})\stackrel{\wedge\:}{d(s})$$

(33)

$$\:sC{\stackrel{\wedge\:}{V}}_{C2}\left(s\right)=D{\prime\:}{\stackrel{\wedge\:}{i}}_{L1}\left(s\right)-D{\stackrel{\wedge\:}{i}}_{L2}\left(s\right)+D\stackrel{\wedge\:}{{i}_{L}}\left(s\right)+(-{i}_{L1}-{i}_{L2}+{I}_{L})\stackrel{\wedge\:}{d(s})$$

(34)

$$\:({R}_{L}+s{L}_{L})\stackrel{\wedge\:}{{i}_{L}}\left(s\right)=D{\prime\:}\left({\stackrel{\wedge\:}{V}}_{C1}\right(s)+{\stackrel{\wedge\:}{V}}_{C2}(s\left)\right)-({V}_{C1}+{V}_{C2})\stackrel{\wedge\:}{d\left(s\right)}$$

(35)

By substituting $\widehat{{\overline{i} _{L} }} = \widehat{{\overline{i} _{{L1}} }} + \widehat{{\overline{i} _{{L2}} }}$,$\overline{{I_{L} }} = \overline{{I_{{L1}} }} + \overline{{I_{{L2}} }}$, $\mathop {v_{c} }\limits^{ \wedge } = \widehat{{\overline{{v_{{c1}} }} }} + \widehat{{\overline{{v_{{c1}} }} }}$, $\overline{V} _{C} = \overline{V} _{{C1}} + \overline{V} _{{C2}}$ in above equations we get Equations (36) to (38),

$$sL\widehat{{\overline{{i_{L} }} }}\left( s \right) = (D - D\prime )\widehat{{\overline{{v_{c} }} }}\left( s \right) + \left( {2\overline{V} _{c} } \right)\mathop {d(s}\limits^{ \wedge } ) + \mathop V\limits^{ \wedge } _{{iq}}$$

(36)

$$sC\widehat{{\overline{{v_{C} }} }}\left( s \right) = (D\prime - D)\mathop i\limits^{ \wedge } _{L} \left( s \right) - 2D\prime \mathop {i_{L} }\limits^{ \wedge } \left( s \right) + 2(i_{L} - I_{L} )\mathop {d(s}\limits^{ \wedge } )$$

(37)

$$(R_{L} + sL_{L} )\mathop {i_{L} }\limits^{ \wedge } \left( s \right) = D\prime \widehat{{\overline{{v_{c} }} }}\left( s \right) - \overline{V} _{c} d\mathop {\left( s \right)}\limits^{ \wedge }$$

(38)

Transfer function model

The reaction of one state variable to various small signal disturbances can be obtained in small signal modeling and transitory analysis through linear combinations of adjustable response to individual disturbances^43,44. Hence, the capacitor voltage small signal expression can be given by Eqs. (39),

$$\:\stackrel{\wedge\:}{{v}_{C}\left(s\right)}={G}_{viq}\left(s\right)\cdot\:\stackrel{\wedge\:}{{V}_{iq}}\left(s\right)+{G}_{vd}\left(s\right)\cdot\:\stackrel{\wedge\:}{d\left(s\right)}$$

(39)

where, $\:{G}_{viq}\left(s\right)$ represents the transfer function of input to capacitor voltage and $\:{G}_{vd}\left(s\right)$ the transfer function of control to capacitor voltage.

$$\:{G}_{viq}\left(s\right)={\left.\frac{\stackrel{\wedge\:}{{v}_{C}\left(s\right)}}{\stackrel{\wedge\:}{{V}_{iq}}\left(s\right)}\right|}_{\stackrel{\wedge\:}{d\left(s\right)}=0}=\:\:\:\frac{sL(D{\prime\:}-D)}{{s}^{2}LC+(D-D{\prime\:}{)}^{2}+\frac{2(1-D)sL}{{R}_{L}+s{L}_{L}}}$$

(40)

$$\:{G}_{vd}\left(s\right)={\left.\frac{\stackrel{\wedge\:}{{v}_{C}\left(s\right)}}{\stackrel{\wedge\:}{d}\left(s\right)}\right|}_{\stackrel{\wedge\:}{{v}_{iq}\left(s\right)}=0}=\frac{(1-2D)2{V}_{C}-\frac{2{V}_{C}(1-D)sL}{{R}_{L}+s{L}_{L}}+2({i}_{L}-{I}_{L})sL}{{s}^{2}LC+(D-D{\prime\:}{)2}_{}+\frac{2(1-D{)}^{2}}{{R}_{L}+s{L}_{L}}}$$

(41)

Fig. 2

Magnitude and phase plot of output voltage controlled QZSDMC.

Figure 2 shows the simulated Bode magnitude and phase response of the output voltage-controlled QZSDMC using MATLAB’s Control System Toolbox. The Bode plot was generated by linearizing the small signal state-space equations derived in Equations (31) to (38), with input as the shoot-through duty ratio and output as the capacitor voltage. A Proportional-Integral (PI) compensator was used in the outer voltage control loop to regulate the capacitor voltage. The PI gains were tuned using the Ziegler-Nichols method followed by manual fine-tuning to meet the desired dynamic response. The system exhibits a gain margin of 10.5 dB and a phase margin of 52°, indicating robust stability. These margins are maintained across various operating points, including wind velocities ranging from 4 m/s to 12 m/s, due to the gain scheduling approach embedded within the control loop. This ensures consistent closed-loop performance of the QZSDMC under variable loading and wind conditions.

Modulation schemes for QZSDMC

The shoot through control methods such as simple boost, maximum boost, maximum constant boost and space vector PWM can be applied to QZDMC after certain modification in the carrier envelope. The Carrier Based PWM Technique and Modified Space Vector PWM Technique are employed to analyze the performance of QZSDMC.

Carrier based PWM scheme

In this PWM technique, the carrier waveform has been bounded by the same envelope of three phase voltages $\:{V}_{x},{V}_{y}$ and $\:{V}_{z}$. The top and bottom envelope of carrier waveform formed by the maximum and minimum voltages amongst the three input source voltages⁴⁵. During each switching time period, the triangular carrier is matched with the output reference voltage $\:{V}_{X},{V}_{Y}$and $\:{V}_{Z}$ to get the PWM signals (S_X, S_Y and S_Z). The shoot through pulses are produced by comparing the carrier waveforms with the shoot through reference and these pulses are inserted in the final output PWM signals as shown in Fig. 3.

Fig. 3

Block Diagram for QZSDMC Pulse Generation with Shoot through Insertion.

Modified space vector PWM scheme

In MSVPWM of QZSDMC, the conventional space vector modulation method is introduced with the control of shoot through state⁴⁶. The active states of traditional DMC is maintained as same in the non-shoot through mode of QZSDMC and portion of the zero vector is replaced by the shoot through states in one complete switching period. Based on the number of phases short circuited, there are three possible groups of shoot through vectors such as single phase, two phases and three phases shoot through.

Fig. 4

Modified space vector pulse width modulation technique (a) input current space vector (b) output voltage space vector.

When related to other two techniques, the single output phase shoot through efficiently diminish the switching period of bidirectional switches. Thus, the voltage boosting in modified modulation strategy is achieved by employing single phase shoot through zero vectors. For instance, assume that the input current vector is situated in sector 1 and output line voltage vector is situated in sector 2. As shown in Fig. 4, the active vectors are formed by the active current vectors I₁, I₆ and the active voltage vectors U₁, U₂. Then four active vectors such as xyy, xyx, xzx, xzz and two zero vectors yyy, zzz are formed. The equivalent shoot through zero vectors are denoted as S_tyy, xyS_t, xS_tx, xzS_t, S_tzz. The law of sines is used to calculate the duty ratio of input current ad output voltage vectors as given by Eqs. (42),

$$\begin{aligned} {d_\alpha } & =\frac{{{T_\alpha }}}{{{T_s}}}={m_i}\sin (60^\circ - {\theta _{mi}}) \\ {d_\beta } & =\frac{{{T_\beta }}}{{{T_s}}}={m_i}\sin {\theta _{mi}} \\ {d_\mu } & =\frac{{{T_\mu }}}{{{T_s}}}={m_\nu }\sin (60^\circ - {\theta _{mv}}) \\ {d_\nu } & =\frac{{{T_\nu }}}{{{T_s}}}={m_\nu }\sin {\theta _{m\nu }} \\ \end{aligned}$$

(42)

Also, we have

$$\begin{aligned} {d_{\alpha \mu }} & ={d_\alpha } \cdot {d_\mu } \\ {d_{\alpha \nu }} & ={d_\alpha } \cdot {d_\nu } \\ {d_{\beta \mu }} & ={d_\beta } \cdot {d_\mu } \\ {d_{\beta \nu }} & ={d_\beta } \cdot {d_\nu } \\ \end{aligned}$$

(43)

where,

dα, dβ - Duty ratios of active input current vectors of rectifier stage.

dµ, dv - Duty ratios of active output voltage vectors of inverter stage.

mi - Modulation index of rectifier stage.

mv- Modulation index of inverter stage.

Tx, where x = α,β,µ,v specifies the period of an active vector in a switching cycle Ts.

Then, the output voltage modulation and input current modulation can be combined to obtain four pairs of active vectors and one zero vector.

$$\begin{gathered} {T_1}={d_{\alpha \mu }}{T_s}=m\sin (60^\circ - {\theta _{mi}})\sin (60^\circ - {\theta _{m\nu }}){T_s} \hfill \\ {T_2}={d_{\alpha \nu }}{T_s}=m\sin {\theta _{m\nu }}\sin (60^\circ - {\theta _{mi}}){T_s} \hfill \\ {T_3}={d_{\beta \mu }}{T_s}=m\sin (60^\circ - {\theta _{m\nu }})\sin {\theta _{mi}}{T_s} \hfill \\ {T_4}={d_{\beta \nu }}{T_s}=m\sin {\theta _{m\nu }}\sin {\theta _{mi}}{T_s} \hfill \\ {T_0}={d_{ST}}{T_s} \hfill \\ {T_z}=1 - {T_1} - {T_2} - {T_3} - {T_4} - {T_0} \hfill \\ m={m_i}{m_v} \hfill \\ \end{gathered}$$

(44)

where,$\:0\le\:{\theta\:}_{mi}\le\:6{0}^{o},0\le\:{\theta\:}_{m\nu\:}\le\:6{0}^{o}$, T₁,T_2,T_3,T₄ specifies the switching period of active vectors in a switching period T_s, T₀ denotes shoot through time period, T_z denotes the switching sequence of zero vectors in a switching cycle T_s, m denotes modulation index and d_ST denotes shoot through duty ratio. The switching time period of shoot through zero vectors is adjusted to improve the performance of QZSDMC. However, the active vector remains unchanged.

Controller for QZSDMC based WECS

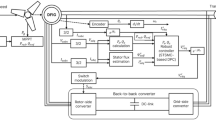
The most important factor in controlling the QZSDMC’s output voltage is the dispersion of the shoot through period. The QZSDMC promises continuous input current, lower harmonics of the output waveform, higher voltage gain, and less switching stresses when the shoot through period is inserted using an appropriate control method. To produce fixed output voltage and frequency a closed loop controller has been used for the suggested QZSDMC. Figure 5 gives the block diagram of Closed Loop Controller for QZSDMC with PMG based DDWECS⁴⁷. To produce PWM pulses for QZSDMC, the PWM controller receives the 3 phase reference voltages (Vx, Vy, and Vz) that were acquired from the closed loop controller. PWM controller provides PWM pulses using two different modulation algorithms, such as CBPWM and ISVPWM⁴⁸. The rotor speed reference ωr* at which maximum power can be harvested has been computed using the measured wind velocity in the closed loop controller’s MPPT control technique. The actual speed of rotor ωr obtained from the PMG is compared with the rotor speed reference ωr* at each wind speed Vω and the resultant signal is fed to a PI controller. After comparing the PI controller’s output with the carrier signal, a control signal that serves as a speed regulator to modify the shoot through duty ratio D is produced.

To regulate active and reactive powers, the closed loop controller has an inner and an outer loop. The Park/Clark Transformation, which converts electrical quantities into a dqo reference frame, is the primary foundation of the closed loop controller. The Park/Clark Transformation is used to convert the three phase load voltages and load currents into dq axis components, such as Vds, Vqs, id, and iq. The actual dq axis current (id and iq) is related with the reference dq axis current (id* and iq*) valued from the obtained reactive power and capacitor voltage separately and the obtained error signals are managed via the PI controllers to provide the reference dq axis voltages (Vds*and Vqs*).

Then, the inverse Park/Clark transformation is used to transform the produced dq-phase voltages into the three-phase reference voltages respectively. The PWM controller receives the attained sinusoidal reference signal as input and uses it to create PWM pulses for the QZSDMC. In QZSDMC, the gain G and Boost Factor B is dependent on Modulation Index M and Shoot through Duty Ratio D. By varying these parameters constant output voltage and frequency can be obtained. Also, the THD in the output voltage and current has to be reduced⁴⁹.

The proposed QZSDMC are known for their ability to handle wide input voltage ranges. However, they can also experience increased voltage stress due to the high voltage boost capability, which may require components with higher voltage ratings. Also, handling faults in quasi-Z-source DMCs can be complex and Ensuring fault tolerance and safe operation under various fault conditions requires sophisticated fault management and protection strategies. These are some of the limitations of QZSDMC^50,51.

Fig. 5

Closed Loop Controller for QZSDMC with PMG based Direct Drive Wind Energy Conversion System.

Results and discussion

Based on characteristics like switching stress, THD and for numerous wind velocity and load situations, the investigations of QZSDMC with CBPWM and ISVPWM schemes, has been conducted. To predict the effectiveness of CBPWM and ISVPWM scheme, the QZSDMC has been simulated in MATLAB/SIMULINK environment and its operation was analyzed for various input and load conditions. The results obtained under two cases are also compared to envisage the better PWM scheme for QZSDMC.

Fig. 6

Simulated Outputs of CBPWM based QZSDMC for (a) Capacitor Voltage (b) Inductor Current and (c) AC link Voltage.

Figure 6a–c shows the voltage in the capacitor, current through the inductor and ac link voltage of QZSDMC with CBPWM technique. It was observed that the voltage across the capacitor was 205 V, the current through the inductor was 90 A and that of AC link voltage was 510 V. To enhance the performance of QZSDMC a novel improved space vector PWM scheme has been investigated. Figure 7a–c shows the capacitor voltage, inductor current and ac link voltage of QZSDMC under ISVPWM scheme for the generated voltage of PMG as 173 V, turbine speed of 130 rpm, D₀ as 0.2 and modulation index 0.8.

Fig. 7

Simulation results of ISVPWM based QZSDMC for (a) Capacitor Voltage (b) Inductor Current and (c) AC Link Voltage.

Fig. 8

Simulated Outputs of CBPWM based QZSDMC for Three Phase (a) Line Voltage and (b) Phase voltage without filter.

Fig. 9

Simulated Outputs of ISVPWM based QZSDMC for Three Phase (a) Line Voltage and (b) Phase Voltage without filter.

Figures 8 and 9 represents the line voltage and phase voltage of CBPWM and ISVPWM based QZSDMC for three phases without filter respectively. According to the results, the ISVPWM scheme’s voltage gain is more than the CBPWM scheme’s. Figure 10 represents the three-phase individual output current of the QZSDMC based on CBPWM and ISVPWM at a 0.25 kW load, respectively.

Fig. 10

Simulation results for (a) CBPWM and (b) ISVPWM based QZSDMC Output Current.

Performance analysis of QZSDMC at different loading conditions

The foremost objective of the simulation is to analyse the QZSDMCs harmonic spectra of output parameters such as line voltage and current under two different PWM Schemes. Figures 11 and 12 represents simulated output voltage and output current harmonic spectra of QZSDMC for both CBPWM and ISVPWM schemes at a load of 0.25 kW. For the CBPWM and ISVPWM schemes, the QZSDMC output line voltage THD is around 2.6% and 1.2%, respectively. The percentage output current THD of CBPWM is 1.05% greater than that of ISVPWM scheme employed in QZSDMC. Thus, the ISVPWM scheme is considered to be the best for efficient operation of QZSDMC.

Figure 13 compares the voltage and current THD at the output of QZSDMC for two PWM methods. The figure makes it clear that, in comparison to the CBPWM scheme for QZSDMC, the THD parameters of the ISVPWM method are lower.

Fig. 11

Simulated output line voltage THD of QZSDMC for (a) CBPWM (b) ISVPWM.

Fig. 12

Simulated output current THD of QZSDMC for (a) CBPWM (b) ISVPWM.

Fig. 13

Comparison of output line voltage and current THD for QZSDMC.

Analysis of switching stress

By raising shoot through duty ratio D0 and the modulation index M, QZSDMC’s voltage gain can be enhanced. By partially or completely substituting shoot-through states for zero states without interfering with active states, the voltage gain of QZSDMC can be boosted. Figures 14 and 15 show the changes in current and voltage stresses in the QZSDMC power switches under the CBPWM and ISVPWM schemes for different shoot through duty ratios, respectively.

Fig. 14

Current stress versus shoot through duty ratio of QZSDMC.

Fig. 15

Voltage Stress Versus Shoot Through duty Ratio of QZSDMC.

The current stress of CBPWM scheme is almost higher than that of ISVPWM scheme for QZSDMC for various D₀. Figures 14 and 15 show that, with D₀ of 0.3, the ISVPWM scheme-based QZSDMC’s voltage stress is 12% lower than the CBPWM scheme’s, and the ISVPM scheme’s current stress is 1 A lower than the CBPWM scheme’s.

Fig. 16

Current Stress of QZSDMC at Different Loading Conditions.

Fig. 17

Voltage Stress of QZSDMC at Different Loading Conditions.

Figures 16 and 17 shows the variations in the current stresses and Voltage stresses of power switches for QZSDMC with CBPWM and ISVPWM scheme at different load conditions. At 1 kW load, the voltage stress of power switches for ISVPWM scheme is about 95 V less than that of CBPWM scheme. Also the current stress of power switches under CBPWM scheme is 1.6 A greater than that of ISVPWM scheme.

Experimental setup

A model has been developed as shown in Fig. 18 to validate the modulation technique and the simulation results of the proposed QZSDMC.

Fig. 18

Prototype experimental setup of QZSDMC.

The control algorithms in Quasi Z Source DMC and ISVPWMM techniques are complex. Implementing these in experimental setups involves hardware-in-the-loop simulations or real-time control, which can introduce uncertainties in the system due to computational limitations or control implementation errors. Limitations in hardware, scalability, and real-time implementation can affect the fidelity of the experimental study. These challenges have been addressed by developing and implementing robust control algorithms that can handle uncertainties and variations in the system’s operation. Also, by employing filtering and noise reduction methods in signal processing the impact of noise on measurements and system performance analysis is reduced.

However, to address the problem of uncertainties and noise encountered in simulation studies of quasi Z-source D-MC based wind energy conversion systems model validation has to be done in which Simulink model results are related with benchmarks to authorize the correctness of the model and ensure it behaves realistically under different conditions. Furthermore, noise disturbances can be reduced by conducting noise analysis to understand its impact on results and applying appropriate filtering methods. By employing these strategies, researchers aim to address.

Fig. 19

Flowchart for Experimental Validation of control scheme employed in QZSDMCs.

The experimental validation method is shown in a flowchart in Fig. 19. A power quality analyser is used to measure the output parameters. The shoot-through pulse generation is a critical part of the QZSDMC control scheme, as it directly influences the converter’s voltage gain and system efficiency. The FPGA is used to synchronize the shoot-through pulses with the main switching signals. This synchronization is achieved by modulating the shoot-through time within the switching period to regulate the duty cycle.

A timing diagram depicting the main switching signals (S1, S2, S3) along with the shoot-through pulse (ST) is shown below. The shoot-through pulses are inserted into the modulation scheme during the zero states of the switching period to avoid overlap with the active states, thereby boosting the voltage gain without compromising system stability. The clock frequency for the FPGA-based pulse generation is set to 100 MHz, ensuring high precision and minimal jitter in the timing control.

The synchronization of the shoot-through pulse with the main switching signals is achieved using a 50% duty cycle for the shoot-through period within each switching cycle. This ensures a balanced voltage boost without causing excessive current stress or harmonics.

The clock precision for the FPGA is maintained within 10 ns, ensuring that the timing control for shoot-through pulses is highly accurate and synchronized with the PWM signal.

Fig. 20

Shoot-through pulse generation and its synchronization with the main switching signals.

The logic diagram illustrating shoot-through pulse generation and synchronization with the main switching signals has been given in Fig. 20. Figures 21 and 22 represent the phase voltage, line voltage, and load current of QZSIMC and QZSDMC respectively.

Fig. 21

Experimental results of ISVPWM-based QZSDMC for line voltages in volts.

Fig. 22

Experimental results of ISVPWM-based QZSDMC for load current in Amps.

Fig. 23

Experimental phase voltage of QZSDMC.

Fig. 24

Experimental Output Line Voltage of QZSDMC.

The experimental phase voltage at the output of QZSDMC under the ISVPWM scheme is shown in Fig. 23. The recommended QZSDMC produces an output phase voltage of 239 V at 50 Hz. The line voltage at the output from experimental set up under ISVPWM scheme is shown in Fig. 24. The experimental line voltage obtained from the QZSDMC is 415.1 V. The experimental output current waveform for all the three phases are revealed in Fig. 25. The magnitude of the output load current is 0.55 A for a load of 0.25 kW. It is apparent that the simulation outputs can be authorized with the investigational results. The shoot through insertion in ISVPWM technique is complex, but it has lesser switching stress and improved voltage transfer ratio.

Fig. 25

Experimental output current of QZSDMC.

Fig. 26

Experimental output voltage THD of QZSDMC for ISVPWM.

Fig. 27

Experimental output current THD of QZSDMC ISVPWM.

The output voltage and current THD of ISVPWM for a load of 0.25 kW is shown in Figs. 26 and 27. The voltage and current THD at the output is almost 4.3% and 2.4%. Thus, from the investigation it can be resolved that the ISVPWM based QZSDMC produces less THD and so, switching losses will be decreased which rises the efficiency of the system. To address the concern about the quantitative comparison with previous publications in terms of key performance metrics, a comparative table that summarizes the performance of the proposed QZSDMC against recent works has been included. This table will focus on key parameters like Total Harmonic Distortion (THD), voltage stress, current stress, voltage gain, control method, and implementation platform. Table 1 shows the comparative performance of the proposed QZSDCM and its comparison with the five recent papers.

Table 1 Comparative performance of the proposed QZSDMC.

This comparative table will clearly show how the QZSDMC with ISVPWM (the proposed converter) outperforms the others in terms of voltage stress, current stress, voltage gain, and other parameters.

Table 2 Comparison of simulation and hardware results of QZSDMC.

Table 2 represents the evaluation of simulation and hardware outputs of QZSDMC for a load of 0.25 kW. From the results that could be observed that the error percentage is very minimal for the line voltage, phase voltage and current parameters at the output. Whereas the voltage and current THD of hardware result is about 3.1% and 2.05% greater than that of simulation results.

Conclusion

The circuit and working principle of a novel QZSDMC topology is examined in the paper together with comprehensive modelling, control techniques, and simulation results. In this work, an extensive analytical evaluation of QZSDMC for PMG based DDWECS has been carried out. A small signal model using state space domain has been derived for QZSDMC and the stability of the system was analysed which showed that the proposed QZSDM converter is stable. The performance of QZSDMC was investigated for different values of input voltages and load conditions. It is verified that the input voltage can be boosted to get the desired constant output voltage by adjusting the shoot through duty ratio between 0.4 and 0.1. The controller was designed with two different switching strategies such as CBPWM and ISVPWM for QZSDMC and its performance were compared by considering the parameters like shoot through duty ratio, output current THD, output voltage THD and switching stress. According to the analysis, the voltage stress of ISVPWM is 100 V lesser than that of the CBPWM scheme for D₀ value of 0.3. Also, an investigational prototype set up for proposed QZSDMC has been fabricated and tested. From the investigational results, it has been found that the output voltage and current THD of the simulation results are 3.1% and 2.05% higher than those of the hardware results, respectively, whereas the actual output voltage and current values are nearly identical. Therefore, it has been demonstrated that the suggested QZSDMC topology is a promising one for PMG-based WECS.