Research on the configuration strategy of active support long-and short-term energy storage devices based on ESD-considered short circuit ratio

Abstract

Although the evaluation of system strength under high penetration of renewable energy sources (RESs) has been widely studied, traditional short-circuit ratio (SCR) indicators mainly focus on the interactions among RESs and are concentrated on steady-state research, neglecting the dynamic regulation effect of energy storage devices (ESDs) on system stability. In addition, most of the existing optimization methods aim to improve economic efficiency and lack system stability analysis based on SCR quantification. Therefore, this paper proposes an ESD-considered short-circuit ratio (ECSCR) that incorporates the contribution of ESDs to the short-circuit capacity of nodes. A bi-layer optimization strategy for the active support long-and short-term energy storage device is developed. The upper-layer optimizes the installation locations of ESDs by maximizing the minimum ECSCR (MinECSCR) on the RES buses, while the lower-layer uses the Newton-Raphson algorithm to dynamically adjust the power distribution of ESD to balance stability and economy. Specifically, when the ECSCR is less than the critical short-circuit ratio (CSCR), the fast-response flywheel energy storage (FES) and battery energy storage (BES) prioritize the restoration of stability; when the ECSCR is greater than the CSCR, the lower-cost thermal energy storage (TES) serves as the main power generation unit to minimize operating costs. The verification of the improved IEEE 9-bus, 39-bus system, and 14-bus system shows that compared with traditional SCR indicators, the proposed ECSCR can significantly enhance the nodal strength and reduce operating costs while ensuring system stability.

Introduction

Driven by factors such as electricity demand and environmental protection requirements, renewable energy source (RESs) and power electronic devices are widely integrated and used in the power system¹, which will change the system characteristics, affecting the stability and reliability of the system². The key issue is the intermittent and uncertain fluctuations of renewable energy, as well as the serious impact of short-circuit faults on the system strength of buses^3,4. Grid strength represents the ability of the connection point between the power system and RESs to keep voltage quality and stability at an ideal level. It is an essential indicator for measuring the power system’s ability to sustain system stable and provide sufficient short-circuit current in the face of faults or disturbances⁵. By accurately measuring and evaluating the system strength, these vulnerabilities can be identified and addressed, which can effectively guide the power grid planning, operation, and dispatching, so as to ensure a secure, reliable and efficient power supply for the new energy power grid. The short-circuit ratio (SCR) is defined as the ratio of the short-circuit capacity of the power grid to the power injected by the connected equipment. It is an index used to measure the grid point strength. Its simplicity and intuitiveness furnish a significant reference for power grid planning and operational decisions⁶. Short circuit ratio is a direct reflection of system stability, which can be improved by increasing power capacity, shortening transmission line length, and other methods to enhance short circuit capacity, thereby increasing the short circuit ratio⁷. The CSCR was denoted as the minimum SCR required to maintain system stability under critical conditions, and it can be used as a critical value for distinguishing weakness in the system⁸.

The traditional SCR ignored the influence among RESs at different buses, which will lead to an inaccurate evaluation of the strength of the nodal system. Based on this, the weight short-circuit ratio (WSCR) developed by ERCOT took into account the influence of the interaction of RESs on the system strength^9,10. However, it presumed that all electrical equipment were interfaced with the one bus. This method can only evaluate the average system strength and be unable to measure the strength of particularly weak points or reflect the interaction among multiple RESs. The generalized short-circuit ratio (gSCR) and the critical generalized short-circuit ratio (CgSCR) were defined to assess multi-infeed system nodal strength¹¹. Site-dependent short-circuit ratio (SDSCR) is proposed², which took into account the influence of the interaction among multiple RESs at different buses on the system strength, and can assess the system strength more accurately according to the distance. However, the SCRs mentioned in the above literatures only considered the interaction among RESs, and did not take into account the interaction among other power output devices such as energy storage devices (ESDs).

In fact, in addition to the aggregated RESs, a substantial number of ESDs have been integrated into the power grid. As an essential technology for power grid power balance, ESD plays a positive role in maintaining system stability through peak regulation, frequency regulation, voltage regulation, and other means^12,13. The influence of ESD needs to be taken into account when accurately evaluating the system strength. Therefore, based on the SDSCR, the integrated short-circuit ratio (ISCR) was proposed¹⁴, which took into account the interactions between all the power output devices in the system. However, the ISCR only considered the interaction between the ESDs and the output power of the RESs and did not consider the supporting role of the ESD in the system short-circuit capacity. Through its rapid response capabilities, ESD can quickly provide additional current through the inverter when a short-circuit fault occurs, thereby increasing the system short-circuit capacity¹⁵. Therefore, it is necessary to establish a new SCR index to reflect the supporting role of ESD in the short-circuit capacity of the system, so as to more accurately represent the role of ESD in enhancing the system strength.

Table 1 Comparison of several types of SCR.

The optimal configuration of ESDs is crucial for ensuring the efficient, safe and economical operation of the power system. An optimized operation method for a centralized shared energy storage station dynamic partitioning strategy was proposed¹⁶, which considers the daily demand of large renewable energy power plants. A universal benchmark evaluation online/real-time energy management strategy for microgrids supported by hybrid energy storage systems was proposed¹⁷. A method for selecting new energy output guarantee rates considering optimal energy storage configuration was proposed¹⁸, determining reasonable rates by maximizing comprehensive benefits. Traditional power grid planning is based on factors such as load demand forecasting and economic construction costs.The application of the SCR can enable the optimal configuration of the power system while ensuring its stability and reliability¹⁹.In addition, existing research mainly focuses on static or quasi-static conditions, and there is a lack of utilization of the complementary characteristics of various ESDs to reflect the performance of the SCR under different dynamic cases in the time scale and to optimize the configuration of ESDs.

On the basis of the above analysis, this paper proposes a new SCR index, ESD-considered short-circuit ratio (ECSCR).The comparison between it and several commonly used SCR is shown in the Table 1. It comprehensively incorporates the interactive effects between the RESs and ESDs in the system, as well as the role of ESD in the system’s short-circuit capacity. Based on the ECSCR and taking costs into account, the ESDs’ location and capacity are optimized with the goal of improving stability, so as to more accurately represent the role of the ESD in enhancing the system strength in the time scale.

The key merits of this study are outlined below.

• 1. The new ECSCR index is proposed. By taking into account the influence of ESDs on the system’s short-circuit capacity, it can more accurately evaluate the system strength and improve it.

• 2. When there are fluctuations in the renewable energy sources in the system, the ECSCR reflects the optimization of the system strength by energy storage in the time scale.

• 3. Based on the ECSCR, an optimization configuration strategy for the active support long- and short- term energy storage device is proposed to optimize the location of the ESDs and its power response, so as to enhance the system stability.

The remaining part of this paper is organized as follows. In Section 2, the ECSCR that incorporates the supporting role of ESDs in the system’s short-circuit capacity is proposed. Based on the ECSCR. Section 3 proposes an optimization configuration strategy for the active support long- and short- term energy storage device. In Section 4, case studies verify the effectiveness of the proposed optimization method in enhancing the system strength. The conclusions are presented in Section 5.

Methods for assessing system stability considering ESDs

SCR is adopted to measure the strength of power systems at a bus. The value of CSCR is generally 3, and the stability of the system can be determined by comparing it with it. The principles are as follows⁶: (1) If the SCR is higher than 3, then the power grid system at that node is very strong. (2) If the SCR is in the 2 to 3, that connection point is weak; (3) If the SCR is below 2, that connection point is very weak; The larger the value of SCR is, the higher the system strength of the power grid is.

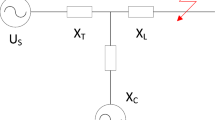
When one RES is connected to the grid system at bus, SCR at bus i can be defined as²⁰:

$$\begin{aligned} SCR_i = \frac{SC_i}{P_{d,i}} \end{aligned}$$

(1)

where $SC_{i}$ is the system short-circuit capacity at bus i, $P_{d,i}$ is the power injection of the RESs at bus i. The system short-circuit capacity can be calculated as

$$\begin{aligned} SC_{i}=\frac{U_{i}^{2}}{Z_{i}}=U_{i}\left| I_{sc,i}\right| \end{aligned}$$

(2)

where $U_{i}$ is the voltage on the bus i, and $Z_{i}$ is the equivalent Thevenin impedance on the bus i. $I_{sc,i}$ is the short-circuit current of bus i. When using the rated voltage $U_{N}$ and rated power $P_{d,N}$ of the bus in the system as reference values, the reference impedance of the system $Z_{b}$ is as follows

$$\begin{aligned} Z_{\textrm{b}}=\frac{\mathrm {U_{N}^{2}}}{\mathrm {P_{d,N}}} \end{aligned}$$

(3)

Substituting $Z_{b}$ into Eq. (1), when the rated value is adopted as the base value by the system, SCR is the reciprocal of the equivalent impedance in per-unit, that is

$$\begin{aligned} SCR_{i}=\frac{1}{|Z_{i}|/Z_{b}}=\frac{1}{|Z_{i,pu}|} \end{aligned}$$

(4)

The SCR defined in (1) only counts the influence of the injected power of a single RES. However, when multiple RESs are connected to the system and they are electrically close to each other, they will interact with each other, thus affecting the system strength of the buses. To solve this problem, the SDSCR is proposed as a measure of the system strength, which takes into account the interactions among multiple RESs at different buses. The SDSCR is defined as

$$\begin{aligned} SDSCR_i=\frac{SC_i}{\sum \limits _{j\in R}\frac{Z_{RR,ij}}{Z_{RR,ii}}P_{R,j}} \end{aligned}$$

(5)

where $P_{R,j}$ is the power injected from bus j; $Z_{RR,ij}$ is the element $(i,j)^{th}$ in the impedance matrix of the node $Z_{RR}$; $\textrm{R}$ is the set of buses connected to RESs. Although ESCR considers the interaction between multiple RESs, it fails to reflect the supporting role of ESDs on bus short-circuit capacity in the system, so it can not reflect the actual strength of the system well. The system with multiple RESs and ESDs connections is illustrated in Fig. 1, and the role of ESDs in power systems is becoming increasingly critical, especially in improving system stability. Therefore, this paper explores the impact of energy storage integration in the evaluation of system strength and proposes an ECSCR index.

Fig. 1

Multi-RESs and ESDs grid-connected system.

It can be shown from Eq. (2) that the short-circuit capacity provided by the system to a certain bus depends on the short-circuit current supplied to that bus. Devices such as ESD increase the short-circuit capacity of the system by providing short-circuit current, thereby increasing the nodal short-circuit ratio. RES is connected to the power grid through an inverter and is generally equivalent to an ideal current source. Grid-forming energy storage and synchronous generators can also support the stability of the large power grid and can be regarded as voltage sources. In this paper, it is assumed that the capacity of the synchronous generator is much smaller than that of the energy storage, and its dynamic response has a relatively small impact on the overall system. Therefore, its effect is ignored when calculating the short-circuit ratio, and the influence of RES and the contribution of ESD are mainly considered. When calculating the short-circuit ratio, the superposition theorem can be used to calculate the short-circuit current when RES is open-circuited and ESD is short-circuited respectively.

For systems with the access of multiple RESs and ESDs, its network equation can be represented as:

$$\begin{aligned} \begin{bmatrix} U_G\\ U_R\\ U_E \end{bmatrix}=\begin{bmatrix}Z_{GG}& Z_{GR}& Z_{GE}\\ Z_{RG}& Z_{RR}& Z_{RE}\\ Z_{EG}& Z_{ER}& Z_{EE}\end{bmatrix}\begin{bmatrix}I_G\\ I_R\\ I_E\end{bmatrix} \end{aligned}$$

(6)

where $U_{G}$, $U_{R}$, $U_{E}$ are the voltage in the synchronous generator (SG) buses, RESs buses and ESD buses; $Z_{GG}$, $Z_{GR}$, $Z_{RR}$, $Z_{RE}$ and $Z_{EE}$ represent the respective bus impedance submatrices; $I_{G}$, $I_{R}$ and $I_{E}$ are currents in the buses connected with SGs, RESs and ESDs.

When the ESDs are short-circuited, the short-circuit current generated by the RESs at bus i is

$$\begin{aligned} I_{sc,R,i}(t)= & \sum _{j\in R}\frac{Z_{eq,RR,ij}}{Z_{eq,RR,ij}+Z_{RR,ii}}I_{R,j}(t) \end{aligned}$$

(7)

$$\begin{aligned} Z_{eq,RR,ij}= & \frac{1}{1/\sum _{k\in E}Z_{RE,jk}} \end{aligned}$$

(8)

where $I_{R,j}(t)$ is the real-time current of RES on bus j; $Z_{eq,RR,ij}$ is the equivalent parallel impedance from busj to other short circuit buses. $Z_{_{RE,ik}}$ is the $(i,k)^{th}$ element in $Z_{_{RE}}$.

When calculating the short-circuit current contribute by the ESDs, set RESs to open circuit, and the equivalent voltage generated by the ESDs at bus i can be obtained through the nodal voltage equation as

$$\begin{aligned} U_{eq,i}(t)=\sum _{k\in E}Z_{RE,ik}I_{E,k}(t) \end{aligned}$$

(9)

where $I_{E,k}(t)$ is the real-time current of ESD at bus k, the short-circuit current generated by the ESDs at bus i is

$$\begin{aligned} I_{sc,E,i}(t)=\frac{U_{eq,i}}{Z_{RR,ii}}=\sum _{k\in E}\frac{Z_{RE,ik}}{Z_{RR,ii}}I_{E,k}(t) \end{aligned}$$

(10)

By superimposing Eqs. (7) and (10), the short-circuit current generated by the RESs and ESDs at bus i is

$$\begin{aligned} \begin{aligned}I_{sc,i}(t)=&I_{sc,R,i}(t)+I_{sc,E,i}(t) \\ =&\sum _{j\in R}\frac{Z_{eq,RR,ij}}{Z_{eq,RR,ij}+Z_{RR,ii}}I_{R,j}(t)&+ \sum _{k\in E}\frac{Z_{RE,ik}}{Z_{RR,ii}}I_{E,k}(t)\end{aligned} \end{aligned}$$

(11)

Substitute Eq. (11) into Eq. (2) to obtain the increasing short-circuit capacity at bus i under the action of RESs and ESDs.

$$\begin{aligned} SC_{RE,i}(t)= \left| \sum _{j\in R}{Z_{R,j}}S_{R,j}(t)+\sum _{k\in E}{Z_{E,k}}S_{E,k}(t)\right| \end{aligned}$$

(12)

where

$$\begin{aligned} Z_{R,j}= \sum _{j\in R}\frac{Z_{eq,RR,ij}}{Z_{eq,RR,ij}+Z_{RR,ii}} \\ Z_{E,k}=\frac{Z_{RE,ik}}{Z_{RR,ii}} \end{aligned}$$

When the injected power $S_{R,j}(t)$ and $S_{E,k}(t)$ in (12) is replaced with the injected power of RESs, $P_{R,j}(t)$ and the injected power of ESDs, $P_{E,k}(t)$. Then substitute it into (5) to obtain the ESD-considered short-circuit ratio, which defined as

$$\begin{aligned} ECSCR_i\left( t\right) = \frac{\left| SC_i+\sum \limits _{j\in R}{Z_{R,j}}P_{R,j}\left( t\right) +\sum \limits _{k\in E}Z_{E,k}P_{E,k}\left( t\right) \right| }{\sum \limits _{j\in R}\frac{Z_{RR,ij}}{Z_{RR,ii}}P_{R,j}\left( t\right) } \end{aligned}$$

(13)

The ECSCR not only takes into account the interactions among the RESs in the system but also reflects the role of the ESDs in enhancing the short-circuit capacity of the buses. Moreover, it can express the system stability under ESD optimization when the power of the RES fluctuates in the time scale. ECSCR can be better applied to solve the dynamic programming problems in the actual system.

Optimized configuration strategy of active support type long- and short-term energy storage device

Transient stability is the foundation of safe and stable operation of power systems, directly related to the safety and reliability of the power grid²¹. Energy storage technology plays an important role in alleviating the intermittency and volatility of RESs and improving the stability of the power system²². ESD can not only enhance the stability of the power system through a rapid response mechanism but also improve the power quality by precisely regulating the active and reactive power outputs. Determining a reasonable configuration of energy storage devices is crucial for ensuring the reliable, economical, flexible, and low-carbon operation of the entire system²³.

Table 2 Common parameter range of ESDs^24,25,26.

The active support type long short-term energy storage system aims to optimize the operational efficiency and stability of the power grid. By combining the advantages of different energy storage technologies, it achieves rapid response and long-term energy management of the power grid. The capacity ratio of short-term and long-term energy storage can be flexibly adjusted according to different application needs to achieve the best economic and operational benefits.A distributed collaborative planning model for energy storage, transmission, and distribution networks considering the characteristics of long-term hydrogen energy storage (h-ESS) and short-term electrochemical energy storage systems (ESS) has been proposed, while ensuring seasonal spatiotemporal power generation and supply levels and eliminating uncertainty and fluctuations in renewable energy²⁷. A strategy for coordinating thermal storage and power storage has been proposed, which actively considers the expansion time fluctuations of load and renewable energy, reduces operating costs, and smooths out renewable energy fluctuations²⁸.

According to the operation time scale, that is, the duration of discharging at the rated power capacity, energy storage devices are divided into short-term energy storage and long-term energy storage²⁹.

Short-term energy storage includes flywheels and battery pack systems with fast response times. Its outstanding advantage lies in its extremely fast response speed, which enables it to complete the charging and discharging processes within a time range from milliseconds to hours. This allows it to quickly balance the instantaneous power fluctuations of the power system. Long-term energy storage can achieve the storage of energy across seasons and months, effectively solving the problem of long-term energy supply shortages²⁷. In this paper, the characteristics of the capacity and response speed of FES, BES, and TES are mainly applied to optimize the fluctuations in power demand during different periods, and their common parameter ranges are shown in Table 2.

FES is a mechanical energy storage technology. It converts electrical energy into kinetic energy and stores it through a high-speed rotating flywheel, and then converts the kinetic energy back into electrical energy when needed. The FES system can complete the charging and discharging process within a few milliseconds, making it highly suitable for dealing with the transient power fluctuations of the power system. In addition, the flywheel can be installed anywhere close to consumers to store electricity for distribution. It has a relatively long service life, usually reaching tens of thousands of cycles³⁰.

BES system refers to a system that uses battery technology to store electrical energy and release it when needed. Its working principle mainly involves converting electrical energy into chemical energy through the charging process storing it in the battery, and then converting the chemical energy back into electrical energy for use during the discharging process. Compared with traditional power generation units, BES can respond more quickly to the changes in the electricity market and provide immediate power support³¹.

TES is a technology that uses chemical reactions to store and release heat. Its working principle is based on reversible endothermic and exothermic chemical reactions. Compared with other forms of energy storage methods, TES can achieve a higher energy density, but the reaction time is relatively long³².

The operating status and location of the RES are restricted by the distribution and availability of natural resources. In contrast, the charging and discharging processes of the ESD can be flexibly controlled according to the demand and status of the power grid. The ESD can be installed on almost any busbar within the power grid. Moreover, since the RES serves as the main power generation unit of the system, and the ESD mainly functions to mitigate the power fluctuations of the RES, we evaluate the strength of the power grid by assessing the ECSCR value of the RES buses.

This section proposes an optimized configuration strategy of active support type long- and short-term energy storage devices, aiming to optimize the system based on maintaining its stability by adjusting the configuration of the ESD. Firstly, at the upper layer the locations of each ESD are optimized to ensure that the ECSCR value of RES bus is maximized. At the lower layer, optimize the output power of each ESD when RES power fluctuates, to achieve system stability with minimal cost.

ESD configuration optimization model

In the upper-layer optimization, the objective function and constraints of the model are shown in (14) and (15).

$$\begin{aligned} f_{upper}= & \max MinECSCR \end{aligned}$$

(14)

$$\begin{aligned} C_{p}= & n_{FES}C_{p,FES}+n_{EES}C_{p,BES}+n_{TES}C_{p,TES} \end{aligned}$$

(15)

where $C_{p}$ is the unit power cost of various ESDs, $n_{FES}$, $n_{EES}$ and $n_{TES}$ are the quantity of ESDs.The construction cost is set to be constant, so that the RESs operate at their rated value and the ESD under different purchase cases is connected at maximum power to calculate the system stability under extreme conditions. Meanwhile, we assume that the system is being studied under normal operating conditions. Therefore, the voltage of each node is close to its rated value, and the voltages of different nodes are considered to be close to each other. The criteria for the optimal location of the ESD should follow the following principles.

The Enhanced White Shark Optimizer (EWSO)³³ is employed for the upper-layer optimization to determine the optimal installation locations of ESDs. EWSO is a metaheuristic algorithm inspired by the foraging behavior of great white sharks, incorporating three movement behaviors: wave sensing, random search, and fish school tracking.

First, determine the installation buses of the RESs. The ESD position update formula for EWSO is as follows:

$$\begin{aligned} w_{k+1}^i = 0.5 \cdot \left[ \text {rand} \cdot \left( w_{\text {best}} - w_k^i \right) + \text {rand} \cdot \left( w_{\text {rand}} - w_k^i \right) \right] + \beta \cdot \text {rand} \cdot \left( w_k^i - w_k^j \right) \end{aligned}$$

(16)

where $w_k^i$ is the current position of the white shark i, $w_{\text {best}}$ is the global best solution, $w_{\text {rand}}$ is a randomly selected individual, and $\beta$ is a direction coefficient adjusted dynamically based on fitness values to enhance population diversity. Position update in random search phase:

$$\begin{aligned} w_{k+1}^{i}= {\left\{ \begin{array}{ll} w_{k}^{i} \oplus \text {rand}(0,1) \cdot (ub - lb) + lb & \text {if } r_{1} < mv, \\ w_{k}^{i} + v_{k}^{i} / f & \text {otherwise} \end{array}\right. } \end{aligned}$$

(17)

where mv controls the exploration-exploitation balance, and f is a frequency parameter.The specific parameters and formula settings are detailed in the literature. $r_{1}$ is a random number between 0 and 1. When the ESD is installed on different buses, determine the minimum value of the ECSCR (MinECSCR) of the RES bus under each installation condition. Then, the best installation situation is when its MinECSCR is maximum. If the maximum values of the MinECSCR are equal under some installation situations, the optimal installation situation is the one where the maximum value of the ECSCR (MaxECSCR)is the largest. The above principles can ensure the stability of the nodes when optimizing the location of the ESD. In summary, the expressions of MinECSCR and MaxECSCR are shown in (18) and (19), where represents the number of installation situations.

$$\begin{aligned} & \max \begin{bmatrix}\min \left( ECSCR_1,...,ECSCR_R\right) _1,\\ ...,\min \left( ECSCR_1,...,ECSCR_R\right) _n\end{bmatrix} \end{aligned}$$

(18)

$$\begin{aligned} & \max \begin{bmatrix}\max \left( ECSCR_1,...,ECSCR_R\right) _1,\\ ...,\max \left( ECSCR_1,...,ECSCR_R\right) _n\end{bmatrix} \end{aligned}$$

(19)

The final optimal configuration scheme satisfies that under a certain construction cost, it can maximize the minimum ECSCR value among all RES nodes. If multiple schemes have the same MaxMinECSCR value, the one with a higher maximum ECSCR value is selected to ensure better overall strength of the system.

ESD time-varying power optimization model

In the lower-layer optimization, the objective function and constraints of the model are shown in Eqs (20) to (23).

$$\begin{aligned} & f_{lower}=\max (\alpha ECSCR-\beta C_{e}) \end{aligned}$$

(20)

$$\begin{aligned} & s.t.{\left\{ \begin{array}{ll}0\le P_E(t)\le \overline{P}_E \\ -R_E\le P_E(t)-P_E(t-1)\le R_E \\ ECSCR_i>CSCR& \end{array}\right. } \end{aligned}$$

(21)

$$\begin{aligned} & (\alpha ,\beta )={\left\{ \begin{array}{ll}(\alpha _1,\beta _1)& ECSCR<3\\ (\alpha _2,\beta _2)& ECSCR\ge 3\end{array}\right. } \end{aligned}$$

(22)

$$\begin{aligned} & C_{e}=C_{e,FES}P_{FES,t}+C_{e,BES}P_{BES,t}+C_{e,TES}P_{TES,t} \end{aligned}$$

(23)

where $C_{e,FES}$, $C_{e,BES}$ and $C_{e,TES}$ represent the unit electricity cost of ESDs respectively.$P_{FES,t}$, $P_{BES,t}$ and $P_{TES,t}$ represents the output power of each ESD during time period t; $\alpha$ and $\beta$ are the weight coefficients for ECSCR and cost, Eq. (20) represents using different weight coefficients for optimization when the system is stable and unstable. In the simulation verification, $(\alpha ,\beta )$ are (10, 1) and (1, 2) respectively.

The optimized constraints are as follows.

• (1) Real time power constraint

  $$\begin{aligned} {\left\{ \begin{array}{ll}\textbf{0}\le P_{FES}(t)\le \overline{P}_{FES}\\ \textbf{0}\le P_{EES}(t)\le \overline{P}_{EES}\\ \textbf{0}\le P_{TES}(t)\le \overline{P}_{TES}& \end{array}\right. } \end{aligned}$$

  (24)

  where $P_{FES}(t)$, $P_{BES}(t)$ and $P_{TES}(t)$ are the real-time powers of FES, BES and TES; $\overline{P}_{FES}$, $\overline{P}_{BES}$ and $\overline{P}_{TES}$ are the power upper limit of various ESDs.

• (2) Power ramp rate constraint

  $$\begin{aligned} {\left\{ \begin{array}{ll}-R_{FES}\le P_{FES}(t)-P_{FES}(t-1)\le R_{FES}\\ -R_{BES}\le P_{BES}(t)-P_{BES}(t-1)\le R_{BES}\\ -R_{FES}\le P_{TES}(t)-P_{TES}(t-1)\le R_{TES}& \end{array}\right. } \end{aligned}$$

  (25)

  where $R_{FES}$, $R_{BES}$ and $R_{TES}$ are the power ramp rates, which represent the power change rate of ESDs.

• (3) Short- Circuit Ratio constraint

  $$\begin{aligned} ECSCR_i>CSCR \end{aligned}$$

  (26)

Table 3 Optimization Process for System Stability and Economy.

CSCR is set to 3 in this paper, and Eq. (26) ensures that the system strength of the bus is greater than the critical value.

The Newton-Raphson algorithm is used for optimization in this paper. The Newton-Raphson algorithm is an effective algorithm for solving nonlinear problems, which usually has better convergence and higher accuracy^34,35. According to Eq. (20), the objective function is changed to

$$\begin{aligned} F(x)&=\alpha ECSCR(x)-\beta C_e(x) \end{aligned}$$

(27)

$$\begin{aligned} x&=\left[ P_{E,1},P_{E,2},...P_{E,k}\right] ^{T} \end{aligned}$$

(28)

The power optimization iteration of ESD is as follows

$$\begin{aligned} x^{n+1}=x^{n}-H^{-1}(x^{n})\nabla F(x^{n}) \end{aligned}$$

(29)

where

$$\begin{aligned} \left. H\left( x^n\right) =\left[ \begin{array}{cccc}\frac{\partial ^2ECSCR^n}{\partial ^2P_{E,1}^n}& \frac{\partial ^2ECSCR^n}{\partial P_{E,1}^n\partial P_{E,2}^n}& \cdots & \frac{\partial ^2ECSCR^n}{\partial P_{E,1}^n\partial P_{E,k}^n}\\ \frac{\partial ^2ECSCR^n}{\partial P_{E,2}^n\partial P_{E,1}^n}& \vdots & \vdots & \vdots \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial ^2ECSCR^n}{\partial P_{E,k}^n\partial P_{E,1}^n}& \cdots & \cdots & \frac{\partial ^2ECSCR^n}{\partial ^2P_{E,k}^n}\end{array}\right. \right] \\ \nabla F(x^n)=\begin{bmatrix}\alpha \frac{\partial ECSCR^n}{\partial P_{E,1}^n}-\beta \frac{\partial C_{e}^n}{\partial P_{E,1}^n}\\ \alpha \frac{\partial ECSCR^n}{\partial P_{E,2}^n}-\beta \frac{\partial C_{e}^n}{\partial P_{E,2}^n}\\ \vdots \\ \alpha \frac{\partial ECSCR^n}{\partial P_{E,k}^n}-\beta \frac{\partial C_{e}^n}{\partial P_{E,k}^n}\end{bmatrix} \end{aligned}$$

In the lower-layer optimization, it is divided into two stages. When ECSCR<CSCR, priority is given to optimizing ECSCR. Through rapid adjustment of FES and BES, ECSCR quickly reaches 3, indicating that the system is relatively stable; When ECSCR>CSCR, priority is given to optimizing C, so that the lower cost TES power plays a major role, and the BES power gradually decreases to reduce costs. The flowchart and steps of the optimization configuration algorithm for long- and short-term energy storage devices are shown in Fig. 2 and Table 3, respectively.

Fig. 2

The optimization process of system stability and economy based on ECSCR.

Case studies

Table 4 The parameters of the ESD used in the simulation.

To validate the effectiveness of the proposed ECSCR, we constructed an improved IEEE 9-bus system, as shown in Fig. 3. Some parameters of the three types of ESD are shown in Table 4.

Fig. 3

IEEE 9-bus System Structure³⁶.

Effectiveness verification for ECSCR

ECSCR was compared with SDSCR and ISCR in a 9-bus model. In this example, two RESs are installed on bus 4 and 5 respectively, and the installation positions of the two ESDs are also on bus 4 and 5. Change the output power of RESs and ESDs constant and compare ESCR, ISCR, and ECSCR . The different operating conditions and comparison situations are shown in Tables 5 and 6.

Table 5 Power injection situations of RESs and ESDs.

Table 6 The values of different Short-Circuit Ratio.

A comparison of Cases 1 to 3 reveals that when the total output power of the system remains constant, the ECSCR of buses 4 and 5 shows a gradual upward trend as the ESD power increases. This indicates that the ESD parameter has the effect of enhancing the system strength of the buses. Comparing case 3–5, it is observable that when the RES output power in the system is constant, the smaller the ESD power is, the smaller the ECSCR is, while the ESCR remains unchanged and the ISCR increases, which contradicts the enhancing effect of ESD on system strength. This proves that ECSCR can better enhance system stability when ESD is involved.

The validity of the optimization strategy has been initially confirmed through BES. Two RESs are respectively installed at bus 5 and 6, and the BES is installed at bus 5. Comparing ECSCR with it without ESD access, Eq. (13) is rewritten as:

$$\begin{aligned} ECSCR_i\left( t\right) =\frac{\left| SC_i+\sum \limits _{j\in R}Z_{R,j}P_{R,j}\left( t\right) \right| }{\sum \limits _{j\in R}\frac{Z_{RR,ij}}{Z_{RR,ii}}P_{R,j}\left( t\right) }\end{aligned}$$

(30)

When the power of the RESs fluctuates, the ECSCR at bus 5 and the power of the BES are shown as Figs. 4 and 5. In the beginning, when the ECSCR is greater than 3, it indicates that the system is stable and the BES does not participate in the optimization. As the power fluctuation of the RESs reduces the system strength, the BES starts to adjust to make the ECSCR rise, and then it stabilizes at the critical value of 3. Since the cost of the BES is relatively high, it is often used in combination with the TES to improve the economy and efficiency of the energy system.

Fig. 4

Comparison of ECSCR with and without BES optimization.

Fig. 5

The power change of BES.

The optimization under two RESs in the IEEE 9-bus system

In this example, two RESs with 30 MW are installed at bus 5 and 6 respectively, and the ESDs are optimized using the optimization strategy proposed in Section 3.

Optimization of the ESD Location

Set the total construction cost to $C_{p}=$40,000,000\$ and obtain the quantity of at least one FES, BES and TES by using Eq. (15), as shown in the Table7.

After obtaining the quantity of each ESD, calculate the ECSCR of the RES bus under different installation bus conditions according to Eqs. (13) and (16). From the Table 8, it can be seen that the ECSCR is the highest in case 2. It can be concluded that the optimal configuration for ESD is one FES installed at bus 3, one BES installed at bus 8, and two TESs installed at bus 3 and 8.

Table 7 The case of the installation quantity of FES, BES, and TES.

Table 8 The maximum value situation of MinECSCR under each configuration.

Optimization of the ESD Power

Connect FES, BES, and TESs to the system according to the optimal configuration mentioned above, with an initial power of 0. Simulate power fluctuations by varying the two RESs around 30 MW. From Figs. 6 and 7, it can be seen that at bus 5 and 6, when the RES power fluctuates, the ECSCR without ESD support is less than 3, indicating a weak system. After ESD intervention, FES and BES respond first, and the power of TES slowly increases due to its low ramp rate. When it reaches a CSCR value, the higher cost BES power begins to decrease, and in the later stage, TES mainly provides stable support, while FES and BES play a role in rapid adjustment.

Fig. 6

The Comparison situation of grid strength under ESD optimization in different buses.

Fig. 7

The power optimization process of FES, BES and TESs.

Fig. 8

Comparison of ECSCR optimization between the optimal location and the other two locations.

To further verify that this location is the optimal one, two installation locations with the second largest and the smallest MinECSCR in case 2 of Table 6 are selected, which are 8, 8, 8, 3, and 5, 6, 6, 5 respectively. Taking bus 5 as an example, the ECSCR values in the case of installation at buses 3, 8, 3, and 8 are respectively subtracted from those in the previous two cases, as shown in the Fig. 8.

Fig. 9

Comparison of ECSCR with and without ESDs optimization at Bus 31.

Fig. 10

The sum power optimization process of FESs, BES, and TESs.

The optimization under four RESs in the IEEE 39-bus system

Fig. 11

IEEE 39-bus System Structure³⁶.

The IEEE 39-bus system is used to further verify the effectiveness of the proposed method. As shown in the Fig. 11, there are a total of 4 RESs in the system, each with a rated capacity of 100 MW, which are installed at buses 31, 32, 33, and 35 respectively. It is assumed that the total construction cost of the ESD is $C_{p}=$75,000,000\$, and the potential installation buses of the ESD are 10, 11, 12, 13, 31, 32, 33, 34, and 35. According to the upper-layer optimization method proposed in Section 3, the optimal configuration of the ESDs is as follows: four FESs are installed at buses 11, 34, 34, and 34 respectively, one BES is installed at bus 12, and two TESs are installed at bus 34. The method is the same as before and will not be repeated here.

Connect the ESDs to the system according to the above optimal configuration. When the power of the RESs fluctuates, the optimization situation of the system strength of bus 31 is shown in Figs. 9 and 10. The main functions of the FESs and the BESs are to respond quickly to improve system stability and to conduct rapid adjustments in the later stage of stabilization. The TES has a slow response and plays a major role in the later stage to reduce the operation cost.

The optimization under three RESs in the IEEE 14-bus system

Fig. 12

IEEE 14-bus System Structure³⁷.

In this section, the IEEE 14-bus system shown in Fig. 12 is used to verify the proposed ECSCR index and optimization method. The standard IEEE 14-bus model can provide a standardized research platform for studying the operating characteristics of microgrids, optimizing control strategies, and analyzing the stability of power systems. Three RESs are installed at buses 4, 6, and 10, respectively, with each unit having a rated capacity of 20 MW. The total construction cost constraint of ESD is set to $C_{p}=$45,000,000\$. In the upper-level optimization, the EWSO algorithm is used to search for the optimal ESD installation positions within the range of buses 1–14. The obtained optimal configuration scheme is as follows: one FES installed at bus 14, one BES installed at bus 14, and three TESs installed at buses 7, 7, and 13, respectively.

Figure 13 shows the time-varying curve of the ECSCR value at bus 4 with and without ESD optimization. It can be seen that without ESD support, the ECSCR value decreases with the fluctuation of RES power and falls below CSCR = 3 multiple times, indicating insufficient system strength. However, after ESD is put into optimization, the ECSCR value is basically maintained above 3. Especially when the RES power fluctuates significantly, the ECSCR quickly returns to the safe range through the rapid response of FES and BES, which proves that the proposed strategy effectively improves the bus strength.

Fig. 13

Comparison of ECSCR with and without ESDs optimization at Bus 4.

Fig. 14

The sum power optimization process of FESs, BES, and TESs.

Figure 14 presents the power variation of each ESD during the optimization process. When the ECSCR is higher than CSCR, the system is in a stable state, and TES with lower cost serves as the main power output unit. As the RES power fluctuation causes the ECSCR to drop below 3, FES and BES respond preferentially and rapidly increase their power output to enhance the system strength; at the same time, the power of TES gradually increases due to its slow ramping rate. When the ECSCR returns to above 3, to reduce the operating cost, the power output of FES and BES gradually decreases, and TES becomes the main supporting unit, while FES and BES are responsible for coping with rapid fluctuations. This process reflects the coordinated optimization of short-term and long-term energy storage, which not only ensures system stability but also improves economic efficiency. The above results show that the ECSCR-based two-layer optimization strategy can effectively coordinate the operating characteristics of different types of energy storage in the IEEE 14-bus system, significantly enhance the system strength, and optimize the operating cost under the premise of ensuring stability.

Conclusion

This paper has addressed the issue of power system strength assessment under the integration of high penetration RESs and has proposed a new short-circuit ratio index, ECSCR, which has taken into account the contribution of ESDs. This index quantified the dynamic supporting role of ESDs in the short-circuit capacity of nodes, making up for the deficiency of the traditional SCR that only focused on the interaction among RESs. Based on the ECSCR, a bi-layer optimization strategy has designed. The upper-layer optimized the installation locations of ESDs by maximizing the MinECSCR, and the lower-layer has used the Newton-Raphson algorithm to dynamically adjust the power distribution of ESDs to balance system stability and economy. Verifications in the improved IEEE 9-bus and 39-bus system has shown that when the total output power of the system is constant and the ESD power gradually increases, the ECSCR of bus4 is 5.47–12.81% higher than that of SDSCR without considering the ESD effect. In the RES power fluctuation experiment, the optimization algorithm used also ensured that ECSCR could be maintained above 3. The ECSCR index significantly enhanced the grid strength, ensured the stability of the system under RES fluctuations, and reduced operating costs through the optimization of ESDs configuration. The research results has provided new theoretical support for the planning and operation of power systems with a high proportion of RESs. In summary, the proposed ECSCR index and optimization algorithm are applicable to both transmission grids and microgrids, providing reliable technical support for microgrid planning with high penetration of renewable energy.