Modeling dysentery spread and the impact of public awareness on control dynamics

Abstract

Dysentery remains a leading cause of morbidity and mortality in developing regions, exacerbated by poor sanitation and limited access to healthcare. This study develops a novel mathematical model to analyze the transmission dynamics of dysentery and evaluate the effectiveness of control strategies, with a specific focus on the impact of public awareness. The model uniquely stratifies the population into compartments based on health education status and disease severity, allowing for a nuanced analysis of intervention impacts. We derived a key epidemiological threshold, the basic reproduction number, to determine the conditions for disease elimination or persistence. Our analysis demonstrates that a disease-free equilibrium is locally and globally stable when this threshold is below one. Furthermore, we employed optimal control theory to simulate and compare three intervention strategies: public awareness campaigns, hygiene and sanitation improvements, and treatment of infected individuals. Numerical simulations reveal that while each intervention alone reduces disease burden, a combined strategy is the most effective and cost-efficient approach to curtailing outbreaks. These findings underscore the critical importance of integrated public health policies that synergize education, prevention, and treatment for effective and sustainable dysentery control.

Introduction

Dysentery is a severe gastrointestinal disease characterized by inflammation of the intestines, typically caused by bacterial or amoebic infections, and marked by symptoms such as bloody diarrhea, abdominal pain, and fever. It primarily affects vulnerable populations, such as children under five and those in impoverished settings with limited access to clean water and sanitation. The main cause is the bacteria Shigella dysenteriae, but other organisms like Salmonella and Entamoeba histolytica can also cause the disease. Transmission occurs through the fecal-oral route, and symptoms typically appeal within one to three days of exposure.

Globally, diarrheal illness is a significant concern, especially in underdeveloped nations. While it can be treated and prevented, diarrhea remains one of the five leading causes of death in these regions. Based on various studies, the second most common cause of death among children under five varies depending on the region and context^1,2. About $40\%$ of deaths in children worldwide are due to pneumonia and diarrhea each year, with 18 percent of pediatric deaths under five years of age linked specifically to diarrhea. According to reports, diarrheal illnesses claim the lives of nearly 5,000 children every day, with 78 percent of these deaths occurring in Africa and Southeast Asia¹.

Diarrheal illnesses come in three main forms, and they often affect children under the age of five. One type, known as dysentery diarrhea, is particularly severe and involves loose or watery stools with blood. This condition is usually caused by either Entamoeba histolytica, a type of amoeba, or Shigella dysenteriae, a bacteria. Another type is acute watery diarrhea, which can lead to rapid dehydration due to significant fluid loss. This type is often caused by Rotavirus or bacteria like Vibrio cholerae or Escherichia coli, and typically lasts for a few days or hours. The third type is persistent diarrhea, which lasts for 14 days or more and may or may not involve blood. This form is more common in malnourished children or those with underlying health conditions².

Dysentery, a serious infection causing bloody diarrhea, continues to be a major health issue in many low- and middle-income countries. Shigella dysenteriae is a major cause of dysentery, leading to symptoms like fever, nausea, vomiting, and cramps³. The presence of blood and mucus in diarrhea is due to microorganisms invading and destroying the cells lining the small intestine and colon. However, dysentery can also be caused by other pathogens, such as Campylobacter jejunijejuni, enteroinvasive E. coli, Salmonella spp., and Entamoeba histolyticahistolytica³. The Shigella bacteria are categorized into four main groups: A (S. dysenteriae), B (S. flexneri), C (S. boydii), and D (S. sonnei). These groups have various subtypes, with S. dysenteriae serotype 1being particularly notorious for causing severe infections due to its production of Shiga toxin³.. Transmission occurs through the fecal-oral route, with illness manifesting one to three days post-infection. Most people with mild cases of the infection start feeling better on their own within a week. However, whether you’re showing symptoms or not, you can still spread the infection to others if you don’t practice good hand hygiene. This can happen through direct contact with contaminated feces, or by touching food, water, or objects that then come into contact with someone else^2,3.

Bacterial pathogens, including Shigella spp., Escherichia coli, and Entamoeba histolytica, are the primary causes of dysentery, leading to significant morbidity and mortality, particularly in young children. Despite advancements in medical science and public health, Dysentery continues to be a major problem in areas where sanitation is poor, clean water is scarce, and healthcare is hard to access. In these places, the disease can spread quickly and easily, putting many people at risk⁴.

Dysentery can manifest in varying degrees of severity, ranging from mild to life-threatening. In severe cases, it can lead to dehydration, malnutrition, and even life-threatening infections. To combat dysentery, it’s essential to provide prompt re-hydration treatment, administer antibiotics judiciously, and implement preventive measures to reduce transmission. However, the growing threat of antibiotic resistance has made treatment more complex, highlighting the need for a better understanding of disease dynamics to develop more effective control strategies^4,5.

In the fight against infectious diseases like dysentery, mathematical modeling has emerged as a powerful tool. By combining clinical data with mathematical models, researchers can simulate disease spread, evaluate the impact of interventions, and predict outcomes. This approach enables public health officials to optimize strategies, make informed decisions, and potentially alleviate the burden of disease on affected communities⁶.

Several mathematical models have been developed to understand diarrheal diseases. Abolaban⁴ focused on statistical prevalence, while Olutimo et al.⁷ incorporated vaccination and treatment. Berhe et al.¹⁰ conducted sensitivity analysis on a dysentery model. Our work builds upon these by introducing a compartment for awareness-based susceptibility ($S_e$) and distinguishing between mild ($I_m$) and severe ($I_s$) infectious states, which allows for a more granular analysis of intervention impacts. Furthermore, we employ optimal control theory, not just for treatment but also for awareness campaigns and hygiene promotion, providing a comparative framework for public health strategy^18,19

Despite being preventable and treatable, dysentery persists due to complex socio-behavioral and environmental factors. This motivates the need for models that go beyond biological transmission to incorporate human behavior. The novelty of this paper is threefold: We introduce a compartmental model that explicitly tracks an educated susceptible class ($S_e$) whose infection risk is reduced due to awareness, a feature often omitted in prior models. We differentiate between mildly and severely infected individuals ($I_m$, $I_s$), acknowledging their different transmission potentials and healthcare needs. We employ optimal control theory to evaluate and optimize the cost-effectiveness of combined public health interventions, providing a practical framework for resource allocation.

Furthermore, we conducted a detailed sensitivity analysis to identify the most influential parameters affecting the disease’s spread. By targeting these parameters, public health officials can design more effective intervention strategies. Our analysis of the disease’s long-term behavior and the conditions required for disease eradication or persistence provides valuable insights for policymakers.

Model formulation

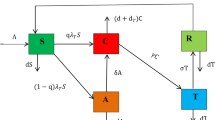
A mathematical model has been created to study the spread of dysentery and assess how treatments and public awareness affect the disease’s dynamics. The population is segmented into six groups: those with minimal or no education on dysentery prevention strategies ($S_u$), those educated and informed about preventive strategies ($S_e$), individuals exposed to the disease (E), moderately ill patients ($I_m$), severely infected patients ($I_s$), those who have recovered, and the general population at time t.

New individuals join the population at a rate of $\psi$, with a fraction $k$ receiving education. Among these, some already know dysentery prevention techniques. Public awareness campaigns can educate the rest at a rate of $\gamma$, which measures the campaigns’ success in spreading awareness.

Those susceptible to the disease can become infected by contact with infected individuals, at a rate of $\lambda$ for the uneducated, and $\epsilon \lambda$ for the educated, with the latter having a reduced rate of infection due to their understanding of prevention. This highlights education’s key role in lowering infection risk.

Once infected, individuals develop either moderate or severe symptoms at rates of $\tau \pi$ and $(1-\tau )\pi$, respectively. This variability illustrates that some show mild symptoms while others experience severe ones.

The model also includes recovery rates ($\phi _1$ for moderate and $\phi _2$ for severe cases), progression from mild to severe infection ($\sigma$), and natural mortality ($\mu$). Natural mortality refers to deaths unrelated to dysentery, while disease mortality concerns deaths caused by the disease. The rate of progression from mild to severe reflects how quickly symptoms worsen, while recovery rates indicate the pace of recovery.

These six categories make up the total population $N(t)$ at any time $t$, offering a detailed view of dysentery transmission and how interventions like treatment and awareness campaigns shape the disease’s dynamics.

Model diagrams

Figure 1 shows a simple schematic diagram to illustrate the dynamics of the model, where the solid arrows represent transitions between compartments, with accompanying expressions denoting the per capita flow rates.

Fig. 1

Schematic diagram illustrating the dynamics of the model. Solid arrows represent transitions between compartments, with accompanying expressions denoting the per capita flow rates.

Model equations

The model equations are given by:

$$\begin{aligned} \begin{aligned} \frac{dS_e}{dt}=k\psi +\gamma S_u-(\mu +\epsilon \lambda )S_e\\ \frac{dS_u}{dt}=\psi (1-k)-(\mu +\gamma +\lambda )S_u\\ \frac{dE}{dt}=\lambda (S_u+\epsilon S_e)-(\mu +\pi )E\\ \frac{dI_s}{dt}=\tau \pi E +\sigma I_m-(\mu +\delta _1+\phi )I_s\\ \frac{dI_m}{dt}=(1-\tau )\pi E-(\mu +\delta _2+\sigma +\Phi )I_m\\ \frac{dR}{dt}=\phi I_s+\Phi I_m-\mu R \end{aligned} \end{aligned}$$

(1)

The force of infection, $\lambda$, which measures the per capita rate at which susceptible individuals become infected, is defined as:

$$\begin{aligned} \lambda = \frac{\beta (I_m + I_s)}{N}. \end{aligned}$$

(2)

Model assumptions and justification

• Awareness and Education ($\gamma$, k): A fraction k of new recruits enter the educated class, reflecting baseline health literacy. The rate $\gamma$ at which uneducated individuals become educated models the efficacy of ongoing public health campaigns. This education refers to functional health knowledge about dysentery prevention (e.g., hand washing, safe food/water practices)⁹.

• Dysentery’s disease-induced mortality rates ($\delta _1$ and $\delta _2$) vary based on infection severity. Severely infected individuals ($\delta _1 = 0.01$ per day) face a higher mortality risk due to rapid dehydration and fatal complications, whereas mildly infected individuals ($\delta _2$) have a significantly lower risk. These parameters are crucial for modeling dysentery’s fatal potential, particularly in children under five, who are disproportionately affected, with approximately 525,000 deaths annually attributed to diarrheal diseases as reported by the World Health Organization (WHO)¹⁵

• Differential Infection ($\epsilon$): The factor $\epsilon \in (0,1)$ reduces the infectivity for the $S_e$ class, justified by the assumption that educated individuals practice preventive measures, thus reducing their effective contact rate.

• Initial Conditions: The system (1) is analyzed subject to the initial conditions: $S_e(0) = S_{e0}> 0$, $S_u(0) = S_{u0}> 0$, $E(0) = E_0 \ge 0$, $I_m(0) = I_{m0} \ge 0$, $I_s(0) = I_{s0} \ge 0$, $R(0) = R_0 \ge 0$.

Variables and parameters

In the table below, Table 1, we provide some variables and parameters that are used in the model, accompanied by their description.

Table 1 Variables and parameters used in the model.

Fundamental characteristics of the model

Feasibility and positivity of the solution

For this part of the analysis, we assumed that all variables and parameters have non-negative values, meaning $t \ge 0$.

Feasibility of solutions

The model’s set of possible solutions that stay within certain boundaries is defined by:

$$\begin{aligned} K={(S_e,S_u,E,I_m,I_s,R)\in \mathbf {R^6_{+}}|N(t)=S_e(t)+S_u(t)+E(t)+I_m(t)+I_s+R(t)} \end{aligned}$$

This assertion was satisfied by the lemma that follows.

Lemma 1

(Boundedness of Solutions) The closed set ${\mathcal {K}} = \left\{ (S_e, S_u, E, I_m, I_s, R) \in {\mathbb {R}}_+^6 : N \le \frac{\psi }{\mu } \right\}$ is positively invariant and attracting for the system (1).

Proof

Adding all equations in the system (1) gives the rate of change of the total population:

$$\frac{dN}{dt} = \psi - \mu N - \delta _1 I_s - \delta _2 I_m.$$

Since $\delta _1 I_s + \delta _2 I_m \ge 0$, it follows that $\frac{dN}{dt} \le \psi - \mu N$. This is a standard first-order linear differential inequality. The solution can be compared to the equation $\frac{dQ}{dt} = \psi - \mu Q$, which has the solution $Q(t) = \frac{\psi }{\mu } + \left( Q(0) - \frac{\psi }{\mu }\right) e^{-\mu t}$. By comparison, $N(t) \le Q(t)$ if $N(0) = Q(0)$. Therefore, $\limsup _{t \rightarrow \infty } N(t) \le \frac{\psi }{\mu }$. Thus, the set ${\mathcal {K}}$ is positively invariant a-+nd attracts all solutions in ${\mathbb {R}}_+^6$¹⁶. $\square$

Positivity of solution

Lemma 2 

(Positivity of solution) Given non-negative initial conditions in ${\mathcal {K}}$, the solutions $S_e(t), S_u(t), E(t), I_m(t), I_s(t), R(t)$ of the system (1) remain non-negative for all time $t> 0$^9,10,22.

Proof

Consider the equation for the uneducated susceptible population:

$$\frac{dS_u}{dt} = \psi (1-k) - (\mu + \gamma + \lambda ) S_u.$$

This can be rewritten as:

$$\frac{d}{dt} \left[ S_u(t) \cdot \exp \left( \mu t + \gamma t + \int _0^t \lambda (s) ds \right) \right] = \psi (1-k) \exp \left( \mu t + \gamma t + \int _0^t \lambda (s) ds \right) .$$

Integrating from 0 to t gives:

$$S_u(t) = S_u(0) e^{-(\mu + \gamma )t - \int _0^t \lambda (s) ds} + \psi (1-k) e^{-(\mu + \gamma )t - \int _0^t \lambda (s) ds} \int _0^t e^{(\mu + \gamma )s + \int _0^s \lambda (\zeta ) d\zeta } ds.$$

Since all terms on the right-hand side are non-negative for all $t> 0$, it follows that $S_u(t) \ge 0$. The non-negativity of the other state variables can be proven similarly by applying an integrating factor to each corresponding equation, demonstrating that the positive orthant ${\mathbb {R}}_+^6$ is invariant. $\square$

Analysis of the model

Disease-free equilibrium point

A disease-free equilibrium (DFE) is a state where no one in the community is infected. To find this point, we need to calculate where the number of infected people stays at zero over time.

$$\begin{aligned} \frac{dS_e}{dt}=\frac{dS_u}{dt}=\frac{dE}{dt}=\frac{dI_m}{dt}=\frac{dI_s}{dt}=\frac{dR}{dt}=0. \end{aligned}$$

Solving the system of equation at $E=0,I_m=0,I_s=0$ we get the disease free equilibrium DFE point $(\epsilon ^*)$ of the model as

$$\begin{aligned} \xi ^* = (S_e^*, S_u^*, 0, 0, 0, 0) = \left( \frac{\psi ( k(\mu + \gamma ) + \gamma ) - \gamma k}{(\mu + \gamma )\mu },\ \frac{\psi (k + 1)}{\mu + \gamma },\ 0,\ 0,\ 0,\ 0 \right) . \end{aligned}$$

When the disease is gone, the total population will stabilize at a fixed number, $N^*$, which is calculated by dividing the recruitment rate, $\psi$, by the mortality rate, $\mu$. i.e.

$$\begin{aligned} N^*=\frac{\psi }{\mu }. \end{aligned}$$

Basic reproduction number

The basic reproduction number, $R_0$, tells us how many people one infected person can spread the disease to. It’s a crucial number that helps us understand how diseases spread and how to control them. If $R_0$ is 1, the disease will stick around. If it’s less than 1, the disease will start to die out. But if it’s more than 1, the disease will likely spread and keep going. Knowing $R_0$ helps us make smart decisions about how to deal with outbreaks.

To figure out $R_0$, we use a method called the next-generation matrix, which is calculated as $FV^{-1}$. This involves two key parts: F, which shows how quickly new infections happen, and V, which deals with how people move between different stages of the disease.

$$\begin{aligned} & F=\left[ \begin{array}{ccc} 0& {\frac{\beta \, \left( S_{e}\,\epsilon +S_{u} \right) }{N}}& {\frac{\beta \, \left( S_{e}\,\epsilon +S_{u} \right) }{N}}\\ 0& 0& 0\\ 0& 0& 0\end{array} \right] \end{aligned}$$

(3)

$$\begin{aligned} & V= \left[ \begin{array}{ccc} k_{2}& 0& 0\\ -\tau \,\pi & -\sigma & k_{3}\\ - \left( 1-\tau \right) \pi & k_{4}& 0\end{array} \right] . \end{aligned}$$

(4)

The inverse of V is given as

$$\begin{aligned} & V^{-1} = \left[ \begin{array}{ccc} {k_{2}}^{-1}& 0& 0\\ -{ \frac{ \left( -1+\tau \right) \pi }{k_{2}\,k_{4}}}& 0& {k_{4}}^{-1}\\ {\frac{\pi \, \left( k_{4}\,\tau -\sigma \,\tau +\sigma \right) }{k_{2}\,k_{3}\,k_{4}}}& {k_{3}}^{-1}& {\frac{\sigma }{k_{3}\,k_{4}}}\end{array} \right] \end{aligned}$$

(5)

$$\begin{aligned} & FV^{-1}= \left[ \begin{array}{ccc} -{\frac{\beta \, \left( S_{e}\,\epsilon +S_{u} \right) \left( -1+\tau \right) \pi }{Nk_{2}\,k_{4}}}+{\frac{\beta \, \left( S_{e}\,\epsilon +S_{u} \right) \pi \, \left( k_{4}\,\tau -\sigma \,\tau +\sigma \right) }{Nk_{2}\,k_{3}\,k_{4}}}& {\frac{\beta \, \left( S_{e}\,\epsilon +S_{u} \right) }{Nk_{3}}}& {\frac{\beta \, \left( S_{e}\,\epsilon +S_{u} \right) }{Nk_{4}}}+{\frac{\beta \, \left( S_{e}\,\epsilon +S_{u} \right) \sigma }{Nk_{3}\,k_{4}}} \\ 0& 0& 0\\ 0& 0& 0\end{array} \right] \end{aligned}$$

(6)

$$\begin{aligned} & = \left[ \begin{array}{c} 0\\ 0\\ {\frac{\beta \,\pi \, \left( -S_{e}\,\epsilon \,k_{3}\,\tau +S_{e}\, \epsilon \,k_{4}\,\tau S_{e}\,\epsilon \,\sigma \,\tau +S_{e}\,\epsilon \,k _{3}+S_{e}\,\epsilon \,\sigma S_{u}\,k_{3}\,\tau +S_{u}\,k_{4}\,\tau -S_{u}\,\sigma \,\tau +S_{u}\,k_{3}+S_{u}\,\sigma \right) }{Nk_{2}\,k_{3}\,k _{4}}}\end{array} \right] . \end{aligned}$$

(7)

The basic reproduction number is given as

$$\begin{aligned} R_0= {\frac{\beta \,\pi \, \left( S_{e}\, \epsilon \,k_{4}\,\tau -S_{e}\,\epsilon \,k_{3}\,\tau -S_{e}\,\epsilon \,\sigma \,\tau +S_{e}\,\epsilon \,k_{3}+S_{e}\,\epsilon \,\sigma -S_{u}\,k_{3}\,\tau +S_{u}\,k_{4}\,\tau -S_{ u}\,\sigma \,\tau +S_{u}\,k_{3}+S_{u}\,\sigma \right) }{Nk_{2}\,k_{3}\,k_{4}}}. \end{aligned}$$

(8)

The basic reproduction number after substituting $S_{u}^{*},S_{e}^{*},N^{*},k_{3}$ and $k_{4}$ is given as

$$\begin{aligned} R_{0}= {\frac{\pi \,\beta \, \left( \left( \delta _{2}+\Phi -\phi -\delta _{1} \right) \tau +\sigma +\delta _{1}+\mu +\phi \right) \left( \left( \epsilon \,k+k+1 \right) \mu +\gamma \,\epsilon \right) }{ \left( \mu + \gamma \right) \left( \mu +\pi \right) \left( \mu +\delta _{1}+\phi \right) \left( \mu +\delta _{2}+\sigma +\Phi \right) }}, \end{aligned}$$

(9)

Biological interpretation of ${\mathcal {R}}_0$

While the full expression for ${\mathcal {R}}_0$ is mathematically complex, it can be interpreted intuitively by decomposing it into core epidemiological components. The basic reproduction number represents the average number of new infections generated by a single infectious individual in a completely susceptible population. Our expression,

$${\mathcal {R}}_0 = \frac{\pi \beta \left( (\delta _2 + \Phi - \phi - \delta _1) \tau + \sigma + \delta _1 + \mu + \phi \right) \left( (\epsilon k + k + 1) \mu + \gamma \epsilon \right) }{(\mu + \gamma )(\mu + \pi )(\mu + \delta _1 + \phi )(\mu + \delta _2 + \sigma + \Phi )},$$

can be understood in terms of the following factors:

• Effective Transmission Rate ($\beta$): This is the base rate of contact capable of spreading the disease. It is scaled by the term.

  $$\frac{ (\epsilon k + k + 1) \mu + \gamma \epsilon }{(\mu + \gamma )}$$

  which represents the effective susceptible population. This term is less than 1 and captures the reduction in transmission due to public awareness; a portion of the population ($S_e$) has a lower risk of infection (reduced by $\epsilon$ ).

• Infection Generation: The numerator terms involving $\pi$ and the large bracket represent the potential of an exposed individual to generate new infections. This includes:

  • The rate at which exposed individuals become infectious ($\pi$).

  • The probability that an infection will be mild or severe ($\tau$ and $1-\tau$), and the different paths to recovery or progression ($\sigma$) that contribute to the overall infectious output.

• Infectious Period: The terms in the denominator $(\mu + \delta _1 + \phi )$ and $(\mu + \delta _2 + \sigma + \Phi )$ represent the average duration of infectiousness for the severely and mildly infected classes, respectively. A longer infectious period (smaller denominator) increases ${\mathcal {R}}_0$.

Therefore, ${\mathcal {R}}_0> 1$ implies that the combined effect of transmission risk, speed of progression, and duration of illness is sufficient for the disease to invade a population. Conversely, interventions that reduce any of these components—such as awareness campaigns (reducing $\beta$ and the effective susceptible pool), hygiene measures (reducing $\beta$), or treatment (reducing the infectious period by increasing $\phi$ and $\Phi$)—can push ${\mathcal {R}}_0$ below 1, leading to disease elimination.

Local stability of disease-free equilibrium

To determine if a disease will spread or die out, we analyze the stability of the disease-free equilibrium. By building a Jacobian matrix and simplifying the equations around this point, we can figure out if the disease will take hold or fade away^13,20,21.

Theorem 1

(Local stability of DFE) The disease-free equilibrium $\xi ^*$ of the system (1) is locally asymptotically stable if ${\mathcal {R}}_0 < 1$ and unstable if ${\mathcal {R}}_0> 1$.

Proof

The local stability of the DFE is determined by the eigenvalues of the Jacobian matrix of the system (1), evaluated at $\xi ^* = (S_e^*, S_u^*, 0, 0, 0, 0)$.

The Jacobian matrix $J(\xi ^*)$ is given by:

$$J(\xi ^*) = \begin{pmatrix} -(\mu + \gamma ) & \gamma & 0 & -\epsilon \beta S_e^*/N^* & -\epsilon \beta S_e^*/N^* & 0 \\ 0 & -(\mu + \gamma ) & 0 & -\beta S_u^*/N^* & -\beta S_u^*/N^* & 0 \\ 0 & 0 & -(\mu + \pi ) & \beta (\epsilon S_e^* + S_u^*)/N^* & \beta (\epsilon S_e^* + S_u^*)/N^* & 0 \\ 0 & 0 & \tau \pi & -(\mu + \delta _2 + \sigma + \Phi ) & \sigma & 0 \\ 0 & 0 & (1-\tau )\pi & 0 & -(\mu + \delta _1 + \phi ) & 0 \\ 0 & 0 & 0 & \Phi & \phi & -\mu \end{pmatrix}$$

This matrix has a block-triangular structure. The eigenvalues are given by the eigenvalues of the two sub-matrices on the diagonal^20,21:

• 1. The sub-matrix corresponding to the non-infected compartments ($S_e, S_u, R$).

• 2. The sub-matrix corresponding to the infected/exposed compartments ($E, I_m, I_s$).

The sub-matrix for the non-infected compartments is:

$$J_1 = \begin{pmatrix} -(\mu + \gamma ) & \gamma & 0 \\ 0 & -(\mu + \gamma ) & 0 \\ 0 & 0 & -\mu \end{pmatrix}$$

This matrix is lower triangular. Its eigenvalues are its diagonal entries: $-(\mu + \gamma )$, $-(\mu + \gamma )$, and $-\mu$. All are real and negative.

The stability of the DFE is therefore determined by the eigenvalues of the infectious subsystem sub-matrix ($E, I_m, I_s$)^20,21:

$$J_2 = \begin{pmatrix} -(\mu + \pi ) & \beta (\epsilon S_e^* + S_u^*)/N^* & \beta (\epsilon S_e^* + S_u^*)/N^* \\ \tau \pi & -k_4 & \sigma \\ (1-\tau )\pi & 0 & -k_3 \end{pmatrix}$$

where $k_3 = (\mu + \delta _1 + \phi )$ and $k_4 = (\mu + \delta _2 + \sigma + \Phi )$.

The characteristic equation of this matrix is given by $\det (J_2 - \Lambda I) = 0$:

$$\det \begin{pmatrix} -(\mu + \pi ) - \Lambda & A & A \\ \tau \pi & -k_4 - \Lambda & \sigma \\ (1-\tau )\pi & 0 & -k_3 - \Lambda \end{pmatrix} = 0$$

where $A = \beta (\epsilon S_e^* + S_u^*)/N^*$.

This expands to the following cubic characteristic equation:

$$\Lambda ^3 + C_1\Lambda ^2 + C_2\Lambda + C_3 = 0$$

where the coefficients $C_1, C_2, C_3$ are functions of the model parameters.

According to the Routh-Hurwitz criterion for a cubic polynomial, all roots have negative real parts (i.e., the DFE is stable) if and only if^20,21: 1. $C_1> 0$ 2. $C_3> 0$ 3. $C_1C_2 - C_3> 0.$

After extensive algebraic manipulation, it can be shown that the condition $C_1C_2 - C_3> 0$ simplifies to $(1 - {\mathcal {R}}_0)> 0$. The other conditions ($C_1> 0$, $C_3> 0$) are always true for positive parameter values^20,21.

Therefore, the DFE is locally asymptotically stable if and only if ${\mathcal {R}}_0 < 1$. If ${\mathcal {R}}_0> 1$, the condition $C_1C_2 - C_3> 0$ is violated, indicating a positive eigenvalue exists, and the DFE is unstable. $\square$

Global stability of disease-free equilibrium

Theorem 2

(Global stability of DFE) When the reproduction number $R_0$ is below 1, the disease-free state is stable, and the disease will eventually disappear. But if $R_0$ is above 1, the disease will stick around, and the disease-free state becomes unstable¹³.

Proof

Two essential conditions, $F_1$ and $F_2$, as stated in¹⁰, need to be satisfied to establish the theorem. To show that the reproduction number $R_0 < 1$, the model can be represented as follows.

$$\begin{aligned} & \frac{dA_1}{dt}=X(A_1,A_2), \\ & \frac{dA_2}{dt}=Y(A_1,A_2);Y(A_1,0)=0. \end{aligned}$$

The uninfected population is denoted by $A_1 \in \mathbf {R^3_{+}}$, comprising three components $(S_e^*, S_u^*, R^*)$, while the infected population is represented by $A_2 \in \mathbf {R^4_{+}}$, consisting of four components $(E^*, I_s^*, I_m^*)$. The disease-free equilibrium is given by $\xi ^*=(A_1^*, 0)$, where $A_1^* = (N^*, 0)$. For $A_1^*$ to be globally asymptotically stable, the first condition is

$$\begin{aligned} \frac{dA_1}{dt}=X(A_1,A_2)= \begin{bmatrix} k\psi +\gamma S_u^{*}-(\mu +\epsilon \lambda )S_e^{*}\\ \psi (1-k)-(\mu +\gamma +\lambda )S_u^{*}\\ -\mu R^* \end{bmatrix}. \end{aligned}$$

Solving the ordinary differential equations (ODEs), we have

$$\begin{aligned} & S_{e}^*(t)= \frac{k\psi +\gamma S_u^{*}}{\mu }+S_{e}^*(0)e^{-(\mu +\epsilon \lambda ) t}-\frac{k\psi +\gamma S_u^{*}}{(\mu +\epsilon \lambda )}e^{-(\mu +\epsilon \lambda ) t} \\ & S_{u}^*(t)= \frac{\psi (1-k)}{(\mu +\gamma +\lambda )}+S_{u}^*(0)e^{-(\mu +\gamma +\lambda )t}-\frac{\psi (1-k)}{(\mu +\gamma +\lambda )}e^{-(\mu +\gamma +\lambda )t}, \\ & R^*(t)= R^*(0)e^{-\mu t}. \end{aligned}$$

It is evident from the system of equations (1) that, regardless of the initial values of $S_e^*(t)$, $S_u^*(t)$, and $R^*(t)$, as $t \rightarrow \infty$, the sum $S_e^*(t) + S_u^*(t) + R^*(t)$ approaches $N^*(t)$. This indicates global asymptotic stability at the equilibrium point $A^*_1 = (N^*, 0)$. The next step is to verify the second condition, which requires demonstrating that.

$$\begin{aligned}\tilde{Y}(A_1, A_2) = GA_2 - Y(A_1, A_2) \ge 0 \end{aligned}$$

where

$$\begin{aligned} G=\begin{bmatrix} -k_{2}& {\frac{\beta \, \left( \epsilon \,S_{e}+S_{u} \right) }{N}}& {\frac{\beta \, \left( \epsilon \,S_{e}+S_{u} \right) }{N}}\\ \tau \pi & \sigma & -k_{3}\\ \left( 1-\tau \right) \pi & -k_{4}& 0 \end{bmatrix}. \end{aligned}$$

$$\begin{aligned} Y(A_1,A_2)= \begin{bmatrix} \frac{\beta (I_m^*+I_s^{*})}{N^*}(S_u+\epsilon S_e)-(\mu +\pi )E\\ (\tau \pi E +\sigma I_m-(\mu +\delta _1+\phi _1)I_s\\ (1-\tau )\pi E-(\mu +\delta _2+\sigma +\phi _2)I_m) \end{bmatrix}. \\ \tilde{ Y}(A_1, A_2) = GA_2 - Y(A_1, A_2) =\begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}. \end{aligned}$$

That is $\tilde{Y}(A_1,A_2)=\begin{bmatrix} 0&0&0 \end{bmatrix}^T.$

It is evident that $\tilde{Y}(A_1,A_2)=0$ $\square$

Endemic equilibrium point (EEP)

Epidemiological models describe an equilibrium point as a steady-state where a disease remains in the population at a constant level, with new infections balancing recoveries. This stable prevalence of the disease indicates its persistence. In epidemiology, the concept of the endemic equilibrium point represents a long-term stable condition of disease in a community, acting as a reference for strategies aimed at disease control and elimination¹². The endemic equilibrium points are defined as follows:

$$\begin{aligned} S_e^{**}={\frac{ \left( \left( \mu +\lambda \right) k+\gamma \right) \psi }{ \left( \epsilon \,\lambda +\mu \right) \left( \mu +\gamma +\lambda \right) }},\end{aligned}$$

(10)

$$\begin{aligned} S_u^{**}={\frac{\psi \, \left( k+1 \right) }{\mu +\gamma +\lambda }},\end{aligned}$$

(11)

$$\begin{aligned} E^{**}={\frac{\lambda \left( \left( \epsilon \,k-k+1 \right) \mu +\epsilon \, \left( \gamma +\lambda \right) \right) \psi }{ \left( \mu +\pi \right) \left( \mu +\gamma +\lambda \right) \left( \epsilon \,\lambda +\mu \right) }},\end{aligned}$$

(12)

$$\begin{aligned} I_m^{**}={\frac{\lambda \,\pi \, \left( \tau +1 \right) \psi \, \left( \left( \epsilon \,k-k+1 \right) \mu +\epsilon \, \left( \gamma +\lambda \right) \right) }{ \left( \mu +\pi \right) \left( \mu +\delta _{2}+\sigma +\Phi \right) \left( \mu +\gamma +\lambda \right) \left( \epsilon \,\lambda +\mu \right) }},\end{aligned}$$

(13)

$$\begin{aligned} I_{s}^{**}={\frac{\lambda \,\pi \, \left( \tau \left( \left( k\mu +\gamma +\lambda \right) \epsilon -\mu \, \left( k-1 \right) \right) +1 \right) \psi \,\sigma }{ \left( -\pi \,\tau +\mu +\phi +\delta _{1} \right) \left( \mu +\delta _{2}+\sigma +\Phi \right) \left( \mu \left( \mu +\gamma +\lambda \right) +\pi \left( \mu +\gamma +\lambda \right) \right) \left( \epsilon \,\lambda +\mu \right) }},\end{aligned}$$

(14)

$$\begin{aligned} R^{**}={\frac{\lambda \,\pi \, \left( \left( \pi \,\tau -\mu -\phi -\delta _{1} \right) \Phi -\phi \,\sigma \right) \left( \tau -1 \right) \left( \left( k\mu +\gamma +\lambda \right) \epsilon -\mu \, \left( k-1 \right) \right) \psi }{\mu \, \left( -\pi \,\tau +\mu +\phi +\delta _{1} \right) \left( \mu +\delta _{2}+\sigma +\Phi \right) \left( \mu \left( \mu +\gamma +\lambda \right) +\pi \left( \mu +\gamma +\lambda \right) \right) \left( \epsilon \,\lambda +\mu \right) }}, \end{aligned}$$

(15)

Global stability of endemic equilibrium point

Theorem 3

(Global stability of EEP) When $R_0$ is greater than 1, the disease becomes a persistent presence in the population, and this state is stable. On the other hand, if $R_0$is less than 1, the disease won’t maintain a steady presence, and this state is unstable^9,10.

Proof

Using the Goh-Voltera formulation provided in¹⁰, we assembled the Lyapunov function candidate.

$$\begin{aligned} \begin{aligned} V(t)&=\epsilon _1\bigg (S_e-S_{e}^{**}-S_{e}^{**}\,\ln \left( {\frac{S_e}{S_{e}^{**}}} \right) \bigg ) +\epsilon _2\bigg (S_u-S_{u}^{**}-S_{u}^{**}\, \ln \left( {\frac{S_u}{S_{u}^{**}}} \right) \bigg ) +\epsilon _3\bigg (E-E^{**}-E^{**}\,\ln \left( {\frac{E}{E^{**}}} \right) \Bigg )\\&\quad +\epsilon _4\bigg (I_m-I_{m}^{**}-I_{m}^{**}\,\ln \left( {\frac{I_{m}}{I_{m}^{**}}} \right) \bigg ) +\epsilon _5\bigg (I_s-I_{s}^{**}-I_{s}^{**}\,\ln \left( {\frac{I_s}{I_{s}^{**}}} \right) \bigg ) \end{aligned} \end{aligned}$$

(16)

Taking into account $\epsilon _i=1$ $(i=1,2,...6)$ for simplicity, we calculate the time derivative of V along the system’s trajectory, and obtain

$$\begin{aligned} V'(t)=\left( 1-{\frac{S_{e}^{**}}{S_e}} \right) S_{e}^{\prime }+\left( 1-{\frac{S_{u}^{**}}{S_u}} \right) S_{u}^{\prime }+\left( 1-{\frac{E^{**}}{E}} \right) E^{\prime }+\left( 1-{\frac{I_{m}^{**}}{I_m}} \right) I_{m}^{\prime }+\left( 1-{\frac{I_s^{**}}{I_s}} \right) I_s^{\prime } \end{aligned}$$

(17)

Substituting $S_{e}^{\prime },S_{u}^{\prime },E^{\prime },I_{m}^{\prime },I_{s}^{\prime }$ into Eq. (40)

$$\begin{aligned} \begin{aligned} V'(t)&=\left( 1-{\frac{S^{**}}{S}} \right) (k\psi -(\mu +\epsilon \lambda )S_e) + \left( 1-{\frac{S_{u}^{**}}{S_u}} \right) \left( \psi (1-k)-(\mu +\gamma +\lambda )S_u\right) \\&\quad + \left( 1-{\frac{E^{**}}{E}} \right) \lambda (S_u+\epsilon S_e)-(\mu +\pi )E + \left( 1-{\frac{I_{m}^{**}}{I}} \right) \left( \tau \pi I_s-(\mu +\delta _1+\phi _1)I_s \right) \\&\quad + \left( 1-{\frac{I_{s}^{**}}{I_{s}}} \right) \left( (1-\tau )\pi E-(\mu +\delta _2+\sigma +\phi _2)I_m \right) . \end{aligned} \end{aligned}$$

(18)

Expanding Eq. (41), we have

$$\begin{aligned} \begin{aligned} V'(t) &= \bigg ( \left( k\psi - (\mu + \epsilon \lambda )S_e\right) - \left( \frac{S^{**}}{S} \left( k\psi - (\mu + \epsilon \lambda )S_e\right) \right) \bigg ) \\&\quad + \bigg ( \left( \psi (1 - k) - (\mu + \gamma + \lambda )S_u \right) - \left( \frac{S_u^{**}}{S_u} \left( \psi (1 - k) - (\mu + \gamma + \lambda )S_u \right) \right) \bigg ) \\&\quad + \bigg ( \left( \lambda (S_u + \epsilon S_e) - (\mu + \pi )E \right) - \left( \frac{E^{**}}{E} \left( \lambda (S_u + \epsilon S_e) - (\mu + \pi )E \right) \right) \bigg ) \\&\quad + \bigg ( \left( \tau \pi E - (\mu + \delta _1 + \phi _1)I_s \right) - \left( \frac{I_s^{**}}{I_s} \left( \tau \pi E - (\mu + \delta _1 + \phi _1)I_s \right) \right) \bigg ) \\&\quad+ \bigg ( \left( (1 - \tau )\pi E - (\mu + \delta _2 + \sigma + \phi _2)I_m \right) - \left( \frac{I_m^{**}}{I_m} \left( (1 - \tau )\pi E - (\mu + \delta _2 + \sigma + \phi _2)I_m \right) \right) \bigg ) \end{aligned} \end{aligned}$$

(19)

At a steady state, we get the following from system (1):

$$\begin{aligned} \begin{aligned}& k\psi \ge (\mu +\epsilon \lambda )S_e\\& \psi (1-k)\ge (\mu +\gamma +\lambda )S_u\\& (\lambda (S_u+\epsilon S_e)\ge (\mu +\pi )E)\\& \tau \pi I_s\ge (\mu +\delta _1+\phi _1)I_s\\& (1-\tau )\pi E\ge (\mu +\delta _2+\sigma +\phi _2)I_m.\\ \end{aligned} \end{aligned}$$

(20)

Substituting Eq. (43) and simplifying, we obtained

$$\begin{aligned} V'(t)= \bigg (2-\frac{S_{e}^{**}}{S_e}-\frac{S_e}{S_{e}^{**}}\bigg )+ \bigg (2-\frac{S_{u}^{**}}{S_u}-\frac{S_u}{S_{u}^{**}}\bigg )+ \bigg (2-\frac{E^{**}}{E}-\frac{E}{E^{**}}\bigg )+ \bigg (2-\frac{I_{s}^{**}}{I_s}-\frac{I_s}{I_{s}^{**}}\bigg )+ \bigg (2-\frac{I_m^{**}}{I_m}-\frac{I_m}{I_m^{**}}\bigg ) \end{aligned}$$

(21)

The arithmetic mean is greater than or equal to the geometric mean based on the relationship between the two measures.

$$\begin{aligned} \begin{aligned} V'(t)= \bigg (2-\frac{S_{e}^{**}}{S_e}-\frac{S_e}{S_{e}^{**}}\bigg )\le 0, \bigg (2-\frac{S_{u}^{**}}{S_u}-\frac{S_u}{S_{u}^{**}}\bigg )\le 0, \bigg (2-\frac{E^{**}}{E}-\frac{E}{E^{**}}\bigg )\le 0, \bigg (2-\frac{I_{m}^{**}}{I_m}-\frac{I_m}{I_{m}^{**}}\bigg )\le 0, \\ \bigg (2-\frac{I_s^{**}}{I_s}-\frac{I_s}{I_s^{**}}\bigg ) \le 0. \end{aligned} \end{aligned}$$

(22)

Thus, $V' \le 0$. The equality $V' = 0$ is satisfied only when $S_e = S_e^{**}, E = E^{**}, S_u = S_u^{**}, I_m = I_m^{**}, I_s = I_s^{**}$. This suggests that the system’s only stable state is the endemic equilibrium (EE) $\xi ^{**}$. Using Lasalle’s invariance principle, we can conclude that the model’s EE $\xi ^{**}$is globally asymptotically stable (GAS)¹². $\square$

Optimal control problem

In this section, we develop a control system based on model (1) and specify an objective function to optimize. We derive the necessary conditions for obtaining the optimal control solution. Optimal control is selected due to its established effectiveness, flexibility, and ability to manage complex systems, enabling us to evaluate outcomes and compare strategies.

This approach provides a robust framework for controlling dysentery transmission, outperforming alternative methods such as feedback control, adaptive control, fuzzy control, and sliding mode control. To effectively implement the optimal control strategy, collaboration with public health officials, decision support systems, training, and community engagement is essential.

Potential implementation sites include schools, healthcare facilities, and community centers. However, addressing challenges related to data quality, resource constraints, and community engagement is crucial for successful implementation. By overcoming these challenges, we can ensure the effective translation of our optimal control strategy into practice, ultimately reducing the transmission of dysentery.

$$\begin{aligned} \begin{aligned} \frac{dS_e}{dt}&= k\psi + \gamma S_u - (\mu + \epsilon \lambda +u_2) S_e, \\ \frac{dS_u}{dt}&= \psi (1 - k) - (\mu + \gamma + \lambda +u_1) S_u, \\ \frac{dE}{dt}&= \lambda (S_u + \epsilon S_e) - (\mu + \pi +u_2) E, \\ \frac{dI_s}{dt}&= \tau \pi E + \sigma I_m - (\mu + \delta _1 + \phi +u_3) I_s, \\ \frac{dI_m}{dt}&= (1 - \tau ) \pi E - (\mu + \delta _2 + \sigma + \Phi +u_3) I_m, \\ \frac{dR}{dt}&= \phi I_s + \Phi I_m - \mu R. \end{aligned}\end{aligned}$$

(23)

The control variables are:

• $u_1:$ Public awareness effort on the uneducated susceptible population

• $u_2:$ Effort for proper sanitation and personal hygiene on the exposed and educated susceptible classes.

• $u_3:$ Chemotherapy treatment on the infected class.

Our goal is to minimize the impact of the disease by reducing the number of infected individuals while also considering the cost of control measures¹¹.

$$\begin{aligned} J = \int _0^T \left[ A I_s(t) + B I_m(t) + \frac{1}{2} \left( C_1 u_1(t)^2 + C_2 u_2(t)^2 + C_3 u_3(t)^2 \right) \right] dt, \end{aligned}$$

The choice of weights in the objective functional is a critical step. The coefficients A and B represent the societal or economic cost per unit time per severely and mildly infected individual, respectively. These costs can include healthcare expenses, lost productivity, and patient suffering. The coefficients $C_1$, $C_2$, and $C_3$ represent the unit costs of implementing the respective control measures per unit time (e.g., cost of running awareness campaigns, providing sanitation facilities, and administering chemotherapy).

While the specific values of these weights can vary based on local economic conditions, their relative value determines the priority of the optimizer. For this theoretical study, we set $A> B> 0$ to reflect the higher burden of severe cases, and $C_1, C_2, C_3> 0$. The qualitative results—the ranking of intervention strategies—are robust to a wide range of positive weight values. The goal is to minimize the total cost, which is the sum of the disease burden and the intervention expenses. As long as $0 \le u_i(t) \le 1$ for $i = 1, 2, 3$ and $t \in [0, T]$, all measurable functions $u_i(t)$ satisfy the conditions of the admissible control set, denoted by ${\mathcal {U}}$, under the system dynamics. In this scenario, the weights for the impacted groups are $A$ and $B$, while the costs associated with the control interventions are $C_1$, $C_2$, and $C_3$, corresponding to $u_1(t)$, $u_2(t)$, and $u_3(t)$, respectively. To simplify the process, we minimize the objective functional $J(u^*)$ using Pontryagin’s Minimum Principle. By reducing the problem to minimizing the Hamiltonian function, the minimization task becomes more straightforward. The Hamiltonian function, denoted as $H$, is defined as follows^23:.

$$\begin{aligned} H = A I_m(t) + B I_{s}(t) + \frac{1}{2}C_{1}u_{1}^{2} + \frac{1}{2}C_{2}u_{2}^{2} + \frac{1}{2}C_{3}u_{3}^{2} + \sum _{i=1}^{6}\lambda _{i}(t)f_{i}(t, S_e, S_u, E, I_m, I_s, R) \end{aligned}$$

(24)

In this context, the adjoint variables are denoted by $\lambda _i(t)$, while the control inputs are represented by $u_1, u_2, u_3$, and the constants by $A, B, C_1, C_2, C_3$. The functions $f_i(t, S_e, S_u, E, I_m, I_s, R)$ represent the right-hand sides of the system equations. The adjoint vector $\lambda (t)$ is a 6-dimensional vector function defined over the interval [0, T] and taking values in ${\mathbb {R}}^6$. The components of this vector, $\lambda _1, \lambda _2, \lambda _3, \lambda _4, \lambda _5$, and $\lambda _6$, correspond to their respective state variables.

Pontryagin’s minimum principle

Theorem 4

(Existence of Optimal control) Let’s say we find the best control strategy $u^*(t)$ that minimizes the cost J(u(t)). This would lead to optimal outcomes for the population, represented by $S_e^*, S_u^*, E^*, I_m^*, I_{s}^*, R^*$. To achieve this, we need to consider certain conditions and introduce additional variables $\lambda _1$ to $\lambda _6$ that help us find the optimal solution.

$$\begin{aligned} \begin{aligned} \frac{d\lambda _1}{dt}&= -\frac{\partial {\mathcal {H}}}{\partial S_e} = \lambda _3 \lambda - \lambda _1 (\mu + \epsilon \lambda + u_2), \\ \frac{d\lambda _2}{dt}&= -\frac{\partial {\mathcal {H}}}{\partial S_u} = \lambda _3 \lambda - \lambda _2 (\mu + \gamma + \lambda + u_1), \\ \frac{d\lambda _3}{dt}&= -\frac{\partial {\mathcal {H}}}{\partial E} = -\lambda _3 (\mu + \pi + u_2), \\ \frac{d\lambda _4}{dt}&= -\frac{\partial {\mathcal {H}}}{\partial I_s} = -\lambda _4 (\mu + \delta _1 + \phi _1 + u_3) + \phi \lambda _6, \\ \frac{d\lambda _5}{dt}&= -\frac{\partial {\mathcal {H}}}{\partial I_m} = -\lambda _5 (\mu + \delta _2 + \sigma + \phi _2 + u_3) + \Phi \lambda _6, \\ \frac{d\lambda _6}{dt}&= -\frac{\partial {\mathcal {H}}}{\partial R} = -\lambda _6 \mu . \end{aligned}\end{aligned}$$

(25)

Subject to the transversality conditions:$\lambda _i(T) = 0, \quad i = 1, \ldots , 5$

Furthermore, the transversality conditions guarantee that the adjoint variables become zero at the final time $T$, which is a crucial requirement for optimality.

$$\begin{aligned}\begin{aligned} u _1^* =min\bigg (max\bigg (0, \frac{\lambda _2 S_u }{C_1}, \bigg ),1\bigg ),\\ u _2^* =min\bigg (max\bigg (0, \frac{\lambda _3 E + \lambda _1 S_e}{C_2} , \bigg ),1\bigg ),\\ u _3^* =min\bigg (max\bigg (0,\frac{\lambda _4 I_s}{C_3} , \bigg ),1\bigg )\end{aligned} \end{aligned}$$

Proof

We calculate the adjoint variables after identifying the optimal control functions through Pontryagin’s Minimum Principle. Specifically, the following procedure is employed to obtain the adjoint variables¹¹:

$$\begin{aligned} H = A I_m(t) + B I_{s}(t) + \frac{1}{2}C_{1}u_{1}^{2} + \frac{1}{2}C_{2}u_{2}^{2} + \frac{1}{2}C_{3}u_{3}^{2} + \sum _{i=1}^{6}\lambda _{i}(t)f_{i}(t, S_e, S_u, E, I_m, I_s, R) \end{aligned}$$

(26)

Defining the Hamiltonian $H$ for the system we have

$$\begin{aligned} {\mathcal {H}}&= A I_s + B I_m + \frac{1}{2} \left( C_1 u_1^2 + C_2 u_2^2 + C_3 u_3^2 \right) \\&\quad + \lambda _1 \left( k \psi + \gamma S_u - (\mu + \epsilon \lambda + u_2) S_e \right) \\&\quad + \lambda _2 \left( \psi (1 - k) - (\mu + \gamma + \lambda + u_1) S_u \right) \\&\quad + \lambda _3 \left( \lambda (S_u + \epsilon S_e) - (\mu + \pi + u_2) E \right) \\&\quad + \lambda _4 \left( \tau \pi I_s + \sigma I_m - (\mu + \delta _1 + \phi _1 + u_3) I_s \right) \\&\quad + \lambda _5 \left( (1 - \tau ) \pi E - (\mu + \delta _2 + \sigma + \phi _2 + u_3) I_m \right) \\&\quad + \lambda _6 \left( \phi I_s + \Phi I_m - \mu R \right) . \end{aligned}$$

The adjoint equations are obtained by calculating the negative partial derivatives of the Hamiltonian concerning each state variable¹¹.

$$\begin{aligned} \begin{aligned} \frac{d\lambda _1}{dt}&= -\frac{\partial {\mathcal {H}}}{\partial S_e} = \lambda _3 \lambda - \lambda _1 (\mu + \epsilon \lambda + u_2), \\ \frac{d\lambda _2}{dt}&= -\frac{\partial {\mathcal {H}}}{\partial S_u} = \lambda _3 \lambda - \lambda _2 (\mu + \gamma + \lambda + u_1), \\ \frac{d\lambda _3}{dt}&= -\frac{\partial {\mathcal {H}}}{\partial E} = -\lambda _3 (\mu + \pi + u_2), \\ \frac{d\lambda _4}{dt}&= -\frac{\partial {\mathcal {H}}}{\partial I_s} = -\lambda _4 (\mu + \delta _1 + \phi _1 + u_3) + \phi \lambda _6, \\ \frac{d\lambda _5}{dt}&= -\frac{\partial {\mathcal {H}}}{\partial I_m} = -\lambda _5 (\mu + \delta _2 + \sigma + \phi _2 + u_3) + \Phi \lambda _6, \\ \frac{d\lambda _6}{dt}&= -\frac{\partial {\mathcal {H}}}{\partial R} = -\lambda _6 \mu . \end{aligned}\end{aligned}$$

(27)

To find the best control strategy, we take the Hamiltonian and set its partial derivatives with respect to $u_1(t)$, $u_2(t)$, and $u_3(t)$ equal to zero

$$\begin{aligned} \begin{aligned} \frac{\partial H}{\partial u_1(t)} = C_1 u_1 - \lambda _2 S_u = 0,\\ \frac{\partial H}{\partial u_2(t)} = C_2 u_2 - \lambda _3 E - \lambda _1S_e = 0,\\ \frac{\partial H}{\partial u_3(t)} =C_3 u_3 - \lambda _4 I_s = 0.\end{aligned}\end{aligned}$$

(28)

Thus, the optimal controls $u_1(t)$, $u_2(t)$, and $u_3(t)$ are:

$$u_1^*(t) = \frac{\lambda _2 S_u }{C_1},$$

$$u_2^*(t) = \frac{ \lambda _3 E + \lambda _1 S_e}{C_2},$$

$$u_3^*(t) = \frac{\lambda _4 I_s}{C_3}.$$

$$\begin{aligned} & u_1^*(t) = \left\{ \begin{array}{rcl} {0} & \text{ for } & \frac{\partial H}{\partial u_1} <0\\ \frac{\lambda _2 S_u }{C_1}, & \text{ for } & \frac{\partial H}{\partial u_1} =0 \\ 1 & \text{ for } & \frac{\partial H}{\partial u_1}>0 \end{array}\right. \end{aligned}$$

(29)

$$\begin{aligned} & u_2^*(t) = \left\{ \begin{array}{rcl} {0} & \text{ for } & \frac{\partial H}{\partial u_2} <0\\ \frac{ \lambda _3 E + \lambda _1 S_e}{C_2} , & \text{ for } & \frac{\partial H}{\partial u_2} =0 \\ 1 & \text{ for } & \frac{\partial H}{\partial u_2}>0 \end{array}\right. \end{aligned}$$

(30)

$$\begin{aligned} & u_3^*(t) = \left\{ \begin{array}{rcl} {0} & \text{ for } & \frac{\partial H}{\partial u_3} <0\\ \frac{\lambda _4 I_s}{C_3}& \text{ for } & \frac{\partial H}{\partial u_3} =0 \\ 1 & \text{ for } & \frac{\partial H}{\partial u_3}>0 \end{array}\right. \end{aligned}$$

(31)

$\square$

Optimal control verification

By ensuring that the Hessian matrix is positive definite, which is necessary for establishing a local minimum, we can evaluate the convexity of the Hamiltonian function $H$ concerning the control variable $u$ and confirm the optimality of $u_{i}^{*}$. The second-order partial derivatives of $H$ with respect to the control variables $u_1$, $u_2$, and $u_3$ form the Hessian matrix $H_u$ of the Hamiltonian. The Hessian matrix is:

$$H_u = \begin{bmatrix} \frac{\partial ^2 H}{\partial u_1^2} & \frac{\partial ^2 H}{\partial u_1 \partial u_2} & \frac{\partial ^2 H}{\partial u_1 \partial u_3} \\ \frac{\partial ^2 H}{\partial u_2 \partial u_1} & \frac{\partial ^2 H}{\partial u_2^2} & \frac{\partial ^2 H}{\partial u_2 \partial u_3} \\ \frac{\partial ^2 H}{\partial u_3 \partial u_1} & \frac{\partial ^2 H}{\partial u_3 \partial u_2} & \frac{\partial ^2 H}{\partial u_3^2} \end{bmatrix}$$

Since the Hamiltonian $H$ is quadratic in $u_1$, $u_2$, and $u_3$, the Hessian matrix is:

$$H_u = \begin{bmatrix} C_1 & 0 & 0 \\ 0 & C_2 & 0 \\ 0 & 0 & C_3 \end{bmatrix}$$

Verify positive definiteness

A Hessian matrix is positive definite if all its leading principal minors are positive¹¹.

• The first leading principal minor is $C_1$, which is positive if $C>0$

• The second leading principal minor is $\begin{vmatrix} C_1&0 \\ 0&C_2\end{vmatrix} =C_1 C_2$, which is positive since $C_1$ and $C_2$ are positive.

• The determinant of the Hessian matrix is $\begin{vmatrix} C_1&0&0 \\ 0&C_2&0 \\ 0&0&C_3\end{vmatrix} = C_1 C_2 C_3$, which is positive since $C_1$, $C_2$, and $C_3$ are positive.

The Hessian matrix is positive definite; hence, the controls are optimal.

Numerical simulation

For the numerical simulations, the parameter values listed in Table 2 were utilized. These values were chosen to ensure the model exhibited biologically plausible dynamics, such as a basic reproduction number ${\mathcal {R}}_0> 1$ conducive to studying an endemic scenario. The justification for each parameter value, especially those not directly sourced from literature, is provided in Table 2. Parameters labeled Assumed were assigned a biologically plausible value within ranges typical of infectious diseases to ensure model stability and realistic dynamics. Parameters labeled Fitted were adjusted within their plausible biological ranges to achieve a specific model behavior (e.g., an endemic equilibrium with ${\mathcal {R}}_0> 1$). The primary goal of this study is the qualitative analysis of intervention strategies; the model is designed to be theoretically consistent rather than to precisely replicate a specific outbreak.

Table 2 Model parameters with values, justification, and sources.

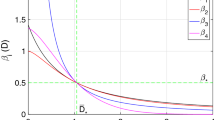
Sensitivity analysis

We examined how changes in key biological parameters affect the reproduction number $(R_0)$ of dysentery. Using a sensitivity analysis, we identified which parameters have the most significant impact on $R_0$. This helps us understand which factors contribute to the spread of the disease and which ones can help control it. By calculating the sensitivity index, we can see which parameters make $R_0$ go up or down.

While the local sensitivity analysis presented here successfully identifies the parameters with the greatest potential influence on ${\mathcal {R}}_0$, it has two primary limitations. First, it assesses sensitivity only at the model’s baseline parameter values and does not explore interactions between parameters. Second, it does not quantify the uncertainty in the model output (${\mathcal {R}}_0$) that results from the uncertainty in the input parameters.

The current local analysis is a vital first step for prioritizing parameters. The logical next step, beyond the scope of this theoretical study, is to apply Techniques such as Latin Hypercube Sampling (LHS) for uncertainty propagation and Partial Rank Correlation Coefficient (PRCC) analysis for global methods to a model calibrated with real-world data to fully assess its robustness and predictive uncertainty.

$$\begin{aligned} X^{R_0}_x =\frac{x}{R_0}\times \frac{\partial R_0}{\partial x} \end{aligned}$$

Where $R_0$ is basic reproduction number and x is parameters.

Table 3 Local sensitivity indices (elasticity) of the basic reproduction number ${\mathcal {R}}_0$ with respect to model parameters, evaluated at the baseline values from Table 2.

Table 3 demonstrates that some model parameters have a positive sensitivity index while others have a negative one. A positive sensitivity index indicates that an increase in the value of these parameters will raise the reproduction number, $R_0$, and vice versa. For example, a sensitivity index value of $X_{\beta }^{R_0}= 1$ implies that a 10 percent reduction in the contact rate parameter $\beta$ will lead to a 10 percent increase in $R_0$, and vice versa.

In essence, sensitivity analysis provides valuable insights into the transmission dynamics, prevention, and control of dysentery. For effective intervention strategies aimed at controlling and preventing the spread of dysentery, it is crucial to decrease parameters with a positive sensitivity index and increase those with a negative sensitivity index. A negative sensitivity index signifies that increasing a parameter with a negative value will lower $R_0$, while decreasing it will raise $R_0$. In Fig. 2, we present a bar chart of the sensitivity index.

Fig. 2

Bar chart representation of sensitivity index.

Result and discussion

Our findings strongly support and provide a mathematical basis for the integrated approach to diarrheal disease control long advocated by global health organizations. The World Health Organization (WHO) and UNICEF’s Integrated Global Action Plan for the Prevention and Control of Pneumonia and Diarrhoea (GAPPD) emphasizes a multi-pronged strategy focusing on protection, prevention, and treatment (WHO, 2013). Our model’s optimal control results directly reflect this philosophy:

• Protection & Prevention: Our awareness control $(u_1)$ and sanitation/hygiene control $(u_2)$ correspond to the GAPPD pillars of

• Protecting children (e.g., through promoting breastfeeding and good nutrition) and preventing infections (e.g., through access to safe water, sanitation, and hygiene education (WASH)).

• Treatment: Our treatment control ($u_3$) aligns with the treating children who are ill pillar, which calls for the provision of appropriate antibiotics and rehydration therapy.

Analytical results

Our study sheds light on how dysentery spreads and what works best to control it. We found that combining awareness campaigns, good hygiene practices, and treatment can be an effective way to tackle the disease. By looking at these factors together, our model gives a more accurate picture of how dysentery outbreaks happen and how to stop them.

Combining Awareness Campaigns with Personal Hygiene and Treatment Our research shows that treatment by itself isn’t enough to stop the spread of dysentery, especially in communities where not everyone has access to it or where immunity is low. However, when we combine treatment with awareness campaigns and good hygiene practices, we can make a big difference. This highlights the need for a comprehensive approach to controlling dysentery outbreaks.

Optimal Control Our study found that the best way to minimize dysentery outbreaks is to combine awareness campaigns, good hygiene practices, and treatment. Awareness campaigns stand out as particularly effective, as they not only reduce the number of people susceptible to the disease but also encourage people to adopt good hygiene habits and seek treatment when needed.

Global Stability and Disease-Free Equilibrium Our analysis shows that if we can keep the disease’s spread under control $(R_0 < 1)$, we can potentially eliminate dysentery. This gives us hope that with effective measures, we can stop the disease from becoming a long-term problem.

Sensitivity Analysis and Key Parameters Our analysis shows that two key factors drive the spread of dysentery: how easily it spreads from person to person and how aware people are of the disease. To control outbreaks, it’s crucial to reduce the spread of the disease through public health measures and increase awareness and treatment.

Numerical results

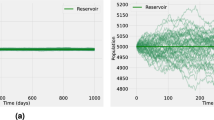
To get a better sense of how our model works, we ran some simulations to see how it behaves under different conditions. We wanted to test our analytical findings and see how changes in parameters affect the outcome. The simulations showed us that if we keep the reproduction number $(R_0)$ below 1, the disease will eventually die out, regardless of the population size. This confirms our theoretical analysis and highlights the importance of keeping $R_0$ low to eradicate the disease. Our simulations also visualized how the disease spreads naturally without any control measures and demonstrated the stability of the disease-free state when $R_0$ is below 1 (See Fig. 3). Figure (4a and b) confirm the global stability of the disease-free equilibrium. They demonstrate that if $R_0 < 1$, the system will eventually reach a dysentery-free state, regardless of population size. Maintaining $R_0 < 1$ is crucial for eradicating the disease from the community, as any outbreak will eventually subside if the basic reproduction number remains below one.

On the other hand, Fig. (5a and b) confirm the global stability of the endemic equilibrium. They show that if $R_0> 1$, the system will reach an endemic state where the disease persists in the population, regardless of size. This highlights the importance of controlling $R_0$ to either eliminate the disease or manage its presence within the community.

Fig. 3

Flow diagram showing the flow of compartment in absence of any control interventions.

Fig. 4

Flow diagram showing dysentery diseases free equilibrium is globally stable for severely infected person. Flow diagram showing dysentery diseases free equilibrium is globally stable for mildly infected person.

Fig. 5

Flow diagram showing dysentery endemic equilibrium is globally stable for severely Infected person. Flow diagram showing dysentery endemic equilibrium is globally stable for severely Infected person Flow diagram showing dysentery endemic equilibrium is globally stable for mildly infected person.

Optimal control simulation results

The visualization presents a comprehensive analysis of optimal control strategies for managing an infectious disease outbreak over a two-year period. The implementation of three distinct control measures—public awareness campaigns, sanitation improvements, and treatment protocols—demonstrates significant effectiveness in reducing disease burden across all measured compartments of the epidemic.

The control effort Fig. (6) reveals interesting temporal patterns in intervention implementation. Awareness campaigns show an initial strong implementation that gradually decreases over time, possibly reflecting the challenge of maintaining public engagement as emergency concerns diminish. Sanitation measures demonstrate a contrasting pattern, with a gradual increase that stabilizes, suggesting these infrastructural improvements become embedded in public health practice. Treatment efforts maintain a consistent level throughout the intervention period, highlighting their fundamental role in disease management. These differential implementation patterns suggest an optimized strategy where immediate awareness campaigns capitalize on heightened public concern during early outbreak stages, sanitation improvements require longer implementation but provide sustained benefits, and treatment maintains a steady-state approach throughout the epidemic period.

The comparison of severe infections with and without control measures demonstrates the most dramatic intervention impact. Without control, severe cases show exponential growth characteristic of uncontrolled epidemics. With interventions, this growth is markedly suppressed, with prevalence maintained at approximately $30-40\%$ of uncontrolled levels throughout the two-year period. This reduction is particularly significant as severe cases typically represent the greatest burden on healthcare systems and contribute most to mortality.

The exposed compartment shows how control measures affect the pool of individuals who are infected but not yet infectious. Interventions reduce both the peak prevalence and duration of exposure, effectively slowing the transmission chain. The gradual divergence between controlled and uncontrolled scenarios suggests that the benefits of interventions compound over time as fewer individuals enter the exposed state.

While mild infections show a similar pattern of reduction under control measures, the relative difference is less pronounced than for severe cases. This may indicate that control measures are particularly effective at preventing progression to severe disease rather than preventing infection entirely. Alternatively, it might suggest that mild cases are more difficult to control through population-level interventions.

The combined impact on total infections demonstrates the population-level benefits of control measures. The intervention strategy appears to delay the epidemic peak and reduce its magnitude substantially. This flattening of the curve has important implications for healthcare system capacity planning and resource allocation during outbreaks.

The percentage reduction figure quantifies the effectiveness of the control strategy, showing increasing benefit over time. The reduction grows from approximately $20\%$ in early stages to nearly $50\%$ by the end of the two-year period. This progressive improvement suggests that control measures have cumulative effects on transmission dynamics, the implemented strategy becomes increasingly cost-effective over time, and sustained intervention is crucial for long-term epidemic control.

The findings support a multi-faceted approach to infectious disease control where early implementation of awareness campaigns capitalizes on initial public responsiveness, investment in sanitation infrastructure provides increasing returns over time, and consistent treatment availability forms the foundation of disease management. The differential effects across disease compartments suggest that control measures may work through different mechanisms, with awareness campaigns likely reducing transmission by modifying behavior, sanitation measures probably reducing environmental contamination and exposure, and treatment directly reducing the infectious period and severity.

Fig. 6

illustrating optimal control strategies for a dysentery disease model. The top panel shows the temporal dynamics of three control measures: awareness campaigns ($u_1$), sanitation efforts ($u_2$), and treatment interventions ($u_3$). Subsequent panels demonstrate the comparative impact of these control strategies on various epidemiological compartments: (a) severely infected population ($I_s$), (b) exposed individuals ($E_s$), (c) total infected population, and (d) mildly infected cases ($I_m$), each comparing scenarios with and without control implementation. The bottom panel quantifies the percentage reduction in total infections achieved through the optimal control approach. Results are shown over a two-year period, highlighting how coordinated control efforts effectively reduce dysentery transmission and disease burden across all infected compartments. The findings emphasize the importance of integrated intervention strategies for controlling dysentery outbreaks.

Limitations and future research directions

While this model offers valuable insights into dysentery dynamics and control, it is important to acknowledge its limitations, which also present significant opportunities for future research.

• The model assumes a homogeneous population, whereas in reality, susceptibility, contact rates, and disease severity are highly age-dependent, with children under five being the most vulnerable group⁸. A logical and valuable extension would be to develop an age-structured model to provide more precise estimates of pediatric disease burden and to evaluate the impact of age-targeted interventions, such as vaccination. Furthermore, the model does not account for seasonality, a known driver of diarrheal disease transmission often linked to factors like rainy seasons. Incorporating a seasonally forced contact rate, $\beta (t)$, would significantly enhance the model’s ability to predict outbreak timing and optimize the scheduling of awareness and prevention campaigns.

• An additional limitation is the deterministic nature of the framework, which predicts average population behavior. For investigating disease extinction in low-prevalence settings or calculating the probability of major outbreaks, a stochastic counterpart to this model would be more appropriate. The model also makes simplifying assumptions regarding lasting immunity and awareness, presuming both are permanent after acquisition. Introducing waning rates for immunity and educated status ($S_e$) would add a layer of realism and facilitate the study of booster campaigns and the long-term sustainability of public health awareness programs.

• Another significant limitation is that the model parameters were estimated from a synthesis of published literature and were not calibrated or validated with real-time outbreak data from a specific region. Consequently, the quantitative predictions (e.g., specific prevalence rates or the exact timeline of an outbreak) are theoretical. The model’s primary strength lies in its qualitative findings—namely, the demonstrated synergy between awareness, hygiene, and treatment and the critical value of a combined strategy over isolated interventions. Future work will involve collaborating with health organizations to fit this model to historical outbreak data from endemic regions, which would significantly enhance its predictive power and practical utility for public health planning.

Conclusion

This study developed a novel mathematical model to analyze the transmission dynamics of dysentery, incorporating the critical roles of public awareness and disease severity—often overlooked in traditional frameworks. The model introduces a dual stratification: an educated susceptible compartment ($S_e$), whose infection risk is reduced through health knowledge, and a separation of infected individuals into mild ($I_m$) and severe ($I_s$) cases, reflecting their differing transmission potentials and healthcare needs.

The analysis confirms that the key to eradication is controlling the basic reproduction number, ${\mathcal {R}}_0$; the disease is eliminated if ${\mathcal {R}}_0 < 1$ but persists if ${\mathcal {R}}_0> 1$ as shown in Figures 4 and 5. A central finding is that treatment alone is insufficient to curb outbreaks. However, when combined with non-pharmaceutical interventions—specifically, awareness campaigns and sanitation improvements—a powerful synergistic effect occurs, leading to a multiplicative reduction in transmission as shown in Fig. 6.

The optimal control analysis provides a rigorous, quantitative framework for policymakers. It demonstrates that while awareness campaigns are the most cost-effective single intervention, offering the best return on investment, the combined strategy of awareness, sanitation, and treatment is unequivocally the most effective for achieving the greatest reduction in infection prevalence and total outbreaks averted.