ThoR: A Motion-Dependent Physics-Informed Deep Learning Framework with Constraint-Centric Theory of Functional Connections for Rainfall Nowcasting

Abstract

Accurate precipitation nowcasting is crucial for mitigating the impacts of extreme weather, especially as climate change increases their frequency and severity. Traditional methods, such as numerical weather prediction and radar extrapolation, face limitations in short-term and high-resolution forecasting. Recently, while deep learning approaches have advanced nowcasting by learning spatiotemporal patterns from radar data, they often suffer from blurry results due to uncertainty predictions and limited physical consistency. To deal with these challenges, we propose ThoR, a Motion-Dependent Physics-Informed Deep Learning Framework with Constraint-Centric Theory of Functional Connections for Rainfall Nowcasting. ThoR integrates attention-centric spatio-temporal modeling with explicit physical constraints derived from partial differential equations (PDEs) for forward simulation, which employs a cascaded-branch architecture that integrates an attention-driven generator with an unsupervised, lead-time-conditioned module for motion field extraction. Physical consistency is enforced by weighted embedding the advection-diffusion equation directly into the optimization objective, establishing a Theory of Functional Connections (TFC) framework tailored for precipitation nowcasting. Extensive experiments on real-world radar datasets demonstrate that ThoR consistently outperforms existing methods in deterministic metrics, particularly at longer lead times and during extreme weather events, highlighting the potential of physics-informed deep learning for operational nowcasting.

Introduction

Weather forecasting, the prediction of future atmospheric conditions such as precipitation, temperature, pressure, and wind, plays a crucial role in both science and society¹. In Vietnam, natural disasters in 2024 resulted in 514 fatalities and economic losses of about 88.748 trillion VND². As a result, accurate weather forecasts have far-reaching social and economic benefits, improving daily decision-making and contributing significantly to numerous sectors, such as agriculture, energy, transportation, and disaster prevention^3,4. Quantitative precipitation nowcasting (QPN) is considered to be one of the most challenging aspects of this field.

Precipitation nowcasting techniques primarily fall into two categories: (1) numerical weather prediction (NWP) and (2) radar echo extrapolation. NWP models simulate atmospheric dynamics based on physical laws; however, they often struggle to produce accurate short-term forecasts due to initialization errors and computational latency^5,6. In contrast, radar-based approaches, such as optical flow estimation and centroid tracking^7,8, offer higher temporal resolution but typically assume conserved reflectivity and smooth motion, assumptions that break down during rapidly evolving convective systems^9,10. Both paradigms exhibit notable limitations in capturing the localized and nonlinear characteristics of precipitation, thereby motivating the exploration of data-driven deep learning (DL) methodologies^11,12. Deep learning (DL) has shown remarkable capability in modeling the complex spatiotemporal patterns inherent in radar reflectivity sequences, eliminating the need for handcrafted heuristics. Recent advances in this domain can be broadly categorized into deterministic and probabilistic approaches, each addressing distinct aspects of precipitation nowcasting challenges.

Deterministic models, such as ConvLSTM¹¹, TrajGRU¹³, and the PredRNN family^12,14, utilize convolutional recurrent architectures to capture spatiotemporal dependencies. Innovations like hierarchical memory cells, attention mechanisms, and motion decomposition have notably enhanced their forecasting performance. However, these models often suffer from blurred predictions, especially at longer lead times. This degradation stems from their reliance on global pixel-wise loss functions, such as Mean Squared Error (MSE), which introduce the “double penalty” problem^15,16 and fail to preserve fine-grained, high-frequency details¹⁷ critical for accurate precipitation forecasts.

In addition to recurrent structures, convolutional neural networks (CNNs) have been employed for spatiotemporal prediction tasks. Architectures like U-Net variants^18,19,20 and direct regression models such as SimVP²¹ encode input sequences and decode future frames in parallel, reducing temporal error propagation. These models leverage multi-scale feature extraction and simple convolutions to maintain spatial resolution efficiently. Nevertheless, despite their structural advantages, CNN-based models continue to produce overly smoothed outputs due to their dependence on global pixel-wise losses, limiting their capacity to capture local uncertainties and sharp precipitation boundaries.

To address the limitations of deterministic frameworks, probabilistic models based on Generative Adversarial Networks (GANs) have been introduced. Models like DGMR²² employ ConvGRU-based generators with stochastic sampling, producing sharper and more realistic radar forecasts. However, adversarial models are not without challenges; issues like mode collapse, limited diversity in generated samples, and difficulties in capturing long-term dependencies persist, restricting their reliability in operational settings.

Recent research has sought to overcome these hurdles through hybrid methodologies that combine deterministic precision with probabilistic expressiveness. Transformer-augmented models, such as ConvLSTM-TransGAN²³ and SAC-LSTM²⁴, leverage self-attention mechanisms to enhance temporal coherence and mitigate error accumulation. Self-clustering techniques, exemplified by ClusterCast²⁵, promote output diversity by dynamically partitioning latent representations, reducing the risk of mode collapse. Furthermore, diffusion-based architectures like DiffCast²⁶ and CasCast²⁷ have emerged as a promising direction. These models decouple the forecasting task into deterministic coarse-scale predictions and stochastic fine-scale residual generation, enabling them to capture both global motion trends and localized uncertainties. By employing guided diffusion processes within a cascaded architecture, these approaches improve fine-grained realism, enhance extreme event prediction, and avoid adversarial training pitfalls.

While architectural innovations address part of the forecasting challenge, the design of objective functions remains equally critical. Conventional global losses inadequately penalize errors in high-intensity rainfall regions, which are infrequent yet meteorologically significant. To counter this, weighted loss formulations amplify penalties for severe events^13,22, while pooling-based losses prioritize large-scale precipitation structures, reducing sensitivity to noise²⁸. Motion-regularized losses enforce physically plausible spatiotemporal dynamics by integrating gradient-based smoothness constraints^29,30. Additionally, probabilistic learning frameworks have proposed differentiable approximations of classification metrics, striking a balance between accuracy across varying rainfall intensities³¹.

A persisting limitation in current DL-based nowcasting systems is their insufficient integration of physical knowledge. Many models act as black boxes, lacking physical interpretability and occasionally violating fundamental atmospheric principles, especially under extreme or out-of-distribution scenarios. To address this, recent studies have begun embedding physical constraints, such as mass conservation and advection dynamics, directly into model architectures and objective formulations^26,32,33.

Among emerging methodologies, the Extreme Theory of Functional Connections (TFC)^34,35 presents a mathematically rigorous framework for embedding physical laws into deep learning models. Unlike traditional physics-informed neural networks (PINNs), which incorporate physics via auxiliary loss terms that are prone to convergence trade-offs, TFC analytically constructs solution spaces that inherently satisfy the governing physical constraints. This approach enables models to maintain physical fidelity while optimizing for data-driven objectives, thus offering a principled pathway to enhance robustness and interpretability in precipitation forecasting applications.

Building on recent advances, we introduce ThoR, a novel physics-informed deep learning framework grounded in the TFC, where spatiotemporal modeling is integrated with explicit physical constraints for precipitation nowcasting. ThoR employs a cascaded-branch architecture, comprising an attention-centric state space generator that captures complex dependencies in both spatial and temporal dimensions, alongside a module that predicts paired advection motion fields to represent dynamic atmospheric flows. These motion fields are utilized in a hybrid manner—both embedded within the generator for precipitation map forecasting and incorporated into the optimization objective via the advection-diffusion equation, thereby reinforcing physical consistency and enhancing predictive accuracy. Through the direct embedding of domain knowledge into the learning process, a significant advancement in nowcasting capabilities is achieved, offering forecasts that are more reliable, interpretable, and physically grounded, particularly under highly dynamic and extreme weather conditions.

To sum up, the principal contributions of this work are as follows:

• We extend the Theory of Functional Connections (TFC) by incorporating the advection-diffusion equation and the associated physical constraints of the motion field directly into the optimization objectives of each component within our framework. This formulation, referred to as Soft TFC with constraint-centric design, enhances the interpretability of the model and improves predictive performance in solving multidimensional partial differential equations (PDEs) for precipitation nowcasting.

• We propose ThoR (A Physics-informed Theory of Functional Connection framework for Rainfall Nowcasting), a hybrid deep learning architecture that integrates attention-based spatiotemporal modeling with explicit physical constraints derived from partial differential equations (PDEs). ThoR facilitates accurate forward simulations of precipitation dynamics by capturing the inherent chaotic behavior of rainfall. It delivers high-quality forecasts across a broad spectrum of rainfall intensities, demonstrating particularly strong performance in predicting extreme precipitation events governed by advective and convective processes—phenomena that have traditionally presented significant modeling challenges.

Results

To rigorously assess the performance of ThoR, we conducted comprehensive empirical evaluations against five state-of-the-art baseline methods: PySTEPS⁸, representing traditional advection-based techniques; NowcastNet³⁶, which employs a physics-informed autoencoder-decoder ensemble; DiffCast²⁶, a deterministic diffusion-based forecasting model; and two representative data-driven spatiotemporal models, PredRNN¹⁴ and TrajGRU¹³.

Experiments were conducted on two geographically and climatologically distinct datasets, each consisting of crops in fixed-length sequences extracted from radar streams: the Multi-Radar Multi-Sensor (MRMS) system³⁷, and radar observations from the Nha Be Weather Radar Station in Ho Chi Minh City³⁸. Each dataset was partitioned into training and testing subsets using a standardized 80/20 split.

To ensure a fair and hardware-agnostic comparison, we reproduced all baseline models using their official open-source implementations and trained them from scratch under identical training and evaluation protocols. This unified experimental framework facilitated a comprehensive and regionally diverse assessment of ThoR’s generalization capabilities and predictive performance.

Problem description

We introduce ThoR, a physics-informed nowcasting framework grounded in conditional generative modeling for precipitation forecasting. The framework operates on an input sequence of observed precipitation fields, denoted as $R_{\text {in}} = \{{R_1, R_2, \cdots , R_t}\} \in \mathbb {R}^{t \times h \times w}$, where t represents the number of input time steps, and h and w correspond to the spatial dimensions (height and width) of each radar-derived precipitation map. The spatiotemporal predictive learning objective is to predict the most probable sequence of future rainfall fields $R_{\text {out}} = \{{R_{t+1}, R_{t+2}, \cdots , R_{t+n}}\} \in \mathbb {R}^{n \times h \times w}$, where n denotes the forecast horizon in time steps.

ThoR adopts a multiple time step forecasting generative formulation, predicting future frames sequentially. This means that ThoR learns the temporal dependencies and physics-based features from a hidden state in order to estimate n future steps given t input steps. The overall forecasting task is cast as a sequential probabilistic estimation:

$$\begin{aligned} P(R_{\text {out}} \mid R_{\text {in}}) = P(R_{t+1}, \cdots , R_{t+n} \mid R_1, \cdots , R_{t}). \end{aligned}$$

(1)

This autoregressive formulation enables the model to leverage the internal motion flow to dynamically refine its latent precipitation representation, rather than solely autoregressing over the precipitation fields themselves. By iteratively updating the motion flow at each step in a knowledge-informed manner, the model effectively captures temporally non-stationary atmospheric dynamics, which subsequently guide the generation of future rainfall fields.

ThoR consists of two main components: (1) an attention-driven spatiotemporal generative network G, parameterized by $\theta$, and (2) a deterministic motion estimation module $M_\phi$, parameterized by $\phi$, which infers large-scale advective motion fields from the observed precipitation sequence. The forecasting task is framed as a hybrid, physics-aware conditional generation problem, incorporating latent stochastic variables $\textbf{z}$ that encode both the extracted advective motion and the fine-grained residual deformations learned by the spatiotemporal encoder. The distribution over future precipitation is given by:

$$\begin{aligned} P(\hat{R}_{t+1:t+n} \mid R_{1:t}, \phi , \theta ) = \int P(\hat{R}_{t+1:t+n} \mid R_{1:t}, M_\phi (R_{1:t}), \textbf{z}; \theta ) \, P(\textbf{z})\, \textrm{d}\textbf{z}. \end{aligned}$$

(2)

In this paper, we train the generator neural networks parametrized by $\theta$ and motion extration network parametrized by $\phi$. Concretely, we use stochastic gradient descent to find a set of parameters $\theta ^*$ and $\phi ^*$ that maximizes the log-likelihood of producing the true target sequence $R_{\text {out}}$ given the input data $R_{\text {in}}$ for all training pairs $\{(R_{\text {in}}, R_{\text {out}})\}_{n=1}^{N}$:

$$\begin{aligned} \theta ^*, \phi ^* = \arg \max _{\theta , \phi } \sum _{n=1}^{N} \log \int P(R^{(n)}_{t+1:t+n} \mid R^{(n)}_{1:t}, M_\phi (R^{(n)}_{1:t}), \textbf{z}; \theta ) \, P(\textbf{z}) \, \textrm{d}\textbf{z}. \end{aligned}$$

(3)

By marginalizing over the latent space $\textbf{z}$, the model ensures that the resulting forecasts are both spatially coherent and probabilistically well-calibrated. The training objective integrates physically grounded constraints with conventional data-driven loss functions, promoting dynamically consistent and meteorologically realistic predictions. This formulation enables ThoR to deliver high-fidelity, probabilistic nowcasts, making it well suited for operational deployment in early warning systems and the real-time monitoring of extreme weather events.

Dataset

The MRMS dataset

The dataset employed in this study is derived from NOAA’s Multi-Radar Multi-Sensor (MRMS) system³⁷, which integrates radar, satellite, surface, upper-air, numerical weather prediction, and climatological data into high-resolution, temporally consistent mosaics. Designed for both operational and research use, MRMS provides over 100 meteorological products widely adopted by agencies such as the NWS, FEMA, and FAA for precipitation estimation and severe weather forecasting (Fig. 1).

Fig. 1

Precipitation maps of three selected regions over the continental United States. Each inset shows a localized precipitation distribution (in mm/h) with top-left corner at coordinates (29.3$^\circ$N, -109.3$^\circ$E), (33.85$^\circ$N, -106.60$^\circ$E), and (38.1$^\circ$N, -81.4$^\circ$E). The color bar on the right indicates precipitation intensity.

We specifically utilize the radar-derived Precipitation Rate field across the continental U.S. from 2016 to 2022 to support radar-based rainfall nowcasting. To improve computational efficiency and focus on high-impact events, we follow the importance sampling protocol from DGMR²², selecting representative $256 \times 256$ pixel subregions centered on high-intensity rainfall at predefined offsets. Temporal subsampling at 10-minute intervals balances resolution with data volume. Precipitation values are clipped to the [0, 76] mm/h range to match radar sensor thresholds and suppress noise.

Each training sample consists of a sequence of 6 past frames (representing the previous hour) and 12 future frames (predicting the next two hours), created using a sliding window. This aligns with standard sequence-to-sequence modeling frameworks for spatiotemporal forecasting.

The Nha Be dataset

This study utilizes a high-resolution radar reflectivity dataset collected by the Nha Be Weather Radar Station, located in Ho Chi Minh City, Vietnam. The station employs Constant Altitude Plan Position Indicator (CAPPI) scans, which provide two-dimensional reflectivity fields at a fixed altitude. Each volume scan comprises a full 360$^\circ$ sweep across multiple elevation angles and is completed approximately every 12 minutes³⁸. The reflectivity data are gridded at a spatial resolution of 500 m, spanning $2305 \times 2881$ grid points (longitude $\times$ latitude), covering the geographical region from $103.960^\circ$E to $109.500^\circ$E and $7.950^\circ$N to $13.360^\circ$N. The temporal resolution is 10 minutes.

To facilitate spatiotemporal analysis, the raw polar radar measurements were interpolated onto a three-dimensional Cartesian grid. Reflectivity fields at an altitude of 2 km were subsequently extracted and used for modeling. Radar reflectivity (Z) is typically expressed on a logarithmic scale as $\textrm{dBZ} = 10 \log _{10}(Z)$. To estimate surface rainfall rates (R, in mm/h), reflectivity values were converted using the empirical reflectivity-rainfall (Z–R) relationship, $Z = a R^b$, where a and b are empirically derived coefficients. In this study, we adopt the canonical values $a = 200$ and $b = 1.6$, which are widely used for convective precipitation regimes. Rearranging yields the rainfall rate as $R = (Z/a)^{1/b}$.

The dataset spans from 1 January to 31 December 2023. For model development, we constructed input-target sequences using the same sliding-window approach: each training sample comprises six historical frames (capturing one hour of past data) used to forecast the subsequent twelve frames (representing a two-hour future horizon). The fine spatial and temporal resolution of this dataset enables detailed modeling and analysis of convective precipitation dynamics across a densely populated tropical environment (Table 1).

Table 1 Specifications of the MRMS and Nha Be Doppler radar datasets.

Experimental setup

All experiments were conducted in a controlled computational environment hosted on Kaggle’s Jupyter Notebook platform. The software stack comprised Python (v3.10.4) and PyTorch (v2.6.0), running on an Ubuntu 20.04 operating system. Hardware resources included an Intel Xeon CPU (2 cores, 4 threads) for general computation, with accelerated deep learning workloads offloaded to an NVIDIA Tesla P100 GPU, leveraging CUDA v12.4 for optimized parallel processing.

The model training regimen was standardized across all experiments. Networks were trained for 100 epochs using the AdamW optimizer, with an initial learning rate of 0.01. To facilitate adaptive convergence, a ReduceLROnPlateau learning rate scheduler was employed. This scheduler continuously monitored the validation loss and dynamically reduced the learning rate by a factor of 0.1 if stagnation was detected over four consecutive epochs (patience = 4). A minimum learning rate threshold of $10^{-6}$ was enforced to maintain numerical precision and prevent premature convergence stalling.

The discriminator architecture was designed following the PatchGAN framework³⁹, which has been empirically validated for high-resolution structured predictions. Specifically, the network comprises five sequential convolutional layers with progressively increasing channel capacities, scaling from 64 to 512 filters. The output is synthesized through a $1 \times 1$ convolution, followed by an adaptive average pooling operation, and finalized with a sigmoid activation to yield a probability map indicative of realness at the patch level. Non-linear activations are applied via LeakyReLU across all hidden layers, while Batch Normalization is utilized for all intermediate layers except the first and final, in alignment with established best practices to stabilize training dynamics without introducing boundary artifacts.

Input to the discriminator is formed by concatenating the conditional context (i.e., the input radar frames) with either the ground truth or the synthetically generated frame, ensuring that the network is conditioned on relevant temporal context during adversarial learning. The discriminator is optimized using the AdamW algorithm, configured with hyperparameters $\beta _1 = 0.5$ and $\beta _2 = 0.999$, and a fixed learning rate of 0.01. To mitigate discriminator overconfidence and foster smoother gradient propagation, we employ a smoothed binary cross-entropy loss with a label smoothing factor of 0.1, a regularization strategy known to enhance GAN stability and generalization.

The map of the United States was generated using the open-source GeoPandas library⁴⁰ with county-level boundaries extracted from the Natural Earth dataset⁴¹, focusing on the mainland U.S. The regional map of Nha Be (Vietnam) was created using the Cartopy library⁴² and public domain Natural Earth coastline data. Radar reflectivity fields, with coordinates extracted from raw files and georeferenced using the Plate Carrée projection, were subsequently overlaid on the Nha Be base map to provide spatial context.

Evaluation metrics

The performance of the proposed precipitation nowcasting model is assessed using three complementary metrics: Mean Squared Error (MSE), Structural Similarity Index Measure (SSIM), and Critical Success Index (CSI). To evaluate sensitivity across rainfall intensities, CSI is computed at three thresholds, 1 mm/h, 8 mm/h and 16 mm/h denoted as CSI(1), CSI(8) and CSI(16).

MSE quantifies the average of the squared differences between predicted and observed values, offering a global measure of numerical accuracy. Unlike RMSE, MSE does not take the square root of the error term, making it more sensitive to larger errors and better suited for optimization in many learning algorithms.

SSIM compares predicted and observed precipitation fields based on local luminance, contrast, and structural patterns. Ranging from $-1$ to 1, higher SSIM values indicate better preservation of spatial structure, which is crucial for applications involving radar reflectivity fields.

CSI, also known as the threat score, quantifies the overlap between predicted and observed binary precipitation events. It is defined as the ratio of true positives to the sum of true positives, false positives, and false negatives. CSI is particularly valuable for imbalanced datasets and rare event detection. The use of multi-thresholds enables evaluation of both light and heavy rainfall events.

Together, MSE, SSIM, and thresholded CSI provide a comprehensive evaluation framework, capturing pointwise accuracy, spatial consistency, and event-level detection performance essential for operational nowcasting.

Experimental results

Quantitative results

As summarized in Table 2, the proposed ThoR model demonstrates consistently favorable results compared to established baseline methods—including PySTEPS, NowcastNet, DiffCast, PredRNN, and TrajGRU—across all evaluation metrics on both the MRMS and Nha Be datasets, evaluated under a unified experimental protocol. When averaged across all evaluated regions, ThoR achieves a Mean Squared Error (MSE) of 41.46, representing a notable reduction compared to NowcastNet (42.31), DiffCast (45.61), TrajGRU (89.82), PredRNN (54.73), and PySTEPS (99.84). This corresponds to a 2.01% improvement in MSE relative to NowcastNet, the strongest-performing baseline, highlighting ThoR’s capability to deliver highly accurate pixel-wise precipitation intensity forecasts.

Table 2 Quantitative comparison of forecasting performance across different methods on the MRMS and Nha Be datasets.

In terms of structural fidelity, ThoR attains an average Structural Similarity Index (SSIM) of 0.91, surpassing PySTEPS (0.785), TrajGRU (0.8125), PredRNN (0.8625) and DiffCast (0.885), while being marginally lower than NowcastNet (0.9025). This indicates ThoR’s robust ability to preserve fine-grained spatial patterns within forecasted rainfall fields, an essential requirement for accurately representing storm morphology.

Regarding precipitation detection, ThoR demonstrates competitive performance across multiple Critical Success Index (CSI) thresholds. Averaged over all regions, ThoR achieves a CSI(1) score of 0.728, outperforming PySTEPS (0.388), TrajGRU (0.454), PredRNN (0.722), and DiffCast (0.753), and closely approximating NowcastNet (0.784). More importantly, ThoR exhibits superior performance in detecting moderate to heavy rainfall events, attaining an average CSI(8) of 0.599, which exceeds the corresponding scores of NowcastNet (0.567), DiffCast (0.578), PredRNN (0.576), TrajGRU (0.2665), and PySTEPS (0.17275).

Notably, ThoR demonstrates a significant advantage in forecasting strong-echo precipitation events, as evidenced by the CSI(16) metric. Across all evaluated regions, ThoR achieves the highest average CSI(16) score of 0.326, surpassing DiffCast (0.328), NowcastNet (0.306), PredRNN (0.304), TrajGRU (0.09375), and PySTEPS (0.100). This indicates ThoR’s enhanced capability in identifying high-intensity, localized precipitation cells, which are critical for flood risk assessment and disaster early warning systems.

Consistent performance trends are also observed on the Nha Be dataset, which characterizes a tropical convective storm regime typical of Southern Vietnam. On this dataset, ThoR achieves the lowest MSE of 49.23 and records a CSI(16) of 0.461, outperforming all baseline methods. While NowcastNet achieves higher SSIM (0.96) and CSI(1) (0.811) scores, ThoR presents a more balanced performance profile, delivering competitive accuracy across MSE, SSIM, and all CSI thresholds. Particularly, ThoR’s superior performance at higher CSI thresholds (CSI(8) and CSI(16)) underscores its robustness in forecasting intense rainfall events, which is essential for effective flood prediction and real-time situational awareness in urban environments such as Ho Chi Minh City.

Fig. 2

Performance changes against different lead time in terms of CSI and SSIM.

To examine how predictive performance evolves with increasing lead time, we present the average Critical Success Index (CSI) and Structural Similarity Index (SSIM) curves in Fig. 2. As expected, performance metrics for all methods degrade as lead time extends, reflecting the growing uncertainty inherent in longer-term forecasts. Nevertheless, our framework consistently maintain superior performance compared to those without it, thereby underscoring the robustness and effectiveness of the proposed approach.

Overall, the proposed ThoR framework exhibits balanced performance across multiple evaluation criteria. The concurrent achievement of low MSE, high SSIM, and strong CSI across multiple thresholds reflects its comprehensive modeling capacity. The improvements in CSI at higher thresholds, particularly CSI(8) and CSI(16), underscore ThoR’s potential for integration into early warning systems where the reliable detection of severe rainfall is paramount. These findings not only demonstrate statistical significance but also practical relevance, highlighting ThoR’s applicability in both continental and tropical forecasting scenarios.

Qualitative results

We conduct a qualitative assessment to evaluate the ability of the models to forecast extreme precipitation events. As illustrated in Fig. 3, ThoR demonstrates greater accuracy in predicting high rainfall intensities. Moreover, ThoR produces sharper forecasts with spectral characteristics that more closely align with radar observations at a 1-hour lead time, while also exhibiting reduced smoothing effects at 2-hour lead times. These findings highlight ThoR’s capability to capture both mesoscale and convective-scale precipitation structures during extreme weather conditions.

Fig. 3

A single prediction at T+10min, T+50min and T+2h lead times with ThoR for three different proposed location using MRMS dataset.

Among the first three case studies, Region 3 features heavy-intensity radar echoes exceeding 12 mm/h, while Regions 1 and 2 are characterized by low-intensity rainfall events. Collectively, these cases encompass both isolated and consecutive precipitation patterns across three geographically distinct regions in the United States, as previously detailed. The corresponding figures present forecast results initiated from the reference time T, with lead times expressed in minutes (e.g., $T + 10\,\textrm{min}$ denotes a 10-minute forecast horizon). For each case, the top row displays the input radar observations, the middle row shows the ground truth, and the bottom row illustrates predictions produced by ThoR, enabling direct visual assessment of forecast accuracy.

In Region 1, the observed precipitation system undergoes gradual dissipation, with weak echoes decaying steadily over time. The proposed model successfully reproduces this weakening trend, demonstrating skill in maintaining both the spatial distribution and temporal evolution of the system throughout the 2-hour forecast horizon. In Region 2, precipitation remains more localized and is characterized by intermittent growth-decay cycles. The forecasts capture the general positioning and intensity of convective cells, although fine-scale variability is somewhat smoothed relative to observations. In Region 3, the precipitation system exhibits pronounced spatiotemporal evolution. Within the 0–2 hour forecast window, low-intensity echo regions progressively contract, whereas areas of heavy precipitation ($>30\,\mathrm {mm/h}$) exhibit modest expansion. Furthermore, strong echo cores ($>40\,\mathrm {mm/h}$) display evidence of intensity amplification while remaining quasi-stationary. This differential behavior between low- and high-intensity echoes reflects the inherent nonlinear interactions between convective updrafts and precipitation particle growth processes within mesoscale convective systems, thereby underscoring ThoR’s capacity to approximate the forward dynamics of partial differential equations in atmospheric modeling.

ThoR also demonstrates robust generalization under tropical weather conditions, as exemplified by a case study from Nha Be, Vietnam. Figure 4 presents forecast results based on data from the Nha Be Radar Station, where ThoR successfully captures the overall morphology of the precipitation field and characterizes its temporal evolution. The framework shows particular strength in modeling the merging processes of precipitation bands, accurately predicting both the intensity and spatial redistribution of precipitation cores.

Fig. 4

A single prediction at T+10min, T+50min and T+2h lead times with ThoR at using Nha Be Dataset.

Figure 5 presents a comparative analysis of ThoR, DiffCast, and NowcastNet in forecasting heavy-intensity precipitation events in Region 3. ThoR consistently excels in preserving the spatial structure and intensity gradients of convective cores, delivering coherent forecasts even at 2-hour lead times. In contrast, DiffCast accurately captures echo positions at shorter horizons but progressively suffers from spatial diffusion and intensity attenuation as lead times increase. NowcastNet, while capable of outlining the broad precipitation extent, tends to over-smooth high-intensity regions, resulting in a systematic underestimation of extreme echoes. Notably, ThoR mitigates common displacement errors observed in existing methods, while retaining sharper spectral characteristics that closely match radar observations. Although ThoR slightly underestimates peak echo intensities, it accurately delineates the spatial footprint and mesoscale organization of severe precipitation, underscoring its enhanced capability for convective-scale nowcasting in extreme weather scenarios.

Fig. 5

Case studies of heavy-intensity precipitation events in MRMS Region 3 (38.1°N, 81.4°E). A single prediction at T+10min, T+50min and T+2h lead times with different models.

To strengthen the qualitative evaluation, we incorporated comparative zoomed-in views of strong echo cores between our framework and state-of-the-art models (NowCastNet and DiffCast), as shown in Fig. 6. These magnified panels provide a clearer inspection of localized precipitation dynamics, particularly within high-intensity regions that are critical for severe weather nowcasting. The results indicate that our model more effectively captures fine-scale reflectivity gradients and maintains the spatial continuity of convective structures, even in complex storm environments. By preserving coherence at the storm-core level while remaining consistent with the broader precipitation field, the proposed ThoR framework demonstrates superior capability in reproducing meteorologically relevant features across multiple spatial scales.

Fig. 6

Comparative zoomed-in views of strong echo cores across different models. Each panel highlights localized high-intensity precipitation regions for clearer assessment of fine-scale dynamics. The proposed ThoR framework captures both reflectivity gradients and spatial continuity more effectively than NowCastNet and DiffCast, underscoring its robustness in representing convective storm structures.

ThoR effectively captures the spatiotemporal evolution of precipitation systems. Although its depiction of precipitation morphology is moderately smoothed, the model accurately reproduces the spatial distribution and temporal progression of observed rainfall fields. It shows strong skill in forecasting regions of heavy precipitation ($>40\,\mathrm {mm/h}$), with predicted patterns closely matching radar observations. However, ThoR tends to systematically underestimate the intensity of extreme precipitation cores ($>50\,\mathrm {mm/h}$) by approximately 4–10 mm/h, despite correctly identifying their locations. This underestimation likely results from the smoothing of local maxima, a consequence of regularization effects inherent to the deep learning architecture. Nonetheless, given the inherent complexity of cyclone propagation and the rarity of extreme precipitation events, further refinement across models is needed to improve the accuracy of rainfall structure forecasting and extreme echo intensity prediction.

Ablation study

Model selection

Figure 7 illustrates the architecture and performance of the proposed ThoR framework, which integrates two complementary cascading modules: a motion extraction network, denoted as $M_{\phi }$, and a generator network designed to jointly model temporal and spatial dependencies. These modules operate within a generative adversarial network (GAN) paradigm, where a discriminator D enforces distributional alignment between predicted and ground-truth precipitation patterns, facilitating the generation of high-fidelity next-hour precipitation forecasts.

To quantify the contribution of each architectural component, we conduct an ablation study comparing the training MSE between three baseline configurations. The first configuration, termed Generator Only, involves a generator that implicitly infers motion information from past observations without explicit motion field supervision, akin to the TrajGRU architecture¹³. The second configuration, referred to as Motion-dependent Generator, incorporates the motion field derived from the motion extraction network into the generator, yet omits the adversarial learning component. The third configuration corresponds to the complete ThoR framework, which synergistically integrates the motion extraction network, generator, and adversarial discriminator.

The comparative results, depicted in Fig. 7, indicate that the Motion-dependent Generator achieves notable improvements over the Generator Only baseline, highlighting the pivotal role of explicit motion extraction in enhancing forecasting accuracy. This observation underscores the effectiveness of disentangling motion estimation from precipitation intensity synthesis, allowing the generator to leverage structured motion cues rather than relying solely on implicit temporal representations. Furthermore, the full ThoR framework yields the highest performance, evidencing the complementary benefits of adversarial learning in refining spatial realism and suppressing artifacts in predicted precipitation fields.

Furthermore, integrating these components into a GAN-based architecture yields a substantial reduction in nowcasting error, highlighting the critical role of adversarial learning in refining the generated precipitation maps.

Fig. 7

Ablation studies on backbone selection.

The full ThoR framework achieves the best performance across all configurations by effectively combining motion-based guidance and adversarial supervision. This demonstrates the complementary advantages of explicit motion modeling and generative learning, reinforcing the importance of semi-supervised strategies in spatiotemporal forecasting. Our findings confirm that incorporating physically meaningful motion fields and adversarial objectives can substantially improve predictive accuracy in precipitation nowcasting.

Objective combination

Table 3 presents an ablation study evaluating the contributions of various loss components in our framework. Specifically, we analyze the effect of the traditional neural network data-driven optimization loss ($\mathscr {L}_\text {NN}$), the physics-informed loss incorporating advection-diffusion constraints ($\mathscr {L}_{\text {physics}}$), the motion consistency loss with Horn-Schunck regularization ($\mathscr {L}_{\text {velocity}}$), and an adversarial learning loss ($\mathscr {L}_{\text {adv}}$).

Using only $\mathscr {L}_\text {NN}$ yields baseline Critical Success Index (CSI) scores of 0.614 at the 1 mm/h threshold and 0.503 at 8 mm/h. Introducing the physics constraint ($\mathscr {L}_{\text {physics}}$) significantly improves CSI(1) to 0.655, whereas incorporating only the motion loss ($\mathscr {L}_{\text {velocity}}$) results in a modest increase to 0.621, suggesting that global physics priors contribute more substantially to dynamic consistency than local motion smoothness.

Combining $\mathscr {L}_\text {NN}$ with both $\mathscr {L}_{\text {physics}}$ and $\mathscr {L}_{\text {velocity}}$ leads to further improvements, achieving 0.713 at 1 mm/h and 0.572 at 8 mm/h. This indicates that global and local physical constraints provide complementary guidance during training.

Finally, the addition of adversarial learning via $\mathscr {L}_{\text {adv}}$ leads to the highest performance, with CSI scores of 0.796 (1 mm/h) and 0.630 (8 mm/h), demonstrating the effectiveness of GAN-based training in enhancing realism and fidelity in precipitation forecasts. Similar trends are observed across higher rainfall thresholds, including CSI(16), underscoring the robustness of the proposed objective design.

Table 3 Ablation studies on Objective Combination.

Figure 8 demonstrates the qualitative impact of progressively integrating different loss functions on forecast performance, corresponding to the ablation cases outlined in Table 3. Training with the neural network loss alone (Case 1) results in overly smoothed forecasts, failing to capture the sharp gradients and localized intensities characteristic of convective cores. Adding the physics-informed constraint (Case 2) enhances the mesoscale structural alignment, though fine-scale details remain underrepresented. The motion consistency loss (Case 3) improves temporal smoothness but does not sufficiently restore spatial precision. Introducing adversarial learning (Case 4) sharpens texture patterns and mitigates over-smoothing, yet certain artifacts, such as misplaced echo regions, persist. The combination of physics and velocity constraints (Case 5) yields forecasts with improved spatial organization and dynamic coherence, bringing predicted structures closer to observed morphologies. Full integration of all loss components (Case 6) achieves the most faithful reproduction of convective-scale features, accurately capturing both intensity peaks and the spatial coherence of strong echo regions. These results underscore the importance of jointly enforcing physical consistency and enhancing generative realism to effectively model the complex dynamics of extreme precipitation events.

Fig. 8

Qualitative comparison of precipitation forecasts across different cases of objective combinations Table 3, using a precipitation event in Region 3 of the MRMS dataset.

Overall, these results highlight the critical role of physics-informed and adversarial losses in improving both accuracy and physical consistency, underscoring the necessity of integrating traditional optimization with domain-specific constraints for robust precipitation nowcasting.

Motion field extraction

Capturing spatiotemporal dynamics is fundamental to accurate precipitation forecasting. Within our framework, the motion field extraction network plays a pivotal role by estimating the displacement of precipitation patterns between successive time frames. As described in Section Unsupervised PINNs Learning for Motion Field Extraction and visualized in Fig. 9, the extracted motion fields exhibit coherent flow structures that closely align with underlying meteorological phenomena, providing essential motion cues to the predictive model.

Fig. 9

Visualization of motion fields extracted by the proposed method. The first row shows the input, the second row presents the predicted motion field at time step T generated by our neural network, and the third row illustrates the subsequent motion field update using Burgers’ Equation. The results demonstrate the model’s ability to capture both large-scale displacement patterns and fine-grained boundary dynamics across diverse precipitation events. Notably, even under sparse precipitation conditions, the extracted fields preserve structural coherence, highlighting the robustness of the learned motion representation.

At time step T, the initial motion field is produced by our physics-informed U-Net, while future time steps (e.g., $T+50$ minutes, $T+2$ hours) are recursively updated via a discretized form of Burgers’ Equation. This integration ensures a physically consistent temporal evolution, allowing the model to simulate realistic precipitation movement without sacrificing spatial fidelity. The motion fields not only capture displacement vectors but also implicitly encode intensity variations, guiding the generative network towards more accurate precipitation evolution.

Ablation studies (Fig. 7) further validate the impact of motion field incorporation. Removing explicit motion guidance leads to noticeable degradation in forecast accuracy, especially for longer lead times. This underscores the importance of structured motion representations in modeling complex atmospheric dynamics, enabling the framework to generate reliable forecasts even under limited observational data.

Methods

Constraint-centric soft TFC for physically consistent precipitation forecasting

Parametric differential equations (DEs) are essential for modeling dynamical systems in fields such as fluid mechanics, meteorology, and finance³⁴. In precipitation nowcasting, deterministic models discretize the atmosphere into spatial grids, evolving physical variables (e.g., moisture, temperature, wind) via PDEs derived from conservation laws. Numerical Weather Prediction (NWP) systems follow this framework but struggle with fine-scale uncertainties due to sensitivity to initial conditions and the chaotic nature of small-scale convection. To overcome these limitations, we propose the Theory of Functional Connections (TFC) as an analytical framework that constructs functional interpolants satisfying PDE constraints, enabling efficient approximation of solutions in high-dimensional, nonlinear spatio-temporal domains.

Our proposed framework integrates rigorous physical laws with deep neural approximators, effectively bridging classical forward modeling via partial differential equations (PDEs) with data-driven learning techniques. By embedding the governing equations of fluid dynamics as hard constraints—both within the model architecture and in the loss formulation—we ensure strict adherence to the intrinsic physical structure of atmospheric motion. This hybrid paradigm enhances predictive fidelity while improving physical interpretability and generalization capacity.

Let the precipitation field be denoted by $R(t, \textbf{x})$, where $t \ge 0$ represents time and $\textbf{x} \in \mathbb {R}^{h \times w}$ denotes spatial coordinates. We aim to approximate a latent solution $f(t, \textbf{x})$ that governs the evolution of R through a parametric partial differential equation (PDE), expressed as:

$$\begin{aligned} \gamma \frac{\partial f}{\partial t} + \mathscr {N}[f; \lambda ] + \varepsilon - \mathscr {U} = 0, \end{aligned}$$

(4)

where $\gamma$ and $\lambda$ are parameters governing the parametric DE system, $\mathscr {N}[\cdot ;\lambda ]$ is a nonlinear differential operator encoding the physical dynamics (e.g., advection and diffusion processes) and parameterized by $\lambda$, $\mathscr {U}$ represents known external forcings, and $\varepsilon$ accounts for modeling uncertainties and observational noise.

Equation (4) provides a unified framework to address both forward simulations, where $\gamma$ and $\lambda$ are given, and inverse problems, where these parameters are inferred from data. In either case, the PDE formulation ensures that the predicted precipitation fields adhere to fundamental physical principles.

According to³⁵, the first step in our physics-informed framework is to approximate the latent solution f, for which we employ a constrained expression (CE) that inherently satisfies the initial and boundary conditions. Specifically, f is formulated as:

$$\begin{aligned} f(R; \varvec{\Theta }) = f_{\text {CE}}(R, g(R); \varvec{\Theta }) = A(R; \varvec{\Theta }) + \mathscr {P}_{\text {null}}[g(R)], \end{aligned}$$

(5)

where $\varvec{\Theta } = [\gamma , \lambda ]^T$ denotes the collection of system parameters. The term $A(R; \varvec{\Theta })$ is analytically constructed to satisfy the known initial precipitation state, while $\mathscr {P}_{\text {null}}$ projects the free-function g(R) onto the space of functions that respect the imposed constraints. The free-function g(R) is approximated by a deep neural network designed to capture residual dynamics not explicitly represented by A.

Fig. 10

Architecture of the Constraint-Centric soft TFC framework, integrating PDE dynamics into a deep learning pipeline for precipitation forecasting.

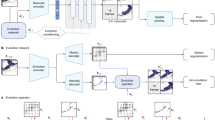
The overall model architecture, illustrated in Fig. 10, consists of two core components. First, a motion estimation network parameterized by $\phi$ extracts latent velocity fields $\textbf{V} = (u, v)$ from historical precipitation observations. Second, a generator network parameterized by $\theta$ synthesizes future precipitation fields, while enforcing compliance with the governing PDE dynamics such as advection-diffusion and Burgers’ equations.

Under this framework, the free-function g(R) is expressed as:

$$\begin{aligned} g(R) = G(R_{1:t}, M_{\phi }(R_{1:t}); \theta ) = G(R_{1:t}, \textbf{V}; \theta ), \end{aligned}$$

(6)

where $M_{\phi }$ denotes the motion-extraction module that encodes the internal dynamical flow $\textbf{V}$, and G is the neural network generator responsible for synthesizing the precipitation field. This construction allows g(R) to incorporate both the historical precipitation sequence $R_{1:t}$ and its corresponding motion representation, thereby enabling the model to capture spatiotemporal dependencies beyond what is directly observable in $R_{1:t}$ alone.

The latent solution f is then reconstructed through a constrained functional composition, denoted by $f_{\textrm{CE}}(\cdot )$, which guarantees that the learned representation adheres to the prescribed initial and boundary conditions. Importantly, both the initial rainfall state and the choice of activation functions are specified a priori, and are therefore regarded as known quantities. Under this setting, the only unknowns to be learned from data are the trainable output weights $\theta$ and $\phi$, which correspond to the generator and the motion-extraction module, respectively. Hence we can write,

$$\begin{aligned} f(t, R) = f_{\text {CE}}(R, g(R); \varvec{\Theta }) = f_{\text {CE}}(R, \theta , \phi ; \varvec{\Theta }). \end{aligned}$$

(7)

This approach embeds physical constraints directly into the neural architecture, enabling the model to generate predictions that are both data-consistent and physically plausible. By incorporating domain-specific PDEs into the model design, the network is encouraged to respect the inherent physical laws governing precipitation dynamics, effectively bridging the gap between data-driven learning and forward modeling.

As outlined in the preceding discussion, this study focuses exclusively on the class of exact problems in precipitation nowcasting, i.e., problems in which the governing parameters $\varvec{\Theta }$ are assumed to be known within a specified level of accuracy through physics-informed formulations, and the model error is considered negligible. Under these assumptions, the task reduces to computing the latent solution f, which is approximated through the constrained expression $f_{\textrm{CE}}$ introduced above. In this setting, the differential equation in Eq. (4) simplifies to an optimization problem of the form

$$\begin{aligned} \min _{\theta , \phi } \; \mathscr {J} \;=\; \mathscr {L}\!\left( R, f_{\textrm{CE}}(R, \theta , \phi ; \varvec{\Theta }) \right) , \end{aligned}$$

(8)

where $\theta$ and $\phi$ denote the trainable parameters, and $\mathscr {L}(\cdot )$ represents the physics-informed loss functional. Explicitly, the loss is defined as

$$\begin{aligned} \mathscr {L}\!\left( R, f_{\textrm{CE}}(R, \theta , \phi ; \varvec{\Theta }) \right) = \gamma \, f_{\textrm{CE},t} + \mathscr {N}[f_{\textrm{CE}}; \lambda ] - \mathscr {U}, \end{aligned}$$

(9)

Thus, while the nonlinear operator, external forcings, and stochastic noise terms are not explicitly propagated into the optimization stage, they remain inherently represented within the physics-informed loss functional under the stated assumptions. On this basis, the learning process is guided to remain consistent with both observational evidence and the governing physical laws. To achieve this, the ThoR framework defines its total optimization objective as a composite loss, which integrates data fidelity, physical constraint enforcement, and motion coherence into a unified learning signal. Formally, the total loss is expressed as:

$$\begin{aligned} \mathscr {L}(\hat{R}, R; V) = \lambda _{NN}\mathscr {L}_{NN}(R, \hat{R}) + \lambda _{PC}\mathscr {L}_{PC}(\hat{R}, V) + \lambda _{MC}\mathscr {L}_{MC}(V), \end{aligned}$$

(10)

Inspired by the Physics-Informed Neural Networks (PINNs) paradigm⁴³, we formulate a composite loss where the weights $\lambda _{NN}$, $\lambda _{PC}$, and $\lambda _{MC}$ balance the scales of data-driven and physics-based terms, ensuring fair optimization. The term $\mathscr {L}_{NN}(R, \hat{R})$ represents a data fidelity loss, typically the mean absolute error (MAE) between the predicted precipitation field $\hat{R}$ and the observed ground truth R, optimized via standard backpropagation.

The physics-consistency loss $\mathscr {L}_{PC}(\hat{R}, V)$ enforces adherence to the advection-diffusion equation by penalizing residuals computed from $\hat{R}$ and the estimated motion fields V, ensuring physically plausible forecasts. Additionally, $\mathscr {L}_{MC}(V)$ regularizes the motion fields by incorporating priors from Burgers’ equation⁴⁴ and Horn-Schunck smoothness constraints⁴⁵, promoting spatial coherence and dynamic consistency within the predicted flow fields.

This approach represents a mathematically rigorous and physically interpretable instance of soft TFC for precipitation nowcasting, wherein deep neural networks are not merely fitted to data but structured by physical theory. The result is a coherent framework for high-resolution precipitation nowcasting—one that is provably constraint-satisfying, empirically robust, and theoretically grounded.

Unsupervised PINNs learning for motion field extraction

Numerous methodologies have been developed to estimate the motion of objects or surfaces from sequences of temporally ordered images. In the context of weather radar data, optical flow techniques are widely employed to derive a dense flow field that represents the apparent motion of pixels between two consecutive radar frames captured at times t and $t + \Delta t$. When applied to precipitation modeling, the optical flow estimation relies on the brightness constancy assumption, which posits that the intensity of a moving pixel remains invariant over time. This principle forms the foundation of the optical flow constraint equation, which, when interpreted through the lens of fluid dynamics and mass conservation, can be generalized as a form of the continuity equation:

$$\begin{aligned} \frac{\partial R}{\partial t} + (\textbf{V} \cdot \nabla ) R = s. \end{aligned}$$

(11)

In this formulation, R denotes the precipitation field, $\textbf{V}$ represents the motion vector field, and s corresponds to the residual source/sink term, while $\nabla$ indicates the spatial gradient operator. The advection term $(\textbf{V} \cdot \nabla ) R$ captures the flux of precipitation patterns transported by the flow, thereby quantifying the mass leaving the system through advection. This term serves as a first-order approximation of the precipitation difference before and after the advection operation, whereas the residual term s accounts for local intensity changes not explained by pure translation. Consequently, the continuity equation imposes a physical constraint that enhances the fidelity of precipitation motion field estimations derived from radar observations.

Our objective is to accurately predict the underlying flow field from sequences of precipitation observations using a data-driven, physics-informed neural network framework. The first component of our framework estimates motion fields from sequences of precipitation observations using a physics-informed, unsupervised neural network. We employ a Conditioned discretised U-Net architecture for Operator Learning, which learns a mapping from precipitation sequences $R_{1:t}$ to the corresponding velocity field at time t, denoted by $\textbf{V}_t = (u_t, v_t)$. Here, $u_t$ and $v_t$ represent the horizontal and vertical velocity components, respectively, as illustrated in Figure 11.

Fig. 11

The architecture of the conditioned U-Net for motion field estimation follows an encoder-decoder design augmented with skip connections. This module is jointly trained alongside the precipitation map generator, while also benefiting from an auxiliary unsupervised learning objective that enforces physics-based constraints on the estimated motion fields. By leveraging these implicit physical priors, the network eliminates the need for explicit ground-truth motion annotations during training.

Drawing inspiration from the Horn-Schunck optical flow method⁴⁶, we incorporate a smoothness regularization term to ensure spatial coherence in the estimated motion fields:

$$\begin{aligned} J_{\textrm{smooth}} = \int \left( |\nabla u|^2 + |\nabla v|^2 \right) \, dx. \end{aligned}$$

(12)

Given the log-normal distribution of precipitation intensities⁴⁷, a weighting function is introduced to balance the influence of light, moderate, and heavy rainfall during training. Following the approach of Ravuri et al.²², we adopt a capped weighting scheme defined as $\textbf{w}(R_t) = \min (24, 1 + r)$, where r denotes the rainfall rate.

Motivated partly by the continuity equation and partly by the observation that large-scale precipitation patterns generally persist longer than smaller ones, the smoothness loss is consequently redefined as:

$$\begin{aligned} J_{\textrm{smooth}} = \left\| \nabla u_t \odot \sqrt{\textbf{w}(R_t)} \right\| _2^2 + \left\| \nabla v_t \odot \sqrt{\textbf{w}(R_t)} \right\| _2^2, \end{aligned}$$

(13)

where $\odot$ represents element-wise multiplication. The spatial gradients $\nabla u_t$ and $\nabla v_t$ are computed using Sobel filters. This formulation imposes stronger regularization in regions of heavy precipitation, ensuring that motion estimates remain physically consistent where accurate modeling is most critical.

To model the temporal evolution of the motion fields, we assume that the sequence $\{\textbf{V}_t\}$ follows the dynamics of the two-dimensional Burgers’ equations, which approximate nonlinear advection-diffusion processes:

$$\begin{aligned} \frac{\partial \textbf{V}}{\partial t} = - (\textbf{V} \cdot \nabla ) \textbf{V} + \mu \nabla ^2 \textbf{V}, \end{aligned}$$

(14)

where $\mu$ is the kinematic viscosity coefficient, and $\nabla ^2$ denotes the Laplacian operator.

For temporal discretization, we employ an explicit Euler scheme. Letting $\Delta t$ denote the time step, and approximating the time derivative using a first-order forward difference:

$$\begin{aligned} \frac{\partial \textbf{V}}{\partial t} \Big |_{t} \approx \frac{\textbf{V}_{t+\Delta t} - \textbf{V}_t}{\Delta t}, \end{aligned}$$

(15)

substitution into Eq. (14) yields the forward Euler update:

$$\begin{aligned} \textbf{V}_{t+\Delta t} = \textbf{V}_t + \Delta t \left[ - (\textbf{V}_t \cdot \nabla ) \textbf{V}_t + \mu \nabla ^2 \textbf{V}_t \right] . \end{aligned}$$

(16)

This recursive formulation allows the model to iteratively generate future motion fields $\textbf{V}_{t+1}$ to $\textbf{V}_{t+n}$ from the initial $\textbf{V}_t$ generated from the learnable neural network. Although conditionally stable, the scheme’s simplicity and differentiability make it particularly well-suited for integration within end-to-end neural architectures that require tractable gradient computations during training. Embedding Eq. (16) within the learning loop ensures that the network generates motion fields adhering to physically plausible advection-diffusion dynamics while maintaining differentiability for backpropagation.

In this manner, the framework synergistically integrates observational data with governing physical laws, allowing the network to learn unsupervised while adhering to the intrinsic dynamics of atmospheric motion. This design principle aligns with the paradigm of physics-informed neural networks, which aim to embed physical knowledge directly into the architecture and training process of machine learning models.

ThoR framework

Skillful nowcasting necessitates the integration of physical principles with advanced statistical learning methodologies³⁶. In pursuit of this objective, we introduce ThoR, a unified neural network framework designed to facilitate end-to-end optimization of forecasting errors. The proposed approach leverages a physics-informed deep generative model, which is conditioned on estimated motion fields, to predict future radar reflectivity based on historical observations. The architecture comprises two principal components: a stochastic generator parameterized by $\theta$, optimized via a discriminator and a physical regularization term, and an unsupervised motion estimation module governed by parameters $\phi$, as illustrated in Fig. 12.

As articulated in³⁶, the multiscale characteristics of atmospheric processes engender intricate dependencies across both spatial and temporal dimensions, which significantly constrain the predictability of weather systems. Convective phenomena, in particular, exhibit acute sensitivity to uncertainties in initial conditions, resulting in rapid amplification of forecasting errors. Such sensitivity imposes intrinsic limitations on conventional advection-based approaches, confining their applicability to spatial resolutions of approximately 20 km and forecast horizons shorter than one hour. Attempts to naively combine neural networks with physical constraints often fail to adequately account for this multiscale variability, leading to distorted mesoscale and convective-scale structures and the emergence of confounding artifacts.

To mitigate these challenges, we propose a modeling strategy wherein the spatiotemporal generation process is conditioned on a learned motion field V. This conditioning mechanism enhances the model’s capacity to capture recurrent structural dependencies across scales. As a result, the ThoR framework effectively integrates physically governed mesoscale patterns with data-driven convective-scale features extracted from radar imagery, yielding accurate and multiscale-consistent forecasts tailored for the nowcasting task.

Fig. 12

(a) The architecture of ThoR, a physics-conditional framework with a deep generative model. The nowcasting encoder captures spatial contextual representations using a recurrent neural network enhanced with spatial aggregation via axial attention blocks. It is conditioned on a physics-informed motion field predicted by the motion extraction network. (b) Detailed structure of the proposed Motion-guided ConvGRU block.

Motion-conditioned temporal encoder

We formulate the precipitation nowcasting task in accordance with the modeling framework defined in Equation 2. The proposed ThoR architecture operates on an input tensor $R_{1:t} \in \mathbb {R}^{t \times h \times w}$, representing a sequence of historical precipitation maps. To effectively capture spatiotemporal dependencies, the input sequence is first encoded into a contextual representation, which is subsequently utilized by the recurrent temporal module.

Specifically, we adopt a convolutional gated recurrent unit (ConvGRU) as the backbone of the temporal sampler, integrating both contextual features and a learned latent state. However, traditional ConvGRUs rely on location-invariant convolutional operations, assuming uniform spatial dynamics—a limitation when modeling complex phenomena such as rotation, scaling, and deformation in precipitation systems. This spatial rigidity hinders their ability to represent heterogeneous motion patterns, particularly in non-stationary meteorological scenarios.

To overcome these limitations, we propose a Motion-Conditioned ConvGRU, which dynamically adapts its spatial receptive field based on estimated motion fields. Unlike conventional recurrent structures, our module conditions the recurrent state updates on flow fields $\{u_t^l, v_t^l\}_{l=1}^{L}$, where L denotes the number of dynamic links. These flow fields are produced by a dedicated Motion Extraction U-Net (Section Unsupervised PINNs Learning for Motion Field Extraction) and encode localized spatial transformations.

Formally, at each time step t, the Motion-Conditioned ConvGRU computes its internal states as follows:

$$\begin{aligned} \begin{aligned} \mathscr {Z}_t&= \sigma \left( \mathscr {W}_{xz} * R_t + \sum _{l=1}^{L} \mathscr {W}_{hz}^l * \text {warp}(\mathscr {H}_{t-1}, u_t^l, v_t^l)\right) , \\ \mathscr {R}_t&= \sigma \left( \mathscr {W}_{xr} * R_t + \sum _{l=1}^{L} \mathscr {W}_{hr}^l * \text {warp}(\mathscr {H}_{t-1}, u_t^l, v_t^l)\right) , \\ \mathscr {H}_t'&= \phi \left( \mathscr {W}_{xh} * R_t + \mathscr {R}_t \circ \left( \sum _{l=1}^{L} \mathscr {W}_{hh}^l * \text {warp}(\mathscr {H}_{t-1}, u_t^l, v_t^l)\right) \right) , \\ \mathscr {H}_t&= (1 - \mathscr {Z}_t) \circ \mathscr {H}_t' + \mathscr {Z}_t \circ \mathscr {H}_{t-1}, \end{aligned} \end{aligned}$$

(17)

where $\sigma (\cdot )$ denotes the sigmoid activation, $\phi (\cdot )$ denotes the hyperbolic tangent (or ReLU depending on implementation), and $\circ$ denotes the Hadamard product. The weights $\mathscr {W}_{hz}^l$, $\mathscr {W}_{hr}^l$, and $\mathscr {W}_{hh}^l$ are $1 \times 1$ convolutional kernels responsible for projecting the hidden state features along dynamic links $l \in L$.

The operation $\text {warp}(\mathscr {H}_{t-1}, u_t^l, v_t^l)$ applies differentiable bilinear sampling to the hidden state $\mathscr {H}_{t-1}$ according to the motion vectors $(u_t^l, v_t^l)$. Given an input tensor $\mathscr {I} \in \mathbb {R}^{C \times H \times W}$ and horizontal and vertical flow fields $\textbf{U}, \textbf{V} \in \mathbb {R}^{H \times W}$, the warped output $\mathscr {M} \in \mathbb {R}^{C \times H \times W}$ at spatial location (i, j) is defined as

$$\begin{aligned} \mathscr {M}_{c,i,j} = \sum _{m=\lfloor i + V_{i,j} \rfloor }^{\lfloor i + V_{i,j} \rfloor + 1} \sum _{n=\lfloor j + U_{i,j} \rfloor }^{\lfloor j + U_{i,j} \rfloor + 1} \mathscr {I}_{c,m,n} \cdot \big (1 - |(i + V_{i,j}) - m |\big ) \cdot \big (1 - |(j + U_{i,j}) - n |\big ), \end{aligned}$$

(18)

where the coordinates $(i + V_{i,j}, j + U_{i,j})$ indicate the continuous sampling location determined by the flow fields. Here, the operator “$\cdot$” denotes scalar multiplication, applied between the pixel intensity $\mathscr {I}_{c,m,n}$ and its bilinear interpolation weights. The factors $\big (1 - |(i + V_{i,j}) - m |\big )$ and $\big (1 - |(j + U_{i,j}) - n |\big )$ represent the vertical and horizontal interpolation weights, respectively, and their product forms the bilinear kernel that scales the contribution of each neighboring pixel. This formulation ensures that the warping operation is fully differentiable with respect to both the input features and the flow fields, enabling seamless integration into end-to-end trainable architectures.

By jointly optimizing the parameters of the Motion Extraction U-Net and the Motion-Conditioned ConvGRU, the model adaptively learns a pixel-level dynamic connectivity pattern that evolves over time. This mechanism empowers the recurrent unit to accurately align its state transitions with complex, non-uniform precipitation dynamics, enhancing its ability to capture temporally evolving spatial patterns.

A comparative illustration of the spatial connectivity structures in standard ConvGRU versus our Motion-Conditioned ConvGRU is provided in Fig. 13. While traditional ConvGRUs utilize static, grid-aligned neighborhoods, our approach dynamically modulates these connections based on the estimated motion fields, yielding spatially adaptive receptive fields tailored to the underlying flow dynamics of precipitation systems.

Fig. 13

(a) Standard ConvGRU assumes fixed recurrent connections across spatial locations, disregarding local motion dynamics. (b) The proposed Motion-Conditioned ConvGRU dynamically adjusts its recurrent connectivity based on the flow fields $u_t$ and $v_t$, enabling adaptive spatiotemporal modeling.

Attention-centric spatial aggregator

One of the fundamental limitations of recursive modeling strategies in precipitation nowcasting is their susceptibility to long-term dependency degradation. The inherently chaotic and nonlinear dynamics of atmospheric processes result in substantial temporal variability and structural shifts in the joint distribution of radar observations. This pronounced non-stationarity, which manifests across multiple temporal scales, significantly impedes the model’s capacity to learn stable and generalizable spatiotemporal features, particularly as the forecast horizon extends.

To address this challenge and to enhance the spatial modeling capabilities of the ThoR framework, our architecture incorporates a dedicated attention module comprising four stacked axial self-attention blocks⁴⁸. Two of these blocks operate along the width axis, while the remaining two are applied along the height axis. In contrast to conventional self-attention mechanisms that require flattening the spatial dimensions and computing pairwise interactions across the entire 2D grid, thereby incurring quadratic computational cost, axial attention decomposes the two-dimensional attention operation into sequential one-dimensional operations along individual spatial axes. Specifically, self-attention is first applied across a single axis, followed by application along the orthogonal axis. This factorization enables the model to capture long-range dependencies with substantially reduced computational overhead while preserving the original input dimensionality, which effectively extract spatiotemporal features and refine the predicted precipitation map sequences.

Physics-guided loss function based on the advection-diffusion equation

To incorporate domain-specific physical knowledge into the learning process, we formulate a physics-informed loss function grounded in the two-dimensional advection-diffusion equation. This PDE characterizes the spatiotemporal evolution of radar reflectivity within a dynamically advecting and diffusing fluid medium. The governing equation is expressed as:

$$\begin{aligned} \frac{\partial R}{\partial t} = -u \frac{\partial R}{\partial x} - v \frac{\partial R}{\partial y} + \nu \left( \frac{\partial ^2 R}{\partial x^2} + \frac{\partial ^2 R}{\partial y^2} \right) , \end{aligned}$$

(19)

where R(x, y, t) denotes the radar reflectivity field, u(x, y, t) and v(x, y, t) represent the velocity components in the x and y directions, respectively, and $\nu$ is a scalar diffusion coefficient. This formulation encapsulates the competing effects of advection and diffusion, which are central to the transport of precipitation in atmospheric systems.

To enable differentiable implementation within a neural network, the PDE is discretized using finite difference approximations implemented via convolutional operations. Given a sequence of radar reflectivity fields $R \in \mathbb {R}^{B \times T \times H \times W}$ and corresponding velocity fields $V \in \mathbb {R}^{T \times B \times 2 \times H \times W}$, the physics-based residual loss derived from Equation 19 is defined as:

$$\begin{aligned} J_{physics}(R_t, V_t) = \left\| \frac{R_t - R_{t-1}}{\Delta t} + u_t \frac{\partial R_t}{\partial x} + v_t \frac{\partial R_t}{\partial y} - \nu \left( \frac{\partial ^2 R_t}{\partial x^2} + \frac{\partial ^2 R_t}{\partial y^2} \right) \right\| _2^2, \end{aligned}$$

(20)

where $J_{physics}(R_t, V_t)$ quantifies the deviation from the physically governed evolution of radar reflectivity.

Within our proposed framework, the advection-diffusion equation is incorporated as a regularization term that promotes the generation of predictions exhibiting both temporal and spatial coherence. Specifically, the velocity field $V_{t,t+n}$, estimated by the Motion Extraction Block, is combined with the observed reflectivity frame $R_t$ and the predicted sequence $\hat{R}_{t+1:t+n}$ to enforce physically consistent dynamics over the prediction horizon.

However, it is acknowledged that not all input sequences $R_{1:t}$ adhere strictly to the assumptions that underlie the advection-diffusion model. Rigid enforcement of the physical constraint in such cases may inadvertently impair predictive accuracy. To mitigate this issue, we introduce a dynamic weighting mechanism via a physics importance coefficient p, which adaptively modulates the influence of the physics-based loss. The final physics-informed loss is defined as:

$$\begin{aligned} \mathscr {L}_{\text {physics}} = \frac{1}{p} \cdot \frac{1}{n} \sum _{k=t}^{t+n} J_{\text {physics}}(R_k, V_k), \end{aligned}$$

(21)

where the weighting term $p = e^{\min (\max (J_{\text {physics}}(R_t, V_t), 0), 1)}$ quantifies the consistency between the current observation and the underlying physical model. A smaller residual $J_{\text {physics}}(R_t, V_t)$ indicates greater physical plausibility, resulting in $p \approx 1$ and thus amplifying the influence of the physics-based loss. Conversely, when the residual is large—indicating inconsistency with physical laws—p increases (approaching e), thereby attenuating the contribution of the physics term. This adaptive formulation enables the model to prioritize physical consistency when reliable, while allowing flexibility in the presence of observational noise or deviations from ideal physical behavior.

Objective function

We formulate the precipitation nowcasting task as a generative modeling problem within an adversarial learning framework. In this setting, the proposed ThoR architecture functions as the generator, tasked with synthesizing realistic precipitation sequences from historical meteorological observations. A spatial-temporal discriminator concurrently learns to assess the authenticity of these generated sequences, distinguishing them from observed radar measurements. This adversarial configuration aligns with the standard Generative Adversarial Network (GAN) paradigm, fostering a competitive learning dynamic that progressively enhances the generator’s ability to model the complex statistical properties inherent in precipitation fields.

To guide the generator’s optimization process, we design a composite objective function that balances data fidelity, perceptual realism, and physical consistency. The overall generator loss, denoted as $\mathscr {L}_{\text {Generator}}$, is expressed as a weighted sum of four principal components:

$$\begin{aligned} \mathscr {L}_{\text {Generator}} = \alpha \mathscr {L}_{\text {velocity}} + \beta \mathscr {L}_{\text {physics}} + \gamma \mathscr {L}_{\text {NN}} + \delta \mathscr {L}_{\text {adv}}. \end{aligned}$$

(22)

The term $\mathscr {L}_{\text {velocity}}$ enforces that the estimated motion fields align with physical velocity constraints, ensuring that the modeled flow dynamics remain coherent with atmospheric transport phenomena. $\mathscr {L}_{\text {physics}}$ further constrains the generator to adhere to the advection-diffusion principle, thereby preserving mass conservation and flow continuity throughout the prediction sequence. These two physics-informed terms are essential for embedding domain-specific knowledge into the learning process, promoting physically plausible forecasts.

The term $\mathscr {L}_{\text {NN}}$ encapsulates a suite of neural network-based loss components, designed to promote numerical accuracy and enhance event localization. Specifically, it is formulated as:

$$\begin{aligned} \mathscr {L}_{\text {NN}} = \lambda _1 \mathscr {L}_{L1} + \lambda _2 \mathscr {L}_{L2} + \lambda _3 \mathscr {L}_{\text {ICL}} + \lambda _4 \mathscr {L}_{\text {Huber}}, \end{aligned}$$

(23)

where $\mathscr {L}_{L1}$ and $\mathscr {L}_{L2}$ correspond to the pixel-wise L1 and L2 distance metrics, respectively, enforcing local accuracy by penalizing absolute and squared deviations between predicted and observed precipitation intensities. The $\mathscr {L}_{\text {Huber}}$ loss is incorporated to provide robustness against outliers, mitigating the adverse effects of extreme intensity values that are characteristic of severe weather events.

A key component of $\mathscr {L}_{\text {NN}}$ is the Intensity Consistency Loss, denoted as $\mathscr {L}_{\text {ICL}}$. Standard regression-based losses, such as Mean Absolute Error (MAE) or Mean Squared Error (MSE), are prone to penalizing incorrect spatial placements of high-intensity events twice—once for erroneously predicted regions and again for failing to predict the correct locations. This results in models that favor smoothed, low-confidence predictions, particularly detrimental in nowcasting scenarios where the accurate localization of convective storms is critical. To counteract this, $\mathscr {L}_{\text {ICL}}$ introduces an event-aware loss formulation based on a trinary cross-entropy mask, defined as:

$$\begin{aligned} \mathscr {L}_{\text {ICL}} = \text {CrossEntropy}(M(\hat{x}), M(x)), \quad \text {where} \quad M(x) = {\left\{ \begin{array}{ll} 0 & \text {if } x \in [0, 4) \\ 1 & \text {if } x \in [4, 8) \\ 2 & \text {if } x \ge 8 \end{array}\right. } \quad \text {for } x \in R_{\text {out}} \ \text {(mm/h)}. \end{aligned}$$

(24)

Here, M(x) denotes a discretization function that maps continuous precipitation intensities into categorical bins corresponding to light, moderate, and heavy rainfall regimes. The cross-entropy loss computed between the predicted mask $M(\hat{x})$ and the ground-truth mask M(x) encourages the generator to maintain spatial and intensity-level consistency in high-impact regions, thereby enhancing its ability to accurately capture storm structures.

The adversarial loss component, $\mathscr {L}_{\text {adv}}$, drives the generator towards producing outputs that are perceptually indistinguishable from real observations. This is achieved through the feedback signal provided by the spatial-temporal discriminator, which evaluates both spatial coherence and temporal evolution in the predicted sequences.

The weighting coefficients $\alpha$, $\beta$, $\gamma$, $\delta$, and $\lambda _{1}$ through $\lambda _{4}$ are empirically determined to balance the influence of physical constraints, numerical precision, and perceptual fidelity. Their selection reflects a trade-off between ensuring physically plausible forecasts and optimizing data-driven reconstruction accuracy. To maintain the clarity of exposition, the exact hyperparameter values are provided in the supplementary materials.

This composite objective function equips ThoR with the capability to generate precipitation forecasts that are not only numerically accurate but also physically consistent and perceptually realistic, thereby enhancing its robustness and generalization ability across diverse meteorological conditions.

Conclusion

Short-term forecasting of convective precipitation remains a persistent and critical challenge in atmospheric science, with profound implications for hazard mitigation and the management of weather-sensitive operations. This study introduces ThoR, a novel attention-driven, physics-informed deep learning architecture embedded within the TFC framework. The model approximates the forward solution of convective system dynamics as governed by partial differential equations (PDEs), enabling accurate simulation of storm evolution and intensification.

By leveraging high-resolution radar reflectivity and rainfall rate data from both the Nha Be radar station in Ho Chi Minh City and the U.S. Multi-Radar Multi-Sensor (MRMS) system, ThoR delivers rainfall predictions with lead times of up to two hours. Its probabilistic forecasting capabilities further support adaptive warning thresholds, improving decision-making and reducing false alarm rates in operational contexts. Importantly, ThoR relies solely on rainfall maps as input while incorporating physical constraints directly into its neural architecture. This fusion of data-driven learning and physics-based reasoning provides a principled approach to modeling the spatiotemporal dynamics of convective weather systems, yielding superior generalization across diverse meteorological regimes.

Comprehensive evaluations on both MRMS and Nha Be datasets demonstrate that ThoR consistently surpasses baseline models, achieving lower mean squared error (MSE), higher structural similarity index (SSIM), and enhanced critical success index (CSI), particularly for high-intensity precipitation events. These results highlight ThoR’s capability to accurately capture fine-scale rainfall structures and extreme weather phenomena across different climatic and geographic settings. Future work will focus on extending the forecasting horizon while preserving spatial and temporal precision, deploying the model in real-time operational environments—especially in tropical urban regions—and integrating uncertainty quantification and explainability techniques to enhance trust, transparency, and decision support in high-stakes applications.