Introduction

Image super-resolution (SR) technology shows great potential in various practical applications, including medical imaging1, geological exploration2, remote sensing3, and military scenarios4. Unlike RGB images, which contain only three spectral bands, hyperspectral images (HSI) typically consist of tens to hundreds of bands. Each band covers a narrow spectral range, allowing for the capture of richer spectral information. Image SR techniques can be categorized into two types based on the number of input images: single hyperspectral image super-resolution(SISR)5 and fusion-based hyperspectral image super-resolution6,7. Fusion-based hyperspectral image super-resolution generates high-resolution(HR) images by fusing multiple low-resolution(LR) images of the same scene. This method effectively utilizes the redundant information between images to achieve better super-resolution results. However, it often requires precise registration of the LR images, which can be complex and data-intensive. On the other hand, SISR creates high-resolution images from a single low-resolution input. This approach is simpler and requires less data. It does not need accurate alignment of multiple images, resulting in lower demands on hardware and computational resources. Therefore, SISR has promising prospects for practical applications and is a key focus of current research.

The SISR methods can be categorized based on their development history. These categories include interpolation-based methods, reconstruction-based methods, traditional machine learning-based methods, and deep learning-based methods. Among these, deep learning-based approaches use deep neural networks for image SR. Due to their excellent performance, these methods have gradually become the mainstream in the field. For example, Dong et al.8 proposed a super-resolution neural network composed of three convolutional layers, which became a foundational work in this area. Mei et al.9 introduced a hyperspectral image super-resolution(HSI-SR) method based on a 3D fully convolutional neural network. However, convolution operations have limitations in capturing long-range dependencies in image SR. This limitation arises because the size of the convolution kernel restricts its receptive field, allowing it to only process features of adjacent pixels in one computation. Although stacking multiple convolutional layers can partially alleviate this issue, it is costly and can lead to information decay or loss during transmission. The self-attention mechanism was first introduced by Vaswani et al.10. They designed the Transformer model, which utilizes an encoder-decoder structure. The Transformer is effective at capturing long-range dependencies but requires large amounts of data for training and has high computational complexity. Liu et al.11 proposed a hierarchical Transformer structure that computes feature representations using a shifted window approach. Liu et al.12 employed a self-attention mechanism in the spectral dimension and used 3D convolutions to extract spatial information. Xu et al.13 introduced the spatial-frequency interactive Transformer U-Net (AS\(^3\)ITransUNet), which alternates between upsampling and downsampling to effectively explore the hierarchical features of HSI. Chen et al.14 improved the spatial resolution of HSI by aggregating information across spatial and spectral ranges while maintaining the integrity of the spectral information. Zhang et al.15 proposed an efficient spatial-spectral attention Transformer network with an iterative refinement structure. This network effectively utilizes spatial and spectral information at different scales, generating high-resolution images without requiring training on large-scale datasets.

U-Net was originally proposed by Olaf Ronneberger et al.16 in 2015 to address the challenges of biomedical image segmentation. Its unique structure and ability to restore image details have shown significant advantages in image super-resolution tasks. The U-Net architecture consists of an encoder and a decoder. This design enables the network to simultaneously capture global contextual information and local detail information. The skip connections in U-Net allow high-resolution feature maps from the encoder to be directly passed to the corresponding decoder. This mechanism helps retain more details from the original image. Thanks to efficient context information fusion and skip connections, U-Net can achieve good performance with relatively few training data. HSI often have high dimensionality and limited training samples, with redundancy present across channels17. Therefore, the application of U-Net shows considerable potential for hyperspectral images. Moreover, Li et al.18 have shown that group convolution plays a vital role in reducing computational load and preventing model overfitting. Inspired by the cross-range spatial-spectral Transformer (CST) proposed by Chen et al.14, we present a cross-range self-attention single HSI-SR method based on the U-Net architecture (Cs\(\_\)Unet). The core of our method is the cross-range spatial-spectral self-attention interaction (CAI) module. This module incorporates cross-range spatial self-attention (CSA) and cross-range spectral self-attention (CSE) from the CST model. This enables the model to capture the relationships between distant pixels and spectral bands. The CAI module contains both CSA and CSE branches. These branches process spatial and spectral information in parallel and merge the processed features. Additionally, we introduce a cross-range grouped convolution upsampling (GCUc) module from previous work to enhance information flow at the top of the U-Net architecture. Finally, we integrate these modules into the U-Net structure for multi-scale feature fusion.

The specific contributions of the proposed method are as follows:

  1. 1.

    We propose a cross-range self-attention single hyperspectral image super-resolution method based on the U-Net architecture. This method captures long-range dependencies in both spatial and spectral dimensions and achieves multi-scale feature fusion. As a result, it enhances the quality of the reconstructed images.

  2. 2.

    We introduce the CAI module, which integrates spatial and spectral self-attention. This module can significantly improve spatial detail and spectral accuracy. The CAI module effectively captures important features within the image and fine-tunes the reconstructed features during the reconstruction process.

  3. 3.

    We construct a single hyperspectral image super-resolution network by integrating the CAI and GCUc modules into the U-Net framework. We adjust the U-Net architecture by adding more skip connections. Additionally, we place the GCUc module at the top to utilize group convolution and progressive upsampling strategies. This approach allows the model to learn fine texture and edge information. Experimental results demonstrate that our proposed method achieves superior image reconstruction compared to other classical methods.

The remainder of this paper is organized as follows: Section introduces methods related to hyperspectral image super-resolution. Section provides a detailed description of the architecture of our proposed Cs\(\_\)Unet method. In Section , we validate the effectiveness of the proposed model architecture through ablation experiments and compare it with other mainstream methods to demonstrate its superiority. Finally, Section summarizes the main findings and suggests directions for future research.

Related work

This section primarily reviews methods related to hyperspectral image SR. It includes both fusion-based hyperspectral image SR and single hyperspectral image SR techniques.

Fusion-based super-resolution methods

Existing fusion-based super-resolution methods typically involve merging low-resolution hyperspectral images (LR-HSI) with high-resolution panchromatic, color, or multispectral images19. Micheal et al.20 designed a cost function based on a spectral mixing model. This approach allows for simultaneous consideration of the relationships among the target high-resolution hyperspectral image(HR-HSI), the LR input HSI, and the HR panchromatic image during the reconstruction process. Akhtar et al.21 proposed simulating the imaging process of HSI as a complex physical process. They deconstructed LR input images into several spectral bases, which are weighted linearly after filtering. They formulated an inverse problem model for generating the target HSI from the LR-HSI and HR multispectral images based on the imaging process. To address the significant modal differences between LR-HSI and HR multispectral/panchromatic images, Li et al.22 designed a cross-spectral scale and shifted window non-local attention network (CSSNet). This network effectively merges LR-HSI with HR multispectral/panchromatic images while alleviating limitations in local feature learning. Since traditional upsampling methods represent pixels in a discrete manner, they often fail to recover continuous spatial and spectral information adequately. To overcome this, Wang et al.23 proposed a spatial-spectral implicit neural representation network (SS-INR) for fusing hyperspectral and multispectral images. Inspired by the high self-similarity of remote sensing HSI, Chen et al.24 proposed a spatial-spectral attention module based on dilated convolution (DSSA) to capture global spatial information. Cao et al.25 proposed an unsupervised multi-level spatiotemporal spectral fusion Transformer (UMSFT), which effectively improves the reconstruction quality of HSI-SR through hierarchical feature fusion and spatiotemporal spectral attention mechanisms. Lin et al.26 introduced the convex/depth image fusion (CODE-IF) algorithm, which achieves good performance in HSI super-resolution. Qu et al.27 proposed a progressive multi-iteration registration fusion collaborative optimization network for unregistered HSI-SR. This network refines registration and fusion results at multiple levels to reconstruct the registered HR-HSI. It applies registration and fusion collaborative optimization blocks iteratively. This process occurs at various levels to achieve the goal.Cao et al.28 also introduced an unsupervised hybrid Transformer-CNN (uHNTC) for efficient fusion of multi-/hyperspectral images without requiring degradation information. These methods perform well, but they rely on a well-registered high-resolution auxiliary image, which is difficult or often impossible to obtain in practice.

Single hyperspectral image super-resolution

SISR methods rely solely on a single LR-HSI for SR. This approach is more flexible in data acquisition compared to fusion-based HSI-SR methods, which depend on additional data sources. Li et al.18 introduced the grouped deep recursive residual network (GDRRN). This network uses a global residual structure to enhance its architecture. Within this structure, it incorporates grouped recursive modules. These modules help in better describing complex nonlinear mapping relationships while maintaining a compact design. Xie et al.29 proposed the deep feature matrix factorization (DFMF) method. This approach combines features extracted by deep neural networks (DNN) with non-negative matrix factorization strategies. It is used for the SR reconstruction of HSI in real scenes. Wu et al.30 formulated the HSI-SR problem as a least-squares problem integrating global reconstruction and local rank regularization. Mei et al.31 employed a convolutional neural network (CNN) to enhance both spatial and spectral resolution. They constructed a complete 3-D CNN. This network is intended to learn the end-to-end mapping. It maps low spatial resolution multispectral images (LR-MSI) to their corresponding HR-HSI. Arun et al.32 presented a convolution-deconvolution framework. Liu et al.33 introduced a novel CNN-based HSI-SR method called spectral grouping and attention-driven residual dense network (SGARDN). This method models all spectral bands and focuses on exploring spatial-spectral features. Jiang et al.34 proposed a framework with shared network parameters using grouped convolution and progressive upsampling. Li et al.35 explored the relationship between 2D and 3D convolutions. They alternated between 2D and 3D units to address structural redundancy. This approach also enhanced learning capabilities in the 2D spatial domain. By doing so, they were able to share spatial information during reconstruction. Long et al.36 introduced the dual self-attention swin Transformer super-resolution network (DSSTSR). This network leverages the representation ability of shifted window Transformers. It uses these Transformers to learn spectral sequence information. This information is gathered from adjacent bands of HSI. Xu et al.13 proposed a spatial-spectral interactive Transformer U-Net (AS\(^{3}\)ITransUNet) for HSI-SR. This method employs a group reconstruction strategy to alleviate computational burdens from the high spectral dimensions of HSI. The U-Net design alternates upsampling and downsampling to effectively explore the hierarchical features of HSI. They introduced the spatial-spectral interactive Transformer (SSIT) block. This block is used to extract spatial-spectral features from hyperspectral images. They integrated the SSIT block into the encoder and decoder of the U-Net. Xu et al.37 proposed a super-resolution framework consisting of three modules: spatial feature reconstruction, edge refinement, and spectral information reconstruction. These modules complement each other to better maintain spatial resolution and spectral fidelity. Compared to existing methods, the proposed approach introduces a c ross-range self-attention mechanism that simultaneously models both local and global spatial-spectral feature interactions, effectively addressing the limitations of some existing methods in capturing long-range dependencies. Moreover, by optimizing the U-Net architecture and integrating a multi-scale feature fusion strategy, the issue of feature loss is significantly mitigated.

Proposed method

The proposed method aims to address the limitations of CNN in capturing global dependencies. It also seeks to improve upon existing methods in extracting spatial-spectral feature information. To achieve this, we have integrated spatial-spectral self-attention with the U-Net architecture to construct the Cs\(\_\)Unet network. This approach effectively utilizes both local-global spatial information and spatial-spectral information. It is worth noting that our proposed CS_Unet is inspired by both the classical U-Net architecture and the CST method, but it is fundamentally different from U-Net-based methods (e.g. AS3ITransUNet) and CST in several aspects. Specifically, CS_Unet is built upon the traditional U-Net architecture, whereas AS3ITransUNet employs a variant U-Net design with alternating up- and down-sampling blocks. In contrast, CST is not based on the U-Net architecture at all, but adopts a different network framework.

Cs\(\_\)Unet network architecture

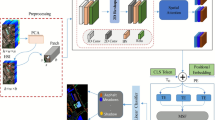
The proposed Cs\(\_\)Unet architecture is illustrated in Fig. 1. This structure is designed based on the principles of the U-Net architecture, incorporating an encoder-decoder framework. It employs multiple downsampling and upsampling operations to enlarge the receptive field. Additionally, a grouped convolution upsampling module is added at the top of the U-Net architecture. This integration introduces more residual connections, enabling the network to learn a greater variety of hierarchical features. As a result, this enhances the richness and diversity of feature representation, thereby strengthening the model’s ability to learn these features.

Fig. 1
figure 1

Overall framework of the proposed Cs\(\_\)Unet.

Full size image

For clarity, we denote the LR-HSI as \(I_{LR}\in \mathbb {R} ^{h\times w\times C}\) , where \(I_{BR}\in \mathbb {R} ^{H\times W\times C}\) represents the image obtained through bicubic interpolation upsampling of the LR-HSI. The model-generated high-resolution image is denoted as \(I_{SR}\in \mathbb {R} ^{H\times W\times C}\) , while the original high-resolution image is represented as \(I_{HR}\in \mathbb {R} ^{H\times W\times C}\) . Here, h(H) and w(W) represent the height and width of the LR-HSI(HR-HSI), respectively. The variable C indicates the number of spectral bands, and r is the upscaling factor, set to 4, meaning \(H=4h\) and \(W=4w\). The process of degrading HR-HSI to obtain the corresponding LR-HSI can be expressed as

$$\begin{aligned} I_{LR}=\mathrm {D(}I_{HR})+n^*, \end{aligned}$$
(1)

where \(\mathrm {D(}\cdot )\) represents the bicubic interpolation downsampling method, and \(n^*\) denotes the noise.

The proposed Cs_Unet method can predict \(I_{SR}\) from the given \(I_{LR}\). This process is denoted as

$$\begin{aligned} I_{SR}=\mathrm {H(}I_{LR}), \end{aligned}$$
(2)

where \(\mathrm {H(}\cdot )\) represents the mapping function of the Cs\(\_\)Unet network. On one hand, for the input \(I_{LR}\), it is first fed into two concatenated GCUc modules, i.e.,

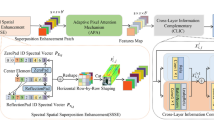
$$\begin{aligned} F_G=\textrm{H}_{\textrm{G}}(\textrm{H}_{\textrm{G}}(I_{LR})), \end{aligned}$$
(3)

where \(\textrm{H}_{\textrm{G}}(\cdot )\) represents the mapping function of the GCUc module, and \(F_G\) denotes the features obtained after the \(I_{LR}\) is processed through the two concatenated GCUc modules. The specific GCUc network architecture, as shown in Fig. 2 , it replaces the \(\mathrm { S^{2}AF}\) module in the original GCU structure with the CAI module38. This change is made to consider global context information. Additionally, it helps capture long-range dependencies in the data. The GCUc network employs a group convolution upsampling strategy, with an upsampling factor of 2, therefore the concatenation of the two GCUc modules achieves a 4-fold enlargement of the input image.

Fig. 2
figure 2

Structure of the GCUc module.

Full size image

On the other hand, \(I_{LR}\) is first upsampled by \(4\times\) using bicubic interpolation to obtain \(I_{BR}\), which is then fed into the main architecture of the U-Net network, as shown in Fig. 1. The process is formulated as

$$\begin{aligned} I_{BR}=\textrm{Bi}\left( I_{LR} \right) , \end{aligned}$$
(4)

where \(\mathrm {Bi(}\cdot )\) represents the bicubic interpolation upsampling method. We first extract shallow features from \(\ I_{BR}\) using a convolutional layer with a kernel size of 3\(\times\)3. During this process, the number of channels is doubled. This can be expressed as

$$\begin{aligned} F_S=\textrm{Conv}_{3\times 3}(\ I_{BR} ), \end{aligned}$$
(5)

where \(\textrm{Conv}_{3\times 3}(\cdot )\) represents the convolution mapping function with a kernel size of 3\(\times\)3. \(F_S\) denotes the shallow features extracted from the \(\ I_{BR}\) through convolution. Subsequently, the CAI module is used to extract the deep features of the image as follows:

$$\begin{aligned} F_d=\textrm{H}_{\textrm{C}}(F_s), \end{aligned}$$
(6)

where \(\textrm{H}_{\textrm{C}}(\cdot )\) represents the mapping function of the CAI module. \(F_d\) denotes the deep features extracted from the shallow features after passing through the CAI module. Following the CAI module, a convolution operation is applied to downsample the feature map by a factor of 2, while the number of channels is doubled. This process can be denoted as

$$\begin{aligned} F_{dn1}=\textrm{H}_{\textrm{dn}1}(F_d), \end{aligned}$$
(7)

where \(\textrm{H}_{\textrm{dn}1}(\cdot )\) represents the convolution operation function for downsampling. \(F_{dn1}\) denotes the features obtained after the first downsampling operation on the deep features. Next, the CAI module is applied again to enhance the spatial and spectral information of the feature map, i.e.,

$$\begin{aligned} F_{d1}=\textrm{H}_{\textrm{C}}(F_{dn1}), \end{aligned}$$
(8)

where \(F_{dn1}\) represents the features of \(F_{dn1}\) after passing through the CAI module. The features of \(F_{d1}\) are then fed into the second convolutional downsampling operation, resulting in the features \(F_{d2}\) after the second downsampling. This can be expressed as:

$$\begin{aligned} F_{dn2}=\textrm{H}_{\textrm{dn}2}(F_{d1}), \end{aligned}$$
(9)

where \(\textrm{H}_{\textrm{dn}2}(\cdot )\) represents the second convolutional downsampling operation. At the bottom of the U-Net architecture, the CAI module is added again. This addition encourages the model to learn different levels of structural and detail information. It enhances the model’s ability to capture long-range dependencies. This process can be expressed as:

$$\begin{aligned} F_{d2}=\textrm{H}_{\textrm{C}}(F_{dn2}), \end{aligned}$$
(10)

where \(F_{d2}\) represents the output features of the CAI module at the bottom of the U-Net architecture. After this, the model performs the first stage of upsampling on the feature map. The structure of the upsampling module is based on the method described in38, as shown in Fig. 3. It primarily uses the PixelShuffle technique39 to upsample the feature map by a factor of 2. The upsampling module is followed by a convolution layer with a 1\(\times\)1 kernel size to adjust the number of channels, matching the quantity of channels in \(F_{d1}\). This processing can be expressed as:

$$\begin{aligned} F_{up1}=\textrm{Conv}_{1\times 1}(\textrm{H}_{\textrm{up}}(F_{d2}))\oplus F_{d1}, \end{aligned}$$
(11)

where \(\textrm{Conv}_{1\times 1}(\cdot )\) represents the 1\(\times\)1 convolution operation function. \(\textrm{H}_{\textrm{up}}(\cdot )\) denotes the upsampling operation mapping function. “\(\oplus\)” represents element-wise addition operation. \(F_{up1}\) indicates the features obtained after the first stage of upsampling and convolution. Subsequently, a CAI module is used to enhance the feature representation, and the result is concatenated with \(F_{dn1}\).

$$\begin{aligned} F_{du1}=\textrm{H}_{\textrm{C}}(F_{up1})\Vert F_{dn1}, \end{aligned}$$
(12)

where “\(\Vert\)” represents the concat operation. \(F_{du1}\) denotes the features obtained after the concat operation. A convolution with a 1\(\times\)1 kernel size is then applied to reduce the number of channels before entering the second stage of the upsampling module, as shown in Fig. 3. Subsequently, another convolution with a 1\(\times\)1 kernel size is used to further reduce the channels. The features from \(F_d\) are then combined with this feature through a skip connection, resulting in the features \(F_{up2}\).

$$\begin{aligned} F_{up2}=\textrm{Conv}_{1\times 1}(\textrm{Conv}_{1\times 1}(F_{du}))\oplus F_d \end{aligned}$$
(13)

\(F_{up2}\) is concatenated with \(F_S\) after passing through the CAI module, resulting in \(F_{du2}\). This can be expressed as

$$\begin{aligned} F_{du2}=\textrm{H}_{\textrm{C}}(F_{up2})\Vert F_S{.} \end{aligned}$$
(14)

To ensure that the dimensions are consistent for element-wise addition with the features \(F_G\) output by the GCUc module at the top of the U-Net, two convolution layers are used to transform the number of channels in \(F_{du2}\), resulting in \(F_u\). This process can be expressed as:

$$\begin{aligned} F_u=\textrm{Conv}_{1\times 1}(\textrm{Conv}_{1\times 1}(F_{du2})), \end{aligned}$$
(15)
Fig. 3
figure 3

Upsampling module.

Full size image

Finally, we employ a residual connection operation. This allows the network to learn the difference between the input and output directly. It helps the model alleviate the gradient vanishing problem and improve learning efficiency. The downsampled \(I_{BR}\) obtained from \(I_{LR}\) using bicubic interpolation, the output \(F_G\) from the top GCUc module, and the output features \(F_u\) from the main U-Net module are added together element-wise to produce the model output \(F_u\). Equation (16) shows the operation,

$$\begin{aligned} F_{out}=F_G\oplus F_u\oplus I_{BR}. \end{aligned}$$
(16)

In summary, the proposed Cs\(\_\)Unet network can capture features at different scales. By incorporating global context information at various stages of the network, it helps the network better understand the overall structure of the image, thereby improving the super-resolution results. The use of cross-range self-attention aids in better recovering the edges and textures of the image.

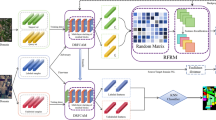
Architecture of the CAI module

The architecture of the CAI module is shown in Fig. 4. It mainly consists of cross-range spectral self-attention (CSE), cross-range spatial self-attention (CSA), layer normalization (LN), and a feedforward neural network layer14. The CAI module first applies LN to each layer’s input to obtain \(F_{LY}\). This normalization stabilizes the data distribution, which stabilizes the training process, reduces issues related to gradient vanishing and explosion, and accelerates convergence. This process can be expressed as follows.

$$\begin{aligned} F_{LY}=\textrm{H}_{\textrm{LY}}(F_{in}), \end{aligned}$$
(17)

where \(\textrm{H}_{\textrm{LY}}(\cdot )\) represents the LN mapping function, while \(\textrm{H}_{\textrm{LY}}(\cdot )\) denotes the input to the CAI module. The subsequent parallel CSE and CSA modules can simultaneously capture important features across channels and spatial dimensions, enhancing the feature representation capability. Following this, an element-wise addition operation fuses the features from different attention mechanisms, improving the overall feature representation to obtain \(F_f\). This process can be expressed as

$$\begin{aligned} F_f=(\textrm{H}_{\textrm{CSE}}(F_{LY})\oplus \textrm{H}_{\textrm{CSA}}(F_{LY}))\oplus F_{in}, \end{aligned}$$
(18)

where \(\textrm{H}_{\textrm{CSE}}(\cdot )\) represents the mapping function of the CSE block, while \(\textrm{H}_{\textrm{CSA}}(\cdot )\) denotes the mapping function of the CSA block. The CSA and CSE modules are used again to further enhance the feature representation capability and capture more detailed information, resulting in the feature \(F_e\), i.e.,

$$\begin{aligned} F_e=\textrm{H}_{\textrm{CSE}}(\textrm{H}_{\textrm{CSA}}(F_f)), \end{aligned}$$
(19)

LN is applied again to the features to ensure stability in their distribution. The feedforward neural network layer performs deeper processing and extraction of features. It achieves this through multiple linear transformations and nonlinear activation functions. This process thereby enhances model performance. Finally, the element-wise addition operation fuses the output features from the feedforward neural network layer with the previous features. This allows the model to simultaneously utilize feature information from different levels, improving the SR effects, the function is thus given by

$$\begin{aligned} F_{out}=\textrm{H}_{\textrm{FF}}(\textrm{H}_{\textrm{LY}}(F_e))\oplus F_e, \end{aligned}$$
(20)

where \(\textrm{H}_{\textrm{FF}}(\cdot )\) represents the mapping function of the feedforward neural network layer, while \(F_{out}\) denotes the output of the CAI layer.

Fig. 4
figure 4

Architecture of the CAI module.

Full size image

In summary, the design combines the LN, CSE, CSA, and FeedForward modules organically, using element-wise addition for feature fusion. This significantly enhances the performance and stability of the image SR model. The comprehensive architecture design strengthens the model’s feature representation capabilities. It achieves this by effectively utilizing crucial information in both channel and spatial dimensions. It also ensures the stability of feature distribution and efficient processing, resulting in higher-quality super-resolution images. Experimental results demonstrate that this approach can provide significant performance improvements. These improvements are particularly evident in image reconstruction tasks.

Loss function

The loss function used in this study is the same as that employed in our previous work38. Extensive ablation experiments have shown that combining L1 loss with GTV loss leads to better reconstruction results compared to using L1 loss alone. The GTV loss is defined as

$$\begin{aligned} L_{GTV}=\frac{1}{N}\left(\frac{\sum \nolimits _{h=1}^H{(}\nabla I_{SR_H}-\nabla I_{HR_H})^2}{H}+\frac{\sum \nolimits _{w=1}^W{(}\nabla I_{SR_W}-\nabla I_{HR_W})^2}{W}\right), \end{aligned}$$
(21)

where \(\nabla I_{SR_H}\) represents the gradient in the vertical direction for each pixel predicted by the model, and \(\nabla I_{HR_H}\) denotes the vertical gradient of each pixel in the Ground Truth. Similarly, \(\nabla I_{SR_W}\) indicates the horizontal gradient for each predicted pixel, while \(\nabla I_{HR_W}\) represents the horizontal gradient in the Ground Truth. H, W and N refer to the height, width, and batch size of the high-resolution images, respectively. Based on these definitions, the loss function utilized in this study is defined as

$$\begin{aligned} L=L_1+\alpha L_{GTV}, \end{aligned}$$
(22)

where the weight \(\alpha\) is set to 1e-3.

Experimental results and analysis

Datasets

The benchmark hyperspectral remote sensing image datasets used in this study are Pavia\(\_\)Center40, Chikusei41 and XiongAn42.

Pavia\(\_\)Center: The Pavia\(\_\)Center dataset comprises hyperspectral images collected by the ROSIS sensor. It is widely used for tasks such as hyperspectral image super-resolution (SR), remote sensing image classification, and target detection. The original image size is 1096\(\times\)1096 pixels with 102 spectral bands (after removing noisy bands). After cropping the unnecessary edges, the final image size is 1096\(\times\)715\(\times\)102.

Chikusei: The Chikusei dataset consists of hyperspectral images acquired using the Hyperspec V-NIR-CIRIS spectrometer, covering the Chikusei area in Ibaraki Prefecture, Japan. The dataset has a ground sampling distance of 2.5 meters and a spectral range from 363 nanometers to 1018 nanometers, containing a total of 128 spectral bands. The image spatial size is 2517\(\times\)2335 pixels.

XiongAn: The XiongAn dataset consists of hyperspectral images acquired by the Shanghai Institute of Technical Physics. The dataset covers a spectral range from 400 nanometers to 1000 nanometers, comprising a total of 256 spectral bands. The spatial resolution of each image is \(3750 \times 1580\)pixels, with each pixel corresponding to a ground sampling distance of 0.5 meters.

Experimental details

In the experiments, we use five commonly used objective quality assessment metrics to measure the model performance, namely Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), Spectral Angle Mapper (SAM), Erreur Relative Globale Adimensionnelle de Synthèse (ERGAS), and Correlation Coefficient (CC).

For the Pavia\(\_\)Center dataset, taking 4\(\times\) SR as an example, we first crop the left section (384\(\times\)715\(\times\)102) for testing and validation. The far left area (256\(\times\)715\(\times\)102) is used to extract 256\(\times\)256 test image patches, while the remaining area is divided into 64\(\times\)64 validation image patches. Importantly, the validation and test sets are completely non-overlapping in the division. The training set is composed of the remaining data, which is further partitioned into overlapping 64\(\times\)64 image patches, ensuring independence among the training, validation, and test sets. With an upsampling factor setting of 4, the overlap region is 32 pixels.

For the Chikusei dataset, taking 4\(\times\) SR as an example, a central region of 2304\(\times\)2048\(\times\)128 is initially cropped. From the left side of the image, a 2304\(\times\)384\(\times\)128 section is selected and divided into non-overlapping test and validation sets. Half of this section is used to create 256\(\times\)256 test samples, and the other half for 64\(\times\)64 validation samples. The remaining area is partitioned into overlapping 64\(\times\)64 patches for the training dataset. With an upsampling factor of 4, the overlap size is 32 pixels.

For the XiongAn dataset, taking 4\(\times\) SR as an example, we first select the leftmost 640 columns from the original image of size \(3750 \times 1580 \times 256\) for testing and validation. Specifically, the first 512 columns are used to extract non-overlapping \(256 \times 256\) patches for the test set, while the remaining 128 columns are partitioned into non-overlapping \(64\times 64\) patches for validation. The rest of the image is used as the training set, which is further divided into overlapping \(64\times 64\) patches. With an upsampling factor of 4, the overlap between adjacent training patches is set to 32 pixels.

After preparing the HR training samples, corresponding LR samples are generated using bicubic interpolation, each with a size of 32\(\times\)32 pixels. To mitigate data scarcity, data augmentation techniques such as rotation and mirroring are applied to enlarge the dataset size fourfold, thereby enhancing the model’s ability to generalize under varying imaging conditions. An initial learning rate of 1e-4 is set, which is halved every 30 epochs. The Adam optimizer is used with parameters \(\beta\)1 =0.9, \(\beta\)2 =0.99, and a weight decay of 1e-5. The kernel size for standard and depthwise convolutions is 3\(\times\)3. All experiments are conducted using the PyTorch framework on an NVIDIA RTX A6000 GPU with 48GB of memory.

Ablation study

The proposed Cs\(\_\)Unet method is based on the U-Net architecture and utilizes the CAI module to extract deep image information. To demonstrate the effectiveness of this method, it is essential to conduct ablation experiments. For this purpose, the training samples from the Chikusei dataset are used as the training dataset for the ablation study. The model’s performance is evaluated using test images from the Chikusei dataset, with a target size of 256\(\times\)256 pixels.

  1. (1)

    To verify the importance of the CAI module in the model, we introduce a variant where the CAI module is replaced with three 3\(\times\)3 convolutional layers. Table 1 summarizes the performance evaluation results, comparing our proposed method (“ours”) with the variant without the CAI module (“ours-w/o CAI”) across three image sizes at an upsampling factor of 4. The results indicate that removing the CAI module leads to a decrease in all evaluation metrics on the test images. By integrating the CAI module, our proposed method effectively combines multidimensional spatial and spectral information, leveraging the richness of hyperspectral images to achieve superior reconstruction results across various test images.

    Table 1 Results of the ablation study on the CAI module.
    Full size table

    The best results are highlighted in red font, where “\(\uparrow\)” indicates that a higher value is better for this metric.

  2. (2)

    Table 2 presents a comparative performance analysis between our proposed method (“Ours”) and a model variant where the CAI architecture is replaced by the SCA architecture from13 (“Ours-CAI->SCA”). The experimental results also demonstrate that the CAI architecture used in our method enhances model performance more effectively.

    Table 2 Ablation study results replacing the CAI Module with SCA.
    Full size table
  3. (3)

    An ablation experiment was conducted to compare the original GCU module from38. In this experiment, a variant was used where \(\mathrm {S^{2}AF}\) in the GCU was replaced by CAI. Table 3 shows the performance comparison between our proposed GCUc (“Ours”) and the version with the original GCU architecture unchanged (“Ours-GCUc-w/o SCA”). The results indicate that replacing \(\mathrm {S^{2}AF}\) with CAI in the GCUc architecture can improve model performance to some extent.

    Table 3 Ablation study results of the CAI module in the GCUc.
    Full size table
  4. (4)

    To verify the effectiveness of the parameter \(\alpha\) in Eq. (22), we conducted experiments and evaluated their performance under different values of \(\alpha\). The results are shown in Table 4. We can find that when \(\alpha\) is set to 0.001, the model achieves the best performance across all metrics, including PSNR, SSIM, SAM, ERGAS, and CC. As a result, we set the parameter \(\alpha\) to 0.001 in the following experiments.

    Table 4 Ablation study of parameter \(\alpha\) in the loss function.
    Full size table

Comparison with seven other representative methods

To verify the performance of the proposed Cs\(\_\)Unet method, we conducted experiments on three public benchmark datasets. The results were compared with seven other representative methods: Deep\(\_\)hs\(\_\)Prior43, GDRRN18, SSPSR34, PUDPN38, PDE-Net44, CST14, and Bicubic45.

Table 5 presents the performance comparison of eight SR techniques on the Chikusei dataset. The comparison is made with an upsampling factor of d=4, with a target size of 256\(\times\)256 for the test samples. The best results are highlighted in bold, and the second-best results are highlighted in italics. As shown in Table 5, the proposed Cs\(\_\)Unet method achieves the better results compared with the other state-of-art methods for five evaluation metrics. Figure 5 provides reconstructed images and their error maps to facilitate visual comparison among the methods. Below each super-resolution image is an error heatmap comparing the reconstruction to the Ground Truth, where darker colors indicate smaller errors and better reconstruction. For further visual comparison, a red rectangular area in the image is selected, and its reconstruction is enlarged in the yellow area. Figure 6 presents the visualization results of typical pixel spectral curves from both the reconstructed images and the Ground Truth for each method. Above all,our proposed method outperforms other competitors both subjectively and objectively.

Fig. 5
figure 5

The Chikusei dataset is displayed, with bands 70, 100, and 36 specifically chosen as the R-G-B channels, while utilizing an upsampling factor of 4. In the visualized figures of this paper, the images shown in the first and third rows are the super-resolution reconstructed images produced by the models, with the corresponding model names labeled above the images. The second and fourth rows respectively display the absolute error maps between the corresponding super-resolution images above and the Ground Truth. The darker the color in the error maps, the better the reconstruction performance.

Full size image
Fig. 6
figure 6

The visual comparison of the spectral curves at the pixel positions (50, 50), (300, 50), and (600, 50) in the Chikusei dataset.

Full size image
Table 5 Quantitative comparison of different methods on the Chikusei dataset.
Full size table

Table  6 reports the quantitative results of all methods on the Pavia_Center dataset test set at scale factors 2, 4, and 8, evaluated using five different metrics. Unlike the PUDPN and CST methods, our approach integrates cross-range spatial and spectral self-attention and employs a U-Net framework. This framework directly connects low-level and high-level features during transmission, preventing information loss through multi-level convolutions and effectively extracting multi-scale features. The results show that the proposed method outperforms other competitors at multiple scale factors and achieves better results on various metrics. Figures 7 and 8 provide subjective quality comparison of reconstruction results on the Pavia\(\_\)Center dataset for various methods. Similar to Fig. 5, each method’s SR result is shown above its corresponding absolute error map. It can be observed that other methods are unable to adequately reconstruct contours and texture details, whereas our approach effectively restores fine structures within the images.

Fig. 7
figure 7

The Pavia\(\_\)Center dataset is visualized by selecting bands 32, 21, and 11 as the R-G-B channels to generate a color image with an upsampling factor of 4.

Full size image
Fig. 8
figure 8

The visual comparison of the spectral curves at the pixel positions (50, 50), (120, 120), and (180, 100) in the Pavia\(\_\)Center dataset.

Full size image
Table 6 Quantitative comparison of different methods on the Pavia_Center dataset.
Full size table

Table 7 presents the performance comparison for different SR methods on the XiongAn dataset. As shown in the table, our proposed method achieves superior performance compared to the other competitors across all five evaluation metrics. Figure 9 presents a visual comparison of the SR reconstruction results produced by each method, along with the corresponding error maps. In addition, Fig. 10 illustrates the spectral curves of the reconstructed image. The above results indicate that our proposed method outperforms other competitors both subjectively and objectively.

Table 7 Quantitative comparison of different methods on the XiongAn dataset.
Full size table
Fig. 9
figure 9

The XiongAn dataset is visualized by selecting bands 120, 72, and 36 as the R-G-B channels to generate a color image with an upsampling factor of 4.

Full size image
Fig. 10
figure 10

The visual comparison of the spectral curves at the pixel positions (50, 50), (100, 310), and (300, 180) in the XiongAn dataset.

Full size image
Table 8 Comparisons of the computational cost of different methods on the Chikusei dataset with an NVIDIA RTX A6000 GPU.
Full size table

Table 8 presents the differences in complexity between the proposed method and other comparative methods. The complexity metrics adopted here include the number of parameters, floating-point operations (FLOPs), training time per epoch, and inference time per image. To ensure the fairness, all models are trained and evaluated under consistent experimental settings, using their original parameter configurations. It should be noted that one of the comparative methods adopts a self-supervised learning paradigm, whose training and inference procedures are fundamentally different from those of supervised methods. Therefore, Table 8 reports only the number of parameters and FLOPs for this method, while training and inference times are not presented.

In terms of computational efficiency, Table 8 indicates higher training and inference costs relative to several baselines. Nevertheless, the gains at \(2\times\) SR-particularly on Pavia\(\_\)Center with higher PSNR/SSIM/CC and lower SAM/ERGAS (Table 6)-justify this overhead for operational use. The inference latency of only a few seconds per image on an RTX A6000 keeps the method within near-real-time constraints, and the additional 2–3 s per image compared to mid-size baselines yields demonstrably better spectral fidelity, which is critical for downstream classification, unmixing, and detection. For higher scaling factors (\(4\times\),\(8\times\)), the improvements are less pronounced and the accuracy–cost trade-off is less favorable; however, even modest quality gains can be valuable in domains with stringent requirements-such as precision agriculture and environmental monitoring-where improved spectral accuracy enhances the reliability of subsequent analyses.

Generalizability to RGB or visible light data

Although our current study is primarily focused on HSI-SR, the core components of our method-such as the U-Net backbone and the cross-range self-attention modules-are fundamentally generic and can, in principle, be adapted to RGB or visible light image super-resolution. Specifically, the cross-range spatial self-attention mechanism can be directly applied to RGB images to capture long-range spatial dependencies. For visible light images, the spectral dimension is typically limited to three channels (R, G, B), so the cross-range spectral self-attention may provide less benefit compared to HSI, where there are hundreds of spectral bands. However, integrating spatial self-attention with conventional upsampling techniques in the U-Net framework could potentially enhance performance in RGB SISR tasks. In addition, fine-tuning the model or re-training it on RGB datasets (e.g., DIV2K, Set5, Set14) could allow effective generalization.

Despite the adaptability, there are several limitations to consider. First, the spectral self-attention branch of our CAI module is specifically designed for high-dimensional spectral data and may not bring the same advantages in RGB settings due to the small number of channels. Second, hyperspectral and RGB images often have different noise characteristics and information redundancy, which might require modifications to the network architecture or loss functions. Third, most existing benchmarks for RGB SISR focus more on perceptual or structural fidelity, while HSI-SR emphasizes both spatial and spectral consistency. Thus, some evaluation metrics and training strategies may need to be reconsidered.

Conclusion

This study presents a novel cross-range self-attention single HSI-SR method based on the U-Net architecture. The cross-range self-attention mechanism effectively captures long-range dependencies in spatial and spectral dimensions, finely adjusting reconstruction features to enhance image quality. By integrating CAI and GCU modules, We optimize the U-Net architecture by adding additional skip connections. Additionally, we employ grouped convolution and progressive upsampling strategies. These enhancements aim to improve the learning of details and edge information. Experiments on two benchmark datasets show that the Cs\(\_\)Unet method excels in both subjective and objective quality metrics, achieving superior reconstruction results. However, the method faces challenges in cross-dataset applications. These challenges arise due to inconsistencies in the number of bands and significant differences in image features. A future research direction is to integrate the proposed network with generative adversarial networks (GANs). This integration aims to better capture global and local information in images and improve the quality of super-resolved images.