Chaotic analysis, hopf bifurcation and collision of optical periodic solitons in (2+1)-dimensional degenerated Biswas–Milovic equation with Kerr law of nonlinearity

Abstract

The main aim of this research study is to examine optical soliton phenomena in a (2+1)-dimensional Schrödinger class nonlinear model that degenerates from Biswas-Milovic equation (BME) using Riccati modified extended simple equation method (RMESEM). This model has particular relevance in the fiber optics domain. The proposed anstaz RMESEM uses a complex structured wave transformation to produce nonlinear ordinary differential equation (NODE) and constraint conditions for Kerr law nonlinearity form of the model. The resulting NODE is assumed to have a closed form solution that converts it into a system of nonlinear algebraic equations via substitution in order to determine fresh variety of optical soliton solutions. The final visualizations of the obtained optical soliton solutions in the form of 3D, contour, and 2D forms demonstrate that the model develops Hopf bifurcation, rogue and internal envelope solitons as a result of the elastic and inelastic collision of optical periodic solitons while the norms of the obtained optical soliton reveal dark and bright kink structures. Using phase portraits and time-series maps, we also study bifurcating and chaotic behavior, observing its presence in the perturbed dynamical system and obtaining favorable results indicating Hopf bifurcation and periodicity. We use a generalized trigonometric function to perturb the planner system for the first time in order carry out chaotic analysis. Furthermore, our results are analyzed and linked to the soliton dynamics in BME, demonstrating the effectiveness of the suggested method as an effective method of identifying novel soliton phenomena within such nonlinear settings.

Introduction

Nonlinear partial differential equations (NPDEs) and Fractional NPDEs (FNPDEs) have been utilized to model a variety of physical phenomena over the past few decades^1,2,3. Many academics have expressed interest in NPDEs, and a wide range of discrete and continuous methods have been developed and applied to different theories, equations, models, and their solutions. Such methods include, extended Fan’s sub-ODE technique⁴, polynomial expansion method⁵, discrete tanh method⁶, Weierstrass elliptic function expansion method⁷, differential-difference Jacobi elliptic functions sub-ODE method⁸, Lie symmetry method⁹, exp-function technique¹⁰, F-expansion approach¹¹, modified Kudryashov method¹², extended trial equation method¹³, extended tanh function technique¹⁴, generalized three-wave method¹⁵, the soliton ansatz method¹⁶, Hirota bilinear technique¹⁷, the variational method¹⁸, modified simple equation approach¹⁹, the first integral method²⁰, the sine-cosine method²¹, the generalised Kudryashov method²², the Riccatti-Bernoulli sub-ODE method²³, the functional variable method²⁴, the Jacobi elliptic function method²⁵, the modified Khater method²⁶, the RMESEM^27,28,29, the $(G'/G)$-expansion method^30,31,32, the tanh-coth method³³, the generalized Kudryashov auxiliary method³⁴, extended direct algebraic method (EDAM)^35,36,37,38 and several additional methods^{39,40,41,42,43,44,45,46,47}.

Among the NPDEs, those pertaining to optics are particularly significant and of great study interest. In the past few decades, several aspects that serve as the basis for research on optical solitons such as physical models of optical solitons⁴⁸, the emergence of some notions pertaining to these models, such as dispersion⁴⁹, perturbation⁵⁰, and refractive index⁵¹, into the literature and highlighting their significance, new findings as a consequence of recent investigations and studies, and their endorsement with laboratory experiments have been identified. These may also include optical fiber technology, which serves as the foundation for modern optical fiber-based communication and internet technologies as well as research on optical nonlinearity in opto-electronic devices that fall under this category⁵². Because of their limited mode area, fibers have a very long interaction length and high density. As a result, these nonlinearities can have significant consequences on fibers, which are frequently unanticipated, hard to detect, and involve very complicated circumstances. As is well known, the quality, efficiency, and speed of transmitting signals in optical fibers are influenced by three primary criteria. These include polarization mode dispersion (PMD)⁵³, chromatic dispersion (CD) or group velocity dispersion (GVD)⁵⁴, and the nonlinear effects⁵⁵. The final one, nonlinear effects, includes the primary nonlinear phenomena that happen in single-mode fibers, including Raman scattering⁵⁶, Kerr effect⁵⁷, and⁵⁸ Brillouin scattering. Numerous applications of this kind have made mathematicians interested in studying optics. This article focuses on the degenerated form of a prominent nonlinear model called BME with Kerr law nonlinearity. The BME equation, which was first presented in 2010⁵⁹, is one of the several models and equations that have been created and presented to investigate the propagation of optical solitons using nonlinear techniques based on the nonlinear Schrödinger equation (NLSE). Numerous investigations have been conducted on the BME equation, which has a special significance in the field of fiber optics⁶⁰. The generalized form of BME is expressed as^61,62,63:

$$\begin{aligned} i ({P}^{n})_{t}-{p}(({P}^{n})_{xx}+({P}^{n})_{yy})-({q}{f}(|{P}|^2)-\kappa ){P}^{n}=0, \end{aligned}$$

(1)

where ${P}={P}(t,x,y)$ is a complex structured wave function that signifies optical field amplitude. Moreover, the general representation of evolution is represented by the first term in (1), followed by the term of general form of the group velocity dispersion term (GVD), the general form of the non-Kerr law nonlinearity is represented by third term which involves $f(\Phi )$ that represents a real-valued algebraic function, $({n}, \quad {n}\ge 1)$ is a parameter that generalizes the model from NLSE to BME while p, q, and ${\kappa }$ are real valued parameters. Moreover, (1) degenerates into the (2+1)-dimensional NLSE version of BME if ${n} = 1$. Assuming that ${n} = 1$, a crucial NLSE form for optical fibers hat is directly relevant to standard silica fibres and has a well-established experimental interpretation, we examine degenerated BME with Kerr law nonlinearity in this work.

Prior to this discovery, a number of previous researchers dealt with BME in different ways to get optical soliton solutions. For example, Altun et al. used Kudryashov’s approach⁶¹ to study dark, brilliant, and singular optical soliton solutions of BME with power, parabolic, and Kerr law nonlinearity. Ahmad discovered both dazzling and dark optical solitons for BME in magneto-optic waveguides based on Kudryashov’s law of refractive index⁶⁴. Pinar used a pair of Kudryashov techniques to create and analyze optical solitons of BME with parabolic law and spatiotemporal dispersion⁶⁵. Ozisik used the Kudryashov technique and the unified Riccati equation expansion methodology to study optical soliton events in the (2+1) and (3+1) forms of the BME⁶⁶. Finally, Raza et al. concentrated the exact arrangement of the BME with Kerr law, power law, parabolic law and dual power law nonlinearity by Exp $(-\varphi (\varepsilon ))$-expansion strategy⁶⁷. They reported more exact travelling wave solutions in a brief shape to the BME condition which concedes physical centrality in applications. However, in the context of the intended model using RMESEM, the formation of Hopf bifurcation, rogue, and internal envelope solitons, as well as the elastic and inelastic collision of optical periodic solitons, have not been investigated and evaluated. This assertion highlights a notable gap in the body of current research. Our research fills this gap by offering a thorough model analysis and outlining the suggested RMESEM approach. The suggested anstaz RMESEM builds NODE and constraint relations for the model’s Kerr law nonlinearity form using a complex structured wave transformation. The resulting NODE is expected to have a close form solution that converts it into a system of nonlinear algebraic equations via substitution in order to identify fresh plethora of optical soliton solutions. The final visualizations of the obtained optical soliton solutions in the form of 3D, contour, and 2D forms demonstrate that the model develops Hopf bifurcation, rogue and internal envelope solitons as a result of the elastic and inelastic collision of optical periodic solitons while the norms |P| of the obtained optical soliton reveal dark and bright kink structures. Using phase portraits and time-series maps, we also examine chaotic and bifurcating behavior, finding that it exists in the perturbed dynamical system and obtaining positive results that show periodicity and Hopf bifurcation. We use a generalized trigonometric function to perturb the planner system for the first time in order carry out chaotic analysis. Additionally, our findings are analyzed and linked to the soliton dynamics in the aimed model, demonstrating the effectiveness of the proposed method as a way to find distinct soliton phenomena in such nonlinear settings.

The remaining article is structured as follows: The applied RMESEM is introduced in Section 2, optical soliton solutions to the aimed model with the application of RMESEM are acquired and presented in Section 3. Results and graphical discussion are covered in Section 4, the chaotic and bifurcation analysis are presented in Section 5, Section 6 concludes our study while last section presents an appendix.

The working methodology of RMESEM

This section describes the RMESEM’s operational procedure to determine soliton solutions for complicated NPDEs. Consider the generic complex NPDE that is shown below^27,28,29:

$$\begin{aligned} A( {P} , {P}_t, {P}_{x}, {P}_{xx}, {P}_{y}, | {P} |, {P} {P}_{ty}, | {P} |_{xy}, \ldots )=0, \end{aligned}$$

(2)

where A is the polynomial of P, ${P}={P}(t,x,y)$ is an unknown complex function, and the subscripts are partial derivatives of P with respect to x , y and t, respectively. The proposed RMESEM’s primary steps are as follows:

Step 1. A complex wave transformation of the form ${P}(t,x,y)=e^{ \xi i}\mathfrak {P}({\phi })$ where $\xi =\xi (t,x,y)$ and $\phi =\phi (t,x,y)$ are linear functions, is firstly performed. In this study, we configure the ensuing complex wave transformation⁶¹:

$$\begin{aligned} {P}(t,x,y)=e^{ \xi i}\mathfrak {P}({\phi }), \quad \text {where} \quad {\phi }=\lambda x+\mu y+\omega t \quad \text {and} \quad \xi =x+y+ t+\vartheta , \end{aligned}$$

(3)

where $\lambda , \mu$, and $\omega$ are wave numbers, $\vartheta$ is phase constant while $\xi$ is a phase component. Equation (2) transforms into the subsequent NODE employing the wave transformation as referred above:

$$\begin{aligned} B(\mathfrak {P},\mathfrak {P}'\mathfrak {P},\mathfrak {P}',\dots )=0, \end{aligned}$$

(4)

where B is a polynomial of $\mathfrak {P}$ and its derivatives, and the primes are the ordinary derivatives of $\mathfrak {P}$ with regard to ${\phi }$.

Step 2. In order to satisfy the homogeneous balance condition, Eq. (4) is sometimes integrated term by term.

Step 3. For Eq. (4), we then assume that the closed-form wave solution is written as follows:

$$\begin{aligned} \mathfrak {P}({\phi })=\sum _{\mathfrak {k}=0}^{\mathfrak {m}}{e}_\mathfrak {k} \left( \frac{{\Pi }'({\phi })}{{\Pi }({\phi })}\right) ^\mathfrak {k}+ \sum _{\mathfrak {k}=0}^{\mathfrak {m}-1}{d}_\mathfrak {k} \left( \frac{{\Pi }'({\phi })}{{\Pi }({\phi })}\right) ^\mathfrak {k} \cdot \left( \frac{1}{{\Pi }({\phi })} \right) , \end{aligned}$$

(5)

where ${d}_\mathfrak {k} (\mathfrak {k}=0,...,\mathfrak {m}-1)$ and ${e}_j (j=0,...,\mathfrak {m})$ stand for the unidentified constants that must be found later, and ${\Pi }({\phi })$ satisfies the ensuing Riccati equation:

$$\begin{aligned} {\Pi }'({\phi })={\varpi }+{\rho } {\Pi }({\phi })+{\varrho }({\Pi }({\phi }))^2, \end{aligned}$$

(6)

where ${\varpi },{\rho }$ and ${\varrho }$ are invariables.

Step 4. The balance number $\mathfrak {m}$ given in Eq. (5) is calculated using the homogeneous balancing principle between the highest nonlinear term and the highest-order derivative term in Eq. (4).

Step 5. Equation (5) is substituted into Eq. (4), or the equation that arises from integrating Eq. (4) and combining the terms with the same powers of ${\Pi }({\phi })$ to obtain an expression in terms of ${\Pi }({\phi })$, using the value of $\mathfrak {m}$ obtained in Step 4. An algebraic system of equations describing the parameters ${e}_j (j=0,...,\mathfrak {m})$ and ${d}_\mathfrak {k} (\mathfrak {k}=0,...,\mathfrak {m}-1)$ with other related parameters is created by comparing the coefficients on both sides of the expression.

Step 6. The algebraic system in Step 5 is solved using the algebraic program Maple to provide the values of ${e}_j (j=0,...,\mathfrak {m})$ and ${d}_\mathfrak {k} (\mathfrak {k}=0,...,\mathfrak {m}-1)$ with other relevant parameters.

Step 7. Soliton solutions to Eq. (2) are obtained by substituting the values of the parameters in Eq. (5) with the solutions of Eq. (6) displayed in Table 1.

Table 1 Families of ${\Pi }({\phi })$ and $\bigg (\frac{{\Pi }'({\phi })}{{\Pi }({\phi })}\bigg )$, wherein ${\eta } ={\rho }^2-4{\varrho } {\varpi }$ and ${\Psi }=\cosh \left( \frac{1}{4}\,\sqrt{\eta }{\phi } \right) \sinh \left( \frac{1}{4}\,\sqrt{\eta }{\phi } \right)$.

The execution of RMESEM

In this section we employ the proposed RMESEM to construct optical soliton solutions for degenerated BME namely NLSE.

The governing equation under Kerr law nonlinearity

According to Kerr law nonlinearity, we substitute $f(\Phi ) = \Phi$ and $n=1$ in (1) which reduces it into the ensuing structure:

$$\begin{aligned} i {P}_{t}-{p}({P}_{xx}+{P}_{yy})-({q}|{P}|^2-\kappa ){P}=0. \end{aligned}$$

(7)

The first step in conducting this study is to apply the wave transformation given in (3) to (7). The following couple of NODEs appears from the real and imaginary parts when Eq. (7) is subjected to this wave transformation:

$$\begin{aligned} \begin{aligned}&( \kappa +2\,{p}-1 ) \mathfrak {P}(\phi ) -{q} \mathfrak {P}^{3}(\phi ) -{p} ( {\lambda }^{2}+{\mu }^{2}) \mathfrak {P}''(\phi )=0,\\&(\omega -2{p}(\lambda +\mu ))\mathfrak {P}''(\phi )=0,\\ \end{aligned} \end{aligned}$$

(8)

respectively. Since $\mathfrak {P}(\phi )\ne 0$ and has the second derivative, thus the second part in (8) gives the following constraint condition:

$$\begin{aligned} \begin{aligned} \omega =2{p}(\lambda +\mu ). \end{aligned} \end{aligned}$$

(9)

With this constraint, the entire model reduced to the following governing NODE:

$$\begin{aligned} ( \kappa +2\,{p}-1 ) \mathfrak {P}(\phi ) -{q} \mathfrak {P}^{3}(\phi ) -{p} ( {\lambda }^{2}+{\mu }^{2}) \mathfrak {P}''(\phi )=0. \end{aligned}$$

(10)

which has Kerr law nonlinearity under the constraint in (9). By demonstrating the homogeneous balancing principle between $\mathfrak {P}^{3}(\phi )$ and $\mathfrak {P}''(\phi )$, we arrive at ${\mathfrak {m}}=1$, stated in (5).

The construction of optical soliton solutions

When ${\mathfrak {m}}=1$ is entered into Eq. (5), the closed form solution for Eq. (10) is obtained as follows:

$$\begin{aligned} \mathfrak {P}({\phi })=\sum _{\mathfrak {k}=0}^{1}{e}_\mathfrak {k} \left( \frac{{\Pi }'({\phi })}{{\Pi }({\phi })}\right) ^\mathfrak {k}+{d}_0 \left( \frac{1}{{\Pi }({\phi })} \right) . \end{aligned}$$

(11)

By putting (11) into (10) and collecting all terms with the same orders of ${\Pi }({\phi })$, we may create an expression in ${\Pi }({\phi })$. Setting all of the coefficients to zero simplifies the expression and yields a system of nonlinear algebraic equations. In the following three (3) distinct sets, Maple is used to solve the resultant system:

Set. 1

$$\begin{aligned} \begin{aligned}&e_{{0}}=e_{{0}},e_{{1}}=0,d_{{0}}=2\,{\frac{\varpi \,e_{{0}}}{\rho }} ,p=p,q=-{\frac{p \left( {\lambda }^{2}+{\mu }^{2} \right) {\rho }^{ 2}}{{2e_{{0}}}^{2}}},\lambda =\lambda ,\mu =\mu ,\kappa =-\frac{1}{2}\,p \left( { \lambda }^{2}+{\mu }^{2} \right) \eta +1-2\,p . \end{aligned} \end{aligned}$$

(12)

Set. 2

$$\begin{aligned} \begin{aligned}&e_{{0}}=-\frac{1}{2}\,\rho \,e_{{1}},e_{{1}}=e_{{1}},d_{{0}}=-\varpi \,e_{{1}} ,p=p,q=-2\,{\frac{p \left( {\lambda }^{2}+{\mu }^{2} \right) }{{e_{{1}} }^{2}}},\lambda =\lambda ,\mu =\mu ,\kappa =-\frac{1}{2}\,p \left( {\lambda }^{2}+{ \mu }^{2} \right) \eta +1-2\,p . \end{aligned} \end{aligned}$$

(13)

Set. 3

$$\begin{aligned} \begin{aligned}&e_{{0}}=\frac{1}{2}\,\rho \,\psi ,e_{{1}}=\psi ,d_{{0}}=-\psi \,\varpi ,p=p,q=q, \lambda =\lambda ,\mu =\mu ,\kappa =-\frac{1}{2}\,p \left( {\lambda }^{2}+{\mu }^{2} \right) \eta +1-2\,p , \end{aligned} \end{aligned}$$

(14)

where $\psi =\sqrt{-2\,{\frac{p \left( {\lambda }^{2}+{\mu }^{2} \right) }{q}}}$.

We get the following innovative families of optical soliton solutions for (7) by taking into account set 1 and applying Eqs. (11) & (3) with the corresponding solution of Eq. (6) shown in Table 1:

Family. 1.1: Considering $\eta <0 \quad \varrho \ne 0$,

$$\begin{aligned} {P}_{1,1}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{2\,\varpi \,e_{{0}}}{\rho } \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}+\frac{1}{2}\,{\frac{\sqrt{-\eta }\tan \left( \frac{1}{2}\,\sqrt{-\eta }\phi \right) }{\varrho }} \right) ^{-1} +e_{{0}} \bigg ) , \end{aligned}$$

(15)

$$\begin{aligned} {P}_{1,2}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{2\,\varpi \,e_{{0}}}{\rho } \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{2}\,{\frac{\sqrt{-\eta }\cot \left( \frac{1}{2}\,\sqrt{-\eta }\phi \right) }{\varrho }} \right) ^{-1} +e_{{0}} \bigg ) , \end{aligned}$$

(16)

$$\begin{aligned} {P}_{1,3}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{2\,\varpi \,e_{{0}}}{\rho } \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}+\frac{1}{2}\,{\frac{\sqrt{-\eta } \left( \tan \left( \sqrt{-\eta }\phi \right) +\sec \left( \sqrt{-\eta }\phi \right) \right) }{\varrho }} \right) ^{-1} +e_{{0}} \bigg ) , \end{aligned}$$

(17)

and

$$\begin{aligned} \begin{aligned} {P}_{1,4}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{2\,\varpi \,e_{{0}}}{\rho } \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}+\frac{1}{2}\,{\frac{\sqrt{-\eta } \left( \tan \left( \sqrt{-\eta }\phi \right) -\sec \left( \sqrt{-\eta }\phi \right) \right) }{\varrho }} \right) ^{-1} +e_{{0}} \bigg ) . \end{aligned} \end{aligned}$$

(18)

Family. 1.2: Considering $\eta >0 \quad \varrho \ne 0$,

$$\begin{aligned} {P}_{1,5}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{2\,\varpi \,e_{{0}}}{\rho } \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{2}\,{\frac{\sqrt{\eta }\tanh \left( \frac{1}{2}\,\sqrt{\eta }\phi \right) }{\varrho }} \right) ^{-1}+e_{{0}} \bigg ) , \end{aligned}$$

(19)

$$\begin{aligned} {P}_{1,6}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{2\,\varpi \,e_{{0}}}{\rho } \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{2}\,{\frac{\sqrt{\eta } \left( \tanh \left( \sqrt{\eta }\phi \right) +i\textrm{sech } \left( \sqrt{\eta }\phi \right) \right) }{\varrho }} \right) ^{-1} +e_{{0}} \bigg ) , \end{aligned}$$

(20)

$$\begin{aligned} {P}_{1,7}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{2\,\varpi \,e_{{0}}}{\rho } \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{2}\,{\frac{\sqrt{\eta } \left( \tanh \left( \sqrt{\eta }\phi \right) -i\textrm{sech } \left( \sqrt{\eta }\phi \right) \right) }{\varrho }} \right) ^{-1} +e_{{0}} \bigg ) , \end{aligned}$$

(21)

and

$$\begin{aligned} \begin{aligned} {P}_{1,8}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{2\,\varpi \,e_{{0}}}{\rho } \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{4}\,{\frac{\sqrt{\eta } \left( \tanh \left( \frac{1}{4}\,\sqrt{\eta }\phi \right) -\coth \left( \frac{1}{4}\,\sqrt{\eta }\phi \right) \right) }{\varrho }} \right) ^{-1}+e_{{0}} \bigg ) . \end{aligned} \end{aligned}$$

(22)

Family. 1.3: Considering $\eta =0, \quad \rho \ne 0$,

$$\begin{aligned} \begin{aligned} {P}_{1,9}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( e_{{0}}-{\frac{e_{{0}}\rho \,\phi }{\rho \,\phi +2}} \bigg ) . \end{aligned} \end{aligned}$$

(23)

Family. 1.4: Considering $\rho =\sigma$, $\varpi =\varsigma \sigma (\varsigma \ne 0)$ and $\varrho =0$,

$$\begin{aligned} \begin{aligned} {P}_{1,10}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( {\frac{e_{{0}} \left( {\textrm{e}^{\sigma \,\phi }}+\varsigma \right) }{{ \textrm{e}^{\sigma \,\phi }}-\varsigma }} \bigg ) . \end{aligned} \end{aligned}$$

(24)

Family. 1.5: Considering $\rho =\sigma$, $\varrho =\varsigma \sigma (\varsigma \ne 0)$ and $\varpi =0$,

$$\begin{aligned} \begin{aligned} {P}_{1,11}(t,x,y)=&e_0 \textrm{e}^{\xi i} . \end{aligned} \end{aligned}$$

(25)

In above solutions, ${\phi }=\lambda x+\mu y+2{p}(\lambda +\mu ) t \quad \text {and} \quad \xi =x+y+ t+\vartheta$.

We get the following innovative families of optical soliton solutions for (7) by taking into account set 2 and applying Eqs. (11) & (3) with the corresponding solution of Eq. (6) shown in Table 1:

Family. 2.1: Considering $\eta <0 \quad \varrho \ne 0$,

$$\begin{aligned} {P}_{2,1}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\varpi \,e_{{1}} \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}+\frac{1}{2}\,{\frac{ \sqrt{-\eta }\tan \left( \frac{1}{2}\,\sqrt{-\eta }\phi \right) }{\varrho }} \right) ^{-1} -\frac{1}{2}\,{\frac{e_{{1}}\eta \, \left( 1+ \left( \tan \left( \frac{1}{2} \,\sqrt{-\eta }\phi \right) \right) ^{2} \right) }{\sqrt{-\eta }\tan \left( \frac{1}{2}\,\sqrt{-\eta }\phi \right) -\rho }}-\frac{1}{2}\,\rho \,e_{{1}} \bigg ) , \end{aligned}$$

(26)

$$\begin{aligned} {P}_{2,2}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\varpi \,e_{{1}} \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{2}\,{\frac{ \sqrt{-\eta }\cot \left( \frac{1}{2}\,\sqrt{-\eta }\phi \right) }{\varrho }} \right) ^{-1} +\frac{1}{2}\,{\frac{e_{{1}}\eta \, \left( \left( \cot \left( \frac{1}{2}\, \sqrt{-\eta }\phi \right) \right) ^{2}+1 \right) }{\sqrt{-\eta }\cot \left( \frac{1}{2}\,\sqrt{-\eta }\phi \right) +\rho }}-\frac{1}{2}\,\rho \,e_{{1}} \bigg ) , \end{aligned}$$

(27)

$$\begin{aligned} {P}_{2,3}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\varpi \,e_{{1}} \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}+\frac{1}{2}\,{\frac{ \sqrt{-\eta } \left( \tan \left( \sqrt{-\eta }\phi \right) +\sec \left( \sqrt{-\eta }\phi \right) \right) }{\varrho }} \right) ^{-1} \nonumber \\&-{ \frac{e_{{1}}\eta \, \left( 1+\sin \left( \sqrt{-\eta }\phi \right) \right) }{\cos \left( \sqrt{-\eta }\phi \right) \left( \sqrt{-\eta } \sin \left( \sqrt{-\eta }\phi \right) -\rho \,\cos \left( \sqrt{-\eta } \phi \right) +\sqrt{-\eta } \right) }}-\frac{1}{2}\,\rho \,e_{{1}} \bigg ) , \end{aligned}$$

(28)

and

$$\begin{aligned} \begin{aligned} {P}_{2,4}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\varpi \,e_{{1}} \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}+\frac{1}{2}\,{\frac{ \sqrt{-\eta } \left( \tan \left( \sqrt{-\eta }\phi \right) -\sec \left( \sqrt{-\eta }\phi \right) \right) }{\varrho }} \right) ^{-1}\\&+{ \frac{e_{{1}}\eta \, \left( \sin \left( \sqrt{-\eta }\phi \right) -1 \right) }{\cos \left( \sqrt{-\eta }\phi \right) \left( \sqrt{-\eta } \sin \left( \sqrt{-\eta }\phi \right) -\rho \,\cos \left( \sqrt{-\eta } \phi \right) -\sqrt{-\eta } \right) }}-\frac{1}{2}\,\rho \,e_{{1}} \bigg ) . \end{aligned} \end{aligned}$$

(29)

Family. 2.2: Considering $\eta >0 \quad \varrho \ne 0$,

$$\begin{aligned} {P}_{2,5}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\varpi \,e_{{1}} \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{2}\,{\frac{ \sqrt{\eta }\tanh \left( \frac{1}{2}\,\sqrt{\eta }\phi \right) }{\varrho }} \right) ^{-1} -\frac{1}{2}\,{\frac{e_{{1}}\eta \, \left( \left( \tanh \left( \frac{1}{2}\, \sqrt{\eta }\phi \right) \right) ^{2}-1 \right) }{\sqrt{\eta }\tanh \left( \frac{1}{2}\,\sqrt{\eta }\phi \right) +\rho }}-\frac{1}{2}\,\rho \,e_{{1}} \bigg ) , \end{aligned}$$

(30)

$$\begin{aligned} {P}_{2,6}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\varpi \,e_{{1}} \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{2}\,{\frac{ \sqrt{\eta } \left( \tanh \left( \sqrt{\eta }\phi \right) +i\textrm{sech} \left( \sqrt{\eta }\phi \right) \right) }{\varrho }} \right) ^{-1}\nonumber \\&-{ \frac{e_{{1}}\eta \, \left( i\sinh \left( \sqrt{\eta }\phi \right) -1 \right) }{\cosh \left( \sqrt{\eta }\phi \right) \left( \rho \,\cosh \left( \sqrt{\eta }\phi \right) +\sinh \left( \sqrt{\eta }\phi \right) \sqrt{\eta }+i\sqrt{\eta } \right) }}-\frac{1}{2}\,\rho \,e_{{1}} \bigg ) , \end{aligned}$$

(31)

$$\begin{aligned} {P}_{2,7}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\varpi \,e_{{1}} \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{2}\,{\frac{ \sqrt{\eta } \left( \tanh \left( \sqrt{\eta }\phi \right) -i\textrm{sech} \left( \sqrt{\eta }\phi \right) \right) }{\varrho }} \right) ^{-1}\nonumber \\&+{\frac{e_{{1}}\eta \, \left( 1+i\sinh \left( \sqrt{\eta }\phi \right) \right) }{\cosh \left( \sqrt{\eta }\phi \right) \left( \rho \,\cosh \left( \sqrt{\eta }\phi \right) +\sinh \left( \sqrt{\eta }\phi \right) \sqrt{\eta }-i\sqrt{\eta } \right) }}-\frac{1}{2}\,\rho \,e_{{1}} \bigg ) , \end{aligned}$$

(32)

and

$$\begin{aligned} \begin{aligned} {P}_{2,8}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\varpi \,e_{{1}} \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{4}\,{\frac{ \sqrt{\eta } \left( \tanh \left( \frac{1}{4}\,\sqrt{\eta }\phi \right) -\coth \left( \frac{1}{4}\,\sqrt{\eta }\phi \right) \right) }{\varrho }} \right) ^{-1} \\&+\frac{1}{4}\,{\frac{e_{{1}}\eta \, \left( 2\, \left( \cosh \left( \frac{1}{4}\,\sqrt{ \eta }\phi \right) \right) ^{2}-1 \right) }{\cosh \left( \frac{1}{4}\,\sqrt{ \eta }\phi \right) \sinh \left( \frac{1}{4}\,\sqrt{\eta }\phi \right) \left( 2 \,\rho \,\cosh \left( \frac{1}{4}\,\sqrt{\eta }\phi \right) \sinh \left( \frac{1}{4}\, \sqrt{\eta }\phi \right) -\sqrt{\eta } \right) }}-\frac{1}{2}\,\rho \,e_{{1}} \bigg ) . \end{aligned} \end{aligned}$$

(33)

Family. 2.3: Considering $\eta =0, \quad \rho \ne 0$,

$$\begin{aligned} \begin{aligned} {P}_{2,9}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\frac{1}{2}\,\rho \,e_{{1}}-2\,{\frac{e_{{1}}}{\phi \, \left( \rho \,\phi +2 \right) }}+\frac{1}{2}\,{\frac{e_{{1}}{\rho }^{2}\phi }{\rho \,\phi +2}} \bigg ) . \end{aligned} \end{aligned}$$

(34)

Family. 2.4: Considering $\eta =0$, in case when $\rho =\varrho =0$,

$$\begin{aligned} \begin{aligned} {P}_{2,10}(t,x,y)=&trivial \ \ solution . \end{aligned} \end{aligned}$$

(35)

Family. 2.5: Considering $\eta =0$, in case when $\rho =\varpi =0$,

$$\begin{aligned} \begin{aligned} {P}_{2,11}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -{\frac{e_{{1}}}{\phi }} \bigg ) . \end{aligned} \end{aligned}$$

(36)

Family. 2.6: Considering $\rho =\sigma$, $\varpi =\varsigma \sigma (\varsigma \ne 0)$ and $\varrho =0$,

$$\begin{aligned} \begin{aligned} {P}_{2,12}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{1}{2}\,e_{{1}}\sigma \bigg ) . \end{aligned} \end{aligned}$$

(37)

Family. 2.7: Considering $\rho =\sigma$, $\varrho =\varsigma \sigma (\varsigma \ne 0)$ and $\varpi =0$,

$$\begin{aligned} \begin{aligned} {P}_{2,13}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\frac{1}{2}\,{\frac{e_{{1}}\sigma \, \left( \varsigma \,{\textrm{e}^{\sigma \, \phi }}+1 \right) }{-1+\varsigma \,{\textrm{e}^{\sigma \,\phi }}}} \bigg ) . \end{aligned} \end{aligned}$$

(38)

Family. 2.8: Considering $\varpi =0$, $\varrho \ne 0$ and $\rho \ne 0$,

$$\begin{aligned} \begin{aligned} {P}_{2,14}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{1}{2}\,{\frac{\rho \,e_{{1}} \left( -\cosh \left( \rho \,\phi \right) + \sinh \left( \rho \,\phi \right) +s_{{2}} \right) }{-\cosh \left( \rho \,\phi \right) +\sinh \left( \rho \,\phi \right) -s_{{2}}}} \bigg ) , \end{aligned} \end{aligned}$$

(39)

and

$$\begin{aligned} \begin{aligned} {P}_{2,15}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\frac{1}{2}\,{\frac{\rho \,e_{{1}} \left( \sinh \left( \rho \,\phi \right) + \cosh \left( \rho \,\phi \right) -s_{{2}} \right) }{\sinh \left( \rho \, \phi \right) +\cosh \left( \rho \,\phi \right) +s_{{2}}}} \bigg ) . \end{aligned} \end{aligned}$$

(40)

In above solutions, ${\phi }=\lambda x+\mu y+2{p}(\lambda +\mu ) t \quad \text {and} \quad \xi =x+y+ t+\vartheta$.

We get the following innovative families of optical soliton solutions for (7) by taking into account set 3 and applying Eqs. (11) & (3) with the corresponding solution of Eq. (6) shown in Table 1:

Family. 3.1: Considering $\eta <0 \quad \varrho \ne 0$,

$$\begin{aligned} {P}_{3,1}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\psi \,\varpi \, \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}+\frac{1}{2}\,{\frac{ \sqrt{-\eta }\tan \left( \frac{1}{2}\,\sqrt{-\eta }\phi \right) }{\varrho }} \right) ^{-1} -\frac{1}{2}\,{\frac{\psi \,\eta \, \left( 1+ \left( \tan \left( \frac{1}{2}\, \sqrt{-\eta }\phi \right) \right) ^{2} \right) }{\sqrt{-\eta }\tan \left( \frac{1}{2}\,\sqrt{-\eta }\phi \right) -\rho }}+\frac{1}{2}\,\rho \,\psi \bigg ) , \end{aligned}$$

(41)

$$\begin{aligned} {P}_{3,2}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\psi \,\varpi \, \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{2}\,{\frac{ \sqrt{-\eta }\cot \left( \frac{1}{2}\,\sqrt{-\eta }\phi \right) }{\varrho }} \right) ^{-1} +\frac{1}{2}\,{\frac{\psi \,\eta \, \left( \left( \cot \left( \frac{1}{2}\, \sqrt{-\eta }\phi \right) \right) ^{2}+1 \right) }{\sqrt{-\eta }\cot \left( \frac{1}{2}\,\sqrt{-\eta }\phi \right) +\rho }}+\frac{1}{2}\,\rho \,\psi \bigg ) , \end{aligned}$$

(42)

$$\begin{aligned} {P}_{3,3}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\psi \,\varpi \, \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}+\frac{1}{2}\,{\frac{ \sqrt{-\eta } \left( \tan \left( \sqrt{-\eta }\phi \right) +\sec \left( \sqrt{-\eta }\phi \right) \right) }{\varrho }} \right) ^{-1}\nonumber \\&-{\frac{\psi \,\eta \, \left( 1+\sin \left( \sqrt{-\eta }\phi \right) \right) }{\cos \left( \sqrt{-\eta }\phi \right) \left( \sqrt{-\eta } \sin \left( \sqrt{-\eta }\phi \right) -\rho \,\cos \left( \sqrt{-\eta } \phi \right) +\sqrt{-\eta } \right) }}+\frac{1}{2}\,\rho \,\psi \bigg ) , \end{aligned}$$

(43)

and

$$\begin{aligned} \begin{aligned} {P}_{3,4}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\psi \,\varpi \, \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}+\frac{1}{2}\,{\frac{ \sqrt{-\eta } \left( \tan \left( \sqrt{-\eta }\phi \right) -\sec \left( \sqrt{-\eta }\phi \right) \right) }{\varrho }} \right) ^{-1}\\&+{\frac{\psi \,\eta \, \left( \sin \left( \sqrt{-\eta }\phi \right) -1 \right) }{\cos \left( \sqrt{-\eta }\phi \right) \left( \sqrt{-\eta } \sin \left( \sqrt{-\eta }\phi \right) -\rho \,\cos \left( \sqrt{-\eta } \phi \right) -\sqrt{-\eta } \right) }}+\frac{1}{2}\,\rho \,\psi \bigg ) . \end{aligned} \end{aligned}$$

(44)

Family. 3.2: Considering $\eta >0 \quad \varrho \ne 0$,

$$\begin{aligned} {P}_{3,5}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\psi \,\varpi \, \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{2}\,{\frac{ \sqrt{\eta }\tanh \left( \frac{1}{2}\,\sqrt{\eta }\phi \right) }{\varrho }} \right) ^{-1} -\frac{1}{2}\,{\frac{\psi \,\eta \, \left( \left( \tanh \left( \frac{1}{2}\, \sqrt{\eta }\phi \right) \right) ^{2}-1 \right) }{\sqrt{\eta }\tanh \left( \frac{1}{2}\,\sqrt{\eta }\phi \right) +\rho }}+\frac{1}{2}\,\rho \,\psi \bigg ) , \end{aligned}$$

(45)

$$\begin{aligned} {P}_{3,6}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\psi \,\varpi \, \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{2}\,{\frac{ \sqrt{\eta } \left( \tanh \left( \sqrt{\eta }\phi \right) +i\textrm{sech} \left( \sqrt{\eta }\phi \right) \right) }{\varrho }} \right) ^{-1}\nonumber \\&-{\frac{\psi \,\eta \, \left( i\sinh \left( \sqrt{\eta }\phi \right) -1 \right) }{\cosh \left( \sqrt{\eta }\phi \right) \left( \rho \,\cosh \left( \sqrt{\eta }\phi \right) +\sinh \left( \sqrt{\eta }\phi \right) \sqrt{\eta }+i\sqrt{\eta } \right) }}+\frac{1}{2}\,\rho \,\psi \bigg ) , \end{aligned}$$

(46)

$$\begin{aligned} {P}_{3,7}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\psi \,\varpi \, \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{2}\,{\frac{ \sqrt{\eta } \left( \tanh \left( \sqrt{\eta }\phi \right) -i\textrm{sech} \left( \sqrt{\eta }\phi \right) \right) }{\varrho }} \right) ^{-1}\nonumber \\&+{\frac{\psi \,\eta \, \left( 1+i\sinh \left( \sqrt{\eta }\phi \right) \right) }{\cosh \left( \sqrt{\eta }\phi \right) \left( \rho \,\cosh \left( \sqrt{\eta }\phi \right) +\sinh \left( \sqrt{\eta }\phi \right) \sqrt{\eta }-i\sqrt{\eta } \right) }}+\frac{1}{2}\,\rho \,\psi \bigg ) , \end{aligned}$$

(47)

and

$$\begin{aligned} \begin{aligned} {P}_{3,8}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( -\psi \,\varpi \, \left( -\frac{1}{2}\,{\frac{\rho }{\varrho }}-\frac{1}{4}\,{\frac{ \sqrt{\eta } \left( \tanh \left( \frac{1}{4}\,\sqrt{\eta }\phi \right) -\coth \left( \frac{1}{4}\,\sqrt{\eta }\phi \right) \right) }{\varrho }} \right) ^{-1} \\&+\frac{1}{4}\,{\frac{\psi \,\eta \, \left( 2\, \left( \cosh \left( \frac{1}{4}\,\sqrt{ \eta }\phi \right) \right) ^{2}-1 \right) }{\cosh \left( \frac{1}{4}\,\sqrt{ \eta }\phi \right) \sinh \left( \frac{1}{4}\,\sqrt{\eta }\phi \right) \left( 2 \,\rho \,\cosh \left( \frac{1}{4}\,\sqrt{\eta }\phi \right) \sinh \left( \frac{1}{4}\, \sqrt{\eta }\phi \right) -\sqrt{\eta } \right) }}+\frac{1}{2}\,\rho \,\psi \bigg ) . \end{aligned} \end{aligned}$$

(48)

Family. 3.3: Considering $\eta =0, \quad \rho \ne 0$,

$$\begin{aligned} \begin{aligned} {P}_{3,9}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{1}{2}\,\rho \,\psi -2\,{\frac{\psi }{\phi \, \left( \rho \,\phi +2 \right) }} +\frac{1}{2}\,{\frac{\psi \,{\rho }^{2}\phi }{\rho \,\phi +2}} \bigg ) . \end{aligned} \end{aligned}$$

(49)

Family. 3.4: Considering $\eta =0$, in case when $\rho =\varrho =0$,

$$\begin{aligned} \begin{aligned} {P}_{3,10}(t,x,y)=&trivial \ \ solution . \end{aligned} \end{aligned}$$

(50)

Family. 3.5: Considering $\eta =0$, in case when $\rho =\varpi =0$,

$$\begin{aligned} \begin{aligned} {P}_{3,11}(t,x,y)=&-{\frac{\psi \textrm{e}^{\xi i}}{\phi }} . \end{aligned} \end{aligned}$$

(51)

Family. 3.6: Considering $\rho =\sigma$, $\varpi =\varsigma \sigma (\varsigma \ne 0)$ and $\varrho =0$,

$$\begin{aligned} \begin{aligned} {P}_{3,12}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{3}{2}\,\psi \,\sigma \bigg ) . \end{aligned} \end{aligned}$$

(52)

Family. 3.7: Considering $\rho =\sigma$, $\varrho =\varsigma \sigma (\varsigma \ne 0)$ and $\varpi =0$,

$$\begin{aligned} \begin{aligned} {P}_{3,13}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{1}{2}\,{\frac{\psi \,\sigma \, \left( \varsigma \,{\textrm{e}^{\sigma \,\phi } }-3 \right) }{-1+\varsigma \,{\textrm{e}^{\sigma \,\phi }}}} \bigg ) . \end{aligned} \end{aligned}$$

(53)

Family. 3.8: Considering $\varpi =0$, $\varrho \ne 0$ and $\rho \ne 0$,

$$\begin{aligned} \begin{aligned} {P}_{3,14}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{1}{2}\,{\frac{\rho \,\psi \, \left( -3\,\cosh \left( \rho \,\phi \right) + 3\,\sinh \left( \rho \,\phi \right) -s_{{2}} \right) }{-\cosh \left( \rho \,\phi \right) +\sinh \left( \rho \,\phi \right) -s_{{2}}}} \bigg ) , \end{aligned} \end{aligned}$$

(54)

and

$$\begin{aligned} \begin{aligned} {P}_{3,15}(t,x,y)=&\textrm{e}^{\xi i} \bigg ( \frac{1}{2}\,{\frac{\rho \,\psi \, \left( \sinh \left( \rho \,\phi \right) + \cosh \left( \rho \,\phi \right) +3\,s_{{2}} \right) }{\sinh \left( \rho \,\phi \right) +\cosh \left( \rho \,\phi \right) +s_{{2}}}} \bigg ) . \end{aligned} \end{aligned}$$

(55)

In above solutions, ${\phi }=\lambda x+\mu y+2{p}(\lambda +\mu ) t \quad \text {and} \quad \xi =x+y+ t+\vartheta$.

Discussion and graphs

This section displays the various optical soliton patterns discovered in the examined degenerated form of BME called NLSE. We were able to get and examine these waveforms in 2D, contour, and 3D graphs using the RMESEM and the Maple program. When the model is transformed into a NODE using a wave transformation, solutions in exponential, hyperbolic, trigonometric, and rational form are generated. The model creates Hopf bifurcation, rogue, and internal envelope solitons as a result of the elastic and inelastic collision of optical periodic solitons, as the shown graphs demonstrate. The findings of this work are highly important to fiber optics, where an understanding of wave behavior is crucial.

Optical periodic solitons are solitons that maintain a waveform of recurrent oscillations throughout time and space. The development of optical periodic solitons is due to the balance between the dispersion p and the nonlinear effects q, n of the BME. Furthermore, we found that the nonlinearity of the Kerr law causes these optical periodic solitons to collide with each other, whereas rogue waves are created by elastic collisions (maintaining their shape after collision) and internal envelope solitons are created by inelastic interactions (energy distribution). The Hopf Bifurcation in 2D graphs is the transition from a stable point of stability to a limit cycle oscillation due to a change in a parameter. This is a hallmark of nonlinear complex systems, where energy redistribution results in persistent oscillating patterns instead of continuous soliton profiles. Hopf bifurcation states that the nonlinear dynamics of the system are changing due to a crucial balance between dispersion and nonlinearity. This bifurcation is strongly tied to the presence of higher-order nonlinear variables in the BME, which introduce dynamical feedback processes. An internal envelope soliton is produced when optical periodic solitons meet inelastically, trapping energy inside an envelope. Nonlinear interactions within a wave packet produce localized structures known as internal envelope solitons. They appear as a soliton inside a larger wave envelope. The dispersion p and the higher-level nonlinear term $q |{P}|^{2} {P}$ help to gradually stabilize this structure. These kinds of structures are frequently seen in non-Kerr optical media and Bose-Einstein condensates. Rogue waves are large, unexpected waveforms that momentarily emerge from a train of apparently regular waves. They have amplitudes that are noticeably larger than those of the surrounding waves and are limited in both space and time. Associated with this phenomenon is modulation instability (MI), which is a characteristic of the non-Kerr law nonlinearity of the model. The emergence of rogue waves after elastic collisions suggests the nonlinear energy concentrating mechanism in BME because the BME contains a higher-level nonlinearity term $q |{P}|^{2} {P}$, which can modulate energy distribution and cause rogue wave emergence in situations where solitons focus the energy they produce locally. Lastly, for norms |P| of the obtained optical soliton reveal dark and bright kink structures. The dark soliton has a dip while the bright is localized soliton which shows peak. These solitons show the intensities of the obtained optical solitons.

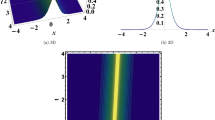
We visually depicted real, imaginary and absolutes of a set of optical solitons. Overall, the profiles of real and imaginary plots show the collision of optical periodic and other solitons while the profiles of norm |P| showed their colliding intensity. These figures have been generated by choosing particular values for the specified and constraint-related parameters that were obtained via the model and solution procedure, and by giving the free parameters random values. The dynamic behavior of the resulting soliton solutions under different parametric selections, such as the generation of envelope solitons, rogue waves, and bifurcating structures, may be observed and verified using this method. Instead of being restricted to preset parameter sets, a wider investigation of solution features is made possible by employing the application of arbitrary values inside a physically feasible range. Moreover, in Figs. 1, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{1,3}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{1,3}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the intensity profiles $|{P}_{1,3}(t,x,y)|$ of ${P}_{1,3}(t,x,y)$ given in (17) at $\varpi = 1, \rho = 1, \varrho = 2, \lambda = 0.0025, \mu = 0.0035, p = 0.005, \vartheta = 0.5, t = 1, e_{0} = 1$. Moreover, the Hopf bifurcations in 2D are shown for $y=0$. Overall, the real and imaginary parts reveal the formation of internal envelope due to the inelastic collisions of optical solitons. In Fig. 2, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{1,6}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{1,6}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the intensity profiles $|{P}_{1,6}(t,x,y)|$ of ${P}_{1,6}(t,x,y)$ given in (20) at $\varpi = 2$, $\rho = 5$, $\varrho = 2$, $\lambda = 0.005$, $\mu = 0.001$, $\vartheta = 1, t = 0$, $e_{0} = 2$. Moreover, the 2D profiles are shown for $x=1$. Overall, the real and imaginary parts reveal the elastic collisions of optical periodic solitons. In Fig. 3, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{1,9}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{1,9}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the intensity profiles $|{P}_{1,9}(t,x,y)|$ of ${P}_{1,9}(t,x,y)$ given in (23) at $\varpi = 5, \rho = 10, \varrho = 5, \lambda = 0.004, \mu = 0.0025, p = 0.15, \vartheta = 2, t = 10, e_{0} = 5$. Moreover, the 2D profiles are shown for $y=0$. Overall, the real and imaginary parts reveal the formation of internal envelope due to the inelastic collisions of optical solitons. In Fig. 4, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{2,5}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{2,5}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the intensity profiles $|{P}_{2,5}(t,x,y)|$ of ${P}_{2,5}(t,x,y)$ given in (30) at $\varpi = 4, \rho = 5, \varrho = 1, \lambda = 0.001, \mu = 0.002, p = 0.075, \vartheta = 1, t = 10, e_{1} = 2$. Moreover, the Hopf bifurcations in 2D are shown for $y=0$. Overall, the real and imaginary parts reveal the elastic collisions of optical periodic solitons. In Fig. 5, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{2,8}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{2,8}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the intensity profiles $|{P}_{2,8}(t,x,y)|$ of ${P}_{2,8}(t,x,y)$ given in (33) at $\varpi = 8, \rho = 10, \varrho = 2, \lambda = 0.035, \mu = 0.065, p = 0.015, \vartheta = 5, t = 20, e_{1} = 5$. Moreover, the 2D dynamics are shown for $x=1$. Overall, the real and imaginary parts reveal the formation of internal envelope due to the elastic collisions of optical periodic solitons. In Fig. 6, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{2,12}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{2,12}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the intensity profiles $|{P}_{2,12}(t,x,y)|$ of ${P}_{2,12}(t,x,y)$ given in (37) at $\varsigma = 2, \sigma = 5, \varpi = \varsigma \sigma , \rho = \sigma , \varrho = 0, \lambda = 0.0025, \mu = 0.0015, p = 0.935, \vartheta = 1, t = 50, e_{1} = 1$. Moreover, the 2D profiles are shown for $y=1$. Overall, the real and imaginary parts reveal the elastic collisions of optical periodic solitons. In Fig. 7, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{3,4}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{3,4}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the intensity profiles $|{P}_{3,4}(t,x,y)|$ of ${P}_{3,4}(t,x,y)$ given in (44) at $\varpi = 2$, $\rho = 2$, $\varrho = 1$, $\lambda = 0.0065$, $\vartheta = 5$, $t = 100$, $d_{0} = 2$, $e_{0} = 1$, $p = 0.005$, $q = 1$, $\mu = 0.002$. Moreover, the Hopf bifurcations in 2D are shown for $y=0.5$. Overall, the real and imaginary parts reveal the inelastic collisions of optical periodic solitons. In Fig. 8, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{3,6}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{3,6}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the intensity profiles $|{P}_{3,6}(t,x,y)|$ of ${P}_{3,6}(t,x,y)$ given in (46) at $\varpi = 5, \rho = 6, \varrho = 1, \lambda = 0.00775, p = 0.0155, \vartheta = 10, t = 5, \mu = 0.001, q = 1$. Moreover, the Hopf bifurcations in 2D are shown for $y=1$. Overall, the real and imaginary parts reveal the formation of rogue wave due to the elastic collisions of optical periodic solitons. Finally in Fig. 9, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{3,15}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{3,15}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the intensity profiles $|{P}_{3,15}(t,x,y)|$ of ${P}_{3,15}(t,x,y)$ given in (55) at $\varpi = 0, \rho = 10, \varrho = 1, \lambda = 0.0085, p = 0.0025, \vartheta = 5, t = 10, q = 2, \mu = 0.002, s_2 = 1$. Moreover, the Hopf bifurcations in 2D are shown for $y=5$. Overall, the real and imaginary parts reveal the formation of rogue wave due to the elastic collisions of optical periodic solitons.

Fig. 1

In this figure, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{1,3}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{1,3}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the bright shaped intensity profiles $|{P}_{1,3}(t,x,y)|$ of ${P}_{1,3}(t,x,y)$ given in (17) at $\varpi = 1, \rho = 1, \varrho = 2, \lambda = 0.0025, \mu = 0.0035, p = 0.005, \vartheta = 0.5, t = 1, e_{0} = 1$. Moreover, the 2D plots are shown for $y=0$.

Fig. 2

In this figure, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{1,6}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{1,6}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the singular dark-bright shaped intensity profiles $|{P}_{1,6}(t,x,y)|$ of ${P}_{1,6}(t,x,y)$ given in (20) at $\varpi = 2, \rho = 5, \varrho = 2, \lambda = 0.005, \mu = 0.001, p = 0.002, \vartheta = 1, t = 0, e_{0} = 2$. Moreover, the 2D profiles are shown for $x=1$.

Fig. 3

In this figure, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{1,9}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{1,9}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the bright shaped intensity profiles $|{P}_{1,9}(t,x,y)|$ of ${P}_{1,9}(t,x,y)$ given in (23) at $\varpi = 5, \rho = 10, \varrho = 5, \lambda = 0.004, \mu = 0.0025, p = 0.15, \vartheta = 2, t = 10, e_{0} = 5$. Moreover, the 2D profiles are shown for $y=0$.

Fig. 4

In this figure, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{2,5}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{2,5}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the dark v-shaped intensity profiles $|{P}_{2,5}(t,x,y)|$ of ${P}_{2,5}(t,x,y)$ given in (30) at $\varpi = 4, \rho = 5, \varrho = 1, \lambda = 0.001, \mu = 0.002, p = 0.075, \vartheta = 1, t = 10, e_{1} = 2$. Moreover, the Hopf bifurcations in 2D are shown for $y=0$.

Fig. 5

In this figure, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{2,8}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{2,8}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the bright shaped intensity profiles $|{P}_{2,8}(t,x,y)|$ of ${P}_{2,8}(t,x,y)$ given in (33) at $\varpi = 8, \rho = 10, \varrho = 2, \lambda = 0.035, \mu = 0.065, p = 0.015, \vartheta = 5, t = 20, e_{1} = 5$. Moreover, the 2D dynamics are shown for $x=1$.

Fig. 6

In this figure, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{2,12}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{2,12}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the dark-bright shaped intensity profiles $|{P}_{2,12}(t,x,y)|$ of ${P}_{2,12}(t,x,y)$ given in (37) at $\varsigma = 2, \sigma = 5, \varpi = \varsigma \sigma , \rho = \sigma , \varrho = 0, \lambda = 0.0025, \mu = 0.0015, p = 0.935, \vartheta = 1, t = 50, e_{1} = 1$. Moreover, the 2D profiles are shown for $y=1$.

Fig. 7

In this figure, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{3,4}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{3,4}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the dark shaped intensity profiles $|{P}_{3,4}(t,x,y)|$ of ${P}_{3,4}(t,x,y)$ given in (44) at $\varpi = 2, \rho = 2, \varrho = 1, \lambda = 0.0065, \vartheta = 5, t = 100, d_{0} = 2, e_{0} = 1, p = 0.005, q = 1, \mu = 0.002$. Moreover, the Hopf bifurcations in 2D are shown for $y=0.5$.

Fig. 8

In this figure, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{3,6}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{3,6}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the kink shaped intensity profiles $|{P}_{3,6}(t,x,y)|$ of ${P}_{3,6}(t,x,y)$ given in (46) at $\varpi = 5, \rho = 6, \varrho = 1, \lambda = 0.00775, p = 0.0155, \vartheta = 10, t = 5, \mu = 0.001, q = 1$. Moreover, the Hopf bifurcations in 2D are shown for $y=1$.

Fig. 9

In this figure, a. 3D, b. contour and c. 2D depict the dynamics of $Re({P}_{3,15}(t,x,y))$, d. 3D, e. contour and f. 2D depict the dynamics of $Im({P}_{3,15}(t,x,y))$ whereas g. 3D, h. contour and i. 2D depict the kink shaped intensity profiles $|{P}_{3,15}(t,x,y)|$ of ${P}_{3,15}(t,x,y)$ given in (55) at $\varpi = 0, \rho = 10, \varrho = 1, \lambda = 0.0085, p = 0.0025, \vartheta = 5, t = 10, q = 2, \mu = 0.002, s_2 = 1$. Moreover, the Hopf bifurcations in 2D are shown for $y=5$.

Phase portraits and chaotic analysis of the governing system

In order to illustrate the chaotic and periodic analysis of the dynamical system, this portion presents phase portraits utilizing bifurcation analysis and time-series analysis.

Phase portraits and hopf bifurcation analysis

We study the emergent dynamical system of the model using the notions of bifurcation theory. The planar dynamical system of Eq. (10) is shown as follows:

$$\begin{aligned} \begin{aligned}&\mathfrak {P}=Z, \\&g(Z,W)= Z'=W ,\\&h(Z,W)=W'=K_1 Z-K_2 Z^3,\\ \end{aligned} \end{aligned}$$

(56)

while, the perturbed dynamical system that is obtained from planner system (56) perturbed with generalized sine function $\sin _m(\delta \phi )$³⁷ is expressed as follows:

$$\begin{aligned} \begin{aligned}&s(Z,W)= Z'=W ,\\&v(Z,W)=W'=K_1 Z-K_2 Z^3+l_0 \sin _m(\delta \phi ),\\ \end{aligned} \end{aligned}$$

(57)

where degree and frequency of the applied external force are represented by the parameters $l_0$ and $\delta$, respectively. Moreover, in above systems

$$\begin{aligned} \begin{aligned}&K_1={\frac{\kappa +2\,{p}-1}{{p} \left( {\lambda }^{2}+{\mu }^{2} \right) }} ,\\&K_2= {\frac{{q}}{{p} \left( {\lambda }^{2}+{\mu }^{2} \right) }} .\\ \end{aligned} \end{aligned}$$

(58)

The planner system exhibits the following Hamiltonian under a specific integral:

$$\begin{aligned} H(Z,W)=\frac{W^2}{2}-\frac{K_1 Z^2}{2}+\frac{K_2 Z^4}{4}. \end{aligned}$$

(59)

For (56), we study the bifurcations of phase portraits in the parameterized space represented by $K_1$ and $K_2$ in the presence of the Hamiltonian constant. The dynamical system analysis along the Z-axis identifies three equilibrium points: $(M_0, 0)$, $(M_1, 0)$, and $(M_2, 0)$, where $M_1$ and $M_2$ are stated as:

$$\begin{aligned} M_0=0, \quad M_1= \sqrt{\frac{K_1}{K_2}}, \quad M_2=-\sqrt{\frac{K_1}{K_2}}. \end{aligned}$$

(60)

Additionally, based on the Jacobian matrix:

$$\begin{aligned} J= \left[ \begin{array}{cc} \frac{\partial g}{\partial Z}& \frac{\partial g}{\partial W}\\ \frac{\partial h}{\partial Z}& \frac{\partial h}{\partial W} \end{array} \right] , \end{aligned}$$

(61)

The system’s Jacobian is:

$$\begin{aligned} |J(Z,W)|=3K_2Z^2-K_1 . \end{aligned}$$

(62)

At an equilibrium point $(M_i,0)$, the eigenvalues $\lambda$ satisfy:

$$\begin{aligned} \lambda = \pm \sqrt{ K_1- 3K_2Z_i^2}, \end{aligned}$$

(63)

which governs the type of equilibrium (center, saddle etc.). Since the linearized dynamics dominate near an equilibrium, thus we discuss the Lyapunov exponents analytically at all equilibria from the eigenvalues of Jacobian matrix represented by (63) as:

• If $K_1- 3K_2Z_i^2<0$, eigenvalues are purely imaginary implies both exponents are zero (i.e. neutrally stable periodic orbit) and the equilibrium point is center.

• If $K_1- 3K_2Z_i^2>0$, eigenvalues are real implies Lyapunov exponents are those real parts i.e. $\lambda _1= -\sqrt{ K_1- 3K_2Z_i^2}$ and $\lambda _2= \sqrt{ K_1- 3K_2Z_i^2}$ and the equilibrium point is saddle.

• If $K_1- 3K_2Z_i^2=0$, we get degenerated equilibrium which needs higher dimension analysis.

We now evaluate the Hopf bifurcation at all equilibria using the eigenvalues of the Jacobean matrix.

1. At $(M_0,0)$: At (0, 0), (63) yields:

$$\begin{aligned} \lambda = \pm \sqrt{K_1}. \end{aligned}$$

(64)

Thus we conclude:

• If $K_1<0$ then the eigenvalue is pure imaginary $\rightarrow \quad (0,0)$ is the centre which implies possibility of a Hopf bifurcation candidate.

• If $K_1>0$ then the eigenvalues are real of opposite signs $\rightarrow \quad (M_0,0)$ is the saddle and implies instability.

As Hopf bifurcation occurs when the real part of a pair of complex conjugate eigenvalues crosses zero, thus, we conclude that when we increase $K_1$ through zero, the real part changes from imaginary to real which implies a Hopf bifurcation may occur at $K_1=0$ (with $K_2>0$ to ensure bounded cubic nonlinearity).

2. Non-zero Equilibria $(M_i,0), \ \ i=1,2$: At these equilibria, eigenvalues satisfy:

$$\begin{aligned} \lambda ^2= -2 K_1, \end{aligned}$$

(65)

Thus we conclude:

• If $K_1>0$ then the eigenvalue is pure imaginary $\rightarrow \quad (M_i,0)$ is the centre which implies possibility of a Hopf bifurcation candidate.

• If $K_1<0$ then the eigenvalues are real of opposite signs $\rightarrow \quad (M_i,0)$ is the saddle and implies instability.

Thus, we conclude that when we decrease $K_1$ through zero, the real part changes from imaginary to real which implies a Hopf bifurcation may occur at $K_1=0$.

Fig. 10

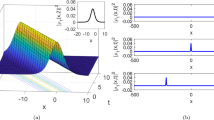
Phase portrait of (56) for $\kappa = 1, {p} = 2, {q} = 2, \lambda = 1, \mu = 3$ with initial conditions $Z(0)=0,W(0)=0.5$.

Remark 1

The phase portrait for (56) in Fig. 10 represents an eight-like homoclinic loop with two centers at $(M_1,0)=(\sqrt{2},0)$ and $(M_2,0)=(-\sqrt{2},0)$ and with a saddle point (0, 0). The phase portrait for (56) in Fig. 11 represents a closed loop with center at (0, 0). The phase portrait for (56) in Fig. 12 represents an eight like homoclinic loop with two centers at $(M_1,0)=(\sqrt{2},0)$ and $(M_2,0)=(-\sqrt{2},0)$ and with a saddle point (0, 0). The phase portrait for (56) in Fig. 13 represents an oval-like limit cycle with center at (0, 0). Finally, the phase portrait for (56) in Fig. 14 represents an eight-like homoclinic loop with two centers at $(M_1,0)=(\sqrt{2},0)$ and $(M_2,0)=(-\sqrt{2},0)$ and with a saddle point (0, 0). The system seems to be acting periodically based on the closed loops and limit cycles centered at the equilibrium point (0, 0) in the phase portrait of (56) in Figs. 11 and 13. This might be interpreted as a dynamic, organized development resulting from energy exchange and the interplay of several solitonic modes. Similarly, closed eight-like homoclinic orbits with centers at $(M_1,0)$ and $(M_2,0)$ in the lobes and with saddle point at (0, 0) are seen in the phase portrait of (56) in Figs. 10, 12 and 14. These phase portraits do not imply chaos as they imply periodic motion inside lobes (represented by closed orbits around each center) which are separated by the homoclinic separatrix. The existence of restricted or constrained periodic motion is indicated by closed loops in the phase portraits. This indicates the presence of persistent soliton cycles, which means that the energy of waves is caught in a repeated motion without dissipating, rather than decaying or growing forever. Instead, the system shifts in a predictable manner. Nonlinear Hamiltonian systems, that preserve energy over time, often exhibit this behavior.

Fig. 11

In this figure, a. quiver plot and b. stream plot represent phase portrait of (56) while c. stream plot represents phase portrait of (57) for $\kappa = -5, {p} = 1, {q} = 1, \lambda = 5, \mu = 1$ with initial conditions $Z(0)=0.1,W(0)=0.1$.

Fig. 12

In this figure, a. quiver plot and b. stream plot represent phase portrait of (56) while c. stream plot represents phase portrait of (57) for $\kappa = 1, p = 1, q = 1, \lambda = 1, \mu = 0$ with initial conditions $Z(0)=0.1,W(0)=0$.

Fig. 13

In this figure, a. quiver plot and b. stream plot represent phase portrait of (56) while c. stream plot represents phase portrait of (57) for $\kappa = 1, p = 1, q = 1, \lambda = 1, \mu = 0$ with initial conditions $Z(0)=1.2,W(0)=0$.

Fig. 14

In this figure, a. quiver plot and b. stream plot represent phase portrait of (56) while c. stream plot represents phase portrait of (57) for $\kappa = 1, p = 1, q = 1, \lambda = 1, \mu = 0$ with initial conditions $Z(0)=0,W(0)=1$.

Chaotic analysis

Throughout this investigation, we have used (57) to examine the chaotic dynamics in the governing system. Using the Gillion transformation, we apply a perturbation term to the planar dynamical system created by converting (10) in order to disrupt the system’s periodic motion and get useful findings of chaotic behavior. To understand this phenomena, a number of techniques from the corpus of current research are employed, including the Lyapunov exponent, time series, Poincaré map, and phase portrait approaches, to show that the model underlying the perturbed dynamical system exhibits chaotic or periodic behavior. The presence of chaotic/periodic dynamics in the perturbed nonlinear system is shown by time-series maps presented by Figs. 15, 16, 17, 18,19 with different initial conditions and with additional suitable parameter values.

Fig. 15

The a. fractal-periodic and b. periodic patterns in perturbed system (57) for $\kappa = 1, {p} = 2, {q} = 2, \lambda = 1, \mu = 3, l_0 = 2, \delta = 2 \pi , m=3$ with initial conditions $Z(0)=0,W(0)=0.5$.

Fig. 16

The a. quasi-periodic and b. quasi-periodic patterns in perturbed system (57) for $\kappa = -5, {p} = 1, {q} = 1, \lambda = 5, \mu = 1, l_0 = 5, \delta = \pi , m=2$ with initial conditions $Z(0)=0.1,W(0)=0.1$.

Fig. 17

The a. quasi-periodic and b. periodic patterns in perturbed system (57) for $\kappa = 1, p = 1, q = 1, \lambda = 1, \mu = 0, l_0 = 0, \delta = \pi , m=4$ with initial conditions $Z(0)=0.1,W(0)=0$.

Fig. 18

The a. quasi-periodic and b. quasi-periodic patterns in perturbed system (57) for $\kappa = 1, p = 1, q = 1, \lambda = 1, \mu = 0, l_0 = 0, \delta = \pi , m=7$ with initial conditions $Z(0)=1.2,W(0)=0$.

Fig. 19

The a. quasi-periodic and b. periodic patterns in perturbed system (57) for $\kappa = 1, p = 1, q = 1, \lambda = 1, \mu = 0, l_0 = 0, \delta = \pi , m=10$ with initial conditions $Z(0)=0,W(0)=1$.

Remark 2

The periodic, quasi-periodic and fractal-periodic oscillations in the time-series plots represented by Figs. 15, 19 for different parameters values and initial conditions are probably due to the complex temporal and spatial growth of the produced periodic solitons. The periodicity of the curve may represent this underlying structure, as periodic solitons show oscillating behavior in both space and time. In Hamiltonian analysis, periodic oscillations show that, despite the system’s complexity and nonlinearity, it exhibits predictable, recurring patterns as opposed to completely chaotic behavior. The quasi-periodic and fractal-periodic cycles in Hamiltonian analysis on the other hand, indicate that the framework is in a state of transition between chaos and order. however, based on the overall time-series plots, the overall system of (57) is periodic but possesses weak chaoticness as revealed by fractal structures.

Conclusion

To summarize, the objective of this work was to investigate optical soliton phenomena in a (2+1)-dimensional Schrödinger class nonlinear model that degenerates from BME, which has particular significance in the fiber optics field. By using a complex structured wave transformation, the proposed anstaz namely RMESEM developed NODE and constraint relations for Kerr law nonlinearity form of the model. The resulting NODE was expected to have a close form solution that converted it into a system of nonlinear algebraic equations via substitution in order to identify fresh plethora of optical soliton solutions. The final visualizations of the obtained optical soliton solutions in the form of 3D, contour, and 2D forms demonstrated that the model develops Hopf bifurcation, rogue and internal envelope solitons as a result of the elastic and inelastic collision of optical periodic solitons while the norms |P| of the obtained optical soliton revealed dark and bright kink structures. Additionally, using phase portraits and time-series maps, we examined bifurcating and chaotic behavior, noting its existence in the dynamical system that was disrupted and obtained positive results that indicated periodicity and Hopf bifurcation. We used a generalized trigonometric function to perturb the planner system for the first time in order carry out chaotic analysis. Additionally, our findings were examined and connected to the soliton dynamics in NLSE, proving that the proposed approach is a successful way to find new soliton phenomena in these nonlinear settings. It should be highlighted, nonetheless, that the suggested approach fails if the largest nonlinear component and the greatest derivative terms do not balance homogeneously. In this case, the technique is unable to balance the nonlinear term with dispersion, which prevents the generation of solitons. Notwithstanding this limitation, the present investigation demonstrates that the methodology employed in this work is highly dependable and successful for nonlinear problems across a range of scientific domains. Finally, the current study aims to carry out a more thorough examination of the stability analysis of solitons in both integer and fractional orders within the parameters of the proposed model in the future.