Enhanced model inversion via frequency disentanglement and latent space optimization

Abstract

Model inversion attacks, which aim to reconstruct private training images from a target model’s outputs, highlight the privacy risks in artificial intelligence systems. Existing methods, relying on generative adversarial networks, face challenges such as frequency-feature coupling, random latent-space sampling with initial points distant from the target identity, and insufficient loss functions for optimizing difficult samples. To address these, this paper proposes three core innovations: frequency decoupling, Top-K initialization, and dynamic focus boundary loss. Specifically, learnable filters disentangle and fuse features at multiple scales, achieving fine-grained frequency decomposition. Top-K initialization retains the best latent codes for each identity, constructing precise latent vectors. The dynamic focus boundary loss, inspired by focal loss, prevents overfitting to easy samples and focuses on difficult ones. Experiments on CelebA, FFHQ, and FaceScrub datasets demonstrate that our method significantly enhances attack performance, especially under large data-distribution shifts.

Introduction

With the rapid development of Deep Neural Networks (DNN), they have been widely used in computer vision, natural language processing, health care, and other fields. However, the high performance of DNNs usually depends on the training of private datasets. Recent privacy attack studies have shown that^2,3,4 model inversion attacks can successfully reconstruct private datasets used for training by using target classification models. Model inversion attacks are divided into white-box and black-box^5,6,7,8 models. This paper will focus on the problem of face image reconstruction under white-box settings. Under the white-box assumption, the attacker has full access to the target model.

Early studies^9,10,11,33 revealed the risk of DNN leaking private data and formalized it as an optimization problem, which realized the sensitive feature values that were as highly likely as possible under the target model by iteratively optimizing data samples in the input space. Subsequent studies have used GAN to improve the efficiency and quality of private data image reconstruction and promote defense¹² technology. Existing MIAs mainly rely on the prior knowledge of the generative model, and the effect of the generative model obtaining prior knowledge from the public data set directly affects the attack performance. From the perspective of model training paradigm, the existing methods mainly cover three types: unsupervised^13,14,35, semi-supervised¹⁵ and supervised^16,18,20 learning frameworks. Compared with semi-supervised and unsupervised training, supervised training can make better use of category information and provide clearer guidance in spatial search. In recent years, research has gradually shifted from white-box to black-box models. However, both white-box¹⁹ and black-box^20,21 attacks in MIA tend to use generative models trained in a supervised manner, and the choice of generative models is more inclined to diffusion models. Although diffusion models show excellent performance in generative ability, the long training time is still a major defect. In this paper, the supervised training GAN is used to achieve excellent attack performance without sacrificing efficiency. Although the existing white-box model MIA has achieved certain results, it still has the following shortcomings:

• 1. Traditional generative adversarial networks lack the ability to explicitly separate frequency band features, resulting in the coupling of low-frequency and high-frequency features within the class, as illustrated in Fig. 1; and the existing conditional normalization of MIA only provides global category guidance, lacking targeted processing of local details and different frequency features.

• 2. Existing model inversion attacks generally adopt a random initialization strategy, but the initial sampling points have no semantic association with any category manifold. To improve the confidence of the target model, the optimization process often amplifies the activation along any direction, causing the potential vector to escape to the outside of the manifold, and finally the generated image deviates from the real data area.

• 3. Previous MIA used the maximum margin loss function as the optimization objective. However, when there is a large difference in data distribution, the maximum margin loss has limited exploration capability in the latent space and cannot focus on those samples that are difficult to recover. This leads to poor performance of the generator when dealing with these difficult samples, thereby affecting the overall attack performance.

Nevertheless, current MIAs still share three core limitations: coupled high- and low-frequency features, random latent codes that easily drift outside the class manifold, and uniform margin losses that neglect hard samples. Existing white-box MIAs have not yet simultaneously solved these three problems. This paper explicitly addresses them by integrating frequency-disentangled generation, manifold-aware Top-K initialization, and difficulty-weighted boundary loss into one unified framework.

Fig. 1

Potential search space for different MI attacks.

To solve the above limitations, this paper proposes an improved model inversion attack method. First, a learnable low-pass-high-pass filter is introduced into cGAN to decompose image features¹ into high-frequency and low-frequency components to realize the explicit separation and processing of different frequency features and avoid the coupling of low-frequency and high-frequency features in the generation process. Then, the label embedding features²² are fused with the image features at multiple scales to provide richer category guidance for the generator, which can more finely control the image generation process and ensure that the generator can capture the detail features related to specific categories at different frequency levels. Secondly, the top K latent codes are retained after the generated samples are scored by the target model, and the mean perturbation is used as the starting point to limit the optimization space to the surrounding range of the corresponding category. Finally, a dynamic focal boundary loss is proposed, which pays more attention to the recovery of difficult samples. By dynamically adjusting the focus of the loss, the optimization process pays more attention to those samples that are difficult to recover, thereby improving the overall attack success rate. The contributions are summarized as follows:

• 1. A generator architecture based on frequency band decoupling and label fusion is proposed to improve the detail and semantic consistency of reconstructed images through multi-frequency feature fusion.

• 2. Top K anchor initialization is proposed to replace random initialization, which anchors the optimization starting point in the real manifold to prevent it from deviating from the real data area.

• 3. A dynamic focal boundary loss is proposed to replace the maximum boundary loss. The deficiency of the existing loss function in dealing with difficult samples and large differences in data distribution, which cannot effectively explore the potential space, is solved.

The experimental results show that the attack method improves the attack performance in various data sets and model architectures and still maintains excellent attack effect in the case of significant distribution differences between public and private data.

Related technologies

Model inversion attack

Fredrikson et al.¹⁰ first studied model inversion attacks in the context of genomic privacy. GMI²³ proposed an inversion attack on the generative model and successfully reconstructed the high-dimensional data. KED_MI¹⁵ proposed to model the private data distribution for each target category instead of optimizing a single data point, and VMI¹³ regarded the optimization process of the attack as variational optimization and performed variational inference. PPA and IF_MI^14,35 use StyleGAN pre-trained on public datasets to attack the target model. LOMMA²⁴ uses knowledge distillation technology to achieve model enhancement, improve the generalization ability of attacks, and alleviate overfitting. PLG_MI¹⁶ uses Conditional Generative Adversarial Network (cGAN) to realize category decoupling, solve the problem of feature coupling of different categories in the latent space, and effectively improve the attack performance under the setting of large data distribution difference. CMD_MI¹⁹ introduces the conditional diffusion model into the white-box scenario and approaches the target distribution through the two-step strategy of pre-training-fine-tuning, to achieve the balance between attack accuracy and fidelity. However, CMD_MI not only takes a long time in the training stage of the diffusion model but also needs an additional 8–10 h for training in the fine-tuning stage, and the attack accuracy is high. However, the method in this paper can consider both accuracy and fidelity without sacrificing efficiency.

Methodology

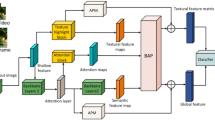
Our attack method is primarily developed to address the limitations of the generator architecture, latent vector sampling, and the attack loss function. Innovations have been made in three key aspects: First, a Frequency Decomposition Fusion Block (FDFB) has been incorporated into the cGAN architecture to enhance the model’s ability to process information at different frequencies. Second, a latent vector initialization method based on Top K class centers has been proposed to improve the sampling efficiency of the latent space. Third, a dynamic focal boundary loss function has been designed to optimize the loss calculation during the attack process. An overview of the attack method is shown in Fig. 2. The specific implementations and advantages of these three methods will be detailed in the order mentioned above.

Fig. 2

Overview diagram of attack methods.

Frequency-band decomposition fusion block

Design of frequency band decoupling fusion block

Inspired by the idea of wavelet transform^17,25, a frequency decomposition fusion block (FDFB) is introduced into cGAN. The core objective is to explicitly divide the intra-class feature space of the generator through frequency band decomposition¹ and pseudo-label fusion and enhance the class-related feature expression by using multi-scale conditional injection to improve the quality of reconstructed images in the inversion attack process. Traditional wavelets use predefined fixed filter banks, while the convolution kernels of FDFB are automatically optimized by backpropagation to achieve parameter learnability. Secondly, the label condition injection is used to introduce the category information into the frequency band, and the high and low frequency components are scaled differently to realize the task-oriented frequency band optimization. The detailed design is shown in Fig. 3.

• 1. Frequency band decoupling: The input image features$F \in {R^{C \times H \times W}}$are decomposed into low-frequency (global structure) components and high-frequency components (local details). The low-frequency components capture the key attributes of the identity to ensure the global semantic consistency of the generated image, and the high-frequency components refine the details of the intra-class diversity to avoid intra-class feature confusion.

$$\begin{gathered} {F_{low}}={\text{Con}}{{\text{v}}_{low}}(F) \hfill \\ {F_{high}}={\text{Con}}{{\text{v}}_{high}}(F - {F_{low}}) \hfill \\ \end{gathered}$$

(1)

where ${\text{Con}}{{\text{v}}_{low}}$ and ${\text{Con}}{{\text{v}}_{high}}$ are both depth-wise separable convolution layers, and the filter bank with band selection characteristics is constructed through the adaptive learning of convolution kernel weights, which respectively simulates the low-pass and high-pass filtering behaviors in the frequency domain. The low-pass is used to retain the overall structure and smooth information of the image, and the high-pass is used to capture the edge details.

Fig. 3

Frequency-band decomposition fusion block.

• 2. Label embedding feature fusion: The category label y is mapped to the class feature vector $E(y) \in {R^D}$,and expanded to the same dimension as the feature map through the spatial broadcast mechanism, and spliced with the low-frequency ${F_{low}}$component and the high-frequency ${F_{high}}$ component respectively. After splicing, the channel is compressed through 1 × 1 convolution to retain the main frequency band features. Finally, the fused low-frequency and high-frequency features are superimposed:

  $${F_{fused}}={\text{Concat}}({F_{low}},E(y))+{\text{Concat}}({F_{high}},E(y))$$

  (2)

• 3. Multi-scale optimization: In this paper, the FDFB module is inserted into each up-sampling block (Block2 to Block5) of the generator, as shown in Fig. 4. Multi-scale condition injections can enhance the class-related feature expression, make up for the deficiency of cgan in the processing of local details, and adopt the progressive feature processing strategy to gradually refine the frequency domain features from the deep layer to the shallow layer.

Fig. 4

Improved generator architecture.

Quantitative analysis of frequency-domain segmentation processing

To verify the necessity of explicitly decomposing image features into low-frequency and high-frequency components, this paper quantitatively analyzes three types of images in the frequency domain: real private images, reconstructed images attacked by non-frequency-division.

generators, and reconstructed images attacked by frequency-division generators. Specifically, each group of images$\:\text{I}$is subjected to two-dimensional discrete Fourier transform to obtain the frequency domain representation $F(I)$, and the low-frequency and high-frequency regions are divided by a circle with the spectral center as the center and the radius r = 16. The low/high energy ratio (LHR) is used as a quantitative index of the coupling strength between low and high frequencies to verify the rationality of the frequency division strategy. The formula is as follows:

$${\text{LHR}}=\frac{{\sum\limits_{{\omega \in {\Omega _{low}}}} {{{\left| {FL(I)(\omega )} \right|}^2}} }}{{\sum\limits_{{\omega \in {\Omega _{high}}}} {{{\left| {FL(I)(\omega )} \right|}^2}} +\epsilon }}$$

(3)

Lower LHR values signify better high-frequency detail preservation and higher image quality, while higher values indicate greater detail loss and poorer quality. The first 200 categories were extracted from the CelebA private training dataset and the reconstructed images of the two attack methods, and 5 images were randomly selected from each category for calculation. Table 1 shows the LHR statistics of the three types of data. As can be seen from the table, the LHR of the generated image without frequency division is 273.94, which is significantly higher than 232.70 of the real image, indicating that the high-frequency details of the image are seriously suppressed and the low-frequency information is excessively dominant during the generation process without frequency division, resulting in the decline of image quality. After frequency decomposition, the LHR falls from 273.94 to 232.23 closer to the real-image value of 232.70 and the standard deviation shrinks from 124.12 to 95.61. These results indicate that, although the ratio still exhibits a certain gap to the real-image level, the strategy reduces low- and high-frequency coupling and.

Table 1 LHR for three image categories.

improves the frequency-domain fidelity of reconstructed images relative to the unfiltered baseline; in other words, it alleviates the coupling problem to a certain extent.

In addition, Fig. 5 shows the spectral comparison of three images of the same category. The LHR of the non-frequency-separated image is significantly higher than that of the real image, with an overly bright spectral center and a dim peripheral high-frequency area, indicating severe coupling between low and high frequencies. In contrast, the image reconstructed after frequency separation shows a significant increase in energy density outside the circle, with the low-frequency falling back and the high-frequency rising. The LHR value drops from 343 to 287, which is closer to the real image’s 190. In other words, the overall spectral distribution is closer to that of the real image.

Fig. 5

Spectral comparison of images within the same category.

Top K class-centric initialization

Traditional methods often use random sampling strategies to initialize the latent vector z, drawing initial values from a Gaussian or uniform distribution. However, this initialization method is highly stochastic, and the initial points may be far from the true distribution area of the target identity, leading to slow optimization convergence. At the same time, when pursuing high confidence, the latent vector is prone to over-optimization, deviating from the true distribution of the real category in the latent space and the decision boundary, resulting in overfitting, which limits the attack accuracy. To address this fundamental deficiency, we innovatively propose a Top K class center initialization strategy to construct a more representative latent vector library (z_bank), thereby providing higher quality initial latent vectors for each identity and constraining the optimization process to be close to the class center in the latent space. The pseudocode for the initialization strategy is as follows:

Algorithm 1. Top K mean-variance initialization

• 1. Candidate sampling: For each target identity$({y_i} \in \{ 0,1, \ldots ,{N_{id}} - 1\} {\text{ }})$, sample M latent vectors from the standard normal distribution to form the selected vector set$\{ {z_i}\} _{{i=1}}^{M}\sim \mathcal{N}(0,I){\text{ }}$, where${z_i} \in {R^{{d_z}}}$.

• 2. Reconstructed image evaluation: By inputting the latent vectors of each category $\{ {z_j}\} _{{j=1}}^{M}$ along with their corresponding labels ${y_i}$ into the generator G to synthesize the corresponding images, $\{ {x_j}=G({z_j},{y_i})\} _{{j=1}}^{M}$ and then inputting the reconstructed images into the target model T, obtaining the predicted confidence on the identity ${y_i}$.

  $${p_j}=\operatorname{Softmax} \left( {T\left( {{x_i}} \right)} \right)$$

  (4)

• 3. Top K filter for selecting high-quality vectors: Based on the evaluation results, a subset ${\{ {z^{(k)}}\} _{k=1}}$ of vectors is selected from the M candidate vectors, consisting of the top K vectors that maximize the confidence of the target identity. This process eliminates many sampling points that are far from the target manifold, significantly reducing the variance of subsequent statistical estimates. These vectors represent directions that can generate images most easily recognized as corresponding identities by the target model.

• 4. Building initial latent vectors: calculate the mean $\mu$and standard deviation $\sigma$of the subset.

$${\mu _i}=\frac{1}{K}\sum\limits_{{k=1}}^{K} {{z^{(k)}}} ,\quad {\sigma _i}=\sqrt {\frac{1}{K}\sum\limits_{{k=1}}^{K} ( {z^{(k)}} - {\mu _i}{)^2}}$$

(5)

Finally, the representation vector of any identity $z_{{bank}}^{{{y_i}}}$ in the vector library is composed of the mean plus a small noise scaled by its standard deviation, where $\alpha$is the noise intensity coefficient. This introduces a moderate level of randomness while maintaining the consistency of identity semantics, which helps to avoid getting trapped in local optima during the optimization process.

$$z_{{{\text{bank}}}}^{{{y_i}}}={\mu _{\text{i}}}+\epsilon \cdot {\sigma _i} \cdot N(0,I) ,\quad \epsilon \sim N(0, {\alpha ^2})$$

(6)

Dynamic focal margin loss

Analysis of limitations of the maximum margin loss function

Previous work¹⁶ introduced the Max Margin Loss ML and Poincare Loss functions to replace the cross-entropy loss function, which solved the problem of gradient disappearance in the attack process, and the maximum boundary loss function achieved excellent attack performance. The core idea of the maximum margin loss is to optimize the classification boundary by maximizing the prediction score of the target class and minimizing the highest competitive score in other categories. The mathematical form is as follows:

$${L_{MM}}(x,{y_c})= - {l_{{y_c}}}(x)+{\hbox{max} _{j \ne {y_c}}}{l_j}(x)$$

(7)

${l_{{y_c}}}$is the output score of the target category, and ${l_j}$ is the highest competitive score in the non-target category. Although the loss function effectively improves the performance of the model inversion attack by directly optimizing the score difference between the target class and the competitive class³⁴, there are still the following limitations:

(1) Equal weight allocation: all samples have the same loss contribution, and there is a lack of targeted attention to difficult samples. (2) Constant-magnitude updates: the constant gradient norm equally updates all samples, so hard examples may receive insufficient effective updates near the decision boundary.

The gradients of the target class score ${l_{{y_c}}}$and the competitive class score ${l_j}$are as follows:

$${\nabla _{{l_{{y_c}}}}}= - 1\quad {\text{ }}\quad {\nabla _{{l_j}}}=1$$

(8)

The differentiation process is as follows, Applying the chain rule to Eq. (7), we first decompose the max-margin loss into two explicit terms:

$${L_{MM}}(x,{y_c})= - {l_{{y_c}}}(x)+{l_j}(x),\quad {\text{where }}j=\arg {\hbox{max} _{k \ne {y_c}}}{l_k}(x),$$

Differentiating with respect to the target-class logit gives

$${\nabla _{{l_{{y_c}}}}}=\frac{{\partial {l_{{y_c}}}(x)}}{{\partial {L_{MM}}}}=\frac{{\partial {l_{{y_c}}}(x)}}{{\partial ( - {l_{{y_c}}}(x))}}+\frac{{\partial {l_{{y_c}}}(x)}}{{\partial {l_j}(x)}}= - 1+0= - 1.$$

Since the maximal competitor ${l_j}(x)$ does not depend on ${l_{{y_c}}}(x)$.

For the competitive-class logit we obtain

$${\nabla _{{l_j}}}=\frac{{\partial {l_j}(x)}}{{\partial {L_{MM}}}}=\frac{{\partial {l_j}(x)}}{{\partial ( - {l_{{y_c}}}(x))}}+\frac{{\partial {l_j}(x)}}{{\partial {l_j}(x)}}=0+1=+1.$$

Regardless of the score difference between the target class and the competing class$\Delta ={l_{{y_c}}} - {l_j}$ (the degree of proximity between the target class and the competing class), the gradient is constant and equal ||∇|| = 1, which makes it difficult for the model to effectively distinguish boundary samples, thereby limiting the model’s ability to adjust the boundary area and failing to prioritize the optimization of difficult samples. The gradient amplitude is always constant, and the same intensity of gradient signal will be applied to produce the following limitations:

• 1. For hard samples: (${l_{{y_c}}}$= 1.0,${l_j}$=0.9,$\Delta$= 0.1) fixed gradient leads to few iterations not enough to produce effective adjustment. Multiple iterations are required to reach the target boundary. At the same time, the gradient noise of simple samples will also affect the effective signal of difficult samples.

• 2. For simple samples: (${l_{{y_c}}}$= 5.0,${l_j}$=0.1,$\Delta$= 4.9) Simple samples are samples that have been optimized and converged. However, fixed gradients will update these samples with the same intensity, causing meaningless oscillations in the converged region and wasting computing resources.

Design of dynamic focal margin loss function

To solve the above problems, this paper proposes a Dynamic Focal^26,27 Margin Loss function (DFML), which is mathematically expressed as:

$${\mathcal{L}_{DFML}}=\frac{{{{(1 - {e^{ - {l_{{y_t}}}}})}^\gamma } \cdot ( - {a_t} \cdot {l_{{y_t}}})}}{{{\text{Target-Class Adaptive Loss}}}}+\frac{{{{(1 - {e^{ - {l_m}}})}^\gamma } \cdot ({a_m} \cdot {l_m})}}{{{\text{Competitive-Class Adaptive Loss}}}}$$

(9)

• 1. Temperature scaling: The logits value of the target model is smoothed and scaled by the temperature parameter to alleviate the influence of extreme values:

  $${\text{out}}=\frac{{{\text{logits}}}}{T}\quad {l_{{y_t}}}=\frac{{{l_{{y_c}}}(x)}}{T}\quad {l_m}=\frac{{{{\hbox{max} }_{j \ne {y_c}}}{l_j}(x)}}{T}$$

  (10)

When T > 1, the probability distribution is smoothed to enhance the sensitivity to difficult samples. When T < 1, the probability distribution is sharpened to accelerate the convergence of simple samples. Secondly, the contribution ratio of the target class ${a_t}$and the competitive class loss ${a_{\text{m}}}$is dynamically adjusted through the weight parameters to enhance the optimization flexibility.

• 2. Focal loss mechanism: Drawing on the idea of Focal Loss, this paper employs the Focal coefficient to achieve adaptive adjustment. That is; by using an exponential function and the parameter to adjust the sample weights, the attack optimization process pays more attention to the low-confidence difficult samples.

  $$\frac{{{{(1 - {e^{ - {l_{{y_t}}}}})}^\gamma } \cdot ( - {l_{{y_{\text{t}}}}})}}{{{\text{Target-Class Adaptive Loss}}}}$$

  (11)

When the confidence of the target class $1 - {{\text{e}}^{ - {l_{{y_t}}}}}$is low, it will become smaller. After multiplying the loss term, the loss value will be amplified, forcing the optimization to increase the target class score faster.

$$\frac{{{{(1 - {e^{ - {l_m}}})}^\gamma } \cdot {l_m}}}{{{\text{Competitive-Class Adaptive Loss}}}}$$

(12)

When the confidence of the interval class$1 - {{\text{e}}^{ - {l_{{y_{\text{m}}}}}}}$is high and close to 1, the loss value remains unchanged. On the contrary, when it is low, the loss value will be amplified, forcing the model to reduce the score of the interval category faster.

Experiment

Experimental setting

Datsets: We use the same three datasets as the previous work¹⁶, namely CelebA, FFHQ and FaceScrub. The CelebA dataset contains 202,599 face images of 10,177 different individuals. FFHQ contains 70,000 high-quality PNG face images at 1024 × 1024 resolution. FaceScrub²⁸ is a large face recognition dataset consisting of 106,863 face images of 530 celebrities, with an average of about 200 images per person.

Target models: We select three deep learning models with different architectures for our experiments. We tested the attack on VGG16, FaceNet64 and ResNet152.

Experimental preparation: The attack experiments are divided into standard attacks and attacks under the condition of large differences in data distribution. According to the previous work, 30,027 images of 1000 identities of CelebA are used as private data sets, and all target models are trained in private data sets. The remaining part that does not intersect with the private dataset is used to train cGAN. Under the standard attack, the cGAN trained based on the CelebA public dataset is attacked. In the case of large differences in the distribution of public and private data sets, ffhq and facescrub are used as public data sets to train cGAN.

Experimental parameter settings: When training GAN, the same settings as in previous studies¹⁶ were adopted. In the inversion attack stage, the Adam optimizer with a learning rate of 0.1 is used, and $\:\beta\:$ = (0.9, 0.999). Randomly initialize 5 times and perform 600 rounds of iterative attacks each time.

Evaluation metrics

Qualitative analysis was performed through visual evaluation results, and quantitative indicators were introduced to ensure the objectivity and repeatability of the evaluation.

Attack accuracy acc: The top-1 and top-5 accuracy of the reconstructed samples on the target class are calculated using an evaluation model that is pre-trained on the same private dataset but with a different architecture from the target model. Here, top 1 accuracy (ACC@1) refers to the proportion of samples where the target class is correctly identified as the most likely class by the evaluation model. Similarly, top 5 accuracy (ACC@5) indicates the proportion of samples where the target class is among the top five most likely classes predicted by the evaluation model. The higher the attack accuracy achieved by the reconstructed image, the more private information is exposed in the data set.

K-Nearest neighbor distance KNN: For a specific target, the shortest feature distance between the reconstructed image and the private image is calculated. This metric is evaluated by calculating the l2 distance between two images in the feature space. The smaller the value, the shorter the distance between the two in the feature space, which means the reconstructed image is closer to the private sample.l.

Initial distance FID: It is often used to evaluate GAN generated images. The feature vector is extracted by InceptionV3 pre-trained on ImageNet, and the distance between the private target data set and the reconstructed image is calculated. The lower the FID value, the better the quality and diversity of the reconstructed image.

Model-inversion attacks synthesize images from latent codes; no clean counterpart of a reconstructed image exists, hence FID/KNN are computed between the reconstructed set and the real private-training set to measure the overall fidelity and proximity of the synthesized images to the actual training data.

Experimental results

Selecting the current state-of-the-art attack methods as baseline experiments includes KED_MI¹⁵, LOMMA²⁴, PLG_MI¹⁶, and CDM_MI¹⁹. LOMMA²⁴, as a plug-and-play enhancement technology, aims to boost attack performance. In this paper, the enhanced GMI and KED_MI are used as baseline experiments. We also compared the performance differences in attack capabilities when using the Top K class center latent vector initialization proposed in this paper versus not using it, with “w/o TK” indicating the method not utilizing it. “↑” and “↓” signify that higher/lower scores represent better attack performance.

Standard setting: Under standard settings, as shown in Table 2, the evaluation metrics of the images reconstructed by our method outperform all baseline experiments. It not only improves the attack accuracy rate but also significantly optimizes KNN and FID. Specifically, compared to PLG_MI, our method reduces the average KNN distance by 68 points, and the FID value by an average of 16%. This indicates that the images reconstructed by our method are closer to the private images. Figure 6 shows a qualitative evaluation visually, where our method reconstructs images that are more realistic in some categories, effectively enhancing the visual similarity to the private dataset. Compared to CMD_MI, which mainly focuses on improving the fidelity of reconstructed images, our method maintains the attack accuracy rate while further optimizing the diversity of generated samples. As shown in Table 2, when comparing the image quality evaluation metrics of the two methods, our method achieves better performance in the FID metric, indicating that the reconstructed images have better quality and diversity. In terms of KNN values, under the attack scenarios based on ResNet152 and VGG16, our method’s KNN values are also superior to CMD_MI. With similar attack performance, our training time only requires 12 h, while CMD_MI requires 48 h of diffusion model training and an additional 6–8 h of model fine-tuning. We also compared the attack effects without using Top K.

Table 2 Attack performance comparison of different target models trained on the celeba Dataset. ↑and ↓ respectively symbolize that higher and lower scores give better attack performance.

Fig. 6

Visual comparison of reconstructed images using different attack methods for the VGG16 target model trained on the CelebA dataset.

latent vector initialization. The comparison results show that the Top K method not only improves the attack ACC but also reduces the KNN distance, indicating that this initialization method can indeed generate higher quality latent vectors.

Large data distribution shifts: In line with the settings of previous studies, we also explored the attack performance under the condition of large distribution differences between public and private training datasets. Table 3 shows the performance when attacking with the FFHQ dataset. Compared with PLG_MI, both the FID value and KNN Dist decreased. Similarly, compared with CMD_MI, our method has a higher attack accuracy and a lower FID value than CMD_MI. In the experiment based on the Facescrub dataset, which is composed of face images crawled from the Internet by web crawlers, we found that most image URL links were invalid. To ensure comparability of the experimental design, the paper strictly followed the same crawling method and dataset processing as PLG_MI and only crawled 23,000 images, resulting in a decrease in the performance of the trained GAN and experimental bias. Although PLG_MI provides pre-trained GAN model nodes, to ensure the validity and fairness of the experimental results, we retrained the corresponding GAN models for comparative experiments according to the training process and parameter settings provided by PLG_MI. Table 4 shows the attack performance of different model architectures when training GANs using the Facescrub dataset based on CelebA. Under the same experimental conditions, our method effectively improved the attack accuracy and significantly reduced the KNN Dist and FID values. The attack accuracy increased by an average of 4%. It is worth noting that when attacking VGG16, the attack accuracy increased by up to 8%. The KNN Dist decreased by an average of 36, and the FID value decreased by an average of 7%. Even without using Top K class center initialization, although the attack accuracy decreased slightly, it still increased by an average of 3%.

Table 3 Attack performance comparison of different target models trained on the FFHQ Dataset. ↑and ↓ respectively symbolize that higher and lower scores give better attack performance.

Table 4 Attack performance comparison across different model architectures during the GAN training phase and the image reconstruction phase. ↑and ↓ respectively symbolize that higher and lower scores give better attack performance.

Ablation study

Ablation study. Based on sampling from the original standard normal distribution latent space (without using Top-K class-centered latent initialization), we further conducted a more detailed and in-depth evaluation of the contributions of the improved generator and loss function. First, we used FFHQ and CelebA as public datasets to attack the three target models trained on CelebA. The design was to use the original cGAN combined with dynamic focal boundary loss to demonstrate the contribution of our designed loss function, and the improved cGAN used maximum boundary loss to evaluate the effect of the improved cGAN, as shown in Table 5. G_o represents the original cGAN, G_n represents the improved cGAN, L_o is the maximum boundary loss function, and L_n is the dynamic focal boundary loss function. Even when using the two methods separately, improvements were observed in attack accuracy, FID values, and KNN distances. The main role of the dynamic focal boundary loss function is to improve the accuracy of model inversion attacks, although it can also slightly improve image reconstruction quality. In comparison, the improved cGAN performs better in KNN and FID, especially in terms of FID values.

Table 5 Ablation study on three target models using the FFHQ and celeba dataset. ↑and ↓ respectively symbolize that higher and lower scores give better attack performance.

Secondly, without employing the Top-K class-centered latent initialization, we conducted attack tests on the three target models trained on the CelebA dataset using FaceScrub as the public dataset. Figure 7 shows the comparison of attack performance using.

Fig. 7

The impact of different loss functions on attack performance.

different loss functions under the PLG_MI cGAN architecture. The use of the DFML loss function increased the attack accuracy on all three target models by more than 5%, and KNN also decreased, although FID was slightly worse. Figure 8 shows the impact of different generators architectures on attack performance when using the ML loss function. The decrease in attack accuracy due to the improved cGAN is because the band decoupling makes the generator fit the feature distribution of the FaceScrub dataset more closely, which leads to a decrease in attack accuracy when there is a large difference in data distribution. However, it performs better in terms of FID.

Fig. 8

The impact of different generators on attack performance.

To further demonstrate the dynamic focal margin loss function, without employing the Top-K class-centered latent initialization. This paper uses the pre-trained generator provided by PLG_MI as the baseline model to compare the Poincaré, maximum margin, and dynamic focal margin loss functions. Specifically, FFHQ and FaceScrub are used as public datasets and CelebA as the private dataset. The VGG16 model is used as the target model to attack the first 100 classes of CelebA. During the 600-iteration attack process, the average values of the gradient, loss, and target logit values are plotted as trend curves. To address the issue that different loss functions, which lead to large differences in gradient and loss values that are difficult to compare, the loss values and gradient values are normalized by dividing them by the absolute value of their initial values. As shown in Figs. 9 and 10, in the first figure, the gradient magnitude of DFML closely tracks that of ML and remains stable throughout the attack. In the second figure, the Poincaré loss remains unchanged, making it difficult to judge the optimization situation. The loss function proposed in this paper does not minimize as quickly and continuously as ML within the same number of iterations because ML cannot effectively identify and optimize difficult samples. It can quickly optimize and reduce the loss value for easy samples. In contrast, the proposed loss.

Fig. 9

Rescaled gradient/loss/logit curves (FFHQ→CelebA).

Fig. 10

Rescaled gradient/loss/logit curves (FascScrub→CelebA).

function focuses more on low-confidence difficult samples and does not waste resources on converged easy samples. This results in slow but stable loss optimization and effectively improves the performance of inversion attacks, which is confirmed by third image. Within 600 iterations, compared with the other two functions, the dynamic focal margin loss function can quickly increase the logits value of the reconstructed samples and reach a higher value.

Using FaceScrub as the common benchmark, we conducted attack tests on three target models trained on CelebA to independently assess the contribution of each module. Taking PLG-MI and our full pipeline as baselines, we systematically compared the differential performance and incremental gains brought by individually introducing TOP-K, FDFB and DFML under three evaluation metrics. As shown in Figs. 11, 12 and 13, individually applying TOP-K leads to minor degradations across all three metrics, remaining almost on par with PLG. In contrast, standalone FDFB notably hurts attack accuracy, whereas DFML effectively boosts it. Moreover,

Fig. 11

Ablation study: attack accuracy Improvement over PLG baseline.

Fig. 12

Ablation study: KNN distance improvement over PLG baseline.

Fig. 13

Ablation study: FID value improvement over PLG baseline.

FDFB clearly outperforms DFML in terms of FID, while KNN distances are largely comparable except for a larger gap on VGG16. Ultimately, combining all three modules yields balanced and consistent improvements across all metrics.

To investigate the differences in enhancing attack performance between DFML, and Top-K class center initialization, we utilized a generator trained on the FaceScrub dataset with the IR152 model, targeting the VGG16 as the model for attack. Using the original node provided by PLG_MI, which was trained on the complete FaceScrub dataset, as our benchmark, we tested the attack performance of DFML, Top-k, and their combination, as well as comparing with the complete method presented in this paper. It should be noted that the cGAN improved in this paper was trained on an incomplete dataset, with a significantly smaller data volume compared to PLG_MI. Despite this, by integrating the three optimization methods, we demonstrated that its attack performance can match that of the original PLG_MI node, which not only reveals the performance differences among the optimization methods but also shows that our method remains effective even when the data volumes are unequal, as shown in Fig. 14.

Fig. 14

The performance comparison analysis of different attack methods.

Firstly, the experimental results clearly demonstrate that DFML can effectively enhance attack performance, showing improvements across all three-evaluation metrics. The Top K method significantly reduces the FID and KNN values, indicating that Top K indeed provides higher quality latent vectors. Secondly, the attack strategy that combines DFML and Top K optimization methods achieved the lowest FID value, dropping below 20, and performed well in terms of attack accuracy, improving by 4% compared to the original model. This result fully confirms the synergistic effect when using both optimization methods in combination. Lastly, the complete method we propose closely approaches the attack performance of the original model node provided by PLG_MI across all three-evaluation metrics. Despite being trained on an incomplete dataset, its performance is comparable to that of the original model trained on a complete dataset, further demonstrating the effectiveness and robustness of our optimization methods.

Conclusion

This paper proposes an enhanced model inversion attack method. First, we inserted a frequency-domain decoupling module into the cGAN and fused its output with label-embedded features to explicitly separate low-frequency and high-frequency components. This allows the generator to learn low-frequency and high-frequency cues for specific categories separately, preventing entanglement that degrades image fidelity. Second, we introduced the Top K category center latent initialization method, which firmly anchors the starting point of optimization within the semantic manifold, effectively suppressing the “runaway” phenomenon of trading high confidence for unrealistic samples. Finally, we proposed a dynamic focal boundary loss function to compensate for the insufficient exploration of hard examples during the optimization process. Extensive experiments demonstrate that this method achieves consistent performance improvements across various model architectures and application scenarios. Future work includes extending the approach to black-box attacks and model inversion attack defense.

(1) Optimization algorithm improvement: Under the black-box model, attackers cannot rely on the gradient information of the target model for optimization. Therefore, the design of efficient optimization algorithms is crucial. In the future, we will explore heuristic optimization algorithms^29,30, such as genetic algorithms. These algorithms can efficiently search for optimal solutions in complex optimization spaces without relying on gradient information, thereby achieving efficient attack optimization. (2) Query efficiency optimization: To cut query costs, we can first pinpoint the image regions that most black-box models rely on. Next, we train (or fine-tune) the generator to keep features in those regions close to the target model’s manifold³¹. During attack we restrict zero-order optimization³² to the latent vectors tied to these fixed spots, adjusting only them to produce high-fidelity reconstructions while keeping the number of black-box queries as low as possible.

Defense strategies: (1) The attack process can be incorporated into the training process of the recognition model, enabling the model to learn how to resist inversion attacks during the training phase and thus possess stronger attack resistance in practical applications. (2) Model inversion attack detection technology can be developed to monitor and identify suspicious attack behaviors in real time. When potential attacks are detected, corresponding defense measures can be taken to counteract them.