Software belief reliability growth model incorporating change point and imperfect debugging based on uncertain differential equation approach

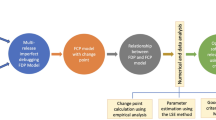
Abstract

Many software reliability growth models (SRGMs) have been proposed by researchers within the context of probability theory to estimate software reliability, remaining number of faults and optimal release time. The Fault Detection Rate (FDR) may vary because of changes in testing strategies. Due to lack of knowledge of software code, the testing team might be unable to rectify the detected faults thereby introducing new faults during the fault correction process. The debugging process is imperfect due to factors like human error, insufficient testing and complex codes resulting in epistemic uncertainty. In this paper, we have proposed a new software belief reliability growth model (SBRGM) using uncertain differential equations to deal with epistemic uncertainty effectively. We have incorporated imperfect debugging and change point based on the approach of belief reliability theory, making this model more accurate as compared to some of the previously developed models. Model parameters estimation methodology is derived using the least square method and Python version 3.10. Calculation of change point is done using empirical data analysis based on the First principle of Derivatives. Three real data sets have been used to validate the proposed model. This research contributes to being more flexible and realistic in dealing with epistemic uncertainty effectively as compared to conventional approaches.

Introduction

In today’s digitalised era, software makes a substantial contribution to the advancements of digital infrastructure from data analytics to customer relationship management systems, and e-commerce platforms to mobile applications. In a heavily competitive market, companies often face immense pressure to keep up with the set standards. Hence, in the Software Development Life Cycle (SDLC), testing phase becomes important and essential. Software engineers are usually supposed to perform their tasks within the allocated time to maintain a competitive edge. Software failures are the result of software errors that could lead to serious aftermaths in our day-to-day activities. A few examples from the past are as described¹: One notable incident occurred on September 17, 1991, when 10 million telephone users were affected for nearly 9 h due to a power failure at AT&T’s switching centre in New York. The deletion of three bits of code in a software upgrade and failed testing were the primary reasons for the software failure before its release in the market. On October 26, 1992, a similar incident occurred when London’s Ambulance Service’s computer-based dispatch system, which had earlier been used to handle 5000 requests per day in emergencies, malfunctioned right after its deployment. Many critically ill patients experienced intense repercussions due to software breakdown, highlighting the risk of system failures.

Not long ago, as mentioned in an article ² on 19 July 2024, a flawed configuration upgrade patch was installed by CrowdStrike for its Falcon sensor software operating on Windows PCs and servers. This faulty upgrade forced systems to enter into a recovery mode or boot loop, resulting in invalid page faults. CrowdStrike Falcon’s close integration with Microsoft Windows kernel led to a Windows system crash. The error was within a sensor configuration in CrowdStrike Falcon. Consequently, approximately 8.5 million systems collapsed and went down and could not restart and reboot effectively, resulting in a heavy economic and financial loss. Since software failure can result in monetary and financial disruptions or sometimes human casualties, the software’s reliability is a necessity^3,4. To guarantee failure-free software and to determine optimal launch time, precise reliability estimation is needed before the software is installed. Hence, software reliability has become one of the major focuses in the current situation⁵. Therefore, SRGMs are considered a tool for discussing software reliability, which estimates and determines software reliability and other related metrics effectively^6,7,8.

Many Software Reliability Growth Models have been developed by prominent researchers to evaluate software reliability with different suppositions and approaches based on probability theory^9,10,11,12. Yamada et al.¹³ for the very first time, applied a stochastic differential equation (SDE) to discuss the number of faults. Subsequently, Kapur et al.¹⁴ developed a generalized Erlang model based on SDE, featuring a logistic error detection function. Li and Pham¹⁵ incorporated factors such as learning behaviour and considered environmental uncertainties to enhance the accuracy of reliability assessments. During the testing phase, due to certain factors like resource allocation and testing knowledge, fault detection rate can be discontinuous and may change at a certain time point, which is referred to as a change point¹⁶. A generalized model has been developed incorporating a change point and logistic testing effort¹⁷.

Because of the intricacy and insufficient knowledge of software system, the testing team might not eliminate detected faults, and additional faults/bugs can also emerge in correction process known as imperfect debugging. Kapur et al.¹⁸ put forward the NHPP-based model taking into account imperfect debugging process. Chatterjee and Shukla [2020] considered imperfect debugging and change point together in the model. Several factors, like skill set, testing productivity, budget al.location, testing methodologies, and approaches, all of which may be uncertain, can affect the testing process²⁰. Probability theory is a mathematical framework to describe this uncertainty. As the software scale broadens, the faults identified during the testing period increase, and the number of bugs identified and rectified by a single debugging process becomes significantly less compared to the total number of faults at the start of the testing process. Various researchers discussed probability theory as advantageous in terms of quantification, risk assessment, and resource allocation in reliability growth models to deal with the uncertainty in the testing phase^9,19,21,22.

Complex software systems consist of various modules and correlations. Uncertainty can take place when faults are associated with other codes of the system. By identifying and managing this uncertainty, software developers and testers can improve fault detection, responses and increase overall software reliability. Software’s fault is based on the fundamental rules of logic and code, behaviour, psychology, testing environment and many more. This uncertainty is mainly due to the cognitive capabilities of software engineers, coding, testing, usage and other situations. The classification of uncertainties includes two types: aleatory and epistemic. Epistemic uncertainty takes place when there is a lack of information, aleatory uncertainty stems from intrinsic inconsistency. Probability theory is adequate for examining aleatory uncertainty but inadequate for measuring epistemic uncertainty as it presumes that complete insights are accessible, see^{20,23,24,25,26}.

Software faults include epistemic uncertainty that cannot be illustrated accurately by probability theory^24,25. To handle epistemic uncertainty in software reliability models, many SRGMs have been established by various scholars^27,28,29,30 under the framework of alternative approaches like Bayesian and fuzzy methods, but these methodologies lack accuracy. Bayesian methods consider the framework of beliefs about a system’s reliability in its modelling process. On the other hand, Zhang et al.³² discussed that fuzzy methods describe uncertainty with fuzzy sets and linguistic variables but yield non-intuitive outcomes, for example, the sum of unreliability and reliability is not one.

To address epistemic uncertainty effectively in SRGMs, it is essential to come up with other possible methods. Uncertainty theory was introduced by Liu³² as a different approach to describe epistemic uncertainty. Uncertainty theory incorporates both epistemic and aleatory uncertainty, providing a comprehensive and systematic framework of software reliability. In comparison to traditional stochastic processes, the Liu process is a stochastic process rooted in uncertainty theory, as it considers increments as normal uncertain variables. The Liu process provides more suitable models for software reliability systems, as the increments in Liu process are independent. Researchers^{24,25,26,33,34} have shown that SBRGMs based on uncertain differential equations have performed better than existing famous models that were based on probability theory. Liu and Kang²⁴ proposed an SBRGM to evaluate properties like mean time between failures, belief reliable time and belief reliability of software reliability, incorporating imperfect debugging based on the uncertainty theory. Liu et al.³⁵ have presented SBRGM based on the methodology and approach of belief reliability and uncertainty theory. This article did not consider that the debugging process is imperfect and new errors can also be introduced. Liu et al.²⁵ developed SBRGM considering change-point based on uncertainty theory and also estimated the software reliability. Garg et al.²⁶ developed an SBRGM based on uncertain differential equations, considering software patching and FDR and Fault correction rate as a two-step process and also investigated belief reliability to optimize the testing cost. Huong³⁶ developed a dynamic event-triggered control method offering an LMI-based solution for uncertain neural networks with time delays. Huong³⁷ introduced a mathematical model to control an uncertain active suspension system by addressing event-triggered finite-time guaranteed cost control. Also, Huong³⁸, in his work, designed a cost controller for an uncertain polytopic fractional-order system with time delays.

Novelty

The novelty of this research is that this is the first one to propose SBRGM incorporating change point and imperfect debugging based on uncertainty theory, which produces better results as compared to probability theory.

Upon further investigation of existing literature, we discovered that previous models based on uncertainty did not consider change-point and imperfect debugging altogether. In fact, in more real-world scenarios, the software is influenced by many things, including the operating environment, testing methodology, and the allocation of resources. To bring our model more in line with reality, we have developed an SBRGM that integrates the change point with imperfect debugging based on uncertain differential equations. The paper provides primary contributions as follows:

• This paper proposes an SBRGM incorporating change point and imperfect debugging altogether.

• A methodology for estimating unknown parameters based on the least squares method is developed, and a code to estimate uncertainty variables present in the model is developed using Python version 3.10.

• A methodology for estimating change point under the framework of empirical data analysis based on the First principle of Derivatives has been proposed.

• The developed model is compared with other well-established models to show its effectiveness and robustness.

The later segments of the paper are arranged subsequently. The basic preliminaries, notations, and assumptions used in the proposed model are described in Sect. “Novelty”. The model formulation and development are represented in Sect. “Basic preliminaries”. Section “Elief reliability evaluation” discusses the techniques of Parameter estimation of unknown parameters. Section “Concept of -path” provides a numerical illustration to demonstrate the model’s applicability with accuracy and precision. The managerial impact of the proposed model is discussed in Sect. “Notations used”. Finally, the conclusion and suggestions for future research scope are summarized in Sect. “Assumptions”.

Basic preliminaries

Let us review some fundamental concepts regarding uncertainty theory³².

Definition 2.1

As discussed by Liu³², a measurable space is denoted by (Γ, $\:\mathcal{L}$), where $\:\mathcal{L}$ is representing a σ-algebra defined over Γ, and Γ being a nonempty set. An uncertain measure $\:\mathcal{M}$: $\:\mathcal{L}$ → [0, 1] is a set function defined on σ-algebra that meets the below-listed fundamentals.

Axiom 1

It states that the measure of the universal set Γ is equal to one. In mathematical terms, this is.

represented as: $\:\mathcal{M}${Γ} = 1. This is known as the Normality Axiom.

Axiom 2

For any event Λ, the sum of the measure of Λ and its complement Λ^c is equal to one.

Mathematically, it is: $\:\mathcal{M}${Λ} +$\:\mathcal{M}${Λ^c} = 1. This is stated as Duality Axiom.

Axiom 3

For every countable sequence of events Λ₁, Λ₂…, mathematical expression is:

$$\:\mathcal{M}\left\{\bigcup\:_{i=1}^{\infty\:}{{\Lambda\:}}_{i}\right\}\le\:\sum\:_{i=1}^{\infty\:}\mathcal{M}\left\{{{\Lambda\:}}_{i}\right\}$$

i.e., the measure of union of these events is less than or equal to the sum of measures of the.

individual events.

This axiom is referred to as Subadditivity Axiom.

Axiom 4

Let (Γ_k, $\:\mathcal{L}$_k,$\:\mathcal{\:}\mathcal{M}$_k) be uncertainty spaces for $\:k$ = 1, 2…, and $\:{{\Lambda\:}}_{\text{k}}$ are arbitrarily.

chosen events from $\:\mathcal{L}$_k for k = 1, 2,..., respectively. Then the product uncertain measure $\:\mathcal{M}$ is an uncertain measure that satisfies the inequality below:

$$\:\mathcal{M}\left\{\prod\:_{k=1}^{\infty\:}{{\Lambda\:}}_{k}\right\}\le\:\underset{k=1}{\overset{\infty\:}{\bigwedge\:}}{\mathcal{M}}_{k}\left\{{{\Lambda\:}}_{k}\right\}$$

This expression explains that the measure of the product of events $\:{{\Lambda\:}}_{\text{k}}$ is less than or equal to minimum of measures of individual events $\:{{\Lambda\:}}_{\text{k}}$. This is known as the Product Axiom.

Definition 2.2

As introduced by Liu³⁹, Liu’s process $\:{C}_{t}$ is an uncertain process that addresses the following three key conditions.

• 1) Continuity and Initial Condition: Almost all sample paths are Lipschitz continuous and initially at.

t = 0, $\:{C}_{0\:}$= 0.

2) Increment Properties: The increments of $\:{C}_{t}$ are independent, which means the behaviour of.

process over disjoint intervals is statistically independent.

3) Distribution of Increments: For any interval $\:t,$ the increment $\:{C}_{l+t}$ $\:{-\:C}_{l}$ follows a normal uncertain.

distribution with an expected value of zero and a variance $\:{t}^{2}$.

Definition 2.3

Let us define an uncertain process^32,39 as $\:{Z}_{t}$ and a Liu process as $\:{C}_{t}$. For closed interval [u, v], the partition is as follows, with u = $\:{t}_{1}$ < $\:{t}_{2}$ < ・ ・ ・ < $\:{t}_{k}$ = v, denote Δ = $\:\underset{1\le\:i\le\:k}{\text{max}}|{t}_{i+1}-{t}_{i}$|. Then, Liu’s integral of $\:{Z}_{t}$ for $\:{C}_{t}$ is given by Eq. (1) and denoted as:

$$\:{\int\:}_{u}^{v}{Z}_{t}d{C}_{t}=\underset{\varDelta\:\to\:0}{\text{lim}}\sum\:_{i=1}^{k}{Z}_{{t}_{i}}({C}_{{t}_{i+1}}-{C}_{{t}_{i}})$$

(1)

under the assumption that a limit exists and finite.

Definition 2.4

Liu³² defined $\:{C}_{t}$ as Liu process (a fundamental concept in uncertainty theory) and denoted f and g as measurable functions. An uncertain differential equation can then be defined in terms of these functions and Liu process by Eq. (2) as:

$$\:d{Z}_{t}\:=\:f(t,{Z}_{t})dt\:+\:g(t,{Z}_{t})d{C}_{t}$$

(2)

with an initial value $\:{Z}_{0}$, which indicates that the solution $\:{Z}_{t}$ complies with the associated uncertain integral equation as described by Eq. (3) as:

$$\:{Z}_{t}={Z}_{0}+{\int\:}_{0}^{t}\:f(l,{Z}_{l})dl\:+\:{\int\:}_{0}^{t}\:g(l,{Z}_{l})d{C}_{l}$$

(3)

Elief reliability evaluation

The proposed model determines the count of detected faults in the testing phase. Software reliability improves/enhances as number of detected defects escalates/rises. In this section, Software belief reliability of the proposed model derived from the belief reliability theory has been discussed as presented below:

Let $\:{t}_{f}\:\:$denote the time required for total detected faults to achieve the predefined critical threshold $\:f$ where $\:f\in\:\left(\text{0,1}\right)$. To determine the belief degree to which software testing could be stopped and released at the time $\:t,\:$.

$\:{\tau\:}_{f}\le\:t,\:$belief reliability is given by $\:R{B}_{f}\left(t\right)=\mathcal{M}\{{\tau\:}_{f}\le\:t\}$.

where,

$$\:{\tau\:}_{f}=\text{inf}\left\{t\ge\:0|S\left(t\right)\ge\:fN\right\}and\:\mathcal{M}\:\text{i}\text{s}\:\text{U}\text{n}\text{c}\text{e}\text{r}\text{t}\text{a}\text{i}\text{n}\:\text{m}\text{e}\text{a}\text{s}\text{u}\text{r}\text{e}$$

As $\:{\tau\:}_{f}$ represents the first hitting of the solution of an uncertain differential equation. The definition of belief reliability is given by some researchers^24,25,26 as:

$$\:R{B}_{f}=1-\text{i}\text{n}\text{f}\left\{\alpha\:\right|\underset{0\le\:s\le\:t}{\text{sup}}{\varPhi\:}_{s}^{-1}\left(\alpha\:\right)\ge\:fN\}$$

(4)

where, $\:{\varPhi\:}_{s}^{-1}\:$is inverse function for belief reliability distribution. Also, as S(t) increases, $\:{\varPhi\:}_{t}^{-1}\left(\alpha\:\right)$ increases for particular $\:\alpha\:.$ Hence, belief reliability can be determined as:

$$\:R{B}_{f}=1-\text{i}\text{n}\text{f}\left\{\alpha\:\right|{\varPhi\:}_{s}^{-1}\left(\alpha\:\right)\ge\:fN\}$$

(5)

where, $\:{\varPhi\:}_{t}^{-1}\left(\alpha\:\right)=E\left(S\left(t\right)\right)+\left[\frac{\sqrt{3}SD\left(S\left(t\right)\right)}{\pi\:}\right]ln\left(\frac{\alpha\:}{1-\alpha\:}\right),\:\:\:\alpha\:\in\:\left(\text{0,1}\right)$, $\:E\left(S\left(t\right)\right)$ and $\:SD\left(S\left(t\right)\right)$ is expectation and standard deviation of random variable, respectively.

Concept of $\:\varvec{\alpha\:}$-path

In uncertain differential equations, the notion of α-path refers to a specific trajectory or solution curve dependent upon parameter α, symbolizing the uncertainty in equations. The α-path method investigates the behaviour of uncertain differential equations by encompassing a range of possible outcomes represented by different values of α. Each value of α corresponds to a specific path of the system of uncertain differential equations. By outlining the graph of numerical solutions for a range of values of , we can depict the -paths, which demonstrates how the system’s behaviour changes as the level of uncertainty varies.

The α-path $\:\left(0<\alpha\:<1\right)\:$of an uncertain differential equation is given below in Eq. (6)

$$\:d{S}_{t}=f\left(t,{S}_{t}\right)dt+g\left(t,{S}_{t}\right)d{C}_{t}$$

(6)

with an initial value, S₀, which is a deterministic function $\:{S}_{t}^{\alpha\:}\:$ with respect to $\:t$ that satisfies the associated ordinary differential equation described in Eq. (7)

$$\:d{S}_{t}^{\alpha\:}=f\left(t,{S}_{t}^{\alpha\:}\right)+\left|g\left(t,{S}_{t}^{\alpha\:}\right)\right|{\varPhi\:}^{-1}\left(\alpha\:\right)dt$$

(7)

where,

$\:{\varPhi\:}^{-1}\left(\alpha\:\right):\:$ a standard normal uncertain variable that follows inverse uncertainty distribution, i.e.,

$$\:{\varPhi\:}^{-1}\left(\alpha\:\right)=\frac{\sqrt{3}}{\pi\:}\text{ln}\frac{\alpha\:}{1-\alpha\:}\:,\alpha\:\:\epsilon\:\left(\text{0,1}\right)$$

Notations used

The notations used are given below:

$\:N$

Total number of initial faults at time ‘t’.

$\:S\left(t\right)$

Cumulative number of detected faults till time ‘t’.

τ : change point.

$\:{\lambda\:}_{1}\left(t,{\theta\:}_{1}\right)$

Fault detection rate per remaining fault for$\:0\le\:t\le\:\tau\:$.

$\:{\lambda\:}_{2}\left(t,{\theta\:}_{2}\right)$

Fault detection rate per remaining fault for$\:\tau\:<t\le\:t$.

$\:{\alpha\:}_{1}$

new fault introduction rate for$\:0\le\:t\le\:\tau\:$.

$\:{\alpha\:}_{2}$

new fault introduction rate for$\:\tau\:<t\le\:t$.

$\:{C}_{t}$

Liu process.

$\:{\sigma\:}_{1}$

Nonnegative constant denoting level of uncertainty for$\:0\le\:t\le\:\tau\:$.

$\:{\sigma\:}_{2}$

Nonnegative constant denoting level of uncertainty for$\:\tau\:<t\le\:t$.

Assumptions

In line with the models^24,26,35, we have taken into account the following presumptions:

• 1) A new bug/error can emerge during the debugging process, reflecting real-world situations where the correction of a fault can introduce new faults inadvertently²⁴. In this paper, we have considered this assumption to understand the concept of imperfect debugging in the proposed model.

• 2) The fault correction process occurs after the fault detection process, representing a sequential and fundamental aspect of software debugging³⁵. This sequential relationship is considered a core assumption in proposing SBRGMs based on uncertainty theory, where faults must be detected before correction.

• 3) The software operates within a finite lifecycle, incorporating development, testing, installation and maintenance within a fixed timeframe. According to Kapur et al.¹⁴, including this finite lifecycle into modeling frameworks aligns with practical realities and allows a more accurate interpretation of fault detection and correction. Here, the software cycle is divided into two intervals- before change point $\:(0\le\:t\le\:\tau\:)$ and after change point $\:(\tau\:<t\le\:\:t)$.

Model development

The software’s life span is subdivided in two intervals in the model:

• Fault detection before change point, i.e. $\:0\le\:t\le\:\tau\:$

• Fault detection after change point, i.e. $\:\tau\:<t\le\:\:t$

Epistemic uncertainties are unavoidable in software faults. Therefore, we are applying the uncertain integral equation to model below equations³⁴:

$$\:S\left(t\right)=S\left(0\right)+\int\:\lambda\:\left(t,\theta\:\right)\left(N-S\left(l\right)\right)dl+\int\:\sigma\:d{C}_{l}$$

(10)

We can deduce the uncertain differential equation as:

$$\:dS\left(t\right)=\lambda\:\left(t,\theta\:\right)\left(N-S\left(t\right)\right)dt+\sigma\:d{C}_{t},\:\:\:\:\:\:S\left(0\right)=s\left(0\right)$$

(11)

Where, $\:\lambda\:\left(t,\theta\:\right)\to\:$ fault detection rate till time ‘t’.

Now, we obtain the following integrals,

$$\:S\left(t\right)=\left\{\begin{array}{c}S\left(0\right)+{\int\:}_{0}^{\tau\:}{\lambda\:}_{1}\left(l,{\theta\:}_{1}\right)\left(N-S\left(l\right)\right)dl+{\sigma\:}_{1}{C}_{t\:\:},\:\:\:\:0\le\:t\le\:\tau\:\:\:\:\:\\\:S\left(\tau\:\:\right)+{\int\:}_{\tau\:}^{t}{\lambda\:}_{2}\left(l,{\theta\:}_{2}\right)\left(N-S\left(l\right)\right)dl+{\sigma\:}_{2}{C}_{t\:\:},\:\:\:\:\tau\:<t\le\:t\:\:\:\end{array}\right.\:\:$$

(12)

Now, we calculate the $\:S\left(t\right)$ i.e. cumulative number of detected faults and belief reliability.

In line with the assumptions^15,25,26, it is presumed that when detected faults are rectified at a given time ‘t’, new faults may be introduced with the introduction rate $\:\alpha\:\left(t\right)$ given by Kapur et al.⁹:

$$\:\alpha\:\left(t\right)=\left\{\begin{array}{c}{\alpha\:}_{1}\:\:\:\:\:0\le\:t\le\:\tau\:\\\:{\alpha\:}_{2}\:\:\:\:\:\tau\:<t\le\:t\end{array}\right.$$

Taking into consideration the change point, we suppose exponential proportional factors to be $\:{\lambda\:}_{1}\left(t,{\theta\:}_{1}\right)={b}_{1}$ and $\:{\lambda\:}_{2}\left(t,{\theta\:}_{2}\right)=\:{b}_{2}$.

Following the approach of Liu integral and uncertain differential equation given by Liu (2007), we obtain the integral equations:

$$\:dS\left(t\right)=\left\{\begin{array}{c}\left(\frac{{b}_{1}}{1-{\alpha\:}_{1}}\right)\left(N-S\left(t\right)\right)dt+\:{\sigma\:}_{1}d{C}_{t},\:\:\:\:\:\:\:\:\:\:0\le\:t\le\:\tau\:,\:\:S\left(0\right)=0\:\:\:\:\:\:\:\:\:\:\:\:\\\:\left(\frac{{b}_{2}}{1-{\alpha\:}_{2}}\right)\left(N-S\left(t\right)\right)dt+\:{\sigma\:}_{2}d{C}_{t},\:\:\:\:\:\:\:\:\:\:\tau\:<t\le\:\tau\:,\:\:S\left(\tau\:\right)=s\left(\tau\:\right)\:\:\:\:\:\:\:\end{array}\right.$$

(13)

where cumulative number of detected faults till time t = 0 is denoted by $\:S\left(t\right)$ and $\:S\left(0\right)$ = 0.

The developed model is a linear uncertain differential equation. The solution for $\:S\left(t\right)$ is given as:

$$\:S\left(t\right)=\left\{\begin{array}{c}N-Nexp\left(\frac{-{b}_{1}t}{1-{\alpha\:}_{1}}\right)+\:{\sigma\:}_{1}exp\left(\frac{{-b}_{1}t}{1-{\alpha\:}_{1}}\right){\int\:}_{0}^{t}\begin{array}{c}{\sigma\:}_{1}exp\left(\frac{{b}_{1}l}{1-{\alpha\:}_{1}}\right)d{C}_{l},\:\:\:\:\:\:\:t\le\:\tau\:\:\:\\\:\:\end{array}\\\:{U}_{2}\left(t\right)\left[S\left(\tau\:\right)+Nexp\left(\frac{{b}_{2}(t-\tau\:)}{1-{\alpha\:}_{2}}\right)-N+{\int\:}_{\tau\:}^{t}\frac{{\sigma\:}_{2}}{{U}_{2}\left(l\right)}d{C}_{l}\:\:\right],\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:t>\tau\:\:\:\:\:\:\end{array}\right.$$

(14)

where,$\:{\:U}_{2}\left(t\right)=\text{e}\text{x}\text{p}\left(\frac{-{b}_{2}(t-\tau\:)}{1-{\alpha\:}_{2}}\right)$

Then, $\:S\left(t\right)$ follows a normal uncertain distribution with the expected value is given by Eq. (15) as

$$\:E\left(S\left(t\right)\right)=\left\{\begin{array}{c}N-Nexp\left(\frac{{-b}_{1}t}{1-{\alpha\:}_{1}}\right),\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:t\le\:\tau\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:N-Nexp\left(\frac{{-b}_{1}t}{1-{\alpha\:}_{1}}-\frac{{b}_{2}\left(t-\tau\:\right)}{1-{\alpha\:}_{2}}\right),\:\:\:\:\:\:t>\tau\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\end{array}\right.$$

(15)

and the standard deviation as

$$\:SD\left(S\left(t\right)\right)=\left\{\begin{array}{c}\left(1-{\alpha\:}_{1}\right)\frac{{\sigma\:}_{1}}{{b}_{1}}\left(1-exp\left(\frac{-{b}_{1}t}{1-{\alpha\:}_{1}}\right)\right),\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:t\le\:\tau\:\:\:\\\:\:\\\:\begin{array}{c}\:\:\\\:\left(1-{\alpha\:}_{1}\right)\frac{{\sigma\:}_{1}}{{b}_{1}}exp\left(-\frac{{b}_{2}\left(t-\tau\:\right)}{1-{\alpha\:}_{2}}\right)\left(1-exp\left(\frac{-{b}_{1}t}{1-{\alpha\:}_{1}}\right)\right)+\left(1-{\alpha\:}_{2}\right)\frac{{\sigma\:}_{2}}{{b}_{2}}\left(1-\text{e}\text{x}\text{p}\left(\frac{-{b}_{2}\left(t-\tau\:\right)}{1-{\alpha\:}_{2}}\right)\right),\:\:t>\tau\:\\\:\:\end{array}\end{array}\right.$$

(16)

Correspondingly, the belief reliability distribution represents the number of detected faults till time ‘τ’ is less than $\:x$ and is described as

$$\:{\varPhi\:}_{t}\left(x\right)={\left(1+exp\left(\frac{\pi\:(E\left(S\left(t\right)\right)-x)}{\sqrt{3}SD\left(S\left(t\right)\right)}\right)\right)}^{-1}$$

(17)

$$\:{\varPhi\:}_{t}^{-1}\left(\alpha\:\right)=E\left(S\left(t\right)\right)+\left[\frac{\sqrt{3}SD\left(S\left(t\right)\right)}{\pi\:}\right]ln\left(\frac{\alpha\:}{1-\alpha\:}\right),\:\:\:\:\alpha\:\in\:\left(\text{0,1}\right)$$

(18)

where, $\:E\left(S\left(t\right)\right)$ and $\:SD\left(S\left(t\right)\right)$ are given in the Eqs. (15) and (16) respectively.

Belief reliability is given as:

$$\:R{B}_{f}\left(t\right)={\left(1+{exp}\left(\frac{\pi\:(fN-E(S\left(t\right))}{\sqrt{3}SD\left(S\right(t\left)\right)}\right)\right)}^{-1}$$

(19)

With the help of Eqs. (6), (7), (13) and (14), the equations of α-paths for proposed model are given below:

$$\:{S}_{t}^{\alpha\:}=s\left(0\right)\text{exp}\left(\frac{{b}_{1}t}{1-{\alpha\:}_{1}}\right)+\left(1+\frac{{\sigma\:}_{1}\left(1-{\alpha\:}_{1}\right)}{{b}_{1}}.\frac{\sqrt{3}}{\pi\:}\text{ln}\left(\frac{\alpha\:}{1-\alpha\:}\right)\right)\left(1-exp\left(\frac{{-b}_{1}t}{1-{\alpha\:}_{1}}\right)\right),\:t\le\:\tau\:$$

(20)

and

$$\:{S}_{t}^{\alpha\:}=S\left(\tau\:\right)\text{exp}\left(\frac{{b}_{2}\left(t-\tau\:\right)}{1-{\alpha\:}_{2}}\right)+\left(1+\frac{{\sigma\:}_{2}\left(1-{\alpha\:}_{2}\right)}{{b}_{2}}.\frac{\sqrt{3}}{\pi\:}\text{ln}\left(\frac{\alpha\:}{1-\alpha\:}\right)\right)\left(1-exp\left(\frac{{-b}_{2}\left(t-\tau\:\right)}{1-{\alpha\:}_{2}}\right)\right),\:\:\:t>\tau\:$$

(21)

Parameter estimation

We devised a two-step method for estimating parameters derived from the least square method and the moment estimation. This section discusses estimating unknown parameters by merging the concept of least squares and moment estimations.

Let us suppose $\:S\left(t\right)$ at a time, $\:{t}_{1}<{t}_{2}<...<{t}_{n\:}$ as s($\:{t}_{1}$), s($\:{t}_{2}$), …, s($\:{t}_{n})$, respectively. Also, assume that a change point occurs at a particular detection time.

To estimate unknown parameters $\:N,\:{\theta\:}_{1},\:and\:{\theta\:}_{2}$ by using the least squares method for each possible change point $\:{t}_{k\:}$, where, $\:k=1,\:2,\dots\:,\:n,\:\:$respectively. In other words, estimates $\:{N}^{*},\:{\theta\:}_{k1}^{*}\:,\:{\theta\:}_{k2}^{*}$ for unknown parameters $\:N,\:{\theta\:}_{1},\:and\:{\theta\:}_{2}$Optimal solutions are determined by minimizing objective functions

$$\:\underset{N,{\theta\:}_{1},{\theta\:}_{2}}{\text{min}}{RSS}_{k}=\sum\:_{i=1}^{n}{\left(s\left({t}_{i}\right)-E\left(S\left({t}_{i}\right)\right)\right)}^{2}$$

(22)

where,

$$\:E\left(S\left(t\right)\right)=\left\{\begin{array}{c}N-Nexp\left(\frac{-{b}_{1}t}{1-{\alpha\:}_{1}}\right),\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:t\le\:{\tau\:}_{j}\:\:\\\:N-Nexp\left(\frac{-{b}_{1}t}{1-{\alpha\:}_{1}}-\frac{{b}_{2}(t-\tau\:)}{1-{\alpha\:}_{2}}\right),\:\:\:\:\:\:\:\:\:\:\:\:t>{\tau\:}_{j},\:\end{array}\right.$$

(23)

j = 1, 2,…,n respectively.

As per the definition, we obtain the difference forms of equations of SBRGM as

$$\:S\left({t}_{i}\right)-S\left({t}_{i-1}\right)=\frac{{b}_{1}}{1-{\alpha\:}_{1}}\left(N-S\left({t}_{i-1}\right)\right)\left({t}_{i}-{t}_{i-1}\right)+{\sigma\:}_{1}\left({C}_{{t}_{i}}-{C}_{{t}_{i-1}}\right)\:\:\:,\:\:\:\:\:t\le\:\tau\:$$

(24)

and

$$\:S\left({t}_{i}\right)-S\left({t}_{i-1}\right)=\frac{{b}_{2}}{1-{\alpha\:}_{2}}\left(N-S\left({t}_{i-1}\right)\right)\left({t}_{i}-{t}_{i-1}\right)+{\sigma\:}_{2}\left({C}_{{t}_{i}}-{C}_{{t}_{i-1}}\right)\:\:\:\:,\:\:\:\:t>\tau\:$$

(25)

for i = 1, 2,…n-1.

Unknown parameters $\:{\sigma\:}_{1}\:and\:{\sigma\:}_{2}$ can be estimated as:

$$\:{\sigma\:}_{1}^{2}=\frac{{\sum\:}_{j=1}^{n-1}(S\left({t}_{i}\right)-S\left({t}_{i-1}\right)-\left(\frac{{b}_{1}}{1-{\alpha\:}_{1}}\right)(N-S\left({t}_{i}\right))\left({t}_{i}-{t}_{i-1}\right){)}^{2}}{{\sum\:}_{j=1}^{n-1}({t}_{i}-{t}_{i-1}{)}^{2}},\:\:\:\:\:\:\:\:t\le\:\tau\:$$

(26)

and

$$\:{\sigma\:}_{2}^{2}=\frac{{\sum\:}_{j=1}^{n-1}(S\left({t}_{i}\right)-S\left({t}_{i-1}\right)-\left(\frac{{b}_{2}}{1-{\alpha\:}_{2}}\right)(N-S\left({t}_{i}\right))\left({t}_{i}-{t}_{i-1}\right){)}^{2}}{{\sum\:}_{j=1}^{n-1}({t}_{i}-{t}_{i-1}{)}^{2}},\:\:\:t>\tau\:$$

(27)

Change point calculation

Identifying the change point from a dataset includes a comprehensive analysis of fault detection trends over time in SRGMs. The conventional approach to identifying the change point involves visually examining the cumulative count of detected faults across time, employing statistical approaches such as time series analysis or regression analysis, change point detection algorithms such as the Bayesian change point detection algorithm etc. The testing team generally possesses the knowledge of the change point in real software testing, represented as τ but in our given dataset, we do not have adequate information regarding the accurate value of τ. To address this, we have applied empirical data analysis for more exact information about τ. The failure increasing rate is given as shown below⁴⁰:

$$\:{z}^{{\prime\:}}\left(t\right)=\underset{{\delta\:t}\to\:0}{\text{lim}}\frac{z\left(t+\delta\:t\right)-z\left(t\right)}{\delta\:t}$$

(28)

where,

• $\:{z}^{{\prime\:}}\left(t\right)\::$ fault detection rate.

• $\:z\left(t\right)\::$ observed cumulative number of detected faults by time $\:t$.

• $\:z\left(t+\delta\:t\right)\::$ observed cumulative number of detected faults by time $\:t+\delta\:t$.

Numerical illustration

Within this segment, we validate our developed model on three real datasets and a comparative analysis is also done with existing well-known models.

Selection of SRGMs

To calculate or predict the effectiveness of the developed model and techniques, a comprehensive literature review was carried out focusing on the mechanism and categorization of SRGMs. The categorization was mainly centred on categories like failure rate models, change point models and Non-Homogeneous Poisson process. At last, 11 SRGMs were taken into consideration as enumerated below in Table 1.

Table 1 m(t) i.e., mean value function of selected SRGMs.

Comparison criteria

A model could be chosen as per its capability to reintegrate the predicted output and the observed failure data can be employed to estimate the software’s future result. Within this segment, we validate our developed model on three real datasets and compare it with other existing models based on the sum of Mean Square Error (MSE) and R². However, the efficiency of SRGMs can be discussed by analyzing models proposing a set of comparison criteria as outlined below:

• The mean square error (MSE) gives the measure of divergence between the calculated values with the actual values of data as given below^9,47:

$$\:MSE=\frac{1}{N-n}\sum\:_{i=1}^{n}{{(y}_{i}-\widehat{m}\left({t}_{i})\right)}^{2}$$

where,

• N - Number of observations.

• $\:{y}_{i}\:$- Total number of faults detected up to time $\:{t}_{i}$.

• $\:m\left({t}_{i}\right)$- Estimated value of cumulative fault number up to time $\:{t}_{i}$ derived from the mean value function, where i = 1, 2…, n.

• $\:n\:$– represents number of parameters included in the model.

Consequently, a lesser value of MSE gives better goodness-of-fit.

• The second criterion implemented to compare the SRGMs is the correlation index of the regression curve equation$\:\left({R}^{2}\right)$ determined as^9,47:

$$\:{R}^{2}=1-\frac{{\sum\:}_{i=1}^{n}({y}_{i}-\bar{m}({t}_{i}){)}^{2}}{{\sum\:}_{i=1}^{n}({y}_{i}-\bar{y}{)}^{2}}$$

where,

• $\:\bar{y}=\frac{1}{n}{\sum\:}_{i=1}^{n}{y}_{i}$. Hence, the greater value of $\:{R}^{2}$ indicates better model performance.

Dataset 1/DS-I

The DS-1 is used to calculate and estimate unknown parameters⁴³. The software, during the testing phase of 19 weeks, took 47.65 CPU hours, and the data set has 328 detected faults. It is shown in Table 2.

Table 2 DS-I (19 weeks)- (Failure data from PL/I database application).

In the beginning, with software failure increasing rate, y′(t) remains relatively stable. This stage aligns with the early phases of testing when testers are trying to know the algorithm and software’s failure mode. After an initial stable stage, y′(t) begins to showcase a significant increase. This rise is attributed to the ability of testers to detect and address faults more effectively. The increase in failure rate touches its peak at a certain point in time, representing the time when the FDR is at its best. Following this peak, y′(t) gradually decreases, implying that testers have resolved almost all faults, and the software is becoming more stable. Eventually, y′(t) stabilizes at a lower rate, suggesting that the software has attained a relatively fault-free state. After employing empirical data analysis, we have identified that the change point for the given DS-I is at 6 weeks as shown in Fig. 1.

Fig. 1

Failures increasing rate for different $\:\delta\:t\:$values for DS-I.

Additionally, we have used SPSS version 20.0 to estimate the unknown parameters of the developed model namely (N, b₁, b₂, α₁, α₂) and we have also developed a code in Google Colab using Python version 3.10 to estimate the unknown parameters which represent uncertainty in the proposed model namely σ₁, σ₂. Additionally, we also used Mathematica version 13.2 to plot graphs to show belief reliability distribution and belief reliability.

The estimated values of unknown parameters are catalogued in Table 3. The expected number of detected faults is more in terms of number than the actual faults given in the data. The graph of the observed and estimated number of detected faults is presented in Fig. 2.

Fig. 2

Observed and expected number of detected faults for DS-I.

Table 3 Estimated values for unknown parameters for DS-I.

Table 4 Model comparisons: MSE and R² for different models for DS-I.

The uncertain differential equation is

$$\:dS\left(t\right)=\left\{\begin{array}{c}\left(21.15-0.05S\left(t\right)\right)dt+\:0.24d{C}_{t},\:\:\:\:\:\:t\le\:6,\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:\left(17.05-0.04S\left(t\right)\right)dt+\:0.05d{C}_{t},\:\:\:\:\:\:\:\:t>6,\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\end{array}\right.$$

(29)

As illustrated in Fig. 3, all the observed values lie within the region between the 0.000000124-path and the 0.996-path of the uncertain differential equation, hence the estimated values are valid and permissible.

Fig. 3

α-paths for DS-I.

Table 4 represents the comparison of the proposed model with other existing models based on MSE and R² criteria. As evident, the proposed model performs better as compared to other existing models.

Now, we plot the graph of belief reliability distribution before and after the change point, i.e. τ = 6, as represented in Fig. 4. The belief reliability distribution at time t = 5 is depicted in Fig. 5. Take into account an example, we can see that ф10 (95) = 0.9053, which indicates that the belief degree that the number of detected faults is less than 95 till t = 10 is 0.9053. Additionally, we outline the graph of belief reliability before and after the change point, i.e. τ = 6, which is displayed in Fig. 6. For given belief distribution function f = 0.05, belief reliability is displayed in Fig. 7.

Fig. 4

Belief reliability distribution for the proposed model before and after the change point at t = 6.

Fig. 5

Belief reliability distribution at time t = 5.

Fig. 6

Belief reliability for the proposed model before and after the change point at t = 6.

Fig. 7

Belief reliability at belief distribution function f = 0.05.

Dataset 2/DS-II

The DS-II is a widely used dataset⁴⁸. It was observed for 22 weeks, during which a sum of 86 faults were identified. The testing effort, determined in CPU hours, accounted for 93 h. We have estimated the change point based on the above-mentioned empirical data analysis for the given DS-II and found it to be 13 weeks. The analysis through graphical representation is shown in Fig. 8.

Fig. 8

Failures increasing rate for different $\:\delta\:t\:$values for DS-II.

Table 5 presents the values of estimated unknown parameters. The graph of the observed and estimated number of detected faults is given in Fig. 9, which also indicates that the expected number of detected faults is greater than the observed faults.

Fig. 9

Observed and expected number of detected faults for DS-II.

Table 5 Estimated values of unknown parameters for DS-II.

Hence, the uncertain differential equation is

$$\:dS\left(t\right)=\left\{\begin{array}{c}\left(6.38-0.042S\left(t\right)\right)dt+\:0.298d{C}_{t},\:\:\:\:\:\:t\le\:13,\:\:\:\:\:\:\:\:\:\:\\\:\left(0.14-0.001S\left(t\right)\right)dt+\:0.463d{C}_{t},\:\:\:\:t>13,\:\:\:\:\:\:\:\:\:\:\:\:\end{array}\right.$$

(30)

As demonstrated in Fig. 10, all the observed data lies within the region within the 0.35-path and 0.99-path of the uncertain differential equation, the estimated values are valid and acceptable.

Fig. 10

α-paths for DS-II.

Table 6 depicts the comparison of our proposed model with other well-established models based on the criteria mentioned above and we can conclude that our proposed model outperforms as compared to mentioned existing models.

Similarly, as in DS-I, we plot the graph belief reliability distribution and belief reliability before and after the change point i.e. τ = 13 which is represented in Figs. 11 and 12 respectively. At a given time, t = 20, the belief reliability distribution is presented in Fig. 13. For particular f = 0.5, belief reliability is represented in Fig. 14.

Fig. 11

Belief reliability distribution for the proposed model before and after the change point at t = 13.

Fig. 12

Belief reliability for the proposed model before and after the change point at t = 13.

Fig. 13

Belief reliability distribution at time t = 20.

Fig. 14

Belief reliability at belief distribution function f = 0.5.

Table 6 Model comparisons: MSE and R² for different models for DS-II.

Dataset 3/DS-III

The data set (DS-III) is extracted from a web-based integrated accounting ERP system (Web ERP) hosted on SourceForge.net⁴⁹, dated from August 2003 to July 2008, where the time unit is in months. A sum of 146 bugs were detected in 60 months. We have identified that the change point using the above-mentioned empirical data analysis for the given DS-III is 56 months. The analysis is shown in Fig. 15.

Fig. 15

Failures increasing rate for different $\:\delta\:t\:$values for DS-III.

Table 7 Estimated values of unknown parameters for DS-III.

Table 7 gives optimized valued of unknown parameters. The expected number of detected faults exceeds the observed number of faults given in the data as shown in Fig. 16.

Fig. 16

Observed and expected number of faults for DS-III.

Hence, the uncertain differential equation is

$$\:dS\left(t\right)=\left\{\begin{array}{c}\left(1.48-0.01\left(t\right)\right)dt+\:0.621d{C}_{t},\:\:\:\:\:\:\:\:t\le\:56,\:\:\:\:\:\:\\\:\left(2060-14.01S\left(t\right)\right)dt+\:1.64d{C}_{t},\:\:\:\:t>56,\:\:\:\:\:\:\end{array}\right.$$

(31)

All the observed data lie in the area within 0.18-path and 0.99-path of uncertain differential equation as shown in Fig. 17. Therefore, all the estimated values are acceptable.

Fig. 17

α-paths for DS-III.

Table 8 represents the comparison of our proposed model with other models based on the criteria mentioned above and we can conclude that our proposed model performs better than other models.

Similarly, as in DS-I, we plot the graph of belief reliability distribution before and after the change point, i.e. τ = 56, which is represented in Fig. 18. At a given time, the belief reliability distribution is similar to the way we calculated in DS-I. Further, we plot the belief reliability before and after the change point, i.e. τ = 56, which is shown in Fig. 19.

Fig. 18

Belief reliability distribution for the proposed model before and after the change point at t = 56.

Fig. 19

Belief reliability for the proposed model before and after the change point at t = 56.

Table 8 Model comparisons: MSE and R² for different models with for DS-III.

Managerial implications

The research paper introduces a new approach to estimate software reliability under uncertainty framework, including factors change point and imperfect debugging. The incorporation of change point and imperfect debugging altogether is the new approach adopted in this paper that identifies significant changes in fault detection rate. Managers can pinpoint these key points in the software lifecycle where changes (like feature additions or major fixes) might impact reliability, and adjust source code, resource allocation, or testing strategies as required. By involving uncertainty directly in the equations, managers can gain better insights into risk factors, including uncertainty, and make well-informed decisions related to software. The integration of uncertainty theory in the model suggests that software managers must be prepared for unexpected changes in system reliability due to external factors, unpredictable bugs, or imperfections in the debugging process. By incorporating this model, managers can develop more reliable risk management strategies, including alternative plans, which deal with the inherent uncertainty in software reliability. This could also result in more anticipatory decision-making when challenges arise. By understanding the impact of change points, imperfect debugging, and the uncertainties inherent in software systems, managers can optimize their workflows, improve resource allocation, and enhance software reliability in an uncertain environment. These characteristics enhance risk assessment and project management. For instance, if the developed model indicates that if debugging phase after the change point is resulting in the reintroduction of faults, then managers can opt to pause the testing, refactor the code, or upskill the staff. Such decisions enhance more informed decisions about optimal release time, cost estimation, and resource allocation. This could result in developing uncertain differential equations with time delays.

Conclusion and future scope

In this research, we have developed a novel software belief reliability growth model incorporating change point and imperfect debugging based on the mathematical approach of uncertainty theory that deals with epistemic uncertainties. This article is the first to integrate change point and imperfect debugging using uncertain differential equations based on belief reliability theory. Using principles of uncertainty theory, our proposed model discusses a more flexible and adaptable approach for estimating software reliability over time. Through numerical illustrations, we showcase the effectiveness of our model in handling the complexities of software development lifecycles and represent a significant contribution to advancing software reliability modelling, offering researchers an important methodology under the framework of uncertain theory. The newly developed model has been validated on three real data sets to generate more effective results. The methodology for estimating the unknown parameters is derived using the least squares method, and the change point is also estimated using empirical data analysis. The proposed model is compared with many other well-known existing SRGMs, and the results conclude that our model performs better than those models. Further, this research can be continued and explored by taking into account aspects like testing effort, multiple change points, time delay, patching and error generation. Other methodologies for estimating parameters can be developed. In future scope of research, time delays can be incorporated into the proposed model.