A meta-learning ensemble framework for robust and interpretable prediction of emergency medical services demand

Abstract

Accurate and robust forecasting of Emergency Medical Services (EMS) demand is crucial for ensuring timely ambulance dispatch and efficient resource allocation, particularly in low-resource public health systems, such as those in India. While most prior EMS forecasting studies have focused on urban settings in developed countries with rich, granular data, limited research has explored district-level forecasting using real-world ambulance dispatch data from India. Moreover, existing models often trade off robustness for accuracy or rely on complex black-box architectures, limiting their interpretability and real-world deployment. This study examines whether a heterogeneous ensemble of interpretable and complementary learners can outperform traditional and state-of-the-art regressors for district-level EMS forecasting, utilizing limited real-world features. To address this challenge, we propose EM-LR (Ensembled Meta-Learner with Linear Regression), a meta-learning framework that integrates four diverse base models−Lasso Regression, Support Vector Regression (SVR), Multilayer Perceptron (MLP), and Extreme Gradient Boosting (XGB)−via a linear regression meta-learner. Unlike prior meta-learners that stack similar tree-based or linear models, EM-LR combines low-variance, diverse learners to enhance robustness while maintaining model interpretability through SHAP-based feature analysis and transparent ensemble weights. Using only temporal and meteorological inputs, EM-LR forecasts daily EMS call volumes across five diverse districts in the state of Uttar Pradesh. We benchmark EM-LR against traditional models and recent advanced variants, including Twin Bounded Least Squares Support Vector Regression (TBLSSVR), Asymmetric-Huber based Extreme Learning Machine (AHELM), and Mexican-Hat Kernelized Large Margin Distribution Machine-based Regression (MHKLDMR), demonstrating superior accuracy and reduced prediction variance. Experimental results show up to 9.5% reduction in RMSE and over 40% variance reduction. EM-LR thus offers a scalable and interpretable forecasting solution tailored to the operational constraints of developing public health systems, supporting data-driven emergency planning and equitable healthcare delivery.

Introduction

Background and motivation

Emergency Medical Services (EMS) are an important component of the public health infrastructure, providing critical and often life-saving assistance in medical emergencies. A responsive and effective EMS system ensures timely care, which directly impacts patient survival rates, especially in trauma and critical care situations. However, EMS systems worldwide, including in low-resource settings such as India, are under increasing pressure due to increased population densities, evolving healthcare demands, and limited resources.

India, in particular, faces unique challenges in EMS planning and delivery. Many districts lack real-time surveillance systems, reliable demand data, or optimized protocols for ambulance allocation. Ambulance response times vary significantly across regions, often due to poor anticipation of demand patterns. In such contexts, district-level EMS demand forecasting becomes a critical planning tool for efficient ambulance deployment and equitable resource allocation. However, research on EMS forecasting in India remains limited, with few studies utilizing real-world ambulance dispatch data at the district level.

Given the critical role of predictive systems in equitable EMS planning, response time−the interval between call receipt and ambulance arrival−has emerged as a core performance metric. Accurate demand forecasting enables timely resource deployment, and numerous studies have leveraged it to guide dynamic ambulance allocation aimed at minimizing delays and improving prehospital care efficiency^1,2,3,4. Various EMS demand studies aim to reduce this response time. The two solutions entail forecasting ambulance demand to meet needs and optimizing ambulance distribution. Comprehensive studies have been conducted on dynamic ambulance allocation models to improve real-time EMS resource management. These models focus on the ongoing redistribution of ambulances in response to fluctuating demand, ensuring optimal coverage across various regions. Recently, several studies have focused on the planning and deployment of ambulances^{5,6,7,8,9,10,11,12}. For instance, Yaseen, Alkhalidi, and Raweshidy⁹ proposed a machine learning and SDN-based system for prioritizing SHE traffic flows. Liu, Li, and Zhang¹⁰ developed a robust optimization model for the optimal distribution of EMS stations. The model aims to optimize the number of ambulances and demand assignments in the EMS system while minimizing the anticipated overall cost. Amorim, Antunes, Ferreira, and Couto¹¹ proposed an approach to EMS resource allocation that improves patient outcomes by combining a mathematical model with a metamodel-based local search technique. Although such methods accelerate response and improve coverage, their effectiveness depends fundamentally on accurate and robust demand forecasting models that can anticipate call volumes under varying regional and temporal conditions.

Forecasting EMS demand helps estimate expected call volumes and temporal fluctuations, forming the foundation of operational planning. Different forecasting horizons serve distinct purposes. Short-term (minute-to-hourly) forecasts are valuable for dynamic ambulance routing and real-time dispatch optimization, while daily-level forecasts are essential for staff scheduling, ambulance station planning, and day-ahead readiness−particularly relevant in data-scarce, low-flexibility systems like those in many Indian districts. Long-term (monthly) forecasts, in contrast, aid in infrastructure and budget planning. Figure 1 illustrates the operational relevance of different forecasting horizons in EMS planning.

Fig. 1

Forecasting horizon and its implications in EMS demand prediction.

Over the years, EMS demand modeling has evolved from traditional statistical techniques to advanced machine learning (ML) frameworks. The regression models^{13,14,15,16,17,18,19,20} have been used extensively to study the influence of several contextual variables on explaining fluctuations in EMS demand. Time series forecasting models^22,23,24,25 rely on historical patterns of demand, along with contextual variables²¹. Graph-based convolutional networks²⁶, and spatio-temporal methods²⁷ have also been proposed to address EMS demand and to enhance resource allocation and emergency response times. Recent advancements in machine learning (ML) have significantly improved the accuracy of EMS demand predictions. Various studies^{28,29,30,31,32,33,34} have recently used ML techniques extensively to predict EMS demand both temporally and spatio-temporally. For instance, Grekousis and Liu²⁸ introduced a new three-level spatial-based artificial intelligence approach to forecast ambulance demand in emergency medical services. The method locates expected emergency events geographically, enabling better resource allocation and faster response times. Abreu et al.²⁹ introduced a data-driven forecasting method to facilitate emergency medical services (EMS) operational decision-making. This method surpasses the limitations of conventional forecasting techniques, enabling the healthcare industry to allocate resources more effectively. Martin, Mousavi, and Saydam³⁰ employed an ensemble-based decision tree model for feature selection, followed by a multilayer perceptron (MLP) artificial neural network model to generate daily, hourly, and spatially distributed predictions of EMS call volume.

Recent advancements in machine learning (ML) have significantly improved the accuracy of EMS demand predictions. While accuracy is a critical metric for predictive models, robustness is equally important, as it defines the model’s ability to deliver consistent results under varying conditions, especially in critical domains such as EMS demand forecasting. Many advanced ML models demonstrate high accuracy but exhibit significant variance across folds or datasets, undermining their reliability. Additionally, many models operate as ”black box” systems, providing limited insight into their decision-making processes. In critical fields such as healthcare, interpretability and robustness are essential for fostering trust, enabling accountability, and providing accurate predictions. This study addresses the triple challenge of accuracy, robustness, and interpretability by proposing EM-LR (Ensembled Meta-Learner with Linear Regression), a SHapley Additive Explanations (SHAP)³⁵ featured meta-learning framework designed to prioritize robustness and interpretability while maintaining competitive accuracy. By carefully curating a set of diverse, stable base models, EM-LR addresses the limitations of single-model approaches and mitigates the destabilizing effects of high-variance predictors. Additionally, SHAP provides a global and local explanation of feature importance, ensuring that the selected features contribute meaningfully to the predictions.

Meta-learning is an approach in machine learning that focuses on optimally combining predictions from multiple base models to enhance overall performance. It has been successfully applied in various domains, including speech recognition, energy forecasting, and natural language processing. In the context of emergency medical services (EMS), prior studies by Ramgopal et al.³⁶ and Megouo et al.³⁷ have explored meta-learning frameworks to forecast EMS dispatches. However, these studies predominantly rely on stacking similar types of base learners, such as generalized linear models, generalized additive models, and tree-based algorithms like Random Forest (RF) and Extreme Gradient Boosting (XGB). For instance, Decision Trees and RF are also used in the ensemble models proposed in³⁸. This lack of model diversity can lead to overfitting and instability, as similar models tend to produce highly correlated predictions³⁸. Moreover, these frameworks are often designed for data-rich environments, limiting their adaptability to regions with sparse data availability. These limitations highlight the need for a robust, interpretable, and generalizable meta-learning ensemble that can perform effectively even in data-scarce EMS settings.

Research gap and study contributions

While ensemble methods have demonstrated strong results in domains such as finance, energy, and NLP, their application to EMS forecasting remains limited, particularly in developing countries. Existing EMS forecasting studies often depend on rich spatial, demographic, or hospital-level variables that are rarely available in public health datasets. Furthermore, past meta-learners have tended to stack similar base models (e.g., tree-based or boosting methods), which increases the risk of overfitting and correlated prediction errors³⁸.

This study investigates whether a heterogeneous, low-variance meta-learning ensemble can achieve accuracy comparable to advanced nonlinear regressors−such as the Asymmetric-Huber Loss function-based ELM (AHELM)³⁹, Twin Bounded Least Squares Support Vector Regression (TBLSSVR)⁴⁰, and Mexican-Hat Kernelized LDMR (MHKLDMR)⁴¹−while maintaining computational efficiency and partial explainability through feature-level insights. The central research question is: ”Can a diverse ensemble of complementary learners forecast daily district-level EMS demand as effectively as complex state-of-the-art models, using only minimal temporal and meteorological features, while ensuring robustness and generalizability in data-scarce environments?”

To this end, we propose EM-LR (Ensembled Meta-Learner with Linear Regression), which strategically combines four diverse base learners−Lasso Regression⁴², Support Vector Regression (SVR)⁴³, Multilayer Perceptron (MLP)⁴⁴, and Extreme Gradient Boosting (XGB)⁴⁵−within a meta-learning framework. These models were chosen for their complementary strengths in handling linearity, nonlinearity, regularization, and structured data. A linear regression meta-learner aggregates its predictions to enhance robustness and maintain model transparency at the ensemble level. SHAP-based feature analysis further strengthens interpretability by identifying key temporal and meteorological drivers of EMS demand.

Key contributions of this study are as follows:

• Contextual novelty: This study is one of the first district-level EMS forecasting models tailored to India’s public health system, utilizing real-world ambulance dispatch data and only minimal features (e.g., day of the week, temperature, humidity, wind speed).

• Algorithmic innovation: We propose EM-LR, a novel heterogeneous meta-learning ensemble that stacks four diverse base learners−spanning linear, kernel, neural, and tree-based paradigms−and integrates them through a transparent linear regression meta-learner. Unlike past EMS meta-learners that rely on homogeneous tree ensembles, EM-LR reduces overfitting and prediction correlation while improving interpretability and robustness^37,38.

• Benchmarking against recent models: We rigorously benchmark EM-LR against both traditional models and recent state-of-the-art regressors such as TBLSSVR, AHELM, MHKLDMR to demonstrate performance gains and variance reduction.

• Explainability via feature analysis integration: We incorporate SHAP- and correlation-based feature relevance analysis within the meta-learning pipeline, enabling transparent understanding of how each temporal and weather variable influences EMS demand.

• Practical deployability and generalization: EM-LR demonstrates strong generalization performance across five demographically diverse districts, despite relying only on minimal temporal and meteorological inputs. This robustness across varied local conditions makes it a promising and scalable forecasting solution for EMS planning in real-world, data-scarce public health settings.

The remainder of this paper is structured as follows: The ”Methods” section details the EM-LR methodology, the ”Experimental Setup” section presents the dataset and experimental design, next, the ”Results and Discussion” section presents performance findings and feature-level insights, and the “Conclusion” section concludes the study.

Methods

Study area

Uttar Pradesh (UP), India’s most populous state, faces significant challenges in managing Emergency Medical Services (EMS) due to its geographical diversity and socio-economic conditions. This study examines five districts−Lucknow, Agra, Kanpur Nagar, Varanasi, and Gorakhpur−selected to represent the diverse characteristics of UP.

Lucknow

Lucknow, the capital of Uttar Pradesh, has a humid subtropical climate. During the study period, Lucknow experienced extremely hot summers, with temperatures reaching as high as $51\,^\circ$C. Winters were cool, with temperatures dropping to around $15\,^\circ$C. The monsoon season brought an average daily rainfall of about 5 mm; the highest recorded rainfall during the study period was 180 mm. Regarding EMS dispatch, the minimum daily dispatch was 0, while the maximum daily demand reached 85. On average, 13 EMS units were dispatched daily during this period.

Agra

Agra has a semiarid climate characterized by distinct summer, monsoon, and winter seasons. Summers were hot and dry, with temperatures as high as $49\,^\circ$C during the study period. Winters were cool, with temperatures dropping to around $4\,^\circ$C. The average daily rainfall in Agra during the study period’s monsoon season was 4.4 mm, with the highest recorded rainfall at 119.7 mm. Regarding EMS dispatch, the minimum daily dispatch was 0, while the maximum daily demand reached 36. On average, 6 EMS units were dispatched each day during this period.

Kanpur Nagar

Kanpur is situated on the banks of the Ganges River and thus has a humid subtropical climate, characterized by hot and dry summers. During the study period, the district’s summer temperature was as high as $51\,^\circ$C. Winters were cooler, with temperatures dropping to around $19\,^\circ$C. During the monsoon season in the study period, Kanpur experienced an average daily rainfall of 4.1 mm, with the highest recorded rainfall reaching 108 mm. Regarding EMS dispatch, the minimum daily dispatch in Kanpur was 0, indicating days with no emergency demands. However, the maximum daily demand reached 41. On average, 8 EMS units were dispatched each day during this period.

Varanasi

Varanasi is in the northern part of Uttar Pradesh and is also located on the banks of the Ganges River. It has hot and humid summers, with temperatures soaring to $51\,^\circ$C. Winters in Varanasi bring cooler temperatures, dropping to around $18\,^\circ$C. During the study period, Varanasi experienced an average daily rainfall of 6.54 mm during the monsoon season, with the highest recorded rainfall reaching 89.5 mm. Regarding EMS dispatch, the minimum daily dispatch in Varanasi was 0, indicating that there were no emergency demands on those days. However, the maximum daily demand reached 24. On average, 5 EMS units were dispatched each day during this period.

Gorakhpur

Gorakhpur is a district in the northeastern part of Uttar Pradesh. It has hot and humid summers, with temperatures soaring up to $48\,^\circ$C. Winters in Gorakhpur bring cooler temperatures, dropping to around $17\,^\circ$C. During the study period, Gorakhpur experienced an average daily rainfall of 1.68 mm during the monsoon season, with the highest recorded rainfall reaching 90.4 mm. Regarding EMS dispatch, the minimum daily dispatch in Gorakhpur was 0, indicating that there were no emergency demands on those days. However, the maximum daily demand reached 51. On average, 11 EMS units were dispatched each day during the study period.

Proposed framework

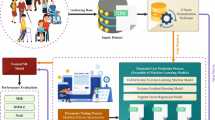
The EM-LR framework (Fig. 2) follows a structured pipeline for EMS demand forecasting. Initially, temporal, meteorological, and historical EMS features are extracted based on prior studies. Feature selection is performed using Pearson correlation and SHAP to identify the most relevant predictors. To assess the incremental value of weather features and feature selection, three model variants are constructed: (i) T using only temporal and historical EMS data, (ii) T+W adding all meteorological features, and (iii) T+W+FS incorporating only the top ten SHAP- and Pearson-ranked features. Each configuration is evaluated to understand trade-offs in performance and complexity. Building upon these, the final EM-LR model ensembles four diverse base learners: Lasso Regression, Support Vector Regression (SVR), Multilayer Perceptron (MLP), and Extreme Gradient Boosting (XGB), using Linear Regression as a meta-learner to capture complementary learning patterns. The optimization of the model’s structure was achieved through the process of hyperparameter tuning. Subsequently, the proposed model was validated using EMS demand data obtained from five discrete locations in Uttar Pradesh, India. The study conducted a comparative analysis of the model’s performance against state-of-the-art persistence models and other machine learning models, including Support Vector Regression (SVR), Random Forest (RF), Extreme Gradient Boosting (XGB), and Multilayer Perceptron (MLP).

Fig. 2

Flow chart of the proposed work.

The study’s methodology underwent rigorous testing and was subjected to a 5-fold cross-validation process to establish the accuracy and reliability of the proposed EM-LR model in predicting EMS demand across different districts. To achieve this, the dataset was partitioned into a training set, a validation set, and a test set. The first four years of data served as the training set, the fifth year’s data as the validation set, and data from the last year of the study period as the test set. The base models are trained with the help of the training set. The validation set compares the performance of different model structures by hypertuning their parameters, such as the regularisation parameter in SVR and Lasso Regression, the optimal number of heights in the XGB, and the number of hidden units in the MLP model. The error rate of the proposed model was measured using the test set. Lasso Regression, MLP, SVR, and XGB each receive the same training data, as shown in Fig. 3. The Linear Regression, which serves as a meta-learner, takes the predicted values of each base model as input. The final result is thus the weighted average of the results from the individual base models.

The input vector consists of three sets of features: meteorological, temporal, and EMS historical features. Let the meteorological features be denoted as $\textbf{x}^m = [x_1^m, x_2^m, \dots , x_{n_m}^m]$, the temporal features be denoted as $\textbf{x}^t = [x_1^t, x_2^t, \dots , x_{n_t}^t]$, and the EMS historical features be denoted as $\textbf{x}^h = [x_1^h, x_2^h, \dots , x_{n_h}^h]$. The input vector can then be written as:

$$\begin{aligned} {X} = [{X}^m, {X}^t, {X}^h] \end{aligned}$$

(1)

Our objective is to create a function that can forecast the EMS demand for the next day, denoted as $t+1$. This prediction will be based on the feature vector of meteorological conditions, time-related factors, and historical data on EMS parameters. Mathematically, the function can be expressed as follows:

$$\begin{aligned} Y_{t+1} = F(X)_t= F({X}^m_t, {X}^t_t, {X}^h_t) \end{aligned}$$

(2)

$Y_{t+1}$ denotes the predicted EMS demand at day $t+1$, and $F(\cdot )$ is the function that maps the input features to the predicted EMS demand. This function $F(\cdot )$ takes the predictions of the 4 base models and can be denoted as:

$$\begin{aligned} F({X})_t=\begin{bmatrix}f_{lr}({X})_t \ f_{svr}({X})_t \ f_{mlp}({X})_t \ f_{xgb}({X})_t\end{bmatrix} \end{aligned}$$

(3)

Where $f_{lr}(X), f_{svm}(X),f_{mlp}(X), f_{xgb}(X)$ denote the predictions of the 4 base models, namely Lasso Regression, SVR, MLP, and XGB. The detailed description of these functions is as follows:

$$\begin{aligned} \begin{aligned} f_{lr}({X})_t=f_{lr}({X}^m_t, {X}^t_t, {X}^h_t)\\ f_{svr}({X})_t=f_{svr}({X}^m_t, {X}^t_t, {X}^h_t)\\ f_{mlp}({X})_t=f_{mlp}({X}^m_t, {X}^t_t, {X}^h_t) \\ f_{xgb}({X})_t=f_{xgb}({X}^m_t, {X}^t_t, {X}^h_t) \end{aligned} \end{aligned}$$

(4)

These predictions from base models go to the linear regressor as 4 input vectors. The linear regressor assigns weights to each of these four input vectors and makes the final prediction as follows:

$$\begin{aligned} F({X})_t = w_0 + {w_1}\cdot {f_{lr}(X)} + {w_2}\cdot { f_{svr}(X)} + {w_3}\cdot { f_{svr}(X)} + {w_4}\cdot {f_{xgb}(X)} \end{aligned}$$

(5)

Where $w_i$ denotes the weights assigned to each of the four base models. The linear regressor optimizes these weights using a cost function that calculates the square of the sum of the differences between the actual EMS demand and the predicted EMS demand. Mathematically, the cost function can be expressed as:

$$\begin{aligned} Cost(w) = \frac{1}{8}\sum _{i=1}^4(y - \hat{y_{i}})^2 + \lambda \sum _{j=1}^4 w_j^2 \end{aligned}$$

(6)

Here Cost(w) is the cost function, y is the actual EMS demand, $\hat{y_{i}}$is the predicted EMS demand for each of the four base models, and $\lambda$ is the regularization parameter.

Fig. 3

Framework of the proposed EM-LR model.

Experimental setup

Data source

The data for this study comes from two sources. The EMS dispatch data was obtained from the GVK-Emergency Management Research Institute in Lucknow, which operates the ”108 Ambulance Service” across UP, providing daily dispatch counts for the five districts. Meteorological data was sourced from the World Weather Online API, including variables such as temperature, precipitation, dew point, pressure, visibility, and wind speed. These weather factors are critical in capturing the environmental influences on EMS demand.

To develop robust EMS demand prediction models, the data underwent preprocessing. Temporal features such as year, month, weekday, and weekend indicators were extracted to capture time-based trends. Meteorological variables were averaged over the preceding seven days to account for lagged effects. Historical EMS dispatch data was included by calculating the average dispatches over the previous seven days and counts from days lagged by 14, 21, and 28 days, capturing short- and long-term trends.

Performance evaluation metrics

The forecasting performance of all models was evaluated using four widely adopted error metrics: Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), Mean Bias Error (MBE), and Mean Absolute Percentage Error (MAPE). These measures collectively capture both the magnitude and direction of prediction errors, enabling a balanced assessment of model accuracy and stability.

MAE and RMSE quantify average deviation and error dispersion, respectively, while MBE indicates systematic bias (under- or over-prediction). MAPE expresses the relative percentage error, facilitating intuitive comparison across districts with varying EMS call volumes. All metrics were computed on the test sets for each district, and lower values indicate superior predictive performance and generalization.

Hyperparameter tuning of baseline and benchmark models

To rigorously evaluate our forecasting framework, we implemented a suite of machine learning models, categorized as either base learners for the proposed ensemble meta-learner (EM-LR) or as comparative benchmark models. The evaluation includes four base learners, including SVR, XGB, MLP, and Lasso Regression. We further benchmarked EM-LR against both traditional and recent advanced variants, including Random Forest (RF), Twin Bounded Least Squares Support Vector Regression (TBLSSVR), Asymmetric-Huber based Extreme Learning Machine (AHELM), and Mexican-Hat Kernelized Large Margin Distribution Machine-based Regression (MHKLDMR). Each model underwent grid search-based hyperparameter tuning to ensure optimal configuration. All experiments employed a consistent train–test split (2013–2017 for training, 2018 for testing), followed by 5-fold cross-validation. Model performance was assessed using four standard evaluation metrics: Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), and Mean Bias Error (MBE). A brief description of each model and its corresponding hyperparameter search space is provided below.

Lasso regression

It is a statistical method that utilizes linear regression with L1 regularization to model the relationship between predictor variables and EMS demand. It works by reducing the regression coefficients of the predictor variables until they reach zero, thereby decreasing the impact of unnecessary or redundant variables and encouraging sparsity in the final model. The values taken for the grid search are as follows:

• fit intercept= [1, 0]

• alpha= [0.005, 0.01, 0.03, 0.05, 0.07, 0.1]

Multilayer perceptron (MLP)

MLP is a neural network composed of many layers of connected neurons, each performing a non-linear change on its input. It was selected for its ability to model nonlinear patterns. The hyperparameters of an MLP that have been tuned are the number of hidden layers, the parameter $\alpha$, and the activation function. The alpha parameter regulates the regularization intensity, while the size of the hidden layer determines the number of neurons present in each layer. The activation parameter specifies the activation function for each layer. The values taken for the grid search for these hyperparameters are as follows:

• hidden layer size= [(24,), (36,), (14,), (14,10), (14,5), (14,14), (24,24), (24,12), (36,24), (36,12)]

• alpha= [$1e^{-8}$, $1e^{-7}$, $1e^{-6}$, $1e^{-5}$, $1e^{-4}$, $1e^{-3}$]

• activation= [relu, identity, tanh]

Support Vector Regression (SVR)

The SVR algorithm is a Support Vector Machine (SVM) version specific for regression tasks. It works by locating the hyperplane that preserves a maximum margin while permitting a specific deviation (specified by the epsilon parameter) from the real target values. SVR is included to capture nonlinear relationships with controlled flexibility. The three hyperparameters tuned in the study are ”fit_intercept”, ”C,” and ”$\epsilon$”. The ’fit_intercept’ parameter determines whether the model should include an intercept term in the regression equation, the ’$\epsilon$’ parameter establishes the margin of error permitted in the model’s predictions, and the ’C’ parameter manages the trade-off between obtaining a good fit on the training data and preventing overfitting. The following values were used to fine-tune these hyperparameters:

• $\epsilon$ = [8, 9, 10, 11, 12, 13, 14]

• fit_intercept = [0,1]

• C = [33, 34, 35, 36, 37, 38, 39, 40, 41]

Extreme Gradient Boosting (XGB)

XGB is a member of the gradient boosting family. It sequentially constructs an ensemble of weak prediction models, typically decision trees, where each successive model is trained to correct the errors made by the previous models. The final forecast is derived by combining the forecasts of all weak models. Four hyperparameters were chosen to tune the XGB model. First is the ’n_estimators’ parameter, which determines the number of trees in the ensemble and influences model performance and training time. The second is ’subsample,’ which refers to the fraction of samples used for training each tree. A lower value reduces the risk of overfitting but may also reduce performance. The ’eta’ hyperparameter, also known as the learning rate, determines the step size when modifying the weights; a smaller value results in more stable convergence. Lastly, the gamma hyperparameter controls the minimal loss reduction necessary to split a leaf, with a higher value resulting in more conservative tree construction. The values taken to tune these hyperparameters were

• n_estimators = range(70, 140, 10)

• subsample = [0.5, 0.75, 1]

• eta = [0.01, 0.05, 0.1, 0.2, 0.3, 0.4]

• gamma = range(150, 310, 10)

Random Forest (RF)

RF is a robust ensemble tree-based model used for EMS forecasting. We tuned three key hyperparameters via grid search: the ’n_estimators’ parameter, which specifies the total number of trees; the ’min_sample_split’ parameter, which specifies the minimum number of samples necessary to split a node; and the ’max_features’ parameter, which specifies the maximum number of features to be randomly selected while the tree is being grown. The range of values used for hyperparameters in the grid search:

• n_estimators = range(300, 500, 25)

• min_sample_split’ = [2, 3, 4, 5, 6, 7]

• max_features = [log2, sqrt]

Asymmetric Huber loss function-based Extreme Learning Machine (AHELM)

AHELM is a robust variant of the Extreme Learning Machine (ELM) that replaces the standard mean-square error loss with an ”asymmetric Huber loss” to improve generalization and resilience to outliers. It combines the fast training of ELM with the robustness of Huber regression by introducing a tunable threshold parameter, $\delta$, that controls the transition between quadratic and linear loss regions. A regularization coefficient $\alpha$ penalizes excessively large output weights, improving stability. The tuned hyperparameters were:

• activation = [‘sigmoid’, ‘tanh’, ‘relu’]

• n_hidden = [25, 50, 75, 100, 150]

• delta = [0.25, 0.5, 0.75, 1.0]

• alpha = [0.001, 0.01, 0.1, 0.5, 1.0]

• learning_rate = [0.001, 0.01, 0.05]

Twin Bounded Least Squares Support Vector Regression (TBLSSVR)

TBLSSVR minimizes two smaller least-squares problems to achieve improved computational efficiency and reduced training complexity compared to traditional SVR. The tuned hyperparameters were:

• C1 = [0.01, 0.1, 1.0, 5.0, 10.0]

• C2 = [0.01, 0.1, 1.0, 5.0, 10.0]

• epsilon = [0.001, 0.01, 0.05, 0.1]

• kernel = [‘linear’, ‘rbf’, ‘poly’]

• gamma = [0.01, 0.05, 0.1, 0.5]

Mexican-Hat Kernelized Large Margin Distribution Machine-based Regression (MHKLDMR)

MHKLDMR integrates a localized dual model regression framework with a Mexican Hat wavelet kernel to capture nonlinear and oscillatory patterns in EMS demand. The following parameters were grid-searched:

• C1 = [0.01, 0.1, 1.0, 5.0]

• C2 = [0.01, 0.1, 1.0, 5.0]

• epsilon = [0.001, 0.01, 0.05, 0.1]

• sigma = [0.25, 0.5, 1.0, 2.0, 3.0]

Results and discussion

This section presents and compares the results of proposed EM-LR with various machine learning models, including traditional models including Extreme Gradient Boosting (XGB), Multi-layer Perceptron (MLP), Random Forest (RF), and Support Vector Regression (SVR), with the benchmark method P-Persistence and the recent advanced variants, including Asymmetric Huber loss function-based Extreme Learning Machine (AHELM), Twin Bounded Least Squares Support Vector Regression (TBLSSVR), and Mexican-Hat Kernelized Large Margin Distribution Machine-based Regression (MHKLDMR). The comparison is conducted for five districts in Uttar Pradesh: Lucknow, Kanpur Nagar, Agra, Gorakhpur, and Varanasi. These districts were selected based on their significance as population centers, encompassing urban, semi-urban, and rural areas. The aim was to comprehensively assess EMS demand patterns across diverse demographic and socioeconomic settings.

Test results

To evaluate the predictive performance of the proposed EM-LR model across the five studied districts, four standard error metrics−Mean Absolute Error (MAE), Root Mean Square Error (RMSE), Mean Absolute Percentage Error (MAPE), and Mean Bias Error (MBE)−were employed (Tables 1, 2, 3, 4, 5). The results demonstrate a consistent and substantial improvement of EM-LR over all baseline models, including MLP, SVR, RF, XGB, and advanced variants such as AHELM, TBLSSVR, and MHKLDMR.

Across all districts, EM-LR achieved the lowest RMSE, confirming its superior ability to capture temporal and meteorological dependencies in EMS dispatch demand. As illustrated in Fig. 4, EM-LR consistently yielded smoother error profiles and reduced prediction volatility compared to both tree-based and neural counterparts. Notably, for Lucknow and Varanasi, EM-LR attained RMSE values of 6.01 and 3.41, respectively−the lowest among all competing models−reflecting its robustness in both high- and low-demand regions. Likewise, in Agra and Kanpur Nagar, EM-LR registered RMSE improvements exceeding 8–12% over the next-best models, while in Gorakhpur, it marginally surpassed SVR and XGB, achieving an RMSE of 5.07.

When compared with recent advanced learners such as AHELM, TBLSSVR, and MHKLDMR, EM-LR demonstrated consistent or superior generalization. For instance, in Lucknow, EM-LR achieved an RMSE of 6.01 compared to 6.90 (AHELM) and 9.21 (TBLSSVR), marking an improvement of 13–35%. In Agra, EM-LR (3.95) outperformed AHELM (4.22) and MHKLDMR (4.20) by approximately 6–7%, while in Kanpur Nagar, it achieved an RMSE of 4.21 versus 4.35 (AHELM) and 4.54 (MHKLDMR). In Gorakhpur, where AHELM (5.73) and MHKLDMR (6.24) performed competitively, EM-LR attained the lowest RMSE (5.07). These results underscore EM-LR’s ability to deliver accuracy and robustness comparable to that of state-of-the-art specialized algorithms, without the added architectural complexity or loss of interpretability.

The MAE and MAPE results (Figs. 5 and 6) further reinforce EM-LR’s superior generalization. For every district, EM-LR exhibited the lowest absolute and percentage errors, signifying enhanced reliability and reduced overfitting across data variants (T, T+W, and T+W+FS). The most pronounced reductions were observed for the T+W+FS configuration, where EM-LR achieved MAPE values as low as 0.32 in Lucknow and 0.35 in Gorakhpur, outperforming all benchmark models by wide margins. These improvements affirm that feature selection (FS) synergistically enhances the ensemble’s stability and interpretability, especially when meteorological factors are integrated.

In addition to minimizing absolute errors, EM-LR effectively mitigated systematic bias. The MBE values show a bias reduction ranging from 37.5% (Lucknow) to 69.4% (Varanasi) relative to traditional regressors, demonstrating that the ensemble does not consistently under- or over-predict dispatch volumes. While SVR achieved the smallest bias for the Gorakhpur district, the EM-LR model remained competitive, yielding an MBE of –0.87, which is within a negligible deviation from the optimal bias margin. In all other districts, EM-LR achieved the lowest or nearly lowest MBE, underscoring its balanced predictive behavior.

In summary, EM-LR delivers consistent, interpretable, and bias-resilient forecasts across diverse operational environments. Its ensemble integration of linear, nonlinear, and tree-based learners allows it to outperform individual base models and contemporary regression alternatives. The uniform superiority of EM-LR across all four metrics highlights its scalability and generalizability for district-level EMS demand forecasting in resource-constrained settings.

Fig. 4

RMSE Comparison of Models across Districts.

Fig. 5

MAE Comparison of Models across Districts.

Fig. 6

MAPE Comparison of Models across Districts.

Table 1 Performance comparison on Agra dataset.

Table 2 Performance comparison on Gorakhpur dataset.

Table 3 Performance comparison on Kanpur Nagar dataset.

Table 4 Performance comparison on Lucknow dataset.

Table 5 Performance comparison on Varanasi dataset.

Statistical significance analysis

To evaluate the statistical reliability of the proposed EM-LR model’s superior forecasting performance, we employed a two-stage non-parametric evaluation based on the t-Friedman test proposed by Liu and Xu⁴⁶, complemented by district-wise paired t-tests for local validation. This combination ensures both global and local statistical verification of EM-LR’s performance gains.

Global comparison using the t-Friedman test

The t-Friedman test is an improvement on the classical Friedman test by integrating Student’s t-tests into the ranking process, thereby accounting for both mean and variance across repeated runs. Algorithms with statistically indistinguishable distributions (at $\alpha _t = 0.05$) receive tied ranks, ensuring a variance-aware and conservative ranking.

Across the four districts and eight competing models on (T+W+FS) variant, the Iman–Davenport extension of the Friedman test produced an $F_{7,21}$ value of 24.02 with a p-value of $3.86\times 10^{-7}$, decisively rejecting the null hypothesis of equal model performance. The resulting average t-Friedman ranks (Table 6) confirm that EM-LR consistently outperformed all benchmarks. A lower rank denotes better predictive accuracy (i.e., lower RMSE).

Table 6 Average t-Friedman ranks of all models across districts (lower is better).

Post-hoc pairwise comparison

After rejecting the null hypothesis globally, we conducted pairwise comparisons between EM-LR (control) and each competing model using the t-Friedman post-hoc procedure. Three multiple-comparison corrections−Holm, Finner, and Bonferroni-Dunn−were applied to control the family-wise error rate at $\alpha = 0.05$. The adjusted results are shown in Table 7.

Table 7 t-Friedman post-hoc comparisons against the EM-LR control model.

The Holm test confirmed that EM-LR is statistically superior to three advanced models−TBLSSVR, AHELM, and MHKLDMR−while the Finner correction additionally marked MLP as marginally inferior. Classical ensemble baselines such as XGB, RF, and SVR exhibited competitive but non-significant differences, reflecting smaller mean gaps and higher variance across districts.

District-wise validation

To complement the global non-parametric analysis, classical paired t-tests⁴⁷ were also conducted between EM-LR and each competing model using RMSE values from five random seeds within each district. These results, summarized in Table 8, reinforce the global findings: EM-LR achieved statistically significant ($p<0.05$) improvements over nearly all baseline and advanced models in Agra, Gorakhpur, Kanpur Nagar, and Lucknow, while Varanasi showed a few non-significant results due to lower variance and more homogeneous data.

Table 8 Paired t-test results between EM-LR and benchmark models across districts.

Overall, the t-Friedman analysis confirmed significant global differences among models, with EM-LR achieving the best average rank and statistically outperforming all advanced baselines under Holm correction. The complementary district-wise t-tests reinforced these results, verifying EM-LR’s consistent superiority across regions. Together, these analyses demonstrate that the proposed ensemble meta-learner delivers statistically significant, robust, and generalizable forecasting performance across diverse geographical contexts.

Feature importance analysis

Feature selection is essential in EMS demand forecasting, as it enhances model accuracy while minimizing redundancy and overfitting. In this study, two complementary approaches−SHAP (SHapley Additive exPlanations) and Pearson correlation analysis−were employed to identify the most influential predictors across districts. SHAP quantifies each feature’s marginal contribution to the model output, effectively capturing non-linear and interaction effects, while correlation analysis highlights strong linear associations with EMS dispatch demand. The integration of both methods ensured that features with either direct or complex relationships were retained for subsequent modeling.

Feature selection was performed independently for each district to account for local variations in EMS patterns and meteorological behavior. The results revealed that Agra and Gorakhpur achieved optimal performance using correlation-based top features, whereas Lucknow, Kanpur Nagar, and Varanasi performed better with SHAP-based top-ten features. Figures 7, 8, 9, 10, 11 illustrate the ranked importance of features for each district.

Across all regions, historical EMS dispatch indicators consistently emerged as dominant predictors. Among the meteorological variables, temperature, dew point, wind speed, precipitation, and pressure showed a notable influence, whereas visibility and previous-day rainfall had a less significant impact. The presence of several non-linear weather effects identified exclusively by SHAP underscores that meteorological factors influence EMS demand in a non-proportional manner.

Temporal variables (year, month, and weekday) exhibited moderate yet consistent relevance. The year variable was a significant predictor across all districts, while the month contributed primarily in Gorakhpur (Fig. 8) and the weekday in Kanpur Nagar (Fig. 9). These variations highlight district-specific temporal dynamics in EMS demand.

To statistically validate the benefits of feature selection, a paired t-test (Table 9) was conducted between the two variants of the EM-LR model, of those trained on all features (T+W) and those trained on selected features (T+W+FS), using five random seeds. The proposed EM-LR model exhibited statistically significant improvement ($p < 0.05$) in most districts, confirming that the reduced feature subset enhanced predictive performance without compromising generality.

Table 9 Paired t-test results for EM-LR model under All-Features and Feature-Selected configurations.

Overall, feature selection improved both interpretability and statistical robustness of the proposed framework. The findings demonstrate that historical EMS trends and nonlinear meteorological interactions jointly govern ambulance dispatch demand.

Fig. 7

Feature importance analysis for Agra District.

Fig. 8

Feature importance analysis for Gorakhpur District.

Fig. 9

Feature importance analysis for Kanpur Nagar District.

Fig. 10

Feature importance analysis for Lucknow District.

Fig. 11

Feature importance analysis for Varanasi District.

Robustness analysis

The models were examined across five random seeds for each district to evaluate the sensitivity of RMSE performance to data partitioning. The variance of RMSE was used as the robustness indicator, where lower variance implies greater stability. As shown in Table 10, 11, 12, 13, 14, the proposed EM-LR generally achieves the lowest or near-lowest variance across districts, indicating high consistency across varying data splits.

In Agra, EM-LR exhibited the most stable performance (variance = 1.59), closely followed by AHELM and MLP, whereas tree-based models, such as RF and XGB, displayed higher fluctuations (Table 10). Kanpur Nagar (Table 12) showed a similar trend, where EM-LR achieved the smallest variance (0.66), with AHELM and MHKLDMR performing competitively and outperforming SVR and RF. For Gorakhpur (Table 11), the differences among EM-LR (1.04), SVR (1.00), and AHELM (0.68) were marginal, suggesting that these models maintained comparable robustness, whereas TBLSSVR and RF exhibited greater sensitivity.

In Lucknow (Table 13), EM-LR (2.34) maintained higher stability than all other models, including the advanced variants, which showed noticeably larger variance under complex temporal patterns. In Varanasi (Table 14), the variances for MLP, SVR, AHELM, and MHKLDMR were relatively close, yet EM-LR still achieved the lowest variance (0.30), confirming its consistent generalization.

Overall, while models such as AHELM and MLP occasionally approached EM-LR in robustness, the proposed ensemble remained the most reliable and balanced performer across all five regions. Its consistent low variance across both traditional and advanced benchmarks underscores its robustness and practical suitability for EMS demand forecasting under diverse operating conditions.

Table 10 Variance of RMSE across different models for the Agra Dataset.

Table 11 Variance of RMSE across different models for the Gorakhpur dataset.

Table 12 Variance of RMSE across different models for the Kanpur Nagar dataset.

Table 13 Variance of RMSE across different models for the Lucknow dataset.

Table 14 Variance of RMSE across different models for the Varanasi dataset.

Conclusion

This study proposed EM-LR, a robust and interpretable meta-learning ensemble framework for forecasting Emergency Medical Services (EMS) demand. Addressing the limitations of conventional ensemble and single-learner models, EM-LR integrates the complementary strengths of Support Vector Regression, Lasso, Multilayer Perceptron, and Extreme Gradient Boosting through a Linear Regression meta-learner. This architecture offers a balanced trade-off between predictive accuracy, variance reduction, and interpretability, essential features for real-time public health decision-making.

Empirical evaluation across five districts in Uttar Pradesh demonstrated that EM-LR consistently outperformed all traditional baselines in terms of both RMSE and variance, achieving up to 20% lower prediction error and over 40% variance reduction compared to the best standalone learners. When benchmarked against recent advanced models such as AHELM, TBLSSVR, and MHKLDMR, EM-LR continued to exhibit comparable or superior robustness while maintaining greater accuracy, underscoring the advantage of its meta-learning design. Statistical validation using the Friedman and post-hoc tests further confirmed the significance of these improvements, establishing EM-LR as a statistically reliable framework for EMS forecasting.

An in-depth feature analysis using SHAP and Pearson correlation revealed that historical dispatch patterns are the most influential predictors, with meteorological and temporal features offering modest incremental gains. This insight reinforces the importance of operational history in short-term EMS forecasting and suggests that weather-based complexity may not always translate to predictive power.

Overall, EM-LR emerges as a practical, transparent, and statistically validated solution for forecasting EMS demand. Its ability to deliver low-error, low-variance predictions without resorting to opaque deep learning architectures makes it a scalable and actionable tool for emergency management agencies. Future work will focus on deploying EM-LR across more districts and integrating probabilistic extensions to account for demand uncertainty and dynamic temporal shifts.