Novel application of sinh cosh optimizer for robust controller design in hybrid photovoltaic-thermal power systems

Abstract

Load frequency control (LFC) is critical for maintaining stability in interconnected power systems, addressing frequency deviations and tie-line power fluctuations due to system disturbances. Existing methods often face challenges, including limited robustness, poor adaptability to dynamic conditions, and early convergence in optimization. This paper introduces a novel application of the sinh cosh optimizer (SCHO) to design proportional–integral (PI) controllers for a hybrid photovoltaic (PV) and thermal generator-based two-area power system. The SCHO algorithm’s balanced exploration and exploitation mechanisms enable effective tuning of PI controllers, overcoming challenges such as local minima entrapment and limited convergence speeds observed in conventional metaheuristics. Comprehensive simulations validate the proposed approach, demonstrating superior performance across various metrics. The SCHO-based PI controller achieves faster settling times (e.g., 1.6231 s and 2.4615 s for frequency deviations in Area 1 and Area 2, respectively) and enhanced robustness under parameter variations and solar radiation fluctuations. Additionally, comparisons with the controllers based on the salp swarm algorithm, whale optimization algorithm, and firefly algorithm confirm its significant advantages, including a 25–50% improvement in integral error indices (IAE, ITAE, ISE, ITSE). These results highlight the SCHO-based PI controller’s effectiveness and reliability in modern power systems with hybrid and renewable energy sources.

Introduction

The main function of load frequency control (LFC) in interconnected power systems is to quickly minimize frequencies and tie-line power deviations after failures and load changes, and to maintain a stable and reliable working point¹. Classical production power plants (thermal generators and gas units) use primary and secondary control cycles for LFCs. However, renewable energy alternatives are widely preferred in power systems today in order to prevent ever-increasing environmental pollution and solve increasing economic problems due to fuel consumption. Photovoltaic (PV) systems are more attractive in terms of renewable energy alternatives and require an effective way to address the LFC problem².

The integration of renewable energy sources, particularly PV systems, into traditional power grids poses challenges related to frequency and voltage control due to their zero or low inertia characteristics. Addressing these challenges requires advanced control strategies, optimization algorithms, and hybrid techniques to enhance the performance of PV-integrated microgrids. In this regard, various control structures and techniques to solve the LFC problem have been studied by researchers. The early proposed methods in the literature can be listed as robust control³, pole placemen⁴, decentralized control⁵, and variable structure⁶. Although these techniques provide the desired performance in the power system, there are some disadvantages that make it difficult to implement them. To overcome these obstacles, alternative techniques such as artificial intelligence-based neural network, sliding mode controller, and fuzzy logic have been proposed^7,8. While these techniques are effective against nonlinear factors in power systems, their complex structures and intensive calculation processes are the biggest disadvantages.

Another proposed alternative to the LFC design problem is the use of metaheuristic algorithms. The biggest advantages of these algorithms are their ability to handle nonlinear functions, their easy integration into the system, and their lack of complex structure^{9,10,11,12,13}. Therefore, recent advancements in metaheuristic algorithms have demonstrated their effectiveness in tackling complex optimization problems in power systems. For instance, an optimized fuzzy logic controller with adaptive membership functions tuned using the sorted position-based grey wolf optimization algorithm was proposed in one of the reported studies¹⁴. The method minimizes discrepancies between reference and control signals, demonstrating improved frequency stability and efficiency in PV-based microgrids. In another study, an adaptive neuro-fuzzy inference system and deep neural network-based controller, optimized using the hybrid honey badger-based grey wolf optimization algorithm was proposed¹⁵. This approach regulates output waveforms, significantly reducing errors and enhancing performance metrics such as switching time and frequency stability in microgrids. The lion algorithm was proposed in a different study¹⁶ for fractional-order proportional-integral controller which was used to design LFC in interconnected power systems. The proposed controller demonstrated superior performance in terms of convergence, gain optimization, and transient stability compared to traditional methods.

It is feasible to encounter a variety of other options that have been reported for LFC. In this context, some of the important algorithms used in literature for the LFC problem can be listed as Lyrebird optimization¹⁷, walrus optimization¹⁸, particle swarm optimization¹⁹, artificial rabbits optimization²⁰, salp swarm algorithm²¹, marine predators algorithm²², modified whale optimization²³, firefly²⁴, teaching–learning based optimization^25,26, and its hybrid version with local unimodal sampling²⁷, hybrid simulated annealing based quadratic interpolation optimizer²⁸, hybrid harmony search and cuckoo optimization²⁹, symbiotic organism search³⁰, Harris hawks optimizer and its enhanced version^31,32, multi-verse optimizer³³, imperialist competitive³⁴, grey wolf optimization³⁵, bees algorithm³⁶, enhanced coyote optimizer³⁷, honey badger³⁸, hybrid whale optimalization algorithm with simulated annealing³⁹, rime algorithm⁴⁰, gorilla troops optimization⁴¹ and wild horse optimizer⁴².

Through these metaheuristic algorithms, different controller structures were designed to solve the LFC problem. Nevertheless, in most of these metaheuristic algorithms some difficulties, such as local minima trap, early convergence, and inadequate ability to search the entire scale of the problem in the higher dimensions, are encountered. Therefore, despite the advancements, limitations in robustness, convergence speed, and adaptability persist, necessitating new solutions. In this regard, this study proposes the sinh cosh optimizer (SCHO)⁴³ as a novel solution to tune a proportional-integral (PI)⁴⁴ controller for the LFC design problem.

The SCHO is one of the latest mathematical based metaheuristic optimization techniques and has been successfully applied to some engineering optimization problems. The biggest advantages of this algorithm can be listed as having a balanced exploration–exploitation, and not being affected by the nature of the problem, along with being simple and flexible. Some applications of the SCHO include automatic voltage regulator design⁴⁵, prediction of biological activities⁴⁶, aircraft pitch angle control⁴⁷ and Parkinson’s disease detection⁴⁸. Considering the success and superiority of the SCHO in engineering problems in the reported studies, this paper proposes the solution to the LFC design problem in a two-area power system consisting of PV and thermal units. The hybrid power system is modeled with Area 1 consisting of a PV-based power system, including a maximum power point tracker (MPPT), and Area 2 comprising a thermal power system with governor, turbine, reheater, and generator dynamics. The optimization objective is to minimize the integral of time-weighted absolute error (ITAE) to achieve rapid stabilization and minimal steady-state errors. Proportional (${k}_{p1}$ and ${k}_{p2}$) and integral (${k}_{i1}$ and ${k}_{i2}$) parameters of the controllers are optimized considering the boundaries adopted in the previous studies. The SCHO is initialized and its unique exploration and exploitation phases ensure efficient global optimization of the PI controller parameters. The proposed SCHO-based PI controller is tested against step load changes, parameter variations, and solar radiation fluctuations. Its performance is compared with (salp swarm algorithm-based PI²¹, whale optimization algorithm-based PI²³ and firefly-based PI²⁴ controllers using metrics such as settling time, overshoot, undershoot, and different error-based performance indices (IAE, ITAE, ISE, ITSE)^49,50,51. Therefore, the proposed SCHO-based PI controller addresses the above-mentioned gaps, achieving faster stabilization and superior error minimization metrics compared to existing methods. The main contributions of this work include:

• 1. The first application of the SCHO algorithm for LFC in hybrid PV-thermal systems.

• 2. Superior performance in minimizing error-based metrics and achieving faster stabilization.

• 3. Enhanced robustness under parameter variations and dynamic conditions, such as solar radiation fluctuations.

• 4. Comprehensive comparison with state-of-the-art methods, demonstrating the proposed approach’s effectiveness and reliability.

Mathematical model of SCHO algorithm

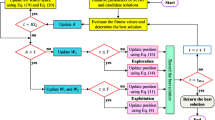
SCHO consists of five important components. These can be listed as initialization phase, exploration phase, exploitation phase, bounded search strategy and switching mechanism, respectively⁴³.

Initialization phase

Like other metaheuristic methods, SCHO starts from randomly selected candidate solutions ($X$), given in Eq. (1), and candidate solutions are updated in each iteration⁴³.

$$X=\left[\begin{array}{ccccc}{x}_{11}& \cdots & {x}_{1j}& \cdots & {x}_{1d}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {x}_{i1}& \cdots & {x}_{ij}& \cdots & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {x}_{N1}& \cdots & {x}_{Nj}& \cdots & {x}_{Nd}\end{array}\right].$$

(1)

Here $N$ is the number of candidate solutions (population size), $d$ is the number of variables in the optimization problem, and ${x}_{ij}$ is ${i}^{th}$ solution’s ${j}^{th}$ position. It is obtained as $X=LB+rand(N,d)\times (UB-LB)$, where $LB$ and $UB$ represent the lower and upper bounds of the variables, respectively, and $rand$ represents the random value between 0 and 1.

Exploration phase

In order to avoid local minima in subsequent iterations, two-stage exploration is used in SCHO and the switch value ($T$) is given in Eq. (2)⁴³.

$$T=floor({t}_{max}/3.6).$$

(2)

Here, floor is the rounding down function in the MATLAB program and ${t}_{max}$ is the maximum number of iterations. In the first exploration phase, position updating is done using the following definition⁴³.

$${X}_{ij}^{t+1}=\left\{\begin{array}{c}{X}_{j}^{best}+{r}_{1}{W}_{1}{X}_{ij}^{t}, {0.5<r}_{2}\\ {X}_{j}^{best}-{r}_{1}{W}_{1}{X}_{ij}^{t}, {0.5>r}_{2}\end{array}\right..$$

(3)

Here ${r}_{1}$ and ${r}_{2}$ are random numbers ranging from 0 to 1, $t$ is the current iteration, ${X}_{ij}^{t}$ and ${X}_{ij}^{t+1}$ are the ${i}^{th}$ solution in the ${j}^{th}$ position for the current iteration and the next iteration, respectively. Solution ${X}_{j}^{best}$ is the best solution of the ${j}^{th}$ position. The weight factor ${W}_{1}$ is given in Eq. (4)⁴³.

$${W}_{1}={r}_{3}{a}_{1}\left[\text{cosh}\left({r}_{4}\right)+0.388\cdot \text{sinh}\left({r}_{4}\right)-1\right].$$

(4)

Here, ${r}_{3}$ and ${r}_{4}$ are random numbers varying between 0 and 1, and ${a}_{1}$ is a parameter that decreases according to the number of iterations and is calculated with the following definition⁴³.

$${a}_{1}=3\cdot \left(0.45-\frac{1.3t}{{t}_{max}}\right).$$

(5)

The position update of the second exploration phase of the SCHO is performed using the following definition⁴³.

$${X}_{ij}^{t+1}=\left\{\begin{array}{c}{X}_{ij}^{t}+\left|0.003\cdot {W}_{2}{X}_{j}^{best}-{X}_{ij}^{t}\right|, {0.5<r}_{5}\\ {X}_{ij}^{t}-\left|0.003\cdot {W}_{2}{X}_{j}^{best}-{X}_{ij}^{t}\right|, {0.5>r}_{5}\end{array}\right..$$

(6)

Here ${W}_{2}={r}_{6}{a}_{2}$ is the weight factor, ${a}_{2}=2\cdot \left(0.5-\frac{t}{{t}_{max}}\right)$ and ${r}_{5}$ and ${r}_{6}$ are random numbers varying between 0 and 1.

Exploitation phase

In SCHO the exploitation is performed within two stages and in the first stage, the positions are being updated via Eq. (7)⁴³.

$${X}_{ij}^{t+1}=\left\{\begin{array}{c}{X}_{j}^{best}+{r}_{7}{W}_{3}{X}_{ij}^{t}, {0.5<r}_{8}\\ {X}_{j}^{best}-{r}_{7}{W}_{3}{X}_{ij}^{t}, {0.5>r}_{8}\end{array}\right..$$

(7)

Here, ${r}_{7}$ and ${r}_{8}$ are random numbers that are produced within [0, 1] and ${W}_{3}$ is a weighting factor represented by Eq. (8)⁴³.

$${W}_{3}={r}_{9}{a}_{1}\left[\text{cosh}\left({r}_{10}\right)+0.388\cdot \text{sinh}\left({r}_{10}\right)\right].$$

(8)

Here, ${r}_{9}$ and ${r}_{10}$ are random numbers changing from 0 to 1. ${r}_{11}$ and ${r}_{12}$ are randomly produced numbers within [0, 1]. The second phase of the exploitation is performed with the following definition⁴³.

$${X}_{ij}^{t+1}={X}_{ij}^{t}+{r}_{11}\frac{\text{sinh}\left({r}_{12}\right)}{\text{cosh}\left({r}_{12}\right)}\left|{W}_{2}{X}_{j}^{best}-{X}_{ij}^{t}\right|.$$

(9)

Bounded search strategy

In SCHO, the potential search areas are fully discovered with the bounded search strategy. The rule for this strategy is given in Eq. (10)⁴³.

$${BS}_{m+1}={BS}_{m}+floor\left(\frac{{t}_{max}-{BS}_{m}}{4.6}\right).$$

(10)

Here, $m$ denotes the positive integers starting from 1 and ${BS}_{1}=floor\left(\frac{{t}_{max}}{1.55}\right)$.

Switching mechanism

With this mechanism, the SCHO ensures the balance and transition between exploration and exploitation. The $sinh$ and $cosh$ based switching mechanism ($A$) used in SCHO is calculated as follows⁴³.

$$A={r}_{13}\left[10-9{\left(\frac{t}{{t}_{max}}\right)}^{\frac{\text{cosh}(t/{t}_{max})}{\text{sinh}(t/{t}_{max})}}\right].$$

(11)

Here, ${r}_{13}$ is a randomly produced number within [0, 1]. In the SCHO algorithm, the exploration phase is executed when $A>1$ and the exploitation phase is executed when $A<1$. The explanatory flow diagram of SCHO is shown in Fig. 1.

Fig. 1

Flowchart for SCHO.

Modeling of photovoltaic and thermal power systems

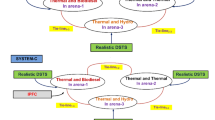
A two-zone power system model is considered to verify the effectiveness of the proposed SCHO-based controller. Area 1 consists of a PV-based system and Area 2 is a thermal power system. The transfer function of the solar PV system, which includes a PV panel, converter, filter and maximum power point tracker (MPPT), is given in Eq. (12)^21,23,24.

$${G}_{PV}\left(s\right)=\frac{-As+B}{{s}^{2}+Cs+D}.$$

(12)

The thermal power system in Area 2 consists of a generator, turbine, reheater and governor components. The transfer functions of these four components are defined in Eqs. (13)–(16), respectively^21,23,24.

$${G}_{gen}\left(s\right)=\frac{{K}_{g}}{s{T}_{g}+1},$$

(13)

$${G}_{tur}\left(s\right)=\frac{{K}_{t}}{s{T}_{t}+1},$$

(14)

$${G}_{rh}\left(s\right)=\frac{{s{T}_{r}K}_{r}+1}{s{T}_{r}+1},$$

(15)

$${G}_{gov}\left(s\right)=\frac{{K}_{ps}}{s{T}_{ps}+1}.$$

(16)

In order to make appropriate comparisons with the SSA-based PI²¹, WOA-based PI²³ and FA-based PI²⁴ control methods in the literature, the values of the parameters of the hybrid PV-thermal power system were chosen as $A=18$, $B=900$, $C=100$, $D=50$, ${K}_{g}=1$, ${T}_{g}=0.08$ s, ${K}_{t}=1$, ${T}_{t}=0.3$ s, ${T}_{r}=10$ s, ${K}_{r}=0.33$, ${K}_{ps}=120$ Hz/puMW, ${T}_{ps}=20$ s, $R=2.5$ Hz/pu, $B=0.8$ pu and ${T}_{12}=0.545$ puMW/Hz⁵². The block diagram of the entire system is shown in Fig. 2.

Fig. 2

Complete model of the system.

Definition of optimization problem

The traditional PI controller consists of proportional (${k}_{p}$) and integral (${k}_{i}$) parameters⁵³. In the PV-thermal power system, one PI controller is recommended for each of the two areas. The transfer function of the PI controller in the PV system region is given in Eq. (17).

$${C}_{area1}\left(s\right)={k}_{p1}+\frac{{k}_{i1}}{s}.$$

(17)

The transfer function of the PI controller in the thermal power system region is given in Eq. (18).

$${C}_{area2}\left(s\right)={k}_{p2}+\frac{{k}_{i2}}{s}.$$

(18)

It is aimed to minimize frequency deviations (($\Delta {f}_{1}$ and $\Delta {f}_{2}$) and tie-line power variations ($\Delta {P}_{tie}$) in the hybrid PV-thermal power system by using PI controllers. In this paper, integral of time weighted absolute error (ITAE) was preferred as the objective function⁵⁴ and its definition is provided as the minimization of Eq. (19).

$$ITAE=\underset{0}{\overset{{t}_{sim}}{\int }}t\cdot (\left|\Delta {f}_{1}\right|+\left|\Delta {f}_{2}\right|+\left|\Delta {P}_{tie}\right|)\cdot dt.$$

(19)

Here, ${t}_{sim}$ represents the simulation time, and it was found sufficient to take it as 30 s in this study. The limits of the parameters of the PI controllers, given in Eq. (20), were considered during the minimization of the ITAE performance metric through the SCHO algorithm.

$${-2\le k}_{p1}, {k}_{i1},{k}_{p2}, {k}_{i2}\le 2.$$

(20)

The interval $[-2, +2$] was selected to ensure a fair comparison with the other approaches-based controllers, as these bounds are consistent with those used in the cited literature. This uniformity in parameter limits ensures that the results accurately reflect the optimization potential of the SCHO relative to other approaches, providing a meaningful and unbiased evaluation of its performance. The parameter bounds defined in Eq. (20) serve as constraints to ensure meaningful optimization and allow a fair comparison with other controller design methods. Additionally, the ITAE objective function minimizes frequency and tie-line power deviations, effectively constraining the system to maintain stability and desired performance metrics.

In order to find the optimal control parameters (${k}_{p1}$, ${k}_{i1}$, ${k}_{p2}$ ve ${k}_{i2}$) in the optimization problem and to adjust the control of the relevant system, the proposed SCHO algorithm was run 30 times, using a population size ($N$) of 40 and the maximum number of iterations of 50. The population size of 40 was chosen to ensure consistency with reported works in the literature, facilitating fair comparisons. Additionally, this value provides an optimal balance between performance and computational efficiency. While reducing the population size would decrease the algorithm’s effectiveness, increasing it would lead to minimal performance gains while introducing additional computational overhead. In the best run, the minimum ITAE objective function value was reached.

Figure 3 illustrates the application of the SCHO to the LFC problem in a two-area hybrid power system. The algorithm initializes with a predefined population size and maximum iterations, then iteratively minimizes the ITAE objective function by assigning optimized PI controller parameters to Area 1 and Area 2. The PI controllers regulate the system to minimize frequency deviations ($\Delta {f}_{1}$, $\Delta {f}_{2}$) and tie-line power deviations ($\Delta {P}_{tie}$) under varying operational conditions, such as parameter variations and load changes. This block diagram provides a holistic view of the SCHO-based controller’s integration and operational workflow within the hybrid power system.

Fig. 3

The application of SCHO to the LFC problem.

Figure 4 shows the change curve of ITAE according to the number of iterations. As can be seen from the figure, with few iterations (${11}^{th}$ iteration), the SCHO algorithm converged to the global value ($\text{min}\left(ITAE\right)=2.9119$) without getting stuck in the local minimum. These results confirm the effectiveness and potential of the balanced exploration–exploitation mechanisms of the SCHO algorithm.

Fig. 4

Evolution curve of SCHO.

Simulation results

Compared methods

In order to demonstrate the stability and superiority of the proposed SCHO-based PI controller over the PV-thermal power system, comparisons were performed using three basic control methods which adopted the same system parameters and the same controller limits. The optimal values of the parameters of the proposed SCHO and the PI controllers based on SSA²¹, WOA²³ and FA²⁴ reported in the literature are listed in Table 1.

Table 1 Optimized PI controller parameters tuned by SCHO, SSA, WOA and FA.

Case studies

A $10\%$ step change ($\Delta {P}_{d1}=0.1$ pu and $\Delta {P}_{d2}=0.1$ pu) in both areas

In this case study, 10% load variations were assumed in the two areas. Comparative system responses of the power system are shown in Figs. 5, 6 and 7. The most important time performance metrics of the system are settling time (${t}_{set}$), undershoot (${U}_{shoot}$) and overshoot (${O}_{shoot}$). When calculating settling times, a tolerance band of ± 0.1 Hz for $\Delta {f}_{1}$ and $\Delta {f}_{2}$ and a tolerance band of ± 0.025 MW for $\Delta {P}_{tie}$ were considered. Besides, the overshoot and undershoot are calculated as the maximum positive and negative deviations from the steady-state value observed during the transient response, respectively. These metrics provide insights into the system’s dynamic behavior and stability following disturbances.

Fig. 5

Variation of frequency in Area 1.

Fig. 6

Variation of frequency in Area 2.

Fig. 7

Variation of tie-line power.

In Fig. 5, frequency changes for Area 1 are plotted over time, and in Table 2, the values of comparative system metrics are provided. Compared to SSA²¹, WOA²³ and FA²⁴ based PI controllers in the literature, the frequency change in Area 1 ($\Delta {f}_{1}$) was suppressed most effectively with the proposed SCHO based PI controller at 1.6231 s. With the proposed control approach, the ${U}_{shoot}$ and ${O}_{shoot}$ values of the oscillations for the $\Delta {f}_{1}$ signal were found to be − 0.1569 Hz and 0.0209 Hz, respectively, and these values are much lower than the values obtained with the three control approaches in the literature.

Table 2 Numerical results of ${U}_{shoot}$, ${O}_{shoot}$ and ${t}_{set}$ for $\Delta {f}_{1}$, $\Delta {f}_{2}$ and $\Delta {P}_{tie}$.

The comparative time response to the $\Delta {f}_{2}$ change for Area 2 is given in Fig. 6 and the numerical values of the system performance metrics are given in Table 2. Looking at the relevant figure and table, the best system response belongs to the system optimized with SCHO, and the frequency change in Area 2 ($\Delta {f}_{2}$) is between − 0.2217 Hz and 0.0459 Hz, and the oscillations were quickly settled into the desired tolerance band in 2.4615 s.

The plots of tie-line power changes ($\Delta {P}_{tie}$) obtained from all control approaches over time are shown in Fig. 7. Numerical values of comparative performance metrics are listed in Table 2. Looking at the table, it is clear that the lowest values of ${t}_{set}$, ${U}_{shoot}$ and ${O}_{shoot}$ metrics are found with the proposed SCHO-based PI control approach. All graphical time responses and numerical findings obtained in this case study show that the dynamics of the system after the fault of the first recommended SCHO tuned PI controller compared to its effective competitors in the literature (PI control methods based on SSA²¹, WOA²³ and FA²⁴) and confirmed its superiority and potential in improving determination.

Influence of solar radiation variation

In this case study, the effectiveness and robustness of the SCHO-based controller in suppressing oscillations was tested by considering random solar radiation changes in Area 1. Figure 8 illustrates the random variations in solar radiation considered during the test period (0–80 s). These variations mimic dynamic changes in PV output, which are common due to environmental factors such as cloud cover and atmospheric conditions.

Fig. 8

Variation of solar radiation.

Figure 9 presents the system’s frequency deviations ($\Delta {f}_{1}$, $\Delta {f}_{2}$) and tie-line power deviation ($\Delta {P}_{tie}$) under solar radiation fluctuations. The SCHO-based PI controller effectively suppresses oscillations, demonstrating its capability to stabilize the system within minimal settling times and low overshoot values. Therefore, the SCHO-based PI controller confirms that it has a robust control structure by successfully and quickly dampening the oscillations in the system during fluctuations in PV power production.

Fig. 9

Time response of load frequency control in solar radiation.

Comparison of well-known integral of error-based performance indices

This section evaluates the effectiveness of different optimization methods for the PI controller design in the load frequency control of a hybrid PV and thermal power system. By leveraging integral error-based performance indices (integral of absolute error (IAE), integral of time-weighted absolute error (ITAE), integral of squared error (ISE), and integral of time-weighted squared error (ITSE)) a comprehensive analysis of the controllers is performed. These indices are mathematically expressed as given in Eqs. (21), (22) and (23).

$$IAE=\underset{0}{\overset{{t}_{sim}}{\int }}(\left|\Delta {f}_{1}\right|+\left|\Delta {f}_{2}\right|+\left|\Delta {P}_{tie}\right|)\cdot dt,$$

(21)

$$ISE=\underset{0}{\overset{{t}_{sim}}{\int }}\left[{(\Delta {f}_{1})}^{2}+{(\Delta {f}_{2})}^{2}+{(\Delta {P}_{tie})}^{2}\right]\cdot dt,$$

(22)

$$ITSE=\underset{0}{\overset{{t}_{sim}}{\int }}t\cdot \left[{\left(\Delta {f}_{1}\right)}^{2}+{\left(\Delta {f}_{2}\right)}^{2}+{\left(\Delta {P}_{tie}\right)}^{2}\right]\cdot dt.$$

(23)

These metrics assess not only the magnitude of the error but also its impact over time, making them critical in judging controller performance in dynamic systems.

Table 3 provides a numerical comparison of the performance indices for the proposed SCHO-based PI controller against other optimization-based controllers. The results indicate that the SCHO-based PI controller outperforms the competing methods in all indices. The SCHO-based controller achieves the lowest values for both IAE and ITAE indices, reflecting minimal accumulated error and a significant reduction in time-weighted errors. This indicates a rapid and efficient suppression of system oscillations. The squared error indices of ISE and ITSE further emphasize the superiority of the SCHO-based approach. The reduced error magnitude and its time-weighted impact signify a more precise and reliable control action over the entire simulation period. The results validate the SCHO algorithm’s balanced exploration and exploitation capabilities, ensuring robust and efficient tuning of the PI controllers. By achieving superior performance in all four indices, the SCHO-based PI controller demonstrates its potential as a reliable solution for LFC challenges in hybrid power systems. The proposed method also illustrates better adaptability and robustness compared to traditional optimization techniques.

Table 3 Comparative performance of different approaches with respect to IAE, ITAE, ISE and ITSE metrics.

Robustness analysis under parameter variations

This section investigates the robustness of the proposed SCHO-based PI controller by examining the system’s response to parameter variations. Robustness is a critical criterion for control systems operating under diverse and unpredictable real-world conditions, as it ensures stability and performance despite variations in system parameters. The test for this section considers the fault scenario with simultaneous $\pm 25\%$ variations in the time constants of key power system components, including the governor, turbine, reheater, and generator. These variations simulate real-world conditions where system parameters may fluctuate due to aging, maintenance, or environmental factors. Figures 10, 11, and 12 illustrate the dynamic responses of the system when subjected to parameter changes in the LFC framework.

Fig. 10

Time response of $\Delta {f}_{1}$ under parameter variation.

Fig. 11

Time response of $\Delta {f}_{2}$ under parameter variation.

Fig. 12

Time response of $\Delta {P}_{tie}$ under parameter variation.

The response of frequency deviation in Area 1 ($\Delta {f}_{1}$), given in Fig. 10, demonstrates the stability and adaptability of the SCHO-based controller. Despite parameter variations, the oscillations are effectively dampened, and the system quickly converges to a stable state. This indicates the controller’s ability to maintain performance, particularly in renewable energy integrated systems like PV power plants where variability is inherent.

The response for frequency deviation in Area 2 ($\Delta {f}_{2}$), given in Fig. 11, associated with the thermal power system, confirms the robustness of the controller in handling variations typical in thermal generation processes, such as fuel supply inconsistencies and mechanical delays. The SCHO-based controller exhibits minimal overshoot and ensures rapid stabilization, showcasing its balanced approach to parameter adaptation.

The tie-line power deviation ($\Delta {P}_{tie}$) response, given in Fig. 12, illustrates the controller’s capacity to stabilize inter-area power flows under parameter uncertainties. The SCHO-based controller minimizes fluctuations and achieves rapid convergence, which is critical for preventing cascading failures and ensuring reliable power exchange between areas. The robustness analysis confirms that the SCHO-based PI controller maintains superior performance under parameter variations. Key performance metrics such as settling time, overshoot, and undershoot remain within acceptable limits across all scenarios. This robustness is attributed to the SCHO algorithm’s effective exploration–exploitation balance, which ensures the controller parameters are well-optimized to handle uncertainties.

Handling of power system non-linearity

Power systems inherently exhibit nonlinear behaviors, such as governor dead-band effects, generation rate constraints, and saturations in various components. These nonlinearities can significantly impact the stability and performance of LFC strategies, making it imperative to evaluate controller robustness under such conditions. The analyses performed in this study, though focused on linear dynamics, indirectly demonstrate the proposed SCHO-based PI controller’s capability to handle nonlinearities through effective damping of oscillations, robustness to parameter variations, and adaptability to dynamic inputs.

As illustrated in “A $10\%$ step change ($\Delta {P}_{d1}=0.1$ pu and $\Delta {P}_{d2}=0.1$ pu) in both areas” and “Robustness analysis under parameter variations” sections, the SCHO-based PI controller effectively minimizes overshoots and settling times under both nominal and perturbed system conditions. Nonlinearities, such as generation rate constraints, are known to exacerbate oscillatory behavior in power systems. The controller’s demonstrated ability to suppress oscillations suggests that it is well-equipped to mitigate the destabilizing effects of such nonlinearities. The robustness analysis in “Robustness analysis under parameter variations” section, which tested the controller under simultaneous parameter variations, serves as an indirect indicator of its performance under nonlinear conditions. Since parameter changes often amplify the impact of system nonlinearities, the controller’s ability to maintain stability and achieve low steady-state errors reflects its resilience to nonlinear effects. The controller’s performance under solar radiation fluctuations (“Influence of solar radiation variation” section) highlights its adaptability to dynamically changing inputs. Nonlinearities introduced by renewable energy sources, such as power output variability and intermittency, are effectively managed by the SCHO-based controller, further indicating its efficiency in nonlinear environments. Moreover, a key advantage of the SCHO is its balanced exploration–exploitation mechanism, which enables it to find global optima in complex problem spaces. Nonlinear systems often result in highly nonconvex optimization landscapes. The SCHO-based PI controller’s demonstrated superior performance in minimizing integral error-based indices (IAE, ITAE, ISE, ITSE) suggests that it can address the challenges posed by nonlinearities effectively.

Conclusions

In this paper, a novel application of the SCHO was proposed for tuning PI controllers to enhance the load frequency control in a two-area hybrid power system consisting of PV and thermal units. By addressing critical challenges such as parameter variations, solar radiation fluctuations, and nonlinear effects, the proposed SCHO-based PI controller demonstrated significant advancements over traditional optimization-based methods, including SSA, WOA, and FA. Key numerical findings that substantiate the efficacy of the proposed method can be explained as follows. Settling times of 1.6231 s and 2.4615 s for frequency deviations in Area 1 and Area 2, respectively, were achieved under step load changes, significantly outperforming the best alternative methods. The tie-line power deviation was stabilized at 1.9986 s, compared to 2.3188 s for SSA, 4.3108 s for WOA, and 2.5018 s for FA. The SCHO-based PI controller recorded the lowest IAE and ISE values at 0.9022 and 0.0773, respectively, indicating its ability to minimize both accumulated and squared errors over time. Time-weighted indices such as ITAE and ITSE further emphasized its superiority, with values of 2.9119 and 0.1097, respectively, surpassing all competing methods. Simulation results confirmed the controller’s robustness to simultaneous parameter variations in governor, turbine, and generator time constants, as well as its adaptability to solar radiation fluctuations. The SCHO algorithm’s balanced exploration and exploitation capabilities, coupled with its ability to avoid local minima, played a pivotal role in achieving these outcomes. The results conclusively establish the proposed SCHO-based PI controller as an effective and reliable solution for LFC in modern hybrid power systems.

Future studies could extend the findings of this research by explicitly incorporating nonlinearities such as governor dead-band effects, generation rate constraints, and saturations in the power system model. Additionally, the application of the SCHO to other renewable energy-integrated systems or multi-area grids with higher levels of complexity presents an exciting avenue for exploration.