Framework development of continuous non-linear Diophantine fuzzy sets and its application to renewable energy source selection

Abstract

Fuzzy sets play a central role in decision-making theory, modeling uncertainty by means of membership grade (MG) and non-membership grade (NMG). Non-linear Diophantine fuzzy sets (N-LDFSs), which are the natural extensions of linear Diophantine fuzzy sets and q-linear Diophantine fuzzy sets, are quite successful in modeling data thanks to their larger domains. However, in an N-LDFS, the MG, NMG and reference parameters (RPs) of an element to a set are given just by a pair of certain numbers from the closed interval [0, 1] that causes a strict modelling. Various types of interval-valued fuzzy sets, multi-fuzzy sets, or circular fuzzy sets change this strict modeling with a sensitive one. In this paper, we propose a theoretical framework for Continuous Non-Linear Diophantine Fuzzy Sets, which introduces continuous functions (CFs) over closed intervals to reduce uncertainty, which represent the MG and NMG functions supported by RPs, which enhance the sensitivity and applicability of decision-making tools. We develop continuous non-linear Diophantine fuzzy algebraic aggregation operators and apply them to a multi-attribute decision-making problem in renewable energy source selection. A case study demonstrates the effectiveness of the proposed CN-LDFS framework using a weighted geometric operator. Comparative analysis with existing methods highlights the superiority and success of our approach in improving decision-making accuracy and reliability.

Introduction

The fuzzy set (FS) concept with membership degree (MD), first put forward by Zadeh¹ in 1965, is a useful tool to handle ambiguous and uncertain information in day-to-day situations. In the context of FSs, Zadeh introduced the important concept of linguistic variables (LVs)². By using LVs, we may translate spoken words into mathematical expressions and apply a number of mathematical techniques to solve MADM problems. The theory of triangular norms, also known as t-norms, was first presented by Schweizer and Sklar in Refs.^3,4. This was in keeping with some of Menger concepts within the framework of probabilistic metric spaces⁵, which became known as statistical metric spaces after 1964. T-norms have been becoming more important in decision-making, statistics, and cooperative game theory since they first appeared in statistical metric spaces. Particularly in fuzzy set theory, fuzzy operations, fuzzy logic, and fuzzy relation equations have been widely used using t-norms⁶. To develop algebraic operations and aggregation operators for fuzzy sets, we frequently utilized t-norm and t-conorm⁷. Xu and Yager⁸ investigated the aggregation of IFNs in connection to the idea. They developed an algorithm that uses operational laws to generate aggregation operators while maintaining the IFN structure. Making use of unique aggregation techniques on crisp numbers is another source of creativity. Both methods are frequently combined into a single formula and are not independent. The Xu and Yager also developed the intuitionistic fuzzy (or ordered) weighted geometric operators and the intuitionistic fuzzy hybrid geometric operator in connection to the first line of inspection. Xu⁹ introduced the intuitionistic fuzzy hybrid aggregation operator and intuitionistic fuzzy (respectively, ordered) weighted averaging operators. Subsequently, Garg¹⁰ used new aggregation operators derived from improvements of the operational rules, while Wei¹¹ proposed induced geometric aggregation operators. The use of geometric aggregation operators to multiple attribute group decision-making problems (MAGDMPs) has become the attention of several researchers in recent years^12,13. Recently, in 2023, Hezam and I.M. Rahman¹⁴ developed a geometric aggregation operator based on the complex Pythagorean fuzzy set (PyFS), and Kumar¹⁵ introduced the geometric operator based on the q-rung orthopair fuzzy set (q-ROFSs). This paper’s main focus is on the modification of geometric operations based on continuous environments to develop continuous non-linear Diophantine fuzzy (C-NLDF) information.

Atanassov is associated with developing the term "intuitionistic fuzzy set (IFS)"¹⁶. As a modified version of IFS, Yager¹⁷ developed the "Pythagorean fuzzy set (PFS)”. The IFS and PFS were standardized by Yager¹⁸, who further developed the idea of the "q-rung orthopair fuzzy set (q-ROFS).” The “membership degree” (MD) and "non-membership degree" (NMD) powers added together for each qth must equal one or be less than one, which is one of the constraints of the q-ROFS. Numerous studies on q-ROFSs have been performed recently; a few of these are cited as^19,20, which are based on the basic principles of operation of q-ROFNs. As mentioned in Refs.^21,22, q-ROFNs also make a significant contribution based on aggregation operators (AOs). In recent years, significant advancements have been made in Multi-Attribute Decision-Making (MADM) and Group Decision-Making (MAGDM) methodologies. However, many of the latest studies do not fully address the complexities involved in these decision-making processes, particularly in contexts that involve uncertainty and imprecision. For instance, recent studies have extended aggregation operators to enhance decision-making in various fields, such as the extension of Einstein average aggregation operators to medical diagnostic approaches under Q-rung orthopair fuzzy soft sets²³, and the development of novel multi-criteria decision-making approaches using interactive aggregation operators of Q-rung orthopair fuzzy soft sets²⁴. Other studies have focused on practical applications, including optimal cloud service provider selection through an MADM framework based on correlation-based TOPSIS with interval-valued Q-rung orthopair fuzzy soft sets²⁵, and the selection of unmanned aerial vehicles for precision agriculture using interval-valued Q-rung orthopair fuzzy information-based TOPSIS methods²⁶. Additionally, transportation decisions in supply chain management have been enhanced by utilizing interval-valued Q-rung orthopair fuzzy soft information²⁷.These studies, among others, highlight the growing need for more advanced decision-making frameworks that can handle complex, uncertain, and dynamic environments. The concept of linear Diophantine fuzzy set (LDFS) was first introduced by Riaz and Hashmi²⁸. By adding difference parameters (RPs) to MD and NMD, LDFS solves the limitations of current approaches. Compared to previous fuzzy models, the LDFS model performs better and is more accurate since RPs has been included. The total number of RPs in LDFSs that have output to MD and NMD, respectively, is limited to a value between 0 and 1. But in some real-life situations, a possibility’s total number of RPs that satisfy the DM-provided criteria is frequently larger than one; hence, LDFS has limited itself to accomplishing the RPs’ objective.

A question arises why we needed the N-LDFS or what are the boundaries of LDFSs that leads us to N-LDFSs.? The limitation of LDFSs is its restriction, i.e. $0{\le \mathcal{A}\mathfrak{M}}_{\mathfrak{D}\varkappa (\eta )}+{\mathcal{B}\mathfrak{N}}_{\mathfrak{D}\varkappa (\eta )}\le 1$ because this condition does not support decision-makers to give their consent to MG and NMG values. Almagrabi et al.²⁹ introduced the idea of a q-rung linear Diophantine fuzzy set (q-RLDFS). In order to achieve this, they covered the space of the MG and NMG’s present structure with respect to the RPs by increasing the qth power of the reference parameters (RPs). Also, the MG, NMG, and RPs are used to further explain the idea of q-RLDFS; the sum of the qth powers to the RPs associated with the MG and NMG is restricted to a range between zero and one. The total number of RPs that DM provides within the framework of LDFS might be greater than one, which shows that the MADM issue would be constrained by the breaking of the LDFS restriction. The idea behind q-RLDFS is that in order to solve the problem and avoid the LDFS controversy, competence is necessary. By increasing the set of allowable Diophantine, more Diophantine can satisfy the boundary limitation as qth increases. The main advantage of the q-RLDF approach is that it considers the qth power of RPs, demonstrating that it may be used for solving DM problems in the real world as well. The q-RLDFS combines the qth power of RFs with MG and NMG already developed in Ref.³⁰, making it more stable and flexible than existing q-ROFSs and LDFSs. It is later referred to as the Non-Linear Diophantine Fuzzy Set (N-LDFS) in Ref.³¹. Furthermore, Shams and Abdullah^32,33 developed the CN-LDF Dombi and CN-LDF Hamacher operators for decision-making problems in 2023 by extending the idea of CN-LDFS to Dombi Norms and Hamacher Norms. Recently, in 2023, Ünver, M., and Olgun, M.³⁴ introduced a new idea by utilizing continuous functions instead of fixed numbers. Motivated by this research, we applied weighted geometric operators on N-LDFNs in addition to including the concept of a continuous function and modified it to a new form called Continuous N-LDF weighted geometric operators.

In recent years, there have been major improvements in fuzzy systems, especially in developing aggregation operators and decision-making methods. For instance, Aczel-Alsina and Dombi aggregation operators have been widely applied in multi-attribute decision-making problems^35,36. Similarly, Sugeno-Weber aggregation operators³⁷ have demonstrated effectiveness in modeling uncertainty, as evidenced in decision-making for solar panel selection³⁸. Moreover, T-spherical fuzzy Dombi Hamy mean operators have introduced innovative approaches to aggregating fuzzy information³⁹. These advancements have inspired novel methods, such as the T-spherical fuzzy Aczel-Alsina-based multi-attribute decision-making approach⁴⁰ and intuitionistic fuzzy Sugeno-Weber frameworks for sustainable digital security⁴¹. For instance, the development of spherical fuzzy Aczel–Alsina aggregation operators has provided a novel means to handle uncertainty in complex decision environments, demonstrating their applicability across various domains⁴². Similarly, a decision analysis algorithm utilizing Frank aggregation within the SWARA framework with p,q-rung orthopair fuzzy information has showcased the potential of such operators in improving decision-making accuracy by leveraging advanced mathematical structures⁴³. Building on these developments, our work extends the capabilities of fuzzy set theory by introducing Continuous Non-Linear Diophantine Fuzzy Sets (CN-LDFSs), providing a more sensitive and robust tool for decision-making under uncertainty.

• i. Review on continuous non-linear diophantine fuzzy set: Recall that the LD $ax+by=c$ equation in number theory is the same as the framework of non-linear Diophantine fuzzy set . The most appropriate name for this developed framework is q-RLDFS, and this name has been modified to N-LDFS. It is unclear what N-LDFS restricts led to CN-LDFS and why we needed the CN-LDFS. Since this situation makes it difficult for decision-makers to reach consensus on MD, NMD, and RPs values, CN-LDFSs are limited, i.e. $0{\le {(\mathcal{A})}^{q}\mathfrak{M}}_{\mathfrak{R}\mathcal{N}(\eta )}+({{\mathcal{B})}^{q}\mathfrak{N}}_{\mathfrak{R}\mathcal{N}(\eta )}\le 1$. However, with N-LDFSs, an element’s MD, NMD, and RPs are only provided by a pair of specific values from the closed interval [0, 1], which results in strict modelling. The need for CN-LDFSs arises because decision-makers in a certain domain are bound. In order to provide decision-making theory especially in application of renewable energy sources, with a more precise tool, we really applied continuous function (CF) in CN-LDFS instead of MD, NMD, and RPs that allow values on a closed interval. We actually investigate functions in addition to points by allowing for the properly big and continuous neighborhoods around the regions.

• ii. Review on Multi-criteria decision making methods: One of the most pressing problems facing society since the beginning of the 20th century has been unclear and misleading information. In many different domains, such as science, technology, economics, management, sociology, neural networks, and autonomous machines, data aggregation is essential for making decisions. Traditionally, people have thought of knowledge of the alternative as a certain amount or linguistic number. Nevertheless, the information is hard to synthesis because of the level of ambiguity involved. The basic goal of the MCDM method, a commonly used intellectual activity tool, is to select among a limited number of options depending on the information supplied by decision-makers (DMs). The MCDM technique proposed by Zhang et al.^44,45,46 is based on consensus. Multi- criteria decision making approaches such as extended TOPSIS⁴⁷, GRA⁴⁸, CODAS⁴⁹, WS⁵⁰, WP⁵¹ and WASPAS⁵² methods are used to assess the best option from a collection of alternatives based on multiple criteria. The TOPSIS method assigns a score to each alternative after calculating the distance between it and the best and worst solutions. The best alternative is then determined to be the one with the highest score. In order to manage ambiguity and imprecision in the decision-making process, Extended TOPSIS combines fuzzy sets and fuzzy logic. The Grey Relational Coefficient Analysis (GRA) approach decides which alternative is best by comparing each one to a reference alternative and selecting the alternative with the highest coefficient. To handle ambiguity and imprecision, extended GRA uses grey theory and grey numbers. The CODAS method calculates the desirability of an alternative, this method uses the Euclidean distance as the primary and the Taxicab distance as the secondary measure, and these distances are calculated according to the negative-ideal point. The alternative which has greater distances is more desirable in the CODAS method.

• iii. Contribution of the study: The current paper’s primary contributions are provided below.

• a. The ideas in this paper are defined as ${\text{C}}^{[a,b]}$ N-LDFS and ${\text{C}}^{[a,b]}$ N-LDFN.

• b. This new idea applies functional analysis techniques from function theory, which are relatively new in the literature, in addition to other continuous structures like interval valued fuzzy sets or circular (intuitionistic) fuzzy sets.

• c. An algorithm is developed to transform ordinary N-LDFS to ${\text{C}}^{[a,b]}$ N-LDFS.

• d. Several algebraic operations, a weighted hybrid and geometric aggregation operator, and the development of a score, quadratic, and expectation functions with Riemann integral are provided for the sets of ${\text{C}}^{[a,b]}$ N-LDFN.

• e. More sensitive information may be carried by DMs when transforming the data to fuzzy values because MCDMs have the ability to access score, quadratic and expectation functions that make a sensitive modeling in fuzzy environment.

• f. The proposed method is compared with other existing models of decision making.

Structure of the article

The paper is organized as follows: Section “Basic concepts” presents the extension of fuzzy sets, including PyFS, q-ROFS, LDFS, and q-RLDFS in their discrete versions. Section “Continuous non-linear Diophantine fuzzy set (CN-LDFS)” introduces the notions of N-LDFS and N-LDFN, along with illustrated examples and comparisons with discrete versions. It also defines score, quadratic, and expectation functions under the Riemann integral and discusses continuous functions. Section “CN-LDF algebraic aggregation operators” defines geometric aggregation operators (CN-LDFWG, CN-LDFOWG, and CN-LDFHWG) and their properties. Section “Algorithm: CN-LDF algebraic aggregation method” proposes a novel algorithm for CN-LDF data based on algebraic operators. Section “Problem statement” presents the problem statement, case study, and numerical example for evaluating renewable energy sources using the proposed methodology. Section “Results and discussion” discusses the results and discussion. Section “Discussion and comparison analysis” compares the proposed method with existing MCDM methods. Section “Advantages and limitations of the proposed algorithm” discusses the advantages and limitations of the proposed work. Section “Conclusion” concludes the paper and outlines the future directions. Acronyms and symbols are defined in Tables 1 and 2.

Table 1 The acronyms listed are used in the present study.

Table 2 The parameters and variables utilized in this work.

Basic concepts

The fuzzy set extensions, such as PyFS, q-ROFS, LDFS, and q-RLDFS or N-LDFS, are included in this section.

Definition 1

Reference¹⁷: The definition of a PyFS ${\mathcal{F}}_{p}$ over a fixed set ϕ is as follows:

$${\mathcal{F}}_{p} = \left\{ {\left( {\eta , {\mathfrak{M}}_{{{\mathcal{F}}p\left( \eta \right)}} , {\mathfrak{N}}_{{{\mathcal{F}}p\left( \eta \right)}} } \right)|\eta \in \phi } \right\},$$

(1)

where ${\mathfrak{M}}_{\mathcal{F}p(\eta )}$ and ${\mathfrak{N}}_{\mathcal{F}p(\eta )}$ are represented MD and NMD respectively, ϕ∈$\left[0, 1\right]$ i.e.

${0\le \left({\mathfrak{M}}_{\mathcal{F}p(\eta )}\right)}^{2}+{\left({\mathfrak{N}}_{\mathcal{F}p(\eta )}\right)}^{2}\le 1$.

Definition 2

Reference¹⁸: The definition of a q-ROFS ${\mathfrak{R}}_{\mathcal{q}}$ over a given set $\upphi$ is:

$${\mathfrak{R}}_{\mathcal{q}}=\left\{\left(\eta , {\mathfrak{M}}_{\mathfrak{R}\mathcal{q}(\eta )}, {\mathfrak{N}}_{\mathfrak{R}\mathcal{q}(\eta )}\right)|\eta \in\upphi \right\},$$

(2)

where ${\mathfrak{M}}_{\mathfrak{R}\mathcal{q}(\eta )}$ and ${\mathfrak{N}}_{\mathfrak{R}\mathcal{q}(\eta )}$ are represented MD and NMD respectively, ϕ∈$\left[0, 1\right]$ i.e.

${0\le \left({\mathfrak{M}}_{\mathfrak{R}\mathcal{q}(\eta )}\right)}^{q}+{\left({\mathfrak{N}}_{\mathfrak{R}\mathcal{q}(\eta )}\right)}^{q}\le 1q>1$.

Definition 3

Reference²⁸: The definition of an LDFS ${\mathfrak{D}}_{\varkappa }$ over a given non-empty reference set ϕ is:

$${\mathfrak{D}}_{\varkappa }=\left\{\left(\eta ,\langle {\mathfrak{M}}_{\mathfrak{D}l(\eta )}, {\mathfrak{N}}_{\mathfrak{D}l(\eta )}\rangle , \langle \mathcal{A},\mathcal{B}\rangle \right):\eta \in\upphi \right\},$$

(3)

where ${\mathfrak{M}}_{\mathfrak{D}\varkappa (\eta )}$, ${\mathfrak{N}}_{\mathfrak{D}\varkappa (\eta )}$, $\mathcal{A}$, $\mathcal{B}$ ∈ $\left[0, 1\right]$ represented MD, NMD and RPs respectively, which satisfy the condition that $0{\le \mathcal{A}\mathfrak{M}}_{\mathfrak{D}\varkappa (\eta )}+{\mathcal{B}\mathfrak{N}}_{\mathfrak{D}\varkappa (\eta )}\le 1$ ∀ η∈ ϕ with $0 \le \mathcal{A}+\mathcal{B}\le 1$.

LDFS failed to reach the RPs objective because, in some real-world situations, the sum of RPs for which an alternative satisfies DM’s requirements may be larger than one. It was suggested that the non-linear Diophantine fuzzy set be used to solve this problem.

Definition 4

Reference²⁹: The definition of a q-rung linear Diophantine fuzzy set (q-RLDFS) ${\mathfrak{R}}_{\mathcal{L}}$ or non-linear Diophantine fuzzy set (N-LDFS) over a particular non-empty reference set ϕ is as follows:

$${\mathfrak{R}}_{\mathcal{L}}=\left\{\left(\eta ,\langle {\mathfrak{M}}_{\mathfrak{R}\mathcal{N}(\eta )}, {\mathfrak{N}}_{\mathfrak{R}\mathcal{N}(\eta )}\rangle , \langle \mathcal{A},\mathcal{B}\rangle \right):\eta \in\upphi \right\},$$

(4)

where ${\mathfrak{M}}_{\mathfrak{R}\mathcal{N}(\eta )}$, ${\mathfrak{N}}_{\mathfrak{R}\mathcal{N}(\eta )}$, $\mathcal{A}$, $\mathcal{B}$ ∈ $\left[0, 1\right]$ represented MD, NMD and RPs respectively, which fulfil the restriction that; $0{\le {(\mathcal{A})}^{q}\mathfrak{M}}_{\mathfrak{R}\mathcal{N}(\eta )}+({{\mathcal{B})}^{q}\mathfrak{N}}_{\mathfrak{R}\mathcal{N}(\eta )}\le 1$, ∀ η∈ ϕ, $q\ge 1$, with 0 ≤ ${(\mathcal{A})}^{q}$+${\mathcal{B}}^{q}$ ≤1, $q\ge 1.$

Continuous non-linear Diophantine fuzzy set (CN-LDFS)

According to the classical concept of NLDFS, pairs of MD, NMD, and RPs, a pair of specific values from the closed interval [0, 1] that result in a strict modelling of an element to a set. Therefore, in this new fuzzy set concept, continuous functions (CF) rather than integers are used to represent the MD, NMD, and RPs of an element to a fuzzy set. In fact, by accounting for the suitably large and continuous neighborhoods of the points, we’re looking at functions as well as points. In order to solve the difference, we proposed the concept of CN-LDFSs, which is capable of handling such circumstances.

Definition 5:

The definition of CN-LDFSs ${\mathcal{M}}_{c}$ over a given non-empty reference set ϕ is as follows:

$${\mathcal{M}}_{C} =\left\{\left(\eta ,\langle {\mathfrak{M}}_{\mathcal{M}C(\eta )}, {\mathfrak{N}}_{\mathcal{M}C(\eta )}\rangle , \langle \mathcal{A},\mathcal{B}\rangle \right):\eta \in\upphi \right\},$$

(5)

where ${\mathfrak{M}}_{\mathcal{M}C(\eta )}, {\mathfrak{N}}_{\mathcal{M}C(\eta )}, \mathcal{A},\mathcal{B}\in C\left[a, b\right]\to [0, 1]$ are represented the MD, NMD and RPs respectively, with “C” shows the CF that belong to the closed interval [0, 1]. These MD, NMD and RPs fulfil the restriction that; $0{\le {(\mathcal{A})}^{q}\mathfrak{M}}_{\mathcal{M}C(\eta )}+({{\mathcal{B})}^{q}\mathfrak{N}}_{\mathcal{M}C(\eta )}\le 1$, ∀ η∈ ϕ, $q\ge 1$, with 0 ≤ ${(\mathcal{A})}^{q}$+${\mathcal{B}}^{q}$ ≤1, $q\ge 1.$ Here is a definition of the degree of hesitation:

$$\Gamma \Phi_{C} = \sqrt[q]{{1 - (\left( {\mathcal{A}} \right)^{q} {\mathfrak{M}}_{{{\mathcal{M}}C\left( \eta \right)}} + \left( {{\mathcal{B}})^{q} {\mathfrak{N}}_{{{\mathcal{M}}C\left( \eta \right)}} } \right),}}$$

(6)

where Γ stands for the relative hesitancy of the RPs. A system’s physical characteristics are influenced by the RPs, which also identify and describe it. Now in CN-LDFSS if $q=1$ then, it is said to be continuous non-linear Diophantine set (CN-LDFS), if $q=2$ then CN-LDFS become continuous non-linear quadratic Diophantine fuzzy set (CN-LQDFS).

Definition 6:

A collection of continuous non-linear Diophantine fuzzy number (CN-LDFN) is defined as:

$${\ell}=\left(\langle {\mathfrak{M}}_{\mathcal{M}C}, {\mathfrak{N}}_{\mathcal{M}C}\rangle , \langle \mathcal{A},\mathcal{B}\rangle \right),$$

(7)

where “ℕ” represent the CN-LDFN which satisfy the following restriction;

• a. $0{\le {(\mathcal{A})}^{q}\mathfrak{M}}_{\mathcal{M}C(\eta )}+({{\mathcal{B})}^{q}\mathfrak{N}}_{\mathcal{M}C(\eta )}\le 1$, $q\ge 1$

• b. 0 ≤ ${(\mathcal{A})}^{q}$+${\mathcal{B}}^{q}$ ≤1, $q\ge 1$

• c. $0{\le {\left(\mathcal{A}\right)}^{q}, \mathfrak{M}}_{\mathcal{M}C\left(\eta \right)},({{\mathcal{B})}^{q}, \mathfrak{N}}_{\mathcal{M}C\left(\eta \right)}\le 1$,

where ${\mathfrak{M}}_{\mathcal{M}C}, {\mathfrak{N}}_{\mathcal{M}C}$ and $\mathcal{A},\mathcal{B}$ ∈ C $\left[\text{0,1}\right]$ where “C” represent the CF on which the MD, NMD and RPs are defined

Score function and accuracy function

The concept of different S.F. and A.F. is updated here with the qth power of RPs in a continuous environment because in this subsection, we develop an accuracy function (A.F.) and score function (S.F.), under the Riemann integral.

Definition 7

Reference³⁴: Consider ${\mathbb{N}}_{r}=\left(\langle \mathfrak{M}, \mathfrak{N}\rangle , \langle \mathcal{A},\mathcal{B}\rangle \right) \in$ CN-LDFNs, then score function (S.F) : CN-LDFNs→ [1, -1] is defined as;

$$\mathfrak{S} \left({\ell}\right)=\frac{1}{4}\left(1+\frac{1}{b-a} {\int }_{a}^{b}(\mathfrak{M}{\mathcal{A}}^{q}-\mathfrak{N}{\mathcal{B}}^{q})dt\right) .$$

(8)

Definition 8

Reference³⁴: The accuracy function (A.F) : C-NLDFNs→ [1, -1] is defined as;

$$\mathfrak{K}\left({\ell}\right)=\frac{1}{4\left(b-a\right)}{\int }_{a}^{b}(\mathfrak{M}{\mathcal{A}}^{q}-\mathfrak{N}{\mathcal{B}}^{q})dt.$$

(9)

For any CN-LDFNs,${\ell}=\left(\langle \mathfrak{M}, \mathfrak{N}\rangle , \langle \mathcal{A},\mathcal{B}\rangle \right)$, note here that $0\le \mathfrak{S} ({\ell})$,$\mathfrak{K}({\mathbb{N}})\le 1$. The larger area under $\mathfrak{M}\mathcal{A}$ and the smaller area under $\mathfrak{N}\mathcal{B}$ implies that ${\mathbb{N}}=\left(\langle \mathfrak{M}, \mathfrak{N}\rangle , \langle \mathcal{A},\mathcal{B}\rangle \right)$ has larger MD and RP. So, larger values under $\mathfrak{S}$ function gives better choices. When the curves are closer the area between them is smaller.

Definition 9

Reference³¹: Let ${{\ell}}_{1}$ and ${{\ell}}_{2}$ be two CN-LDFNs, then the two CN-LDFNs can easily be compared by using S.F and A.F:

• a. If $\mathfrak{S} {{\ell}}_{1}<\mathfrak{S} {{\ell}}_{2}$ then ${{\ell}}_{1}<{{\ell}}_{2}$,

• b. If $\mathfrak{S} {{\ell}}_{1}>\mathfrak{S} {{\ell}}_{2}$ then ${{\ell}}_{1}>{{\ell}}_{2}$,

• c. If $\mathfrak{S} {{\ell}}_{1}=\mathfrak{S} {{\ell}}_{2}$ then ${{\ell}}_{1}\approx {{\ell}}_{2}$,

• d. If ${\mathfrak{K} {\ell}}_{1}<\mathfrak{K} {{\ell}}_{2}$ then ${{\ell}}_{1}<{{\ell}}_{2}$,

• e. If $\mathfrak{K} {{\ell}}_{1}>\mathfrak{K} {{\ell}}_{2}$ then ${\ell}>{{\ell}}_{2}$,

• f. If $\mathfrak{K} {{\ell}}_{1}=\mathfrak{K} {{\ell}}_{2}$ then ${{\ell}}_{1}\approx {{\ell}}_{2}$.

We’ll define the quadratic score function (Q.S.F.) next.

Definition 10

Reference³¹: The quadratic score function (Q.S.F) $\Psi :CN-LDFN(\upphi )\to [-\text{1,1}]$ for CN-LDFN is defined as;

$$\Psi {\ell}=\frac{1}{4}\left(1+\frac{1}{b-a} {\int }_{a}^{b}({\mathfrak{M}}^{2}{\left({\mathcal{A}}^{q}\right)}^{2}-{\mathfrak{N}}^{2}{\left({\mathcal{B}}^{q}\right)}^{2})dt\right).$$

(10)

Definition 11

Reference³¹: The quadratic accuracy function (Q.A.F) $\Upsilon: CN-LDFN(\phi )\to [\text{0,1}]$ for CN-LDFN is defined as;

$$\Upsilon{\ell}=\frac{1}{4\left(b-a\right)}{\int }_{a}^{b}({\mathfrak{M}}^{2}{\left({\mathcal{A}}^{q}\right)}^{2}-{\mathfrak{N}}^{2}{\left({\mathcal{B}}^{q}\right)}^{2})dt.$$

(11)

Definition 12

Reference³¹: Let ${{\ell}}_{1}$ and ${{\ell}}_{2}$ be two CN-LDFNs, then the two CN-LDFNs can easily be compared by using Q.S.F and Q.A.F:

• a. If $\Psi {{\ell}}_{1}<\Psi {{\ell}}_{2}$ then ${{\ell}}_{1}<{{\ell}}_{2}$,

• b. If $\Psi {{\ell}}_{1}>\Psi {{\ell}}_{2}$ then ${{\ell}}_{1}>{{\ell}}_{2}$,

• c. If $\Psi {{\ell}}_{1}=\Psi {{\ell}}_{2}$ then ${{\ell}}_{1}\approx {{\ell}}_{2}$,

• d. If ${\Upsilon {\ell}}_{1}<\Upsilon {{\ell}}_{2}$ then ${{\ell}}_{1}<{{\ell}}_{2}$,

• e. If $\Upsilon {{\ell}}_{1}>\Upsilon {{\ell}}_{2}$ then ${{\ell}}_{1}>{{\ell}}_{2}$,

• f. If $\Upsilon {{\ell}}_{1}=\Upsilon {{\ell}}_{2}$ then ${{\ell}}_{1}\approx {{\ell}}_{2}$.

Definition 13

Reference³¹: Suppose ${\ell}=\left(\langle \mathfrak{M}, \mathfrak{N}\rangle , \langle \mathcal{A},\mathcal{B}\rangle \right)\in CN-LDFN$, then expectation score function (E.S.F) $\upepsilon :CN-LDFN(\phi )\to [\text{0,1}]$ can be defined as;

$$\upepsilon \left({\ell}\right)=\frac{1}{4}\left(1+\frac{1}{b-a} {\int }_{a}^{b}(\left(\mathfrak{M}{\mathcal{A}}^{q}+1\right)-\left(\mathfrak{N}{\mathcal{B}}^{q}+1\right))dt\right).$$

(12)

E.S.F. values fall under [0, 1] instead of [1, 1]. Expectation accuracy function (E.A.F.) is not necessary.

Definition 14

Reference³¹: Assuming ${\mathbb{N}}_{1}$ and ${\mathbb{N}}_{2}$ are two CN-LDFNs, it is straightforward to compare them using E.S.F.

• a. If $\upepsilon {{\ell}}_{1}<\upepsilon {{\ell}}_{2}$ then ${{\ell}}_{1}<{{\ell}}_{2}$,

• b. If $\upepsilon {{\ell}}_{1}>\upepsilon {{\ell}}_{2}$ then ${{\ell}}_{1}>{{\ell}}_{2}$,

• c. If $\upepsilon {{\ell}}_{1}=\upepsilon {{\ell}}_{2}$ then ${{\ell}}_{1}\approx {{\ell}}_{2}$.

In many fuzzy decision-making models, classical Non-Linear Diophantine Fuzzy Sets (N-LDFS) bound to only fixed values, which can lead to certain limitations. For example, when using fixed values, conditions may fail for specific powers (e.g.,$q=4 or above$), as the sum of squared values might not satisfy the required inequalities. This issue can significantly affect the reliability of the results. To address this limitation, we propose using continuous functions instead of fixed values. By doing so, we ensure that the conditions are met across the entire interval, providing more flexibility and accuracy in decision-making. The following example demonstrates how this approach works.

Example 1

let $G=\left(\langle \mathfrak{M}, \mathfrak{N}\rangle , \langle \mathcal{A},\mathcal{B}\rangle \right)\in \text{NLDFS}\left(\phi \right)$. Suppose we have the data in the set that be $G=\left(\langle 1, 1\rangle , \langle 0.9, 0.7\rangle \right)$ for $\phi \in \left\{x\right\}$. Clearly the condition fails here for $q=\text{1,2}..$ because if we take $q=2$ then,${0.9}^{2}+{0.7}^{2}\nleqq 0$, also $1.\left({0.9}^{2}\right)+1.\left({0.7}^{2}\right)\nleqq 1$, but we used $q=4$ then, it may give the result within the interval $\left[\text{0,1}\right]$, hence there may chances to fail the condition in qth power. Therefore we may give help to take the continuous data instead of fixed number, for example we have;

We are taking that same discrete data but here we inserting the continuous function to transfer the data to continuous form. Let ${\ell}=\left(\langle 1.j, 1.\mathcal{K}\rangle , \langle 0.9.j, 0.7.\mathcal{K}\rangle \right)$ be any CN-LDFN, the $\mathfrak{M},$ $\mathcal{A}$: ⟶[0, 1] and $\mathfrak{N}$, $\mathcal{B}$:⟶[0, 1].Now if we defined these two functions by $\mathcal{J}(\text{t})=\frac{(2\text{t}+3)}{6}$ where, $\mathcal{J}(\text{t})\to \left[\text{0,1}\right]$ if $t\in \left[\text{0,1}\right]$ associated with MD $\left(\mathfrak{M}\right)$ and RP $\left(\mathcal{A}\right)$ and $\mathcal{K}\left(t\right)=\frac{({t}^{2}-4t+5)}{6}$ where, $\mathcal{J}(\text{t})\to \left[\text{0,1}\right]$ if $t\in \left[\text{0,1}\right]$ associated with NMD $\left(\mathfrak{N}\right)$ and RP $\left(\mathcal{B}\right)$. So we can easily check the condition by taking integral within the interval $\left[\text{0,1}\right]$. So, by using integration by integrating we may have the result;

$${\int }_{0}^{1}\left[{\ell}\right] ={\int }_{0}^{1}\left(\langle 1.j, 1.\mathcal{K}\rangle , \langle 0.9.j, 0.7.\mathcal{K}\rangle \right)dt$$

$$={\int }_{0}^{1}\left(\left(\left(1.\frac{\left(2\text{t}+3\right)}{6}\right).\left(0.9.\frac{\left(2\text{t}+3\right)}{6}\right)\right)+\left(\left(1.\frac{({t}^{2}-4t+5)}{6}\right).\left(0.7.\frac{({t}^{2}-4t+5)}{6}\right)\right)\right)dt$$

$$=0.639\in \left[\text{0,1}\right]$$

From this we see that the condition satisfied if we use functions instead of fixed values in the MD, NMD and RPs. The result gives us the value in the range of [0, 1] interval. The Table 3 discusses the comparison of difference between N-LDFS and CN-LDFS. The Figs. 1 and 2 show the orientation graph of above defined functions. The graphs both show that they are continuous functions and give the result within the interval $\left[\text{0,1}\right]$.

Table 3 Comparison between N-LDFS and CN-LDFS.

Fig. 1

Graph of function $\mathcal{J}(\text{t})$ within the interval $\left[\text{0,1}\right]$.

Fig. 2

Graph of function $\mathcal{K}\left(t\right)$ within the interval $\left[\text{0,1}\right]$.

Algebraic t-norm and t-conorm

The triangular norm⁶ is a fundamental concept in FS theory that describes the universal union and intersection of FSs. For fuzzy sets, the t-norm and t-conorm are frequently used for developing aggregation operators and algebraic operations^7,8. The algebraic t-norms and t-conorm are defined as follows, given any two real numbers α and β:

$${\mathcal{H}}_{\gamma } \left( {\alpha ,~\beta } \right) = \alpha \otimes \beta = \alpha \beta$$

$${\mathcal{H}}_{\gamma } ^{{ \star }} \left( {\alpha ,~\beta } \right) = \alpha \oplus \beta = \alpha + \beta - \alpha \beta$$

Algebraic operations for CN-LDFNs

In this subsection we are going to define some operational laws based on CN-LDFN. According to the algebraic norm, the operational rules are:

Definition 9:

let ${{\ell}}_{1}=\left(\langle {\mathfrak{M}}_{1}, {\mathfrak{N}}_{1}\rangle , \langle {\mathcal{A}}_{1}, {\mathcal{B}}_{1}\rangle \right)$ and ${{\ell}}_{2}=\left(\langle {\mathfrak{M}}_{2}, {\mathfrak{N}}_{2}\rangle , \langle {\mathcal{A}}_{2}, {\mathcal{B}}_{2}\rangle \right)$ are any two CN-LDFNs, with $\lambda >0$ then, we have to define the basic Algebraic operations for CN-LDFNs as follow;

• a. ${{\ell}}_{1}^{c}=\left(\langle {\mathfrak{N}}_{1}, {\mathfrak{M}}_{1}\rangle , \langle {\mathcal{B}}_{1}, {\mathcal{A}}_{1}\rangle \right)$

• b. $\ell_{1} \oplus \ell_{2} = \left\{ {\begin{array}{*{20}c} {{\mathfrak{M}}_{1} + {\mathfrak{M}}_{2} - {\mathfrak{M}}_{1} {\mathfrak{M}}_{2} ,{ }{\mathfrak{N}}_{1} {\mathfrak{N}}_{2} ,} \\ {\left( {{\mathcal{A}}_{1} } \right)^{q} + \left( {{\mathcal{A}}_{1} } \right)^{q} - \left( {{\mathcal{A}}_{1} } \right)^{q} \left( {{\mathcal{A}}_{1} } \right)^{q} ,\left( {{\mathcal{B}}_{1} } \right)^{q} \left( {{\mathcal{B}}_{1} } \right)^{q} } \\ \end{array} } \right\}$

• c. ${{\ell}}_{1}{\otimes {\ell}}_{2}=\left\{\begin{array}{c}\langle {\mathfrak{M}}_{1}{\mathfrak{M}}_{2},{\mathfrak{N}}_{1}+{\mathfrak{N}}_{2}- {\mathfrak{N}}_{1}{\mathfrak{N}}_{2}\rangle ,\\ \langle {\left({\mathcal{A}}_{1}\right)}^{q}{\left({\mathcal{A}}_{2}\right)}^{q},{\left({\mathcal{B}}_{1}\right)}^{q}{+\left({\mathcal{B}}_{2}\right)}^{q}-{\left({\mathcal{B}}_{1}\right)}^{q}{\left({\mathcal{B}}_{2}\right)}^{q}\rangle \end{array}\right\}$

• d. $\lambda {{\ell}}_{1}=\left\{\begin{array}{c}\langle 1-({1-{\mathfrak{M}}_{1})}^{\lambda },{\left({\mathfrak{N}}_{1}\right)}^{\lambda }\rangle ,\\ \langle 1-({1-{\left({\mathcal{A}}_{1}\right)}^{q})}^{\lambda },{\left({\left({\mathcal{B}}_{1}\right)}^{q}\right)}^{\lambda }\rangle \end{array}\right\}$;$\lambda >0$

• e. ${{{\ell}}_{1}}^{\lambda }=\left\{\begin{array}{c}\langle {({\mathfrak{M}}_{1})}^{\lambda },1-({1-{\mathfrak{N}}_{1})}^{\lambda }\rangle ,\\ \langle {({\left({\mathcal{A}}_{1}\right)}^{q})}^{\lambda },1-({1-{\left({\mathcal{B}}_{1}\right)}^{q})}^{\lambda }\rangle \end{array}\right\}$

Definition 10:

let ${{{\ell}}_{\mathcal{M}C}}_{\gamma }=\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }, {{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\rangle , \langle {\mathcal{A}}_{\gamma }, {\mathcal{B}}_{\gamma }\rangle \right)$ for $\gamma \in \Delta$ be an assembling of CN-LDFNs, Therefore, using the algebraic norm, the following properties may be simply satisfied:

• a. $\bigcup_{\gamma \in \Delta }{{\ell}}_{\gamma }=\left(\left({\text{sup}}_{\gamma \in \Delta }{{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma },{\text{inf}}_{\gamma \in \Delta }{{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\right),\left({\text{sup}}_{\gamma \in \Delta }{\mathcal{A}}_{\gamma },{\text{inf}}_{\gamma \in \Delta }{\mathcal{B}}_{\gamma }\right)\right)$

• b. $\bigcap_{\gamma \in \Delta }{{\ell}}_{\gamma }=\left(\left({\text{inf}}_{\gamma \in \Delta }{{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma },{\text{sup}}_{\gamma \in \Delta }{{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\right),\left({\text{inf}}_{\gamma \in \Delta }{\mathcal{A}}_{\gamma },{\text{sup}}_{\gamma \in \Delta }{\mathcal{B}}_{\gamma }\right)\right)$

Definition 11:

Let ${{\ell}}_{1}=\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{1}, {{\mathfrak{N}}_{\mathcal{M}C}}_{1}\rangle , \langle {\mathcal{A}}_{1}, {\mathcal{B}}_{1}\rangle \right)$ and ${{\ell}}_{2}=\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{2}, {{\mathfrak{N}}_{\mathcal{M}C}}_{2}\rangle , \langle {\mathcal{A}}_{2}, {\mathcal{B}}_{2}\rangle \right)$ be any two C-NLDFNs, with $\lambda >0$, then

• a. ${{\ell}}_{1}={{\ell}}_{2}\Leftrightarrow {{\mathfrak{M}}_{\mathcal{M}C}}_{1}={{\mathfrak{M}}_{\mathcal{M}C}}_{2}$,${{\mathfrak{N}}_{\mathcal{M}C}}_{1}={{\mathfrak{N}}_{\mathcal{M}C}}_{2}$,${\mathcal{A}}_{1}={\mathcal{A}}_{2}$,${\mathcal{B}}_{1}={\mathcal{B}}_{2}$;

• b. ${{\ell}}_{1}\subseteq {{\ell}}_{2}\Leftrightarrow {{\mathfrak{M}}_{\mathcal{M}C}}_{1}\le {{\mathfrak{M}}_{\mathcal{M}C}}_{2}$,${{\mathfrak{N}}_{\mathcal{M}C}}_{1}\ge {{\mathfrak{N}}_{\mathcal{M}C}}_{2}$,${\mathcal{A}}_{1}\le {\mathcal{A}}_{2}$,${\mathcal{B}}_{1}\ge {\mathcal{B}}_{2}$.

Proposition 1:

Let ${{\ell}}_{1}$ and ${{\ell}}_{2}$ belong to CN-LDFNs with real numbers $\lambda >0$; then ${{\ell}}_{1}$ and ${{\ell}}_{2}$ are still CN-LDFNs after applying the operation that is ${{{\ell}}_{1}}^{C}$, ${{\ell}}_{1}\bigcup {{\ell}}_{2}$, ${{\ell}}_{1}\bigcap {{\ell}}_{2}$, l₁⨁l₂, l₁⨂l₂, $\lambda {{\ell}}_{1}$, ${{{\ell}}_{1}}^{\lambda }$ are also C-NLDFNs.

Proof:

Using definitions 9, 10, and 11 above, it is simple to prove these results.

Proposition 2:

Taking three CN-LDF numbers such as; ${{\ell}}_{1}=\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{1}, {{\mathfrak{N}}_{\mathcal{M}C}}_{1}\rangle , \langle {\mathcal{A}}_{1}, {\mathcal{B}}_{1}\rangle \right)$, ${{\ell}}_{2}=\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{2}, {{\mathfrak{N}}_{\mathcal{M}C}}_{2}\rangle , \langle {\mathcal{A}}_{2}, {\mathcal{B}}_{2}\rangle \right)$ and ${{\ell}}_{3}=\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{3}, {{\mathfrak{N}}_{\mathcal{M}C}}_{3}\rangle , \langle {\mathcal{A}}_{3}, {\mathcal{B}}_{3}\rangle \right)$ with $\varphi >0$, Consequently, the following conditions are satisfied:

• a. If ${{\ell}}_{1}\subseteq {{\ell}}_{2}$ and ${{\ell}}_{2}\subseteq {{\ell}}_{3}$ then ${{\ell}}_{1}$ $\subseteq {{\ell}}_{3}$.

• b. ${{\ell}}_{1}\bigcup {{\ell}}_{2}={{\ell}}_{2}\bigcup {{\ell}}_{1}$

• c. ${{\ell}}_{1}\bigcap {{\ell}}_{2}={{\ell}}_{2}\bigcap {{\ell}}_{1}$

• d. ${{\ell}}_{1}\bigcup \left({{\ell}}_{2}\cup {{\ell}}_{3}\right)=\left({{\ell}}_{1}\bigcup {{\ell}}_{2}\right)\bigcup {{\ell}}_{3}$

• e. ${{\ell}}_{1}\bigcap \left({{\ell}}_{2}\bigcap {{\ell}}_{3}\right)=\left({{\ell}}_{1}\bigcap {{\ell}}_{2}\right)\bigcap {{\ell}}_{3}$

• f. ${{\ell}}_{1}\bigcup \left({{\ell}}_{2}\bigcap {{\ell}}_{3}\right)=\left({{\ell}}_{1}\bigcup {{\ell}}_{2}\right)\bigcap \left({{\ell}}_{1}\bigcup {{\ell}}_{3}\right)$

• g. ${{\ell}}_{1}\bigcap \left({{\ell}}_{2}\bigcup {{\ell}}_{3}\right)=\left({{\ell}}_{1}\bigcap {{\ell}}_{2}\right)\bigcup \left({{\ell}}_{1}\bigcap {{\ell}}_{3}\right)$

• h. ${\left({{\ell}}_{1}\bigcup {{\ell}}_{2}\right)}^{c}={{{\ell}}_{1}}^{c}\bigcap {{{\ell}}_{2}}^{c}$

• i. ${\left({{\ell}}_{1}\bigcap {{\ell}}_{2}\right)}^{c}={{{\ell}}_{1}}^{c}\bigcup {{{\ell}}_{2}}^{c}$.

Proof:

It is clear that the previously stated claims are true.

CN-LDF Algebraic aggregation operators

In this part, we develop the CN-LDF aggregation operators using the Algebraic norms.

CN-LDF weighted geometric aggregation (CN-LDFWGA) operator

This part defines the C-NLDF weighted geometric aggregation operators, which are CN-LDFWG, CN-LDFHWG, and CN-LDFWG.

Definition 12:

Consider ${{{\ell}}_{\mathcal{M}C}}_{\gamma }=\left\{\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }, {{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\rangle , \langle {\mathcal{A}}_{\gamma }, {\mathcal{B}}_{\gamma }\rangle \right):\gamma \in \text{N}\right\}$ be a family of CN-LDFNs over the fixed set ϕ and ${\omega }_{i}={\left({\omega }_{1},{\omega }_{2},{\omega }_{3},\dots ,{\omega }_{n}\right)}^{T}$ are the weight with $\sum_{\gamma =1}^{n}{\omega }_{\gamma }=1$, $q\ge 1$; then the CN-LDF weighted geometric (CN-LDFWG) operator as follow and let the transformation $\theta :CN-LDFN\left(\phi \right)\to CN-LDFN(\phi )$

$$CN-LDFHWG\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)={\otimes }_{\gamma =1}^{n}\left({{\ell}}_{\mathcal{M}C\gamma }^{{\omega }_{\gamma }}\right)$$

$$={{\ell}}_{\mathcal{M}C1}^{{\omega }_{1}}\otimes {{\ell}}_{\mathcal{M}C2}^{{\omega }_{2}}\dots \otimes {{\ell}}_{\mathcal{M}Cn}^{{\omega }_{n}}$$

In CN-LDFAWG operator, denote MG and denote NMG, , ℬ denotes the RPs and $q \ge 1.$ Weights are denoted by ω, ${\mathbb{N}}_{\mathcal{M}C\gamma }$ are the CN-LDFNs, where γ∈ N and CN-LDFN (ϕ) combines all CN-LDFNs.

Based on Algebraic product operations rules for CN-LDFNs, we have captured the result displayed in theorem 1.

Theorem 1:

Let ${{{\ell}}_{\mathcal{M}C}}_{\gamma }=\left\{\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }, {{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\rangle , \langle {\mathcal{A}}_{\gamma }, {\mathcal{B}}_{\gamma }\rangle \right):\gamma \in \text{N}\right\}$ be an assembling of CN-LDFNs over the fixed set ϕ and ${\omega }_{i}={\left({\omega }_{1},{\omega }_{2},{\omega }_{3},\dots ,{\omega }_{n}\right)}^{T}$ are the weight with $\sum_{\gamma =1}^{n}{\omega }_{\gamma }=1$ and $q\ge 1$, then by applying the CN-LDFWG operator their aggregated value is also a CN-LDFN, and the transformation $\theta :CN-LDFN\left(\phi \right)\to CN-LDFN(\phi )$ is called CN-LDF Algebraic weighted geometric operator (CN-LDFWG) and define as follow;

$$CN-LDFHWG\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)={\otimes }_{\gamma =1}^{n}\left({{\ell}}_{\mathcal{M}C\gamma }^{{\omega }_{\gamma }}\right)$$

$$=\left(\begin{array}{c}\langle \prod_{\gamma =1}^{n}{\left({{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{n}{\left(1-{{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\right)}^{{\omega }_{\gamma }}\rangle ,\\ \langle \prod_{\gamma =1}^{n}{\left({\left({\mathcal{A}}_{\gamma }\right)}^{q}\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{n}{\left(1-{\left({\mathcal{B}}_{\gamma }\right)}^{q}\right)}^{{\omega }_{\gamma }}\rangle \end{array}\right)$$

(13)

Proof:

By induction method we want to prove this theorem. We put $n = 2$ in Eq. (13). So for CN-LDFNs based on Algebraic product, we obtained the associated result.

(i): Let ${{\ell}}_{1}=\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{1}, {{\mathfrak{N}}_{\mathcal{M}C}}_{1}\rangle , \langle {\mathcal{A}}_{1}, {\mathcal{B}}_{1}\rangle \right)$, ${{\ell}}_{2}=\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{2}, {{\mathfrak{N}}_{\mathcal{M}C}}_{2}\rangle , \langle {\mathcal{A}}_{2}, {\mathcal{B}}_{2}\rangle \right)$ be two CN-LDFNs then built on algebraic product. The left side of Eq. (13) becomes,

$$CN-LDFHWG\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2}\right)={{\ell}}_{\mathcal{M}C1}^{{\omega }_{1}}\otimes {{\ell}}_{\mathcal{M}C2}^{{\omega }_{2}}$$

The right side of Eq. (13) becomes,

$$=\left(\begin{array}{c}\langle {\left({{\mathfrak{M}}_{\mathcal{M}C}}_{1}\right)}^{{\omega }_{1}},1-{\left(1-{{\mathfrak{N}}_{\mathcal{M}C}}_{1}\right)}^{{\omega }_{1}}\rangle ,\\ \langle {\left({\left({\mathcal{A}}_{1}\right)}^{q}\right)}^{{\omega }_{1}},1-{\left(1-{\left({\mathcal{B}}_{1}\right)}^{q}\right)}^{{\omega }_{1}}\rangle \end{array}\right)\otimes \left(\begin{array}{c}\langle {\left({{\mathfrak{M}}_{\mathcal{M}C}}_{2}\right)}^{{\omega }_{2}},1-{\left(1-{{\mathfrak{N}}_{\mathcal{M}C}}_{2}\right)}^{{\omega }_{2}}\rangle ,\\ \langle {\left({\left({\mathcal{A}}_{2}\right)}^{q}\right)}^{{\omega }_{2}},1-{\left(1-{\left({\mathcal{B}}_{2}\right)}^{q}\right)}^{{\omega }_{2}}\rangle \end{array}\right)$$

$$=\left(\begin{array}{c}\langle \prod_{\gamma =1}^{2}{\left({{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{2}{\left(1-{{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\right)}^{{\omega }_{\gamma }}\rangle ,\\ \langle \prod_{\gamma =1}^{2}{\left({\left({\mathcal{A}}_{\gamma }\right)}^{q}\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{2}{\left(1-{\left({\mathcal{B}}_{\gamma }\right)}^{q}\right)}^{{\omega }_{\gamma }}\rangle \end{array}\right)$$

Hence, Eq. (13) is true when we put $n= 2$.

(ii): Assume that Eq. (13) holds for $n= K$,

$$CN-LDFHWG\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)=\left(\begin{array}{c}\langle \prod_{\gamma =1}^{k}{\left({{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{k}{\left(1-{{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\right)}^{{\omega }_{\gamma }}\rangle ,\\ \langle \prod_{\gamma =1}^{k}{\left({\left({\mathcal{A}}_{\gamma }\right)}^{q}\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{k}{\left(1-{\left({\mathcal{B}}_{\gamma }\right)}^{q}\right)}^{{\omega }_{\gamma }}\rangle \end{array}\right)$$

(iii): Now we prove that Eq. (13) holds for $n = K + 1$, Let

$$CN-LDFHWG\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)={\otimes }_{\gamma =1}^{k}{{\ell}}_{\mathcal{M}C\gamma }^{{\omega }_{\gamma }}\otimes {{\ell}}_{\mathcal{M}Ck+1}^{{\omega }_{k+1}}$$

$$=\left(\begin{array}{c}\langle \prod_{\gamma =1}^{k}{\left({{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{k}{\left(1-{{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\right)}^{{\omega }_{\gamma }}\rangle ,\\ \langle \prod_{\gamma =1}^{k}{\left({\left({\mathcal{A}}_{\gamma }\right)}^{q}\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{k}{\left(1-{\left({\mathcal{B}}_{\gamma }\right)}^{q}\right)}^{{\omega }_{\gamma }}\rangle \end{array}\right)\otimes$$

$$\left(\begin{array}{c}\langle {\left({{\mathfrak{M}}_{\mathcal{M}C}}_{k+1}\right)}^{{\omega }_{k+1}},1-{\left(1-{{\mathfrak{N}}_{\mathcal{M}C}}_{k+1}\right)}^{{\omega }_{k+1}}\rangle ,\\ \langle {\left({\left({\mathcal{A}}_{k+1}\right)}^{q}\right)}^{{\omega }_{k+1}},1-{\left(1-{\left({\mathcal{B}}_{k+1}\right)}^{q}\right)}^{{\omega }_{k+1}}\rangle \end{array}\right)$$

$$=\left(\begin{array}{c}\langle \prod_{\gamma =1}^{k+1}{\left({{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{k+1}{\left(1-{{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\right)}^{{\omega }_{\gamma }}\rangle ,\\ \langle \prod_{\gamma =1}^{k+1}{\left({\left({\mathcal{A}}_{\gamma }\right)}^{q}\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{k+1}{\left(1-{\left({\mathcal{B}}_{\gamma }\right)}^{q}\right)}^{{\omega }_{\gamma }}\rangle \end{array}\right)$$

Hence, Eq. (13) is true for $n = K + 1$, which proves the theorem given in Eq. (13).

Theorem 1 (Idompotency):

If ${{\ell}}_{\mathcal{M}C\gamma }=\left\{\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }, {{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\rangle , \langle {\mathcal{A}}_{\gamma }, {\mathcal{B}}_{\gamma }\rangle \right):\gamma \in \text{N}\right\}$ be a family of CN-LDFNs which are all same, i.e. ${{\ell}}_{\mathcal{M}C\gamma }={{\ell}}_{\mathcal{M}C}$ ∀γ, then

${CN-LDFHWG}_{\omega }\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)={{\ell}}_{\mathcal{M}C}$.

Theorem 2 (Boundedness):

Let ${{\ell}}_{\mathcal{M}C\gamma }=\left\{\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }, {{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\rangle , \langle {\mathcal{A}}_{\gamma }, {\mathcal{B}}_{\gamma }\rangle \right):\gamma \in \text{N}\right\}$ be a family of CN-LDFNs, and consider

${{\ell}}_{\mathcal{M}C}^{-}={min}_{\gamma }{{\ell}}_{\mathcal{M}C\gamma }$, ${{\ell}}_{\mathcal{M}C}^{+}={max}_{\gamma }{{\ell}}_{\mathcal{M}C\gamma }$. Then,${{\ell}}_{\mathcal{M}C}^{-}\le {CN-LDFHWG}_{\omega }\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)\le {{\ell}}_{\mathcal{M}C}^{+}$.

Theorem 3 (Monotonically):

Let ${{\ell}}_{\mathcal{M}C\gamma }\left(\gamma \in N\right)$ and ${{\ell}}_{\mathcal{M}C\gamma }^{^\circ }\left(\gamma \in N\right)$ belong to CN-LDFNs, if ${{\ell}}_{\mathcal{M}C\gamma }\le {{\ell}}_{\mathcal{M}C\gamma }^{^\circ }$, ∀γ. Then,

${CN-LDFHWG}_{\omega }\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)\le {CN-LDFHWG}_{\omega }\left({{\ell}}_{\mathcal{M}C1}^{^\circ },{{\ell}}_{\mathcal{M}C2}^{^\circ },\dots ,{{\ell}}_{\mathcal{M}Cn}^{^\circ }\right)$.

Further, we develop the C-NLDF ordered weighted geometric (CN-LDFOWG) operator.

Definition 13:

Consider a family of CN-LDFNs ${{\ell}}_{\mathcal{M}C\gamma }=\left\{\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }, {{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\rangle , \langle {\mathcal{A}}_{\gamma }, {\mathcal{B}}_{\gamma }\rangle \right):\gamma \in \text{N}\right\}$ over the reference set ϕ and ${\omega }_{i}={\left({\omega }_{1},{\omega }_{2},{\omega }_{3},\dots ,{\omega }_{n}\right)}^{R}$ are the weight with $\sum_{\gamma =1}^{n}{\omega }_{\gamma }=1$, $q\ge 1$; then the CN-LDF ordered weighted geometric (CN-LDFOWG) operator as follow and let the transformation $\theta :CN-LDFN\left(\phi \right)\to CN-LDFN(\phi )$

$$CN-LDFOWG\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)={\otimes }_{\gamma =1}^{n}{\left({{\ell}}_{\mathcal{M}C(\delta )\gamma }\right)}^{{\omega }_{\gamma }}$$

$$={{\ell}}_{\mathcal{M}C(\delta )1}^{{\omega }_{1}}\otimes {{\ell}}_{\mathcal{M}C(\delta )2}^{{\omega }_{2}}\dots \otimes {{\ell}}_{\mathcal{M}C(\delta )n}^{{\omega }_{n}}$$

$$\left(\begin{array}{c}\langle \prod_{\gamma =1}^{n}{\left({{\mathfrak{M}}_{\mathcal{M}C(\delta )}}_{\gamma }\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{n}{\left(1-{{\mathfrak{N}}_{\mathcal{M}C(\delta )}}_{\gamma }\right)}^{{\omega }_{\gamma }}\rangle ,\\ \langle \prod_{\gamma =1}^{n}{\left({\left({\mathcal{A}}_{\gamma (\delta )}\right)}^{q}\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{n}{\left(1-{\left({\mathcal{B}}_{\gamma (\delta )}\right)}^{q}\right)}^{{\omega }_{\gamma }}\rangle \end{array}\right)$$

(14)

where the arrangement of (γ∈ N) is (δ(1), δ(2), . . . , δ(n)), for which ${{\ell}}_{\mathcal{M}C\delta }\left(\gamma =1\right)\ge {{\ell}}_{\mathcal{M}C\delta (\gamma )}$ ∀(γ ∈ N).

Theorem 4 (Idompotency):

If ${{\ell}}_{\mathcal{M}C\gamma }=\left\{\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }, {{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\rangle , \langle {\mathcal{A}}_{\gamma }, {\mathcal{B}}_{\gamma }\rangle \right):\gamma =\text{1,2},\dots ,\text{n}\right\}$ be a family of CN-LDFNs which are all same, i.e. ${{\ell}}_{\mathcal{M}C\gamma }={{\ell}}_{\mathcal{M}C}$ ∀γ, then

${CN-LDFOWG}_{\omega }\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)={{\ell}}_{\mathcal{M}C}$.

Theorem 5 (Boundedness):

Let ${{\ell}}_{\mathcal{M}C\gamma }=\left\{\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }, {{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\rangle , \langle {\mathcal{A}}_{\gamma }, {\mathcal{B}}_{\gamma }\rangle \right):\gamma =\text{1,2},\dots ,\text{n}\right\}$ be a family of CN-LDFNs, and consider

${{\ell}}_{\mathcal{M}C}^{-}={min}_{\gamma }{{\ell}}_{\mathcal{M}C\gamma }$, ${{\ell}}_{\mathcal{M}C}^{+}={max}_{\gamma }{{\ell}}_{\mathcal{M}C\gamma }$. Then,

${{\ell}}_{\mathcal{M}C}^{-}\le {CN-LDFOWG}_{\omega }\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)\le {{\ell}}_{\mathcal{M}C}^{+}$.

Theorem 6 (Monotonically):

Let ${{\ell}}_{\mathcal{M}C\gamma }\left(\gamma =\text{1,2},\dots ,\text{n}\right)$ and ${{\ell}}_{\mathcal{M}C\gamma }^{^\circ }\left(\gamma =\text{1,2},\dots ,\text{n}\right)$ belong to C-NLDFNs, if ${{\ell}}_{\mathcal{M}C\gamma }\le {{\ell}}_{\mathcal{M}C\gamma }^{^\circ }$, ∀γ. Then,

${C-NLDFOWG}_{\omega }\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)\le {C-NLDFOWG}_{\omega }\left({{\ell}}_{\mathcal{M}C1}^{^\circ },{{\ell}}_{\mathcal{M}C2}^{^\circ },\dots ,{{\ell}}_{\mathcal{M}Cn}^{^\circ }\right)$.

In the above paragraph, we defined the CN-LDFWG and CN-LDFOWG operators. We now introduce the CN-LDF hybrid weighted geometric (C-NLDFHWG) operator.

Definition 14:

Let ${{\ell}}_{\mathcal{M}C\gamma }=\left\{\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }, {{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\rangle , \langle {\mathcal{A}}_{\gamma }, {\mathcal{B}}_{\gamma }\rangle \right):\gamma =\text{1,2},\dots ,\text{n}\right\}$ be a family of CN-LDFNs over the fixed set ϕ and ${\omega }_{i}={\left({\omega }_{1},{\omega }_{2},{\omega }_{3},\dots ,{\omega }_{n}\right)}^{T}$ are the weight with $\sum_{\gamma =1}^{n}{\omega }_{\gamma }=1$, $q\ge 1$; then the C-NLDF hybrid weighted geometric (CN-LDFHWG) operator as follow and let the transformation $\theta :CN-LDFN\left(\phi \right)\to CN-LDFN(\phi )$

$$CN-LDFHWG\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)={\otimes }_{\gamma =1}^{n}{\left({{\ell}}_{(\delta )\mathcal{M}C\gamma }^{\star }\right)}^{{\omega }_{\gamma }}$$

$$={\left({{\ell}}_{\left(\delta \right)\mathcal{M}C1}^{\star }\right)}^{{\omega }_{1}}\otimes {\left({{\ell}}_{\left(\delta \right)\mathcal{M}C2}^{\star }\right)}^{{\omega }_{2}},\dots , \otimes {\left({{\ell}}_{(\delta )\mathcal{M}Cn}^{\star }\right)}^{{\omega }_{n}}$$

$$= \left(\begin{array}{c}\langle \prod_{\gamma =1}^{n}{\left({{{\mathfrak{M}}^{\star }}_{\mathcal{M}C(\delta )}}_{\gamma }\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{n}{\left(1-{{{\mathfrak{N}}^{\star }}_{\mathcal{M}C(\delta )}}_{\gamma }\right)}^{{\omega }_{\gamma }}\rangle ,\\ \langle \prod_{\gamma =1}^{n}{\left({\left({{\mathcal{A}}^{\star }}_{\gamma (\delta )}\right)}^{q}\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{n}{\left(1-{\left({{\mathcal{B}}^{\star }}_{\gamma (\delta )}\right)}^{q}\right)}^{{\omega }_{\gamma }}\rangle \end{array}\right)$$

(15)

where ${{\ell}}_{(\delta )\mathcal{M}Cn}^{\star }$ is the γth biggest weighted CN-LDF values ${{\ell}}_{\mathcal{M}C(i)}^{\star }$ $\left({{\ell}}_{\mathcal{M}C\left(\gamma \right)}^{\star }={\left({{\ell}}_{\mathcal{M}C(\gamma )}\right)}^{n{\omega }_{\gamma }},\gamma \in N\right)$ and be the weights of ${{\ell}}_{\mathcal{M}C\left(\gamma \right)}^{\star }$ is $\omega ={\left({\omega }_{1},{\omega }_{2},{\omega }_{3},\dots ,{\omega }_{n}\right)}^{T}$ with condition $\omega >0$, $\sum_{\gamma =1}^{n}{\omega }_{\gamma }=1$. If $\omega =\left(\frac{1}{\omega },\frac{1}{\omega },\dots ,\frac{1}{\omega }\right)$ Therefore, CN-LDFHWG and CN-LDFOWG operators are considered to be specific cases. This led to the conclusion that the CN-LDFHWG operator is the generalized form of the CN-LDFWG and CN-LDFOWG operators.

Algorithm: CN-LDF algebraic aggregation method

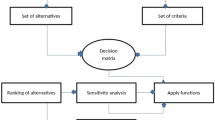
In this subsection, we developed an algorithm based on CN-LDFWG aggregating operations. The most appropriate renewable energy sources for CN-LDF data are found and chosen using the Multi Attribute Decision Making (MADM) problem, which is based on algebraic operators.

Consider the set of alternatives ${\widetilde{A}}_{g}=\left\{{\widetilde{A}}_{1},{\widetilde{A}}_{2},\dots ,{\widetilde{A}}_{m}\right\}$ and ${\widetilde{C}}_{h}=\left\{{\widetilde{C}}_{1},{\widetilde{C}}_{2},\dots {\widetilde{C}}_{n}\right\}$ be the set criteria. Let the weight of criteria ${\omega }_{\gamma }\left(\gamma =\text{1,2},\dots ,n\right)$ are $\omega ={\left\{{\omega }_{1},{\omega }_{2},\dots ,{\omega }_{n}\right\}}^{T}$, with condition that ${\omega }_{\gamma }>0$ $\sum_{\gamma =1}^{n}{\omega }_{\gamma }=1$. Let us we have the CN-LDF decision making (DMs) matrix ${\mathfrak{D}}_{j}={\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{\mathcal{g}\gamma }, {{\mathfrak{N}}_{\mathcal{M}C}}_{\mathcal{g}\gamma }\rangle , \langle {\mathcal{A}}_{\mathcal{g}\gamma }, {\mathcal{B}}_{\mathcal{g}\gamma }\rangle \right)}_{m\times n}$, where ${{\mathfrak{M}}_{\mathcal{M}C}}_{\mathcal{g}\gamma }$ is MD, ${{\mathfrak{N}}_{\mathcal{M}C}}_{\mathcal{g}\gamma }$ is the NMD and ${\mathcal{A}}_{\mathcal{g}\gamma }, {\mathcal{B}}_{\mathcal{g}\gamma }$ are the RPs for which the alternatives $\left({\widetilde{A}}_{\gamma }\right)$ fulfill the criteria $\left({\widetilde{C}}_{\gamma }\right)$.These grades and RPs, ${{\mathfrak{M}}_{\mathcal{M}C}}_{\mathcal{g}\gamma }$,${{\mathfrak{N}}_{\mathcal{M}C}}_{\mathcal{g}\gamma }$,${\mathcal{A}}_{\mathcal{g}\gamma }$,${\mathcal{B}}_{\mathcal{g}\gamma }$ ∈ C $\left[\text{0,1}\right]$, where “C” represent the continuous functions (CF). The condition that will satisfy as, $0\le {\left(\left({\mathcal{A}}^{q}\right){\mathfrak{M}}_{\mathcal{M}C}\right)}_{\mathcal{g}\gamma }+{\left(\left({\mathcal{B}}^{q}\right){\mathfrak{N}}_{\mathcal{M}C}\right)}_{\mathcal{g}\gamma }\le 1$,$\left(\mathcal{g}=\text{1,2},\dots ,m\right)$. We use C-NLDF aggregation operations to solve the MADM problem. For this we have the following algorithm steps;

Input:

Step 1: Construct a group of DMs using CN-LDF data with an appropriate number of alternatives and criteria. Here, ${\mathfrak{D}}_{j}=\left\{{ \mathfrak{D}}_{1},{ \mathfrak{D}}_{2},\dots ,{ \mathfrak{D}}_{\mathcal{k}},{ \mathfrak{D}}_{{\ell}}\right\}$ with weight vector ω represents the decision maker groups. Algebraic operators are used by CN-LDFNs to assess each DM.

Step 2: Normalization of CN-LDF input data before starting the calculations, the input data must be normalized in order to get the most accurate results. Therefore, the following formula may be used to standardize the CN-LDF analysis:

$${\mathbb{N}}_{{\mathcal{M}C}_{\gamma }}=\left\{\begin{array}{c}\left(\langle {{\mathfrak{M}}_{\mathcal{M}C}}_{\mathcal{g}\gamma }, {{\mathfrak{N}}_{\mathcal{M}C}}_{\mathcal{g}\gamma }\rangle , \langle {\mathcal{A}}_{\mathcal{g}\gamma }, {\mathcal{B}}_{\mathcal{g}\gamma }\rangle \right);Same data \\ \left(\langle {{\mathfrak{N}}_{\mathcal{M}C}}_{\mathcal{g}\gamma }, {{\mathfrak{M}}_{\mathcal{M}C}}_{\mathcal{g}\gamma }\rangle , \langle {\mathcal{B}}_{\mathcal{g}\gamma }, {\mathcal{A}}_{\mathcal{g}\gamma }\rangle \right);different data\end{array}\right.$$

Choose the weights assigned to each decision-maker’s perspective.

Calculations:

Step 3: To aggregate the decision information given in matrices ${\widetilde{\mathfrak{D}}}_{k}$ (k = 1, 2, 3) into the collective CN-LDF DM, use Eq. (16) of the CN-LDF Algebraic aggregation operations with weights ${\omega }_{\gamma }\left(\gamma =\text{1,2},\dots ,n\right)$ of criterion ${\widetilde{C}}_{h}$. Where “$\gamma$” shows the number of experts involved in decision making.

$$CN-LDFWG\left({{\ell}}_{\mathcal{M}C1},{{\ell}}_{\mathcal{M}C2},\dots ,{{\ell}}_{\mathcal{M}Cn}\right)=$$

$$\left(\begin{array}{c}\langle \prod_{\gamma =1}^{n}{\left({{\mathfrak{M}}_{\mathcal{M}C}}_{\gamma }\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{n}{\left(1-{{\mathfrak{N}}_{\mathcal{M}C}}_{\gamma }\right)}^{{\omega }_{\gamma }}\rangle ,\\ \langle \prod_{\gamma =1}^{n}{\left({\left({\mathcal{A}}_{\gamma }\right)}^{q}\right)}^{{\omega }_{\gamma }},1-\prod_{\gamma =1}^{n}{\left(1-{\left({\mathcal{B}}_{\gamma }\right)}^{q}\right)}^{{\omega }_{\gamma }}\rangle \end{array}\right)$$

(16)

In a similar manner, we will get the aggregated decision matrix for order and hybrid AOs by using the CN-LDFWOG and CN-LDFHWG operators.

Step 4: Determine each criterion’s combined aggregated value through alternative wise utilizing weights,${\omega }_{\gamma }\left(\gamma =\text{1,2},\dots ,n\right)$ by using the CN-LDF Algebraic operator’s equation above.

Step 5: Calculate each alternative’s score using the S.F., Q.S.F., and E.S.F. definitions above.

Output

Step 6: Ranking the alternatives is based on S.F., Q.S.F., and E.S.F. values.

Step 7: For the final selection, an alternative with the highest score must be selected since it has the highest rank. The proposed technique steps based on algebraic operators for CN-LDF data are shown in Fig. 3.

Fig. 3

CN-LDF algorithm flow chart based on algebraic operators.

Problem statement

This section presents a multi-attribute decision-making (MADM) problem focused on selecting the most suitable renewable energy (RE) source for Pakistan. The case study is inspired by previous works^53,54 and extends them using a novel decision-making model based on Continuous Non-Linear Diophantine Fuzzy (C-NLDF) information. The model utilizes score, quadratic, and expectation functions to evaluate alternatives comprehensively.

Background and importance

The government of Pakistan aims to reduce its dependence on imported energy by promoting the development of renewable energy sources within the country. Due to limited domestic oil and natural gas resources, diversifying energy sources and focusing on renewable energy is critical for ensuring energy security. Pakistan possesses significant potential in renewable energy resources, making it a viable solution for sustainable development and energy independence.

Alternatives and criteria

The decision-making process evaluates five renewable energy alternatives:

${\widetilde{A}}_{1}$: Geothermal energy (GE)

${\widetilde{A}}_{2}$: Solar energy (SE)

${\widetilde{A}}_{3}$: Biomass energy (BE)

${\widetilde{A}}_{4}$: Hydropower energy (RE)

${\widetilde{A}}_{5}$: Wind energy (WE)

These alternatives are assessed based on three primary criteria: economic (${\widetilde{C}}_{1}$​), technical (${\widetilde{C}}_{2}$​), and environmental (${\widetilde{C}}_{3}$​), as shown in Table 4. The prioritization of these criteria reflects the country’s strategic focus:${\widetilde{C}}_{3}$ > ${\widetilde{C}}_{1}$ >${\widetilde{C}}_{2}$, where > denotes preference. The Fig. 4 illustrates the alternatives of defined different energy sources. . The evaluation process prioritizes sub-criteria within each primary criterion based on their importance.

Table 4 Evaluation criteria for renewable energy sources

Fig. 4

Renewable energy from different sources based on defined alternatives.

${\widetilde{C}}_{1}$: Economical attribute contain ${c}_{11}$-Servicelife, ${c}_{12}$-Investment cost, ${c}_{13}$-Operation and maintenance cost, ${c}_{14}$-Energy production cost and ${c}_{15}$-Payback period. There is a strict prioritization between parameters ${c}_{11}$ >${c}_{12}$ >${c}_{13}$>${c}_{14}>{c}_{15}$, here > indicates preferred to.

${\widetilde{C}}_{2}$: Technical attribute contain ${c}_{21}$- Availability, ${c}_{22}$- Capacity, ${c}_{23}$- Resource density, ${c}_{24}$- Efficiency and ${c}_{25}$- Grid compatibility. There is a strict prioritization between parameters ${c}_{21}$ >${c}_{22}$ >${c}_{23}$>${c}_{24}>{c}_{25}$, here > indicates preference.

${\widetilde{C}}_{3}$: Environmental attribute contain ${c}_{31}$- Air pollution, ${c}_{32}$- Noise pollution, ${c}_{33}$- Water usage, ${c}_{34}$- Land use impact and ${c}_{35}$- Biodiversity impact. There is a strict prioritization between parameters ${c}_{31}$ >${c}_{32}$ >${c}_{33}$>${c}_{34}>{c}_{35}$, here > indicates preference.

Additionally, experts are selected from a range of engineering areas within the educational institution in an effort to optimize the impartiality of the results. Then, we use the C-NLDFWG operator to construct a method to multiple-attribute decision-making problems utilizing C-NLDF information, which may be explained by using the following algorithm.

Results and discussion

In this section we discuss the results of the proposed decision making method. The proposed decision making method consists of the following steps:

Step 1: In this step, the algorithm is applied on the input data. The decision maker considers the five kinds of alternatives,$\widetilde{A}=\left\{{\widetilde{A}}_{1},{\widetilde{A}}_{2},\dots ,{\widetilde{A}}_{5}\right\}$, five sub-attributes set, $\widetilde{C}=\left\{{\widetilde{C}}_{1},{\widetilde{C}}_{2},\dots {\widetilde{C}}_{5}\right\}$ and thus, expressed as an expert decision matrices. Using the functions defined by $\mathcal{J}(\text{t})=\frac{(2\text{t}+3)}{6}$ and $\mathcal{K}\left(t\right)=\frac{({t}^{2}-4t+5)}{6}$ which are discussed in example 1. The first function associated with MD ($\mathfrak{M})$ and reference parameter $\mathcal{A}$ and same as second function is associated with NMD $(\mathfrak{N})$ and reference parameter $(\mathcal{B})$ respectively, and thus, we constructed three CN-LDF sub-decision matrices, which are shown in Tables 5, 6, 7.

Table 5 CN-LDF sub-decision matrix 1.

Table 6 CN-LDF sub-decision matrix 2.

Table 7 CN-LDF sub-decision matrix 3.

Step 2: The input data was first finalized by assigning weights according to the total number of experts. Making the final decision now requires considering all perspectives of all renewable sources energy experts weight are $\omega =\frac{1}{n}=\frac{1}{3}$ represent the CN-LDF input data weights where, “n” shows number of experts.

Step 3: We used Eq. (16) to apply the CN-LDFWG operator to the input CN-LDF data, for each alternative, aggregate all of the attribute values. We aggregated the individual decision matrices into a collective CN-LDFWG matrix. For example

$${{\mathfrak{M}}_{\mathcal{M}C}}_{11}=0.1609148974{\left({\left(2t+3\right)}^{3}\right)}^{1/3}$$

and ${{\mathfrak{N}}_{\mathcal{M}C}}_{11}=1-\sqrt[3]{-0.02778{\left({t}^{2}-4.t-1\right)}^{2}\left(0.14500{t}^{2}-0.5800t-0.27500\right)}$.

thus, same aggregated reference parameter (${\mathcal{A}}_{\gamma })$ and reference parameter ${(\mathcal{B}}_{\gamma })$.

Step 4: To aggregate the collective CN-LDFWG table alternative wise, we chose the five different criteria weights which are $\omega ={\left(0.35, \text{0.25,0.2,0.1,0.1}\right)}^{T}$. We repeated step 3, by using Eq. (16), as a result we obtained the aggregated CN-LDFWG values.

Step 5: Determine the score values i.e. S.F, Q.S.F, and E.S.F of each of the aggregated attributes by using Eqs.8, 10, and 12 and thus, we obtained Table 8 for $q=4$.

Table 8 Score value of CN-LDFWG.

Table 6 We ranked the alternatives based on greater score values of S.F, QSF and E.S.F. The result of ranking order is shown in Table 9. The graphical representation is shown in Fig. 5.

Table 9 Score value of CN-LDFWG.

Fig. 5

Graphical representation of different score function using CN-LDFWG operator.

From Table 9, we concluded that ${\widetilde{{\varvec{A}}}}_{4}$ which is Hydropower energy (HE) selected the best overall RE sources obtained from CN-LDFWG operator.

The proposed operators’ performances

The performance of the proposed operators has been evaluated using the provided input data. The result of CN-LDFWG we discussed in detail now in order to determine the order of each of the three experts for CN-LDFHOWG, we first apply E.S.F, which is given in the form of Tables 5, 6 and 7. The Order weighted operator’s reordering step, which reorders all of the input data in decreasing numerical order, is the most important part of it. To get the CN-LDFOWG results, we proceed with the previous algorithm’s steps. The various CN-LDFOWG operator score values are shown in Table 10. The CN-LDFOWG operator ranking table for $q = 4$ is shown in Table 11 and Fig. 6 show the graphical representation of these results.

Table 10 Score value of CN-LDFOWG

Table 11 Ranking of CN-LDFOWG.

Fig. 6

The final ranking based on SF, QSF and ESF under CN-LDFOWG operator

According to Table 11, ${\widetilde{A}}_{4}$ which is Hydropower (HE) energy was chosen as the most environmentally friendly renewable energy source, based on data collected from the CN-LDFOWG operator.

In the hybrid situation, we also added a step to the above method, which is to first aggregate three decision maker’s tables using the CN-LDFHWG operator. Then, for the CN-LDFHWG operator, we used the same steps as in the Algebraic CN-LDFNs approach mentioned above. The CN-LDFHWG operator is then applied independently to each number of the CN-LDF aggregated table that we obtained from step 3, in the same manner that we aggregate in step 3 of the CN-LDFHWG. We have selected five more weights for the five criteria in this aggregate table: 0.3, 0.25, 0.2, 0.15, and 0.1. Each weight is multiplied by five. As a result, the weight vector for the CN-LDF Hybrid WG operator is (1.5, 1.25, 1, 0.75, and 0.5). The CN-LDFH hybrid weighted geometric table is obtained; then, scores is applied to the table, and the criteria are rearranged to produce a hybrid aggregated table. The entire procedure is taken into consideration in step 3. The CN-LDFHWG table is then obtained by moving to the next stages and applying the same steps of the preceding algorithm after step 3. For $q = 4$, the CN-LDFHHWG operator’s score values are shown in Table 12. The operator CN-LDFHWG for $q = 4$ is ranked in Table 13.the results are graphically shown in Fig. 7. Based on Table 13, we concluded that ${\widetilde{A}}_{4}$, the Hydropower energy chose the best overall renewable sources energy among the operators of CN-LDFHWG.

Table 12 Score value of CN-LDFHWG.

Table 13 Ranking of CN-LDFHWG.

Fig. 7

Graphical ranking of CN-LDFHWG operator based on S.F, Q.S.F and E.S.F.

It’s important to remember that the suggested method provides the same outcome for any scoring function. The CN-LDFWG, CN-LDFOWG and CN-LDFHWG operator for renewable energy sources is ranked graphically in Figs. 5, 6 and 7 with the Hydropower energy coming as the best option overall. The overall graphical ranking of the CN-LDFWG, CN-LDFOWG, and CN-LDFHWG operators for renewable sources energy are shown in Fig. 8, with the Hydropower energy coming as the best alternative overall.

Fig. 8

Overall graphical ranking of CN-LDFWG operators based on different score functions.

Discussion and comparison analysis

In this part, we illustrate how well the three CN-LDF Algebraic Aggregation operators can deal with DMPs from daily life by comparing them to the existing method. The fuzzy set theory, in particular in N-LDFS, results in restricted modelling since the MD, NMD, and RPs of an element to a set are only provided by two specific integers from the closed interval [0, 1]. In this work, we provide a new idea of fuzzy sets utilizing continuous functions (CFs) that accept values over a closed interval, enabling decision making theory a more sensitive tool. This new concept of FS is substituting numbers with CFs for transmitting the MD and NMD of an element to an FS. We really consider the suitably big and continuous neighborhoods of the points, therefore we are not just studying with points but also functions. This method is exciting because it primarily provides valuation spaces for IFSs, PyFS, q-ROFSs, LDFSs, and N-LDFSS using CF techniques. Table 14 provided a basic comparison between the proposed and existing concepts. We verify our proposed approach by comparing it with the MCDM methods. For the purpose of to achieve this, we are using the same three expert decision matrices about the evolution of renewable source energy.

Table 14 CN-LDFS comparison research with previous methods.

Comparison with extended WASPAS

This part compares the proposed strategy with existing MCDM method extended WAPAS, for the purpose of to achieve this, we are using the same continuous three expert decision matrices data about the evolution of renewable source energy as CN-LDF sets. Next, we used the expert weights (0.4, 35, and 0.25) and found the aggregated decision matrix using the equations (13, 14 and 15). After that, apply the steps of the extended WASPAS method. The result is given in Table 15.

Table 15 Output of various existing MCDM methods.

Comparison with extended CODAS

In this subsection we compare our proposed method with existing MCDM method extended CODAS, for this again we are using that same continuous input data of CN-LDFNs in the form of three experts decision matrices. Next we used the same expert weight (0.4, 0.35 and 0.25) and determined the aggregated matrix using aggregation equation’s (13, 14 and 15). After that with help of extended CODAS step we get the final result shown in Table 15.

Comparison with extended GRA

This section compares our suggested approach with an existing one again called extended GRA, for this we have taken the same input data of CN-LDFNs in decision matrices. Next by using the same expert weight (0.4, 0.35 and 0.25) we get the aggregated decision matrix. After by utilizing the steps of extended EDAS we get the final which is shown in Table 15.

After that comparison of these existing techniques, we compared our proposed method with more different MCDM methods include extended TOPSIS, WS and WP methods for that input data with same experts weight (0.4, 0.35 and 0.25). These results are shown in Table 15. The ranking among these different MCDM techniques and proposed technique are listed in Table 16 that looks similar the proposed ranking method. The proposed approach and existing methods are ranked graphically in Fig. 9.

Table 16 Ranking proposed and different existing methods.

Fig. 9

The final result of different MCDM methods and CN-LDF score values.

Superiority and comparison of proposed method and existing method

CN-LDFSs are more superior than existing N-LDFS³³ because here, in CN-LDFSs we used continuous functions (CF) instead of fixed values; the MD, NMD, and RPs are represented by continuous form by using CF, that makes this structure a more sensitive model that may be used in the continuous environment for MCDM theory. However, it might be difficult to determine the precise values of the MD, NMD, and RPs for the N-LDFS in some circumstances. To fill this research gap, Shams³¹ developed N-LDFSs and changed the concept of q-LDFSs. We then applied algebraic operators to N-LDFSs to get a more modified concept by involving the continuous functions (CF). By including the continuous data, we are able to incorporate the suitably big and continuous neighborhoods of the points later called CN-LDFWG aggregation operators into our research of both points and functions.

Advantages and limitations of the proposed algorithm

Advantages

• The use of continuous functions in the proposed algorithm allows for more accurate representation of membership and non-membership degrees and reference parameters.

• The algorithm accommodates a wide range of decision-making problems, particularly in renewable energy selection, through its adaptable framework.

• The integration of continuous fuzzy sets provides a more sensitive and refined approach to handling uncertainty and imprecision in decision-making.

• The proposed method outperforms traditional methods, such as the geometric operator, in terms of accuracy and robustness when applied to real-world case studies.

Limitations

• The use of continuous functions and advanced aggregation operators increases the computational complexity. This may limit the scalability of the model for large-scale decision-making problems with many alternatives and attributes.

• The effectiveness of the proposed method heavily depends on the availability and quality of data. Inaccurate or incomplete data may impact the reliability of the results.

• The performance of the method can be sensitive to the selection of reference parameters, which may require further refinement in real-world applications.

• The study’s methodology allows flexibility in selecting functions, but not all functions may be suitable for every decision-making context, which could limit the applicability of the results.

Conclusion

In this study, we focus on the development of Continuous Non-linear Diophantine Fuzzy Sets (CN-LDFSs) for the selection of the best renewable energy sources using continuous functions (CFs) to represent Membership Degree (MD), Non-membership Degree (NMD), and Reference Parameters (RPs). The CN-LDFS framework is extended with the CN-LDFWG aggregation operator, along with CN-LDFOWG and CN-LDFHWG operators, utilizing geometric properties. A case study is conducted to demonstrate the application of the proposed Multi-Attribute Decision-Making (MADM) methods for renewable energy selection. Finally, Hydropower Energy (HE) is identified as the optimal renewable energy source. We also compare the proposed approach with existing methods, highlighting the advantages and effectiveness of the proposed methodology in handling complex decision-making scenarios involving multiple attributes and criteria. Afterwards, we discuss some of the advantages and limitations of the proposed approach.

This work presents some interesting ideas for further study. The continuous non-linear Diophantine fuzzy decision making methods N-LDF GRA, N-LDF EDAS, N-LDF TOPSIS, N-LDF VIKOR, and N-LDF CODAS, as well as their hybrid approaches, may also be used in this study. The proposed method can be used in the future to solve challenges related to medical diagnostics and the evaluation of health care waste treatment technology. In addition, more extended Banach lattice algebras and other norms, like the ${L}_{p}$ norm, can be taken into consideration in place of continuous function spaces that nevertheless have a unit closed ball with a maximum element.