Introduction

Fifth-generation (5G) technology represents a fundamental advancement in wireless communication, delivering enhanced performance through increased speeds, reduced latency, and expanded network capacity compared to its predecessors1. A key aspect of 5G is its use of various frequency bands, including the sub-6 GHz band (FR1). Sub-6 GHz 5G can support a higher density of connected devices, making them perfect for smart cities, connected homes, and industrial Internet of Things (IoT) applications. The n78 band is a crucial frequency band for 5G sub-6 GHz networks, operating between 3,300 and 3,800 MHz. Often referred to as the 3.5 GHz band or C-band, it is known for its balance of coverage and capacity. The n78 band employs time-division duplexing, allowing the same frequency to be used for uplink and downlink at different times. This method enhances spectrum efficiency and boosts overall network performance. In addition, the Citizens Broadband Radio Service (CBRS) is a 150 MHz spectrum band within the 3.5 GHz range (3,550 MHz to 3,700 MHz). This service (i.e., BRS) is essential for applications such as mobile network densification, fixed wireless access, and the creation of private networks.

Low sidelobe level (SLL) antennas are needed in 5G sub-6 GHz networks for reducing interference and enhancing signal quality2. These antennas minimize the power radiated in unwanted directions, thereby boosting the overall performance of the communication system. Low SLL antennas ensure clearer and more reliable connections by suppressing sidelobes, which is particularly important for the dense deployment of 5G networks. Two common techniques for achieving antenna arrays with low SLL are amplitude tapering and employing slant-polarized antenna3. Designing low SLL antenna arrays involves non-uniform amplitude distributions such as binomial, Chebyshev, and Taylor distributions. The non-uniform amplitudes of these antenna elements are typically achieved using unequal-power dividing networks. However, these low-sidelobe antennas often have complex structures due to using power dividers. The second technique shifts the antenna’s polarization to the diagonal plane of a uniformly excited square array, effectively suppressing SLL4,5,6,7. The main drawback of these antennas is their multi-layered and complex structure, especially for large arrays.

Over the years, a large variety of printed low SLL antennas were implemented using various printed circuit board (PCB)-based technologies, including microstrip8,9,10,11,12,13,14,15and substrate-integrated waveguide (SIW)16,17,18,19,20,21. These antennas provide benefits such as a low profile, cost-efficiency, and versatility in manufacturing and integration. However, they are limited by low power handling capacity and high insertion loss. Conversely, hollow waveguide (HW) antennas, while larger and more expensive, provide high gain, superior efficiency, and robust power handling, making them well-suited for long-distance and high-power communication systems. Consequently, numerous low SLL antenna arrays utilizing HWs have been investigated22,23,24,25,26,27,28,29. In22, a nonequal waveguide power divider was proposed to excite the radiation slots with a non-uniform amplitude distribution, resulting in an SLL of −25 dB over a frequency band from 14.15 to 16.25 GHz. However, this antenna array suffers from structure complexity and narrow bandwidth (13.8%). The design of a 2 × 2-element cavity-backed slot array with 13.4 dBi gain, 15% fractional bandwidth, −12dB SLL and 95% efficiency was reported in24. In25, a low-sidelobe cavity-backed slot antenna array was proposed with 18.2 dBi gain, −20dB SLL, and 94% radiation efficiency. In27, a 2 × 2-element cavity-backed slot array with 6.2% bandwidth, 97% total efficiency, 10.4–11 dBi realized gain and SLL of −14 dB was proposed. The design of a low-sidelobe 1 × 10-element slot array exhibited 13.1 dBi gain, −24.1dB SLL, and 1.8% fractional bandwidth28. The main drawback of that design is its ultra-narrow bandwidth.

To overcome the limitations of existing low SLL antenna arrays, this paper proposes a novel all-metal cavity-backed slot antenna array. The design directly excites each radiating slot through the cavity layer, eliminating the need for a complex power divider. The desired non-uniform amplitude distribution for SLL reduction is achieved by strategically positioning the radiating slots. Most of the cavity-backed slot arrays that use a single large cavity to excite the radiating slots exhibit narrow bandwidth. To overcome the bandwidth constraints typically associated with single-cavity designs, our proposed architecture incorporates two adjacent cavities with an integrated power divider. This configuration allowed us to achieve exceptional performance metrics, including a measured peak gain of 20.2 dBi and efficiency exceeding 90% across a 25% bandwidth spanning 3.1 to 4 GHz specifications that, to our knowledge, represent the first demonstration of such comprehensive performance in a fabricated low SLL cavity-backed antenna array.These features make the proposed antenna a promising candidate for sub-6 GHz networks requiring high gain, high efficiency, wide bandwidth, and low SLL.

The remainder of this paper is organized as follows: Sect. 2 explains the overall configuration of proposed antenna. The design methodology and simulated results of the proposed non-uniform excited cavity-backed slot array is presented in Sect. 3. Sections 4 and 5 discusses optimization process and the fabrication and measurement results, respectively. Finally, conclusions are provided in Sect. 6.

Fig. 1
figure 1

Exploded perspective view of configuration of the proposed cavity-backed slot array antenna.

Full size image

Antenna configuration

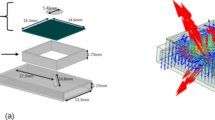
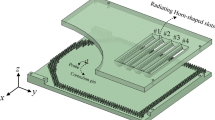
The configuration of the proposed antenna is illustrated in Fig. 1. The structure includes radiating elements in the top layer, two cavities in the middle layer, and a feeding network in the bottom layer, forming a three-layer metallic structure. This antenna features several key components: a 2-way coaxial-fed power divider, a cavity layer, 16 radiating slots arranged in a 4 × 4 array, and rectangular sidewalls employed as reflectors. The radiating slots are positioned on the top side of the cavity, while two coupling apertures are located on the bottom side. Input energy from the coaxial-to-waveguide transition is distributed to the coupling slots. Two matching steps at the waveguide ends facilitate a 2-way power division with minimal reflection loss across the 3–4 GHz operating band. The vertical sidewalls reduce off-axis radiation, minimizing sidelobes and improving overall performance. The frequency band of interest in the design is 3–4 GHz for various sub-6 GHz applications. The simulations and optimizations are performed by employing CST Microwave Studio.

Antenna analysis and design

Array factor

The array factor (AF) for a planar 4 × 4-element array illustrated in Fig. 2(a) in the xy-plane is:

$${\text{AF}}(\theta ,\varphi )\,=\,\sum\limits_{{n=1}}^{4} {\sum\limits_{{m\,=1}}^{4} {{I_{mn}}{e^{j{\alpha _{mn}}}}{e^{j{\psi _{mn}}}}} }$$
(1)
Fig. 2
figure 2

(a) Geometry of 4 × 4-element planar antenna array. (b) Normalized AF in principal planes.

Full size image

where

$${\psi _{mn}}=\,\beta \left( {{{x^{\prime}}_{mn}}\sin \theta \cos \varphi +{{y^{\prime}}_{mn}}\sin \theta \sin \varphi } \right)$$
(2)
$${\alpha _{mn}}=\, - \beta \left( {{{x^{\prime}}_{mn}}\sin {\theta _0}\cos {\varphi _0}+{{y^{\prime}}_{mn}}\sin {\theta _0}\sin {\varphi _0}} \right)$$
(3)

where θ0 and φ0 define the main pointing direction, β is the phase constant of wave in free space, and Imn and αmn are the amplitude and phase of excitation. Given that all eight radiation elements are uniform in size, the critical factor for achieving the desired radiation performance is the spacing between the elements. Amplitude weighting, also called tapering, is a well-known technique used in array antenna design to reduce SLL. By adjusting the amplitude of the signals fed to each element in the array, the overall radiation pattern can be shaped to minimize sidelobes. Common amplitude weighting methods include using various distributions that gradually decrease the amplitude of the signals toward the edges of the array. This smooth tapering helps suppress sidelobes while maintaining the main lobe’s integrity, thereby enhancing the antenna’s signal-to-noise ratio and overall efficiency.

For this design, amplitude tapering along the y-axis is considered. This approach enables achieving the desired low SLL in the yz-plane. For instance, the AF corresponding to the in-phase excitation with amplitude coefficients of

$$\left[ {\begin{array}{*{20}{c}} {0.53}&{0.53}&{0.53}&{0.53} \\ 1&1&1&1 \\ 1&1&1&1 \\ {0.53}&{0.53}&{0.53}&{0.53} \end{array}} \right]$$
(4)

for radiating elements and half-wavelength element spacing results in an SLL of −20 dB in the yz-plane of a broadside radiation pattern. The AF is calculated using (1)-(4) and illustrated in Fig. 2(b). To reduce the SLL in the xz-plane, we need to employ a different technique, which is discussed next.

Fig. 3
figure 3

(a) Geometry of radiation slot array. (b) Configuration of cavity layer.

Full size image
Fig. 4
figure 4

Electric field distribution of cavity layer in 3.5 GHz.

Full size image

Cavity-backed Radiation slots

As shown in Fig. 3(a) and (b), the radiation slots are initially identical and symmetrically arranged on the top surface of the cavity layer. This antenna features elements in a 4 × 4 configuration along the x- and y-axes. The slots are symmetrically positioned and exhibit symmetrical phase and amplitude excitation about the origin. The top side of the cavity features radiating slots, and the bottom side hosts two coupling apertures. The input energy from the feed layer is entered to the cavities through the coupling apertures for exciting the radiation slots. Taking into account the configuration of the radiating slots, it is evident that slots 1 and 2 have similar excitation characteristics. However, given that slot 2 is positioned further from the coupling slot, the amplitude of the excitation current is likely to be less than that of slot 4. This aspect of the current tapering can be utilized to reduce the side lobe level (SLL) in the yz-plane. The electric field distribution as shown in Fig. 4, indicates that the operational mode of cavities is TE150, and its resonance frequency is given by:

$${f_r}\,=\,\frac{1}{{2\sqrt {{\mu _o}{\varepsilon _0}} }}\sqrt {{{\left( {\frac{1}{{{W_C}}}} \right)}^2}+{{\left( {\frac{5}{{{L_C}}}} \right)}^2}} .$$
(5)
Fig. 5
figure 5

Configuration of radiation slot array with rectangular sidewalls as reflectors.

Full size image
Fig. 6
figure 6

Normalized radiation pattern of cavity-backed slot array with sidewalls with different heights. (a) yz-plane and (b) xz-plane.

Full size image

Rectangular sidewalls as Reflector in Radiation Layer

As stated, by tapering the current amplitude of radiation elements along y-axis according to (5), the desired low SLL (−20 dB) in the yz-plane is achieved. Considering that the distribution of the excitation current of the radiating elements is assumed to be uniform along the x-axis, the SLL in the xz-plane is approximately −13 dB. To reduce this value, it is required to employ another technique. As illustrated in Fig. 5, four rectangular sidewalls with the same height and thickness are employed as a reflector for reducing undesirable radiations in side directions. The rectangular sidewalls help to minimize leakage current, which can cause diffraction at the edges of the metal plates surrounding the radiating slots. The idea is similar to employing a cylindrical shroud within a paraboloidal reflector enclosure to suppress the far-out sidelobes30. In addition, the height of the rectangular sidewalls must be optimized to achieve low SLL in the xz-plane. To demonstrate the impact of this parameter, the radiation patterns of the antenna with different rectangular sidewall heights are displayed in Fig. 6. The results indicate that the undesirable radiation of the antenna in the yz-plane is below −20 dB, attributed to the tapered amplitude of the element excitation currents. Consequently, adding rectangular sidewalls does not further enhance the SLL in this plane. However, using sidewalls with appropriate height reduces the SLL to approximately −20 dB in the xz-plane.

Fig. 7
figure 7

(a) Geometry of probe-fed waveguide power divider. (b) Off-centerline probe-fed rectangular waveguide.

Full size image

Feed Layer

A two-way power divide is required to ensure the cavity-backed slot array antenna is appropriately excitable. This power divider can be realized using a probe-fed rectangular waveguide junction. As depicted in Fig. 7, instead of using a conventional waveguide T-junction, a probe with a radius of RP is placed exactly in the middle of two adjacent waveguides but not on the centerline of each of them. The impedance seen from the connector can be adjusted by changing this offset from the center OP along with the length of the probe LP. As illustrated in Fig. 7, the waveguide has cross-sectional dimensions WW×HW. The corners of waveguides are chamfered, and two stepped sections (LM×WM×HM) are incorporated at the waveguide ends to facilitate the transformation of electromagnetic energy from the rectangular waveguides to the cavity layer via coupling slots, minimizing reflection loss.

The effect of height (HM) and width (WM) of matching steps on the performance of an antenna array was investigated by conducting several parameter studies (Fig. 8). It is evident that these geometrical parameters significantly impact the return loss at the input port of the antenna. The electric field distribution of the proposed power divider is displayed in Fig. 9.

Equivalent Circuit Model for feed layer

Detailed discussions on the classical setup of a rectangular waveguide to coaxial-line transition, with the probe located on the centerline of the waveguide’s wide wall, can be found in the literature31,32,33,34. Since the electric current on the thin probe can be approximated by I0 sink0(LP-z), the input resistance can be determined as:

$${R_0}\,=\,\frac{{{Z_{T{E_{10}}}}}}{{k_{0}^{2}{H_W}{W_W}}}{\tan ^2}\frac{{{k_0}{L_P}}}{2}$$
(6)
Fig. 8
figure 8

Effect of height and width of matching steps the input reflection of the antenna.

Full size image
Fig. 9
figure 9

Electric field distribution of power divider in 3.5 GHz.

Full size image

where k0 = ω/c and ZTE10 is the impedance of TE10 mode in the rectangular waveguide given by:

$${Z_{T{E_{10}}}}\,=\,\frac{{120\pi }}{{\sqrt {1 - {{\left( {\frac{\lambda }{{2{W_W}}}} \right)}^2}} }}$$
(7)

A closed-form expression for the input resistance of an off-centerline probe can be obtained as follows: The fundamental mode’s electric field in a rectangular waveguide is parallel to the probe axis, with its distribution across the waveguide axis described by E0 cos(πOP/WW). In this equation, E0 denotes the electric field intensity at the waveguide centerline. Consequently, the power delivered by a probe offset from the centerline by OP is determined by the E-field’s transverse position dependence, resulting in:

$$P\,=\,{P_0}\,{\cos ^2}\left( {\frac{{\pi {O_P}}}{{{W_W}}}} \right)$$
(8)

where P0 represents the power delivered by the probe when it is positioned at the centerline of the waveguide’s broad wall (OP = 0). Consequently, the input resistance of a probe positioned off the centerline of the waveguide can be expressed as:

Fig. 10
figure 10

Equivalent circuit of coaxial-waveguide junction.

Full size image
Fig. 11
figure 11

Comparison of S-parameters obtained with CST and the equivalent circuit model.

Full size image
$${R_{in}}\,=\,\frac{{{R_0}}}{{{{\cos }^2}\left( {\frac{{\pi {O_P}}}{{{W_W}}}} \right)}}\,=\,\frac{{{Z_{T{E_{10}}}}}}{{k_{0}^{2}{H_W}{W_W}}}{\tan ^2}\left( {\frac{{{k_0}{L_P}}}{2}} \right)\left( {1+{{\tan }^2}\left( {\frac{{\pi {O_P}}}{{{W_W}}}} \right)} \right)$$
(9)

An appropriate and simple equivalent circuit for the coaxial to rectangular waveguide junction aids conceptual design and enhances understanding of its functionality33. Figure 10 depicts a simple equivalent circuit of the junction. The probe passes through an aperture in the broad wall, modeled by an equivalent inductor (L1) and capacitor (C1). The proper equivalent circuit model for the probe in the waveguide includes a parallel combination of L2 and C2, which is connected in a shunt with the waveguide line. An ideal transformer is employed to scale the load impedances outside the waveguide environment. The scattering matrix corresponding to an ideal n:1 transformer is given by35:

$$[S]\,=\,\frac{1}{{{n^2}+1}}\left[ {\begin{array}{*{20}{c}} {{n^2} - 1}&{2n} \\ {2n}&{1 - {n^2}} \end{array}} \right]$$
(10)

Extracting the elements of the equivalent circuit yields n = 1.29, L1 = 46.41 pH, L2 = 754.58 pH, C1 = 4.63 pF, and C2 = 2.01 pF. The S-parameters for these extracted values are shown in Fig. 11, demonstrating a reasonable agreement with the CST full-wave simulation results.

Table 1. Optimized values for the geometrical parameters of the cavity-backed slot array.
Full size table
Fig. 12
figure 12

Electric field distribution of cavity-backed slot array antenna in 3.5 GHz.

Full size image

Power Handling

The capacity of the proposed antenna to handle peak power relies on the dimensions of the structure. The maximum handled power Pmax can be calculated as follows:

$${P_{\hbox{max} }}\,=\,\,{\left( {\frac{{3 \times {{10}^6}}}{{{{\left| E \right|}_{\hbox{max} }}}}} \right)^2}$$
(11)

wherein represents the peak electric field value in the structure, calculated under the assumption of an input power of 1 W. As illustrated in Fig. 12, |E|max at 3.5 GHz is 7226 V/m. Consequently, the antenna peak power handling capability is 172.3 kW.

Optimization process

The design process for the proposed cavity-backed slot array antenna, using a three-layer structure, involves these steps:

  • Set the Design Frequency (f0): Choose this frequency at the center of the desired bandwidth.

  • Define Radiating Slot Dimensions (LS×WS): Ensure these dimensions cause radiation over the target frequency range. Start with initial values of λ0/2 × λ0/4 and set element spacing at λ0/2.

  • Specify Cavity Dimensions (LC×WC×HC): Begin with initial dimensions of λ0 × λ0/2 × λ0/4.

  • Configure Waveguide Power Divider Dimensions: For a 1-to-2 rectangular waveguide-based power divider, start with width and height values of λ0 and λ0/2, respectively. Matching step dimensions can be initially λ0 (length), λ0/4 (width), and λ0/4 (height).

Fig. 13
figure 13

3-D radiation patterns of slot array antenna at (a) 3.3 and (b) 3.8 GHz.

Full size image

  • Determine Coaxial Line to Waveguide Transition: Begin with a probe length and offset of λ0/4 and λ0/8, respectively.

  • Optimize the Design: Fine-tune 14 parameters, listed in Table 1., ensuring each parameter’s allowable range is centered on its initial value, considering ± 50% variations.

The optimization of the geometrical parameters of the proposed antenna geometry enables the attainment of the desired input reflection coefficient, gain, and SLL. This optimization is accomplished through the Trust Region Framework optimization method in CST Microwave Studio. The design specifications are met using CST’s optimization tools with an appropriate fitness function defined as:

$$fitness\,=\,{\left( {\frac{1}{M}\sum\limits_{{m\,=\,1}}^{M} {\left( {{{\left| {{S_{11}}({f_m})} \right|}^2}+{{\left| {G({f_m}) - {G_0}} \right|}^2}+{{\left| {{\text{SLL}}({f_m}) - {\text{SL}}{{\text{L}}_0}} \right|}^2}} \right)} } \right)^{0.5}}$$
(12)

where the input reflection coefficient and gain of the antenna at M frequency samples (fm) over the required frequency band are represented by S11(fm) and G(fm), respectively. The minimum realized gain and SLL are selected as G0 = 20 dBi and SLL0 = −20 dB for the optimization procedure. On a Windows 10 system with an Intel Xeon Gold 6136 CPU (3.5 GHz, two processors, 36 cores) and 576 GB of RAM, the optimization process takes less than one minute per full structure simulation.

The values of the final optimized parameter are detailed in Table 1.. The 3-D radiation patterns of the optimized antenna at 3.3 and 3.8 GHz are displayed in Fig. 13. Observe that the simulated realized gain is approximately 20 dBi over the desired frequency bandwidth.

Fabrication, measurement and discussion

Measurement results

The concept was illustrated by fabricating a prototype of the cavity-backed slot array antenna using aluminum. Figure 14 presents the fabricated prototype under test. The standard N-type connectors used have a probe diameter of 3 mm. S11 measurement of the prototype is conducted using an Anritsu 37,347 C network analyzer. Figure 15 compares the simulated and measured S- parameters, revealing that the measured |S11| < −10 dB bandwidth ranges from 3.1 to 4 GHz. The slight discrepancy between the measurement and simulation values can be caused by fabrication tolerance.

Fig. 14
figure 14

The photographs of the fabricated antenna array under test.

Full size image
Fig. 15
figure 15

Simulated and measured (a) input reflection coefficient and (b) realized gain and total efficiency of cavity-backed slot array antenna.

Full size image

The far-field radiation pattern and gain are measured in an anechoic chamber with a resolution of 1° rotation. The normalized simulated and measured radiation patterns of the antenna array are shown in Fig. 16. Consistent with the simulation responses, the measured radiation pattern exhibits no beam squint. The measured peak gain of the antenna is approximately 20.2 dBi, compared to the simulated gain of 20.7 dBi, with a reduced SLL of −19 dB. The measured results align well with the simulations, validating the design. Minor deviations between the measured and simulated results may be attributed to fabrication tolerances and inaccuracies in the measurement setup.

Discussion

Table 2 compares the performances of previously reported cavity-backed array antennas with the proposed design. With a fractional bandwidth of 25.3% from 3.1 GHz to 4 GHz, our three-layer structure surpasses the limited bandwidth of most single-cavity-backed slot arrays. By employing a cavity layer with two adjacent rectangular cavities and an appropriate power divider, our antenna achieves the broadest impedance bandwidth among similar designs while maintaining low SLL, high gain, and acceptable total efficiency. These characteristics render it highly suitable for sub-6 GHz communications.

Fig. 16
figure 16

Simulated (solid lines) and measured (dashed-lines) normalized radiation patterns of antenna array in E- and H-planes at 3.3 GHz (a and b) and 3.8 GHz (c and d).

Full size image

Conclusion

This study presents the design and implementation of an all-metal wideband slot array antenna tailored for 5G sub-6 GHz networks. The comprehensive validation through simulations and experimental measurements confirms the antenna’s capability for wideband operation with high gain, low reflection loss, and high efficiency over the frequency band from 3.1 to 4 GHz. Overall, the proposed low SLL wideband antenna is crucial for enhancing signal clarity and mitigating interference, which are essential for 5G and next-generation wireless communications.

Table 2 Performance comparison of the cavity-backed antenna arrays.
Full size table