Introduction

The exponential growth of artificial intelligence has intensified the demand for advanced memory technologies that offer higher performance, higher efficiency, and enhanced scalability. Traditional memory systems such as dynamic random access memory (DRAM) are reaching their physical and technical limitations, prompting the exploration of alternative solutions. Among the emerging candidates, resistive random access memory (RRAM) has gained significant attention due to its unique advantages and the potential to meet the high requirements of next-generation memory applications1.

RRAM is characterized by its simple metal-insulator-metal (MIM) structure, where various insulating materials are sandwiched between two metal electrodes. This architecture not only simplifies fabrication processes, but also allows for versatility in material selection, enabling tailored electrical properties. Interestingly, the fundamental structure of RRAM closely resembles that of a capacitor, suggesting the potential for dual functionality that integrates both resistive and capacitive properties within a single device.

However, despite the structural similarity to capacitors, most research on RRAM devices has focused primarily on resistive switching, where the device transitions between high-resistance state (HRS) and low-resistance state (LRS) in response to applied voltage. While some studies have investigated the coexistence of resistive and capacitive switching in RRAM, they were mainly limited to experimental observations through measurements, and specialized simulations for precise mechanism analysis have rarely been studied2,3,4.

In this study, we measured RRAM using an Al/Al2O3/HfO2/SiOx/p+-Si stack structure. Pulse measurement results showed that when continuous set pulses were applied, LRS and high-capacitance state (HCS) coexisted, whereas the HRS and low-capacitance state (LCS) were observed with continuous reset pulses. This is contrary to the assumption based on the known operating principles of RRAM, which suggest that the formation of conductive filament (CF) requires local dielectric breakdown of the insulator, leading to a weakened capacitance. This correlation implies that there is an inherent mechanism that governs changes in resistance and capacitance within the device. Therefore, in this study, we established two main hypotheses. First, variations in the oxide-silicon interface trap charge cause changes in the device capacitance due to Joule heating within the conductive filament when in the LRS. Second, variations in device capacitance are driven by oxygen (O2-) ion migration and release within the oxygen reservoir layer (ORL) under different resistance states.

To verify these hypotheses, we utilized COMSOL Multiphysics, which can simultaneously simulate electrical and thermodynamic properties. The simulation results for both hypotheses supported our experimental observations. Using the mechanisms revealed in this study, we present the possibility of ultra-high-density memory. Using the coexistence of resistive and capacitive memory effects can dramatically increase the integration density of memory devices, potentially leading to innovative technology that meets future demands for ultra-high-density memory.

Fig. 1
figure 1

Analyses of Al/Al2O3/HfO2/SiOx/p+-Si device. (a) Device fabrication process, (b) TEM images for EDS mapping, (c) Schematic of device structure, cross-sectional HR-TEM image of Al/Al2O3/HfO2/SiOx/p+-Si, and EDS line scan of Al, O, Hf, Si.

Full size image

Methods

For preparing the oxide memristors, a heavily doped p-type silicon substrate was sequentially cleaned by ultrasonication in acetone, isopropyl alcohol, and deionized water for 15 minutes. The p-type doped silicon functioned as the bottom electrode. A 20 nm thick hafnium dioxide film, serving as a stable resistive switching layer(RSL), was deposited on the substrate through atomic layer deposition (ALD) (CN1, ALD Dual Chamber System). An 80 nm thick aluminum film, serving as the top electrode, was thermally evaporated at 2 Å/s under a pressure of 10−6 Torr. The samples were then annealed at 300 °C for 1 hour to promote the formation of interfacial layers. The processing procedure is illustrated in Fig. 1a. The electrical characteristics of the device were assessed using a Keysight 4156C and a Keithley 4200A-SCS. DC measurements were conducted using the high-resolution source measurement unit (HRSMU) to achieve high accuracy in reading current. Pulse measurements were performed using the pulse generation unit (PGU) and the ultra-fast pulse measurement unit (PMU), which operate to generate and measure pulses almost simultaneously. Capacitance measurements were executed using the multi-frequency capacitance-voltage unit (CVU). Unless specified otherwise, measurements were conducted at room temperature (25 °C).

Fig. 2
figure 2

(a) Typical I–V characteristics of the device under compliance current (10mA). Inset shows the forming process. (b) High resistance and low resistance values during ten DC cycles (c) Ohmic conduction mechanism for LRS and trap-controlled SCLC mechanism for HRS. (d) RRAM resistance retention property and (e) capacitance retention property. (f) Temperature-dependent C-V characteristics. (g) The schematic of state transition due to the generation of oxygen vacancies and O2- ions under the applied voltage. (h) R-C measurement results demonstrating both resistive and capacitive switching under pulse scheme. (i) Pulse scheme of R-C measurement for one sequence.

Full size image

Results and discussion

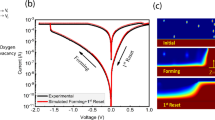
Figure 1b presents the energy-dispersive X-ray spectroscopy (EDS) mapping of the HfO2 based RRAM device after processing, showing a notable difference in the expected distribution of each component. The distinct presence of Al, Hf, O, and Si elements within their respective layers confirms that the fabrication process proceeded as intended. A more detailed analysis is provided in Fig. 1c, which includes a high-resolution transmission electron microscopy (HR-TEM) image and EDS line scanning, revealing the atomic concentrations of these elements. Although only the HfO2 layer was deposited initially, the annealing process resulted in the formation of an Al2O3 layer between Al and HfO2, and an SiOx layer between HfO2 and p+- Si. To evaluate the basic electrical characteristics, DC sweep based electrical measurements were performed. The I–V characteristics for 10 cycles are presented in Fig. 2a. The sweep followed the numbered sequence shown in the graph. The set and reset operations occurred at positive and negative voltages, respectively, confirming the device’s bipolar switching behavior. Additionally, as shown in the inset graph, the device required a forming process at approximately 2.5 V with a compliance current (CC) of 100 μA before DC sweep, suggesting a filament-type device. The HRS and LRS over 10 cycles show an on/off ratio of approximately 3, as depicted in Fig. 2b. To further understand the conduction mechanism, an analysis was conducted using the log-log plot of the set curve, as presented in Fig. 2c. In both HRS and LRS cases, the slope slightly increases from 1 (\(\sim\) 1.32) or remains close to 1 at lower voltages, which can be explained by Ohm’s law as Eq. (1).

$$\begin{aligned} J=qn_{0}\mu \frac{V}{t} \end{aligned}$$
(1)

At higher voltages, however, the HRS slope increases to approximately 2, following with Child’s law as Eq. (2), while the LRS maintains a slope of 1 across all voltage ranges, which indicates that the conduction mechanism is dominated by space-charge-limited conduction (SCLC)5,6.

$$\begin{aligned} J_{TFL}=\frac{9}{8}\mu \varepsilon \theta \frac{V^{2}}{t^{3}} \end{aligned}$$
(2)

So, as the applied voltage increases in the HRS, the trap density becomes progressively filled, enabling sufficient movement of free carrier, which leads to a transition to the LRS. Other I–V curves also exhibit this SCLC mechanism, as illustrated in Fig. S1. Fig. 2d and e display the retention measurement results of the resistance and capacitance, respectively. During the 4000 seconds, the on/off ratio of resistance and capacitance remained approximately 10 times.

We also performed the temperature dependent capacitance-voltage (C-V) measurements sweeping from − 3.5 to 3.5 V with 1 kHz frequency, while applying a compliance current to suppress the device forming process. At all applied voltages, the marked increase in capacitance was observed with increasing temperature, as shown in Fig. 2f. Moreover, the presence of accumulation, depletion, and inversion regions was revealed, similar to those observed in a conventional MOS capacitor. An interesting observation is that the overall capacitance decreases as the measurement frequency increases regardless of temperature. This behavior is due to the parasitic capacitance of the bottom electrode, which becomes more influential at higher frequencies, degrading device performance. However, its impact remains minimal in the 1 kHz. The details about frequency dependent measurements are provided in Fig. S2.

Furthermore, the Al2O3 layer is expected to function as an ORL, storing oxygen ions in the set state7. Consequently, the overall state transition under the applied voltage can be described as illustrated in Fig. 2g. To confirm the coexistence of resistive and capacitive switching, continuous pulse measurement was carried out. The measurement proceeded as pulse application \(\rightarrow\) resistance reading \(\rightarrow\) capacitance reading in a single sequence. During the pulse application step, pulse of 1.6 V or − 1.4 V with a 100 ms width was applied to induce LRS and HRS. In the resistance reading step, resistance was read by performing a DC sweep from 0 V to 0.3 V. Afterwards, capacitance was measured using an AC voltage with an amplitude of 0.02 V and 1 kHz frequency as shown in Fig. 2i. This entire process was repeated 40 times, and changes in resistance and capacitance were recorded at each iteration, starting from the pristine state.

Fig. 3
figure 3

(a) Schematic of the modeled device and environment in COMSOL simulation. (b) Shape changes of the CF in the device between the LRS and HRS. (c) Simulation of current variation based on the relationship between the number of CFs. (d) Current variation resulting from changes in the CF shape and gap formation. (e) Voltage dependent Joule heating changes in CF.

Full size image

The results, as shown in Fig. 2h, demonstrate that the LRS and HCS coexist during 20 set cycles, while the HRS and low capacitance state (LCS) coexist during 20 reset cycles. This finding is contrary to the expectation that the formation of CF, which involves localized dielectric breakdown, would lead to a reduction in capacitance.

Thus, we aimed to perform simulations to evaluate the two aforementioned hypotheses. To achieve this, it was necessary to simulate both electrical and thermodynamic properties simultaneously. For this purpose, COMSOL Multiphysics, which meets all these requirements, was employed in this study.

Modeling and physics module

We established a simulation environment and modeled the device to resemble the actual measurement conditions as closely as possible. All simulations were performed in three dimensions. Based on analysis of the real measurement environment, three main types of heat transfer were identified.

First, conduction occurs as the lower part of the bottom electrode remains in direct contact with the metal chuck of the probe station. This contact facilitates heat conduction. The metal chuck serves as a substantial heat sink for the device and allows rapid dissipation of heat. Second, convection is present as the remaining parts of the device are exposed to ambient air, resulting in convective heat transfer to the surrounding environment. Finally, radiation takes place at all interfaces of the device, governed by the Stefan–Boltzmann law8.

Therefore, we modeled an air-filled space of dimensions 50 × 50 × 50 μm, without airflow and created an Al/Al2O3/HfO2/SiOx/p+-Si device with an area of 1 × 1 μm within it, as depicted in Fig. 3a. Additionally, the lower part of the bottom electrode was set to a fixed temperature of room temperature, as it acts as a heat sink and rapidly dissipates the generated heat. The air was defined as an electric insulator and heat radiation was specified to be simulated at the interfaces of device. Here are the four physics modules used in COMSOL for our simulations: (All simulations were principally based on a time-dependent study).

  • Electric Current Module: The Electric Current Module is computed according to the following Eq. (3).

    $$\begin{aligned} \triangledown \cdot J=0, \quad J=\sigma _{c}E+\varepsilon \tfrac{\partial E}{\partial t}, \quad E=-\triangledown V \end{aligned}$$
    (3)

    The first equation represents the law of current conservation, while the second equation expresses the current density in terms of displacement current and Ohm’s law. Last equation is derived from Maxwell’s equations and describes the relationship between the electric field and electric potential. Here, \(\sigma _{c}\) denotes conductivity, \(\varepsilon\) represents permittivity, and V stands for electric potential.

  • Heat transfer in solids Module: The Heat transfer in solids Module is computed according to the following Eq. (4).

    $$\begin{aligned} \rho C_{p}\tfrac{\partial T}{\partial t} - \triangledown \cdot (\kappa \triangledown T) = Q_{s} \end{aligned}$$
    (4)

    This equation is based on Fourier’s law and the heat conduction equation. Here, T represents temperature in Kelvin, k denotes thermal conductivity, \(C_p\) stands for specific heat capacity, \(\rho\) represents density, and \(Q_s\) denotes the heat source.

  • Multiphysics Module: The Multiphysics Module is computed according to the following Eq. (5).

    $$\begin{aligned} Q_{s} = J \cdot E \end{aligned}$$
    (5)

    This module establishes a coupling between current density and electric field, representing the electromagnetic heat source generated by Joule heating.

  • Electric Circuit Module: This module connects the modeled device to an electric circuit. By utilizing the voltage source of the module, various functions of voltage can be applied to the device.

Fig. 4
figure 4

Energy band diagram for RRAM (a) before contact and (b) after contact. Enlarged Band Diagram of the SiOx/Si Interface and corresponding equivalent circuit under various conditions. Accumulation is shown in (c) at room temperature and (f) at high temperature, depletion in (d) at room temperature and (g) at high temperature, and inversion in (e) at room temperature and (h) at high temperature.

Full size image

Next, we should consider the extent of the RSL in which the filament forms. As illustrated in Fig. S3a, the SiOx layer deposited beneath HfO2 has a Si-O bond dissociation energy similar to that of the Hf-O bond9. Moreover, several studies have demonstrated that SiOx can function as an RSL, suggesting that filament formation may occur simultaneously in both the HfO2 and SiOx layers upon voltage application10,11. Consequently, filament formation has been modeled to extend across both the HfO2 and SiOx layers, as depicted in Fig. 3b. All material parameters used for the simulation are provided in Table 1.

Table 1 Material parameter12,13,14,15,16,17,18,19.
Full size table

It is also considered to determine the precise size of the CF in the switching layer. Wei et al.20 observed that the diameter of the filaments is typically on the order of a few to tens of nanometers. However, since this observation is based on a highly localized cell area, there is potential for multiple filaments to form as bundles in larger areas21,22. Thus, rather than determining the precise radius and amount of CFs in the device, we focused on observing the current variation as the number of CFs changed, and we performed simulations to verify the basic characteristics.

We varied the number and radius of CFs within the RSL, then applied a pulse with an amplitude of 1.6 V and 100 ms width to measure the resulting current. The results, as shown in Fig. 3c, indicate that the current increased significantly as the number of CF increased and their radius expanded. This behavior aligns with the characteristics observed in typical filament-type RRAM.

Finally, it is crucial to determine the shape of the CF in each resistance state of the RRAM device. In practical RRAM devices, CF does not form a perfect geometric shape. However, in the LRS, the CF is often represented as a cylindrical structure with an increased horizontal dimension23,24,25.

The critical aspect, however, lies in the determination of the shape of CF during the HRS after the reset process. Many studies have reported that applying a reset voltage to the device creates a gap at the end of the CF, disrupting the filament connection and leading the device into the HRS. The formation of this gap indicates a recombination of O2- ions stored in the ORL with oxygen vacancies that consist of filament. Typically, this recombination starts from the outer region of the CF, primarily at one of its ends, which is connected to either the electrode or the ORL. Consequently, a cylindrical CF could transform into a conical shape with a gap appearing at its terminal26,27. To validate this, we modeled a perfect cylindrical CF and gradually reduced the radius of its upper end, which is in contact with the ORL, simulating a conical transformation until a gap was formed. The current was measured by applying a 0.3 V pulse. As we expected, the simulation results indicated that as the upper radius of the CF decreased, the current gradually decreased, and abrupt decrease in current was observed once the gap formed. (see Fig. 3d). However, our device exhibited a gradual decrease in current during the reset process, as confirmed through measurements (see Fig. 2a). Furthermore, pulse measurements demonstrated a current on/off ratio of 3, suggesting that the CF within the device might not fully disconnect in the HRS. Instead, a partially incomplete CF may still connect the two electrodes.

Furthermore, the recombination of O2- ions and oxygen vacancies can occur at the bottom of the device or at the HfO2/SiOx interface. Therefore, we conducted simulations considering all possible cases and the results indicated that the CF shape in the HRS would not significantly affect the simulation results28,29,30 (see Fig. S4).

Additionally, Fig. 3e illustrates the variation in Joule heating of the CF as the voltage changes. At 0.4 V, the maximum temperature almost reached 200 °C, while at 1.6 V, Joule heating increased to1000 °C.

Based on our simulations, we ultimately determined a cylindrical CF with a radius of approximately 6 nm to represent the LRS, and a conical CF with a top radius of about 2 nm to represent the HRS. We also assumed the formation of nine filaments, since current at 0.3 V read produces approximately 200 μA in the LRS and about 40 μA in the HRS. These results lead an on/off ratio of roughly 3–4, which is consistent with our experimental measurements. (see Fig. S3b for details).

Simulation results

The first hypothesis suggests that the observed capacitance variation originates from an increase in interface trap charge activated by Joule heating. Interface traps, typically found in metal-oxide-semiconductor (MOS) structures, are generated primarily at the insulator-semiconductor interface, where they capture charges and contribute to the formation of the interface trap capacitance, Cit31. The RRAM device of this study, which employs a Si substrate, is expected to exhibit charge traps at the oxide-silicon interface. In particular, the non-stoichiometric SiOx layer that directly contacts Si is leading to a greater possibility of oxygen vacancies (traps) being generated32. Consequently, interface traps are more likely to significantly affect the capacitance variation.

To assess the influence of interface traps by temperature, temperature-dependent C-V measurements were performed (see Fig. 2f). The result indicates a tendency for the appearance of accumulation, depletion, and inversion regions, and they demonstrate that the overall capacitance increases as the temperature rises. For a more detailed analysis, an energy band diagram was performed and examined using a band diagram simulation. Fig. 4a represents the state before contact, while Fig, 4b illustrates the state after contact33,34,35,36. Due to heavy boron-doped Si, the Fermi level (EF) is observed to overlap (or lie slightly below) the valence band edge (Ev), and Si energy bandgap narrowing is evident37. Furthermore, the high doping concentration limits the formation of the depletion width (and bending of Si), thereby reducing the influence of Cdep in the depletion region and resulting in a more gradual C-V curve.

If the internal temperature of the device is assumed to remain at room temperature, in the accumulation region, the EV, intrinsic Fermi level (Ei), and the conduction band edge (EC) are located above the EF (see Fig. 4c). We also considered that interface traps located below Ei act as donor-like traps, while those above Ei function as acceptor-like traps38. Thus, if all traps are located above the EF, positive charge is generated at the interface (due to donor-like traps), suggesting that CSiOx and Cit are connected in series.

Fig. 5
figure 5

(a) Temperature distribution contour maps along Cut Plane 1 for LRS and HRS. (b) Temperature distribution at the SiOx/Si interfaces observed via Cut Plane 2 under the LRS and HRS. To clearly distinguish the temperature difference at the entire interface, the temperature caused by Joule heating in the filament was set to black. (c) Cross-sectional schematic of the device structure showing Cut Plane 1 and Cut Plane 2. (d) Equivalent circuit of the interface considering the temperature-dependent variation of Cit under the read voltage applied.

Full size image

If the applied voltage is further increased, the device enters the depletion region, where the bending of the energy bands causes some donor-like traps to shift below EF and capture electrons. (see Fig. 4d). So, compared to the accumulation region, Cit is expected to increase at the circuit level.

Moreover, if the device was located in the inversion region, most donor-like traps, and even some acceptor-like traps, are positioned below EF, which is likely to result in negative charge dominating at the interface. (see Fig. 4e) In other words, it is suggested that Cit is connected in parallel with Cdep, thereby increasing the overall capacitance.

The interface charge density Qit can be expressed as the integral over the band gap energy of the trap-state density \(D(E_{it})\) multiplied by the trap occupation probability \(f(E_{it})\)39,40 as

$$Q_{{it}} = - q\int_{{E_{V} }}^{{E_{C} }} D \left( {E_{{it}} } \right) \times f\left( {E_{{it}} } \right)dE,\quad f\left( {E_{{it}} } \right) = \frac{1}{{1 + g \cdot \exp \left[ {\frac{{E_{{it}} - E_{F} }}{{kT}}} \right]}},$$
(6)

where \(E_{it}\) denotes the energy level of trap state and g denotes degeneracy factor.

Therefore, as the temperature increases, f (Eit) increases exponentially, which in turn causes Qit to increase (see Fig. S5).

However, we should also consider the capture and emission rates of both electrons and holes in the interface traps, which can be described by the Shockley-Read-Hall (SRH) model. Based on the SRH model, the capture and emission of electrons (\(R_{cn}\) and \(R_{en}\)) and holes (\(R_{cp}\) and \(R_{ep}\)) are expressed as

$$R_{{cn}} = C_{n} \left[ {N_{{it}} \left( {1 - f\left( {E_{{it}} } \right)} \right)} \right] \times n,\;R_{{en}} = n^{\prime } C_{n} N_{{it}} f\left( {E_{{it}} } \right),\;C_{n} = v_{{th,n}} \sigma _{n} ,\;n^{\prime } = N_{c} \exp \left[ { - \frac{{E_{C} - E_{{it}} }}{{kT}}} \right]$$
(7)
$$R_{{cp}} = C_{p} \left[ {N_{{it}} f\left( {E_{{it}} } \right)} \right] \times p,\;R_{{ep}} = p^{\prime }C_{p} \left[ {N_{{it}} \left( {1 - f\left( {E_{{it}} } \right)} \right)} \right],\;C_{p} = v_{{th,p}} \sigma _{p} ,\;p^{\prime } = N_{v} \exp \left[ { - \frac{{E_{{it}} - E_{v} }}{{kT}}} \right],$$
(8)

where \(V_{th,n}\) and \(V_{th,p}\) denote thermal velocities of electrons and holes, \(\sigma _{n}\) and \(\sigma _{p}\) denotes capture cross-sections of electrons and holes, \(n^{\prime }\) and \(p^{\prime }\) denote effective electron and hole concentrations, respectively, and \(N_{it}\) denotes interface trap density.

Under ideal conditions, since the net electron capture rate (\(R_{n}=R_{cn}-R_{en}\)) is equal to the net hole capture rate (\(R_{p}=R_{cp}-R_{ep}\)) , \(f(E_{it})\) can be expressed as shown in Eq. (9).

$$\begin{aligned} f(E_{it})=\frac{C_{p} p^{\prime }+C_{n}n}{C_{n}(n+ n^{\prime } )+C_{p}(p+ p^{\prime })} \end{aligned}$$
(9)

However, we consider the temperature increases, \(R_{cn}\) and \(R_{en}\) increase exponentially due to factors \(n^{\prime }\) and \(p^{\prime }\). In this case, because the Si is boron heavy-doped, the hole concentration is overwhelmingly high, indicating that the hole emission rate becomes very large at elevated temperatures. Consequently, \(f(E_{it})\) can be reformulated as

$$\begin{aligned} f_{high}(E_{it})=\frac{C_{p} p^{\prime }}{C_{p}(p+ p^{\prime })}\cong 1 \end{aligned}$$
(10)

,which shows that it converges to 1 with increasing temperature. Thus, it is suggested that as the device temperature increases, donor-like traps will tend to emit holes, while acceptor-like traps will tend to capture electrons. Therefore, in the accumulation region, Cit increases itself (see Fig. 4f) and in the depletion and inversion regions, where Cit and Cdep are connected in parallel, the entire capacitance of the device is expected to increase (see Fig. 4g and h). COMSOL simulation was performed to examine how the temperature of the SiOx/Si interface changes upon voltage application. Following the application of 100 ms set and reset pulses in both LRS and HRS, cross-sectional slices were extracted along the directions indicated by cut plane 1 and cut plane 2 (see Fig. 5c). As shown in Fig. 5a, significant Joule heating is observed in the LRS due to the CF, whereas Joule heating is rarely observed in the HRS.

For more details, Fig. 5b illustrates the overall temperature distribution at the SiOx/Si interface only for each resistance state, with the CF-induced temperature variation highlighted in black for easier comparison. In the LRS, the heat transfer resulting from the CF’s Joule heating leads to an overall device temperature increase of approximately over 30 °C on average. In contrast, in the HRS, there is no significant heat transfer, and the temperature remains nearly unchanged from room temperature. In summary, in the LRS under a 1.6 V bias, the increase in interface temperature results in a parallel combination of Cit and Cdep. Conversely, in the HRS, even with a -1.4 V bias, the temperature did not change much, leading to no significant change in Cit. Thus, the equivalent circuit can be depicted as shown in Fig 5d, when a read voltage is applied in each state. These findings are consistent with our experimental measurements, in which LRS coexists with the HCS and HRS coexists with LCS.

Fig. 6
figure 6

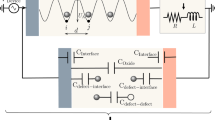
(a) Illustration of O2- ion concentrations change in ORL with resistance state changes. (b) Simulated capacitance values over a 1 ms period (1kHz) for both HRS and LRS states reveal that the LRS exhibits higher capacitance than the HRS. Inset graph shows the capacitance ratio between HRS and LRS. (c) The average capacitance changes with each resistance state including pristine state. (d) Final equivalent circuit model considering both hypothesis 1 and hypothesis 2, when read voltage is applied.

Full size image

Interestingly, as shown in Fig. 2f, once a trap captures an electron, it continues over an extended period, even after the device temperature has returned to room temperature. Thus, when a negative voltage is applied to switch from LRS to HRS, the reversed electric field is likely to cause the trapped electrons to be emitted, thereby reducing the overall capacitance. (This phenomenon can be explained by the Poole-Frenkel effect). Moreover, since the device in the HRS is in the accumulation region, the absence of Cdep also contributes to the decrease in overall capacitance.

The second hypothesis concerns the variation in capacitance resulting from changes in O2- ions within the ORL. During the set/reset cycle, O2- ions are generated in the switching layer, temporarily stored in the ORL, and then recombine with oxygen vacancies that form the CF. This process can subsequently affect the resistance change in ORL. As shown in Fig. 6a, due to O2- ions, excessive ion concentration in ORL (as observed in the LRS) results in a significant reduction in resistance. Conversely, if O2- ions are removed from the ORL, the resistance increases again.

Accordingly, we utilized the current module in COMSOL to calculate the device current and capacitance by varying the electrical conductivity of Al2O3, which serves as the ORL. Simulations were conducted by applying a sinusoidal voltage with a 0.5 V amplitude at a frequency of 1 kHz for 1 ms, consistent with the measurement. Since the Al2O3, HfO2, and SiOx that composite insulator layer exhibit both resistive and capacitive characteristics, the device can be represented by an equivalent circuit in which each layer is modeled as a resistor and a capacitor connected in parallel. Also, when a sinusoidal voltage \(V_{sin}\) is applied, the total current of device, which is the sum of the resistive current(\(I_{resistive}\)) and the capacitive current(\(I_{capacitive}\)), can be expressed in terms of current component :

$$\begin{aligned} & I_{{total}} + = I_{{resistive}} + i_{{capacitive}} = \frac{{0.5}}{R} \cdot \sin (2\pi ft) + 0.5 \cdot C \cdot 2\pi f \cdot \cos (2\pi ft), \\ & {\text{where}}\;\;f = 1\;kHz \\ \end{aligned}$$
(11)

The \(I_{resistive}\) is in phase with the voltage, while the displacement current has a 90-degree phase difference, forming a cosine waveform. Therefore, at each half-cycle of the 1 kHz frequency signal, such as at t = 0 ms, 0.5 ms, 1 ms, etc., the \(I_{resistive}\) cancels out, allowing us to obtain a pure \(I_{capacitive}\) component. Using this, the capacitance of the stack structure can be quantitatively derived using well-known capacitance equation: \(i(t) = C \times dV(t)/dt\).

As a result of the simulations, in the pristine state, the capacitance was approximately 0.15 fF, which demonstrates a similar trend to the analytical calculation result 4.9 fF. Subsequently, in the LRS, the capacitance was found to be on average 0.85 nF during 1 ms, whereas in the HRS, it decreased to approximately 0.18 nF, indicating changes in dielectric properties corresponding to the state transition. (see Fig. 6b and c) In other words, the injection of O2- ions throughout the ORL layer can be considered as evidence that CAl2O3 becomes shorted.

Finally, we present the equivalent circuit model reflecting our hypotheses 1 and 2 in Fig. 6d. In the LRS, the increased O2- concentration in the Al2O3 layer reduces its resistance, thereby making the CAl2O3 negligible. Furthermore, due to the elevated temperature at the SiOx/Si interface, the trapped electrons cause Cit to connect in parallel with Cdep, leading to the coexistence of the HCS state. In contrast, in the HRS, the reduced O2- concentration in the Al2O3 layer results in a non-negligible CAl2O3, and with no significant temperature change at the SiOx/Si interface, Cit remains connected in series, leading to the coexistence of the LCS state.

Conclusion

In this study, we investigated the resistive and capacitive switching characteristics of Al/Al2O3/HfO2/SiOx/p+-Si device. The material composition and thickness of each layer in the device were confirmed through TEM and EDS analyses, while the I–V characteristics demonstrated bipolar resistive switching. Furthermore, by applying continuous pulses, the coexistence of resistance and capacitance switching was observed, with LRS and HCS, as well as HRS and LCS, coexisting. To understand the switching mechanism, we conducted two different simulations using COMSOL Multiphysics.

In the first simulation, the temperature change of SiOx/Si interfaces due to Joule heating was analyzed. In the LRS, when a pulse voltage was applied, the temperature at the core of the CF increased to over 1000 °C, while heat transfer caused the SiOx/Si interface temperature to rise approximately 45 °C. In contrast, in the HRS, even when a pulse voltage was applied, the CF core temperature remained around 200 °C and the interface temperature did not exceed about 25 °C. This indicates that only in the LRS does the increase in interface temperature lead to an elevated Cit, thereby increasing the overall device capacitance.

In the second simulation, the capacitance was measured by varying the ORL O2- ion concentration at LRS and HRS. Since the insulator contains both resistive and capacitive components, the pure capacitive current was obtained by subtracting the resistive current from the total current induced by a sinusoidal voltage. The results showed that the capacitance was approximately 0.18 nF in the HRS state, but increased to around 0.85 nF in the LRS state, yielding a ratio of approximately 4.6. This is because, in the LRS, the increased O2- ion concentration in the ORL enhances its conductivity, shorting its effective capacitance and thus increasing the overall capacitance.

In summary, both simulations agree with our experimental results, supporting the coexistence of LRS with HCS and HRS with LCS. Moreover, the presence of the ORL and the SiOx/Si interface in the RRAM device is considered essential for the coexistence of resistive and capacitive memory effects, suggesting that their utilization could lead to innovative technologies capable of meeting future demands for ultra-high-density memory.