A PSO weighted ensemble framework with SMOTE balancing for student dropout prediction in smart education systems

Abstract

Student dropout is a critical issue that affects not only educational institutions but also students’ mental well-being, career prospects, and long-term quality of life. The ability to predict dropout rates accurately enables timely interventions that can support students’ academic success and psychological resilience. However, the imbalanced nature of student dropout datasets often results in biased and less effective predictive models. To address this, we propose a Particle Swarm Optimization (PSO)-Weighted Ensemble Framework integrated with the Synthetic Minority Oversampling Technique (SMOTE). This methodology balances the dataset using SMOTE, optimizes model hyperparameters, and fine-tunes ensemble weights through PSO to improve predictive performance. The framework achieves 86% accuracy, an AUC score of 0.9593, and enhanced dropout class metrics, including an F1-Score of 0.8633, precision of 0.8633, and recall of 0.86. Compared to Ant Colony Optimization (ACO) and Firefly algorithms, which achieve accuracies of 83% and 85% respectively, our approach demonstrates up to a 3% improvement in key performance metrics. Additionally, in comparison to individual baseline models used in ensemble model Random Forest (RF) with SMOTE (83.5% accuracy, 0.95 AUC) and XGBoost (XGB) with SMOTE (82.7% accuracy, 0.95 AUC), the proposed framework significantly enhances predictive reliability. Furthermore, PSO offers computational efficiency advantages over Firefly and Ant Colony Optimization, reducing hyperparameter tuning time while improving ensemble performance. The proposed framework is scalable and adaptable for real-world applications, particularly in educational institutions, where it can aid in early intervention strategies to mitigate dropout rates.

Introduction

Student dropout is a significant issue in educational systems. It is impacting both traditional classroom settings and online learning environments. Dropouts are students who leave their studies before completing their degree or advancing to the next academic level, often due to factors such as personal issues, dissatisfaction with the education system, or logistical challenges¹. Mostly, developing countries are facing this problem. School dropout rates show a critical societal challenge². The United Nations has established a Sustainable Development Goal (SDG) to improve the quality of education. Improving student retention is a key aspect of meeting these objectives by 2030. In India, significant strides have been made to increase enrollment rates. It has a Gross Enrollment Ratio (GER) of 97% at the elementary level and 80% at the secondary level. However, continued low retention rates and poor learning outcomes undermine these advancements³. The 2020 National Education Policy aims to achieve a 100% GER at the school level by 2030. The country also faces dropout rates that remain a significant challenge. As a result, ensuring that students remain enrolled through graduation has become a central focus of policy. Artificial Intelligence (AI) techniques have a major role in solving these issues. It provides valuable insights that facilitate data-driven decision-making in the education system⁴.

Machine learning (ML) has shown considerable efficacy in predicting dropout rates among higher education students. Employing machine learning approaches, such as predictive modeling, allows educators to pinpoint areas for student growth and offer learning metrics during the course of education¹⁵. Optimization with machine learning methods has improved efficiency not only for education but also for other domains^31,32

The application of these methods can facilitate the creation of early warning systems, detect students at risk of withdrawing early, and provide essential support¹⁶. A significant difficulty exists in the imbalanced composition of dropout datasets, where the gap in dropout rates between conventional classrooms and online platforms biases predictions towards the majority class. This disparity limits the ability of machine learning algorithms to effectively identify students at risk of attrition⁵.

Expanding on these challenges, existing dropout prediction models often fail to adequately address class imbalance, leading to poor recall for minority classes. Traditional models rely on simple statistical approaches or rule-based systems, which lack the adaptability and generalization capabilities of machine learning³⁴. Addressing these shortcomings requires a robust method that can handle data imbalance while optimizing model performance. We have proposed SMOTE-based machine learning classifiers using PSO-optimized algorithms to address this issue. The classifiers use SMOTE to make fake samples for the minority group. This fixes the problem of uneven data in the preprocessing phase. PSO has been chosen over other optimization techniques such as GA, ACO, and the Firefly Algorithm because of its ability to efficiently explore the search space while maintaining computational efficiency. Unlike GA, which relies on crossover and mutation, PSO leverages swarm intelligence to converge faster to optimal solutions. Furthermore, compared to ACO and the Firefly Algorithm, PSO requires fewer hyperparameter adjustments and has demonstrated higher stability in ensemble weight optimization. Hyperparameter tuning methods have been performed to improve prediction accuracy. These methods are the PSO, ACO, and Firefly algorithms. These optimization methods also determine the weights for the ensemble methods.The proposed approach differentiates itself from traditional dropout prediction models by integrating SMOTE-based balancing techniques with PSO-driven hyperparameter tuning. This dual approach improves model fairness and improves the accuracy of the prediction for minority classes, addressing a major limitation of previous studies. Using these methods, the proposed model accurately improves the prediction of dropouts.

The highlights of the proposed work are as follows.

• 1. An in-depth background study has been performed to find limitations in existing models. These limitations have helped to find motivation for the research work.

• 2. A novel PSO-weighted ensemble framework with SMOTE is proposed. It includes a RF and XGB classifier for prediction and PSO to optimize hyperparameters and ensemble weights.The proposed strategy is unique in integrating data balance, model improvement, and ensemble techniques to improve prediction performance.

• 3. The proposed method was compared with ACO and Firefly, demonstrating its superior performance in handling imbalanced datasets.

• 4. Interpreting the model using SHAP (XAI), emphasizing key attributes’ impact on predictions, and revealing the framework’s decision-making process.

• 5. The proposed framework achieves an improvement of up to 3% in critical metrics compared to the baseline methods.

The remaining sections are organized as follows: In the ’Related Work’ section of this paper, the review of the literature is discussed. ’Methods and Materials’ covers the methodology, including the data set used, the ML models used, the Ensemble Approach, the data balancing techniques used, and the optimizations (PSO, ACO, Firefly) used to both hyper-tune the baseline ML classifier and find the optimal weights for the ensemble approach. The proposed System Architecture discusses the proposed methodology. The experimental setup discusses the platform and evaluation metrics used to conduct and evaluate experiments. The Results and Discussion Section discusses the experiment results and its effects. The last section is the Conclusion.

Related Work

An important emphasis of educational data mining is student dropout prediction (SDP). Its main goal is to identify kids at risk of dropping out to provide early interventions. This review of the literature examines SDP from many perspectives using research findings. S1⁶ solved the SDP dataset class imbalance problems with Optimized SMOTE and machine learning classifiers. The approach was 0.99 accurate. NNs outperformed other classifiers with accuracy 0.68, recall 1.00, F1 0.91, and AUC-ROC 0.98. The approach focuses on reducing the imbalance in the data set to increase predicted accuracy.

The data set from Czech Technical University was analyzed by S2⁷using a support vector machine (SVM) with a Radial Basis Function (RBF) kernel. Their model obtained an F1 score of 0.90 ± 0.09, a recall of 0.64 ± 0.09, a precision of 0.69 ± 0.08, and an accuracy of 0.77 ± 0.05. The difficulty in consistently using SVM-RBF in some datasets is highlighted by the inconsistency of these findings. S3⁸leveraged DeepFM, a deep factorization machine model, in the HarvardX Person-Course Academic Year 2013 Deidentified Dataset. The methodology demonstrated excellent performance with an accuracy of 99%, precision of 0.98, recall of 0.99, F1 score of 0.98, and AUC-ROC score of 0.92. These results illustrate the effectiveness of DeepFM in capturing both linear and nonlinear relationships in educational datasets. S4⁹used SMOTE in combination with Random Forest (RF) and SVM to predict dropout of students. Data was collected from both internal and external sources. The model achieved an accuracy of 0.741 ± 0.005 and an F1 score of 0.84 ± 0.02. The results emphasize the utility of ensemble methods such as RF in improving dropout prediction when combined with SMOTE. S5¹⁰developed a multi-feature fusion approach to improve dropout prediction. They performed a prediction on the KDD CUP 2015 dataset.They had 0.8885 accuracy, 0.899 precision, 0.9627 recall, and 0.9311 F1 score. S6¹¹ compared linear regression (LR), decision tree (DT), random forest (RF), support vector machine (SVM), deep neural network (DNN) and lightGBM. The investigation included 20,050 student records from 2013 to 2022. LightGBM offers 0.955 accuracy, 0.867 precision, 0.814 recall, and 0.840 F1 score.

S7¹²applied several algorithms, such as Logistic Regression, Decision Tree, Random Forest, LightGBM, Support Vector Machines, and XGBoost, on a school dataset Random Forest performed best, with 0.94 accuracy, 0.9523 precision, 0.9393 recall, 0.9703 F1 score, and 0.895 AUC-ROC. Ensemble approaches have a great predicted accuracy, as shown in these data.S8¹³utilized AutoML in conjunction with hyperparameter optimization methods, including grid search and randomized search, on a dataset comprising 385,634 records, which was subsequently preprocessed to yield 168,162 samples. RF and grid search optimization achieved 0.99 accuracy, 0.84 precision, and 0.98 F1 score. S9¹⁴conducted an exploration of multiple deep learning methodologies, encompassing CNN, LSTM, and hybrid models such as Bagging CNN-LSTM³³ and Bagging LSTM-LSTM, utilizing the KDD CUP 2015 dataset. The Bagging LSTM-LSTM model outperformed others with an accuracy of 0.91896, precision of 0.919, recall of 0.9899, and F1 score of 0.98. The review highlights several research gaps in student dropout prediction (SDP), including limited use of cohesive ensemble frameworks, inadequate integration of data balancing techniques such as SMOTE with model optimization, reliance on traditional hyperparameter tuning methods instead of advanced techniques such as Particle Swarm Optimization (PSO), and the absence of holistic strategies combining data preprocessing, model improvement, and ensemble learning. To address these gaps, this study proposes a novel PSO-weighted ensemble framework with SMOTE, which integrates RF and XGB classifiers for prediction while leveraging PSO to optimize hyperparameters and ensemble weights. This unique approach effectively combines data balancing, model enhancement, and ensemble techniques to deliver improved prediction performance, offering a significant advancement in SDP methodologies. This study highlights the potential of ensemble deep learning models to tackle complex educational datasets. Table 1 presents a brief description of SDP.

Table 1 Comparison of Methodologies and Results from Various Studies.

Methods and materials

This section outlines the methods used to create models to predict student dropout using machine learning classifiers. Machine learning classifiers are used on diverse student data, encompassing demographic information, academic achievement, and behavioral data, to create models that can precisely forecast student dropout rates. According to studies, the efficacy of machine learning classifiers in predicting student dropouts differs depending on the particular data and the problem being addressed. In this study, three different data balancing approaches(SMOTE¹⁷, ADASYN¹⁸, RU¹⁹) are compared to address the problem of data imbalance. After evaluating each data balancing approach using five baseline ML Classifiers, Best Data Balancing approach is chosen with top performing baseline ML classifiers, which are then further combined using proposed optimized weighted ensemble approach. In this paper, three different optimization techniques are used for comparison, that is, PSO²⁰, ACO²¹, and Firefly²² optimization. Figure 1 and Algorithm 1 represent the SDP workflow diagram, which includes data pre-processing, hyperparameter selection, and comparison of the results of optimized SMOTE-based ML classifiers. The data preparation steps, different optimized ML classifiers, and the architecture of the proposed optimized neural network classifier are described in the following subsections.

Fig. 1

Student Dropout Prediction Workflow.

Algorithm 1

Student Dropout Prediction Workflow Steps

Dataset

In our study, we used the publicly available dataset titled Predict Student Dropout and Academic Success from the UCI Machine Learning Repository²³. This dataset provides a comprehensive view of academic performance, including features such as demographics, academic records, and socioeconomic indicators, which are crucial in understanding student outcomes. The dataset is highly imbalanced as shown in Figure 4 with total of 4424 rows out of which 2209 are labeled as ’Graduate’, 1421 as ’Dropout’ and 794 as ’Enrolled’. There are a total of 36 features in the dataset including demographics features such as ’Gender’, ’ Nationality’, Economical Features such as ’GDP’, ’Inflation Rate’ and more with Target feature(Graduate, Enrolled, Dropout). Data Preparation is a very important step before using Machine Learning Classifiers and in this paper we have performed data collection, cleaning, transformation, splitting, and balancing. To handle class imbalances within the data, we evaluated multiple balancing techniques, including SMOTE, ADASYN, and Random Under-sampling (RU). Subsequently, advanced machine learning algorithms were applied and their performance was optimized using ensemble methods and meta-heuristic optimization techniques.

Data balancing techniques

Data balancing is essential for effective Student Dropout Prediction due to the significant class imbalance in the dataset, as mentioned in the above section. This imbalance challenges machine learning algorithms, leading to biases towards the majority class and misclassifying the class with fewer instances. We have chosen SMOTE, ADASYN, and random subsampling (RU) because they offer distinct advantages in addressing class imbalance in our data set. SMOTE generates synthetic samples by interpolating between minority class instances, enhancing diversity, and improving classifier performance by expanding the minority class without duplication. ADASYN further refines this by focusing on harder-to-classify examples, adapting the sampling density to improve class separation and overall model accuracy, especially in complex decision boundaries. However, RU simplifies the dataset by randomly removing instances from the majority class, helping to balance the data and reduce computational load, which is particularly beneficial when working with large datasets. These techniques, with their complementary strengths, were selected to improve model performance, ensure efficient training, and mitigate the impact of class imbalance.

Synthetic Minority Oversampling Technique (SMOTE)

SMOTE is a commonly utilized method for mitigating class imbalance by creating synthetic samples for the minority class.Let $X = \{x_1, x_2, \ldots , x_n\}$ represent the set of minority class instances in the feature space, where $x_i \in \mathbb {R}^d$. The method creates new synthetic samples $x_{\text {new}}$ through interpolation between a selected sample from the minority class $x_i$ and one of its closest neighbors $k$ $x_j$ (commonly $k = 5$). The synthetic instance is calculated as:

$$\begin{aligned} x_{\text {new}} = x_i + \lambda \left( x_j - x_i \right) \end{aligned}$$

(1)

Here, $\lambda$ is a random value in the range $[0, 1]$. By systematically applying this process, SMOTE generates additional synthetic samples until the desired balance is achieved, thereby enhancing the representation of the minority class in the dataset.

ADASYN

Adaptive Synthetic (ADASYN) sampling is an advanced oversampling technique that builds upon SMOTE by adaptively focusing on minority class instances that are harder to classify. Given a data set where $X = \{x_1, x_2, \ldots , x_n\}$ represents the samples of the minority class and $Y = \{y_1, y_2, \ldots , y_m\}$ represents the samples of the majority class in a feature space $\mathbb {R}^d$, ADASYN generates synthetic samples as follows:

• 1. Density Ratio Calculation: For each minority class sample $x_i$, compute the density ratio $r_i$ based on the number of majority class samples $\Delta _i$ among its $K$-nearest neighbors:

  $$\begin{aligned} r_i = \frac{\Delta _i}{K \cdot n}, \end{aligned}$$

  (2)

  where $n$ is the total number of minority class samples, and $K$ is the neighborhood size.

• 2. Adaptive Sample Generation: Determine the total number of synthetic samples $g_i$ for each minority instance $x_i$:

  $$\begin{aligned} g_i = \frac{G \cdot r_i}{\sum _{i=1}^n r_i}, \end{aligned}$$

  (3)

  where $G$ is the total desired number of synthetic samples. Instances with higher $r_i$ values (more difficult to classify) receive more synthetic data.

• 3. Synthetic Sample Creation: Generate synthetic samples $x_{\text {new}}$ for each $x_i$ using linear interpolation. Select a minority neighbor $x_j$ from the $K$-nearest neighbors of $x_i$, and compute:

  $$\begin{aligned} x_{\text {new}} = x_i + \lambda (x_j - x_i), \end{aligned}$$

  (4)

  where $\lambda \in [0, 1]$ is a randomly generated value.

By focusing on difficult-to-classify samples, ADASYN adjusts the decision boundary of the classifier to better accommodate complex regions of the minority class, improving model performance on imbalanced datasets.

Random Under-Sampling(RU)

Random Undersampling (RU) is an efficient technique for handling class imbalance, particularly effective in scenarios such as student dropout prediction where the number of dropout classes is significantly lower than those of graduate students.

Let the original dataset $D$ be defined as:

$$\begin{aligned} D = \{(x_1, y_1), (x_2, y_2), \dots , (x_n, y_n)\} \end{aligned}$$

(5)

where $x_i$ represents the feature vector, and $y_i \in \{0, 1\}$ indicates the class label

Given:

• $N_0$: the number of majority class instances

• $N_1$: the number of minority class instances, where $N_0 \gg N_1$.

RU aims to balance the dataset by randomly selecting a subset of the majority class to match the size of the minority class $N_1$. The resulting balanced dataset $D' \subset D$ is given by:

$$\begin{aligned} D' = \left\{ (x, y) \in D \mid y = 1 \right\} \cup R \left( \left\{ (x, y) \in D \mid y = 0 \right\} , N_1 \right) , \end{aligned}$$

(6)

where $R(\cdot , N_1)$ represents the random selection of $N_1$ majority class samples.

This method effectively reduces the imbalance by undersampling the majority class, ensuring that both classes have equal representation in the training data.

Machine learning classifiers

Logistic regression

Logistic regression (LR)²⁴ is a machine learning technique used for binary classification tasks. Estimates the probability of an outcome using a logistic function, thus constraining the output to the interval [0,1]. The hypothesis for LR is expressed as:

$$\begin{aligned} h_\theta (x) = \frac{1}{1 + e^{-\theta ^T x}} \end{aligned}$$

(7)

where $h_\theta (x)$ denotes the predicted probability, $\theta$ denotes the parameter vector, and $x$ is the input feature vector. The model training involves minimizing the log-loss function, which quantifies the disparity between predicted values and true labels, thus ensuring effective classification outcomes.

Random forest

Random Forest (RF)²⁵ is a group learning technique that is predominantly applied to classification and regression problems. It operates by constructing numerous decision trees during the training phase and then derives the class label using a majority vote, or it averages the predictions for regression tasks. The prediction made by the Random Forest classifier is mathematically given by

$$\begin{aligned} \hat{y} = \text {majority\_vote}\left( T_1(x), T_2(x), \dots , T_n(x) \right) \end{aligned}$$

(8)

where $T_i(x)$ denotes the prediction made by the $i$-th decision tree for the input $x$, and $n$ indicates the total count of trees. Through this aggregation of predictions, RF mitigates overfitting and enhances model generalization, making it particularly effective for managing high-dimensional and imbalanced datasets.

Decision tree

Decision Trees (DT)²⁶ represent a widely adopted machine learning approach applicable to both classification and regression problems. These models decompose the data set into smaller groups based on feature values, forming a structure that resembles a tree. The decision-making mechanism utilizes splitting criteria such as Gini Impurity or Information Gain. The formula used to compute Gini impurity is:

$$\begin{aligned} G = 1 - \sum _{i=1}^{k} p_i^2 \end{aligned}$$

(9)

Here, $p_i$ represents the fraction of instances in class $i$, and $k$ indicates the number of classes. To predict an output $y$ for a given input $x$, the tree follows a path from the root node down to a leaf node determined by specific feature conditions. Decision trees are known for their interpretability and competence with datasets that exhibit non-linear decision boundaries.

K Nearest Neighbor

The K-Nearest Neighbors (KNN) algorithm²⁷ is a straightforward and intuitive supervised learning technique designed for classification and regression applications. It works by locating the $k$ closest data points to a specific query point in the feature space, using a selected distance metric, such as the Euclidean distance. The Euclidean distance $d$ between two points $\mathbf {x_1} = (x_{11}, x_{12}, \ldots , x_{1n})$ and $\mathbf {x_2} = (x_{21}, x_{22}, \ldots , x_{2n})$ is determined by the equation:

$$\begin{aligned} d(\mathbf {x_1}, \mathbf {x_2}) = \sqrt{\sum _{i=1}^{n} (x_{1i} - x_{2i})^2} \end{aligned}$$

(10)

In classification scenarios, KNN associates the query point with the class that appears most often among its $k$-nearest neighbors. In regression cases, the result is usually the average or median of the values of neighbors. As a non-parametric algorithm, KNN does not involve a separate training phase, making it easy to implement, although it can be computationally demanding when applied to large datasets.

Extreme gradient boosting

Extreme Gradient Boosting (XGBoost)²⁸ represents a sophisticated form of gradient boost that is optimized for rapid performance and efficiency in both classification and regression applications. This technique aggregates predictions from an ensemble of weak learners, commonly decision trees, by minimizing a differentiable loss function through gradient descent. The model is developed iteratively, with each subsequent tree addressing the errors of its predecessors. The objective function of XGBoost is given as:

$$\begin{aligned} \mathcal {L}(\Theta ) = \sum _{i=1}^{n} l(y_i, \hat{y}_i) + \sum _{k=1}^{K} \Omega (f_k) \end{aligned}$$

(11)

where:

• $l(y_i, \hat{y}_i)$ is the loss function that measures the difference between the actual value $y_i$ and the predicted value $\hat{y}_i$.

• $\Omega (f_k)$ is the regularization term to penalize the complexity of the $k$-th tree $f_k$, expressed as:

  $$\begin{aligned} \Omega (f_k) = \gamma T + \frac{1}{2} \lambda \Vert w\Vert ^2 \end{aligned}$$

  (12)

  where $T$ is the number of leaves in the tree, $\gamma$ is the penalty for adding a leaf, $\lambda$ controls the regularization of the weights of the $L_2$ leaves $w$.

XGBoost employs the second-order Taylor expansion to approximate the loss function, improving optimization efficiency. Its ability to handle missing data, regularization, and parallel processing makes it highly effective for structured data tasks.

Weighted classifier ensemble

The Classifier Ensemble (CE)technique²⁹ improves classification accuracy by combining predictions from multiple base models. In a CE framework, the input dataset is processed through n classifiers, each trained on the complete feature space. The output of these classifiers is then passed to a combination scheme which consolidates individual predictions into a final decision. In this paper, we adopted a weighted ensemble approach as shown in Figure 2 to enhance predictive performance by combining the output of multiple base models.

Fig. 2

Flowchart of Weighted Ensemble Method.

In this approach, the final prediction is calculated as a weighted sum of the predictions from individual models. Let $P_i$ denote the prediction probability of the i -th model, and $w_i$ represent its corresponding weight. The final ensemble prediction, $P_{\text {Ensemble}}$, is formulated as:

$$\begin{aligned} P_{\text {Ensemble}} = \sum _{i=1}^{n} w_i \cdot P_i, \end{aligned}$$

(13)

where n is the number of base models, and the weights satisfy $\sum _{i=1}^{n} w_i = 1$. These weights are optimized using advanced optimization techniques, such as particle swarm optimization (PSO), ant colony optimization (ACO), and the firefly algorithm, to maximize prediction accuracy. This method leverages the strengths of individual models while mitigating their weaknesses, resulting in a robust and reliable ensemble prediction framework.

XAI-SHAP

SHAP (SHapley Additive Explanations)³⁰ serves as a comprehensive framework to elucidate the predictions of machine learning models. It applies principles from cooperative game theory to equitably allocate the influence of each feature on a model’s outcome. By calculating the marginal contribution of each feature to the model’s prediction, SHAP values quantify the influence exerted by each feature. The SHAP value for a feature $i$ is given by:

$$\begin{aligned} \phi _i = \sum _{S \subseteq N \setminus \{i\}} \frac{|S|! \, (|N| - |S| - 1)!}{|N|!} \, \left[ f(S \cup \{i\}) - f(S)\right] \end{aligned}$$

(14)

where:

• $N$ is the set of all the features.

• $S$ is a subset of $N$ that does not include the features$i$.

• $|S|$ is the size of the subset $S$.

• $f(S)$ is the prediction of the model using only the features in $S$.

• $f(S \cup \{i\}) - f(S)$ represents the marginal contribution of the feature $i$ to the model’s output.

SHAP has the following key properties:

• Efficiency: The sum of the SHAP values is equal to the difference between the model prediction and the baseline.

• Symmetry: If two features contribute equally, their SHAP values are identical.

• Additivity: SHAP values provide a consistent explanation when combining features.

In practice, SHAP values are computed using approximation methods, such as TreeSHAP for tree-based models, which ensures computational efficiency. SHAP is widely used in Explainable AI (XAI) to provide insight into feature importance, visualize local explanations for individual predictions, and understand the behavior of global models.

Optimization techniques

Particle Swarm Optimization(PSO)

Particle Swarm Optimization (PSO) is an optimization algorithm that draws inspiration from the collective behavior seen in flocks of birds and fish schools. Within PSO, a group of particles serves as candidates to solve the optimization task. Each particle modifies its current position and velocity considering both its own best known position ($p_i$) and the best placed particle currently in the swarm ($g$). The velocity and position are updated according to the following rules:

$$\begin{aligned} v_{i}(t+1) = w \cdot v_{i}(t) + c_1 \cdot r_1 \cdot (p_{i} - x_{i}(t)) + c_2 \cdot r_2 \cdot (g - x_{i}(t)), \end{aligned}$$

(15)

$$\begin{aligned} x_{i}(t+1) = x_{i}(t) + v_{i}(t+1), \end{aligned}$$

(16)

where $v_i$ and $x_i$ denote the velocity and position of the particle $i$, $w$ is the inertia weight, $c_1$ and $c_2$ are acceleration coefficients, $r_1$ and $r_2$ are random numbers uniformly distributed in $[0, 1]$, and $t$ represents the iteration number. The goal of PSO is to iteratively converge to the optimal solution by exploring the search space through particle movement.

Ant Colony Optimization(ACO)

Ant Colony Optimization (ACO) is an algorithm inspired by nature, specifically designed to mimic ant foraging behavior. In the ACO framework, artificial ants iteratively build solutions by navigating the problem’s search space, making use of pheromone trails and heuristic knowledge. The likelihood of an ant $k$ transitioning from node $i$ to node $j$ is determined by:

$$\begin{aligned} P_{ij}^{k} = {\left\{ \begin{array}{ll} \frac{[\tau _{ij}]^\alpha [\eta _{ij}]^\beta }{\sum _{l \in \mathcal {N}_{i}^{k}} [\tau _{il}]^\alpha [\eta _{il}]^\beta }, & \text {if } j \in \mathcal {N}_{i}^{k}, \\ 0, & \text {otherwise}, \end{array}\right. } \end{aligned}$$

(17)

where $\tau _{ij}$ is the value of the pheromone on the edge $(i, j)$, $\eta _{ij}$ is the heuristic information (e.g. the inverse of the distance), $\alpha$ and $\beta$ are parameters that control the influence of the pheromone and the heuristic information, and $\mathcal {N}_{i}^{k}$ is the set of nodes that the ant has yet to visit $k$.

After all ants complete their solutions, the pheromone trails are updated as follows.

$$\begin{aligned} \tau _{ij} = (1 - \rho ) \cdot \tau _{ij} + \sum _{k=1}^{m} \Delta \tau _{ij}^{k}, \end{aligned}$$

(18)

where $\rho \in [0, 1]$ is the rate of evaporation, $m$ is the number of ants, and $\Delta \tau _{ij}^{k}$ is the pheromone deposited by the ant $k$, defined as:

$$\begin{aligned} \Delta \tau _{ij}^{k} = {\left\{ \begin{array}{ll} \frac{Q}{L^k}, & \text {if ant } k \text { uses edge } (i, j), \\ 0, & \text {otherwise}, \end{array}\right. } \end{aligned}$$

(19)

where $Q$ is a constant and $L^k$ is the length of the solution constructed by ant $k$. ACO iteratively updates the pheromone trails to guide the ants toward better solutions, enabling convergence to an optimal or near-optimal solution.

Firefly optimization

The Firefly Algorithm (FA) is a nature-inspired metaheuristic approach modeled after the luminescent behavior of fireflies. This algorithm employs the principle of attractiveness, which is directly related to the intensity of a firefly’s glow. The brightness $I$ of a firefly located at position $x_i$ is calculated by the objective function $f(x_i)$:

$$\begin{aligned} I_i \propto f(x_i), \end{aligned}$$

(20)

where brighter fireflies attract other fireflies. The movement of a firefly $i$ toward a brighter firefly $j$ is governed by the following equation.

$$\begin{aligned} x_i = x_i + \beta \cdot e^{-\gamma r_{ij}^2} \cdot (x_j - x_i) + \alpha \cdot \epsilon , \end{aligned}$$

(21)

where:

• $x_i$ and $x_j$ are the positions of fireflies $i$ and $j$,

• $r_{ij} = \Vert x_i - x_j\Vert$ is the distance between the fireflies,

• $\beta$ is the attractiveness at $r = 0$,

• $\gamma$ is the light absorption coefficient,

• $\alpha$ is a randomization parameter, and

• $\epsilon$ is a random vector drawn from a uniform distribution.

The attractiveness $\beta$ decreases with distance and is given by:

$$\begin{aligned} \beta = \beta _0 \cdot e^{-\gamma r_{ij}^2}, \end{aligned}$$

(22)

where $\beta _0$ is the initial attractiveness. The randomization component helps fireflies escape the local optima and explore the search space.

The algorithm iteratively updates the positions of fireflies, ensuring that they converge toward the global optimum, guided by the principle that brighter (better) solutions attract less bright ones.

Proposed system architecture

The proposed system aims to predict student dropout using a dataset that includes features such as academic performance and demographics. To address the class imbalance in the dataset, various balancing techniques, including SMOTE, ADASYN, and Random Under-sampling (RU), were evaluated using five baseline ML classifiers (RF, LR, DT, XGB, and KNN). From the results, it has been found that SMOTE with RF and XGB outperform others.Then to further enhance model performance, optimization techniques such as Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and Firefly Algorithm are applied to tune both hyperparameters and the weights for ensemble of RF and XGB. The ensemble model, using optimized weights, combines the predictions of both models to improve accuracy. The performance of the system is assessed using metrics such as accuracy, precision, recall, F1 score, and AUC, with visualizations like ROC curves and confusion matrices to provide a comprehensive evaluation of the model’s predictive capabilities. This approach ensures robust dropout prediction while addressing class imbalance, making the model more reliable and accurate for educational decision-making. Figure 3 and Algorithm 2 show the complete proposed system architecture.

Algorithm 2

Proposed System: Algorithm

Fig. 3

Proposed System Architecture.

Experimental setup

An extensive experimental framework is established to assess the efficacy of the suggested methodology for predicting student dropout, aiming to tackle the issue of imbalance. An unbalanced student dropout dataset? from UCI, encompassing demographic details, academic performance, and institutional information, has been utilized for the empirical investigation. The dataset undergoes preprocessing through the encoding of categorical variables and the management of missing values. This experiment utilizes 80% of the data for training the machine learning classifiers, while the remaining 20% is allocated for testing, so assuring a rigorous evaluation. The empirical outcomes of the baseline machine learning classifiers and the enhanced SMOTE-based machine learning classifiers have been illustrated using several visualization approaches grounded on the evaluation measures employed, namely accuracy, precision, recall, F1 score, and AUC-ROC. We have implemented the experiments on Kaggle Platform with Python3, GPU Support and 30GB RAM. To evaluate the model performance, the following metrics are used, and in equations the following abbreviations are used: TP(True Positives), TN(True Negatives), FP(False Positives), FN(False Negatives).

• 1. Accuracy(ACC):

  $$\begin{aligned} \text {Accuracy} = \frac{TP + TN}{TP + TN + FP + FN} \end{aligned}$$

  (23)

• 2. Precision(P):

  $$\begin{aligned} \text {Precision} = \frac{TP}{TP + FP} \end{aligned}$$

  (24)

• 3. Recall(R):

  $$\begin{aligned} \text {Recall} = \frac{TP}{TP + FN} \end{aligned}$$

  (25)

• 4. F1 Score:

  $$\begin{aligned} \text {F1 Score} = 2 \cdot \frac{\text {P} \cdot \text {R}}{\text {P} + \text {R}} \end{aligned}$$

  (26)

• 5. ROC AUC (Receiver Operating Characteristic Area Under the Curve): This metric evaluates the ability of a binary classifier to distinguish between positive and negative classes across various threshold settings. The ROC curve plots the True Positive Rate (Sensitivity) against the False Positive Rate (1-Specificity). The AUC (Area Under the Curve) value ranges from 0 to 1, where a value closer to 1 indicates a better-performing model.

Results and discussion

Uneven class distribution affects the ability to anticipate student dropout rates in physical and online schooling. Dropout is much lower than retention in physical mode courses. Online, dropout rates are greater than non-dropout rates. ML classifiers often prefer accuracy by correctly predicting the majority class while overlooking the minority class. The next subsections examine baseline ML classifier results utilizing unbalanced and balanced data sets.

Results on imbalanced dataset

Dataset used in this study is highly imbalanced as shown in Figure 4 where it is clear that the number of dropout (class 0), enrolled (class 1) are less than Graduate (class 2). We have applied five baseline ML classifiers and the results are shown in Table 2 and the ROC comparison is shown in Figure 5. The results indicate that XGB achieves the highest overall accuracy of 76.9%, followed by RF, but the performance of all classifiers highlights the challenges posed by class imbalance, particularly for the enrolled class. In this category, all classifiers show low precision and recall values, with XGB attaining the highest F1 score of 0.471, which remains relatively low. RF and DT follow with F1 scores of 0.370 and 0.383, respectively, while LR and KNN achieve F1 scores of 0.313 and 0.305. XGB and RF are outperforming other ML classifiers with highest F1 score in both Graduate and Dropout Classes. The ROC comparison chart shows that XGB and RF are outperforming others with an AUC score of 0.88 and 0.86 respectively.

Fig. 4

Class Distribution in Original(Imbalanced Dataset): class 0 - Dropout, 1 - Enrolled, 2 - Graduate.

Fig. 5

ROC Curve of ML Classifiers on Imbalanced Dataset.

Table 2 Performance of ML Classifiers on Imbalanced Dataset.

Results on SMOTE balanced dataset

Here, we have applied the SMOTE technique to balance the dataset, and the class-wise distribution after data balancing is shown in Figure 6. The results shown in Table 3 help visualize the impact of data balancing. For the enrolled class, RF and XGB outperform others with F1 scores of 0.814 and 0.803, respectively, with both models showing high precision and recall. The mean F1 score for the enrolled class is 0.719, which shows a significant improvement compared to the results of the unbalanced dataset. For the dropout class, RF achieves the highest F1 score of 0.856 followed by XGB with 0.833. And for Graduate Class, XGB leads obtained maximum F1-Score of 0.844 followed by RF with 0.836. The overall mean F1-Score for Dropout and Graduate class is 0.7608, 0.7518 respectively, showing consistent performance across models. In general, Random Forest and XGB outperform other classifiers in all classes, with the highest accuracy and F1 scores, making them the most reliable models for this data set. Figure 7 shows the ROC comparison of all five ML classifiers on the SMOTE Balanced Dataset and shows that XGB and RF perform best with AUC values of 0.95.

Fig. 6

Class Distribution after SMOTE Data Balancing: class 0 - Dropout, 1 - Enrolled, 2 - Graduate.

Fig. 7

ROC Curve Comparison of ML Classifiers for SMOTE Balanced Dataset.

Table 3 Performance of ML Classifiers on SMOTE Balanced Dataset.

Results on ADASYN balanced dataset

This section shows the results of the ADASYN Balanced Dataset with the class distribution plot in Figure 8 and the performance comparison in Table 4. Just like SMOTE ADASYN also helps in overcoming the data balancing problem as seen in the case of Imbalanced dataset. For Enrolled Class, XGB achieves highest F1-Score of 0.813 followed by 0.765 and for Dropput ad Graduate Classes, also XGB outperforms others by F1-Scores of 0.836 and 0.844 respectively. The mean F1 score for the Enrolled Class is 0.695 which shows that ADASYN is not as effective as SMOTE. In general, XGB consistently outperforms other classifiers in all classes, followed by RF. Figure 9 shows the ROC comparison of all five ML classifiers on the balanced data set ADASYN and shows that XGB and RF perform best with AUC values of 0.95.

Fig. 8

Class Distribution after ADASYN Data Balancing: class 0 - Dropout, 1 - Enrolled, 2 - Graduate.

Fig. 9

ROC Curve Comparison of ML Classifiers for ADASYN Balanced Dataset.

Table 4 Performance of ML Classifiers on ADASYN Balanced Dataset.

Results on RU balanced dataset

This section shows the results of the RU balanced dataset with the class distribution plot in Figure 10 and the performance comparison in Table 5. Of the three data balancing techniques that we have used in this paper, RU performs the worst with a mean F1 score of 0.553 for the Enrolled class, showing that RU does not show adequate improvement. Similarly, for dropout and graduate mean F1 scores of 0.6806 and 0.6772 shows that RU shows the weakest performance across all classes, particularly for Enrolled. Figure 11 shows the ROC comparison of all five ML Classifiers on the RU balanced data set and shows that XGB and RF are performing best with AUC values of 0.87 and 0.86 respectively.

Fig. 10

Class Distribution for RU Balanced Dataset: class 0 - Dropout, 1 - Enrolled, 2 - Graduate.

Fig. 11

ROC Curve Comparison of ML Classifiers for RU Balanced Dataset.

Table 5 Performance of ML Classifiers on RU Balanced Dataset.

Selecting best data balancing approach

In this section, we have compared and analyzed the performance of three data balancing techniques (SMOTE, ADAYSN, and RU). Table 6 compares the mean performance of the mentioned data balancing techniques on the five baseline ML classifiers. The mean accuracy comparison plot shown in Figure 12 shows that SMOTE performs best with a mean accuracy of 74.44% followed by ADASYN with 72.50%. We have also compared the mean score of precision, recall and the F1 score and are shown in Figure 13, 14, 15, respectively. Figure 16 shows the Precision-Recall Curves for all considered approaches and it can be seen that SMOTE Balancing approach is outperforming all other in AUCPR Values. The plots also highlight that SMOTE outperforms others in each evaluation metric. So SMOTE is selected as the Data Balancing Approach to further enhance the performance of SDP. Now to select the best Baseline ML Classifier we have plotted the accuracy comparison plot in Figure 17 showing the accuracy comparison of five Baseline ML Classifiers in the SMOTE balanced dataset, which helps to conclude that RF and XGB perform best with the highest accuracy. Figures 18 and 19 present the confusion matrix of RF and XGB in the SMOTE balanced data set. Overall, balancing techniques like SMOTE and ADASYN significantly improve the classification of Dropout and Enrolled classes compared to the Imbalanced Dataset and SMOTE perform best.

Table 6 Mean Performance Comparison of Different Dataset Balancing Techniques.

Fig. 12

Mean Accuracy for Different Data Balancing Approach.

Fig. 13

Mean Precision Comparison Chart.

Fig. 14

Mean Recall Comparison Chart.

Fig. 15

Mean F1 Score Comparison Chart.

Fig. 16

Precision-Recall Curve for (a) Imbalanced Dataset, (b) SMOTE Balanced Dataset, (c) ADASYN Balanced Dataset, (d) RU Balanced Dataset.

Fig. 17

Accuracy Comparison of ML Classifier for SMOTE Balanced Dataset.

Fig. 18

Confusion Matrix of RF on SMOTE Balanced Dataset.

Fig. 19

Confusion Matrix of XGB on SMOTE Balanced Dataset.

Results on proposed methodology

Evidence from the previous section indicates that SMOTE is the most successful approach for handling class imbalance in our dataset, with Random Forest (RF) and XGBoost (XGB) identified as the most efficient baseline machine learning classifiers.Figure 20 shows the feature distribution (For Inflation Rate Feature) before and after SMOTE. It shows a comparison of inflation rate distributions before and after applying SMOTE. The top histogram shows the original data with an uneven distribution that features several peaks, particularly around values 1.5 and 3, with counts ranging from approximately 200 to 800. After SMOTE application (bottom histogram), the overall pattern remains similar but with increased sample counts across most bins, with the highest peak now exceeding 1000 counts around the 1.5 inflation rate value. This transformation maintains the multimodal nature of the distribution while addressing potential class imbalance issues by generating synthetic samples, making the dataset more suitable for machine learning applications that require balanced class representation.

In this study, we optimized the weighted ensemble machine learning classification using Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and Firefly Algorithm (FA) to fine-tune RF, XGB, and ensemble weights. Each optimization technique explores a predefined search space and optimizes hyperparameters to minimize the fitness function, defined as the negative accuracy score ($-\text {accuracy\_score}$). For RF, the search space includes n_estimators (10–200), max_depth (1–50), min_samples_split (2–20), and min_samples_leaf (1–10), while for XGB, the optimized parameters are learning_rate (0.01–0.3), max_depth (1–10), n_estimators (10–200), and subsample (0.5–1.0). The Firefly Algorithm is implemented with $n\_fireflies = 20$, $\alpha = 0.5$, $\beta = 0.2$, and $\gamma = 1.0$, exploring a parameter grid with $n\_iterations$ (10, 20, 50), $\alpha$ (0.1, 0.5, 1.0), $\beta$ (0.1, 0.2, 0.5), and $\gamma$ (0.5, 1.0, 2.0). PSO optimizes RF and XGB within specified lower and upper bounds and is also applied for ensemble weight optimization, using a weight search space (0–1), swarmsize = 30, and maxiter = 50. Similarly, ACO refines the ensemble weights using pheromone-based updates to improve the performance of the model. The convergence criterion for all optimization methods is based on the selection of the best parameters after a predefined number of iterations, ensuring an optimal balance between exploration and exploitation in search space traversal.

Fig. 20

Feature(Inflation Rate) Distribution Before and After SMOTE Balancing.

Table 8 shows the Hyper-tuned parameters and Optimized Weights for RF and XGB. The results shown in Table 7 show that the PSO-based ensemble classification model performs better with the highest accuracy of 86% and an AUC score of 0.9593 which is also presented with the comparison of the baseline ML Classifiers (RF and XGB in SMOTE) in Figures 21 and 22. For the dropout class, PSO performs the best with an F1 score of 0.88, achieving a high precision of 0.93 and a recall score of 0.83. ACO and Firefly deliver similar F1 scores of 0.86, but differ slightly in precision and recall, with Firefly having slightly higher precision value 0.92 than for ACO with a score of 0.91. In the Enrolled class, PSO again outperforms with an F1-Score of 0.84, supported by a balanced precision of 0.82 and recall of 0.86. ACO and Firefly both achieve similar F1-Scores of 0.83, but Firefly has a slightly lower recall of 0.84 compared to ACO’s with F1-Score of 0.86. For the Graduate class, PSO leads with an F1-Score of 0.87, followed by ACO with 0.86 and Firefly with 0.85. The confusion matrix for the optimized PSO, ACO and Firefly weighted ensemble models is shown in Figures 24, 23, 25, respectively.

In general, PSO demonstrates the best performance in all classes, particularly in terms of F1 score and AUC, making it the most effective optimization technique in this comparison. ACO and Firefly offer competitive results but fall slightly behind in precision and recall for the Dropout and Graduate classes.

Table 7 Performance Metrics for Different Optimization Methods.

Fig. 21

Comparison of Proposed Weighted Ensemble Approach with Base Line Classifiers.

Fig. 22

ROC Comparison between PSO, ACO, Firefly Optimized Ensemble Approach.

Fig. 23

Confusion Matrix for ACO Optimized Ensemble.

Fig. 24

Confusion Matrix for PSO Optimized Ensemble.

Fig. 25

Confusion Matrix for Firefly Optimized Ensemble.

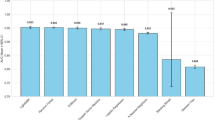
The box plot shown in Figure 26 compares the accuracy of three optimization techniques: PSO ACO and Firefly over 10 runs. Among these, PSO demonstrates the best performance with a higher median accuracy and relatively lower variability, indicating stable and consistent results. Although Firefly optimization also shows competitive performance with a slightly broader range, ACO exhibits the lowest median accuracy and a noticeable outlier, suggesting it may be less effective in this scenario. Therefore, PSO emerges as the most reliable and optimal choice on the basis of accuracy.

Fig. 26

Box Plot of Accuracy Comparison of Optimization Approaches.

Table 8 Hyper-parameters and Weights using Different Optimization.

We have also compared Proposed Approach with state-of-the-art Deep Learning Models and Existing Work. The results shown in Table 9 demonstrate that the proposed model achieves the highest Macro F1 score of 0.863, outperforming all other classifiers. In particular, it shows better predictive performance across all classes, particularly in distinguishing dropout students with an F1 score of 0.88. Compared to other optimization-based approaches, such as CatBoost + Optuma (0.860) and LightGBM + Optuma (0.857), the proposed framework offers a slight but crucial improvement. Traditional deep learning models, such as CNN (0.763) and LSTM (0.673), exhibit lower macro F1 scores. The results highlight the effectiveness of PSO-Weighted Ensemble learning with SMOTE in improving classification balance and precision, making it a promising approach to predict student dropout and early intervention strategies.

Table 9 Comparison with State of Art Deep Learning Models and Existing Work.

Effect of proposed approach - discussion

Here we have shown the effectiveness of the proposed approach which uses SMOTE Data Balancing combined with a PSO Weighted Ensemble of RF and XGB Baseline Classifiers. Figures 27, 28, 29 show the comparison between the proposed approach with best preforming Baseline Classifier(XGB) in Imbalanced Dataset. From the results shown in the graphs, it is concluded that the proposed approach shows improvement in all three evaluation metrics. Precision, recall, and F1 score. In the earlier section, we have shown that for an imbalanced dataset, Enrolled Class is showing very poor precision, recall, and F1-Score values as the number of instances for the said classes are very low compared to other. However, as we can see from the plots, maximum improvement is shown in enrolled classes for all three metrics, which shows the effectiveness of using the SMOTE data-balancing approach.

Fig. 27

Precision Comparison between XGB(Imbalanced) and Proposed(PSO Optimized Ensemble).

Fig. 28

Recall Comparison between XGB(Imbalanced) and Proposed(PSO Optimized Ensemble).

Fig. 29

F1-Score Comparison between XGB(Imbalanced) and Proposed(PSO Optimized Ensemble).

XAI analysis

The SHAP-based feature importance ranking for the Proposed Approach as shown in Figure 31 highlights “Curricular units 2nd sem (approved)” as the most influential feature, with a SHAP value around 0.8, followed by “Curricular units 1 st sem (approved)” and “Tuition fees up to date,” both scoring approximately 0.5. Academic performance indicators dominate the top positions, confirming their strong predictive power. The mid-tier characteristics include socioeconomic factors such as scholarship status, admission grade, and economic indicators such as GDP and inflation rate, while demographic and administrative factors, including nationality, marital status, and parental occupation, rank lowest with SHAP values less than 0.1. The SHAP summary graph shown in Figure 30 reinforces these findings, showcasing the hierarchical importance of academic metrics and illustrating the continuous distribution of their impacts on predictions. Features such as tuition fee status display binary patterns, while academic metrics show nuanced effects. Socioeconomic and demographic factors, though less influential, provide additional context, and the visualization effectively demonstrates how each feature contributes to predicting student outcomes.

Fig. 30

SHAP Feature Value Summary Plot.

Fig. 31

Mean SHAP Value Plot for Features.

TOPSIS analysis

In this paper, we conducted a comparative analysis of multiple models using the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS). This method evaluates models based on multiple performance metrics to determine which model is closest to the best ideal while maintaining the greatest distance from the worst ideal. TOPSIS is based on two primary distance measures. The first, $D^+$, represents the distance of a model from the best ideal values in all the criteria considered. The second, $D^-$, denotes the distance from the ideal worst values. These distances are computed using the Euclidean distance formula.

The relative proximity to the ideal solution is calculated as follows.

$$\begin{aligned} C^* = \frac{D^-}{D^+ + D^-} \end{aligned}$$

(27)

A model with a higher value of $C^*$ is considered to perform better, as it is closer to the ideal solution and farther from the least desirable outcomes.

Based on TOPSIS results as shown in Table 10, the PSO model achieved the highest relative closeness score of 1.0000, indicating that it is the best performing model in this evaluation. The Firefly model ranked second with a relative closeness of 0.6614, followed by RF(SMOTE) and ACO. The XGB(SMOTE) model had the lowest relative closeness score of 0.0000, suggesting that it is the least favorable among the evaluated models.

This study demonstrates the effectiveness of TOPSIS in objectively ranking machine learning models by incorporating multiple performance metrics into a single evaluation framework.

Table 10 TOPSIS Ranking of Models Based on Distance Measures (Corrected Values).

Paired t-test analysis

In this paper, we conducted a paired t-test to compare the PSO model against other models (ACO, Firefly, RF(SMOTE), and XGB(SMOTE)) based on accuracy. The paired t-test is used to determine whether there is a statistically significant difference between two related samples. The test statistic is computed using the formula:

$$\begin{aligned} t = \frac{\bar{X}_1 - \bar{X}_2}{\frac{s}{\sqrt{n}}} \end{aligned}$$

(28)

where:

• $\bar{X}_1$ and $\bar{X}_2$ are the mean values of the two models,

• $s$ is the standard deviation of the differences,

• $n$ is the number of observations.

The null hypothesis ($H_0$) states that there is no significant difference between the PSO model and other models, while the alternative hypothesis ($H_1$) suggests that a significant difference exists. A p-value below 0.05 indicates that we reject $H_0$, meaning that the models perform significantly differently.

The results in Table 11 show that PSO significantly outperforms all other models since all p-values are below 0.05. This confirms that the differences in accuracy between PSO and other models are statistically significant.

Table 11 Paired t-test Results Comparing PSO with Other Models.

Conclusion and future scope

This study introduces a PSO-Weighted Ensemble Framework integrated with SMOTE to address the challenges of imbalanced datasets in Student Dropout Prediction (SDP). The proposed approach outperforms traditional machine learning classifiers, achieving accuracy of 86% and an AUC score of 0.9593. Particle Swarm Optimization (PSO) consistently surpasses other optimization methods, such as Ant Colony Optimization (ACO) and Firefly algorithms, in all performance metrics in dropout, enrolled, and graduate classes. The novelty of the method lies in the combination of ensemble optimization techniques with SMOTE, improving data balance and model performance. Beyond academic performance, student dropout has profound implications for mental health, stress levels, and long-term career prospects. By enabling early detection of at-risk students, the framework facilitates timely interventions that not only improve academic success but also contribute to psychological well-being. The experimental results highlight the effectiveness of the framework in accurately identifying at-risk students and facilitating targeted interventions by educational institutions. The model can be integrated into online learning platforms for real-time risk assessment and generalizes across different education levels with slight adjustments in retraining. Periodic retraining, particularly at the start of each academic year, would enhance adaptability to evolving student data. However, deployment must address regulatory challenges, ensuring compliance with student data privacy laws, while integrating seamlessly with existing academic systems. To enable real-world adoption, future work should explore deployment strategies, such as integrating the model into existing student management systems for real-time analysis. In addition, the study is limited by its generalizability across diverse educational institutions and scalability to large datasets. Future research could focus on incorporating deep learning architectures and exploring explainable AI techniques to enhance interpretability, scalability, and robustness of the framework in different educational settings.