A hybrid framework of feature selection and interpretability for dissolved oxygen prediction in drinking water treatment plants

Abstract

Accurate prediction of dissolved oxygen (DO) is essential for the sustainable operation of drinking water treatment plants. Conventional approaches often rely on a single feature selection method, which can result in biased or inconsistent identification of key predictors. This study proposes a sequential hybrid framework that integrates Mutual Information (MI), Mean Decrease in Impurity (MDI), Permutation Importance, and SHAP interpretability to achieve robust and transparent DO prediction. Filter-based (MI) and embedded (MDI) methods were first employed for initial relevance screening, followed by performance-based validation using Permutation Importance, while SHAP provided both global and local interpretability and reconciled ranking discrepancies. Seven influent water quality parameters were used to train Random Forest (RF) and XGBoost (XGB) models. Feature importance analysis consistently identified historical DO, water temperature, and turbidity as the dominant predictors, whereas pH and NO₂ had minimal influence. Dimensionality reduction preserved predictive accuracy while reducing model complexity by up to 70%, thereby enhancing computational efficiency. Both models demonstrated strong performance (R² = 0.928 for RF and 0.942 for XGB; RMSE < 0.27 mg/L) with narrow 95% confidence intervals. The proposed framework provides a reliable, interpretable, and cost-effective solution for real-time DO monitoring in drinking water treatment systems and offers a transferable methodology for other environmental modeling applications.

Introduction

Clean water is an essential requirement for a thriving society, as domestic, industrial, and agricultural activities rely heavily on its availability, quality, and long-term sustainability^1,2. DO is a critical parameter for evaluating water quality in drinking water treatment plants (DWTPs), although its operational significance varies considerably depending on raw water characteristics. DO becomes particularly vital in polluted, stagnant, or low-flow raw waters, where low oxygen levels foster anaerobic conditions. These conditions promote the release of undesirable constituents—such as iron, manganese, and ammonia—and stimulate the proliferation of pathogenic or nuisance microorganisms, thereby significantly complicating treatment processes^3,4,5. In anaerobic groundwater sources, adequate DO is indispensable for biological filtration systems to effectively oxidize and remove iron, manganese, and ammonium, ensuring compliance with drinking water standards^4,5. Likewise, in stratified or eutrophic reservoirs, hypoxic or anoxic conditions in hypolimnetic layers can trigger the release of metals and nutrients from sediments, severely impairing raw water quality^6,7. DO is also crucial for aerobic biological processes, such as slow sand filtration, where insufficient oxygen or flow interruptions can induce anoxic zones, compromising filtration efficiency and overall treatment reliability⁸. Conversely, in clean, well-oxygenated raw waters with minimal pollution loads, DO plays a less critical operational role, yet it remains a valuable indicator of overall water quality and system stability^9,10. In predominantly physico-chemical treatment trains—such as coagulation–flocculation or advanced oxidation processes—DO has limited direct influence but can still affect secondary phenomena, including corrosion and redox-mediated reactions¹¹. This highly context-dependent role of DO underscores the need for robust predictive modeling approaches to enable optimized DO management across diverse raw water conditions—the central focus of the present study.

Recent advances in ML have provided powerful tools for modeling complex, nonlinear, and multivariate systems, offering superior alternatives to conventional statistical methods^12,13,14. Numerous studies have shown that ML algorithms—including artificial neural networks (ANNs), RF, support vector machines (SVMs), and hybrid ensembles—can accurately predict water quality parameters in treatment systems^15,16,17. However, ML models applied to high-dimensional datasets are prone to overfitting, elevated computational demands, and reduced interpretability. The inclusion of redundant or irrelevant variables further compromises model robustness and predictive accuracy, highlighting the critical importance of effective feature selection^18,19.

Most previous DO prediction studies have relied on a single feature selection technique or standalone ML models, often yielding inconsistent results or overlooking key predictors^20,21. For instance, Chen et al. (2020) employed ensemble and traditional ML models (e.g., ANN, SVM) to predict DO in surface waters using parameters such as NH₃-N, COD, and pH; however, their approach remained heavily dependent on large datasets, sensitive to data quality, and did not incorporate multiple feature selection methods for enhanced robustness²². Similarly, Zhi et al. (2021) applied LSTM networks for continental-scale riverine DO forecasting, achieving moderate performance (Nash–Sutcliffe efficiency ≥ 0.4 at 74% of sites), yet the model struggled with sparse time-series data and lacked automated feature optimization, potentially missing important nonlinear interactions²³. More recently, Sidek et al. (2024) used RF and gradient boosting algorithms for riverine water quality index prediction (incorporating DO and BOD), but emphasized persistent challenges in handling regional variability and achieving adequate model interpretability²⁴. Different feature selection techniques operate on distinct principles—e.g., statistical dependency (mutual information), impurity-based ranking (mean decrease in impurity), or performance perturbation (permutation importance)—and can therefore produce inconsistent or even contradictory variable rankings. Relying on a single method risks introducing methodological bias, omitting influential predictors, or failing to capture complex nonlinear relationships²⁵. Moreover, the vast majority of existing DO modeling studies have focused on natural water bodies (rivers, lakes, estuaries) or wastewater treatment plants, with relatively little attention devoted to DO dynamics within DWTPs. In DWTPs, operational processes such as coagulation, filtration, and disinfection introduce unique challenges that significantly alter oxygen behavior^26,27,28. This research gap exacerbates problems of overfitting, computational inefficiency, and limited interpretability.

To overcome these limitations, the present study introduces an innovative hybrid framework that systematically integrates three complementary feature selection techniques—MDI, permutation importance, and MI—with SHAP (SHapley Additive exPlanations) for interpretability. This multifaceted, sequential pipeline leverages the strengths of filter-based, embedded, and model-agnostic methods while substantially reducing dimensionality and computational burden²⁵. The principal contributions of this work are twofold: (1) the first systematic application of hybrid feature selection specifically for DO prediction in drinking water treatment plants, addressing a critical gap relative to the predominant focus on rivers and wastewater systems^26,27,28; and (2) the development of a robust, decision-oriented sequential pipeline that integrates mutual information, MDI, permutation importance, and SHAP analysis to reliably identify key predictors, enhance model interpretability, and improve predictive accuracy.

The proposed framework is termed “hybrid” not simply because multiple techniques are employed, but because they are strategically integrated into a cohesive, sequential workflow: initial rankings from filter (MI) and embedded (MDI) methods are rigorously validated using a model-agnostic wrapper (permutation importance), while SHAP provides both global and local explanations to confirm the most robust predictors. This synergistic approach effectively mitigates the weaknesses of individual methods, resulting in a more reliable, transparent, and explainable modeling process for DO dynamics in DWTPs.

Materials and methods

Study area and data collection

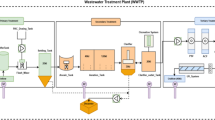
This study was conducted using full-scale operational data from Ahvaz Water Treatment Plant, Khuzestan Province, Iran (31°19’N, 48°40’E). The plant supplies drinking water to approximately 450,000 inhabitants and has a nominal capacity of 150,000 m³/day, treating raw water sourced from the Karun River. The treatment train comprises coagulation–flocculation, sedimentation, rapid sand filtration, and chlorination. A comprehensive 10-year dataset (April 2011–April 2021) was acquired from the plant’s quality control laboratory and Supervisory Control and Data Acquisition (SCADA) system. Ahvaz has a hot desert climate (Köppen BWh), with summer temperatures frequently exceeding 45 °C, mild winters (10–15 °C), and low annual precipitation (~ 230 mm, concentrated in winter). The Karun River, Iran’s longest river (950 km), has a mean annual discharge of approximately 575 m³/s but exhibits strong seasonal and interannual variability due to upstream dam operations, irrigation withdrawals, and occasional floods. These factors drive substantial fluctuations in key influent parameters, particularly turbidity and temperature. Seven inlet water quality parameters were selected as predictors: dissolved oxygen (DO), nitrite (NO₂⁻), chloride (Cl⁻), electrical conductivity (EC), turbidity, pH, and temperature. The outlet DO (measured at the clear water reservoir) served as the target variable. All measurements were taken daily at 8:00 AM to ensure consistency and minimize diurnal effects. Input parameters were sampled immediately after filtration (pre-chlorination), whereas output DO was measured at the clear water reservoir outlet.

The measurements were not performed by the authors; rather, the study relied on historical records routinely collected by the Khuzestan Water and Wastewater Company in strict accordance with national and international drinking water standards (Iranian National Standards and WHO guidelines). The laboratory-based monitoring protocol was retained because it provides the highest analytical accuracy for parameters requiring precise chemical or physicochemical determination—results upon which real-time operational decisions at the plant are based. The geographical location of the treatment plant and raw water intake is shown in Fig. 1.

Fig. 1

Geographical location of Ahvaz water treatment plant and the Karun River raw water intake, Khuzestan province, Iran.

Data preprocessing and exploratory data analysis

Descriptive statistics, including the mean, median, standard deviation, minimum, and maximum values, were calculated for all variables. The normality of data distributions was assessed using the Shapiro–Wilk test (α = 0.05), complemented by visual inspection of histograms²⁹. Outliers were evaluated and either removed or retained based on their relevance to the experimental context to ensure robust preprocessing. Box-and-whisker plots were employed to visualize data distributions, identify outliers, and assess interquartile ranges. As the dataset was originally collected for experimental monitoring rather than predictive modeling, several preprocessing steps were required to adapt it for machine learning application³⁰. Although the primary models used in this study (RF and XGB) are scale-invariant, standard normalization (z-score transformation) was applied to center the data around a mean of zero and a standard deviation of one. This step helps manage data variability, reduce the influence of extreme values, ensure consistency in exploratory analysis, and maintain compatibility with scale-sensitive algorithms such as artificial neural networks. Accordingly, all input features were transformed using the standard normalization equation.

$${\textbf Z}= \frac{ ( {\bf x}_{\bf i } - {\varvec \mu })}{( {\varvec \sigma }) }$$

(1)

where $\:\text{Z}$ is standardized value of initial variable $\:{\varvec{x}}_{\varvec{i}}$, $\:\varvec{\mu\:}$ is the mean, and $\:\varvec{\sigma\:}\:$is the standard deviation.

Additionally, to detect and address multicollinearity among the input features, Pearson correlation analysis was performed using Eq. (2), quantifying the linear relationships between each pair of variables^31,32.

$$\:{r}_{xy}=\frac{{\sum\:}_{i=1}^{n}({x}_{i}-\stackrel{-}{x}){\sum\:}_{i=1}^{n}({y}_{i}-\stackrel{-}{y})}{\sqrt{{\sum\:}_{i=1}^{n}{({x}_{i}-\stackrel{-}{x})}^{2}}\sqrt{{\sum\:}_{i=1}^{n}{({y}_{i}-\stackrel{-}{y})}^{2}}}$$

(2)

where $\:{r}_{xy}$ is correlation coefficient between two variables (x and y), $\:\stackrel{-}{x}$ and $\:\stackrel{-}{y}$ are average of x_i and y_i, respectively.

2.3. Machine learning Estimation models

The dataset was randomly divided into two subsets: a training set (80%) and a testing set (20%). Previous studies have shown that allocating only 60% of the data for training may be insufficient to adequately represent the overall dataset and capture its underlying patterns³³. Two machine learning models were employed to estimate DO concentrations using other water quality parameters as predictor variables. RF is an ensemble learning method for regression and classification that constructs multiple decision trees using bootstrapped subsets of the data and aggregates their outputs to produce a robust and generalized prediction. XGBoost is a supervised machine learning algorithm applicable to regression, classification, and ranking tasks. It represents an optimized implementation of the gradient boosting framework, specifically designed to improve both computational efficiency and predictive performance³⁴. To ensure optimal model performance and reproducibility, hyperparameters for both RF and XGBoost models were optimized using a grid search strategy combined with 5-fold cross-validation applied to the training dataset. The hyperparameter search spaces are summarized in Table 1. The optimal set of hyperparameters was selected based on the highest coefficient of determination (R²) achieved during cross-validation.

Table 1 Hyperparameter grids explored during grid search with 5-fold cross-validation. Optimal parameters were selected based on the highest R² score on the validation folds.

Feature selection and interpretability

One of the major challenges in environmental modeling, particularly in predictive applications, is the high dimensionality of input variables. Incorporating a large number of predictors can increase the risk of overfitting, raise computational complexity, and reduce model interpretability³⁵. Consequently, identifying the most influential variables through systematic feature selection and importance analysis is a critical step toward improving model performance, enhancing transparency, and extracting meaningful environmental insights³⁶. To address these challenges, this study adopts a comprehensive, multi-perspective feature selection framework that integrates filter-based, embedded, wrapper-based, and explainable artificial intelligence (XAI) approaches. These methods are combined within a sequential pipeline designed to leverage their complementary strengths while mitigating individual limitations. The framework begins with filter-based MI and MDI methods for efficient initial screening of relevant predictors. This is followed by permutation importance to validate feature relevance through unbiased, perturbation-based assessment, and finally by SHAP (SHapley Additive exPlanations) for interpretable refinement of feature contributions at both global and local levels. By integrating these techniques, the proposed framework mitigates methodological biases—for example, the tendency of MDI to overestimate the importance of correlated features through validation via permutation importance—while capturing diverse aspects of feature relevance, including nonlinear dependencies (MI), model-specific importance (MDI), and prediction sensitivity to feature perturbation (permutation). The use of SHAP further ensures transparent and robust interpretation of feature effects. Overall, this consensus-driven strategy reduces the likelihood of overlooking critical predictors, such as historical DO levels or water temperature, and enhances the reliability and interpretability of the predictive models.

Mean decrease in impurity (MDI)

Mean Decrease in Impurity (MDI) was employed as an embedded feature importance measure inherent to tree-based learning algorithms, including RF and XGBoost. MDI quantifies the contribution of each feature during model training by measuring the reduction in node impurity attributable to splits based on that feature. This approach is computationally efficient and directly aligned with the internal learning mechanism of tree-based models.

Specifically, MDI estimates feature importance by averaging the impurity reduction contributed by a given feature across all trees in the ensemble. Despite these advantages, MDI is known to exhibit bias toward continuous variables or features with high cardinality, as such features are more likely to be selected for node splitting, potentially leading to an overestimation of their importance. For a feature _Xj, the MDI is calculated as:

$$\:MDI=\left({X}_{j}\right)=\frac{1}{T}{\sum\:}_{t=1}^{T}\sum\:_{n\in\:{N}_{t}}{\varDelta\:}_{i}(n,{X}_{j})$$

(3)

Where:

T: Number of trees in the ensemble (e.g., Random Forest).

$\:{N}_{t}$

Set of nodes in tree t where feature $\:{X}_{j}$ is used for splitting.

$\:{\varDelta\:}_{i}(n,{X}_{j})$

Reduction in impurity at node n due to splitting on feature $\:{X}_{j}$, calculated as.

$$\:{\varDelta\:}_{i}(n,{X}_{j})=i\left(n\right)-(\frac{\left|{N}_{n,left}\right|}{\left|{N}_{n}\right|}i\left({n}_{left}\right)+\frac{\left|{N}_{n,right}\right|}{\left|{N}_{n}\right|}i\left({n}_{right}\right))$$

(4)

$\:i\left(n\right)$

Impurity at node n (e.g., Gini impurity or entropy).

$\:\left|{N}_{n}\right|$

Number of samples at node n.

$\:\left|{N}_{n,left}\right|$, $\:\left|{N}_{n,right}\right|$: Number of samples in the left and right child nodes after the split.

Gini impurity for a node:

$\:i\left(n\right)=1-{\sum\:}_{k-1}^{K}{p}_{k}^{2}$, where $\:{p}_{k}$is the proportion of class k at node n.

Entropy:

$$\:i\left(n\right)=-{\sum\:}_{k-1}^{K}{p}_{k}\text{l}\text{o}\text{g}\left({p}_{k}\right).$$

MDI averages the impurity reduction across all nodes and trees where the feature is used.

Permutation importance

Permutation Importance was used as a model-agnostic, wrapper-based technique to overcome potential biases associated with embedded methods. This approach evaluates feature relevance by randomly shuffling the values of a given feature and measuring the resulting degradation in model performance. For a feature $\:{X}_{j}$, the importance of permutation is:

$$\:PI\left({X}_{j}\right)={Score}_{\text{o}\text{r}\text{i}\text{g}\text{i}\text{n}\text{a}\text{l}}-{Score}_{\text{p}\text{e}\text{r}\text{m}\text{u}\text{t}\text{e}\text{d}}$$

(5)

Where:

$\:{Score}_{\text{o}\text{r}\text{i}\text{g}\text{i}\text{n}\text{a}\text{l}}$

model performance metric (here, negative MAE on the validation fold) obtained using the original data.

$\:{Score}_{\text{p}\text{e}\text{r}\text{m}\text{u}\text{t}\text{e}\text{d}}:\:$Corresponding score after randomly shuffling the values of feature $\:{X}_{j}\:$while keeping all other features unchanged.

A large positive PI value indicates that the model relies heavily on $\:{X}_{j}$, confirming its true predictive importance. By averaging over multiple random permutations, the effect of random noise is minimized, yielding stable and reliable importance rankings.

This step served as the final, model-agnostic validation layer in our sequential hybrid framework, ensuring that only predictors consistently ranked as critical across all three complementary methods (MI, MDI, and permutation importance) were retained for the final modeling phase.

Mutual information (MI)

Mutual Information (MI) was incorporated as a filter-based method to capture nonlinear dependencies between individual features and the target variable (DO) without assuming any specific predictive model. MI quantifies the amount of information gained about the target variable Y by knowing feature $\:{X}_{j}$.

For discrete variables:

$$\:MI({X}_{j},Y)=\sum\:_{x\in\:{X}_{j}}\sum\:_{y\in\:Y}p\left(x,y\right)\text{l}\text{o}\text{g}\left(\frac{p(x,y)}{p\left(x\right)p\left(y\right)}\right)$$

(6)

Where:

$\:p(x,y)$

Joint probability distribution of $\:{X}_{j}$and Y.

p(x), p(y): Marginal probability distributions of $\:{X}_{j}$and Y.

For continuous variables, the integral form is used:

$$\:MI({X}_{j},Y)=\iint\:p\left(x,y\right)\text{l}\text{o}\text{g}\left(\frac{p(x,y)}{p\left(x\right)p\left(y\right)}\right)$$

(7)

In practice, MI is often estimated using methods like k-nearest neighbors or kernel density estimation due to the difficulty of estimating continuous distributions.

SHAP (SHapley additive exPlanations)

SHAP were employed to enhance model interpretability using a game-theoretic framework. SHAP values assign each feature a contribution to the model’s prediction for a specific instance by averaging its marginal contribution across all possible feature subsets. For a feature $\:{X}_{j}$, the SHAP value for an instance x is:

$$\:{{\varnothing}}_{j}\left(x\right)=\sum\:_{S\in\:N\left\{j\right\}}\frac{\left|S\right|!(\left|N\right|-\left|S\right|-1)!}{\left|N\right|!}$$

(8)

Where:

N: Set of all features.

S: Subset of features excluding $\:{X}_{j}$.

$\:{f}_{x}$ (S): Model prediction for instance x using only the features in S.

∣S∣,∣N∣: Number of features in subset S and total features, respectively.

$\:{f}_{x}$ (S $\:\cup\:\:\left\{j\right\}-{f}_{x}\left(S\right)$): Marginal contribution of feature $\:{X}_{j}$ when added to subset S.

The SHAP value $\:{\varnothing\:}_{j}\left(x\right)\:$represents the contribution of feature $\:{X}_{j}$ to the difference between the model’s prediction and the expected (average) prediction.

For tree-based models, SHAP uses an efficient algorithm (TreeSHAP) to compute these values without explicitly evaluating all coalitions.

Hybrid sequential feature selection framework

The three complementary feature importance techniques were combined into a robust, sequential, and synergistic pipeline (Fig. 2):

• 1. Mutual information (filter method) and mean decrease in impurity (embedded method within Random Forest) were first applied in parallel for rapid, computationally efficient preliminary screening of the seven candidate predictors.

• 2. Permutation importance (model-agnostic wrapper) was then employed on the highest-ranked features to correct known biases of tree-based embedded methods, particularly the overestimation of continuous or high-cardinality variables.

• 3. Finally, SHAP (SHapley Additive exPlanations) analysis was performed on the refined subset to provide both global and local interpretability, quantifying the magnitude, direction (positive or negative), and potential nonlinear interaction effects of each predictor on outlet dissolved oxygen concentration.

This hybrid, consensus-driven framework effectively mitigates the inherent limitations and biases of individual techniques, leverages their complementary strengths, and yields a highly reliable and transparent feature ranking. By requiring consistent high importance across all three methodologically distinct approaches, the pipeline substantially reduces the risk of omitting truly influential predictors—ultimately identifying inlet DO and water temperature as the dominant drivers of outlet DO in the studied full-scale drinking water treatment plant.

Fig. 2

Feature Selection Workflow in Environmental Modeling Using MDI, Permutation Importance, MI, and SHAP.

Evaluation of metrics of models

In the present study, the performance of the models was rigorously evaluated using validated statistical metrics to ensure their accuracy and generalizability. This study employed several evaluation criteria, including Mean Squared Error (MSE), Mean Absolute Error (MAE), Coefficient of Determination (R²), Root Mean Squared Error (RMSE), and Explained Variance Score (EVS) to comprehensively analyze and compare the predictive performance and validity of the machine learning models. These metrics collectively offer a robust understanding of the models’ reliability, error magnitude, and explanatory power^37,38,39. The equations for these measures are given below:

$$\:\text{M}\text{S}\text{E}=\frac{1}{\text{n}}\sum\:_{\text{i}=1}^{\text{n}}{({Y}_{i}^{exp}-{Y}_{i}^{pred})}^{2}$$

(9)

$$\:MAE=\:\frac{\sum\:_{i=1}^{n}\left|{Y}_{i}^{exp}-{Y}_{i}^{pred}\right|}{n}$$

(10)

$$\:{\text{R}}^{2}=1-\:\frac{\sum\:_{i=1}^{n}{\left({Y}_{i}^{exp}-{Y}_{i}^{pred}\right)}^{2}}{\sum\:_{i=1}^{n}{\left({Y}_{I}^{exp}-{Y}_{ave}^{exp}\right)}^{2}}\:\:\:$$

(11)

$$\:RMSE=\sqrt{\frac{\sum\:_{i=1}^{n}{\left({Y}_{i}^{exp}-{Y}_{i}^{pred}\right)}^{2}}{n}}\:\:\:$$

(12)

$$\:EVS=1-\frac{Var\:({Y}_{i}^{exp}-{Y}_{i}^{pred})}{Var\:{Y}_{i}^{exp}}\:$$

(13)

Here, $\:{Y}_{i}^{pred}$ and $\:{Y}_{i}^{exp}$ denote the ith anticipated and experimental values, respectively. $\:{Y}_{ave}^{exp}$ is the meaning of the experimental values, and n is the quantity of experimental values. In an ideal model, the values of RMSE, R², MAE, and MSE would be 0, 1, 0, 0, and 1, respectively⁴⁰.

Results and discussion

Descriptive statistics and data distribution

Descriptive statistics of the water quality parameters used as input variables for dissolved oxygen (DO) prediction are summarized in Table 2. The mean DO concentration at the plant outlet was 6.92 mg/L, while the influent water exhibited a slightly higher mean value of 7.08 mg/L, indicating moderate oxygen depletion during the treatment process. The relatively low standard deviation of DO (approximately 0.98 mg/L) suggests limited temporal variability, which is indicative of stable operational conditions at the treatment plant.

The input water quality parameters, including NO₂, Cl, EC, turbidity, pH, and T, exhibited considerable variability. NO₂ concentrations were generally low, with a mean value of 0.01 mg/L, indicating minimal nitrogen-related contamination. In contrast, chloride concentrations showed substantial fluctuations (mean = 311.28 mg/L; SD = 121.56 mg/L), likely reflecting variations in disinfection practices or source water characteristics. EC and turbidity also displayed wide ranges (EC: 1033–3310 µS/cm; turbidity: 1.61–11,000 NTU), which may be attributed to seasonal effects, hydrological variability, or changes in raw water sources. The pH values remained within a neutral to slightly alkaline range (7.41–8.41), while water temperature varied from 10.21 to 31.41 °C, capturing both cold and warm operational periods. Collectively, the observed variability across these parameters underscores the necessity of incorporating multiple input variables to achieve accurate and robust DO prediction in the modeling framework.

Table 2 Descriptive statistics (mean, standard deviation, minimum, and maximum) of water quality parameters measured at input and output parameters.

The histograms of the water treatment plant dataset (Fig. 3) provide valuable insight into the distributional characteristics of the variables relevant to DO prediction. The DO concentration at the plant outlet exhibits an approximately normal distribution, reflecting well-controlled treatment conditions and indicating suitability for regression-based modeling approaches. In contrast, the influent DO shows a right-skewed distribution, highlighting variability in raw water quality that may be attributed to seasonal dynamics and fluctuations in organic loading.

Among the input variables, NO₂ demonstrates a pronounced right-skewed distribution, suggesting sporadic nitrogen inputs into the system. Cl and EC display approximately symmetric distributions, indicative of relatively stable ionic conditions within the treatment process. Turbidity exhibits strong right skewness, likely resulting from episodic sediment influxes or short-term disturbances in source water quality. The pH distribution reveals a bimodal pattern, which may be associated with diurnal buffering effects or variations in chemical dosing practices. T also follows a right-skewed distribution, capturing seasonal thermal variability and its potential influence on biological treatment processes.

Overall, these distributional characteristics emphasize the heterogeneous nature of the input variables and underscore the importance of robust machine learning models capable of capturing nonlinearity and variability in DO prediction.

Fig. 3

Histograms of normalized input (DO-input, NO₂-input, Cl-input, EC-input, Turbidity-input, pH-input, T-input) and output (DO-output) variables.

Box plot analysis (Fig. 4) revealed distinct distributional patterns among the input variables. Both DO output and its corresponding input values exhibited relatively symmetrical distributions around the median, with a moderate number of outliers. NO₂ showed limited variability, indicating a narrow observation range. EC and Cl presented wider distributions with several outliers, while turbidity demonstrated the greatest variability, with extreme values far exceeding the upper quartile. pH and temperature showed moderate spreads, with temperature exhibiting fewer extreme outliers compared to pH. The observed variability among input parameters highlights their differing influence on DO prediction. The narrow range of NO₂ suggests limited predictive power, whereas the wide distributions and extreme outliers in turbidity and EC indicate that these variables could introduce substantial variability into the modeling process. The relatively balanced distribution of DO input further supports its role as a strong predictor of DO dynamics.

.

Fig. 4

Box plots of normalized input (DO, NO₂, Cl, EC, Turbidity, pH, T) and output variables, showing data distribution and outliers.

These findings highlight the importance of applying feature engineering and normalization techniques to handle skewed distributions and outliers, thereby improving the robustness and accuracy of predictive models. The observed patterns are consistent with previous studies. Xie, et al. , reported substantial variations in input parameters, indicating significant fluctuations in water quality entering treatment plants. Similarly, Li, et al. found that electrical conductivity, flow velocity, and both influent and effluent turbidity were highly skewed, reflecting pronounced variability in raw water quality. Furthermore, Ahmed and Lin²⁹ evaluated the normality of predictor variables using the Kolmogorov–Smirnov test and confirmed that the data for DO prediction were non-normally distributed. Overall, these results demonstrate that the dataset adequately represents plant dynamics and provides a solid foundation for accurate modeling of DO.

Model performance

The results of DO prediction using RF and XGBoost models are summarized in Table 3, with their comparative performance illustrated in Fig. 5. Hyperparameter optimization via Grid Search enhanced model robustness, particularly for XGBoost, while maintaining high accuracy suitable for real-time DO monitoring. Both models demonstrated strong predictive performance, with R² values of 0.928 for RF and 0.942 for XGBoost, explaining over 93% of the variance in DO. RF slightly outperformed XGBoost across most evaluation metrics (MSE: 0.073 vs. 0.059; MAE: 0.194 vs. 0.172; RMSE: 0.271 vs. 0.244), while XGBoost achieved marginally higher explained variance (EVS: 0.942 vs. 0.928). The superior robustness of XGBoost is likely attributed to its ensemble averaging, which effectively captures nonlinear relationships among input variables.

The high performance of both models underscores the strong dependency of DO on key water quality parameters, including NO₂, Cl, EC, turbidity, pH, and temperature. These results confirm that machine learning approaches can reliably predict DO, thereby supporting real-time monitoring and optimization of water treatment processes.

Table 3 Summarizes the performance of the machine learning models—RF and XGBoost —in predicting DO using all input parameters.

The scatter plots for the XGBoost model show a strong agreement between predicted and observed DO values, with most points tightly clustered around the ideal $\:y=x$line across the full range of measured concentrations. The 95% confidence interval (CI), defined by residual bounds of − 0.4609 to 0.4919 mg/L, encompasses most predictions, reflecting stable and reliable model performance. Additionally, the low RMSE of 0.244 mg/L confirms the high prediction accuracy of XGBoost. These results demonstrate the model’s ability to capture complex nonlinear relationships governing DO dynamics in the treatment process, influenced by interacting physicochemical factors such as temperature, turbidity, and historical DO conditions.

Similarly, the RF model exhibits strong predictive capability, with predicted values closely aligned with the ideal line and minimal systematic bias. RF shows a slightly wider 95% CI (− 0.5149 to 0.5452 mg/L) and a higher RMSE (0.271 mg/L) compared to XGBoost, indicating marginally lower precision. Nevertheless, its ensemble-based structure enables robust generalization by reducing variance and effectively handling nonlinear relationships among input variables. Overall, both models demonstrate reliable performance with minimal deviation from the $\:y=x$line, confirming the effectiveness of the applied preprocessing and feature selection strategies in mitigating the influence of skewed variables such as turbidity and NO₂. The consistently lower error metrics and higher explained variance achieved by XGBoost highlight its slightly superior predictive performance. These findings align with previous studies, including Garabaghi, et al. ²¹, who reported strong performance of RF models for DO prediction, while other investigations on aeration process optimization have shown that gradient boosting approaches can achieve enhanced accuracy under complex operational conditions²⁷.

Fig. 5

Scatter plots of predicted versus observed DO concentrations (in mg/L) for (a) XGBoost and (b) Random Forest models. The solid line represents the ideal 1:1 relationship (y = x). The shaded area denotes the 95% confidence interval of the predictions.

Feature importance and ranking stability across multiple techniques

Feature importance and ranking stability across multiple techniques are summarized in Fig. 6.

Fig. 6

(Left) Radar plot of normalized feature importance scores for DO-input, T-input, turbidity-input, Cl-input, EC-input, pH-input, and NO₂-input obtained from the four methods (MDI, permutation importance, mutual information, and SHAP). (Right) Stacked bar chart showing how many times each input variable was assigned to a given rank (Rank 1 to Rank 7) across the four-feature selection and interpretability techniques. Higher bars in the upper ranks (e.g., Rank 1–2) indicate more consistent identification of a variable as important, whereas taller bars in lower ranks (e.g., Rank 6–7) reflect consistently low importance.

Figure 6. (Left) Radar chart illustrating normalized importance scores (scaled 0–1) for DO-input, T-input, turbidity-input, Cl-input, EC-input, pH-input, and NO₂-input, as determined by four feature selection and interpretability techniques: MDI, Permutation Importance, MI, and SHAP. A larger radar area indicates higher importance and stronger consensus among the methods. (Right) Stacked bar chart showing the frequency with which each variable achieved a specific rank (1–7) across the four techniques. Higher bars at upper ranks (Rank 1–2) indicate consistent identification as important, while taller bars at lower ranks (Rank 6–7) indicate consistently low importance. Variables are ordered by average rank from top to bottom, allowing independent interpretation. For instance, DO-input achieved Rank 1 in all four methods, confirming it as the most consistently important predictor. T-input ranked second across all methods, whereas NO₂-input was frequently assigned the lowest rank (Rank 7 in three out of four methods), indicating weak and inconsistent contribution. Overall, the stacked bar chart facilitates identification of robust predictors for effluent DO.

Interpretation of feature ranking stability

The distribution of ranks (1–7, lower ranks indicate higher importance) assigned to each input across the four evaluation techniques is summarized as follows:

• DO-input: Rank 1 in all methods (average = 1.0).

• T-input: Rank 2 in all methods (average = 2.0).

• Turbidity-input: Rank 3 in three methods, Rank 5 in one method (average = 3.5).

• Cl-input: Rank 3 in one method, Rank 4 in two methods, Rank 5 in one method (average = 4.0).

• EC-input: Rank 4 in two methods, Rank 5 in one method, Rank 7 in one method (average = 5.0).

• pH-input: Rank 6 in all methods (average = 6.0).

• NO₂-input: Rank 5 in one method, Rank 7 in three methods (average = 6.5).

These rankings reveal a clear hierarchy among input variables, with DO-input and T-input consistently dominant, while pH-input and NO₂-input exhibit the lowest importance.

Physical and process-based interpretation of feature importance

DO-input consistently ranks first (average = 1.0), reflecting strong autocorrelation in DO dynamics. In aquatic and treatment systems, DO concentrations evolve gradually, so recent historical measurements capture essential temporal dependencies not fully represented by other physicochemical parameters. T-input ranks second (average = 2.0) due to its direct influence on oxygen solubility and biological activity. Higher temperatures reduce oxygen solubility and alter microbial metabolism and BOD, making temperature a key driver of DO variability, consistent with findings by Yaseen et al. ⁴². Turbidity-input (average rank = 3.5) ranks third. Elevated turbidity, often associated with phytoplankton blooms, may enhance DO through photosynthesis, whereas low turbidity conditions introduce more complex interactions between biological and environmental processes^42,43. Cl-input (average rank = 4.0) exerts moderate influence. While chloride does not directly control oxygen levels, elevated concentrations may indicate contamination sources or ionic changes affecting microbial activity and oxidative processes. EC-input (average rank = 5.0) reflects overall ionic strength. High EC values indicate dissolved salts or nutrients that indirectly influence DO through microbial activity, osmotic stress, or chemical equilibria, providing supplementary predictive information.

pH-input and NO₂-input exhibit the lowest importance (average ranks = 6.0 and 6.5). Although pH affects chemical equilibria and microbial processes⁴⁴, its variability within normal operational ranges is insufficient to strongly impact DO. Similarly, NO₂ influences oxygen consumption via nitrification but is secondary to the dominant effects of DO history, temperature, and turbidity.

Advantages of the multi-technique (Hybrid) framework

The proposed multi-technique framework mitigates bias associated with relying on a single feature selection method. For example, using only MDI would correctly identify DO and temperature as key predictors but might underestimate the consistent role of turbidity, which is highlighted by Permutation Importance and SHAP. Conversely, MI overestimates Cl-input (ranked third), while model-based methods consistently place it lower (average rank = 4.0), suggesting its statistical association with DO is not fully actionable for predictive performance.

The framework applies convergent validity: features consistently ranked highly across multiple methods are considered core predictors. Conflicting signals are resolved by giving greater weight to performance-based techniques (particularly Permutation Importance), while SHAP provides contextual explanations by revealing interaction effects. This yields a balanced, interpretable, and defensible feature set superior to any single technique. Comparative analysis shows that single-technique approaches can lead to inconsistent rankings (e.g., MI overestimating Cl-input, reducing R² by 1–3%) and suboptimal performance (e.g., MDI bias increasing RMSE by ~ 5%). The hybrid approach achieves consensus, effective dimensionality reduction (excluding low-importance features like pH and NO₂), and superior metrics (RMSE reduced to 0.244 mg/L), demonstrating enhanced robustness and efficiency.

Model performance in context of existing literature

The high predictive accuracy achieved by both RF and XGBoost models (R² > 0.93, RMSE < 0.26 mg/L) is comparable to, and in some cases exceeds, recent reports for DO prediction in water systems. For example, Garabaghi et al. (2023) 21 reported R² = 0.91 using Random Forest for wastewater treatment. Liu et al. (2024) 20, employing a hybrid ML approach, achieved RMSE ≈ 0.30 mg/L. In the context of drinking water treatment—an area with comparatively less attention—our models demonstrate competitive and reliable accuracy, validating the effectiveness of the proposed hybrid feature selection framework. The narrow confidence intervals (Fig. 3) further confirm robustness and reliability, highlighting the potential of this approach for real-time monitoring and operational decision-making.

Results of DO prediction using feature-engineered inputs

To assess the robustness and generalizability of machine learning models in predicting DO with feature-engineered inputs under dimensionality reduction, a Taylor diagram (Fig. 7) was employed.

Fig. 7

Taylor diagram comparing the performance of RF and XGBoost models under different feature elimination scenarios. Correlation coefficients (R), RMSE, and standard deviations of predicted versus observed values are illustrated relative to the observed data (black star).

The diagram simultaneously visualizes correlation, RMSE, and standard deviation across different reduced input sets. For XGBoost, variations in input combinations caused only minor changes in prediction accuracy, indicating robustness to dimensionality reduction. Similarly, RF consistently achieved high accuracy across all reduced input scenarios. Notably, RF slightly outperformed XGBoost in RMSE, particularly under reduced dimensionality, highlighting its ability to capture nonlinear dependencies and variable interactions even with fewer predictors.

The most effective feature combinations included T, turbidity, and Cl, alongside DO input, reflecting their direct influence on DO dynamics. This aligns with environmental understanding: DO indicates biological activity, turbidity reflects suspended particulate matter, and temperature governs physicochemical processes, collectively explaining the majority of variance in DO. Overall, targeted feature selection can reduce input dimensionality by up to 70% while maintaining predictive accuracy, supporting cost-effective and efficient environmental monitoring strategies.

Generalized guidance for framework application

The proposed hybrid framework can be generalized for various environmental modeling applications:

Data Preparation

Implement preprocessing steps such as normalization and outlier handling to account for domain-specific variability, including seasonal hydrological patterns or sensor noise in air quality data.

Technique integration

Begin with filter-based methods (e.g., MI) for rapid screening of high-dimensional datasets, followed by embedded (MDI) and wrapper (Permutation) approaches for validation, and apply SHAP for interpretability. Adjust method selection according to model type (e.g., tree-based models for efficiency, neural networks for complex interactions).

Handling divergences

Use convergent validity to prioritize features consistently ranked highly across multiple methods, giving greater weight to performance-based techniques (e.g., Permutation Importance) in cases of conflicting signals, as demonstrated in the DO prediction case.

Customization and evaluation

Tune hyperparameters via cross-validation and assess models using domain-relevant metrics (e.g., RMSE for continuous predictions, precision for classification). Evaluate generalizability on hold-out datasets.

Applications beyond DO

The framework can be extended to predicting pollutant concentrations in wastewater, air quality indices using meteorological data, or ecosystem health indicators integrating biological variables, emphasizing reduced dimensionality for real-time, computationally efficient monitoring.

Conclusions

This study demonstrates that machine learning models—particularly Random Forest (RF) and XGBoost—can reliably predict DO concentrations in drinking water treatment plants. The integration of multiple feature selection and interpretability techniques enhanced predictive performance and enabled robust identification of the most influential variables. Historical DO, water temperature, and turbidity consistently emerged as the dominant predictors, reflecting the combined effects of temporal continuity and physicochemical processes on oxygen dynamics. Dimensionality reduction decreased computational complexity by up to 70% without compromising model accuracy, highlighting the efficiency and practicality of the proposed framework for real-time water quality monitoring. By focusing on treated drinking water, this study addresses a gap in existing literature and provides actionable insights for optimizing aeration strategies, energy consumption, and overall process efficiency.

.

Despite the high predictive accuracy, several limitations should be noted. The analysis is based on a 10-year dataset from a single location (Ahvaz, Iran), and feature importance may differ under other climatic conditions or treatment configurations. Moreover, biological indicators such as Biochemical BOD and COD were not included due to data availability, and the use of daily averaged data may obscure short-term DO fluctuations. Future studies should incorporate high-frequency sensor data, a broader range of biological and operational variables, and extend the framework to inverse modeling for optimized aeration control.

Compared to single-technique approaches, which may introduce methodological biases and overlook key interactions, the hybrid framework offers superior robustness. It improves model accuracy, enhances interpretability through consensus validation, and maintains computational efficiency, making it particularly valuable for complex environmental systems such as DWTPs.

Beyond DO prediction, the proposed multi-technique framework provides a generalizable workflow for environmental modeling tasks involving high-dimensional and correlated data, offering improved transparency, robustness, and interpretability across a wide range of applications.