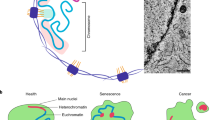
Abstract
Nuclear atypia is a hallmark of cancer. A recent model posits that excess surface area, visible as folds/wrinkles in the lamina of a rounded nucleus, allows the nucleus to take on diverse shapes with little mechanical resistance. Whether this model is applicable to normal and cancer nuclei in human tissues is unclear. We image nuclear lamins in patient tissues and find: (a) nuclear laminar wrinkles are present in control and cancer tissue but are obscured in hematoxylin and eosin (H&E) images, (b) nuclei rarely have a smooth lamina, and (c) wrinkled nuclei assume diverse shapes. Deep learning reveals the presence of extreme nuclear laminar wrinkling in cancer tissues, which is confirmed by Fourier analysis. These data support a model in which excess surface area in the nuclear lamina enables nuclear shape diversity in vivo. Extreme laminar wrinkling is a marker of cancer, and imaging the lamina may benefit cancer diagnosis.
Similar content being viewed by others
Introduction
Nuclear morphological alterations, or nuclear atypia, have been associated with human cancers for over 150 years1. Nuclear atypia is critical in the diagnosis of breast carcinoma2, breast ductal carcinoma in situ (DCIS)3, thyroid carcinoma4, skin carcinoma5, ovarian carcinoma6, and precancerous dysplasia of the larynx7. Nuclear atypia includes features such as larger nuclear size, altered heterochromatin, more prominent nucleoli, and nuclear shape alterations8. How nuclear shapes become abnormal in cancer is not understood.
Variations in nuclear shapes may result from changes in the mechanical properties of the nucleus in cancer9. Indeed, cancer nuclei tend to be softer than normal nuclei10, due to alterations in nuclear lamin levels, particularly a decrease in lamin A/C levels11. Lamin A/C is a component of the nuclear lamina, a stiff two-dimensional sheath that underlies the nuclear envelope. The resistance of the nuclear lamina to extension and the resistance of nuclear contents to volume compression underlie the stability of the nucleus to changes in shape12,13,14. A loss of lamin A/C eliminates the resistance to areal extension, resulting in irregular nuclear shapes.
However, the nuclear lamina resists extensional deformation only in extreme nuclear shapes where the lamina is smooth12,15, such as the flattened nuclei in cell culture. We and others have reported that the nuclear lamina in non-extreme shapes, such as those in 3D culture or in elongated or rounded nuclei, tend to form folds and wrinkles16,17,18,19,20,21,22,23,24. These folds, which we have quantified as excess surface area relative to a sphere of the same volume as the nucleus25, imply that the nuclear lamina does not resist extensional strain so long as these folds are present. The presence of excess area in the lamina provided support for a recent ‘drop model’ of nuclear shaping in which the nuclei offer little mechanical resistance to deformation as long as these folds/wrinkles in the nuclear lamina allow them to take on diverse shapes26. The model predicts that nuclei will be soft or compliant in human tissue cells and become stiff only when the lamina is smooth, consistent with recent measurements15. Given that a smooth lamina is present only in extreme nuclear shapes, such as flattened or elongated nuclei, nuclei with a smooth lamina should be rare in vivo, as cells and nuclei in a 3D environment are less likely to be flattened.
Here, we tested the following predictions of this model for nuclear shaping in human tissues: (a) nuclear laminar folds and wrinkles are present in cells in diverse tissues, (b) nuclei with a smooth lamina are relatively rare, and c) nuclei assume a wide range of shapes when wrinkles/folds are present. We further determined whether laminar wrinkling is a quantifiable, diagnostically valid morphological marker of human cancers27.
Results
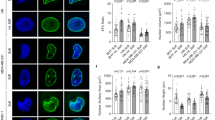
Nuclei in diverse control and cancer tissues have a wrinkled nuclear lamina
The drop model predicts that rounded nuclei contain laminar folds/wrinkles. Supplementary Fig. 1 illustrates this, where MDCK cells in 2D culture are both flatter and less wrinkled than those in an acinus, consistent with the hypothesis that nuclei geometrically develop folds in their rounded shapes. We reasoned that in contrast to cultured cells, epithelial nuclei in human patient tissues are unlikely to be flattened because cells in vivo do not adhere to flat and stiff smooth surfaces but rather adhere to a three-dimensional extracellular matrix. Thus, there should be folds and wrinkles in the nuclear lamina in normal as well as cancer tissues, unless cancer causes nuclear flattening or reduces the area of the nuclear lamina at a constant nuclear volume. Therefore, we imaged the nuclear lamina in diverse patient tissues, including grade 1–3 cancer tissues and cancer adjacent or normal tissues. We immunostained formalin-fixed paraffin-embedded (FFPE) human tissue microarrays for lamin B1 and pan-cytokeratin as a marker of normal epithelial and carcinoma cells and performed high-resolution confocal microscopy using head and neck, skin, ovarian, breast, colon, and thyroid tissues (Fig. 1). Most nuclei in cytokeratin-stained cells had some degree of folding/wrinkling in the nuclear lamina, in both control and cancer tissues. The only tissue that had predominantly nuclei with a smooth lamina was pure breast ductal carcinoma in situ (DCIS). Patients with DCIS who also had invasive carcinoma elsewhere had a visually higher percentage of nuclear wrinkling than those with pure DCIS. These data confirm our predictions that nuclei in diverse normal and cancer tissues in vivo contain folds/wrinkles in the nuclear lamina, and nuclei with a smooth lamina are rare in vivo. Visual inspection, which was also shown quantitatively by deep learning in Fig. 3, suggested an increased prevalence of laminar wrinkling in all cancer types relative to controls.
a Formalin-fixed paraffin-embedded (FFPE) tissue stained for lamin B1 (yellow or gray) and pan-cytokeratin (magenta), imaged at 20× (left) and 60× (middle). The right columns show zoomed regions from the 60× image. Head and Neck (HN) tissue. b Skin (SK). CAT: Cancer Adjacent Tissue. c Ovarian (OV). d Breast (BR). e Colon (CO). f Thyroid (TH). Scale bars are 100, 20, and 5 µm for 20×, 60× inset, and 60× zoom, respectively.
Nuclei with a wrinkled lamina should assume diverse shapes because there is little mechanical resistance to shape deformation14. In contrast, nuclei with smooth lamina should be “stiff” to deformation, resulting in a narrower range of shapes. To test this prediction, we compared shapes in DCIS, where the lamina was smoother, vs. invasive breast carcinoma, where nuclei were wrinkled. We computed the perimeter of the shapes in excess to that of a circle of the same area. The standard deviation of the excess perimeter was significantly higher in invasive cancer compared to DCIS, confirming that nuclear shapes are highly variable when there are more folds/wrinkles in the nuclear lamina (Fig. 2a). The diversity of nuclear shapes in wrinkled nuclei in invasive carcinoma as opposed to smooth nuclei in DCIS is also apparent visually (Fig. 2b).
a Excess perimeter distribution for pooled ductal carcinoma in situ (DCIS) patient nuclei and pooled breast cancer nuclei. Mean values were calculated from DCIS (n = 1882) and invasive cancer (n = 4575) nuclei. Error bars present standard deviations. b Collage of nuclei observed in formalin-fixed paraffin-embedded (FFPE) DCIS tissue sample (left) and invasive cancer samples (right) stained for lamin B1. c Frozen normal and cancer breast tissue fixed with acetone and stained for lamin B1. Scale bar is 5 µm. d Top: FFPE tissue section exhibiting shrinkage in the form of empty spaces (visible in brightfield) stained for lamin B1 (yellow) and pan-cytokeratin (magenta). Scale bar is 20 µm for 60× and 5 µm for zoomed. Below are zoomed regions from the lamin B1 image above (gray). e FFPE tissue sections featuring adjacent smooth and wrinkled nuclei. Scale bar is 5 µm. All images were taken at 60×.
Nuclear wrinkles are not an artifact of tissue processing
Although FFPE samples are the workhorse of pathological diagnosis, and nuclear abnormalities observed in these samples inform routine diagnosis, FFPE sample preparation may contribute to nuclear wrinkling. Therefore, we stained frozen, acetone-fixed normal, and breast cancer tissue for lamin B1. Unlike FFPE tissue, which is fixed in formalin for 24 to 48 h, our frozen tissue was snap-frozen in the gas phase of liquid nitrogen after embedding in an optimum cutting temperature compound and was then fixed for only 15 min in acetone. Our frozen tissue did not undergo the FFPE heat- and pH-based antigen retrieval process to reduce excessive crosslinking from lengthy formalin fixation. Unlike FFPE tissue, which is washed with xylene and ethanol, frozen tissue is air-dried before blocking. Despite these major processing differences, nuclear wrinkling was also observed in frozen cancer and control tissues (Fig. 2c). As shrinkage due to formalin fixation28,29 or other factors30 may cause nuclear wrinkling, we examined some FFPE tissue samples with shrinkage, indicated by blank spaces31, and found cases with smooth nuclei in these regions, demonstrating that tissue shrinkage does not necessarily result in wrinkled nuclei (Fig. 2d). Further, we found many examples of adjacent smooth and wrinkled nuclei in the same FFPE tissue sample for diverse tissue types (Fig. 2e). Finally, as processing artifacts cannot explain the systematic and reproducible differences in nuclear laminar wrinkling across tissue types (Fig. 1), it is very unlikely that nuclear wrinkles are sample preparation artifacts.
Extreme nuclear wrinkling is a morphological feature of diverse cancers
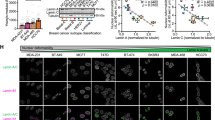
Our results demonstrated that the nuclear lamina in both control and cancer tissues contains folds/wrinkles, but nuclear laminar irregularities appeared to be more common in cancer compared to control tissue (Fig. 1). To quantify wrinkling, we used deep learning to classify nuclear laminar irregularities. Based on visual inspection of thousands of nuclei, we chose five classification categories, (1) out-of-focus/wrongly-cropped nuclei, (2) smooth nuclei, (3) nuclei with low frequency contour waviness, (4) nuclei with high frequency contour waviness, and 5) nuclei with inner wrinkles (Fig. 3a). We found that inner wrinkling and high frequency contour waviness represented distinct types of extreme nuclear wrinkling. Inner wrinkles appeared due to deep invaginations in the lamina, while surface wrinkling without deep invaginations appeared as high frequency contour waviness, which corresponds closely with the “star-like” or “garland-like” nuclei reported in emerin-stained thyroid carcinoma samples32,33.
a Examples of nuclei sorted into classes 0–5 for deep learning model training. 0 = invalid nuclei, 1 = smooth, 2 = low frequency contour waviness, 3 = high frequency contour waviness, and 4 = inner wrinkles. b ResNet50 architecture of our model. An input image is processed through a 7×7 convolutional layer followed by max pooling. The network includes multiple residual learning blocks increasing in depth and complexity, each containing convolutional layers of varying filter sizes, with skip connections to ensure efficient training and feature extraction by mitigating the vanishing gradient problem. After feature extraction, we used an average pooling layer and a fully connected layer with a softmax function to classify the images into the five categories. c Bar plots showing the normalized corrected count of nuclei in each class. i. Head and neck; n = 1851, 2605, 1619, 1943, 1737 nuclei for adjacent, grades 1–3, respectively. ii. Skin; n = 848, 4180, 1637, 1487, 890 nuclei for adjacent, basal cell carcinoma (BCC), grades 1–3. iii. Ovary; n = 197, 3009, 2685, 10044, 1933, 3223, 4507 nuclei for control, mucinous, low grade serous, high grade serous, grades 1–3 endometrioid adenocarcinoma. iv. Breast; n = 3223, 2095, 859, 4296, 1054 nuclei for adjacent, ductal carcinoma in situ (DCIS), grades 1–3. v. Colon; n = 1458, 2147, 7011, 2521 nuclei for adjacent, grades 1–3. vi. Thyroid; n = 303, 10412 nuclei for normal and cancer, respectively. Error bars present a 95% confidence interval of the mean. *False discovery rate adjusted p < 0.05 by the Benjamini–Hochberg procedure.
To train the deep learning algorithm, we used Cellpose34 to segment and crop nuclei from confocal microscopy images of control and breast cancer tissue and then sorted them manually into the five nuclear shape categories. Only nuclei in pan-cytokeratin-expressing cells that passed a focus test were included in the analysis, thereby excluding about 45% of nuclei. These cropped images were used to train a multi-class classifier (Fig. 3b). We implemented a transfer learning approach using a pre-trained ResNet50 model, which was fine-tuned to our specific dataset (see methods). The deep learning model was trained on several thousand segmented nuclei, with a high overall classification accuracy of 90.26%, confirming the robustness of the model. The model achieved a high overall F1-score of 0.9014 and an area under the receiver operating characteristic curve (AUC) value of 0.9809, indicating excellent precision, recall, and discriminative ability across classes. Class-specific performance, expressed in the confusion matrix, was 88.21% for smooth nuclei, 90.65% for low frequency contour waviness, 94.29% for high frequency contour waviness, 90.63% for inner wrinkles, and 86.02% for less typical nuclei (out of focus). We used this model to classify nuclear wrinkling types across diverse cancer cell types whose nuclei were cropped the same as the training data. The model sorted thousands of nuclei from the control and cancer grades 1–3 for each tissue type, with 50–80 patients per tissue type. Patient information is included in Supplementary Table 1. Tumor grade was determined as the majority decision based on the grades of two external pathologists and the grade provided by the tissue supplier’s pathologists. In the few cases where all three evaluations differed, we assigned the grade provided by the tissue supplier company. Results were quantified using a corrected, normalized count considering individual class accuracies.
We found that low frequency contour waviness in the nuclear lamina was the most prevalent wrinkling type in every cancer and control tissue (Fig. 3c, Supplementary Table 2, and Supplementary Data 1), consistent with our observations in Fig. 1, in which even control tissues exhibited wrinkling. Breast, skin, and thyroid cancers exhibited a similar pattern, with smoother nuclei more prevalent in adjacent tissue and reduced in cancerous tissues. Conversely, high frequency wrinkles were consistently more frequent in cancer tissue compared to control tissue in these three cancer types. Notably, breast DCIS tissue had a high fraction of smooth nuclei, consistent with our visual observations (Fig. 1). Head and neck cancer tissues had fewer smooth nuclei in cancer tissue compared to control. Nuclei with inner wrinkles were more prevalent in this cancer type compared to high frequency contours. Ovarian and colon cancer tissues had a low frequency of smooth nuclei in adjacent tissue, consistent with our visual observations (Fig. 1). Although the high frequency contours were much more prevalent in tissue from ovarian cancer vs. the control, tissue from colon cancer showed more subtle differences in extreme wrinkling compared to control tissue. Collectively, these findings show that extreme wrinkling of the nuclear lamina, comprising high frequency wrinkles and inner wrinkles, is a morphological hallmark of diverse cancers.
We also found that extreme nuclear wrinkling was more prevalent in ovarian, breast, colon, and thyroid cancers that had lymph node involvement (Fig. 4 and Supplementary Table 3). We used the TNM classification, where an N value greater than or equal to 1 represents lymph node involvement. This result, consistent with the trend observed in tumor grades (Fig. 3c), indicates that extreme nuclear wrinkling may be associated with cancer progression and metastatic potential. In this analysis, head neck, and skin tumors were excluded due to the low number of lymph node metastases observed in these tissues in our dataset.
Bar plots show the normalized corrected count of nuclei in each wrinkling class. i. Ovary; n = 134, 16944, 2414 nuclei for control, TNM grade N0, and N1, respectively. ii. Breast; n = 2541, 5124, 2489, 510 nuclei for control, N0–N2. iii. Colon; n = 1458, 7479, 2514, 1686 nuclei for control, N0–N2. iv. Thyroid; n = 303, 8395, 1601 nuclei for control, N0, and N1. Error bars present a 95% confidence interval of the mean. *False discovery rate adjusted p < 0.05 by the Benjamini–Hochberg procedure. Patient information is in Supplementary Table 3.
Elliptical Fourier analysis reveals that laminar contour irregularity is higher in cancer tissues
To confirm that the high frequency laminar contour waviness revealed by the deep learning model was more common in cancers, we also used elliptical Fourier analysis, which specifically quantifies contour irregularities35. For the Fourier analysis, we needed accurate segmentation of nuclear contours; however, segmentation of the nucleus using Cellpose was unsuccessful as it tended to smooth out micron and sub-micron variations in the nuclear contour. Given that imaging nuclear lamins produces a clearly delineated thin boundary, we adapted a previously developed method used to segment microtubules36 to segment the nuclear shape (Supplementary Fig. 2a). Briefly, the method approximated nuclear segmentation using the deep learning program Cellpose, then normal lines were computationally drawn around the Cellpose mask, and the point on each line with maximum intensity was taken as the most likely location of the nuclear lamina. Limited smoothing connected the points around the nuclear contour. This method resulted in clear and visually accurate segmentation of the nuclear contour (Supplementary Fig. 2a). We performed elliptical Fourier analysis on the segmented contours and calculated the elliptical Fourier coefficient (EFC) ratio for each nucleus (see methods for the definition of this parameter). The EFC ratio varied inversely with the visible level of nuclear irregularity and was a much more sensitive metric than the commonly used solidity parameter (Supplementary Fig. 2b). Our segmentation and EFC ratio quantification methods applied to a standard field of view are shown in a heat map in Supplementary Fig. 2c.
Using the same approach to restrict our analysis to only in-focus nuclei from cytokeratin-stained cells described above, we compared the distributions of EFC ratios visually via kernel density estimate (KDE) plots (Fig. 5) and formally via robust statistical tests for means and scales (standard deviations) between control and pooled cancer grades and between each cancer type. As a positive control, we also computed nuclear area, which is higher in cancer8, and compared their distributions. To address potential imbalances in the number of nuclei per sample and their impact on the statistical analysis, Nnuclei distinct nuclei were randomly selected from the set of all imaged nuclei per sample, separately for each tissue type. A total of R = 100 random data subsets were generated for each tissue type and the common number Nnuclei of nuclei in each subset was set to the minimum number of nuclei imaged across all samples within that tissue type (Supplementary Table 4). Subsequently, we performed KDE analyses separately in each random data subset. The estimated kernel densities from the R = 100 random subsets were combined by averaging (i.e., mixing the densities with equal weights). The computed test statistics obtained across the random replicates were also combined via averaging (meta-analysis), and the resulting approximate chi-squared p-values were derived from the averaged test statistics (Fig. 5). EFC ratios varied between control and cancer tissue depending on cancer type, with a lower EFC ratio for head and neck and skin cancer compared to control tissues and a higher EFC ratio for colon cancer. In ovarian, breast, and thyroid cancer, there was a trend toward lower EFC ratios compared to control tissues, but differences in the mean values lacked statistical significance. In contrast, nuclear area was higher in cancer tissue compared to control tissue in all cancer types. These results suggest that nuclear contour irregularity is a marker for a subset of cancers. Given that deep learning detects differences in extreme wrinkling across all cancers, the small differences in EFC ratios in some cancers may reflect the inability of elliptical Fourier analysis to fully capture nuclear wrinkling, especially folds inside the nuclear body. Also, the small differences in some cases may be due to low frequency contour waviness, which is similar across cancer and control tissues and may be as frequent or more frequent than high frequency waviness. This might mask the contribution of low EFC ratios, which represent the high frequency waviness, in the comparisons.
Kernel density plots show the distribution of elliptical Fourier coefficient (EFC) ratios and nuclear areas for control and cancer tissues and for different tumor grades. The estimated kernel densities from the R = 100 random subsets were combined by averaging (see Methods). a Head and neck tissue; n = 1508, 1951, 1336, 250, 1603, 5140 nuclei for adjacent, grades 1–3, and pooled tumor grades, respectively. b Skin tissue; n = 762, 3724, 1658, 1509, 907, 4074 nuclei for adjacent, basal cell carcinoma (BCC), grades 1–3, and pooled grades. c Ovarian tissue; n = 58, 1530, 2027, 7085, 1382, 2074, 3251, 6707 nuclei for control, mucinous, low grade serous, high grade serous, grades 1–3 endometrioid adenocarcinoma, and pooled grades. d Breast tissue; n = 2455, 1918, 819, 3859, 1054, 5732 nuclei for adjacent, ductal carcinoma in situ (DCIS), grades 1–3, and pooled grades. e Colon tissue; n = 904, 1416, 5987, 2110, 9513 nuclei for adjacent, grades 1–3, and pooled grades. f Thyroid tissue; n = 69, 6030 nuclei for adjacent and cancer. p values for equality of means and homogeneity of scales obtained from the Kruskal-Wallis test and the Fligner test and adjusted using Benjamini-Hochberg false discovery rate corrections are labeled.
To address this complication, we performed a linear discriminant-based posterior probability analysis to compare the probabilities of tumor grade or control for a given EFC ratio magnitude. We calculated the posterior probabilities, defining discrimination boundaries of cancer adjacent tissue vs. tumor grades under a uniform/flat prior assumption for tumor grade proportions, using a linear discriminant analysis of log-transformed nuclear EFC ratios, nuclear areas, and nuclear aspect ratios (Supplementary Fig. 3). EFC ratio values associated with control vs. cancer nuclei were significantly different with a clear separation between control tissue and cancer grades. Consistent with the results obtained using the deep learning analysis, low EFC ratios, corresponding to high frequency contour waviness, were especially predictive of cancer grades. These results confirm the results of the deep learning analysis that cancer is characterized by extreme nuclear wrinkling.
Discussion
Nuclear atypia is a common characteristic of human cancers. How nuclear shapes are established and maintained in human tissues and how they become abnormal in cancers is not understood. The drop model, which explains the role of the nuclear lamina in nuclear shaping25,26, predicts that a wrinkled nucleus can assume a range of shapes with little mechanical resistance. As the drop model was based only on in vitro experiments, here, we explored some predictions of the model for nuclear shapes in tissues.
We found that the nuclear lamina in diverse control and cancer tissues had folds/wrinkles accompanied by a wide variety of nuclear shapes. In a minority of tissues, the nuclear lamina was smooth, as it is in in vitro cultures, which is likely because nuclei in tissues rarely take on extremely flattened shapes as they do in culture. Further, we would expect predominantly wrinkled nuclei in patient tissues, as the lamina is assembled in a wrinkled state during mitosis because it forms around the non-smooth surface presented by postmitotic chromosomes37. In fact, this characteristic is directly visible in patient tissues (Supplementary Fig. 4). Our findings support the hypothesis that wrinkled nuclei are compliant15, yielding diverse nuclear shapes in tissues.
Nuclear wrinkling was common across diverse tissues; however, extreme wrinkling was more prevalent in cancer tissues than in control tissues in all cancer types studied. We quantified extreme wrinkling using both deep learning and elliptical Fourier analysis. Both methods demonstrated that extreme wrinkling, marked by increased waviness of the nuclear contour, was more frequent in cancer tissue.
The gold standard for cancer diagnosis is hematoxylin and eosin (H&E) imaging of tissue samples. Although nuclear shape irregularities have been quantified from H&E images38,39,40,41,42,43,44,45,46,47, it is unlikely that the high frequency wrinkling observed in lamin stains is visible in H&E images because hematoxylin yields a solidly stained nucleus, precluding sensitive visualization of nuclear contours. When we stained and imaged a tissue section using H&E and an adjacent section for lamin B1, we found that the lamin B1 stained nuclei showed the greater spatial detail that is necessary for visualizing wrinkling compared with the H&E images. Images of nuclei from the same field of a tissue sample immunostained for lamin B1 and counterstained with DAPI (4’,6-diamidino-2-phenylindole), which also stains DNA, confirmed this observation (Supplementary Fig. 5). The inability of DNA stains to produce detailed visualizations of nuclear contours is supported by studies using lamin27 or emerin32,33,48,49 stains, which have diagnostic or prognostic utility. In emerin-stained breast tissue in which nuclei were classified manually as having either low or high nuclear envelope pleomorphism (NEP), there was a correlation between NEP and lymph node metastasis48. This study identified folds in the nuclear contours of breast cancer cells but not in control tissues, perhaps because of the few control samples. In contrast, we observed nuclear folds in many of our control samples. Other studies used emerin stains in thyroid tissue samples to assist in the diagnosis of papillary thyroid carcinoma in borderline cases by providing a clearer image of the nuclear shape33,49. In these studies, a pathologist classified emerin-stained nuclei into different shape categories, including nuclei with garlands that we would consider to have high frequency contour waviness, and nuclei with grooves that appeared to be a type of inner nuclear wrinkling.
Others have used lamin or emerin stains to quantify nuclear shape. One group used deep learning on images of lamin-stained ovarian tissue and datasets of nuclear shape factors from lamin-stained images to successfully sort nuclei into healthy or cancer groups. However, they did not consider nuclear wrinkling and did not restrict the analysis to any cell types in their classification50. Another study of wrinkling in lung cancer measured the difference in perimeter between hematoxylin-stained and emerin-stained nuclei to estimate the occurrence of nuclear grooves or cytoplasmic inclusions51. Although this study indirectly quantified nuclear wrinkling, it required two nuclear stains to calculate the less precise excess perimeter value. In contrast, our study identified wrinkled nuclei in both cancer and control tissue and used deep learning and quantitative techniques to assess the degree of wrinkling. We found that segregating nuclei into the correct classes revealed extreme wrinkling as a hallmark of cancer. The quantitative Fourier analysis of nuclear contours supported this finding.
Based on our results, we suggest that using lamin-stained images as input for AI/deep learning in digital pathology to determine the extent of nuclear wrinkling could improve cancer diagnosis and prognosis for multiple tissue types, especially head and neck, skin, breast, and thyroid cancers. Lamin staining is a relatively inexpensive addition to standard pathology workflows. Although we used fluorescence microscopy, immunohistochemistry is an alternative method that is more common in pathology labs. Imaging the folds/wrinkles will likely require at least 40× magnification with a high numerical aperture ( ~ 1). Deconvolution of images obtained with a camera can result in images that approach the image quality from a confocal microscope32.
One caveat with our analysis is that, depending on the way tissues are sectioned and the extent of nuclear wrinkling, a wrinkled nucleus may appear more or less wrinkled52, or even smooth. However, as we imaged thousands of nuclei per condition (grade), these differences should be averaged across and even within samples.
The cause of extreme nuclear wrinkling in cancer tissues is not clear. To determine whether nuclear indentation by perinuclear actin explains nuclear laminar wrinkles17, we immunostained a tissue sample for lamin B1 and F-actin (Supplementary Fig. 6). Some cells contained visible perinuclear F-actin. In half of the cells that contained perinuclear F-actin, the F-actin fiber was associated with at least one laminar wrinkle. Nevertheless, even in these nuclei, other wrinkles were not visibly associated with perinuclear actin. Therefore, perinuclear actin does not explain most of the nuclear wrinkling observed in our tissue sections. Also, a visual inspection of contiguous tumor cell clusters did not indicate an obvious trend in wrinkling from the center to the edge of the clusters (Supplementary Fig. 7), indicating that location in the tumor does not explain higher wrinkling.
We have previously proposed that wrinkling may be induced geometrically in nuclei by rounding up flattened cells12. The rounding of a flattened nucleus with a smooth lamina at a constant volume induces wrinkles geometrically because a sphere provides the minimum surface area for a given volume. Likewise, cell rounding may occur in some cancers, due perhaps to crowding of proliferating cells. Further, the area of the nuclear lamina may be higher for a given nuclear volume in cancer compared to control tissue. Alternatively, irregular shapes may result from the depletion of lamin A/C, which occurs in diverse cancers53 and is associated with a worse prognosis54,55. In vitro, migrating lamin A/C null mouse embryonic fibroblasts deform without an apparent limit on areal expansion when they are indented by external, slender obstacles56. Consistent with these prior experiments, we observed a significantly lower lamin A/C:B1 ratio in breast cancer tissue compared to control tissue (Supplementary Fig. 8 and Supplementary Table 5), but no differences between breast cancer tissues of different grades. Among different cancer types, there were only minor differences in lamin A/C:B1 ratios between control and cancer tissue. Thus, a decrease in the lamin A/C:B1 ratio does not explain the systematic differences in nuclear wrinkling between control and cancer tissue.
Overall, we demonstrated that the nuclear shapes observed in diverse tissues are consistent with the drop model in which nuclei resist deformation only when the nuclear lamina is smooth12 and that a difference in the extent and type of nuclear laminar wrinkling is a characteristic morphological feature of diverse human cancers. The difference in nuclear wrinkling was identified by deep learning algorithms and quantitative analysis of segmented nuclear contours. Thus, extreme nuclear wrinkling is a potential morphological cancer biomarker that can be identified by digital pathology.
Methods
FFPE tissue immunostaining and imaging
Microarrays of 5-µm thick FFPE tissues (TissueArray) were deparaffinized with xylene, rinsed in ethanol, and rehydrated with a gradient of ethanol to deionized water. Heat-induced antigen retrieval was performed using a 1× universal antigen retrieval solution (Abcam) in an instant pot on the high setting for 20 min. The tissue was rinsed and blocked with blocking buffer (3% w/v bovine serum albumin, 1% v/v goat serum, and 0.1% Triton X-100 in phosphate-buffered saline (PBS)). Samples were incubated overnight at 4 °C with the primary antibodies in blocking buffer, including rabbit anti-lamin B1 (Abcam, Ab229025, diluted 1:2000), mouse anti-lamin A/C (Santa Cruz Biotech, sc-376248, diluted 1:100), and guinea pig anti-pan-cytokeratin antibody (LS-Bio, LS-B16812, diluted 1:50). Tissue was then incubated with secondary antibodies in PBS, including goat anti-rabbit Alexa Fluor 405 (Invitrogen, A48264, diluted 1:500), goat anti-rabbit Alexa Fluor 488 (Invitrogen, A11034, diluted 1:500), goat anti-guinea pig Alexa Fluor 594 (Invitrogen, A11076, diluted 1:500), and goat anti-mouse Alexa Fluor 647 (Invitrogen, A21235, diluted 1:500) for 1 h at room temperature (RT). DNA was counterstained with DAPI (Thermo Fisher Scientific, diluted to 1 µg/ml) for 5 min. Tissues were rinsed and mounted with Diamond Antifade mountant (Thermo Fisher Scientific) and imaged on an Olympus confocal microscope FV3000 with 20× (N.A. = 0.80) and 60× (N.A. = 1.50) objectives. Images for the lamin A/C:B1 ratio experiments were collected with a 60× objective (N.A. = 1.30) at constant laser intensity, gain, and offset settings so that imaging settings would not artificially change staining intensity between imaging fields. Brightness and contrast enhancements were applied to some images shown in the figures but not applied to those used for calculations.
FFPE tissue H&E staining and imaging
Tissue was deparaffinized as described above, incubated with hematoxylin for 3 min, rinsed, exposed to a differentiator (0.3% v/v HCl in 70% ethanol) for 2–3 s, rinsed, and treated for bluing with Scott’s tap water substitute. The tissue was then treated with 80% ethanol before incubation with eosin for 10 s. The tissue was rinsed and treated with xylene, mounted with DPX mountant (Sigma-Aldrich), and imaged on an Olympus confocal microscope with a 60× objective (N.A. = 1.50) and color camera (Olympus DP23).
Frozen tissue immunostaining
Unstained frozen tissue (OriGene Technologies) was stored at −80 °C. After a brief thawing, the tissue was fixed in ice-cold acetone for 10 min, which was removed prior to air-drying the samples for 20 min. The tissue samples were rinsed, blocked, and immunostained as described above for FFPE tissue immunostaining. F-actin staining was performed overnight at 4 °C in blocking buffer with mouse anti-F-actin (Abcam, ab205, diluted 1:100), followed by incubation in PBS with goat anti-mouse Alexa Fluor 647 (Invitrogen, A21235, diluted 1:500) for 1 h at RT.
Cell culture, staining, and imaging
Human head and neck cancer cell line HN (Deutsche Sammlung von Mikroorganismen und Zellkulturen GmbH) was grown in a humidified incubator at 37 °C and with 5% CO2 and cultured in Dulbecco’s Modified Eagle’s Medium with 4.5 g/l glucose (Corning), supplemented with 10% v/v donor bovine serum (Gibco) and 1% v/v penicillin/streptomycin (Corning). HN cells were rinsed with PBS before fixing with 4% paraformaldehyde (Alfa Aesar) for 15 min at RT. After treatment with permeabilization buffer (0.1% Triton X-100 (Thermo Fisher Scientific) and 1 mg/ml bovine serum albumin (Thermo Fisher Scientific) in PBS) for 1 h and blocking in superblock (Thermo Fisher Scientific) for 30 min, HN cells were exposed to primary antibodies in superblock overnight at 4 °C, including rabbit anti-lamin B1 (Abcam, Ab229025, diluted 1:500) and mouse anti-lamin A/C (Santa Cruz Biotechnology, sc-376248, diluted 1:200). Secondary staining was done at RT in PBS for 1 h and 40 min with goat anti-mouse Alexa Fluor 488 (Invitrogen, A32723, diluted 1:200) and goat anti-rabbit Alexa Fluor 647 (Invitrogen, A21244, diluted 1:200) antibodies. HN cells were imaged at 20× (N.A. = 0.80) with constant laser power settings so that imaging settings would not artificially change staining intensity between imaging fields.
MDCK cells were cultured in high glucose DMEM (Thermo Fisher Scientific), supplemented with 10% v/v Plenty (Omeat/Plenty Bio) and 1% v/v penicillin-streptomycin mix. For imaging of 2D MDCK cells, 35 mm glass bottom dishes were first coated with 1 μg/ml fibronectin (Corning) for 1 h, washed thrice with PBS, and seeded with cells. The cells were allowed to spread and fixed for imaging. For 3D acinar cultures, Nunc Lab Tek II 8-well chamber slides (Thermo Fisher Scientific, #155409) were coated with 15 μl of growth-factor-reduced (GFR) Matrigel (Corning) in each well and allowed to polymerize for at least 1 h at 37 °C. Then, the MDCK cells were trypsinized from tissue culture plates and suspended in the growth medium supplemented with 2% v/v Matrigel at a final concentration of 5 cells/µl. 400 μl aliquot of cells was added to each well of the chamber slide, and the cells were allowed to form acini for 7–12 days before fixation. The growth medium was changed every 3–5 days. 2D and 3D acinar MDCK samples were fixed with warm 2% paraformaldehyde for 10–15 min at 37 °C and washed thrice with PBS for 5 min each. The cells were permeabilized using 0.5% Triton X-100 in PBS for 30 min at RT, followed by 1-hour incubation with an immunofluorescence buffer (130 mM NaCl; 7 mM Na2HPO4; 3.5 mM NaH2PO4; 7.7 mM NaN3; 0.1% BSA; 0.2% Triton X-100; 0.05% Tween-20) supplemented with 10% goat serum at RT. The samples were incubated with rabbit anti-lamin A/C primary antibody (Abcam, diluted 1:1000) overnight at 4 °C, washed thrice with PBS, and incubated with goat anti-rabbit Alexa Fluor 594 secondary antibody (Abcam, diluted 1:1000) for 2 h at RT. Fixed-cell fluorescence imaging of 2D MDCK cells was performed using an Olympus FV3000 confocal microscope at 60× (N.A. = 1.5), whereas acini were imaged with an ImageXpress Ht.ai spinning disk confocal microscope (Molecular Devices) at 40× (N.A. = 1.15) with a 0.1 μm step size between z-slices.
Transfection with siRNAs
Depletion of lamin A/C level was performed using siRNA transfection according to the manufacturer’s protocol (Invitrogen). HN cells were cultured in a 12-well plate in antibiotic-free media at transfection with 0.5% lipofectamine RNAiMAX transfection reagent (Invitrogen) and 0.5% siRNA (Dharmacon, siGENOME Non-Targeting siRNA Pool #2, D-001206-14-05, target sequences: UAAGGCUAUGAAGAGAUAC, AUGUAUUGGCCUGUAUUAG, AUGAACGUGAAUUGCUCAA, UGGUUUACAUGUCGACUAA; LMNA siGENOME SMARTpool siRNA, D-004978-01, target sequence: GAAGGAGGGUGACCUGAUA) in the reduced serum Opti-MEM medium (Gibco). After 96 h, transfected cells were passed onto fibronectin-coated dishes and allowed to spread overnight before fixation the next day.
Segmentation of nuclear contour in tissue array images
Raw confocal images of tissue arrays were segmented using Cellpose34 for the initial identification of nuclei, except for control ovarian tissue, where high background and few epithelial nuclei necessitated manual generation of masks by tracing around the nuclear contour. The generated nuclear masks and the raw images were imported into MATLAB, where a customized MATLAB code was developed for precise segmentation and subsequent nuclear morphometric analysis. Nuclei touching the image border or below an empirically determined area threshold were eliminated to remove small debris or imaging artifacts. Since the bulk masks generated from Cellpose did not capture details like folds and wrinkles on nuclear contours, a more precise segmentation approach was employed where the intensity maxima were traced on each normal line along the bulk nuclear periphery, achieving sub-pixel resolution for delineating precise nuclear contours. Following precise segmentation, additional filters were applied to refine the selection of nuclei of interest. A contrast filter calculated the lamin intensity ratio between the maximum pixels and the pixels covered by normal lines for each nucleus. Nuclei with a contrast ratio below 1.5, indicating a blurry contour, were excluded. Similarly, a pan-cytokeratin filter calculated the pan-cytokeratin intensity ratio between the ring area outside the nucleus vs. inside. Nuclei with a pan-cytokeratin ratio below 1, indicative of non-epithelial cells, were also excluded.
Deep learning
For the nuclear morphological analysis, we implemented a deep learning approach to classify the types of nuclear wrinkling (out of focus/invalid nuclei, smooth, low frequency contour waviness, high frequency contour waviness, and inner wrinkles). Nuclei identified by the Cellpose algorithm that passed quality filters were cropped as individual images. A custom MATLAB code was built to annotate the five classes of the cropped nuclei from breast cancer tissue samples. These annotated images served as inputs to train a multi-class classifier. We implemented a transfer learning approach using a pre-trained ResNet50 model57, which was fine-tuned to our dataset. Transfer learning allowed us to utilize the comprehensive feature-detection capabilities of ResNet50, which had been initially trained on ImageNet dataset58, thereby accelerating our training process and enhancing the model accuracy with limited data. ResNet50, a convolutional neural network architecture known for its deep residual learning framework, is particularly effective in handling vanishing gradients, allowing the training of much deeper networks. This model features 50 layers, including residual blocks with skip connections to preserve gradient flow and bottleneck layers that reduce computational burden as they maintain processing depth. ResNet50 uses global average pooling to reduce overfitting and decrease the total number of parameters, enhancing its efficiency.
The training pipeline included a series of data augmentation techniques to enhance model robustness and address data imbalance due to varied representations of nuclear types across samples. Transformations included resizing to 224 × 224 pixels, random horizontal and vertical flips, rotations up to 15 degrees, color jittering for brightness, contrast, and saturation adjustments, random affine transformations, and center cropping to maintain focus on the nucleus. Normalization was performed with specific mean and standard deviation values typical for pre-trained networks on ImageNet. To counter data imbalance, these augmentation techniques were combined with resampling methods to equalize class presence in the training set. We expanded its applications to predict nuclear wrinkling types in other cancer types that were not in the initial dataset, as nuclear shapes are similar across each tissue type, enabling generalization of our model across all tissue types studied. Results were quantified using a corrected normalized count, considering individual class accuracies, providing a robust assessment of nuclear morphological variations.
Nuclear morphometric analysis
Nuclear irregularity was quantified using an elliptical Fourier analysis, as reported previously35. This approach approximates nuclear shapes by decomposing the shape into a series of harmonic ellipses59. The precise segmented contour was fitted using a series of elliptic harmonics, defined by Fourier series coefficients that were calculated from the x and y coordinates of the nuclear outline. 15 harmonic ellipses were employed in this study to effectively capture the complexity of irregular nuclei while avoiding overfitting smooth nuclei, which was verified by Fréchet distance calculations (Supplementary Fig. 9) and was also suggested in the literature35,60. Each single elliptic harmonic at different frequencies can be geometrically visualized as a pair of orthogonal semiaxes. The first-frequency Fourier coefficients describe a rough ellipsoidal shape, and the Fourier coefficients at higher frequencies approximate more convoluted outlines. To quantify the shape irregularity, EFC ratio is defined as the ratio of the length sum of the major and minor semiaxes at the first frequency to the sum of semiaxes lengths for the subsequent 14 harmonics at higher frequencies. A regular nuclear contour, where the first-frequency elliptic harmonic captures most of the contour with small axis lengths at higher frequencies, has a larger EFC ratio. Conversely, an irregular nuclear contour requires larger axes lengths at higher frequencies, resulting in a lower EFC ratio. Other parameters such as nuclear cross-section area \(A\), perimeter \(P\), solidity, and aspect ratio were quantified using the MATLAB Image Processing Toolbox. Excess perimeter was calculated by
where \({P}_{{circle}}\) is the perimeter of the circle and is geometrically related to \(A\) by
To quantify the level of lamin based on staining brightness, the mean pixel intensity was calculated within a peripheral area approximately 1 μm wide surrounding the nuclear contour for each nucleus.
Statistical analyses
To compare the proportions of nuclei belonging to four different wrinkling categories (smooth, low frequency, high frequency, and inner wrinkles as determined by the deep learning classifier) across different cancer grades and sites, we conducted a series of multi-class multinomial logistic regression models. We developed a separate model for each cancer site. These models used the expected/corrected counts (raw counts determined by the deep learning classifier multiplied by the probability of correct classification) of nuclei in the four wrinkling categories as multivariate responses, with cell types (cancer grades and adjacent cells) serving as explanatory variables. The models were fitted using the method of maximum likelihood. From each fitted model, we (a) estimated the probabilities (proportions) of each nuclear wrinkling category for adjacent and various cancer grades, along with their 95% confidence intervals, and (b) formally tested the differences between the probabilities of each wrinkling category across different cancer grades using marginal probability contrasts. To account for the multiplicity of hypothesis tests, we applied the Benjamini–Hochberg false discovery rate adjustment61,62. The results are presented in Fig. 3, which displays the estimated probabilities of each wrinkling category (normalized corrected counts) with their 95% confidence intervals represented by vertical bars with error whiskers. The corresponding pairwise test results are visualized through horizontal lines.
To compare the distributions of nuclear EFC ratios and areas for different cell types, we obtained kernel density estimates using default Gaussian kernels as implemented in the density function in R for the nuclear EFC ratios and areas, separately for each cell type—control, BCC (skin), DCIS (breast), serous and mucinous (ovary), and cancer—with individual grades in one set of analysis and all grades combined in another. To address potential imbalances in the number of nuclei per sample and their impact on the final KDE plots, as well as on the means and scales comparisons, we applied random data subsampling to ensure homogeneity in the number of nuclei per sample in each random subset. Specifically, Nnuclei distinct nuclei were randomly selected from the set of all imaged nuclei per sample, separately for each tissue type. A total of R = 100 random data subsets were generated for each tissue type and the common number Nnuclei of nuclei in each subset was set to the minimum number of nuclei imaged across all samples within that tissue type (Supplementary Table 4). KDE analysis was performed for the EFC ratios and nuclear areas separately for the adjacent, pooled cancer, and grade-specific cancer cells, and separately in each random data subset. Comparisons of the means and scales for the nuclear measurements were conducted using the Kruskal-Wallis test63 and the Fligner test64, respectively, for both adjacent vs. pooled cancer cells (two-sample) comparisons and adjacent vs. grade-specific cancer cells (multi-sample) comparisons. The estimated kernel densities from the R = 100 random subsets were combined by averaging (i.e., mixing the densities with equal weights). The computed test statistics obtained across the random replicates were also combined via averaging (meta-analysis), and the resulting approximate chi-squared p-values were derived from the averaged test statistics. This analysis was carried out separately for each metric (EFC ratio; nuclear area), measure (mean; scale), comparison (adjacent vs. pooled cancer; adjacent vs. grade-specific cancers), and tissue combination. The multiplicity of the p-values was addressed using Benjamini-Hochberg false discovery rate corrections61,62, and the adjusted p-values are reported in Fig. 5.
To assess cancer grade-specific discriminative information embedded in the nuclear wrinkling measurements, we performed a posterior probability analysis based on linear discriminants separately for each cancer site and nuclear morphometric measurements (EFC ratio, area, and aspect ratio). With a log-normal probability distribution assumption—effectuated by a normality assumption on the log-transformed measurements—made separately for each of the three nuclear morphometric measurements at each cancer site, a linear discriminant analysis was performed to obtain the discrimination boundaries for adjacent, BCC (skin), DCIS (breast), individual cancer grade cells and all cancer cells combined (grouping all individual grades). In the absence of reliable population-level (prior) estimates for the prevalence/proportions of the different cancer grades, a flat/uniform probability distribution allocating equal weights to the different cancer grades was assumed. The flat prior provides a way to assess the discriminative information solely in the nuclear morphometry measurements by invoking a theoretical population where the different cancer grades and adjacent cells are equally prevalent. From the computed linear discriminants, the resulting posterior probabilities for a nucleus to be one of the different cell types—adjacent or one of the different cancer grades—were obtained for a range of values of the underlying nuclear morphometric measurement. The resulting posterior probabilities were plotted on the y-axis as a function of the nuclear morphometric measurement on the x-axis, yielding curves that were color-coded by the cell type (Supplementary Fig. 3).
Data availability
The datasets used and analyzed during the current study are available from the corresponding author on reasonable request.
Code availability
The underlying code for this study is not publicly available but may be made available to qualified researchers on reasonable request from the corresponding author. Segmentation of nuclear contour and nuclear morphometric analysis were performed using custom MATLAB scripts (version R2024a). The data preprocessing, augmentation, and fine-tuning pipeline for nuclear wrinkling classification was implemented using a custom Python script with PyTorch (version 2.4.1+cu121) and torchvision (version 0.19.1+cu121). Statistical analyses for comparing wrinkling categories, EFC distribution, and posterior probability were performed using custom R scripts (version 4.3.0).
References
Beale, L. Examination of sputum from a case of cancer of the pharynx and the adjacent parts. Arch. Med 2, 1860–1861 (1860).
Krishnamurti, U. G., Fitzgibbons, P. L., Connolly, J. L. Protocol for the Examination of Resection Specimens from Patients with Invasive Carcinoma of the Breast, https://www.cap.org/protocols-and-guidelines/cancer-reporting-tools/cancer-protocol-templates#protocols (2023).
Fitzgibbons, P. L., Connolly, J. L. Protocol for the Examination of Biopsy Specimens from Patients with Ductal Carcinoma In Situ (DCIS) of the Breast https://www.cap.org/protocols-and-guidelines/cancer-reporting-tools/cancer-protocol-templates#protocols (2021).
Mete, O. Protocol for the Examination of Specimens From Patients With Carcinomas of the Thyroid Glan, https://www.cap.org/protocols-and-guidelines/cancer-reporting-tools/cancer-protocol-templates#protocols (2023).
Seethala, R. R. Protocol for the Examination of Specimens from Patients with Cutaneous Squamous Cell Carcinoma of the Head and Neck, https://www.cap.org/protocols-and-guidelines/cancer-reporting-tools/cancer-protocol-templates#protocols (2022).
Crothers, B. A. Protocol for the Examination of Specimens From Patients With Primary Tumors of the Ovary, Fallopian Tube, or Peritoneum, https://www.cap.org/protocols-and-guidelines/cancer-reporting-tools/cancer-protocol-templates#protocols (2023).
Seethala, R. R. Protocol for the Examination of Specimens From Patients With Cancers of the Larynx https://www.cap.org/protocols-and-guidelines/cancer-reporting-tools/cancer-protocol-templates#protocols (2023).
Fischer, E. G. Nuclear morphology and the biology of cancer cells. Acta Cytol. 64, 511–519 (2020).
Singh, I. & Lele, T. P. Nuclear morphological abnormalities in cancer: a search for unifying mechanisms. Results Probl. Cell Differ. 70, 443–467 (2022).
Deville, S. S. & Cordes, N. The extracellular, cellular, and nuclear stiffness, a trinity in the cancer resistome-a review. Front Oncol. 9, 1376 (2019).
Dubik, N. & Mai, S. Lamin A/C: Function in Normal and Tumor Cells. Cancers 12, https://doi.org/10.3390/cancers12123688 (2020).
Lele, T. P., Dickinson, R. B. & Gundersen, G. G. Mechanical principles of nuclear shaping and positioning. J. Cell Biol. 217, 3330–3342 (2018).
Dahl, K. N., Kahn, S. M., Wilson, K. L. & Discher, D. E. The nuclear envelope lamina network has elasticity and a compressibility limit suggestive of a molecular shock absorber. J. Cell Sci. 117, 4779–4786 (2004).
Wang, T.-C. et al. Matrix stiffness drives drop like nuclear deformation and lamin A/C tension-dependent YAP nuclear localization. Nat. Commun. 15, 10151 (2024).
Tang, W. et al. Indentation induces instantaneous nuclear stiffening and unfolding of nuclear envelope wrinkles. Proc. Natl Acad. Sci. USA 120, e2307356120 (2023).
Dickinson, R. B., Katiyar, A., Dubell, C. R. & Lele, T. P. Viscous shaping of the compliant cell nucleus. APL Bioeng. 6, 010901 (2022).
Cosgrove, B. D. et al. Nuclear envelope wrinkling predicts mesenchymal progenitor cell mechano-response in 2D and 3D microenvironments. Biomaterials 270, 120662 (2021).
Swift, J. & Discher, D. E. The nuclear lamina is mechano-responsive to ECM elasticity in mature tissue. J. Cell Sci. 127, 3005–3015 (2014).
Jackson, J. A. et al. Scaling behaviour and control of nuclear wrinkling. Nat. Phys. 19, 1927–1935 (2023).
Katiyar, A. et al. Nuclear size changes caused by local motion of cell boundaries unfold the nuclear lamina and dilate chromatin and intranuclear bodies. Soft Matter 15, 9310–9317 (2019).
Neelam, S., Hayes, P. R., Zhang, Q., Dickinson, R. B. & Lele, T. P. Vertical uniformity of cells and nuclei in epithelial monolayers. Sci. Rep. 6, 19689 (2016).
Lomakin, A. et al. The nucleus acts as a ruler tailoring cell responses to spatial constraints. Science 370, eaba2894 (2020).
Venturini, V. et al. The nucleus measures shape changes for cellular proprioception to control dynamic cell behavior. Science 370, eaba2644 (2020).
Kim, D.-H. et al. Volume regulation and shape bifurcation in the cell nucleus. J. cell Sci. 128, 3375–3385 (2015).
Dickinson, R. B. & Lele, T. P. Nuclear shapes are geometrically determined by the excess surface area of the nuclear lamina. Front Cell Dev. Biol. 11, 1058727 (2023).
Dickinson, R. B. & Lele, T. P. A new function for nuclear lamins: providing surface tension to the nuclear drop. Curr. Opin. Biomed. Eng. 28, https://doi.org/10.1016/j.cobme.2023.100483 (2023).
Bussolati, G. Proper detection of the nuclear shape: ways and significance. Rom. J. Morphol. Embryol. 49, 435–439 (2008).
Chen, C. H. et al. Shrinkage of head and neck cancer specimens after formalin fixation. J. Chin. Med. Assoc. 75, 109–113 (2012).
Kshithi, K. et al. Effect of formalin fixation on tumour size and margins in head and neck cancer specimens. Acta Otorhinolaryngol. Ital. 42, 434–440 (2022).
Horn, C. L. & Naugler, C. Breast specimen shrinkage following formalin fixation. Pathol. Lab Med Int 6, 11–14 (2014).
Rastogi, V. et al. Artefacts : A Diagnostic Dilemma - A Review. J. Clin. Diagn. Res 7, 2408–2413 (2013).
Asioli, S. & Bussolati, G. Emerin immunohistochemistry reveals diagnostic features of nuclear membrane arrangement in thyroid lesions. Histopathology 54, 571–579 (2009).
Kinsella, M. D., Hinrichs, B., Cohen, C. & Siddiqui, M. T. Highlighting nuclear membrane staining in thyroid neoplasms with emerin: review and diagnostic utility. Diagn. Cytopathol. 41, 497–504 (2013).
Stringer, C., Wang, T., Michaelos, M. & Pachitariu, M. Cellpose: a generalist algorithm for cellular segmentation. Nat. Methods 18, 100–106 (2021).
Tamashunas, A. C. et al. High-throughput gene screen reveals modulators of nuclear shape. Mol. Biol. cell 31, 1392–1402 (2020).
Wu, J. et al. Effects of dynein on microtubule mechanics and centrosome positioning. Mol. Biol. Cell 22, 4834–4841 (2011).
Naetar, N., Ferraioli, S. & Foisner, R. Lamins in the nuclear interior - life outside the lamina. J. Cell Sci. 130, 2087–2096 (2017).
Tipoe, G. L. & White, F. H. Quantitative assessment of normal and potentially premalignant epithelium at different levels of human colorectal crypts. Histol. Histopathol. 13, 395–404 (1998).
Tan, P. H., Goh, B. B., Chiang, G. & Bay, B. H. Correlation of nuclear morphometry with pathologic parameters in ductal carcinoma in situ of the breast. Mod. Pathol. 14, 937–941 (2001).
Axelrod, D. E. et al. Effect of quantitative nuclear image features on recurrence of Ductal Carcinoma In Situ (DCIS) of the breast. Cancer Inf. 6, 99–109 (2008).
Wang, X. et al. Prediction of recurrence in early stage non-small cell lung cancer using computer extracted nuclear features from digital H&E images. Sci. Rep. 7, 13543 (2017).
Lu, C. et al. An oral cavity squamous cell carcinoma quantitative histomorphometric-based image classifier of nuclear morphology can risk stratify patients for disease-specific survival. Mod. Pathol. 30, 1655–1665 (2017).
Rawat, R. R., Ruderman, D., Macklin, P., Rimm, D. L. & Agus, D. B. Correlating nuclear morphometric patterns with estrogen receptor status in breast cancer pathologic specimens. NPJ Breast Cancer 4, 32 (2018).
Whitney, J. et al. Quantitative nuclear histomorphometry predicts oncotype DX risk categories for early stage ER+ breast cancer. BMC Cancer 18, 610 (2018).
Nag, R., Chatterjee, J., Paul, R. R., Pal, M. & Das, R. K. in 2018 International Conference on Current Trends towards Converging Technologies (ICCTCT). 1-6 (IEEE).
Ji, M. Y. et al. Nuclear shape, architecture and orientation features from H&E images are able to predict recurrence in node-negative gastric adenocarcinoma. J. Transl. Med 17, 92 (2019).
Dodington, D. W. et al. Analysis of tumor nuclear features using artificial intelligence to predict response to neoadjuvant chemotherapy in high-risk breast cancer patients. Breast Cancer Res. Treat. 186, 379–389 (2021).
Bussolati, G., Marchio, C., Gaetano, L., Lupo, R. & Sapino, A. Pleomorphism of the nuclear envelope in breast cancer: a new approach to an old problem. J. Cell Mol. Med 12, 209–218 (2008).
Coban, I. et al. Emerin expression in well differentiated epithelial lesions of thyroid: implications in papillary thyroid carcinoma diagnosis and predicting malignant behavior. Pathol. Oncol. Res. 21, 357–366 (2015).
Sengupta, D. et al. A deep hybrid learning pipeline for accurate diagnosis of ovarian cancer based on nuclear morphology. PLoS One 17, e0261181 (2022).
Kobayashi, S. et al. Image analysis of the nuclear characteristics of emerin protein and the correlation with nuclear grooves and intranuclear cytoplasmic inclusions in lung adenocarcinoma. Oncol. Rep. 41, 133–142 (2019).
Papotti, M., Manazza, A. D., Chiarle, R. & Bussolati, G. Confocal microscope analysis and tridimensional reconstruction of papillary thyroid carcinoma nuclei. Virchows Arch. 444, 350–355 (2004).
Irianto, J., Pfeifer, C. R., Ivanovska, I. L., Swift, J. & Discher, D. E. Nuclear lamins in cancer. Cell Mol. Bioeng. 9, 258–267 (2016).
Bell, E. S. et al. Low lamin A levels enhance confined cell migration and metastatic capacity in breast cancer. Oncogene 41, 4211–4230 (2022).
Urciuoli, E. et al. Nuclear Lamins and Emerin Are Differentially Expressed in Osteosarcoma Cells and Scale with Tumor Aggressiveness. Cancers12, https://doi.org/10.3390/cancers12020443 (2020).
Katiyar, A. et al. The Nucleus Bypasses Obstacles by Deforming Like a Drop with Surface Tension Mediated by Lamin A/C. Adv. Sci. 9, e2201248 (2022).
He, K. M., Zhang, X. Y., Ren, S. Q. & Sun, J. Deep Residual Learning for Image Recognition. Proc Cvpr Ieee, 770-778, https://doi.org/10.1109/Cvpr.2016.90 (2016).
Deng, J. et al. ImageNet: A Large-Scale Hierarchical Image Database. Cvpr: 2009 IEEE Conf. Comput. Vis. Pattern Recognit. s 1-4, 248–255 (2009).
Diaz, G., Zuccarelli, A., Pelligra, I. & Ghiani, A. Elliptic Fourier analysis of cell and nuclear shapes. Comput. Biomed. Res. 22, 405–414 (1989).
Lammerding, J. et al. Lamins A and C but not lamin B1 regulate nuclear mechanics. J. Biol. Chem. 281, 25768–25780 (2006).
Benjamini, Y. & Hochberg, Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc.: Ser. B (Methodol.) 57, 289–300 (1995).
Benjamini, Y. & Yekutieli, D. The control of the false discovery rate in multiple testing under dependency. Ann. Stat. 29, 1165–1188 (2001).
Holander, M. & Wolfe, D. A. Nonparametric statistical methods. New York: John Wilew and Sons Inc. Publications 497 (1973).
Conover, W. J., Johnson, M. E. & Johnson, M. M. A comparative study of tests for homogeneity of variances, with applications to the outer continental shelf bidding data. Technometrics 23, 351–361 (1981).
Acknowledgements
TPL, CPRIT Scholar in Cancer Research, acknowledges support from NIH U01 CA225566 and CPRIT Established Investigator Award RR200043. VCS is supported by the National Institute of Dental and Craniofacial Research (R21DE032344) and the VA Office of Research and Development (1I01CX002776). The content of this manuscript does not represent the views of the Department of Veterans Affairs or the U.S. Government. We thank K. Myers for her input at an earlier stage of this project.
Author information
Authors and Affiliations
Contributions
TCW, CRD, IS, and TPL conceived the study. TCW, CRD, SM, HP, SC, VCS, and TPL wrote the manuscript. TCW developed code for the segmentation of nuclear contours and Fourier analysis, quantified nuclear shapes, developed code to sort nuclei for deep learning analysis, and presented the visualization of quantification. CRD performed tissue staining and imaging experiments, developed the H&E staining and frozen tissue staining protocol, and sorted nuclei to create the training data set for the deep learning analysis. SM trained the deep learning model. HP cultured, stained, and imaged the MDCK 2D and 3D acinar cell culture. SA performed transfection of siRNAs. IS developed the FFPE immunostaining protocol. VT and DGR graded all tissue samples used in the manuscript. SC, TCW, and CRD performed statistical analysis.
Corresponding author
Ethics declarations
Competing interests
VCS is a consultant and equity holder for Femtovox Inc (unrelated to current work). TCW, CRD, SM, HP, SA, IS, VT, DGR, SC, and TPL declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wang, TC., Dollahon, C.R., Mishra, S. et al. Extreme wrinkling of the nuclear lamina is a morphological marker of cancer. npj Precis. Onc. 8, 276 (2024). https://doi.org/10.1038/s41698-024-00775-8
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41698-024-00775-8