Abstract
Common genetic variation detected by genome-wide association studies (GWAS) partially explains variability in the spectrum of cardiac phenotypes. In this work, we explore genetic correlations among 58 cardiac-related traits/diseases, detecting novel ones. We subsequently employ multi-trait analysis of GWAS (MTAG), which meta-analyzes genetically correlated traits, to improve genomic loci discovery and prediction in atrial fibrillation (AF), coronary artery disease (CAD), and heart failure (HF). We identify 19 novel loci specific for AF, 131 for CAD, and 141 for HF. Polygenic scores (PGS) in 15,177 Canadian individuals show similar results when PGS are derived from conventional GWAS versus MTAG summary statistics, although MTAG-PGS improve prediction and discrimination of CAD in females [∆R2 1.735% (95% Confidence Interval (CI): 0.609–2.856); Net reclassification index 0.208 (95%CI: 0.139–0.277)]. This work describes new relevant genetic correlations among cardiac-related traits/diseases and supports MTAG to improve loci discovery in common cardiovascular diseases and potentially improve the prediction of CAD in females.
Similar content being viewed by others
Introduction
Genome-wide association studies (GWAS) have mapped numerous single-nucleotide polymorphisms (SNP) in loci implicated in molecular mechanisms altered in common complex diseases, thus providing guidance in the investigation of novel drug targets1.
Atrial fibrillation (AF), coronary artery disease (CAD), and heart failure (HF) are common heart diseases, with a prevalence of 8%2, 2.5%3 and 2.5%4, respectively. The genetic substrate of these diseases is partly explained by genomic loci harboring common genetic variants in the general population. This substrate may overlap with cardiovascular (CV) diseases and traits, and such overlap can be quantified using genetic correlation.
Polygenic scores (PGS) intend to account for the genetic susceptibility due to common genetic variants, i.e., SNPs, and may be useful for the susceptibility to disease assessment in order to set up preventive strategies among high-risk individuals.
Multi-trait analysis of genome-wide association studies (MTAG) boosts statistical power by joint analysis of genetically correlated traits, fitting the results to the genetic correlation matrix and allowing the inclusion of overlapping samples among the included GWAS. MTAG was shown to enhance loci discovery and increase the variance explained by PGS in genetically correlated complex traits such as depressive symptoms, neuroticism, and subjective well-being5.
The objectives of this study were (1) To investigate the genetic correlations (rg) among cardiovascular traits and diseases (CVT/D) and assess causal relationships of novel correlations, (2) to empower genomic locus discovery in AF, CAD and HF by leveraging relevant genetic correlations with CVT/D using MTAG, and (3) to evaluate the added value of MTAG to improve PGS-based disease prediction and discrimination in common CV diseases.
Results
Heritability and genetic overlap among cardiovascular traits and diseases
A comprehensive analysis encompassing common CV diseases such as AF2,6, CAD7 and HF4 as well as rare heritable heart diseases and cardiometabolic traits was performed. The complete list of phenotypes and included studies appears in Supplementary Data 1. The study workflow is shown in Fig. 1.
AF, atrial fibrillation and atrial flutter; AUC, area under the curve; BMI, body mass index; CAD, coronary artery disease; DCM, dilated cardiomyopathy; GWAS, genome-wide association studies; HF, heart failure; LDL, low-density lipoprotein; maxFDR, maximum false discovery rate, which calculates the maximum type I error in the analysis; MHIBB, Montreal Heart Institute Biobank; Neff, effective sample size; PGS, polygenic scores; SBP, systolic blood pressure; UKB, United Kingdom Biobank. aNielsen et al.6, bNelson et al.7, cShah et al.4, dAragam et al.21, eLevin et al.22. *Another large AF GWAS with partly non-overlapping samples (Roselli et al.2).
We computed SNP heritability (h2SNP) using Linkage Disequilibrium Score regression (LDSC)8 for all the included CV phenotypes, which ranged from 0.05 to 0.27 (Supplementary Data 2). For binary traits (diseases), h2SNP on a liability scale ranged from 0.03 (for HF) to 0.17 (for type 2 diabetes mellitus, T2DM) (Supplementary Data 3).
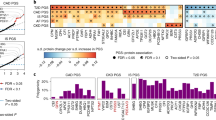
We then computed pairwise rg for 1,770 CVT/D pairs using LDSC. A total of 443 unique pairwise rg were significant at a false discovery rate (PFDR) < 0.05 (Fig. 2 and Supplementary Data 2), of which 325 yielded absolute rg above 0.20. AF, CAD and HF showed 12, 21 and 23 significant rg, respectively, depicted in Fig. 3 and Supplementary Data 4–6. These findings and their contextualization in the literature are described in the Supplementary Note.
Genetic correlations of the included 58 cardiovascular traits and diseases using Linkage Disequilibrium Score Regression8 all values in Supplementary Data 2. Non-significant correlations (P > 0.05 after correction for false discovery rate) are set to 0 and shaded in gray. Abbreviations specified in Supplementary Data 1.
On the left, barplots depicting genetically correlated traits with atrial fibrillation and flutter [AF], coronary artery disease [CAD], and heart failure [HF] at a significance level PFDR ≤ 0.05. rg and 95% confidence intervals are represented; all rg values appear in Supplementary Data 4–6. On the right, hierarchical clustering of the traits with rg > 0.20 and PFDR ≤ 0.01 with AF, CAD and HF. The Euclidean distance and the complete method were used to obtain three clusters grouping the traits significantly correlated with AF, CAD, and HF. For each of the 3 clusters, the trait with the highest genetic correlation with the trait of interest was selected for multi-trait analysis of GWAS (marked with an asterisk). PFDR, P-value corrected by false discovery rate; rg, genetic correlation. Other abbreviations as per Supplementary Data 1.
A novel correlation that attracted our attention is myocardial trabeculation, measured as a fractal dimension of the endocardium trabeculae of the left ventricle (LV)9 with cardiac electrical parameters. Myocardial trabeculation in apical and midventricular segments (CMTAp-MidV) showed significant and relevant genetic correlations with ventricular repolarization, specifically with ST segment amplitude at 80 ms after the QRS on the ECG (rg −0.35 and 0.28, respectively, for inferior [ST80INF] and aVR leads). Also of interest, the significant correlation between CMTAp-MidV with AF (rg 0.15 to 0.21), and of trabeculation in basal segments with exercise heart rate (HR; rg −0.31) and HR variability (rg −0.33).
In order to explore the potential causal relationship of CMTAp-MidV with cardiac repolarization and AF, we performed two-sample Mendelian Randomization (TwoSampleMR) analyses10. CMTAp-MidV instrumental SNPs did not show a causal effect on cardiac repolarization, nor did cardiac repolarization have a causal effect on AF when employing ST80INF summary statistics. Given that TwoSampleMR relies on significant SNPs in the exposure that are also present in the outcome, and that the summary statistics of ST80INF stem from a study with limited statistical power (N = 15,943) which employed a genotyping array with a relatively low number of SNPs (~2.3 M)11, we believed that this could have influenced the negative results. To further explore the genetic correlations we found, and based on previous literature linking early repolarization prevalence with higher prevalence of AF12, and vice versa13, we performed additional analyses employing a more recent GWAS with a larger sample size (N = 63,706)14. Among the 500 ECG amplitudes across the cardiac cycle analyzed in Verweij et al.14, we selected ECG amplitude at 44 ms after the R peak (ECG44) for its known relationship with early repolarization14. CMTAp-MidV depicted a causal effect on cardiac repolarization proxied by ECG44 (P = 0.033). Notably, cardiac repolarization (ECG44) was shown to have a consistent causal effect on AF (P = 0.023), but CMTAp-MidV did not show a significant causal effect on AF. MR-PRESSO15 and MRlap16 discarded the abovementioned causal associations are driven by horizontal pleiotropy or overestimation due to sample overlap (Supplementary Data 7 includes detailed results and explanation; depiction in Supplementary Fig. 1).
Genetic loci discovery through multi-trait analysis of GWAS (MTAG)
In order to unravel novel genetic loci implicated in AF, CAD, and HF, we performed MTAG for each of those common heart diseases5. MTAG leverages genetically correlated traits to increase power for locus discovery. For each of the 3 diseases, correlated traits were clustered in 3 groups based on pairwise rg (Fig. 3). Within each of the 3 clusters, we then selected the trait with the highest rg with the disease of interest (i.e., AF, CAD or HF). Restricting the number of included traits to 4 allows for estimation of the upper bound of the false discovery rate (maxFDR; see the Methods). The following traits were included in the MTAG. For the AF MTAG using Nielsen et al. GWAS6, we included body mass index (BMI)17, HF4 and another AF GWAS by Roselli et al.2, as this was a large GWAS with partly non-overlapping samples with Nielsen et al. These traits had pairwise rg with AF Nielsen et al. GWAS of 0.21, 0.56 and 1, respectively. For the CAD MTAG employing the Nelson et al. study7, we included HF4, low-density lipoprotein (LDL)18 and systolic blood pressure (SBP)19, which have pairwise rg with CAD Nelson et al. GWAS of 0.72, 0.22 and 0.34, respectively. For the HF MTAG using the GWAS by Shah et al.4, we included AF6, CAD7 and dilated cardiomyopathy (DCM)20, which showed pairwise rg of 0.56, 0.72 and 0.56 with HF. We estimated maxFDR to be 0.2%, 1.6% and 0.4% for the AF, CAD and HF analysis, respectively (Supplementary Data 8). MTAG significantly increased the mean χ2, equivalent to an increase in the effective sample size (Neff) for a conventional GWAS from 228,221 to 296,021 for AF, from 224,727 to 310,368 for CAD, and from 180,076 to 358,418 for HF (Supplementary Data 8).
We identified 19 novel loci at genome-wide significance (P < 5 × 10−8) associated with AF, 89 with CAD, and 52 with HF (Table 1, Supplementary Data 9-11). Two recently published GWAS in CAD (Aragam et al.21) and HF (Levin et al.22) were employed for the identification of additional novel loci by MTAG, leading to the identification of 42 and 89 loci not identified by the conventional GWAS (Supplementary Data 26–27). Of those, 19 and 37 overlapped with novel MTAG loci detected using Nelson et al. (CAD) and Shah et al. (HF), and an additional 23 and 52 were further identified for CAD and HF, respectively (Table 1). Novel loci were defined as not identified by the original published single-trait GWAS summary statistics2,4,6,7,21,22.
Among the 291 novel MTAG loci, 134 (46%) were either reported at P ≤ 5 × 10−8 in other published GWAS (which may include partially overlapping or independent cohorts) or had P ≤ 0.005 in an independent case-control GWAS (FinnGen), with a large proportion being reported for the first time in this work (Supplementary Data 9–11, 26–27). Only 13 of the novel loci identified through MTAG were not nominally significant in the original GWAS of the disease of interest, although 3 of them were confirmed to be associated with the trait of interest in the independent FinnGen cohort. The Miami plots showing single-trait and multi-trait results are depicted in Fig. 4. Figure 5 shows the effect estimates of each leading SNP of the MTAG loci on all traits included in the analysis. Figures of the additional MTAG analyses are included in Supplementary Figs. 2 and 3. All data are available in Supplementary Data 9–11, 26–27.
Miami plots from the summary statistics of the original studies and from the MTAG results. Panels (A, B, and C) depict Miami plots for atrial fibrillation and flutter [AF], coronary artery disease [CAD], and heart failure [HF], respectively. The plots of Nielsen et al. for AF, Nelson et al. for CAD and Shah et al. for HF, are depicted at the top, and from the disease-specific MTAG results at the bottom. In AF, MTAG increased the number of identified significant loci from 119 to 138, in CAD from 50 to 135, and in HF from 11 to 61. This led to the identification of 19 novel loci not reported in the original summary statistics for AF, 89 for CAD and 52 for HF. Red dashed line shows the genome-wide significance threshold (P = 5 × 10−8).
For each novel MTAG loci the lead SNP Z-score of the disease risk allele (beta divided standard error) from all the traits included in each MTAG analysis is represented. SNP identifiers along the x-axis represent the locus number (Supplementary Data 9–11) followed by the genomic position (in GRCh37) and the risk allele. Abbreviations: CV, cardiovascular, other abbreviations and references as per Fig. 1 and Supplementary Data 1.
MAGMA tissue expression and gene-set functional analysis from MTAG summary statistics are shown in Supplementary Data 15–23, 30–35 and Supplementary Fig. 4. In AF, MAGMA gene-property analyses to assess positive relationships between disease-gene associations and tissue specific gene expression profiles depicted AF associated genes tissue specificity in the heart, esophagus, uterus, skeletal muscle, cervix, colon, tibial, coronary and aorta arteries, bladder and fallopian tube. CAD-associated genes had significantly increased tissue expression in the coronary, aorta and tibial arteries, uterus, cervix, colon, fallopian tube, esophagus, heart atrial appendage, lung, bladder, visceral omentum and ovary tissue. HF-associated genes showed tissue specificity in the heart atrial appendage, tibial, coronary and aorta arteries, uterus, cervix and ovary. Interestingly, significantly increased specific tissue expression of disease-associated genes was detected in more tissues after MTAG, mostly in CAD and HF, and notably in genes expressed in the gastrointestinal and female reproductive systems, rich in smooth muscles. The tissue expression pattern of CAD-associated genes after MTAG (Nelson et al.) was very similar to that of the conventional single-trait GWAS by Aragam et al., supporting the specificity of the tissue expression pattern detected after MTAG (Supplementary Fig. 4). The gene-set analysis identified cardiac depolarization, repolarization, regulation of heart rate by cardiac conduction, muscle contraction, tissue development, atrial septation and regulatory region DNA/RNA binding in AF; macromolecular complex remodeling, heart development, collagen, triglyceride, chylomicron and LDL metabolism in CAD; and muscle structure and tissue development, cell differentiation encompassing cardiomyocyte/striated myocytes, membrane raft formation, and cell cycle progression, apoptosis and cellular transformation encompassing MYC, CDKN1A/RUNX3 and TGF-β regulation pathways, as well as RNA transcription initiation and DNA/RNA binding processes in HF.
Genes mapping to novel MTAG loci (using the Open Targets variant to gene algorithm) are listed in Table 1 and Supplementary Data 9–14, 26–29 and the more relevant ones due to mechanistic insight or support by other studies are described briefly in the Discussion and the Supplementary Note. GTEx tissue expression for all prioritized genes is depicted in Supplementary Fig. 5.
Genomic risk prediction
We next sought to assess whether PGS derived from MTAG summary statistics improved disease-status prediction and discrimination in AF, CAD and HF. Specifically, we derived multiple PGS using LDpred223 from the originally published single-trait summary statistics and those enhanced after the multi-trait analysis (MTAG) (PGSsingleT and PGSmultiT, respectively), which were assessed in a cohort of 15,177 unrelated individuals enrolled in the Montreal Heart Institute biobank [MHIBB, 97.7% European ancestry, 59.5% male, age at last follow-up 64 ± 11, baseline characteristics shown in Table 2], a cohort completely independent of AF and HF-PGS derivation data, and with a small overlap with CAD-PGS derivation data, for which we performed sensitivity analyses.
Disease-specific PGSsingleT and PGSmultiT were significantly associated with AF, CAD and HF in the testing cohort, using both univariable and multivariable logistic regression models with correction for sex, age and the first 4 genotypic principal components, except for HF PGSsingleT (Supplementary Data 36). PGSmultiT yielded very similar area under the curve (AUC) and phenotype explained variance by the model (Nagelkerke’s R2, referred to hereafter as R2) to PGSsingleT in AF [∆AUC = 0.001 (95% Confidence Interval (CI): −0.003, 0.005); ∆R2 0.053% (95%CI: −0.305, 0.421)] and CAD [∆AUC = 0.003 (95%CI: −0.003, 0.009); ∆R2 0.103% (95%CI: −0.493, 0.687)]. In contrast, HF PGSmultiT model significantly increased the AUC, although AUCs were overall low, and did not significantly increase R2 [∆AUC = 0.017 (95%CI: 0.002, 0.033); ∆R2 0.072% (95%CI: −0.029, 0.224)] (Fig. 6, Supplementary Data 36).
Area under the curve (AUC) from logistic regression model with the disease as an outcome (atrial fibrillation and flutter [AF], coronary artery disease [CAD] and heart failure [HF]) and the disease-specific candidate polygenic score as a predictor. The models including the single-trait polygenic scores (PGSsingleT) are represented in blue and the multi-trait ones (PGSmultiT) in red. On the left, the PGS univariate models are depicted and, on the right, the PGS models adjusted for age at last follow-up, sex and the four first principal components of genetic ancestry are shown. PGS developed by LDpred2, using the United Kingdom Biobank linkage disequilibrium reference panel (N = 362,320 individuals). The validation (N = 2500) and testing datasets (N = 12,677) consisted of unrelated individuals from the Montreal Heart Institute Biobank cohort. AUC shown are those from the testing dataset. For the female cohort, 997 individuals were included in the validation dataset and 5152 in the testing dataset. For the male cohort, 1503 individuals in the validation dataset and 7525 in the testing dataset. Representation of the AUCs corresponding to the best LDpred2 method, defined as the one with highest Wald-Z in the validation dataset in each disease. 95% confidence intervals are represented. Significant differences in the discrimination ability assessed using ∆AUC, Net Reclassification Index and Integrated Discrimination Improvement marked with an asterisk (*). The lack of model calibration in HF only-PGS models indicates caution in the interpretation of these results (Supplementary Data 36). Interestingly, PGS derived from the multi-trait summary statistics (PGSmultiT) improved prediction and discrimination in CAD in females (Supplementary Data 37). Abbreviations: PGS, polygenic score.
PGSsingleT and PGSmultiT were compared using the Net Reclassification Index (NRI), and the Integrated Discrimination Improvement (IDI). NRI and IDI supported the ∆AUC results. PGSmultiT did not supply significant improvement compared to PGSsingleT for AF and CAD [NRIAF 0.002 (95%CI: −0.036,0.041), IDIAF 0.000 (95%CI: −0.001,0.002); NRICAD 0.005 (95%CI: −0.030,0.041), IDICAD 0.001 (95%CI: −0.002,0.003)]. Regarding HF, PGS models were poorly calibrated for the univariable PGS models (Supplementary Fig. 6), thus the NRI should be interpreted with great caution24 [NRIHF 0.057 (95%CI: 0.007, 0.106); IDIHF 0.00047 (95%CI: 0.00009, 0.00085)].
In HF, PGS performed differently in the validation compared to the testing dataset, where the PGS including all variants as causal (i.e., infinitesimal method) performed better in the larger testing cohort (Supplementary Fig. 7, Supplementary Data 41) and PGSmultiT models obtained better calibration and significant reclassification when assessing this PGS (Supplementary Fig. 8, Supplementary Data 36). The poor model calibration and the different PGS performance in the validation and testing cohorts in HF may be due to the distinctive characteristics of these datasets reflecting HF etiological diversity, which is covered in more detail in the discussion and the Supplementary Note. Of note, the testing dataset had a lower proportion of patients with CAD, and a lower proportion of individuals receiving medication for HF with reduced ejection fraction (EF) compared to the validation dataset, and therefore, a possible higher prevalence in the testing dataset of patients with HF with preserved EF, which might support a higher etiological diversity in this subset of patients and explain why the infinitesimal methods performed better in the testing dataset (Supplementary Fig. 9 and Supplementary Data 41).
We then explored whether PGSmultiT may outperform PGSsingleT in females and males separately. As was the case for the overall cohort, PGSmultiT and PGSsingleT performed similarly for AF and HF. Of interest, in CAD we observed significantly increased explained variance and discrimination ability in females for the PGSmultiT models compared to PGSsingleT [∆R2 1.725% (95%CI: 0.609, 2.856); ∆AUC 0.019 (95%CI: 0.006, 0.033)], resulting in significantly improved reclassification: NRICAD-F 0.208 (95%CI: 0.139, 0.277) and IDICAD-F 0.011 (95%CI: 0.007, 0.015). PGSmultiT did not enhance the model in males (∆AUC 0.001 (95%CI: −0.006, 0.009); ∆R2 −0.100% (95%CI: -−0.879, 0.676)], with an NRICAD-M −0.012 (95%CI: −0.058, 0.033) and IDICAD-M 0.000 (95% CI: −0.058, 0.033) (Fig. 6, Supplementary Data 37). Of clinical interest is the observation that PGSmultiT, compared to PGSsingleT, provided numerically higher relative and absolute risk of CAD in females in the top PGS percentiles, although this did not reach statistical difference (Supplementary Fig. 10 and Supplementary Data 38).
CAD PGSsingleT and PGSmultiT were derived from a meta-analysis of CAD GWAS7, which includes samples genotyped on the Illumina Infinium Exome beadchip from the MHIBB. The overlap between MHIBB and the derived PGS concerned ~1.5% of the SNPs in ~6% of cases and 2% of controls in the CAD GWAS meta-analysis. We performed sensitivity analyses which confirmed a significant association of CAD PGS when removing the overlapping samples from the MHIBB, and when deriving PGS from an older CAD GWAS which did not include MHIBB samples25, and supported the findings in the main analysis. Results of these sensitivity analyses are presented in the Supplementary Note and Supplementary Data 36–37.
For a comprehensive analysis we also derived the PGS using LDpred1 and traditional linkage disequilibrium (LD)-based clumping and P-value thresholding (C-T)26 (see full description of the approach in the Methods). Extensive results are available in Supplementary Fig. 9 and Supplementary Data 39–41.
Discussion
The findings of our work can be summarized as follows: (1) CVT/D have shared genetic architecture as demonstrated by the 325 relevant pairwise genetic correlations found among the 58 included traits, some of which are novel, and for whom causal relationships were assessed; (2) By leveraging such genetic correlations, multi-trait analysis of GWAS using MTAG empowers locus discovery in common CV diseases, identifying 19, 131, and 141 novel loci for AF, CAD, and HF, respectively; (3) Genomic risk prediction through genome-wide PGS provides similar results for single-trait and multi-trait derived scores in AF and CAD, and inconclusive results in HF; (4) Multi-trait derived PGS show improved disease explained variance and discriminative ability for CAD in females, but not in males.
In our genetic correlation analyses, we reproduced prior findings from genetic and epidemiological studies and the new correlations fall within the expected. Among the novel correlations in AF, we highlight the correlation of this electrical disease with trabeculation in left ventricular mid-ventricular and apical segments, which in turn correlate with ECG myocardial repolarization. Mendelian randomization (MR) analyses showed a causal effect of apical and mid-ventricular myocardial trabeculation on myocardial repolarization on the surface ECG, which in turn showed a causal association with AF. The former may be attributable to the development of the conduction system, bundle branches and the peripheral ventricular conduction system, including Purkinje fibers, from the ventricular trabeculae27, and to the role Purkinje-muscle junction plays in the heterogeneity of transmural repolarization28. The causal effect of ECG44 on AF may correspond to the capture of initial ventricular repolarization and late atrial repolarization mechanisms by the surface ECG datapoint at 44 ms after the R peak. In Verweij et al.14, a PGS on AF showed significant associations with ECG amplitude from -250 to 125 ms before and after the R peak, respectively, supporting that the amplitudes corresponding to the P-wave, PR, QRS and ST surface ECG segments are related to AF mechanisms. Likewise, the lead SNPs in ECG44 significant loci (N = 10) mapped to genes previously associated with AF: KCND3, CASQ2, SCN10A, NKX2-5 and GOSR22,6. These mechanistic crossovers warrant further investigation to gain a deeper understanding of these associations.
The overlapping genetic structure of the included CVT/D allowed us to select the most relevant ones to enhance disease-specific effect estimates for AF, CAD and HF through MTAG. MTAG methodology has been previously used mostly in neurologic and psychiatric diseases5,29,30,31,32,33,34,35,36,37,38,39,40,41, in hypertrophic cardiomyopathy (HCM)20,42, and recently in HF22. The hierarchical clustering approach our group uses for selecting the traits to be included in MTAG may be useful to other researchers in the setting of numerous multiple relevant associations with the trait of interest. By selecting traits from different clusters, we include traits with less overlapping genetic architecture in the MTAG analysis. In previous unpublished interim analyses of recent work by our group, we observed that the selection of 3 traits by pre-determined clustering provides an increase in statistical power similar to that of including more traits genetically correlated with the trait of interest42. Importantly, the joint MTAG analysis of 4 traits, including those with the highest rg with the trait of interest from each cluster, allows the calculation of the maxFDR, which controls the conformity of the included traits with the MTAG assumptions and which is specially relevant in the absence of an independent (and large enough) cohort to replicate the novel MTAG loci.
Recently, Levin et al. conducted an MTAG analysis on HF using their HF GWAS (Neff = 428,755) together with LV ejection fraction (LVEF, rg −0.29, P = 4.51 × 10−11), LV end-systolic volume (rg 0.36, P = 3.73 × 10−16) and LV end-diastolic volume (rg 0.33, P = 2.98 × 10−13). In the MTAG conducted by Levin et al., 23 loci not identified by the conventional GWAS were found using MTAG. The increase in χ2 and maxFDR were not reported. In contrast, when we performed an MTAG analysis employing the summary statistics of Levin et al. we found 89 additional loci to the GWAS. The main difference between the approaches is that while Levin et al. included highly inter-correlated traits in the MTAG analysis (LV volumetric traits), with a relatively small sample size (N = 36,041) and moderate rg with HF, the clustering approach we employed led to the inclusion of more diverse traits which also displayed high genetic correlation with HF, namely AF(rg 0.56, P = 3.10 × 10−61), CAD (rg 0.72, P = 7.38 × 10−80) and DCM (rg 0.56, P = 1.81 × 10−8).
In our study, MTAG uncovered 19, 131, and 141 loci in AF, CAD, and HF that had not been identified in the included single-trait GWAS, of which a large proportion are novel, i.e., not reported in other GWAS contained in the GWAS Catalog, UK biobank (UKB), and FinnGen databases. In the absence of independent replication, caution is warranted since it is possible that some of those novel loci are false positive. MTAG allows for an estimation of the upper bound of the false discovery rate. In all our analyses, the maxFDR was <5% suggesting that the risk for false positive results is likely low. In addition, we queried the GWAS catalog and PheWAS in FinnGen and UKB for the 291 novel loci; 134 (46%) were either reported at P ≤ 5 × 10−8 in other published GWAS (which may include the used datasets) or had P ≤ 0.005 in the independent FinnGen cohort; and 96% showed nominal significant in the original GWAS. This further supports the robustness of the MTAG results presented in this work.
Among genes mapping to novel loci, we identify pathophysiological pathways congruent with the mechanisms of each disease and with relevant potential therapeutic implications. Among the new AF loci, rs2209073 on chromosome 17 mapped to the SRR gene, responsible for the synthesis of D-serine, a co-agonist of NMDA receptors whose activation has shown a role in reduced HR variability and enhanced AF inducibility in animal models43. In CAD, the NPR3 gene mapping rs1173727 on chromosome 5 codes for a natriuretic peptide receptor whose inhibition provides cardioprotective role for CAD according to MR44. In HF, genes mapped to novel loci on chromosome 5 (TBX5, lead SNP rs10507248) and 12 (NKX2-5, lead SNP rs2277923) are involved in cardiac development and congenital heart disease and have been demonstrated to interact with the promoter of cardiac-specific natriuretic peptide precursors45,46,47. In addition, MTAG loci in HF mapped numerous genes involved in cytoskeleton structure, which have a known role in cardiomyopathy and emerged as a therapeutic target for reducing stiffness in HF48,49, such as CORO6 and BCAS3 (mapped to rs11655587 and rs4968535, respectively, on chromosome 17) and SWAP70 (mapped to rs360153 on chromosome 11). See detailed description in the Supplementary Note.
To further assess the utility of MTAG in common CV diseases, we evaluated its ability to overcome the power limitation in SNP effect estimation under the hypothesis that MTAG-derived PGS would improve those estimates and PGS-based disease prediction.
Our PGS assessed a cohort of 15,177 patients from the MHIBB, a hospital-based cohort including individuals predominantly of French-Canadian ancestry. The MHIBB was previously used to successfully validate other CAD PGS50. In this work, we replicate previous results of other PGS tested in the MHIBB and report new PGS results in line with those derived and tested in other cohorts such as the UKB23,51 (Supplementary Data 40). The MHIBB is a cardiology hospital cohort in which there is obvious enrichment of CV diseases. The discrimination parameters employed in this work (AUC, continuous NRI and IDI) are not affected by disease prevalence52.
In Turley et al.5, MTAG developers obtained improvements in R2 values of PGS models derived from MTAG results versus conventional summary statistics from GWAS. Such R2 improvements were close to what would be expected based on the observed increase in the mean χ2 statistics. In our study, we also obtained an increase in mean χ2 in the MTAG summary statistics of the three diseases, but this was not reflected in improved R2 with MTAG in the overall cohort results (Supplementary Data 36). The main differences with Turley et al., apart from the nature of the diseases of interest, are that herein we calculate the PGS by the improved version of LDpred, LDpred2. LDpred2 allows LD matrix calculation within a wider window size of 3 cM with respect to its previous version, LDpred1, allowing better predictive performance for long-range LD regions and fewer polygenic traits23. In addition, in our main analysis we employed LDpred2-grid, which prioritizes SNPs effect sizes based on a prior assumption of the genetic architecture of the disease according to a diverse spectrum of hyperparameters [fraction of causal variants (ρ) and h2SNP], rather than LDpred1-infinitesimal, which adjusts SNP effects employing nominal h2SNP and assuming all variants are causal (ρ = 1). When looking at LDpred2 and LDpred1 infinitesimal results in the present work, as performed in Turley et al., PGSmultiT did provide improvement with respect to PGSsingleT (Supplementary Data 36, 39–41), although those were not the PGS that performed better based on the Wald-Z in the validation dataset. From our work, we deduce that the improvement of SNP-phenotype associations provided by MTAG in common cardiac diseases does not translate into improved genetic prediction when deriving PGS using LDpred2-grid. We hypothesize this is because common cardiac diseases dispose of a large sample-size GWAS and LDpred2-grid adequately identifies the genetic architecture of the disease and weights SNPs according to their probability of being causal, altogether rendering relevant SNPs effect estimates for disease prediction adequately captured and re-estimated. In the current work LDpred2-grid method outperformed LDpred2-infinitesimal in AF and CAD, supporting that prioritization of relevant variant effects instead of all improves disease prediction in these diseases. The LDpred2 method is different from classical methods such as C-T, which employ unadjusted SNP effects prioritized according to P-value. In the latter scenario, MTAG enhanced summary statistics, with a larger number of significant loci (P ≤ 5 × 10−8), outperform conventional GWAS in predicting common CV diseases (CAD and HF) when employing low P-value thresholds (Supplementary Fig. 11).
Interestingly, even if MTAG-derived PGS did not enhance PGSsingleT models, they did not impair genomic prediction either, thereby MTAG did not add noise to the single-trait summary statistics, i.e., MTAG did not bias the estimate of the effect toward correlated traits away from the real effect on the trait of interest.
HF analyses yielded low h2SNP and accordingly HF models showed low R2. PGS models in HF showed poor calibration and different performance in the validation and testing datasets, i.e., the randomly created cohorts for validation and testing of PGS had distinct clinical characteristics (Table 2) and different performance of the PGS hyperparameters (Supplementary Data 41, Supplementary Fig. 12). The PGS including the highest fraction of causal variants (infinitesimal method) provided the best calibration and prediction when assessing the (larger) testing dataset (see further details in Supplementary Note), and MTAG did enhance performance when employing this PGS. This points to greater polygenicity or etiological diversity of the disease, a scenario in which MTAG may be useful for improved prediction. Our findings are consistent with the fact that HF is a syndrome with several subtypes -preserved or reduced EF - and underlying aetiologies, and potentially opposing mechanisms (e.g., hypercontractile in HCM vs. hypocontractile in DCM)20, so GWAS of these subtypes and aetiologies separately will be more useful in providing mechanistic insight in the future. Similarly, Shah et al. stated that HF GWAS revealed lower statistical power and lower number of genetic associations compared to other studies with similar Neff, suggesting the heritability of HF may be more attributable to underlying disease subtypes than to the common final pathway4. Despite low h2SNP, HF had many significant rg. HF depicted high genetic overlap with CAD (rg 0.72) and several overlapping correlations with CAD, consistent with the high CAD prevalence in the cohorts included in the HF GWAS by Shah et al. This may raise concerns as to whether the HF correlations obtained were specific to HF or mediated by CAD, but it is reassuring that traits with high genetic overlap with HF such as DCM (defined as non-ischemic, rg 0.56, P = 2.20 × 10−7) were not correlated to CAD (rg 0.11, P = 0.32), as expected. In addition, PGSmultiT grid and infinitesimal models depicted similar and better performance, respectively, than the PGSsingleT ones. These last two findings suggest that MTAG does not introduce a bias toward CAD-related mechanisms independent of HF.
The stratified analysis by sex yielded similar results for AF and HF as those observed in the overall cohort. This was not the case for CAD where there was no improvement by PGSmultiT in males but PGSmultiT in females significantly outperformed PGSsingleT. The PGS derivation summary statistics stem from a cohort mostly constituted by males7, and thus, MTAG may have helped to uncover relevant mechanisms in the underrepresented female subgroup. In females, PGSmultiT obtained a significant increase in prediction and discrimination parameters, with increased explained variance by the model, an improved classification as represented by the NRI, and significantly better differentiation of prediction between affected and non-affected as shown by the IDI. In line with these results, CAD-associated genes after MTAG depicted higher tissue expression specificity in the feminine reproductive system as also shown by Aragam et al.21 After the enhancement, CAD explained variance by PGSmultiT in females was still lower than that in males, similarly to previously reported lower h2SNP and genetic variance in females than in males53,54. While some analyses support genetic overlap of mechanisms of CAD in men and women (LDSC rg of CAD GWAS in males and females is not statistically different from 1)53,54, sex-stratified studies have identified differential effect between sexes of autosomal SNPs in CAD21,55,56,57,58. Although performing stratified analysis, these studies were mostly underpowered to detect female-specific associations (small female sample size). Among the previously described female-specific-variants, in our study MTAG increased significance in one, but not the other [rs715 (CPS1)58: single-trait P = 0.057, multi-trait P = 8 × 10−5; rs7696877 (MYOZ2)21: single-trait P = 0.003, multi-trait P = 0.013). A possible explanation for sex differences in the CAD h2SNP is the exclusion of sex chromosomes from GWAS even though there are recommendations on how to perform GWAS including them59 and there is strong agreement to do so in upcoming studies. Future specific research on sex-specific genetic and environmental mechanisms of CAD may help to explain sex differences in this entity. MTAG can be a promising tool to overcome statistical power limitations due to lower available sample sizes in females.
One of the limitations of MTAG is that only those SNPs represented in all included traits are analyzed, so some relevant SNPs for the trait of interest may be excluded and limit loci discovery and predictive power of the final summary statistics, since even if the SNP to trait association statistic (i.e., χ2) is improved, the number of represented SNPs is dropped. Similarly, for the use of LDpred2 it is recommended to employ only the subset of HapMap3 SNPs (N = 1,120,696), which may also compromise the final predictive ability due to the possible omission of relevant SNPs. Another important limitation of our work is that in order to calculate LDSC genetic correlations, only predominantly European populations were included, therefore our results may not be transferable to other cohorts with different ancestry. MTAG assumes that all SNPs share the same variance-covariance matrix of effect sizes across the included traits in the analysis, which might lead to deviations in the actual estimates. However, maxFDR, which estimates the maximum probability that the previous assumption is violated, was low in all our analyses, and, in addition, we confirmed a high proportion of the MTAG loci, supporting the robustness of the findings. Still, we recommend interpreting the new loci with caution, especially for the few that were nonsignificant in single-trait summary statistics at a nominal P-value threshold and were not confirmed in other studies. In this work, we only assessed the improvement of genomic prediction using the MTAG methodology, without obtaining an improvement in prediction. Other approaches implementing multiple traits may be beneficial to improve genetic prediction, in addition to increasing the sample size of ancestrally diverse populations60.
Altogether, our research provides novel insight into the genetic overlap and causal relationships among cardiometabolic traits/diseases and shows that the integration of shared genetic underpinnings using MTAG contributes to the discovery of new trait-specific loci and unravels the pathophysiological basis in AF, CAD, and HF. Multi-trait PGSs yield similar discrimination and prediction in CAD and AF, and non-conclusive results for HF, although they point to better performance (when PGS methods including all variants as causal are considered). Furthermore, MTAG enabled improvement in discriminative and predictive capabilities for CAD-PGS in females.
Methods
Compilation and quality control on study summary-level data
CVT/D with publicly available GWAS summary statistics were compiled, prioritizing those with the largest sample size and power, encompassing 58 traits/diseases and 60 summary statistics. The complete list of phenotypes and included studies appears in Supplementary Data 1. The study workflow is shown in Fig. 1.
We included studies comprising European ancestry individuals (or mostly European individuals) to be able to compute pairwise LDSC rg.
The summary statistics were generated as described in the original GWAS (see Supplementary Data 1 for references). They were processed according to the standard quality control procedures61 and transformed into the input format required for the software tools to be used: LDSC8 and MTAG5.
LDSC genetic correlation
Genetic overlap of the included CVT/D was analyzed using LDSC and the detected rg served as a guidance for the selection of the traits to be incorporated in the joint analysis using MTAG.
For the LDSC analyses we employed the LD scores reference panel from the Broad Institute computed using European individuals from the 1000 Genomes Project62.
Among 1770 non-repeated comparisons (marked in the Unique Pairs column in the Supplementary Data 2), LDSC rg with P-value < 0.05 after correcting for multiple comparisons using Benjamini & Hochberg false discovery rate method (PFDR) were considered significant (Supplementary Data 2). To select the traits significantly correlated with AF, CAD and HF, the correction was performed individually for each disease of interest (Supplementary Data 4–6).
LDSC outputs h2SNP on an observed scale for binary traits, i.e., using the disease prevalence in the GWAS sample. h2SNP on a liability scale was computed for these traits and reported in the Supplementary Data 3, along with the population prevalence used for its calculation.
Mendelian randomization
The MR main analyses were performed using the R package “TwoSampleMR” (mrcieu.github.io/TwoSampleMR/)10 Directionality of causal relationships was confirmed using the Steiger test. The inverse variance weighted (IVW) method was employed in the main analysis, and the weighted median, weighted mode and Egger method were employed as sensitivity analyses. Instrumental SNPs were selected if associated with the trait of interest at P ≤ 5 × 10−8 and pruned to select independent SNPs (using an LD r2 threshold of 0.001 when employing the LD reference panel of European individuals in 1000 Genomes). Instrumental SNPs strength was assessed using the F-statistic. Heterogeneity and horizontal pleiotropy were assessed using the Q-statistic and the Egger intercept. We confirmed the robustness of our results by using MR-PRESSO15 and MRlap16 to correct IVW results for bias due to horizontal pleiotropy or sample overlap, respectively, if present. MR-PRESSO was employed to obtain IVW results corrected for horizontal pleiotropy via outlier removal. MRlap employs the LDSC intercept to adjust MR results for sample overlap and assesses the difference between observed and corrected results. The causal relationships reported as significant have been confirmed by the weighted median sensitivity analysis method and after ruling out overestimation due to sample overlap (by MRlap) and/or horizontal pleiotropy (by Egger intercept test and MR-PRESSO). Detailed methodology and results are supplied in Supplementary Data 7.
Multi-trait analysis of GWAS
We performed MTAG analyses for AF, CAD and HF.
As per software requirements, before performing MTAG, all SNPs with minor allele frequency (MAF) < 0.01 were filtered out.
The increase in statistical power through MTAG was measured by means of the increase in the mean χ2. The increase in the mean χ2 was in turn employed to estimate the sample size that would be needed for a standard GWAS (not MTAG) to obtain an increase in statistical power such as that obtained with the MTAG5:
where N GWAS corresponds to the sample size of the GWAS of interest.
For binary traits, input summary statistics N corresponded to the effective sample size (Neff) as recommended in the MTAG publication5:
To ensure the reliability of our results, we calculated the upper bound of the false discovery rate (maxFDR), which calculates the type I error in the dataset for the worst-case scenario: SNPs that have a null effect for some traits but a non-null effect for others. The maxFDR increases with lower genetic correlation and wider difference in the summary statistics mean χ2 between the included traits. χ2 scales with sample size and h2SNP.
To be able to calculate MTAG maxFDR, we conducted MTAG using 4 traits per each analysis, otherwise its calculation is computationally not feasible.
To select the traits to be included in each MTAG analysis we conducted a cluster analysis for the traits significantly correlated with each of the diseases of interest: AF, CAD and HF. Clustering was performed for traits with relevant LDSC rg (≥0.20) that is statistically significant (PFDR ≤ 0.01). The trait with the highest genetic correlation from each cluster was selected, which allowed to include traits with high overlapping genetic structure with the trait of interest but not between them.
Hierarchical clustering was performed using the absolute value of the rg, the Euclidean distance and the complete method (Fig. 3).
For the AF MTAG we employed Nielsen et al.6 summary statistics as the main trait. In addition, we included another GWAS on the same trait by Roselli et al.2, as it had partly non-overlapping samples with Nielsen et al., and the meta-analysis of those studies was not publicly available. Nielsen et al. summary statistics were selected as the main AF trait as they had higher mean χ2 (Supplementary Data 8).
For the new MTAG analysis using new summary statistics published in CAD (Aragam et al.21) and HF (Levin et al.22), we kept the same features used for the main analysis, using updated summary statistics if available (Supplementary Data 24), and did not combine (1) Nelson et al. with Aragam et al. nor (2) Shah et al. with Levin et al. (similarly to what we did for AF), as these cohorts were already included in the Aragam et al. and Levin et al. GWAS, respectively.
For the HF MTAG, the initially selected traits included AF, CAD and systolic blood pressure (SBP)19 (Supplementary Fig. 13) but it yielded a maxFDR of 40.9%. This was presumed to be due to imbalanced statistical power between HF (mean χ2 = 1.14) and SBP (mean χ2 = 2.84), as described above. We then excluded blood pressure traits and performed a new clustering analysis that led to the selection of DCM as the fourth trait for the HF MTAG, yielding a maxFDR of 0.4% (Supplementary Data 8).
Annotation and functional analyses
The annotation and functional mapping of the new generated summary statistics was conducted using FUMA v1.5.3 (https://fuma.ctglab.nl/)63 and Open Targets v22.10 (https://genetics.opentargets.org/)64,65.
Genomic risk loci were defined in FUMA. We clumped independent SNPs at a LD r2 > 0.1 and merged LD blocks with distance ≤250 kb. This led to a number of loci slightly different from the ones reported in the original summary statistics (Supplementary Data 9–11, 26–27). MTAG novel loci were defined as not identified by the original published single-trait GWAS summary statistics (at a significance level P ≤ 5 × 10−8) and without overlapping boundaries with those, i.e., not in Nielsen et al.6, Roselli et al.2, nor in meta-analysis reported in Roselli et al. for AF, not in Nelson et al.7 for CAD, not reported in Shah et al.4 in the case of HF and not reported in Aragam et al.21 and Levin et al.22 for the new CAD and HF analyses.
We looked up the novel MTAG loci in other GWAS publications through FUMA and OpenTargets. FUMA retrieves GWAS associations from the GWAS Catalog for all the variants included in a locus. The GWAS Catalog contains associations at a significance level of P ≤ 1 × 10−5, in our case, we filtered for P ≤ 5 × 10−8. OpenTargets retrieves GWAS associations (P ≤ 5 × 10−8) in the UKB, FinnGen and/or GWAS Catalog repositories. In the query, OpenTargets uses the specified variants (in our case the list of the novel MTAG lead variants), and those in high LD r2 (>0.7) or in the same credible set, i.e., set of independent variants in a locus (after conditional analysis) likely to be causal at a 95% confidence interval. In addition, Open Targets was also used to query PheWAS associations (P ≤ 5 × 10−3) for the novel MTAG lead variants in independent datasets (FinnGen). We report those loci associated with AF, CAD and HF, respectively, at either (1) a genome wide significant level in partially overlapping or independent cohorts (P ≤ 5 × 10−8), or (2) at P ≤ 5 × 10−3 in the FinnGen independent cohort, as detailed in Table 1 and Supplementary Data 9–11, 26–27.
Functional mapping and prioritization of causal genes was conducted using Open Targets, which integrates information on molecular phenotype quantitative trait loci experiments, chromatin interaction experiments, in silico functional predictions and the distance between the variant and each gene’s canonical transcription start site. The genes with the highest variant to gene score for each lead variant are reported in Table 1 and in Supplementary Data 9–11, 26–27, and the whole list of associated genes is reported in Supplementary Data 12–14, 28–29.
Summary statistics functional analyses were conducted using MAGMA gene-set and tissue expression functions in FUMA.
Polygenic scores
PGS derivation data
PGSsingleT were derived from the previously published available GWAS summary statistics on AF (Nielsen et al.6), CAD (Nelson et al.7), and HF (Shah et al.4), and the PGSmultiT from the summary statistics that we generated through MTAG for each disease.
PGS calculation in the target data
PGS were calculated in a population of 15,177 unrelated individuals with complete array genotype and detailed phenotypic data. Individuals were recruited from the André and France Desmarais Hospital Cohort of the MHIBB. All participants provided informed consent to be included in the biobank. The MHIBB protocol was approved by the Montreal Heart Institute’s Scientific and Ethics Committees. This study conforms to the Helsinki declaration and, in addition to the aforementioned committees, was also approved by the Cohort Management Committee.
Genotyping of the DNA samples from the MHIBB cohort (n ~ 17,000) was performed on the Illumina GSAv3.0_MD by the Beaulieu-Saucier Pharmacogenomics Centre, together with the pre-imputation quality control which was performed using the previously described pyGenClean tool (1.8.3)66. SNP positions are in build GRCh38. Genome-wide imputation was performed on the TOPMed Imputation Server (version 1.5.7) using Eagle (version 2.4) for phasing and Minimac4 (version 1.0.2) for imputation. BGEN post-imputation files were further filtered and SNPs with MAF < 0.001, imputation quality value < 0.3, indels, multiallelic variants and SNPs with a Hardy Weinberg equilibrium exact test P-value < 1 × 10−10 were filtered out. Among the 17,000 individuals of the MHIBB cohort only non-1st or 2nd degree related individuals were kept, as individuals with close relatedness can lead to overfitted results. After this filtering, 15,428,698 SNPs and 15,177 individuals were included as target data for the PGS calculation.
The baseline characteristics of the MHIBB cohort are described in Table 2. Baseline data analyses were conducted in R (version 4.0.2). Continuous variables were presented as mean ± standard deviation or median [interquartile range], and these were compared using the t-test for independent samples or the Mann-Whitney U test. Categorical variables were reported as frequencies (%) and Fisher’s exact test was used for comparison.
PGS were derived using LDpred223 in the main analysis. For a comprehensive analysis of the value of MTAG in genetic risk prediction in cardiovascular diseases according to the different PGS methodologies, we also derived the PGS employing LDpred126 and C-T methods. Prior to the calculation of the PGSs, the summary statistics were converted to GRCh38 assembly using the liftover function available at the UCSC Genome Browser67, to be consistent with the genetic build of the MHIBB, the target data. LDpred is a genome-wide PGS derivation method that adjusts GWAS summary statistics SNP effect estimates based on their probability of being causal and LD information from a reference panel. LDpred2 allows LD matrix calculation within a wider window size of 3 cM with respect to its previous version, LDpred1, allowing better predictive performance for long-range LD regions and fewer polygenic traits23. Both LDpred1 (original software) and LDpred2 (improved version) have an infinitesimal method that considers all variants as causal [fraction of causal variants (ρ = 1)], both have a grid or Gibbs method, where LDpred2 employs a larger number of hyperparameters with respect to LDpred1 (ρ from 7 to 21, h2SNP from 1 to 4, and a sparse option which learns effects that are exactly 0), and LDpred2 also has an auto method, which learns the hyperparameters from the summary statistics and therefore does not require a validation cohort. C-T method selects SNPs based on a user-specified P and LD r2 values.
The MHIBB cohort was divided into a validation cohort, composed of 2500 individuals and used to select the best performing hyperparameters, and a testing cohort of 12,677 individuals in which the best performing PGSs were evaluated.
To select the best combination of hyperparameters for LDpred2-Grid, those parameters corresponding to the logistic regression model with the disease as the outcome and the disease-specific candidate PGS as the predictor with the highest Wald-Z in the validation cohort were selected. Subsequently, the best LDpred2-PGS (among the auto, grid and infinitesimal methods) was selected in the validation cohort, also based on the Wald-Z from the logistic model, and this was used to compare PGSsingleT and PGSmultiT performance in the MHIBB testing dataset (N = 12,677).
To select the best hyperparameters for LDpred1 and C-T methods the same approach based on the Wald-Z was followed. For the analyses stratified by sex and CAD sensitivity analyses, best LDpred2-grid and best LDpred2 method were re-selected based on the Wald-Z.
The validation cohort also was employed to calculate the LD reference panels for C-T, LDpred1 and LDpred2 methods. For LDpred2, as allowed by the method, we also used in the analysis an external reference panel of 362,320 individuals from the United Kingdom Biobank (UKB), whose results are the ones presented in the main results. All results are presented in Supplementary Data 39–41.
PGS testing
Univariate logistic regression models with the disease as the outcome and the disease-specific candidate PGS as the predictor, and multivariate logistic regression models including sex, age at last follow-up and the first four genotypic principal components as covariates were evaluated.
The following outcome definitions were established:
We coded as prevalent AF all patients having atrial fibrillation or atrial flutter in the MHIBB, the same diagnoses included in Nielsen et al.6 Controls were selected as not having atrial fibrillation or atrial flutter.
Prevalent CAD was defined as the occurrence at any time of fatal or nonfatal myocardial infarction (MI), percutaneous transluminal coronary angioplasty (PTCA) or coronary artery bypass grafting (CABG) and controls were selected to be free of MI, PTCA or CABG. Our definition was similar to the one used by Nelson et al.7, but this one also included patients with unstable angina and chronic ischemic heart disease as cases for the summary statistics we employed (SOFT).
Prevalent HF was defined as diagnosed by a cardiologist based on clinical notes, hospitalization or death report. In addition, individuals LVEF ≤ 45% were coded as having HF. Individuals with preserved EF along with left atrium > 34 ml/m² or increased indexed LV mass in the echocardiography (>115 g/m² in men, >95 g/m² in women); diastolic dysfunction, defined as E/e’ >13 or lateral e’ < 9; and/or NT-proBNP≥600 pg/ml were also coded under the diagnosis of HF in the MHIBB database and used for the HF prevalent definition in the present study. Controls were selected to be free of HF. Our definition was in line with the one used by Shah et al.4, in which the diagnosis of the 26 cohorts was based on the combination of the following parameters: Physician diagnosis or adjudication in 18 cohorts, ICD codes (discharge ± cause of death) in 12 cohorts, imaging in 15 cohorts, natriuretic peptides in 1 cohort and HF treatment in 9 cohorts. To assess whether the definition of HF in the MHIBB was too inclusive with regard to the HF with preserved EF inclusion criteria, two additional definitions were analyzed, whose results are available in Supplementary Data 41:
I. Cases were those with HF who also had an NT-proBNP ≥125 pg/ml when available, excluding those patients without NT-proBNP and a diagnosis of HF from the analysis, and keeping as controls those without HF.
II. Cases were defined as having severe HF, which included HF patients who received a heart transplant, carried a ventricular assist device, or had experienced HF with a NYHA functional class III-IV.
Nagelkerke’s R2 and AUC were assessed through the rms R package (version 6.2-0), confidence intervals were created for 10,000 bootstrapping samples using boot (version 1.3-2), and AUCs were compared using the pROC package (version 1.18.2) and the roc.test() function, which employs the Delong method68. NRI and IDI were assessed using the R package Hmisc (version 4.7-0). For calibration plots, 1000 bootstrapping samples were used and the continuous calibration curve was smoothed using the lowess method69. All analyses were conducted in R (version 4.0.2).
Data availability
All sources of GWAS summary statistics employed in this study are detailed in Supplementary Data 1. The analyses reported in this article rely on previously published software, and the tools employed are listed in the Methods section. Summary statistics generated with MTAG are available on the GWAS catalog (accession numbers GCST90668073-GCST90668077), and PGS derived from both single-trait and multi-trait summary statistics are available on the PGS catalog (publication ID PGP000759 and score IDs PGS005287-5306). Access to MHIBB individual-level information requires prior approval by the institution. The details of the requirements can be found at https://www.icm-mhi.org/.
References
Behan, F. M. et al. Prioritization of cancer therapeutic targets using CRISPR-Cas9 screens. Nature 568, 511–516 (2019).
Roselli, C. et al. Multi-ethnic genome-wide association study for atrial fibrillation. Nat. Genet. 50, 1225–1233 (2018).
Yang, C. et al. Polygenic risk for coronary artery disease in the Scottish and English population. BMC Cardiovasc. Disord. 21, 586 (2021).
Shah, S. et al. Genome-wide association and Mendelian randomisation analysis provide insights into the pathogenesis of heart failure. Nat. Commun. 11, 163 (2020).
Turley, P. et al. Multi-trait analysis of genome-wide association summary statistics using MTAG. Nat. Genet. 50, 229–237 (2018).
Nielsen, J. B. et al. Biobank-driven genomic discovery yields new insight into atrial fibrillation biology. Nat. Genet. 50, 1234–1239 (2018).
Nelson, C. P. et al. Association analyses based on false discovery rate implicate new loci for coronary artery disease. Nat. Genet. 49, 1385–1391 (2017).
Bulik-Sullivan, B. et al. An atlas of genetic correlations across human diseases and traits. Nat. Genet. 47, 1236–1241 (2015).
Meyer, H. V. et al. Genetic and functional insights into the fractal structure of the heart. Nature 584, 589–594 (2020).
Hemani, G. et al. The MR-Base platform supports systematic causal inference across the human phenome. Elife 7 (2018).
Verweij et al. Twenty-eight genetic loci associated with ST-T-wave amplitudes of the electrocardiogram. Hum. Mol. Genet 25, 2093–2103 (2016).
Watanabe, H. et al. Clinical characteristics and risk of arrhythmia recurrences in patients with idiopathic ventricular fibrillation associated with early repolarization. Int J. Cardiol. 159, 238–240 (2012).
Hasegawa, Y. et al. Early repolarization and risk of lone atrial fibrillation. J. Cardiovasc. Electrophysiol. 30, 565–568 (2019).
Verweij, N. et al. The genetic makeup of the electrocardiogram. Cell Syst. 11, 229–38 e5 (2020).
Verbanck, M., Chen, C. Y., Neale, B. & Do, R. Detection of widespread horizontal pleiotropy in causal relationships inferred from Mendelian randomization between complex traits and diseases. Nat. Genet. 50, 693–698 (2018).
Mounier, N. & Kutalik, Z. Bias correction for inverse variance weighting Mendelian randomization. Genet. Epidemiol. 47, 314–331 (2023).
Pulit, S. L. et al. Meta-analysis of genome-wide association studies for body fat distribution in 694 649 individuals of European ancestry. Hum. Mol. Genet. 28, 166–174 (2019).
Surakka, I. et al. The impact of low-frequency and rare variants on lipid levels. Nat. Genet. 47, 589–597 (2015).
Evangelou, E. et al. Genetic analysis of over 1 million people identifies 535 new loci associated with blood pressure traits. Nat. Genet. 50, 1412–1425 (2018).
Tadros, R. et al. Shared genetic pathways contribute to risk of hypertrophic and dilated cardiomyopathies with opposite directions of effect. Nat. Genet. 53, 128–134 (2021).
Aragam, K. G. et al. Discovery and systematic characterization of risk variants and genes for coronary artery disease in over a million participants. Nat. Genet. 54, 1803–1815 (2022).
Levin, M. G. et al. Genome-wide association and multi-trait analyses characterize the common genetic architecture of heart failure. Nat. Commun. 13, 6914 (2022).
Prive, F., Arbel, J., Vilhjalmsson, B. J. LDpred2: better, faster, stronger. Bioinformatics 36, 5424–5431 (2020).
Thomas, L. E., O’Brien, E. C., Piccini, J. P., D’Agostino, R. B. & Pencina, M. J. Application of net reclassification index to non-nested and point-based risk prediction models: a review. Eur. Heart J. 40, 1880–1887 (2019).
Nikpay, M. et al. A comprehensive 1,000 Genomes-based genome-wide association meta-analysis of coronary artery disease. Nat. Genet. 47, 1121–1130 (2015).
Vilhjalmsson, B. J. et al. Modeling linkage disequilibrium increases accuracy of polygenic risk scores. Am. J. Hum. Genet. 97, 576–592 (2015).
van Weerd, J. H. & Christoffels, V. M. The formation and function of the cardiac conduction system. Development 143, 197–210 (2016).
Walton, R. D. et al. Influence of the Purkinje-muscle junction on transmural repolarization heterogeneity. Cardiovasc. Res. 103, 629–640 (2014).
Deak, J. D. et al. Genome-wide association study in individuals of European and African ancestry and multi-trait analysis of opioid use disorder identifies 19 independent genome-wide significant risk loci. Mol Psychiatry 27, 3970–3979 (2022).
Seligowski, A. V., Misganaw, B., Duffy, L. A., Ressler, K. J. & Guffanti, G. Leveraging large-scale genetics of PTSD and cardiovascular disease to demonstrate robust shared risk and improve risk prediction accuracy. Am J Psychiatry 179, 814–823 (2022).
Carcel-Marquez, J. et al. A polygenic risk score based on a cardioembolic stroke multitrait analysis improves a clinical prediction model for this stroke subtype. Front. Cardiovasc. Med. 9, 940696 (2022).
Guo, P. et al. Pinpointing novel risk loci for Lewy body dementia and the shared genetic etiology with Alzheimer’s disease and Parkinson’s disease: a large-scale multi-trait association analysis. BMC Med. 20, 214 (2022).
Wang, H., Yi, Z. & Shi, T. Novel loci and potential mechanisms of major depressive disorder, bipolar disorder, and schizophrenia. Sci. China Life Sci. 65, 167–183 (2022).
Meyers, J. L. et al. A genome-wide association study of interhemispheric theta EEG coherence: implications for neural connectivity and alcohol use behavior. Mol. Psychiatry 26, 5040–5052 (2021).
Liu, K. et al. A combined analysis of genetically correlated traits identifies genes and brain regions for insomnia. Can. J. Psychiatry 65, 874–884 (2020).
Liu, L. et al. A trans-ethnic two-stage polygenetic scoring analysis detects genetic correlation between osteoporosis and schizophrenia. Clin. Transl. Med. 9, 21 (2020).
Yang, X. L. et al. Three novel loci for infant head circumference identified by a joint association analysis. Front. Genet. 10, 947 (2019).
Chung, J. et al. Genome-wide association study of cerebral small vessel disease reveals established and novel loci. Brain 142, 3176–3189 (2019).
Pei, Y. F. et al. Joint association analysis identified 18 new loci for bone mineral density. J. Bone Min. Res. 34, 1086–1094 (2019).
Chung, W. et al. Efficient cross-trait penalized regression increases prediction accuracy in large cohorts using secondary phenotypes. Nat. Commun. 10, 569 (2019).
Lam, M. et al. Large-Scale Cognitive GWAS Meta-Analysis Reveals Tissue-Specific Neural Expression and Potential Nootropic Drug Targets. Cell Rep. 21, 2597–2613 (2017).
Tadros, R. et al. Large-scale genome-wide association analyses identify novel genetic loci and mechanisms in hypertrophic cardiomyopathy. Nat. Genet. 57, 530–538 (2025).
Shi, S. et al. Activation of N-methyl-d-aspartate receptors reduces heart rate variability and facilitates atrial fibrillation in rats. Europace 19, 1237–1243 (2017).
Cronje, H. T. et al. Genetic evidence implicating natriuretic peptide receptor-3 in cardiovascular disease risk: a Mendelian randomization study. BMC Med. 21, 158 (2023).
Xu, J. H. et al. Prevalence and spectrum of NKX2-5 mutations associated with sporadic adult-onset dilated cardiomyopathy. Int. Heart J. 58, 521–529 (2017).
Steimle, J. D. & Moskowitz, I. P. TBX5: A. Key regulator of heart development. Curr. Top. Dev. Biol. 122, 195–221 (2017).
Hiroi, Y. et al. Tbx5 associates with Nkx2-5 and synergistically promotes cardiomyocyte differentiation. Nat. Genet. 28, 276–280 (2001).
Caporizzo, M. A. & Prosser, B. L. The microtubule cytoskeleton in cardiac mechanics and heart failure. Nat. Rev. Cardiol. 19, 364–378 (2022).
Ehler, E. Actin-associated proteins and cardiomyopathy-the ‘unknown’ beyond troponin and tropomyosin. Biophys. Rev. 10, 1121–1128 (2018).
Wunnemann, F. et al. Validation of genome-wide polygenic risk scores for coronary artery disease in French Canadians. Circ. Genom. Precis Med. 12, e002481 (2019).
Khera, A. V. et al. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nat. Genet. 50, 1219–1224 (2018).
Pencina, M. J., D’Agostino, R. B. Sr. & Steyerberg, E. W. Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Stat. Med. 30, 11–21 (2011).
Nikpay, M., Stewart, A. F. R. & McPherson, R. Partitioning the heritability of coronary artery disease highlights the importance of immune-mediated processes and epigenetic sites associated with transcriptional activity. Cardiovasc. Res. 113, 973–983 (2017).
Bernabeu, E. et al. Sex differences in genetic architecture in the UK Biobank. Nat. Genet. 53, 1283–1289 (2021).
Sakkers, T. R. et al. Sex differences in the genetic and molecular mechanisms of coronary artery disease. Atherosclerosis 384, 117279 (2023).
Consortium CAD et al. Large-scale association analysis identifies new risk loci for coronary artery disease. Nat. Genet. 45, 25–33 (2013).
Huang, Y. et al. Sexual differences in genetic predisposition of coronary artery disease. Circ. Genom. Precis Med. 14, e003147 (2021).
Hartiala, J. A. et al. Genome-wide association study and targeted metabolomics identifies sex-specific association of CPS1 with coronary artery disease. Nat. Commun. 7, 10558 (2016).
Konig, I. R., Loley, C., Erdmann, J. & Ziegler, A. How to include chromosome X in your genome-wide association study. Genet. Epidemiol. 38, 97–103 (2014).
Patel, A. P. et al. A multi-ancestry polygenic risk score improves risk prediction for coronary artery disease. Nat. Med. 29, 1793–1803 (2023).
Marees, A. T. et al. A tutorial on conducting genome-wide association studies: Quality control and statistical analysis. Int J. Methods Psychiatr. Res. 27, e1608 (2018).
Genomes Project, C. et al. A global reference for human genetic variation. Nature 526, 68–74 (2015).
Watanabe, K., Taskesen, E., van Bochoven, A. & Posthuma, D. Functional mapping and annotation of genetic associations with FUMA. Nat. Commun. 8, 1826 (2017).
Ghoussaini, M. et al. Open Targets Genetics: systematic identification of trait-associated genes using large-scale genetics and functional genomics. Nucleic Acids Res. 49, D1311–D1320 (2021).
Mountjoy, E. et al. An open approach to systematically prioritize causal variants and genes at all published human GWAS trait-associated loci. Nat. Genet. 53, 1527–1533 (2021).
Lemieux Perreault, L. P., Provost, S., Legault, M. A., Barhdadi, A. & Dubé M. P. pyGenClean: efficient tool for genetic data clean up before association testing. Bioinform. 29, 1704–1705 (2013).
Kent, W. J. et al. The human genome browser at UCSC. Genome Res. 12, 996–1006 (2002).
Robin, X. et al. pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinform. 12, 77 (2011).
Austin, P. C. & Steyerberg, E. W. Graphical assessment of internal and external calibration of logistic regression models by using loess smoothers. Stat. Med. 33, 517–535 (2014).
Acknowledgements
The authors would like to thank all the patients who volunteered to be included in the Montreal Heart Institute Biobank cohort. Also, we would like to acknowledge Vincent Bourgeault from the Montreal Heart Institute Hospital for his support during this project. We thank the authors of the GWAS listed in Supplementary Data 1 for generously sharing their summary statistics, including the members of the CHARGE Inflammation Working Group. The study is in part supported by the Philippa and Marvin Carsley cardiology chair. P.J. is also supported by Takeda Canada and CIHR Institute of Genetics Rare Diseases Fellowship (TAK401439). Julia C.-T. is also supported by the Montreal Heart Institute Foundation and the Fonds de recherche du Québec. S.d-D. holds the Université de Montréal Beaulieu-Saucier Chair in Pharmacogenomics. M.-P.D. holds the Canada Research Chair in Precision medicine data analysis. R.T. holds the Canada Research Chair in Translational Cardiovascular Genetics. The funders played no role in study design, data collection, analysis and interpretation of data, or the writing of this manuscript.
Author information
Authors and Affiliations
Contributions
Jean-Claude T. and R.T. share senior authorship. R.T. and P.J. designed the study. P.J. performed the genomic and statistical analyses and drafted the initial manuscript. Y.L. and A.J. contributed to data collection and analysis. E.G. and L.-P.L.-P. facilitated the access to the MHIBB data. Jean-Claude T. is the principal investigator of the MHIBB, coordinated by D.B. M-P.D., who is the director of the Beaulieu-Saucier Pharmacogenomics Center, in charge of the MHIBB genotypic information. A.N. and M.W.T. provided statistical support. Julia C.-T., N.L., G.L., S.d-D. and C.R.B. provided scientific guidance. R.T. provided mentoring and close supervision of the analyses and the interpretation of the results. All authors participated in the edition and revision of the manuscript. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
S.d-D. reports grants outside the submitted work from AstraZeneca and RMS/Dalcor. M.-P.D. has patents unrelated to this work: “Methods for Treating or Preventing Cardiovascular Disorders and Lowering Risk of Cardiovascular Events” issued to Dalcor, no royalties received; “Genetic Markers for Predicting Responsiveness to Therapy with HDL-Raising or HDL Mimicking Agent” issued to Dalcor, no royalties received; and “Methods for using low dose colchicine after myocardial infarction”, assigned to the Montreal Heart Institute. M.-P.D. reports equity interest in Dalcor, unrelated to this work. Jean-Claude T. has received research grants from Amarin, AstraZeneca, Ceapro, DalCor, Esperion, Ionis, Novartis, Pfizer and RegenXBio; honoraria from AstraZeneca, DalCor, HLS Therapeutics, Pendopharm and Pfizer; holds a minor equity interest in DalCor; and is an author of a patent on pharmacogenomics-guided CETP inhibition. R.T. receives research support from BMS Canada.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Jordà, P., Lai, Y., Jeuken, A. et al. Genetic analyses across cardiovascular traits: leveraging genetic correlations to empower locus discovery and prediction in common cardiovascular diseases. npj Genom. Med. 10, 65 (2025). https://doi.org/10.1038/s41525-025-00515-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41525-025-00515-2