Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

The actin cortex acts as a mechanical memory of morphology in confined migrating cells

Nature Physics volume 21, pages 1451–1461 (2025)Cite this article

Subjects

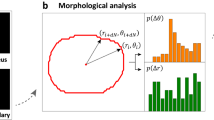
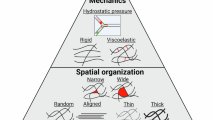
Abstract

Cell migration in narrow microenvironments occurs in numerous physiological processes. It involves successive cycles of confinement and release that drive important morphological changes. However, it remains unclear whether migrating cells can retain a memory of their past morphological states that could potentially facilitate their navigation through confined spaces. We demonstrate that local geometry governs a switch between two cell morphologies, thereby facilitating cell passage through long and narrow gaps. We combined cell migration assays on standardized microsystems with biophysical modelling and biochemical perturbations to show that migrating cells have a long-term memory of past confinement events. The morphological cell states correlate across transitions through actin cortex remodelling. These findings indicate that mechanical memory in migrating cells plays an active role in their migratory potential in confined environments.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: A morphological switch ensures a successful crossing on long bridges.
Fig. 2: Impact of symmetry-breaking and polarization states on cell dynamics.
Fig. 3: Morphological switch dynamics and mechanical memory.
Fig. 4: Pharmacological perturbation of mechanical memory dynamics.
Fig. 5: Geometrical perturbation of the mechanical memory dynamics.

Similar content being viewed by others

Data availability

All data are available upon request to the corresponding authors. Source data are provided with this paper.

Code availability

Codes are available upon request to D.B.B.

References

  1. Jiang, C. Switch of cell migration modes orchestrated by changes of three-dimensional lamellipodium structure and intracellular diffusion. Nat. Commun. 14, 5166 (2023).

    Article  ADS  Google Scholar 

  2. Yang, C., Tibbitt, M. W., Basta, L. & Anseth, K. S. Mechanical memory and dosing influence stem cell fate. Nat. Mater. 13, 645–652 (2014).

    Article  ADS  Google Scholar 

  3. Nasrollahi, S. Past matrix stiffness primes epithelial cells and regulates their future collective migration through a mechanical memory. Biomaterials 146, 146–155 (2017).

    Article  Google Scholar 

  4. Lauffenburger, D. A. & Horwitz, A. F. Cell migration: a physically integrated molecular process. Cell 84, 359–369 (1996).

    Article  Google Scholar 

  5. Friedl, P. et al. Migration of coordinated cell clusters in mesenchymal and epithelial cancer explants in vitro. Cancer Res. 55, 4557–4560 (1995).

    Google Scholar 

  6. Brückner, D. B. et al. Stochastic nonlinear dynamics of confined cell migration in two-state systems. Nat. Phys. 15, 595–601 (2019).

    Article  Google Scholar 

  7. Fink, A. et al. Area and geometry dependence of cell migration in asymmetric two-state micropatterns. Biophys. J. 118, 552–564 (2020).

    Article  ADS  Google Scholar 

  8. Brückner, D. B. et al. Learning the dynamics of cell–cell interactions in confined cell migration. Proc. Natl Acad. Sci. USA 118, e2016602118 (2021).

    Article  Google Scholar 

  9. Brückner, D. B., Ronceray, P. & Broedersz, C. P. Inferring the dynamics of underdamped stochastic systems. Phys. Rev. Lett. 125, 058103 (2020).

    Article  ADS  Google Scholar 

  10. Weigelin, B., Bakker, G.-J. & Friedl, P. Intravital third harmonic generation microscopy of collective melanoma cell invasion. IntraVital 1, 32–43 (2012).

    Article  Google Scholar 

  11. Ilina, O. et al. Cell–cell adhesion and 3D matrix confinement determine jamming transitions in breast cancer invasion. Nat. Cell Biol. 22, 1103–1115 (2020).

    Article  Google Scholar 

  12. Lee, J. W. N. & Holle, A. W. Engineering approaches for understanding mechanical memory in cancer metastasis. APL Bioeng. 8, 021503 (2024).

    Article  Google Scholar 

  13. Doyle, A. D., Wang, F. W., Matsumoto, K. & Yamada, K. M. One-dimensional topography underlies three-dimensional fibrillar cell migration. J. Cell Biol. 184, 481–490 (2009).

    Article  Google Scholar 

  14. Versaevel, M., Grevesse, T. & Gabriele, S. Spatial coordination between cell and nuclear shape within micropatterned endothelial cells. Nat. Commun. 3, 671 (2012).

    Article  ADS  Google Scholar 

  15. Maiuri, P. et al. Actin flows mediate a universal coupling between cell speed and cell persistence. Cell 161, 374–386 (2015).

    Article  Google Scholar 

  16. Mosier, J. A. et al. Extent of cell confinement in microtracks affects speed and results in differential matrix strains. Biophys. J. 117, 1692–1701 (2019).

    Article  ADS  Google Scholar 

  17. Yevick, H. G., Duclos, G., Bonnet, I. & Silberzan, P. Architecture and migration of an epithelium on a cylindrical wire. Proc. Natl Acad. Sci. USA 112, 5944–5949 (2015).

    Article  ADS  Google Scholar 

  18. Wang, W. Y., Davidson, C. D., Lin, D. & Baker, B. M. Actomyosin contractility-dependent matrix stretch and recoil induces rapid cell migration. Nat. Commun. 10, 1186 (2019).

    Article  ADS  Google Scholar 

  19. Hennig, K. et al. Stick-slip dynamics of cell adhesion triggers spontaneous symmetry breaking and directional migration of mesenchymal cells on one-dimensional lines. Sci. Adv. 6, 5670 (2020).

    Article  ADS  Google Scholar 

  20. Brückner, D. B. & Broedersz, C. P. Learning dynamical models of single and collective cell migration: a review. Rep. Prog. Phys. 87, 056601 (2024).

  21. Corne, T., Sieprath, T. & Vandenbussche, J. Deregulation of focal adhesion formation and cytoskeletal tension due to loss of A-type lamins. Cell Adhes. Migr. 11, 447–463 (2017).

    Article  Google Scholar 

  22. Pouthas, F. et al. In migrating cells, the Golgi complex and the position of the centrosome depend on geometrical constraints of the substratum. J. Cell Sci. 121, 2406–2414 (2008).

    Article  Google Scholar 

  23. Schmidt, C. J. Microtubule control of migration: coordination in confinement. Curr. Opin. Cell Biol. 86, 102289 (2024).

    Article  Google Scholar 

  24. Wu, C. et al. Arp2/3 is critical for lamellipodia and response to extracellular matrix cues but is dispensable for chemotaxis. Cell 148, 973–987 (2012).

    Article  Google Scholar 

  25. Pollard, T. D. & Borisy, G. G. Cellular motility driven by assembly and disassembly of actin filaments. Cell 112, 453–465 (2003).

    Article  Google Scholar 

  26. Flommersfeld, J., Stöberl, S., Shah, O., Rädler, J. O. & Broedersz, C. P. Geometry-sensitive protrusion growth directs confined cell migration. Phys. Rev. Lett. 132, 098401 (2024).

    Article  ADS  Google Scholar 

  27. Brückner, D. B. et al. Geometry adaptation of protrusion and polarity dynamics in confined cell migration. Phys. Rev. X 12, 031041 (2022).

    Google Scholar 

  28. d’Alessandro, J. et al. Cell migration guided by long-lived spatial memory. Nat. Commun. 12, 4118 (2021).

    Article  ADS  Google Scholar 

  29. Chalut, K. J. & Paluch, E. K. The actin cortex: a bridge between cell shape and function. Dev. Cell 38, 571–573 (2016).

    Article  Google Scholar 

  30. Jawahar, A., Vermeil, J., Heuvingh, J., du Roure, O. & Piel, M. The third dimension of the actin cortex. Curr. Opin. Cell Biol. 89, 102381 (2024).

    Article  Google Scholar 

  31. Truong Quang, B. A. et al. Extent of myosin penetration within the actin cortex regulates cell surface mechanics. Nat. Commun. 12, 6511 (2021).

    Article  ADS  Google Scholar 

  32. Zhang, J., Guo, W.-H. & Wang, Y.-L. Microtubules stabilize cell polarity by localizing rear signals. Proc. Natl Acad. Sci. USA 111, 16383–16388 (2014).

    Article  ADS  Google Scholar 

  33. Belly, H. D. et al. Cell protrusions and contractions generate long-range membrane tension propagation. Cell 186, 3049–3061 (2023).

    Article  Google Scholar 

  34. Chugh, P. & Paluch, E. K. The actin cortex at a glance. J. Cell Sci. 131, jcs186254 (2018).

    Article  Google Scholar 

  35. Fritzsche, M. et al. Self-organizing actin patterns shape membrane architecture but not cell mechanics. Nat. Commun. 8, 14347 (2017).

    Article  ADS  Google Scholar 

  36. Bergert, M., Chandradoss, S. D., Desai, R. A. & Paluch, E. Cell mechanics control rapid transitions between blebs and lamellipodia during migration. Proc. Natl Acad. Sci. USA 109, 14434–14439 (2012).

    Article  ADS  Google Scholar 

  37. Clark, A. G., Dierkes, K. & Paluch, E. K. Monitoring actin cortex thickness in live cells. Biophys. J. 105, 570–580 (2013).

    Article  ADS  Google Scholar 

  38. Chaigne, A. et al. A soft cortex is essential for asymmetric spindle positioning in mouse oocytes. Nat. Cell Biol. 15, 958–966 (2013).

    Article  Google Scholar 

  39. Hakim, V. & Silberzan, P. Collective cell migration: a physics perspective. Rep. Prog. Phys. 80, 076601 (2017).

    Article  ADS  Google Scholar 

  40. Selmeczi, D., Mosler, S., Hagedorn, P. H., Larsen, N. B. & Flyvbjerg, H. Cell motility as persistent random motion: theories from experiments. Biophys. J. 89, 912–931 (2005).

    Article  ADS  Google Scholar 

  41. Mitterwallner, B. G., Schreiber, C., Daldrop, J. O., Rädler, J. O. & Netz, R. R. Non-Markovian data-driven modeling of single-cell motility. Phys. Rev. E 101, 032408 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  42. Brückner, D. B. & Hannezo, E. Tissue active matter: integrating mechanics and signaling into dynamical models. Cold Spring Harb. Perspect. Biol. 17, a041653 (2025).

    Article  Google Scholar 

  43. Ziebert, F. & Aranson, I. S. Computational approaches to substrate-based cell motility. npj Comput. Mater. 2, 16019 (2016).

    Article  ADS  Google Scholar 

  44. Shao, D., Rappel, W.-J. & Levine, H. Computational model for cell morphodynamics. Phys. Rev. Lett. 105, 108104 (2010).

    Article  ADS  Google Scholar 

  45. Sadhukhan, S. et al. Modeling how lamellipodia-driven cells maintain persistent migration and interact with external barriers. Phys. Rev. Res. 7, 013319 (2025).

    Article  Google Scholar 

  46. Marchetti, M. C., Joanny, J. F. & Ramaswamy, S. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143 (2013).

    Article  ADS  Google Scholar 

  47. Ron, J. E., Monzo, P., Gauthier, N. C., Voituriez, R. & Gov, N. S. One-dimensional cell motility patterns. Phys. Rev. Res. 2, 033237 (2020).

    Article  Google Scholar 

  48. Zadeh, P. & Camley, B. A. Inferring nonlinear dynamics of cell migration. PRX Life 2, 043020 (2024).

    Article  Google Scholar 

  49. Sens, P. Stick-slip model for actin-driven cell protrusions, cell polarization, and crawling. Proc. Natl. Acad. Sci. USA 117, 24670–24678 (2020).

    Article  ADS  Google Scholar 

  50. Grevesse, T., Versaevel, M., Circelli, G., Desprez, S. & Gabriele, S. A simple route to functionalize polyacrylamide hydrogels for the independent tuning of mechanotransduction cues. Lab Chip 13, 777 (2013).

    Article  Google Scholar 

  51. Grevesse, T., Versaevel, M. & Gabriele, S. Preparation of hydroxy-PAAm hydrogels for decoupling the effects of mechanotransduction cues. J. Vis. Exp. 28, 51010 (2014).

    Google Scholar 

  52. Vercruysse, E. et al. Geometry-driven migration efficiency of autonomous epithelial cell clusters. Nat. Phys. 20, 1492–1500 (2024).

    Article  Google Scholar 

  53. Ciccone, G. et al. Epithelial cell mechanoresponse to matrix viscoelasticity and confinement within micropatterned viscoelastic hydrogels. Adv. Sci. 12, 2408635 (2025).

    Article  Google Scholar 

  54. Strale, P.-O. et al. Multiprotein printing by light-induced molecular adsorption. Adv. Mater. 28, 2024–2029 (2016).

    Article  Google Scholar 

  55. Stringer, C., Wang, T., Michaelos, M. & Pachitariu, M. CellPose: a generalist algorithm for cellular segmentation. Nat. Methods 18, 100–106 (2021).

    Article  Google Scholar 

  56. Efron, B. Bootstrap methods: another look at the jackknife. Ann. Stat. 7, 1–26 (1979).

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We are grateful to members of S.G.’s laboratory for feedback and suggestions. We thank E. Hannezo, J. O. Rädler, M. Piel, O. du Roure and J. Heuvingh for inspiring discussions. Y.K. and S.G. acknowledge J. B. Braquenier from Nikon Instruments Belux and the Nikon BioImaging Lab in Leiden (the Netherlands) for their support with the Nikon Spatial Array Confocal enhanced-resolution confocal microscopy. We thank D. S. Herrador and M. Balland for their help in improving the microprinting method. D.B.B. was supported by the NOMIS Foundation as a NOMIS Fellow and by an EMBO Postdoctoral Fellowship (ALTF 343-2022). Y.K., M.L. and S.G. acknowledge funding from the University of Mons (FEDER Prostem Research Project no. 1510614, Wallonia DG06), the F.R.S.-FNRS (Epiforce Project no. T.0092.21, Cellsqueezer Project no. J.0061.23 and Optopattern Project no. U.NO26.22) and the Interreg projects ANTIRESI and MICROPLAITE, which are financially supported by Interreg France-Wallonie-Vlaanderen (Fonds Européen de Développement Régional). Y.K. and M.L. are financially supported by F.R.S.-FNRS as FRIA Grantee FNRS and Postdoctoral Fellow (Chargé de Recherches), respectively. Y.K. and S.G. acknowledge le Fonds pour la Recherche Médicale dans le Hainaut (FRMH). G.C. was supported by a grant from the Biotechnology and Biological Sciences Research Council (grant no. BB/V007483/1).

Author information

Authors and Affiliations

  1. SYMBIOSE Lab, Research Institute for Biosciences, CIRMAP, University of Mons – UMONS, Mons, Belgium

    Yohalie Kalukula, Marine Luciano & Sylvain Gabriele

  2. London Centre for Nanotechnology, University College London, London, UK

    Gleb Simanov & Guillaume Charras

  3. Institute for the Physics of Living Systems, University College London, London, UK

    Gleb Simanov & Guillaume Charras

  4. Department of Cell and Developmental Biology, University College London, London, UK

    Gleb Simanov & Guillaume Charras

  5. Biozentrum, University of Basel, Basel, Switzerland

    David B. Brückner

  6. Department of Physics, University of Basel, Basel, Switzerland

    David B. Brückner

  7. Institute for Science and Technology Austria, Klosterneuburg, Austria

    David B. Brückner

Authors
  1. Yohalie Kalukula
    View author publications

    Search author on:PubMed Google Scholar

  2. Marine Luciano
    View author publications

    Search author on:PubMed Google Scholar

  3. Gleb Simanov
    View author publications

    Search author on:PubMed Google Scholar

  4. Guillaume Charras
    View author publications

    Search author on:PubMed Google Scholar

  5. David B. Brückner
    View author publications

    Search author on:PubMed Google Scholar

  6. Sylvain Gabriele
    View author publications

    Search author on:PubMed Google Scholar

Contributions

S.G. and Y.K. conceived of the project, and S.G. supervised the project. Y.K. developed the micropatterns and performed the time-lapse cell experiments, cell tracking and confocal imaging. D.B.B. developed the theoretical model and performed the simulations. M.L. contributed to the experiments and commented on the paper. G.C. provided cell lines and commented on the paper. G.S. conceived of the Arpc1b MCF-10A cell line. Y.K., D.B.B. and S.G. analysed the data and prepared the figures. The article was written by Y.K., D.B.B. and S.G. and read and corrected by all authors, who each contributed to the interpretation of the results.

Corresponding authors

Correspondence to David B. Brückner or Sylvain Gabriele.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Falko Ziebert and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Examples of morphological switch on glass fiber and in 3D collagen fiber matrix.

(a) Time-lapse sequence of a single MDCK epithelial cell migrating on a smooth glass wire (diameter = 5.3 µm). After detaching from the tissue, the epithelial cell rounds up and migrate on the glass fiber. The temporal evolution of the long cell axis and the migration speed indicates that the cell morphological switch from an elongated to a compacted morphology is associated with an increase in migration speed. Scale bar, 50 µm. Adapted with permission from 17. (b) Time-lapse sequence of a single fibroblast (NIH3T3) migrating in a 3D matrix composed of aligned collagen fibers. Scale bar, 50 µm. The temporal evolution of the long cell axis and the migration speed indicates that the cell morphological switch from an elongated to a compacted morphology is associated with an increase in migration speed with a maximum speed around 80 µm/min. Adapted with permission from 18.

Source data

Extended Data Fig. 2 Semi-infinite narrow segments.

(a) Theoretical expectation of the percentage of compacted cell on the bridge of dumbbells (W = 6 µm and L = 160 µm) with square area of 1600 µm2 versus 1D semi-infinite line of W = 6 µm and L = 500 µm. On 6 µm line, percentage of compacted cell is expressed as the percentage of time spent under the compacted morphology over a 20-hour time-lapse. (b) Time-lapse sequence of a compacted cell morphology migrating on a one-dimensional (1D) micropatterned line of W = 6 µm and L = 500 µm. Scale bar, 20 µm. (c) Representative color-coded trajectories with elongated (CSI < 0.4) and compacted (CSI > 0.4) morphologies. (d) Percentage of compacted cells on the bridge of dumbbells (W = 6 µm and L = 160 µm) with square area of 1600 µm2 (n = 56, N = 16) versus 1D semi-infinite line of W = 6 µm and L = 500 µm (n = 10, N = 2). On 6 µm line, percentage of compacted cell is expressed as the percentage of time spent under the compacted morphology over a 20-hour time-lapse.

Source data

Extended Data Fig. 3 Analysis of memory dynamics from cell trajectories.

(a) Selection of n = 55 color-coded single cell trajectories of individual MCF-10A cells migrating on FN dumbbell micropatterns for 20 hours. Trajectories on the bridge are color-coded by state: elongated (CSI < 0.4) and compacted (CSI > 0.4) morphologies. (b) State trajectories computed from position trajectories in (A). A morphological state is assigned to each transition on the bridge, based on the morphological state adopted for most time-points during each transition. (c) Memory analysis tree diagram for events C (compacted transition) and E (elongated transition) obtained from state trajectories in (b). Numbers of the branches indicate probabilities. (d) Trajectories of successful and unsuccessful transitions, defined as follows: in successful transitions, the cell (nucleus) enters the bridge and transmigrates to the other island. In unsuccessful transitions, the nucleus enters the bridge and returns to the same island. Fraction of unsuccessful, successful and total transition, which are repartitioned into two categories, elongated and compacted.

Extended Data Fig. 4 Morphological switching dynamics and mechanical memory on 320 µm-long bridges.

(a) Representative sequence of a back-and-forth motion of an individual MCF-10A cell migrating on an FN dumbbell micropattern with a 320 µm-long bridge. (b) Selection of n = 50 color-coded cell trajectories of individual MCF-10A cells migrating on FN dumbbell micropatterns for 30 hours. Trajectories on the bridge are color-coded with elongated (CSI < 0.4) and compacted (CSI > 0.4) morphologies, and square zones. (c) Statistical tree representation of the experimental probabilities for elongated and compacted states over three generation of successive crossings (N ≥ 3 replicates for each condition). (d) Histogram representation of the probabilities for elongated, P(E), and compacted, P(C), states for various combinations of morphological switches: elongated to elongated P(E | E), compacted to compacted P(C | C), elongated to compacted P(E | C) and compacted to elongated P(C | E). Data are presented as mean values ± SD.

Source data

Extended Data Fig. 5 Physico-chemical footprints.

(a) Schematic representation of the two experimental procedures used to assess pattern conditioning by migrating cells. Cells were seeded on human plasma (hp) fibronectin (FN) micropattern, then detached and fixed either (i) after 5 hours (before the time-lapse) or (ii) 24 hours (after the time-lapse) of culture on micropatterns. (b) Epifluorescence images showing human plasma fibronectin, cellular laminin and cellular FN in control conditions after t = 5 h and t = 24 h of cell culture (top to bottom). Scale bar, 50 μm. (c) Normalized laminin intensity for control (n = 62 patterns, N = 3), 5-hour conditioning (n = 67 patterns, N = 3), and 24-hour conditioning (n = 46 patterns, N = 3). (d) Normalized fibronectin intensity from control (n = 73 patterns, N = 3), 5-hour conditioning (n = 125 patterns, N = 3), and 24 hour-conditioning (n = 74 patterns, N = 3). Boxplots range from the first quartile (Q1) to the third quartile (Q3), with the median (50th percentile) indicated by a line. Whiskers extend from the box to the minimum and maximum data points within 1.5 times the interquartile range.**p < 0.01, ns = not significant (Kruskal-Wallis test).

Source data

Extended Data Fig. 6 Spatial distribution of microtubule filaments.

Confocal microscopy images in enhanced-resolution mode of the basal planes of (a) elongated (left) and (b) compacted (right) cell morphologies. β-tubulin staining (inverted image) and the cell body outline is represented with a black dashed line. Scale bar, 20 µm. In bottom images, β-tubulin filaments in elongated and compacted cells were color-coded according to their spatial orientation. Scale bar, 20 µm. Distribution of the normalized intensity of microtubules (c) at the front and (d) at the rear of elongated (n = 3, N = 2) and compacted (n = 2, N = 2) cell morphologies. (e) Front-to-rear tubulin intensity ratio of elongated (n = 48, N = 3) and compacted (n = 54, N = 3) morphologies during crossing events. Boxplots range from the first quartile (Q1) to the third quartile (Q3), with the median (50th percentile) indicated by a line. Whiskers extend from the box to the minimum and maximum data points within 1.5 times the interquartile range. ****p < 0.0001 (Student’s t test).

Source data

Extended Data Fig. 7 Myosin cortex in elongated and compacted cells.

Typical equatorial focal plane obtained in enhanced-resolution microscopy showing the spatial distribution of phosphorylated myosin light chain (p-MLC) at the actin cortex in (a-b) elongated and (c-d) compacted cells. Plot profiles in (b) and (c) shows the normalized intensity of actin and p-MLC as a function of the distance from the membrane. (e) Full width at half maximum (FWHM) for myosin cortex in elongated (orange, n = 29) and compacted (purple, n = 29) cells. Boxplots range from the first quartile (Q1) to the third quartile (Q3), with the median (50th percentile) indicated by a line. Whiskers extend from the box to the minimum and maximum data points within 1.5 times the interquartile range. ****p < 0.0001 (Student’s t test). Scale bars, 10 µm.

Source data

Extended Data Fig. 8 Effect of a nocodazole treatment on confined migration.

(a) Time-lapse sequence of a compacted cell entering a bridge before (control, CTRL) and after treatment with nocodazole (orange). CTRL is DMSO for nocodazole experiments. Scale bar, 10 µm. White arrows show the direction of migration. (b) Cell shape index on bridge for CTRL (n = 21, N = 5) and nocodazole-treated cells (n = 23, N = 6). (c) Cell area on square for CTRL (n = 18, N = 6) and nocodazole-treated cells (n = 22, N = 7). (d) Successful crossing percentage for CTRL (n = 146, N = 18) and nocodazole-treated cells (n = 33, N = 8) and (e) dwell time on square for CTRL (n = 22, grey) and nocodazole-treated cells (n = 12, light orange). Boxplots range from the first quartile (Q1) to the third quartile (Q3), with the median (50th percentile) indicated by a line. Whiskers extend from the box to the minimum and maximum data points within 1.5 times the interquartile range.****p < 0.0001 and n.s. = not significant (Student’s t test).

Source data

Extended Data Fig. 9 Thickness of the actin cortex in cells spread on squares.

Enhanced-resolution confocal images of (a) a partial spreading and (b) a full spreading of epithelial cells on FN square of 1600 µm2. Cells are immunostained for F-actin with phalloidin (in green) and DNA with DAPI (in bue). Inverted images show normal and side views of the actin cytoskeleton at the apical side. The spreading rate is 50.1% for partial spreading (a) and 87.2% for full spreading (b). Scale bars, 20 µm. (c) Full width at half maximum (FWHM) represents the actin cortex thickness for partial (n = 14, N = 4) and full (n = 18, N = 4) spreading conditions. Boxplots range from the first quartile (Q1) to the third quartile (Q3), with the median (50th percentile) indicated by a line. Whiskers extend from the box to the minimum and maximum data points within 1.5 times the interquartile range. ****p < 0.0001 (Student’s t test).

Source data

Extended Data Fig. 10 Experimentally measured and simulated percentages of successful crossing on interconnected dumbbell micropattern.

Percentages of successful crossing with (a) 900 µm2 squares for elongated (E, n = 34, N = 3) and compacted (C, n = 34, N = 3) and (b) 2500 µm2 squares for elongated (E, n = 50, N = 3) and compacted (C, n = 50, N = 3). Experimentally measured and model-estimated percentages of repolarization during successful crossing on interconnected dumbbell micropattern with (c) 900 µm2 squares for elongated (E, n = 21, N = 3) and compacted (C, n = 30 cells, N = 3)cells and (d) 2500 µm2 squares for elongated (E, n = 41, N = 3) and compacted (C, n = 27 cells, N = 3) cells. Data are presented as mean values ± SD. ****p < 0.0001 (Student’s t test).

Source data

Supplementary information

Supplementary Information

Supplementary Figs. 1–8, Video captions 1–18 and Theory note.

Reporting Summary

41567_2025_2980_MOESM3_ESM.mp4

Supplementary Video 1. Time-lapse sequences showing the back-and-forth motion of an individual MCF-10A epithelial cell on dumbbell-shaped fibronectin micropatterns with bridge lengths of 40 µm, 80 µm, 120 µm, 160 µm and 320 µm and square ends measuring 40 µm × 40 µm. The cell is imaged in differential interference contrast (DIC) mode, with the micropattern labelled with rhodamine-conjugated fibronectin and the nucleus stained with Hoechst. The scale bar represents 20 µm and 50 µm for 320 µm bridge length, the frame rate is 3 min per frame.

41567_2025_2980_MOESM4_ESM.mp4

Supplementary Video 2. Typical sequence of automatic tracking of an individual MCF-10A cell observed in DIC mode and analysed using the Fiji plugin Cellpose 2.0, which provides the cell outline for each frame. This enables the determination of the cell’s spreading area, perimeter and the coordinates of the cell front, rear and centre of mass.

41567_2025_2980_MOESM5_ESM.mp4

Supplementary Video 3. Representative time-lapse sequences (t = 20 h) showing the elongated and compacted morphologies adopted by an individual MCF-10A epithelial cell during its back-and-forth motion on a dumbbell-shaped fibronectin micropattern with a bridge length of 160 µm. The cell is imaged using differential interference contrast (DIC) microscopy, with the micropattern labelled with rhodamine-conjugated fibronectin and the nucleus stained with Hoechst. The scale bar represents 20 µm, and images were captured at 3-min intervals.

41567_2025_2980_MOESM6_ESM.mp4

Supplementary Video 4. Representative time-lapse sequences showing both a failed (t = 24 h) and a successful (t = 3 h and 51 min) crossing event during the back-and-forth motion of an individual MCF-10A epithelial cell on a dumbbell-shaped fibronectin micropattern with a bridge length of 160 µm. The cell is imaged using differential interference contrast (DIC) microscopy, with the micropattern labelled with rhodamine-conjugated fibronectin and the nucleus stained with Hoechst. The scale bar represents 20 µm, and images were captured at 3-min intervals.

41567_2025_2980_MOESM7_ESM.mp4

Supplementary Video 5. Time-lapse sequences of actin retrograde flow in both elongated and compacted lamellipodia, observed in confocal mode using a ×100 silicone objective (N.A. = 1.35). Images were acquired at a rate of one frame every 1.25 s for a total duration of 5 min.

41567_2025_2980_MOESM8_ESM.mp4

Supplementary Video 6. High-resolution confocal Z-stack sequence (Nikon Spatial Array Confocal, NSPARC) of an elongated cell morphology, obtained usinga galvano scanner at × 60 magnification (Plan Apo oil immersion objective, N.A. 1.42) with a step size of 0.10 μm for three channels (DAPI, TRITC and FITC).Actin filaments are shown in black, and DAPI is shown in blue.

41567_2025_2980_MOESM9_ESM.mp4

Supplementary Video 7. High-resolution confocal Z-stack images (Nikon Spatial Array Confocal, NSPARC) of a compacted cell morphology, obtained using agalvano scanner at × 60 magnification (Plan Apo oil immersion objective, N.A. 1.42) with a step size of 0.17 μm for three channels (DAPI, TRITC and FITC).Actin filaments are shown in black, and DAPI is shown in blue.

41567_2025_2980_MOESM10_ESM.m4v

Supplementary Video 8. Schematic movies of simulations of elongated (top), compacted (middle) and switching (bottom) cells moving through the confiningdumbbell pattern. Colour of the dot indicates state of polarization (orange: elongated, a = 1; purple: compacted, a = –2), and arrow indicates the polarity of thecell. Plots on the right indicate simultaneous migration trajectories along the x direction. The dumbbell-shaped micropattern is composed of a bridge of 160 μmin length and 6 μm in width connected at each extremity to a square of 40 μm × 40 μm.

41567_2025_2980_MOESM11_ESM.mp4

Supplementary Video 9. Series of time-lapse sequences in DIC mode of an epithelial cell (MCF-10A) migrating on a dumbbell-shaped fibronectinmicropattern, featuring a bridge 160 μm in length and 6 μm in width, with square ends measuring 40 μm × 40 μm. The first and second sequences depict,respectively, an elongated and a compacted cell both expressing Golgi targeted CellLight Golgi-GFP BacMam 2.0 (red) and the nucleus is stained blue withHoechst. The third sequence depicts a migrating MCF-10A cell expressing ArpC1B–mScarlet. Arp2/3 complex localization is shown in black with the nucleusin blue stained with Hoechst. Scale bar, 50 μm.

41567_2025_2980_MOESM12_ESM.mp4

Supplementary Video 10. Time-lapse sequences of a morphological switch from an elongated to a compacted state, captured in epifluorescence mode with actinfilaments labelled using SPY555-FastAct™ (t = 24 h) and in DIC mode (t = 24 h). The epithelial cell (MCF-10A) migrates on a dumbbell-shaped fibronectinmicropattern, featuring a bridge 160 μm in length and 6 μm in width, with square ends measuring 40 μm × 40 μm. The nucleus is stained blue with Hoechst.Scale bar, 40 μm.

41567_2025_2980_MOESM13_ESM.mp4

Supplementary Video 11. Time-lapse sequence in DIC mode of an epithelial cell (MCF-10A) migrating on fibronectin microstripe measuring 500 µm in length and 6 µm in width (t = 20 h). The nucleus is stained blue with Hoechst. Scale bar, 10 µm.

41567_2025_2980_MOESM14_ESM.mp4

Supplementary Video 12. Successive time-lapse sequences in DIC mode of an individual epithelial cell (MCF-10A) migrating on a dumbbell-shapedfibronectin micropattern, featuring a bridge 160 μm in length and 6 μm in width, with square ends measuring 40 μm × 40 μm. Nocodazole-treated cells exhibita loss of polarity, characterized by oscillations in the first sequence. In the second sequence, the cells fail to enter the bridge, and in the third sequence, theyremain compacted while also failing to enter the bridge. In the first sequence, the cell is treated with 2.5 μM nocodazole at t = 1 h and 30 min (t = 30 h). In thesecond and third sequences, the cell is treated with 2.5 μM nocodazole at t = 2 h and 30 min (t = 30 h).

41567_2025_2980_MOESM15_ESM.mp4

Supplementary Video 13. Time-lapse sequence in DIC mode of an epithelial cell (MCF-10A) migrating on a dumbbell-shaped fibronectin micropattern,featuring a bridge 160 μm in length and 6 μm in width, with square ends measuring 40 μm × 40 μm (t = 20 h and 55 min). The cell is treated with 20 nMLatrunculin B at t = 03 h and 50 min. Scale bar, 10 μm.

41567_2025_2980_MOESM16_ESM.mp4

Supplementary Video 14. Time-lapse sequence in DIC mode of an epithelial cell (MCF-10A) migrating on a dumbbell-shaped fibronectin micropattern,featuring a bridge 160 μm in length and 6 μm in width, with square ends measuring 40 μm × 40 μm (t = 21 h and 40 min). The cell is treated with 10 μMY27632 at t = 03 h and 15 min. Scale bar, 50 μm.

41567_2025_2980_MOESM17_ESM.mp4

Supplementary Video 15. Time-lapse sequence in DIC mode of an epithelial cell (MCF-10A) migrating on a dumbbell-shaped fibronectin micropattern,featuring a bridge 160 μm in length and 6 μm in width, with square ends measuring 30 μm × 30 μm (t = 20 h). The fibronectin micropattern is red and thenucleus in blue. Scale bar, 20 μm.

41567_2025_2980_MOESM18_ESM.mp4

Supplementary Video 16. Time-lapse sequence in DIC mode of an epithelial cell (MCF-10A) migrating on a dumbbell-shaped fibronectin micropattern, featuring a bridge 160 µm in length and 6 µm in width, with square ends measuring 50 µm × 50 µm (t = 20 h). The fibronectin micropattern is depicted in red, and the nucleus is stained blue. Scale bar, 20 µm.

41567_2025_2980_MOESM19_ESM.mp4

Supplementary Video 17. Time-lapse sequence in DIC mode of an epithelial cell (MCF-10A) migrating on a dumbbell-shaped fibronectin micropattern, featuring a bridge 160 µm in length and 6 µm in width, with square ends measuring 50 µm × 50 µm (t = 20 h). The cell is treated with 1 nM of Jasplakinolide 30 min before the beginning of the time-lapse experiment. The fibronectin micropattern is depicted in red, and the nucleus is stained blue. Scale bar, 20 µm.

41567_2025_2980_MOESM20_ESM.mp4

Supplementary Video 18. Time-lapse sequences in DIC mode of an MCF-10A cell migrating on interconnected dumbbell-shaped micropatterns with 160-μmlongbridges and square deconfinement zones of 2500 μm² (first sequence) and 900 μm² (second sequence). The first sequence spans 59 h and 54 min, and thesecond sequence lasts 17 h and 30 min. The nucleus is stained blue with Hoechst. Scale bar, 100 μm.

Source data

Source Data Fig. 1

Fig. 1b–d,h,i.

Source Data Fig. 2

Fig. 2a–c,e,h–j,l,m–p.

Source Data Fig. 3

Fig. 3b,d,f,h,k,i.

Source Data Fig. 4

Fig. 4b–d,f–h.

Source Data Fig. 5

Fig. 5c–e,g,h,m.

Source Data Extended Data Fig. 1

Extended Fig. 1a,b.

Source Data Extended Data Fig. 2

Extended Fig. 2a,c,d.

Source Data Extended Data Fig. 4

Extended Fig. 4b,d.

Source Data Extended Data Fig. 5

Extended Fig. 5c,d.

Source Data Extended Data Fig. 6

Extended Fig. 6c–e.

Source Data Extended Data Fig. 7

Extended Fig. 7b,d,e.

Source Data Extended Data Fig. 8

Extended Fig. 8b–e.

Source Data Extended Data Fig. 9

Extended Fig. 9.

Source Data Extended Data Fig. 10

Extended Fig. 10a–d.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kalukula, Y., Luciano, M., Simanov, G. et al. The actin cortex acts as a mechanical memory of morphology in confined migrating cells. Nat. Phys. 21, 1451–1461 (2025). https://doi.org/10.1038/s41567-025-02980-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-025-02980-z

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing