The flexible Lomax-G family with estimation methods and applications in hydrology and biomedicine

Abstract

In this article, we introduce and investigate a new family of continuous distributions, termed the new Lomax-G (NLx-G) family, constructed via a novel generator. Several mathematical properties are derived, including quantile functions, mixture representations, and moments, together with different estimation methods. A notable special case, the NLx-exponential (NLxEx) distribution, is emphasized for its flexibility in modeling diverse data behaviors. The performance of the proposed model is examined through a comprehensive convergence analysis of estimators and supported by an extensive simulation study, which indicates that the maximum likelihood estimator performs best. To demonstrate practical utility, the NLxEx distribution is applied to three real-world datasets from hydrology, biomedical sciences, and insurance. In addition to standard goodness-of-fit measures, fitting plots are provided as further diagnostics. Across all applications and in comparison with several competing exponential-type models, the NLxEx distribution consistently yields the best fit, confirming its robustness and adaptability.

Introduction

The Pareto type II distribution, also known as the Lomax (Lx) distribution, was introduced by¹. This distribution has a wide range of applications, including in actuarial science, economics, and more. Furthermore, it has proven to be valuable in reliability engineering, particularly in endurance testing problems, as well as in survival analysis, where it serves as an alternative distribution, as highlighted by researchers in² and³. Its ability to model data with asymmetrical characteristics makes it particularly useful in these fields.

Due to its versatile applications, various modified and enhanced versions of the Lx distribution have been proposed in recent literature. Notable examples include the weighted Lx distribution³, transmuted Lomax distribution⁴, exponential Lx distribution⁵, exponentiated Lx distribution⁶, gamma Lx distribution⁷, Poisson–Lx distribution⁸, McDonald Lx distribution⁹, Weibull Lx distribution¹⁰, power Lx distribution¹¹, and the minimum Lindley–Lx distribution¹². Additionally, several recent papers, including those cited from¹³–¹⁸, are highly recommended for further reading.

In this article, we introduce a new family of distributions called the new Lomax-G (NLx-G) family. The NLx-G family is derived from the Lx distribution and the T-X family¹⁹. A key feature of the NLx-G family is its ability to generate both bimodal and unimodal density shapes, depending on the specific sub-models.

The NLx-G family possesses the following desirable properties:

• The “probability density function” (PDF) of the NLx-G family has a simple closed-form expression, making it suitable for modeling and analyzing real-life data across various applied fields.

• The additional parameters in the NLx-G family provide flexibility, enabling its sub-models to accommodate a wide range of failure rate shapes.

• The densities of the NLx-G sub-models offer further flexibility, allowing for the modeling of diverse distribution shapes.

• The NLx-exponential (NLxEx) distribution, a special sub-model within the NLx-G family, provides consistently better fit to real-life datasets as compared to other competing exponential models.

The proposed NLx-G family represents a new class of probability distributions constructed by combining the Lx baseline with the T–X family framework. This construction endows the family with several desirable features that distinguish it from existing Lx extensions. In particular, the NLx-G framework offers closed-form tractability while providing additional parameters that allow for flexible modeling of a wide spectrum of density shapes–including right-skewed, left-skewed, symmetric, bimodal, J-shaped, and reversed J-shaped forms–as well as diverse hazard rate behaviors such as increasing, decreasing, bathtub, and modified bathtub patterns. Its versatility is further illustrated in Section 2, where several special sub-models are derived using different baselines. Among these, the NLxEx sub-model is studied in detail and shown to outperform other exponential-type models when applied to real datasets; however, it is not designed to compete directly with other Lx-based families, but rather to demonstrate the general strength and flexibility of the NLx-G generator. In addition, this work evaluates a broad range of estimation methods for NLxEx, across various sample sizes and parameter settings, offering practical guidelines for applied statisticians. Collectively, these aspects highlight that the NLx-G family extends beyond current Lx generalizations while maintaining mathematical simplicity and broad applicability.

Another motivation of this paper is to evaluate the performance of various estimators for the NLxEx distribution across sample sizes and parameter values. Additionally, we aim to provide a guideline for selecting the most appropriate estimation method for the NLxEx distribution, which we believe will be valuable to applied statisticians.

The rest of this article is structured as follows: Section 2 presents four distinct models from the NLx-G family, accompanied by graphs illustrating their density and hazard functions. In Section 3, we derive essential mathematical properties of the new family. In Section 5, we discuss various estimation methods for the NLx-exponential (NLxEx) distribution, along with simulation studies assessing these methods. Section 6 provides an analysis of two real-world datasets to evaluate the overall performance of the NLxEx model. Finally, Section 7 offers concluding remarks.

The NLx-G family

This section introduces the definition of a newly proposed family, which is based on the classical Lx distribution and the T-X family, using the function $H(\Pi ; y, \, \varvec{\nabla })={G\left( x; \varvec{\psi }\right) \left( 2-G\left( x; \varvec{\psi }\right) \right) /\bar{G} \left( x; \varvec{\psi }\right) }$.

If a random variable Y follows the Lx distribution, the “cumulative distribution function” (CDF) and the associated PDF are given by:

$$\begin{aligned} \Pi \left( y; \alpha , \, \beta \right) =1-(1+\beta \, y)^{-\alpha },\quad y>0 \end{aligned}$$

and

$$\begin{aligned} \pi \left( y; \alpha , \, \beta \right) =\alpha \, \beta \, (1+\beta \, y)^{-\alpha -1}. \end{aligned}$$

We define the flexible NLx-G family by replacing y with the function $H(\Pi ; y, \, \varvec{\nabla })$ into the CDF of the Lx distribution, $\Pi _{\alpha , \,\beta }(y)$. Hence, the CDF of the NLx-G family follows as

$$\begin{aligned} F\left( x;\alpha , \, \beta , \,\varvec{\psi }\right)= & \alpha \,\beta \, \int _{0}^{H(\Pi ; y, \, \varvec{\nabla })} (1+\beta \, y)^{-\alpha -1}\,dy \nonumber \\= & 1-\left( 1+\beta \left\{ o(x;\varvec{\psi })[2-G(x;\varvec{\psi })]\right\} \right) ^{-\alpha }, \quad x\in \Re , \end{aligned}$$

(1)

where $\alpha$ and $\beta$ represent positive shape parameters, $o(x;\varvec{\psi })=G(x;\varvec{\psi })/\bar{G}(x;\varvec{\psi })$, $\bar{G}(x;\varvec{\psi })=1-G(x;\varvec{\psi })$ and $\varvec{\psi }$ is the vector of parameters for the baseline CDF G(.).

The corresponding PDF of the NLx-G family has the form

$$\begin{aligned} f(x; \alpha ,\beta ,\varvec{\psi })=\frac{\alpha \, \beta \, g(x;\mathbf {\varvec{\psi }})}{\bar{G}(x;\varvec{\psi })^2} \left\{ 1+ \left[ G(x;\varvec{\psi })-1 \right] ^{2} \right\} \left( 1+\beta \left\{ o(x;\varvec{\psi })[2-G(x;\varvec{\psi })]\right\} \right) ^{-\alpha -1}. \end{aligned}$$

(2)

The survival function (SF) of the new generator reduces to

$$\begin{aligned} S(x; \alpha ,\beta ,\varvec{\psi })=\left( 1+\beta \left\{ o(x;\varvec{\psi })[2-G(x;\varvec{\psi })]\right\} \right) ^{-\alpha }. \end{aligned}$$

The “hazard rate function” (HRF) of the NLx-G family is

$$\begin{aligned} h(x; \alpha ,\beta ,\varvec{\psi })= \frac{ \alpha \, \beta \, \xi (x;\varvec{\psi }) \left\{ 1+ \left[ G(x;\varvec{\psi })-1 \right] ^{2} \right\} }{\bar{G}(x;\varvec{\psi }) \left( 1+\beta \left\{ o(x;\varvec{\psi })[2-G(x;\varvec{\psi })]\right\} \right) }, \end{aligned}$$

where $\xi (x;\varvec{\psi })=g(x;\varvec{\psi })/\bar{G}(x;\varvec{\psi })$ refers to the baseline HRF.

The reversed HRF is given by

$$\begin{aligned} r(x; \alpha ,\beta ,\varvec{\psi })=\frac{ \alpha \, \beta \, \xi (x;\varvec{\psi }) \left\{ 1+ \left[ G(x;\varvec{\psi })-1 \right] ^{2} \right\} \left( 1+\beta \left\{ o(x;\varvec{\psi })[2-G(x;\varvec{\psi })]\right\} \right) ^{-\alpha -1}}{ \bar{G}(x;\varvec{\psi }) \left[ 1-\left( 1+\beta \left\{ o(x;\varvec{\psi })[2-G(x;\varvec{\psi })]\right\} \right) ^{-\alpha } \right] }. \end{aligned}$$

The cumulative HRF is defined as

$$\begin{aligned} H(x; \alpha ,\beta ,\varvec{\psi })= -\log \left( 1+\beta \left\{ o(x;\varvec{\psi })[2-G(x;\varvec{\psi })]\right\} \right) ^{-\alpha }. \end{aligned}$$

Special sub-models of the NLx-G family

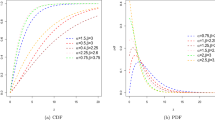
This section emphasizes the versatility of the NLx-G family by presenting several special cases using baseline models such as the exponential (Ex), Burr XII (BXII), Weibull (W), and Kumaraswamy (Ku) distributions. The specific sub-models within the NLx-G family are the NLx exponential (NLxEx), NLx Burr XII (NLxBXII), NLx Weibull (NLxW), and NLx Kumaraswamy (NLxKu) distributions. These sub-models offer a wide range of possible density shapes, including right-skewed, symmetrical, left-skewed, bimodal, unimodal, J-shaped, and reversed J-shaped curves. Additionally, they can model various aging and failure patterns, such as increasing, upside-down bathtub, decreasing, constant, bathtub, and increasing-decreasing-increasing (or modified bathtub) HRFs. Figures 1, 2, 3 and 4 illustrate these diverse density and failure rate shapes for all the mentioned sub-models.

NLxEx distribution

Consider the PDF of the baseline Ex distribution with parameter $\lambda >0$, which is given by $g(x;\lambda )=\lambda e^{-\lambda x}, x>0$. The key functions of the NLxEx distribution are defined in Equations (3)–(6). Here, $\alpha >0$ and $\beta >0$ correspond to the shape parameters, and $\lambda >0$ denotes the scale parameter.

Hence, the CDF of the NLxEx distribution is given by

$$\begin{aligned} F(x)=1-\left[ 1+\beta \left( e^{\lambda x} - e^{-\lambda x}\right) \right] ^{-\alpha }, \,\, x>0. \end{aligned}$$

(3)

The PDF of the NLxEx distribution takes the form

$$\begin{aligned} f(x)=\alpha \beta \lambda e^{\lambda x}\left( 1+e^{-2\lambda x}\right) \left[ 1+\beta \left( e^{\lambda x} - e^{-\lambda x}\right) \right] ^{-\alpha -1}, \end{aligned}$$

(4)

Equation (4) defines the PDF of the NLxEx distribution, where the exponential terms shape the skewness and tail behavior, while the parameters $\alpha$ and $\beta$ control the peakedness and heaviness of the distribution.

The HRF, defined as the ratio of the PDF to the SF, describes the instantaneous risk of failure at time x, conditional on survival up to that point. The HRF of the NLxEx model reduces to

$$\begin{aligned} h(x)=\frac{\alpha \beta \lambda e^{\lambda x}\left( 1+e^{-2\lambda x}\right) }{1+\beta \left( e^{\lambda x} - e^{-\lambda x}\right) }. \end{aligned}$$

(5)

The quantile function (QF) of the NLxEx distribution follows, by inverting (3), as

$$\begin{aligned} Q_{x}(u)= \frac{1}{\lambda } \ln \left( \frac{z-1+\sqrt{\left( z-1\right) ^2+4\beta ^{2}} }{2 \beta } \right) , \end{aligned}$$

(6)

where $z=(1-u)^{-1/\alpha }$. A random variable with density (4) is denoted by $X\sim$NLxEx$(\alpha , \beta , \lambda )$. Figure 1 displays the density and HRF plots of the NLxEx distribution.

Fig. 1

Plots of the PDF and HRF for the NLxEx distribution, illustrating the effects of different parameter values.

NLxBXII distribution

Consider the PDF of the baseline BXII distribution with parameters $c> 0$, $k> 0$, which is given by $g(x;c,k)=ck x^{c-1}(1+x^c)^{-k-1}, x>0$. Then, the PDF and HRF of the NLxBXII distribution are given by

$$\begin{aligned} f(x)=\alpha \beta c k x^{c-1} \frac{1+(1+x^c)^{-2k}}{(1+x^c)^{k+1}} \left\{ 1+\beta \left[ \frac{1-(1+x^c)^{-2k}}{(1+x^c)^{-k}}\right] \right\} ^{-\alpha -1}, \,\, x>0 \end{aligned}$$

and

$$\begin{aligned} h(x)=\alpha \beta c k x^{c-1} (1+x^c)^{-k-1}\frac{1+(1+x^c)^{-2k}}{1+\beta \left[ \frac{1-(1+x^c)^{-2k}}{(1+x^c)^{-k}}\right] }, \end{aligned}$$

respectively, where $\alpha , \beta , c, k$ are positive parameters.

Figure 2 presents the PDF and HRF plots for the NLxBXII distribution for different values of its parameters.

Fig. 2

Plots of the PDF and HRF for the NLxBXII distribution, illustrating the effects of different parameter values.

NLxW distribution

Consider the PDF of the W distribution, with positive parameters $c>$ and k, which is given by $g(x;c,k)=ck x^{k-1} e^{-c x^k}$, $x> 0$. Then, the PDF and HRF of the NLxW distribution take the forms

$$\begin{aligned} f(x)=\alpha \beta c k x^{k-1} \left( e^{c x^k}+e^{2c x^k}\right) \left[ 1+\beta \left( e^{c x^k}-e^{-c x^k}\right) \right] ^{-\alpha -1},\,\, x>0, \,\, \alpha , \beta ,c,k>0 \end{aligned}$$

$$\begin{aligned} h(x)=\alpha \beta c k x^{k-1} \frac{e^{c x^k}+e^{-c x^k}}{1+\beta \left( e^{c x^k}-e^{-c x^k}\right) }. \end{aligned}$$

Figure 3 provides some density and HRF curves for the NLxW distribution.

Fig. 3

Plots of the PDF and HRF for the NLxW distribution, illustrating the effects of different parameter values.

NLxKu distribution

Consider the PDF of the baseline Ku model, with parameters $c> 0$ and $k> 0$, which is defined by $g(x;c,k)=ck x^{c-1} (1-x^c)^{k-1}$, $x\in (0,1)$. Then, the PDF and HRF of the NLxKu distribution are defined (for $0<x<1$) by

$$\begin{aligned} f(x)=\alpha \beta c k x^{c-1} \frac{1+(1-x^c)^{2k}}{(1-x^c)^{k+1}} \left\{ 1+\beta \left[ \frac{1-(1-x^c)^{2k}}{(1-x^c)^{k}}\right] \right\} ^{-\alpha -1}, \,\, \alpha , \beta ,c,k>0 \end{aligned}$$

(7)

and

$$\begin{aligned} h(x)=\alpha \beta c k x^{c-1} (1-x^c)^{-k-1}\frac{1+(1-x^c)^{2k}}{1+\beta \left[ \frac{1-(1-x^c)^{2k}}{(1-x^c)^{k}}\right] }. \end{aligned}$$

(8)

Plots for the PDF and HRF of the NLxKu distribution are illustrated in Fig. 4.

Fig. 4

Plots of the PDF and HRF for the NLxKu distribution, illustrating the effects of different parameter values.

Properties of the proposed family

In this section, we derive some fundamental mathematical properties of the NLx-G family. Throughout, we use the following notational conventions: $g(x;\varvec{\psi })=g(x)$ and $G(x;\varvec{\psi })=G(x)$ denote the PDF and CDF of the baseline distribution, respectively, while $F(x;\alpha ,\beta ,\varvec{\psi })=F(x)$.

Linear representation

A convenient linear expression for the CDF and PDF of the NLx-G family is introduced below.

Using the series expansion $(1+y)^{-n}=\sum _{i=0}^{\infty }\genfrac(){0.0pt}0{-n}{i}y^{i}$, where n is not an integer, the CDF of the NLx-G family can be expressed in terms of an infinite series as follows:

$$\begin{aligned} F(x)= 1-\sum _{i=0}^{\infty }\genfrac(){0.0pt}0{-\alpha }{i} \beta ^{i} \frac{G(x)^{i}[2-G(x)]^{i}}{\bar{G}(x)^{i}}, \end{aligned}$$

where $\bar{G}(x)=1-G(x)$.

Using the following two series expansions:

$$\begin{aligned} (1-y)^n= & \sum _{j=0}^{\infty } \left( {\begin{array}{c}n\\ j\end{array}}\right) (-1)^j y^j, \\ (1+y)^n= & \sum _{k=0}^{\infty } \left( {\begin{array}{c}n\\ k\end{array}}\right) y^k, \end{aligned}$$

and after some algebraic manipulation, the preceding expression simplifies to:

$$\begin{aligned} F(x)=1+\sum _{i,j,k=0}^{\infty }\genfrac(){0.0pt}0{-\alpha }{i}\genfrac(){0.0pt}0{i}{j}\genfrac(){0.0pt}0{j-i}{k}(-1)^{k+1}\beta ^{i}G(x)^{i+k}. \end{aligned}$$

Accordingly, the CDF of the NLx-G family can be represented by the following infinite series expansion:

$$\begin{aligned} F(x)=1+\sum _{i,k=0}^{\infty }\,a_{i,k}\,G(x)^{i+k} \end{aligned}$$

(9)

where $a_{i,k}=\sum _{j=0}^{\infty }\, (-1)^{k+1}\,\beta ^{i} \,\genfrac(){0.0pt}0{-\alpha }{i}\,\genfrac(){0.0pt}0{i}{j}\,\genfrac(){0.0pt}0{j-i}{k}$.

Taking the derivative of Equation (9), the PDF of the NLx-G family is given by:

$$\begin{aligned} f(x)=\sum _{i,k=0}^{\infty }\,{d_{i,k}}\,h_{i+k-1}(x), \end{aligned}$$

(10)

where ${d_{i,k}}=(i+k)\,a_{i,k}$ and $h_{i+k-1}(x)=g(x) G(x) ^{i+k-1}$ is the PDF of the NLx-G family with power parameter $(i+k-1)$.

Moments and generating function

The $r^{th}$ moment about the origin for X can be expressed as

$$\begin{aligned} \mu _{r}^{\prime }=E(X^{r})=\,\int _{0 }^{\infty }\,x^{r}\,f(x)dx. \end{aligned}$$

By applying Equation (10), the preceding expression simplifies to

$$\begin{aligned} \mu _{r}^{\prime }=\sum _{i,k=0}^{\infty }d_{i,k}\,\int _{0 }^{\infty }\,x^{r}\,h_{i+k-1}(x)dx. \end{aligned}$$

Then, we get

$$\begin{aligned} \mu _{r}^{\prime }=\sum _{i,k=0}^{\infty }\, {d_{i,k}}\,\, E(Y_{i+k-1}^{r}), \end{aligned}$$

(11)

where $Y_{i+k-1}$ refers to the exponentiated-G (exp-G) random variable with power parameter $i+k-1$. The mean of X, say $\mu _{1}^{\prime }$, follows from (11) with $r=1$.

Equation (11) provides the closed-form expression for the $r^{th}$ moment. The derivation follows by substituting the NLx-G density into the general definition of the moment and expanding the binomial terms. This compact result highlights how the additional parameter $\alpha$ influences higher-order moments.

From the ordinary moments, one can compute the skewness and kurtosis using standard relationships. The $n^{th}$ central moment of a random variable X, denoted $M_{n}$, is given as:

$$\begin{aligned} M_{n}=E(X-\mu )^{n}=\underset{h=0}{\overset{n}{\sum }}(-1)^{h}\,\left( {\begin{array}{c}n\\ h\end{array}}\right) \,(\mu _{1}^{\prime })^{n}\,\mu _{n-h}^{\prime }. \end{aligned}$$

Two expressions for the moment generating function (MGF) of X, given by $M_{X}\left( t\right) =E\left( e^{t\,X}\right)$, are provided below. The first is derived directly from Equation (10):

$$\begin{aligned} M_{X}\left( t\right) =\sum _{i,k=0}^{\infty } {d_{i,k}}\,M_{i+k-1}\left( t\right) , \end{aligned}$$

where $M_{i+k-1}\left( t\right)$ is the MGF of $Y_{i+k-1}$. Therefore, $M_{X}\left( t\right)$ can be calculated using the exp-G MGF.

Equation (10) also leads to an alternative representation of $M_{X}\left( t\right)$, given by:

$$\begin{aligned} M_{X}\left( t\right) =\sum _{i,k=0}^{\infty } {d_{i,k}}\,\tau \left( t,i+j\right) , \end{aligned}$$

(12)

where $\tau \left( t,i+j\right)$ is defined as $\int \nolimits _{0}^{1}\exp \left[ t\,Q_{G}\left( u\right) \right] \,u^{i+j}du$, where $Q_{G}(u)=G^{-1}(u)$ denotes the QF associated with the baseline distribution $G\left( x\right)$.

Equation (12) gives the MGF of the NLx-G distribution, obtained by applying the series expansion of the exponential function and interchanging the order of summation and integration. This representation is useful for characterizing distributional properties and for deriving cumulants.

In Table 1, numerical values are reported for the first four raw moments ($\mu ^{\prime }_1$, $\mu ^{\prime }_2$, $\mu ^{\prime }_3$, $\mu ^{\prime }_4$), the variance ($V_ar$), skewness ($\Omega _1$), kurtosis ($\Omega _2$) and the coefficient of variation ($C_V$) of the NLxEx distribution under different parameter settings.

Table 1 provides some numerical results for the first four moments, denoted by $\mu ^{\prime }_1$, $\mu ^{\prime }_2$, $\mu ^{\prime }_3$, and $\mu ^{\prime }_4$, variance ($V_ar$), skewness ($\Omega _1$), kurtosis ($\Omega _2$) and the coefficient of variation ($C_V$) of the NLxEx distribution for different values of its parameters. The NLxEx distribution demonstrates significant flexibility in shape characteristics–including central tendency, variability, skewness, and tail weight–depending on parameter settings. This suggests its suitability for modeling a wide range of real-world data behaviors.

Figure 5 depicts the skewness and kurtosis of the NLxEx distribution for different parameter settings. The skewness plot shows that the distribution can capture both negative and positive asymmetry, indicating its flexibility in modeling left- and right-skewed data. The kurtosis plot demonstrates that, within the explored parameter ranges, the distribution exhibits platykurtic behavior (kurtosis $< 3$), reflecting light-tailed characteristics. These properties highlight the adaptability of the NLxEx model in describing diverse data shapes.

Table 1 Summary of the first four moments, $V_ar$, $\Omega _1$, $\Omega _2$, and $C_V$ for the NLxEx distribution.

Fig. 5

Plots of the skewness and kurtosis for the NLxEx distribution under different parameter values.

Incomplete moments

The first incomplete moment (FIM), denoted $I_{1}$, is a valuable tool, particularly for deriving measures such as mean deviations, the Bonferroni curve, and the Lorenz curve. These curves are widely applied in disciplines such as economics, reliability engineering, demography, insurance, and healthcare.

The $s^{th}$ incomplete moment of X, denoted $I_{s}\left( t\right)$, follows from Equation (10) and is defined as:

$$\begin{aligned} I_{s}\left( t\right) =\int _{0 }^{t}\,x^{s}\,f(x)dx=\sum _{i,k=0}^{\infty } {d_{i,k}}\,\int _{0 }^{t}\,x\,h_{i+k-1}\left( x\right) dx. \end{aligned}$$

(13)

The mean deviations of X about the mean, denoted $\delta _{1}$, and about the median, denoted by $\delta _{2}$, have the forms

$$\begin{aligned} \delta _{1}=E(|X-\mu _{1}^{\prime }|)=2\mu _{1}^{^{\prime }}F(\mu _{1}^{\prime })-2\varphi _{1}(\mu _{1}^{\prime }) \end{aligned}$$

and

$$\begin{aligned} \delta _{2}=E\left( \left| X-M\right| \right) =\mu _{1}^{\prime }-2\varphi _{1}\left( M\right) , \end{aligned}$$

where $F(\mu _{1}^{\prime })$ follows easily from (1) and M denotes the median, say $M=Median(X)=Q(0.5)$.

Hence, we provide two ways to determine $\delta _{1}$ and $\delta _{2}$. The first using the general equation for $I_{1}\left( t\right)$, which can be derived from (13) as

$$\begin{aligned} I_{1}\left( t\right) =\sum _{i,k=0}^{\infty } {d_{i,k}}\,I_{i+k-1}\left( x\right) , \end{aligned}$$

where

$$\begin{aligned} I_{i+k-1}\left( x\right) =\int _{0 }^{t}\,x\,h_{i+k-1}\left( x\right) dx \end{aligned}$$

is the FIM of $Y_{i+k-1}$.

An alternative general expression for $I_{1}\left( t\right)$ is given by:

$$\begin{aligned} I_{1}\left( t\right) =\sum _{i,k=0}^{\infty } {d_{i,k}}\,v_{i+k-1}\left( t\right) , \end{aligned}$$

where

$$\begin{aligned} v_{i+k-1}\left( t\right) =(i+k-1)\,\int \nolimits _{0}^{G\left( t\right) }\,Q_{G}\left( u\right) \,u^{i+k}du, \end{aligned}$$

can be calculated numerically.

The expressions for $I_{1}\left( t\right)$ can also be utilized to construct the Bonferroni and Lorenz curves, which are defined, for a given probability level $\pi$, as follows $B(\pi )=I_{1}\left( q\right) /(\pi \mu _{1}^{\prime })$ and $L(\pi )=I_{1}\left( q\right) /\mu _{1}^{\prime }$, where $q=Q(\pi )$ is the QF of X evaluated at $\pi$ and $\mu _{1}^{\prime }$ denotes the first (raw) moment of X.

Moments of the residual lifetime

For the NLx-G family, the $n^{th}$ moment of the residual lifetime, defined as $a_{n}(t)=E[(X-t)^{n}\mid X>t],~n=1,2,\ldots$, simplifies to:

$$\begin{aligned} a_{n}(t)=\frac{\int _{t}^{\infty }(x-t)^{n}dF(x)}{1-F(t)}. \end{aligned}$$

Accordingly, the formulation becomes:

$$\begin{aligned} a_{n}(t)=\frac{1}{1-F(t)}\,\sum _{i,k=0}^{ \infty } {d_{i,k}}^{*}\int _{t}^{\infty }\,x^{r}\,h_{i+k-1}(x), \end{aligned}$$

where

$$\begin{aligned} {d_{i,k}}^{*}= {d_{i,k}}\overset{n}{\underset{r=0}{\sum }}\left( {\begin{array}{c}n\\ r\end{array}}\right) \left( -t\right) ^{n-r}. \end{aligned}$$

Moment of reversed residual lifetime

The $n^{th}$ moment of the reversed residual lifetime of X is defined by

$$\begin{aligned} A_{n}(t)=E\left[ (t-X)^{n}\mid X\le t\right] \text { for }t>0\text { and }n=1,2,\ldots \end{aligned}$$

Then, $A_{n}(t)$ for the NLx-G family is expressed as

$$\begin{aligned} A_{n}(t)=F^{-1}(t)\int _{0}^{t}(t-x)^{n}dF(x). \end{aligned}$$

Consequently, the $A_{n}(t)$ of X takes the form:

$$\begin{aligned} A_{n}(t)=F(t)^{-1}\, {d_{i,k}}^{**}\int _{0}^{t}\,x^{r}\,h_{i+k-1}(x), \end{aligned}$$

where

$$\begin{aligned} {d_{i,k}}^{**}= {d_{i,k}}\overset{n}{\underset{r=0}{\sum }}\left( -1\right) ^{r}\left( {\begin{array}{c}n\\ r\end{array}}\right) t^{n-r}. \end{aligned}$$

Methods of estimation

“Lambert-G” In this section, we estimate the unknown parameters of the NLxEx distribution using six different estimation methods: “maximum likelihood” (ML), “least squares” (LS), “Cramér–von Mises” (CVM), “weighted least squares” (WLS), “Anderson–Darling” (AD), and “right-tail AD” (RTAD). Throughout this section, let $X_1, X_2..., X_n$ denote a random sample of size n, and let $X_{(1)}, X_{(2)}..., X_{(n)}$ represent the corresponding order statistics.

To obtain the ML estimators of the parameters $\alpha , \beta$, and $\lambda$ of the NLxEx distribution, we maximize the log-likelihood function given by:

$$\begin{aligned} \ell= & n \log \alpha +n \log \beta +n \log \lambda +\sum _{i=1}^{n}\lambda x_i+\sum _{i=1}^{n}\log \left( 1+e^{-2\lambda x_i}\right) \\ & -(\alpha +1)\sum _{i=1}^{n}\log \left[ 1+\beta \left( e^{\lambda x_i}-e^{-\lambda x_i}\right) \right] . \end{aligned}$$

The ML estimators are the solutions to the following system of likelihood equations. Differentiating with respect to $\alpha$, we obtain

$$\begin{aligned} \frac{\partial \ell }{\partial \alpha }=\frac{n}{\alpha }-\sum _{i=1}^{n}\log \left[ 1+\beta \left( \frac{1-\vartheta _i^{2}}{\vartheta _i}\right) \right] =0. \end{aligned}$$

Similarly, differentiating with respect to $\beta$ yields

$$\begin{aligned} \frac{\partial \ell }{\partial \beta }=\frac{n}{\beta }-(\alpha +1)\sum _{i=1}^{n}\frac{1-\vartheta _i^{2}}{\vartheta _i\big [1+\beta \big (\frac{1-\vartheta _i^{2}}{\vartheta _i}\big )\big ]}=0. \end{aligned}$$

Finally, differentiating with respect to $\lambda$ gives

$$\begin{aligned} \frac{\partial \ell }{\partial \lambda }=\frac{n}{\lambda }+\sum _{i=1}^{n}x_i-\sum _{i=1}^{n}\frac{2\, x_i \, \vartheta _i^{2}}{1-\vartheta _i^{2}}-(\alpha +1)\sum _{i=1}^{n}\frac{\beta x_i (1+\vartheta _i^{2})}{\vartheta _i\big [1+\beta \big (\frac{1-\vartheta _i^{2}}{\vartheta _i}\big )\big ]}=0, \end{aligned}$$

where $\vartheta _i=e^{-\lambda x_i}$.

The above equations form a nonlinear system that does not admit closed-form solutions. Hence, the ML estimators $(\hat{\alpha }, \hat{\beta }, \hat{\lambda })$ must be obtained numerically using iterative optimization methods such as Newton–Raphson.

The LS estimators²⁰ of $\alpha , \beta$ and $\lambda$ can be determined by minimizing the following function

$$\begin{aligned} W_1(\alpha ,\beta ,\lambda )=\sum \limits _{i=1}^{n}\left[ F(x_{(i)};\alpha ,\beta ,\lambda )-\frac{i}{n+1}\right] ^{2}=\sum \limits _{i=1}^{n}\left[ 1-\left\{ 1+\beta \left( \frac{1-\vartheta _{(i)}^{2}}{\vartheta _{(i)}} \right) \right\} ^{-\alpha }-\frac{i}{n+1}\right] ^{2}, \end{aligned}$$

where $\vartheta _{(i)}=e^{-\lambda x_{(i)}}$.

In addition, the LS estimators are derived by solving the following non-linear equations simultaneously:

$$\begin{aligned} \frac{\partial W_1(\alpha ,\beta ,\lambda )}{\partial \alpha }= & \sum \limits _{i=1}^{n} \delta ^{(1)}_i\left[ 1-\left\{ 1+\beta \left( \frac{1-\vartheta _{(i)}^{2}}{\vartheta _{(i)}}\right) \right\} ^{-\alpha }-\frac{i}{n+1}\right] =0,\\ \frac{\partial W_1(\alpha ,\beta ,\lambda )}{\partial \beta }= & \sum \limits _{i=1}^{n} \delta ^{(2)}_i\left[ 1-\left\{ 1+\beta \left( \frac{1-\vartheta _{(i)}^{2}}{\vartheta _{(i)}}\right) \right\} ^{-\alpha }-\frac{i}{n+1}\right] =0 \end{aligned}$$

and

$$\begin{aligned} \frac{\partial W_1(\alpha ,\beta ,\lambda )}{\partial \lambda }=\sum \limits _{i=1}^{n} \delta ^{(3)}_i\left[ 1-\left\{ 1+\beta \left( \frac{1-\vartheta _{(i)}^{2}}{\vartheta _{(i)}}\right) \right\} ^{-\alpha }-\frac{i}{n+1}\right] =0, \end{aligned}$$

where

$$\begin{aligned} \delta ^{(1)}_i= & -\left[ 1+\beta \left( \frac{1-\vartheta _{(i)}^{2}}{\vartheta _{(i)}}\right) \right] ^{-\alpha }\log \left[ 1+\beta \left( \frac{1-\vartheta _{(i)}^{2}}{\vartheta _{(i)}}\right) \right] , \end{aligned}$$

(14)

$$\begin{aligned} \delta ^{(2)}_i= & \alpha \frac{1-\vartheta _{(i)}^{2}}{\vartheta _{(i)}} \left[ 1+\beta \left( \frac{1-\vartheta _{(i)}^{2}}{\vartheta _{(i)}}\right) \right] ^{-\alpha -1} \end{aligned}$$

(15)

and

$$\begin{aligned} \delta ^{(3)}_i=\alpha \, \beta \, x_{(i)}\, \frac{1+\vartheta _{(i)}^{2}}{\vartheta _{(i)}} \left[ 1+\beta \left( \frac{1-\vartheta _{(i)}^{2}}{\vartheta _{(i)}}\right) \right] ^{-(\alpha +1)}. \end{aligned}$$

(16)

The WLS estimators of $\alpha , \beta$ and $\lambda$ can be determined by minimization

$$\begin{aligned} W_2(\alpha ,\beta ,\lambda )= \sum \limits _{i=1}^{n}\frac{(n+1)^{2}(n+2)}{i(n-i+1)}\left[ 1-\left\{ 1+\beta \left( \frac{1-\vartheta _{(i)}^{2}}{\vartheta _{(i)}}\right) \right\} ^{-\alpha }-\frac{i}{n+1}\right] ^{2} \end{aligned}$$

The CVM minimum distance estimation method is introduced by²¹. The CVM estimators of $\alpha , \beta$ and $\lambda$ can be obtained by minimizing the following function:

$$\begin{aligned} W_3(\alpha ,\beta ,\lambda )= & \frac{1}{12n}+\sum \limits _{i=1}^{n} \left[ F(x_{(i)};\alpha ,\beta ,\lambda )-\frac{2i-1}{2n}\right] ^{2}\\ & =\frac{1}{12n}+\sum \limits _{i=1}^{n}\left[ 1-\left\{ 1+\beta \left( \frac{1-(e^{-\lambda x_{(i)}})^{2}}{e^{-\lambda x_{(i)}}}\right) \right\} ^{-\alpha }-\frac{2i-1}{2n}\right] ^{2}. \end{aligned}$$

The AD estimation method is introduced by²². The AD estimators for $\alpha , \beta$ and $\lambda$ can be determined by minimizing the following quantity

$$\begin{aligned} W_4(\alpha ,\beta ,\lambda )=-n-\frac{1}{n}\sum \limits _{i=1}^{n}(2i-1) \left[ \log \{F(x_{(i)};\alpha ,\beta ,\lambda )\}-\log \{1-F(x_{(n+1-i)}; \alpha ,\beta ,\lambda )\}\right] . \end{aligned}$$

Equivalently, to obtain the AD estimators, one must solve the following equations simultaneously:

$$\begin{aligned} \frac{\partial W_4(\alpha ,\beta ,\lambda )}{\partial \alpha }= & -\frac{1}{n}\sum \limits _{i=1}^{n}(2i-1) \left[ \frac{\delta _i^{(1)}(\alpha ,\beta ,\lambda )}{F(x_{(i)};\alpha ,\beta ,\lambda )} -\frac{\delta _{(n+1-i)}^{(1)}(\alpha ,\beta ,\lambda )}{1-F(x_{(n+1-i)};\alpha ,\beta ,\lambda )}\right] , \\ \frac{\partial W_4(\alpha ,\beta ,\lambda )}{\partial \beta }= & -\frac{1}{n}\sum \limits _{i=1}^{n}(2i-1) \left[ \frac{\delta _i^{(2)}(\alpha ,\beta ,\lambda )}{F(x_{(i)};\alpha ,\beta ,\lambda )} -\frac{\delta _{(n+1-i)}^{(2)}(\alpha ,\beta ,\lambda )}{1-F(x_{(n+1-i)};\alpha ,\beta ,\lambda )}\right] \end{aligned}$$

and

$$\begin{aligned} \frac{\partial W_4(\alpha ,\beta ,\lambda )}{\partial \lambda }=-\frac{1}{n}\sum \limits _{i=1}^{n}(2i-1) \left[ \frac{\delta _i^{(3)}(\alpha ,\beta ,\lambda )}{F(x_{(i)};\alpha ,\beta ,\lambda )} -\frac{\delta _{(n+1-i)}^{(3)}(\alpha ,\beta ,\lambda )}{1-F(x_{(n+1-i)};\alpha ,\beta ,\lambda )}\right] , \end{aligned}$$

where $\delta ^{(1)}_i, \delta ^{(2)}_i$ and $\delta ^{(3)}_i$ are given in Equations (14)-(16).

To estimate $\alpha , \beta$, and $\lambda$ using the RTAD method, we minimize the following function:

$$\begin{aligned} W_5(\alpha ,\beta ,\lambda )=\frac{n}{2}-2\sum \limits _{i=1}^{n}\left[ \log \{ F(x_{(i)};\alpha ,\beta ,\lambda )\} \right] +\frac{1}{n}\sum \limits _{i=1}^{n}(2i-1) \log \{1-F(x_{(n+1-i)};\alpha ,\beta ,\lambda )\}. \end{aligned}$$

Simulation analysis

In this section, we develop a numerical study to compare the behavior of different estimators. We generate $N=1000$ random samples of sizes $n = 50, 100, 200, 500$ and 750 from the NLxEx distribution. Fifteen combinations of parameters are assigned including: Set-1: $(\alpha =0.5, \beta = 2, \lambda = 1)$, Set-2: $(\alpha = 2, \beta =1.2, \lambda =0.5 )$, Set-3: $(\alpha =2.5, \beta =1, \lambda =1.5 )$, Set-4: $(\alpha =1.5, \beta =0.8, \lambda =0.2 )$, Set-5: $(\alpha =1, \beta =0.5, \lambda =1.4 )$, Set-6: $(\alpha = 3, \beta = 1.8, \lambda =2 )$, Set-7: $(\alpha =1.2, \beta =1, \lambda =0.8 )$, set-8: $(\alpha = 2.2, \beta = 2, \lambda =0.2 )$ , set-9: $(\alpha = 1.8, \beta = 1.5, \lambda =1.2 )$ , set-10: $(\alpha = 0.2, \beta = 1.4, \lambda =2.5 )$, set-11: $(\alpha = 2, \beta = 2.2, \lambda =1 )$, set-12: $(\alpha = 1.6, \beta =1.1, \lambda =0.6 )$, set-13: $(\alpha = 1.7, \beta = 0.9, \lambda =2.3 )$ , set-14: $(\alpha =2.8, \beta = 1.4, \lambda =0.6 )$ and set-15: $(\alpha =0.6, \beta = 1.7, \lambda =1.1 )$. The average estimates (AEs) of $\alpha , \beta$ and $\lambda$ are determined using six estimation approaches for each sample, along with the mean squared errors (MSEs) for each estimate.

The AE and MSE are defined by

$$\begin{aligned} \widehat{AE(n)}=\frac{1}{N}\sum \limits _{i=1}^{N}\hat{\varvec{\theta }}_{i}, \quad \widehat{MSE(n)}=\frac{1}{N}\sum \limits _{i=1}^{N}(\hat{\varvec{\theta }}_{i}-\varvec{\theta })^2, \end{aligned}$$

where $\varvec{\theta }=(\alpha ,\beta ,\lambda )^{T}$.

The numerical values for the AEs and MSEs are calculated for all parameter combinations using the ML, LS, WLS, CVM, AD, and RTAD methods, and are presented in Tables 2–6. In each table, the first column corresponds to the AE, while the second culomn displays the MSEs for each estimate. Our simulation study reveals that all the estimation methods exhibit consistency, meaning that the MSE decreases as the sample size increases. When comparing the different estimation methods, the results in these tables indicate that the ML method generally provides the most accurate parameter estimates for $\alpha$, $\beta$, and $\lambda$, in terms of MSEs. Therefore, the ML method is the most effective for estimating the parameters of the NLxEx distribution based on MSEs performance.

Convergence analysis of estimators

The convergence behavior of the proposed estimators for the NLxEx distribution has been investigated through a comprehensive simulation study, as presented in Tables 2, 3, 4, 5 and 6. Across all considered parameter sets, the AEs tend to approach the true parameter values as the sample size n increases, confirming the consistency of the ML, LS, WLS, CVM, AD, and RTAD estimators.

In general, the MSE of each estimator decreases with increasing sample size, reflecting improved estimation precision. The ML estimator consistently exhibits the lowest MSE across almost all parameter sets and sample sizes, indicating superior efficiency. The RTAD estimator also performs well, particularly for small to moderate sample sizes, due to its robustness against extreme observations. LS and WLS estimators show acceptable performance, though they occasionally yield larger MSE values in small samples. Similarly, the CVM and AD estimators are competitive but can be sensitive to sample variability.

However, some anomalies were observed: for certain estimators and parameter sets, the MSE slightly increases with larger sample sizes. This phenomenon can be attributed to finite-sample effects, numerical instability, or the influence of extreme values in simulated datasets, particularly when the underlying distribution is highly skewed or heavy-tailed. Such behavior is more pronounced in the LS, WLS, CVM, and AD estimators, whereas ML and RTAD remain largely stable.

Figures 6 and 7 display the AEs and MSEs of the NLxEx parameters for different sample sizes. The results clearly show that all estimators are consistent, with accuracy and efficiency improving as the sample size increases. Among the methods, ML and RTAD perform best, yielding the lowest AEs and MSEs across parameter settings. In contrast, LS and WLS improve gradually and converge to the true values as the sample size grows, while AD and CVM occasionally show larger errors for small samples.

From a practical standpoint, these findings suggest the following guidelines for applied use:

• ML estimator: most suitable for moderate to large samples due to high efficiency and stable convergence.

• RTAD estimator: preferable when robustness is critical or for small-sample scenarios.

• LS, WLS, CVM, and AD estimators: viable alternatives, but users should exercise caution with small or skewed datasets owing to occasional increases in error.

Overall, the convergence analysis highlights ML and RTAD as offering the best balance of efficiency and robustness, while confirming the consistency of all estimators under increasing sample sizes.

Table 2 The AEs and MSE obtained from various estimation methods for the NLxEx distribution.

Table 3 The AEs and MSE obtained from various estimation methods for the NLxEx distribution.

Table 4 The AEs and MSE obtained from various estimation methods for the NLxEx distribution.

Table 5 The AEs and MSE obtained from various estimation methods for the NLxEx distribution.

Table 6 The AEs and MSE obtained from various estimation methods for the NLxEx distribution.

Fig. 6

AEs versus sample size for selected parameter sets of the NLxEx distribution..

Fig. 7

MSEs versus sample size for selected parameter sets of the NLxEx distribution..

Real-world data applications

In this section, we present three applications to real-life datasets to empirically illustrate the potential of the new family.

The first dataset, analyzed by²³, shows the spatial differences in flood levels recorded at various stations along the river course. The data values are: 11.75, 3.60, 1.96, 11.48, 4.79, 10.43, 3.80, 13.29, 1.97, 14.18, 5.78,12.34, 5.76, 5.66, 6.30, 8.51, 6.76, 7.84, 9.18, 10.24, 11.45, 10.25, 11.81, 12.78, 13.06, 10.13, 14.40, 6.27, 13.98, 16.22, 7.65, 17.06, 7.99.

The second dataset contains the survival times (in days) for 72 guinea pigs infected with virulent tubercle bacilli, as reported by²⁴ and analyzed by²⁵. This species was chosen because of its pronounced susceptibility to human tuberculosis. The survival times are: 0.1, 0.33, 0.44, 0.56, 0.59, 0.72, 0.74, 0.77, 0.92, 0.93, 0.96, 1, 1, 1.02, 1.05, 1.07, 07, .08, 1.08, 1.08, 1.09, 1.12, 1.13, 1.15, 1.16, 1.2, 1.21, 1.22, 1.22, 1.24, 1.3, 1.34, 1.36, 1.39, 1.44, 1.46, 1.53, 1.59, 1.6, 1.63, 1.63, 1.68, 1.71, 1.72, 1.76, 1.83, 1.95, 1.96, 1.97, 2.02, 2.13, 2.15, 2.16, 2.22, 2.3, 2.31, 2.4, 2.45, 2.51, 2.53, 2.54, 2.54, 2.78, 2.93, 3.27, 3.42, 3.47, 3.61, 4.02, 4.32, 4.58, 5.55.

The third dataset originates from the insurance domain and serves to demonstrate the practical utility of the NLxEx distribution. It consists of monthly unemployment insurance records covering the period from July 2008 to April 2013, comprising 58 observations. The data were released by the Department of Labor, Licensing, and Regulation, State of Maryland, USA. Although the full dataset contains 21 variables, our analysis concentrates exclusively on the seventh variable. The data are publicly available at: https://tinyurl.com/4en5cdsj. The observed values are: 18.2, 8.0, 30.1, 16.3, 22.7, 11.1, 26.6, 26.9, 18.9, 31.2, 20.6, 24.3, 40.7, 49.3, 56.9, 55.0, 50.7, 49.4, 46.6, 79.2, 87.9, 78.9, 63.7, 61.7, 60.8, 68.8, 69.2, 54.8, 55.9, 65.4, 65.5, 53.7, 52.7, 50.7, 52.9, 61.3, 47.5, 49.6, 58.9, 56.0, 47.4, 46.5, 46.9, 57.9, 44.5, 45.7, 44.1, 53.1, 41.8, 37.1, 48.2, 32.7, 42.8, 37.6, 47.4, 32.2, 35.6.

For all datasets, we compare the NLxEx distribution with several competing Ex models, including the Lomax Ex (LEx)²⁶, exponentiated transmuted Ex (ETLEx)²⁷, exponentiated Gumbel Ex (EGEx)²⁸, Burr XII Ex (BXIIEx)²⁹, transmuted generalized Ex (TGEx)³⁰, and Topp–Leone odd log-logistic Ex (TLOLLEx)³¹ distributions.

The model selection is based on information criteria (IC), including the negative log-likelihood ($-\hat{\ell }$), “Bayesian IC” (BIC), Akaike IC” (AIC), “Hannan–Quinn IC” (HQIC), and “corrected AIC” (CAIC), along with “goodness-of-fit” statistics such as the “Cramér–von–Mises” ($W^{*}$), “Anderson–Darling” ($A^{*}$), and “Kolmogorov–Smirnov” (KS) tests with its corresponding p-value (KS p-value). All analyses in this study are conducted using R software.

Tables 7, 8 and 9 report the ML estimates and their corresponding standard errors (SEs, in parentheses) for the fitted models across the three datasets. The associated goodness-of-fit statistics are summarized in Tables 10, 11 and 12, which compare the performance of the NLxEx distribution with that of the competing exponential-type models. According to all reported measures, the NLxEx distribution consistently provides the best fit among the considered models.

Table 7 The ML estimates and their corresponding SEs (in parentheses) for the first dataset.

Table 8 The ML estimates and their corresponding SEs (in parentheses) for the second dataset.

Table 9 The ML estimates and their corresponding SEs (in parentheses) for the third dataset.

Table 10 The goodness-of-fit measure values for the NLxEx distribution and other competing models for the first dataset.

Table 11 The goodness-of-fit measure values for the NLxEx distribution and other competing models for the second dataset.

Table 12 The goodness-of-fit measure values for the NLxEx distribution and other competing models for the third dataset.

Figures 8, 11, and 14 display the fitted PDFs and empirical CDFs of the NLxEx and competing models for the three datasets. Figures 9, 12, and 15 further illustrate the fitted density and empirical CDF of the NLxEx distribution alone for each dataset. In addition, the quantile–quantile (QQ) plots in Figs. 10, 13, and 16 provide a graphical assessment of the fit for the NLxEx and alternative models. These plots reinforce the numerical findings in Tables 10, 10 and 12, clearly demonstrating that the proposed NLxEx distribution offers a superior fit compared to the competing exponential-type distributions.

Fig. 8

Plots of the fitted PDFs and empirical CDFs for the NLxEx distribution and other competing models based on the first dataset.

Fig. 9

Plots of the fitted density and empirical CDF for the NLxEx distribution based on the first dataset.

Fig. 10

QQ plots of the NLxEx distribution and its competing models based on the first dataset..

Fig. 11

Plots of the fitted PDFs and empirical CDFs for the NLxEx distribution and other competing models based on the second dataset.

Fig. 12

Plots of the fitted density and empirical CDF for the NLxEx distribution based on the second dataset.

Fig. 13

QQ plots of the NLxEx distribution and its competing models based on the second dataset..

Fig. 14

Plots of the fitted PDFs and empirical CDFs for the NLxEx distribution and other competing models based on the third dataset.

Fig. 15

Plots of the fitted density and empirical CDF for the NLxEx distribution based on the third dataset.

Fig. 16

QQ plots of the NLxEx distribution and its competing models based on the third dataset.

Conclusions

In this work, we introduced a new and flexible class of lifetime distributions, the new Lomax–G (NLx–G) family, which incorporates two additional shape parameters to enhance the modeling flexibility of common baselines such as the exponential, Burr XII, Weibull, and Kumaraswamy distributions. Several key mathematical properties of the family were derived, and four important sub-models were highlighted. These sub-models are capable of generating a wide variety of density shapes–including symmetric, skewed, unimodal, bimodal, J-shaped, and reversed J-shaped forms–as well as diverse hazard rate structures, such as increasing, decreasing, bathtub, constant, upside-down bathtub, and more complex increasing–decreasing–increasing shapes.

For one of the most important sub-models, the NLx-exponential (NLxEx) distribution, parameter estimation was studied using a broad set of methods, including ML, LS, WLS, CVM, AD, and RTAD. A detailed convergence analysis confirmed that all estimators are consistent, with ML and RTAD providing the most reliable balance of efficiency and robustness across different sample sizes.

The practical utility of the proposed family was validated through the analysis of three real-world datasets from reliability and survival contexts. Across all cases, the NLxEx distribution provided the best overall fit relative to competing exponential-type models, as confirmed by both numerical goodness-of-fit criteria and graphical tools (fitted densities, empirical CDFs, and QQ plots). Overall, the results demonstrate that the NLx–G family offers a powerful and versatile modeling framework, capable of capturing complex data patterns and improving fit over existing exponential-type distributions. Future research could further extend this work by exploring Bayesian inference, regression structures, or multivariate generalizations within the NLx–G framework.