Introduction

Effective and economical assembly line design is essential for raising production and profitability in the manufacturing sector. An assembly line with proper design may minimise waste, cut down on downtime, and increase production speed while also lowering total operating expenses. The total cost of a product is significantly influenced by its assembly process, making the optimization of the assembly line a critical factor for cost reduction1. Task allocation, workstation arrangement, material flow dynamics, and the incorporation of automated systems like robots and machines are important factors to take into account when building an effective assembly line. To attain the best possible performance and cost effectiveness, each of these components needs to be carefully examined and coordinated. In order to overcome this difficulty, researchers and industry professionals have developed incredibly productive and economical assembly methods, like robotic assembly lines. With the industry shift from manual labour to automated systems, assembly lines incorporating robots are referred to as the robotic assembly line. Task allocation among robots in an assembly line is of crucial importance for creating a highly efficient and optimised production process. It plays a key role in reducing costs, maximising productivity, and ensuring the timely production of high-quality goods. The overall cost of an assembly line is a critical factor in determining its operational efficiency, profitability, and long-term sustainability. It encompasses multiple cost components such as robot cost, setup cost, maintenance and energy cost, and downtime cost. By minimising these costs, manufacturers can achieve cost-effective products and increase competitive advantage. Moreover, consumption is a critical consideration in the implementation of robotic systems.

Fysikopoulos et al.2 found that energy expenses comprise approximately 9–12% of the overall manufacturing cost in car production. A 20% reduction in energy consumption can lead to a 2–2.4% decrease in the final manufacturing cost. Lowering energy use not only helps maintain industrial competitiveness but also reduces environmental impact. Consequently, efforts to reduce energy consumption, improve production efficiency, and lower assembly line costs are highly important. Robotic assembly lines are complex systems where optimizing for a single objective, such as minimizing cycle time, often leads to inefficiencies in other areas, like cost. Traditional methods may not sufficiently address the need to balance multiple conflicting objectives simultaneously. This paper, therefore, concentrates on optimizing the assembly line by minimizing cycle time, energy consumption, and overall assembly costs.

Literature review

In 1991, Rubinovitz and Bukchin first introduced the robotic assembly line balancing (RALB) problem. With the main goal of reducing the overall number of workstations required, they concentrated on assigning the best robot to each workstation to complete the tasks. In recent years, robotic assembly line balancing has emerged as a complex and evolving area of research. Various approaches have been explored to address the challenges in this field, including traditional methods, mathematical models, genetic algorithms, heuristic techniques, multi-objective optimization, and machine learning3 To better accommodate the dynamic nature of robotic assembly lines and factors such as task variability and robot failures, further research is needed to develop more effective and efficient algorithms. These studies have investigated various methods and strategies to maximise work distribution and resource allocation for a well-balanced assembly line. Improving robotic assembly lines’ general productivity, efficiency, and cost-effectiveness is the main goal of these studies. The total cost approach is one strategy that has been developed to solve this problem. It takes into account the goal of reducing the overall number of robots utilised while distributing the same amount of work among all stations. This method reduces idle time at each station and guarantees that the assembly line runs successfully and efficiently4. Optimising the assignment of parts, assembly duties, and tools on a serial robotic assembly line was a challenge that5 took on. Their goal was to reduce the overall number of robot cells needed while still meeting a number of restrictions. In order to attain an ideal robot assignment to line stations and a balanced distribution of labour among those stations, Levitin et al.6 focused on the RALB problem.

Gao et al.7 investigated the type II robotic assembly line balancing problem, which involves assigning assembly tasks to workstations, where each workstation selects an available robot to perform the tasks, with the aim of reducing the cycle time. Additionally researching the type II robotic assembly line balance problem, Yoosefelahi et al.8 created an evolution strategies method for a multi-objective model. Nilakantan et al. (2014)9 introduced the Particle Swarm Optimisation (PSO) technique and a hybrid Cuckoo Search and Particle Swarm Optimisation (CS-PSO) to address a distinct type II robotic assembly line balancing problem (RALB-II). Their goal was to reduce the cycle time, and in comparison to other well-known metaheuristics, their suggested approach produced encouraging results10.

In 2016, Rabbani et al.11 investigated the use of multi-objective metaheuristics in the solution of a type II robotic mixed-model assembly line balance problem. Similarly, Li et al. (2018)12 investigated discrete cuckoo search algorithms for the two-sided robotic assembly line balance problem. They added neighbour operations to the original cuckoo search algorithm.

The total cost approach takes into account both the variable operational expenses related to each workstation and the annualized fixed costs for equipment, such as robots and workstations. Manufacturers can enhance the productivity and reduce costs on their assembly lines by adopting the Total cost approach. This method offers numerous advantages in the design and balancing of robotic assembly lines. First of all, it enables firms to take labour and equipment costs into account when making decisions. Second, it ensures the best possible use of resources by assisting in the achievement of a more evenly distributed workload among workstations. Finally, the Total Cost Approach gives producers a numerical assessment of the productivity and efficacy of their robotic assembly lines.

The advantages of incorporating various optimisation techniques with the total cost approach have been investigated by other researchers. In order to optimise the overall cost of robotic assembly lines, Guo et al. (2016)13 suggested a hybrid optimisation strategy that incorporated genetic algorithms and particle swarm optimisation. The benefits of using various optimisation techniques to improve the efficacy and affordability of assembly line designs were brought to light by their study.

Moreover, case studies have been carried out to assess the overall cost approach’s efficacy in practical situations. In a case study published in 2018, Liu et al.14 used the total cost approach to optimise a robotic assembly line for a car manufacturing. The outcomes indicated considerable cost savings and increased overall effectiveness, confirming the total cost approach’s practical usefulness. The Total Cost Approach works very well when the Non-Dominated Sorting Genetic Algorithm is used. The Pareto-optimal solutions for workload balancing in robotic assembly lines with several robot types are found using this technique.

Furthermore, manufacturers can optimise their robotic assembly line to achieve higher productivity, lower labour costs, and enhanced overall profitability by applying the Total Cost Approach and the Non-Dominated Sorting Genetic Algorithm. The relevant research that emphasise the value of the total cost approach and the application of non-dominated sorting genetic algorithms (NSGAs) in obtaining optimised assembly line designs are the main focus of this review of the literature. Regarding optimisation methods, NSGAs have drawn notice due to their superiority in producing Pareto solutions. NSGA was used by15 to optimise robotic assembly line designs while taking a number of factors into account, including cost, cycle time, and energy consumption. Their research showed that NSGA-based optimisation techniques can successfully resolve conflicts between goals and enhance assembly line efficiency.

Overall, the research points to the significance of designing and balancing robotic assembly lines using a total cost approach. Manufacturers can achieve cost-effective assembly lines by taking into account a variety of cost elements, including purchase, maintenance, and energy costs. The capacity to reconcile competing goals and produce ideal solutions is further improved by the application of NSGAs and other optimisation approaches. The suggested total cost method and the application of NSGAs in creating effective and well-balanced robotic assembly lines are fully supported by these investigations.

In robotic assembly lines, a robot is allocated to workstation, and each robot completes a sequence of assembly tasks to achieve a certain objective. Assigning the most appropriate robot to each station and achieving an effective balance on the assembly line for a number of assembly cells (stations) or at the required production rate are the two main goals of robotic assembly line balancing. Robot assignment and balancing quality have a direct impact on robotic assembly line performance16. The selection of an appropriate robot to carry out activities in a workstation is essential for an effective robotic assembly line. The current RALB approaches ignore the entire assembly cost in favour of analysing setup, robot, and energy costs independently.

In recent years, robotic assembly line balance has attracted a lot of attention as a complicated and developing field of study. To solve the difficulties in this subject, a variety of strategies have been investigated, including conventional methodologies, mathematical models, genetic algorithms, heuristic methods, multi-objective optimisation, and machine learning techniques. In order to address the dynamic nature of robotic assembly lines and take into account real-time aspects like task variations and robot failures, additional research is required to create more effective and efficient algorithms. Table 1 provides a summary of the literature on the Robotic Assembly Line Balancing (RALB) problem, categorized by the specific objectives addressed and the solution methodologies employed. The analysis reveals that no existing study simultaneously considers the optimization of costs, cycle time, and workstation minimization. This gap in the literature underscores the necessity of our research, which aims to integrate these objectives into a unified framework for robot allocation.

Table 1 Summary of objectives considered in the literature for RALBP.
Full size table

This paper examines how tasks are assigned to robots in robotic assembly line balancing, taking total cost into account. Energy, setup, and robot costs are all included in the overall cost of assembly. It is not always the case that cutting individual expenses will result in a lower overall cost of assembly. Although it’s not always the case, time-based allocation frequently helps to minimise assembly cost. The entire cost-based robot allocation method, which concurrently optimises cycle time and cost, leads to cost-effective RALB. Complex algorithms and programming are needed to optimise robotic assembly line balancing.

In light of recent developments in industrial robotics, we study robotic assembly line balance issues, which have a big influence on the dependability and productivity of production systems. A precedent map27 summarises earlier studies in the RALB literature. Over time, the subject has expanded, with survey papers25,28,20,21,31 addressing a range of aims. Yılmaz32 introduced an ε-constrained approach to address the integrated scheduling problem, focusing on minimising total operation costs and achieving workload balance in a U-shaped assembly line. Yilmaz and Durmusoglu26 investigated the scheduling of a manufacturing system that combined cell and functional areas and included walking workers. Ö. F. Yılmaz33 developed a mathematical model for a U-shaped assembly line balancing problem, considering worker heterogeneity. They applied axiomatic design to maximize output and minimize waste. Lean manufacturing principles were applied, resulting in a 23% increase in production volume. The study also showed a 12% reduction in idle time, 38% decrease in workload imbalance, and a 23% increase in production volume. Recently, the authors of Ref.34 based on the problem specifications and constraints, a novel generic multi-objective optimization model with objectives including the makespan, the average flow time, and the total workload imbalance is formulated. Use non-dominated sorting genetic algorithm-II (NSGA-II) to solve this problem.

However, there hasn’t been much research done on line balancing issues with costs and variable processing times in the literature [see Ref.1, for a recent work on this topic]. Given that RALB is known to be an NP-hard issue and that heuristic techniques are computationally efficient; they are being used extensively. Our study differs from previous research in two respects: first, it considers all costs as the overall cost of robotic assembly lines; second, it uses Pareto front and non-dominated sorting to give trade-off solutions between cycle time and total cost, as both goals are incompatible. It is crucial to take the big picture into account in order to create an assembly process that is cost-effective, as opposed to concentrating only on cutting cycle times or individual prices. The entire cost-based robot allocation approach makes sure that all pertinent variables are taken into account, which results in an assembly process that is more productive and economical.

This research study differs from existing literature in mainly two ways. Firstly, the RALB problem addressed in this paper considers the comprehensive total cost of robotic assembly lines, integrating robot cost, set up cost, and energy cost into a balanced optimisation framework for the assignment of tasks processed by robots. Secondly, the conflicting nature of two objectives, cycle time and total cost, where improvement in one typically results in deterioration of the other. To address this, non-dominated sorting and Pareto front analysis are employed to provide trade-off solutions, enabling decision makers to balance these competing objectives effectively.

Allocating the proper robot to the proper work station and assigning the suitable task to the suitable station in order to decrease the cycle time, increase the line efficiency, and reduce the total cost make the problem more complex.

The main contributions of the study are summarized as follows:

  • The study presents a novel approach to robotic assembly line balancing that simultaneously optimize cycle time and overall costs of the assembly.

  • A mathematical model is developed that integrates initial, setup, maintenance and energy cost factors into the optimization process, providing a more holistic view of assembly line efficiency.

  • The effectiveness of the proposed approach is validated with three case study problems using the non-dominated sorting genetic algorithm (NSGA-II), with results compared to traditional methods to demonstrate its efficacy.

The remainder of the paper is organised as follows: Section "Mathematical model formulation" provides the problem description and the mathematical formulation of the Robotic Assembly Line Balancing Problem (RALBP). Section "Computational experiments and numerical insights" outlines the details of the case study problem. The procedural steps and implementation of the non-dominated sorting genetic algorithm (NSGA) for solving the RALBP is given in Section "Non-dominated Sorting Genetic Algorithm". Section "Results and discussion" presents the results and discussion. Finally, Section "Concluding remarks" offers the concluding remarks.

Mathematical model formulation

This section first describes the problem descriptions and assumptions before presenting a mathematical model of the problem.

Problem description

The Robotic Assembly Line Balancing Problem (RALBP) is a combinatorial optimization problem that involves assigning a set of tasks to a set of workstations and assigning to each workstation while also assigning a suitable robot to make a final product. A set of Ni tasks, I = {1,2, …, i, …, Ni}, needs to be completed in a set of Nj workstations, J = {1,2, …, j, …, Nj} to select one of the sets of Nr robots, {1, 2…r, …, Nr} to process the assigned tasks without violating the precedence relationship. Each robot r has different capabilities such as task time or cost to perform assembly tasks. The processing time of task i depends on the type of robot r used and is denoted as tir. The robot setup cost to perform task i is SCir. The total cost of assembly includes setup cost, robot cost and energy cost. The main objective here is to assign tasks with precedence requirements to an ordered sequence to the robotic workstations in a multi- objective manner (i.e.) minimize cycle time and total cost simultaneously. The objectives considered in this paper are:

  • Minimize the cycle time for a specified number of workstations (f1)

  • Minimize total cost which includes setup cost, robot cost and energy cost (f2)

Mathematical model

The notations used in the mathematical model are given below.

Sets

 I The set of tasks = {1,2, …, i, …, Ni}

 J The set of workstations = {1,2, …, j, …, Nj}

 R The set of robots = {1, 2…r, …, Nr}

Indices:

 i, h

assembly task; i = 1, 2, …, Ni; i is predecessor task of h

 r

robot; r = 1, 2, …, Nr

 j

workstation; j = 1, 2, …, Nj

Parameters:

 C

Cycle time

 Nj

Number of workstations

 Ni

Number of tasks

 Nr

Number of robots

 Di

Set of immediate predecessors of task i in the precedence network

 tir

Processing time of task i by robot r

 ts

Station time

 γr

robot (r)’s discount rate, 0 ≤ γr < 1

 Cr

Procurement cost of robot of type r

 Ct

Total cost

 SCri

robot (r)’s setup cost for performing task i

 Ψ

a huge positive number

 Np

Number of populations

 Ng

Number of generations

 CEC

Cost per unit energy consumption

 Opct

Operational power consumption per unit time

 Spct

Standby power consumption per unit time

Decision variables:

\({X}_{ijr}\)

\(\left\{\begin{array}{l}1, if\, task\, i \,is \,assigned \,to \,workstation\, j\, and \,robot \,r\, is \,assigned \,to\, wokstaion\, j\\ 0, otherwise\end{array}\right.\)

\({Y}_{jr}\)

\(\left\{\begin{array}{l}1, if \,robot \,r \,is \,assigned \,to \,workstation\, j \\ 0, otherwise\end{array}\right.\)

Assumptions

The basic assumptions in this study are given as follows:

  • There are r types of robots available, and there is no limit on the quantity of robots for each type.

  • The task processing time is dependent on the type of robot assigned to it.

  • A task can only be assigned to one station and one robot.

  • Robot setup times are considered due to the time-consuming nature of setup processes.

  • Buying multiple robots of the same kind comes with a discount and has a set price for each type of robot

  • Cost per unit energy consumption is assumed to be Indian Rupees (INR) 40.

  • Operational power consumption per unit of time is assumed to be 0.3.

  • Standby power consumption per unit of time is assumed to be 0.03.

Objective functions

$${Minimize, f}_{1}=C$$
(1)
$$\begin{aligned} Minimize,f_{2} & = \left( {\sum\limits_{{r = 1}}^{{N_{r} }} {\sum\limits_{{j = 1}}^{{N_{j} }} {\sum\limits_{{i = 1}}^{{N_{i} }} S } } C_{{ri}} .X_{{ijr}} } \right) + \left( {\sum\limits_{{r = 1}}^{{N_{r} }} {C_{r} } \left( {1 + \gamma _{r} \left( {\sum\limits_{{j = 1}}^{{N_{j} }} {Y_{{jr}} } - 1} \right)} \right)} \right) \\ & + \left( {C_{{EC}} \sum\limits_{{j = 1}}^{{N_{j} }} {\sum\limits_{{r = 1}}^{{N_{r} }} {\sum\limits_{{i = 1}}^{{N_{i} }} {\left( {O_{{pct}} .d_{{B_{{ir}} }} .Y_{{ijr}} } \right)} } } + S_{{pct}} (C - (d_{{B_{{ir}} }} .Y_{{ijr}} )} \right) \\ \end{aligned}$$
(2)

Subject to:

$$\sum_{i:{B}_{i}\in S({A}_{k})}{Z}_{i}=1;\forall k=0$$
(3)
$$\sum_{i:{B}_{i}\in S({A}_{k})}{Z}_{i}=\sum_{i:{B}_{i}\in P({A}_{k})}{Z}_{i}$$
(4)
$$\sum_{j=1}^{{N}_{j}}\sum_{i=1}^{{N}_{i}}{X}_{ij}=\sum_{i=1}^{{N}_{i}}{Z}_{i}$$
(5)
$$\sum_{r=1}^{{N}_{r}}\sum_{j=1}^{{N}_{j}}\sum_{i=1}^{{N}_{i}}{Y}_{ijr}=\sum_{j=1}^{{N}_{j}}\sum_{i=1}^{{N}_{i}}{X}_{ij}$$
(6)
$$\sum_{i:{B}_{i}\in P({A}_{k})}\sum_{j=1}^{v}{Y}_{vjr}\le \sum_{i:{B}_{i}\in S({A}_{k})}{Y}_{ijr};j=\text{1,2},\dots ,{N}_{j};r=\text{1,2},\dots ,{N}_{r}; \forall v\in prc(i)$$
(7)
$$\sum_{r=1}^{{N}_{r}}\sum_{j=1}^{{N}_{j}}\sum_{i=1}^{{N}_{i}}{Y}_{ijr}{d}_{Bir}\le C$$
(8)

Decision variables

$${X}_{ijr}=\left\{\begin{array}{l}1, \,if\, task\, i\, is\, assigned \,to\, workstation\, j\, and\, robot\, r\, is \,assigned\, to\, wokstaion\, j\\ 0, otherwise\end{array}\right.$$
$${Y}_{jr}=\left\{\begin{array}{l}1, if \,robot\, r\, is\, assigned\, to\, workstation\, j \\ 0, otherwise\end{array}\right.$$

The first objective (f1) in Eq. (1) is to minimize cycle time for the stated number of workstations, and the second objective (f2) in Eq. (2) is to minimize the overall assembly cost. In Eq. (2), the first term represents the robot setup cost, the second term represents the robot cost after the discount price, and the third term represents the energy cost to accomplish jobs. Constraint (3) computes workstation time, ensuring it does not exceed calculated cycle time, and constraint (4) determine task priority connections, possibly specifying the order in which tasks are executed. Constraint (5) ensure that each job is assigned to a single workstation. Constraint (6) specifies the type of robot to be assigned to a particular workstation. Constraint (7) confirm that only one robot can be assigned to each workstation. Constraint (8) limits the total number of robots used, regardless of their types, does not exceed the number of workstations.

Computational experiments and numerical insights

This section evaluates the effectiveness of the proposed total cost approach for the robotic assembly line balancing problem by applying it to two case studies: one based on the work of Yoosefelahi et al.8 and the other derived from Case Study Problem 3 presented in Ref.35.

Case study problem-1

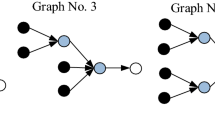
Figure 1 presents the precedence graph for case study problem 1, which includes a total of 10 tasks. Table 2 displays the task time and setup cost required for each robot to complete every task.

Fig. 1
figure 1

Precedence graph for case study problem-1.

Full size image
Table 2 The data for the case study Problem-1.
Full size table

Case study problem-2

The precedence graph for case study problem 2 is shown in Fig. 2 and it has a totally of thirty-five tasks.. Table 3 displays the task time and setup cost values of each robot to perform every task. The purchase cost of each robot with discount cost is given in Table 4.

Fig. 2
figure 2

Precedence graph for case study Problem-2.

Full size image
Table 3 The data for the Case study Problem-2.
Full size table
Table 4 Robot cost and discount cost for each robot.
Full size table

Case study problem-3

The precedence graph for case study problem-3 is given in Fig. 3 and it has a totally of twenty-five tasks[]. Table 5 display the time and setup cost required for completing every task by each robot. The purchase cost of each robot with discount cost is given in Table 4.

Fig. 3
figure 3

Precedence graph for case study problem-3.

Full size image
Table 5 The data for the Case study Problem-3.
Full size table

Non-dominated sorting genetic algorithm

This study chose the Non-Dominated Sorting Genetic Algorithm (NSGA-II) due to its effectiveness in handling multi-objective optimization problems with complex objectives. It efficiently explores large solution spaces, maintains a diverse set of non-dominated solutions, and balances trade-offs between multiple objectives, ensuring a well-distributed Pareto front. Recently, Yilmaz et al. (2024) utilized it to solve similar kind of problems, such as flow shop scheduling, aiming to minimize makespan, average flow time, and overall workload imbalance. The following is a step-by-step implementation of NSGA-II to generate the Pareto front of optimal solutions for robotic assembly line balancing.

Solution representation and Initial population generation

The task assignment and robot allocation vectors are used for encoding and decoding. The task assignment vector is a 1 × Ni vector, where each element represents a workstation. If the i-th element is s, it indicates that task i is assigned to workstation s. Similarly, the robot allocation vector is a 1 × Nr vector, with each element representing a robot. If the s-th element is r, it signifies that robot r is assigned to workstation s. An example of solution representation is depicted in Fig. 4. Tasks 1, 3, and 5 are assigned to workstation 1 and handled by robot 3. Tasks 4, 6, 8, and 2 are allocated to workstation 2, where they are processed by robot 1. Tasks 7, 9, and 10 are assigned to workstation 3 and processed by robot 2.

Fig. 4
figure 4

Illustration of solution representation.

Full size image

A chromosome represents a sequence of genes (tasks), which is randomly generated. To determine the feasibility of each chromosome, an algorithm based on the precedence matrix is employed. This matrix is derived from the precedence network diagram, where each row and column correspond to specific tasks. For instance, if tasks 1, 2, and 3 have no predecessors, their respective columns in the precedence matrix would consist of all zeros. On the other hand, if task 4 is preceded by tasks 1 and 2, its row in the matrix would have ones in the positions corresponding to tasks 1 and 2.

The feasibility of a chromosome is checked as follows: Given an example chromosome (Fig. 4), the algorithm examines each position and its associated task. If a task has a predecessor according to the precedence matrix, it is not suitable for that position. In such cases, the algorithm swaps the task with its predecessor until a feasible solution is obtained.

A precedence matrix is constructed using a precedence network diagram to generate feasible solutions. For example, tasks 1, 2, and 3 have no prior tasks, so the first, second, and third columns of the matrix contain zeros. Task 4, which follows tasks 1 and 2, is represented by ones in the rows corresponding to tasks 1 and 2 in the fourth column, while all other entries in that column are zeros. This method is applied for each task, with ones indicating a precedence relationship and zeros for no dependency. The resulting precedence matrix is shown in Table 6.

Table 6 Precedence matrix.
Full size table
Algorithm 1
figure a

Feasible chromosome generation algorithm.

Full size image

Feasible chromosomes are generated as shown in Fig. 5. In the example chromosome, task 2 is placed in the first position. Referring to the precedence matrix, it is verified that task 2 has no predecessors, making it suitable for this position. Task 8 is placed in the second position, but it has tasks 6 and 7 as predecessors. Since task 7 appears earlier, tasks 8 and 6 are swapped, moving task 6 to the second position. The current position becomes 2, and the chosen position is 7. As the termination condition (where the chosen position is less than or equal to the current position) is not yet met, the process continues. Task 6 is now in position 2, with task 4 as its predecessor. Another swap occurs, moving task 4 to position 2 and task 6 to position 4. The chosen position is 4, but the termination condition is still not fulfilled. The process continues with task 4, which has tasks 1 and 2 as predecessors. In the chromosome, tasks 1 and 2 are positioned at 10 and 1, respectively. Since task 1 is in the later position, tasks 4 and 1 are swapped, placing task 1 in the second position. Now that task 1 is in position 2 and has no predecessors, the termination condition is satisfied.This procedure is repeated for each position in the chromosome to ensure that a feasible solution is generated.

Fig. 5
figure 5

Feasible chromosome generation.

Full size image

Order crossover

Order crossover is a method employed to generate offspring for the next generations in an optimization process. It randomly selects two chromosomes from the population, and the process is illustrated in Fig. 6. Two crossover points, denoted as crossover point 1 and crossover point 2, are randomly selected within the range of tasks. It is ensured that crossover point 2 is greater than crossover point 1. The tasks located between crossover point 1 and crossover point 2 in parent 1 are swapped with the corresponding tasks in parent 2 to create new offspring. As shown in Fig. 6, if crossover point 1 is at position 3 and crossover point 2 is at position 6, tasks 2, 9, 5, and 1 are swapped between the parents to produce child 1, while tasks 1, 4, 9, and 6 remain unchanged to form child 2.

Fig. 6
figure 6

Order crossover.

Full size image

After the swapping, the order crossover continues by searching and assigning tasks in a circular manner. The search starts next to crossover point 2 in the parent and child, respectively. For instance, if the search begins at position 7 in parent 1, which contains task 8, the algorithm checks if task 8 already occupies a position in child 1. Since it does not, task 8 remains in its position in child 1. The algorithm then moves to the next task (i.e., task 3) for the eighth position in child 1, as it is not present there. The search continues, ensuring each task is uniquely assigned to the offspring. The new children generated by order crossover are shown in Fig. 6. However, it is important to note that these children may not be feasible solutions as per the problem constraints. Therefore, a repair algorithm is applied to make the children feasible.

Swap mutation

The swap mutation method is depicted in Fig. 7. After the crossover process, a chromosome is randomly chosen from the population. Two mutation points, let’s say 3 and 7, are then randomly selected within the range of tasks. The tasks at these two points are swapped, effectively exchanging their positions in the chromosome. This swapping creates a new chromosome, which replaces its parent in the population. Once the new population is formed through crossover and mutation, it undergoes a feasibility check using a feasible chromosome generation procedure. This step ensures that the resulting population contains valid solutions that adhere to the problem’s constraints.

Fig. 7
figure 7

Swap mutation.

Full size image

Modified consecutive assignment procedure (mCAP)

In this paper a new assignment method called “mCAP” (modified consecutive assignment procedure), which is derived from the “Consecutive Assignment Procedure” (CAP) originally proposed by Levitin et al. in 2006. Table 7 explains about the allocation of tasks through mCAP for RALB.

Table 7 Total cost estimation.
Full size table
Algorithm 2
figure b

Modified Consecutive assignment algorithm.

Full size image

The Modified Consecutive Assignment Procedure aims to select cumulative tasks randomly while ensuring the cycle time is not violated. It allows any number of tasks to be allocated to each robot. This assignment cycle continues until all tasks are sequentially assigned to workstations. The number of cycles performed equals the number of workstations in the system.

Selection procedure

The selection procedure employed in this study is the Dominant-based selection method. The NSGA is used to identify Pareto fronts from both the parent and offspring chromosomes until the desired number of individuals, matching the population size, is selected. Selection is based on the fitness value’s Pareto front, and the ranking is determined by assessing the domination of one chromosome over others. With a population size of 10, comprising 10 parent chromosomes and their corresponding 10 offspring, the selection process evaluates a total of 20 feasible sequences based on cycle time and total cost. The chromosomes are assigned ranks according to the domination rule. In the first Pareto front, chromosomes 3, 6, and 20 are present, and they dominate other chromosomes in specific aspects. However, none of these chromosomes completely dominate each other, as they may excel in cycle time but not in total cost, or vice versa. This phenomenon persists in subsequent Pareto fronts until a final set of ten chromosomes is ultimately selected for the next generation.

Algorithm 3
figure c

Pseudocode for NSGA.

Full size image

The pseudo code for NSGA (Non-dominated Sorting Genetic Algorithm) used in the multi-objective Robotic Assembly Line Balancing (RALB) is provided in Algorithm 3. The user inputs include the number of populations (Np = 30), the number of workstations (Nj = 5), the number of iterations (Ng = 50), the crossover rate (Crossover rate = 6.67% or 2 chromosomes), and the mutation rate (Mutation rate = 0.67% or 2, 5, 7 genes for case study problems 1, 2, 3, respectively). The iteration process in the algorithm involves incrementing the minimized cycle time to search for further minimization of the total cost, considering the multi-objective nature of the problem. For case study problem 1, the cycle time is incremented by 1 for 50 iterations, starting from the minimum cycle time and increasing until it reaches the minimum cycle time + 50. Similarly, for case study problems 2 and 3, the cycle time is incremented by 500 times. The output of the algorithm includes the minimized cycle time, corresponding total cost, and the task and robot assignments to workstations.

Results and discussion

The task allocations for Case Study Problems 1 and 2 were determined using a total cost-based approach implemented through the Non-dominated Sorting Genetic Algorithm (NSGA). By leveraging NSGA’s multi-objective optimization capabilities, the algorithm effectively explores and identifies task allocation strategies that minimize the overall assembly costs while maintaining production efficiency. Tables 8 and 9 showcase the Pareto front solutions for case studies 1 and 2, respectively, while Figs. 8 and 9 illustrate the Pareto-optimal solutions for minimizing cycle time and total cost for case studies 1 and 2.Yoosefelahi et al.8 examined case studies 1 and 2, focusing on minimizing cycle time, robot setup costs, and robot costs. They employed three variations of multi-objective evolutionary methods to identify Pareto-optimal solutions for various cycle times. Notably, their approach did not account for energy costs (Fig. 10, Table 10).

Table 8 Pareto front solutions for case study problem-1.
Full size table
Table 9 Pareto front solutions for case study problem-2.
Full size table
Fig. 8
figure 8

Pareto front of NSGA-mCAP case study problem-1.

Full size image
Fig. 9
figure 9

Pareto front of NSGA-mCAP case study problem- 2.

Full size image
Fig. 10
figure 10

Pareto front of NSGA-mCAP case study problem-3.

Full size image
Table 10 Pareto front solutions for case study problem-3.
Full size table

Table 11 compares the Pareto solutions for Case Study Problem 1, showing the job assignments to workstations and robots across different cycle times. The results indicate that the allocation based on total cost technique consistently outperforms other methods. Specifically, for the same cycle time values, this technique results in lower overall costs and fewer workstations. Figure 11 illustrates a comparison of these Pareto solutions with the benchmark Pareto solutions for Case Study Problem 1.

Table 11 Comparison of Pareto front solutions based on total cost for case study-1.
Full size table
Fig. 11
figure 11

Comparison of Pareto with benchmark Pareto for the case study problem-1.

Full size image

Table 12 compares the Pareto solutions for Case Study Problem 2, presenting the task assignments to workstations and robots across various cycle times. The findings show that the allocation based on the proposed total cost technique consistently outperforms other methods. Notably, this technique achieves lower overall costs and requires fewer workstations for the same cycle time values. Figure 12 depicts a comparison of Pareto solutions with the benchmark Pareto solutions for Case Study Problem 2.

Table 12 Comparison of Pareto front solutions based on total cost for case study-2.
Full size table
Fig. 12
figure 12

Comparison of Pareto with benchmark Pareto for the case study problem-2.

Full size image

For both case study presented in the research article, it is clear that the allocation based on the proposed total cost approach is indeed superior to other methods in terms of total cost and workstation utilization. One of the strengths of this study is its comprehensive analysis of various allocation techniques and their impact on cost and efficiency. By comparing different methods side by side, the researchers were able to clearly demonstrate the advantages of using the proposed total cost technique. This approach adds credibility to their findings and strengthens their argument for its superiority. Furthermore, the research methodology employed in this study appears to be sound and well-executed. The researchers utilized a combination of theoretical models and simulation techniques to test their hypotheses, providing a robust framework for their analysis. The implementation of total cost based task allocation effectively enhances assembly line productivity. This effect is more apparent with fewer stations, implying the potential gains from station consolidation based on actual scenarios.

Concluding remarks

In this study, a new approach to the robotic assembly line balancing problem is presented. The approach focuses on minimizing both the assembly time and overall cost of the assembly line. The mathematical model considers various costs, including purchase costs, setup costs, maintenance costs, and energy costs. To validate the proposed approach, three case study problems were solved using the Non-dominated Sorting Genetic Algorithm (NSGA), and the results were compared with traditional assembly methods. The findings revealed that minimizing the cycle time also reduces the total assembly cost, highlighting the importance of optimizing both time and cost. Additionally, it was discovered that achieving the minimum cycle time does not always result in the lowest total assembly costs. This insight emphasizes the need to consider both aspects when designing optimal assembly line configurations. The proposed allocation method has significant managerial implications for real-life robotic assembly line systems and can contribute to the development of cost-efficient assembly line designs in the robotic assembly industry to optimize resource allocation strategies and improve operational performance. It is evident that the allocation based on the proposed total cost technique offers significant advantages over other methods in terms of cost efficiency and workstation utilization. Further research in this area could help to refine and expand upon these promising results and explore the application to other types of robotic assembly lines, such as two-sided assembly lines and U-shaped assembly lines.