An integrative TLBO-driven hybrid grey wolf optimizer for the efficient resolution of multi-dimensional, nonlinear engineering problems

Abstract

This research article introduces a hybrid optimization algorithm, referred to as Grey Wolf Optimizer-Teaching Learning Based Optimization (GWO-TLBO), which extends the Grey Wolf Optimizer (GWO) by integrating it with Teaching-Learning-Based Optimization (TLBO). The benefit of GWO is that it explores potential solutions in a way similar to how grey wolves hunt, but the challenge with this approach comes during fine-tuning, where the algorithm settles too early on suboptimal results. This weakness can be compensated by integrating TLBO method into the algorithm to improve its search power of solutions as in teaches students how to learn and teachers are knowledge felicitator. GWO-TLBO algorithm was applied for several benchmark optimization problems to evaluate its effectiveness in simple to complex scenarios. It is also faster, more accurate and reliable when compare to other existing optimization algorithms. This novel approach achieves a balance between exploration and exploitation, demonstrating adaptability in identifying new solutions but also quickly zoom in on (near) global optima: this renders it a reliable choice for challenging optimization problems according to the analysis and results.

Introduction

Optimization is a prevalent mathematical challenge across numerous real-world domains ranging from economics¹, manufacturing process², carriage³, engineering design⁴, systems⁵, machine learning⁶ to resource management. Several metaheuristic algorithms⁶ have been discovered, in recent years, as efficient solvers for such challenging optimization problems with a parameter space characterized by significant non-linearity, multidimensionality and non-differentiability. Although the performance of traditional deterministic techniques performances very well for continuous and differentiable optimization problems, this same method has some intrinsic limitations: On one hand owing to getting stuck in smaller optimum solutions (at local optima) and in contrast with when performing global searches in extremely high dimensional spaces. Consequently, stochastic^7,8,9 and population-based metaheuristic algorithms possess reasonable the equilibrium between exploration (wide-ranging global search) and exploitation (targeted local search) to deliver feasible solutions within acceptable computation time¹⁰.

Recently, several populations based metaheuristic algorithms have been created and the hybrid Grey Wolf algorithm and Teaching-Learning Optimization method are among best of them because of its simplicity, robustness, flexibility. GWO is an algorithm which is constructed upon the behaviour of grey wolves especially for social hunting strategy of the said wolves, which being a good exploration has ability to guide search agents toward very favorable domain of the solution space. In contrast, GWO suffers from ‘premature convergence’ in terms of exploration when solving complex and high-dimensional problems. TLBO, inspired by the pedagogical principle of a master-teacher and apprentice-class learning strategy, utilizes exploitation to improve candidate solutions iteratively on the counterparts. While TLBO is good on local search, it may not work well when it comes to global search process of vast multimodal landscapes.

To combat these issues, a hybrid optimization algorithm which efficiently utilizes the exploration features capability of GWO¹¹ and exploitation competences of TLBO which has been introduced in this research. The proposed hybrid GWO-TLBO algorithm uses an active, social behaviour of grey wolves to navigate the parameter space in conjugation with the learning and teaching phases of TLBO that facilitate in refining solutions for escaping from local optima. This combination of methods is hoped to result a well-balanced optimization process capable of more effectively solve complex, multimodal and high dimensional problems than each algorithm separately.

Advantages of Hybrid Algorithms:

• a. By combining strengths, these algorithms often deliver faster, more accurate, and reliable outcomes than single methods.

• b. They work well for all kinds of problems, from everyday tasks to highly complex challenges in areas like AI and machine learning.

• c. Hybrid algorithms can dig deeper to find better answers, sometimes getting close to the perfect solution.

• d. They adapt better to unexpected changes or noisy data, making them dependable in unpredictable situations.

• e. You can tweak them to fit specific needs, making them a perfect match for unique problems.

• f. They scale up well for tackling massive datasets or problems with many variables.

• g. These algorithms can explore new ideas while still focusing on refining good solutions, avoiding the trap of getting stuck in one spot.

Disadvantages of Hybrid Algorithms:

• a. Mixing different methods isn’t easy—it requires time, expertise, and careful planning.

• b. They often need more computing power and time to run, which might not be practical for all scenarios.

• c. Getting all the settings right for each part of the hybrid algorithm can be tricky and take a lot of trial and error.

• d. It can be hard to figure out how all the pieces interact, making these algorithms harder to understand or explain.

• e. They shine in certain situations but might not work as well for more general or straightforward tasks.

• f. Bringing together different techniques can lead to technical hiccups or inefficiencies during development.

• g. Sometimes, combining too many methods can make the algorithm bloated, with parts that don’t add much value.

• h. Hybrid algorithms can sometimes become too tailored to a specific problem, making them less effective for other situations.

Literature review

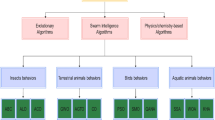
Research in optimization methods has been advancing at an impressive pace, evolving from stochastic and heuristic techniques to more sophisticated metaheuristic¹² and hybrid tactics. These methods aim to discover the greatest optimal solutions by integrating various advantageous features of optimization. This paper reviews the latest studies, focusing on different types of metaheuristic approaches¹³. Generally, populations-based metaheuristics can be categorized as either population-based or single-solution categories, with population-oriented further classified into four groups based upon their inspiration sources which is presented in the following Fig. 1.

Fig. 1

Classification of population-based meta heuristics (PMH) optimization techniques.

• 1. Swarm-based population-based metaheuristics (PMH): PMH mimic such collective behaviour in nature as that of swarms^14,15,16,17 flocks and herds^18,19. Particle Swarm Optimization (PSO)^20,21,22 is a well-known method inspired upon the coordinated movement²³ of birds or fishes in school. Similarly, there are many swarm intelligence techniques²⁴ including DGCO²⁵, LFD²⁶, LCBO²⁷, HHO^{28,29,30,31,32,33,34,35,36,37,38,39}, GWO^11,40,41,42, MFO algorithm^43,44, CS⁴⁵, ALO⁴⁶ and ABC^47,48 etc.⁴⁹.

• 2. Physics-based population-based metaheuristics (PMH): These methods draw on physical laws^50,51,52 and phenomena^{53,54,55,56,57} to guide the interactions of search agents. Simulated Annealing^58,59, for example, leverages thermodynamic principles to simulate the process of heating and cooling materials. Additional examples include Electromagnetic Field Optimization (EFO)³⁶, Multi-Verse Optimization (MVO)⁶⁰, the Gravitational Search Algorithm (GSA)^61,62, Sine–Cosine Algorithm^63,64,65,66, Charged System Search⁶⁷, Photon Search Algorithm⁶⁸, Harmony Search^69,70, Billiards Inspired Optimization (BOA)⁷¹, Henry Gas Solubility Optimization (HGSO)⁷², Central Force Optimization (CFO)⁷³, Transient Search Optimization (TSO)⁷⁴, and Electro Search Optimizer (ESO)⁷⁵.

• 3. Evolution-based population-based metaheuristics (PMH): These methods borrow their behaviour from nature^{7,76,77,78,79,80,81,82,83,84,85,86,87}, and in particular they engage the process of biological evolution^88,89 to change a set of possible solutions (populations) and come up with a best result^90,91,92. GA (Genetic Algorithms)⁹³ are the most popular one, with this we will mix some kind of crossover to create off-springs, and mutation to make more space for optimal solutions^94,95. Meaning, there are also some diverse evolutionary algorithms such as Particle Swarm Optimization (PSO), Genetic Programming^96,97, Ant Colony Optimization (ACO)⁹⁸, Evolutionary Programming (EP)⁹⁹, Dung Beetle Optimizer¹⁰⁰, Biogeography-Based Optimization (BBO)¹⁰¹, Differential Evolution (DE)¹⁰², and Evolutionary Strategy (ES)^103,104.

• 4. Human-based population-based metaheuristics (PMH): These algorithms are developed based on human behaviour and learning processes. Some popular ones include, Teaching Learning Based Optimization (TLBO)^105,106, Human Evolutionary Algorithm (HEA), Group Search Optimizer (GSO)¹⁰⁷, Cultural Algorithm (CA), Human memory optimization¹⁰⁸ and Tabu Search (TS)^109,110

Hybrid approaches^111,112,113 where combining two or more algorithms^{113,114,115,116} results in enhancing performance and free from local optima, are also taking increasingly his place. Recently Proposed Hybrid Methods: Differences between Nonlinear or Linear Hybrid Optimization Techniques^117,118 and Some Recent Work Follows¹¹⁹. The most recent hybrid methods¹²⁰ include the following; Polished Selfish Herd Optimizer (RSHO)¹²¹, Simplified Salp Swarm Algorithm (SSSA)^122,123, Enhanced GWO¹²⁴, Self-Adapted Differential ABC (SADABC)^125,126, Hybrid Crossover Orienter PSO and GWO (HCPSOGWO)¹²⁷, Multi-objective Heat Transfer Search Algorithm (MHTSA)¹²⁸, Multi-Strategy Enhanced SCA (MSESCA)¹²⁹ Historical, Ant Colony Optimization based on Equilibrium, Dynamic Hunting Leadership Algorithm¹³⁰, Cat Swarm Optimization with Dynamic Pinhole Imaging and Golden Sine Algorithm¹³¹, artificial electric field employing cuckoo search algorithm¹³² with refraction learning¹³³, MSAO¹³⁴, Improved Gorilla Troops Optimizer¹³⁵ and IHAOAVOA^136,137. Table 1 summarizes the literature review of the similar recent algorithms and optimizers.

Table 1 Motivation and/or brief analysis of recent population-based metaheuristics.

Mathematical modeling of proposed algorithm

Grey wolf optimizer (GWO)

The Grey Wolf Optimizer (GWO) is an innovative optimization algorithm inspired by the social structure and hunting techniques of grey wolves in the wild. By emulating how these animals organize themselves into hierarchies and collaborate during hunts, GWO effectively navigates complex optimization landscapes. This document presents a comprehensive overview of the GWO algorithm, detailing its fundamental principles and mechanisms. The mathematical equations and formulas that underpin this optimization method is explored, illustrating how they contribute to its ability to find optimal solutions across various problem domains. Through this in-depth examination, a deeper understanding of GWO’s functionality and its applications in addressing real-world optimization challenges is gained.

Pack structure

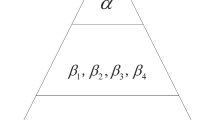
In the GWO algorithm¹¹, the pack structure of the wolves (as shown in Fig. 2) is modeled by categorizing the best solutions as:

• i. Alpha (α): Represents the optimal solution and guides the pack.

• ii. Beta (β): Offers the alternate-best solution.

• iii. Delta (δ): Contributes the tertiary-best solution.

• iv. Omega (ω): Encompasses all other remaining solutions.

Fig. 2

Social hierarchy in grey wolves.

The wolves exhibit a dynamic positional adjustment in response to the directives of the alpha, beta, and delta wolves, while the omega wolves dutifully follow their lead. This intricate interplay among the ranks exemplifies the nuanced leadership dynamics that characterize the social structure of a wolf pack.

Encircling the prey

In the predatory tactics employed by grey wolves, they engage in a coordinated maneuver to encircle their prey during the hunting phase as illustrates in Fig. 3. This intricate behavior can be articulated mathematically as follows:

$$\overrightarrow{D}= \left|\overrightarrow{C}\cdot {\overrightarrow{X}}_{p\left(t\right)}- \overrightarrow{X}\left(t\right)\right|$$

$$\overrightarrow{X}\left(t+1\right)= {\overrightarrow{X}}_{p\left(t\right)}- \overrightarrow{A}\cdot \overrightarrow{D}$$

where X⃗_p(t) denotes the location of the prey, which is synonymous with the optimal best solution, X⃗(t) signifies the position of the grey wolf and A⃗ and C⃗ are defined as the coefficient vectors that play a crucial role in the optimization process.

Fig. 3

Hunting strategy of grey wolves to hunt the prey (2D and 3D view).

The evaluation of the vector coefficients is conducted as follows:

$$\overrightarrow{A}= 2 \cdot \overrightarrow{a}\cdot {\overrightarrow{r}}^{1}- \overrightarrow{a}$$

$$\overrightarrow{C}= 2 \cdot {\overrightarrow{r}}^{2}$$

where a⃗ over the iterations decreases on or after 2 to 0 linearly and r₁, r₂ are the vectors randomized in the range of zero to one.

Hunting (Optimization)

The wolves navigate towards the prey, representing the optimal solution, drawing upon the intelligence and strategic insights of the alpha, beta, and delta wolves. This behavioral pattern can be mathematically articulated as follows:

$${\overrightarrow{D}}_{\alpha }= \left|{\overrightarrow{C}}^{1}\cdot {\overrightarrow{X}}_{\alpha }- \overrightarrow{X}\right|$$

$${\overrightarrow{D}}_{\beta }= \left|{\overrightarrow{C}}^{2}\cdot {\overrightarrow{X}}_{\beta }- \overrightarrow{X}\right|$$

$${\overrightarrow{D}}_{\delta }= \left|{\overrightarrow{C}}^{3}\cdot {\overrightarrow{X}}_{\delta }- \overrightarrow{X}\right|$$

The new positions are updated as:

$${{\overrightarrow{X}}^{1}}= {\overrightarrow{X}}_{\alpha }- {\overrightarrow{A}}^{1}\cdot {\overrightarrow{D}}_{\alpha }$$

$${\overrightarrow{X}}^{2}= {\overrightarrow{X}}_{\beta }- {\overrightarrow{A}}^{2}\cdot {\overrightarrow{D}}_{\beta }$$

$${\overrightarrow{X}}^{3}= {\overrightarrow{X}}_{\delta }- {\overrightarrow{A}}^{3}\cdot {\overrightarrow{D}}_{\delta }$$

Final position of the wolf with best optimum is updated and can be expressed as:

$$\overrightarrow{X}\left(t+1\right)=\frac{\left({\overrightarrow{X}}^{1}+ {\overrightarrow{X}}^{2}+ {\overrightarrow{X}}^{3}\right)}{3}$$

Exploitation phase

To replicate the culminating (Exploiting) phase of the hunt, wherein the wolves engage in an assault on their prey, the value of A⃗ is diminished. When the magnitude of | A⃗ | falls below 1, the wolves are motivated to launch their attack on the prey, thereby converging towards the optimal solution.

Exploration (search for prey)

When |A|> 1, wolves are compelled to wander the parameter space more extensively, distancing themselves from the prey’s location. This behavioral pattern enables the algorithm to circumvent local minima, thereby facilitating a more thorough quest for a global optimum.

Throughout number of iterations, a⃗ decreases from 2 to 0, which balances exploration and exploitation. When |A⃗|< 1, wolves focus more on exploitation, while |A⃗|> 1 emphasizes exploration.

Convergence

Throughout the iterations, a⃗ decreases from it is initial value of 2–0, which balances exploration as well as exploitation. When ∣A⃗∣ < 1, wolves focus more on exploitation, while ∣A⃗∣ > 1 emphasizes exploration.

The Grey Wolf Optimizer guarantees that the wolves can extensively traverse the parameter space in the initial stages of the optimization process. As the progression unfolds, they gradually shift their focus to exploiting the most promising solutions, ultimately converging toward the global optimum.

Teaching–learning-based optimization (TLBO)

In 2011, Rao et al. introduced the Teaching–Learning-Based Optimization (TLBO) algorithm, a population-centric optimization method designed to mimic the educational process of teaching and learning. The said algorithm is stimulated from natural process based on learning and knowledge transfer as done within a classroom setting, where an instructor/supervisor/teacher conveys knowledge to students/learners with a goal of improving their understanding and performance. TLBO has gained significant attention for its simplicity, effectiveness, and the fact that it does not require specific algorithmic parameters such as crossover rates or mutation probabilities, facilitating its implementation across a diverse array of optimization challenges.

Working principle of TLBO

TLBO operates on the fundamental concept that learners (candidate solutions) improve their knowledge (solution quality) through interaction with a teacher and through peer-to-peer learning. The optimization process is classified into two discrete phases: exploration, referred to as teaching, and learning, known as exploitation:

Teacher phase (global exploration)

During the teacher phase, the individual representing the best solution within the population imparts knowledge to the learners, aiming to enhance the overall quality of the population’s mean. The idea is that the teacher tries to bring the learners closer to an optimal solution by adjusting their knowledge. The said process is mathematically expressed as follows:

$${X}_{new}={X}_{old}+r\cdot \left({X}_{best}-{T}_{F}\cdot {X}_{mean}\right)$$

where X_new is the updated solution, X_old is the present solution, X_best is the optimal solution (teacher), X_mean is the mean solution of the population, T_F is the teaching factor, which controls the influence of the teacher, and r is a number randomized between 0 and 1.

This phase focuses on global exploration by allowing learners to discover the parameter space guided by the optimal solution (teacher), thus increasing the probability of finding optimal or near-optimal solutions.

Learner phase (local exploitation)

In the learner phase, the students, or learners, acquire knowledge through their interactions and collaborations with their peers. Pairs of learners are randomly selected, and the better-performing learner attempts to improve the other’s performance. This phase is represented mathematically as:

$${X}_{new}= {X}_{old}+ r \cdot \left({X}_{i}- {X}_{j}\right)$$

or

$${X}_{new}= {X}_{old}+ r \cdot \left({X}_{j}- {X}_{i}\right)$$

where X_i and X_j represent two learners selected at random, and r denotes a randomly generated number. If the newly discovered solution surpasses the prior one in quality, it will replace the existing solution. This phase emphasizes local exploitation by refining solutions through peer-to-peer learning.

Advantages of TLBO

TLBO stands out from other optimization algorithms due to several key advantages:

• a. Parameter-free Optimization: In contrast to numerous population-based algorithms, including Teaching–Learning-Based Optimization, Particle Swarm Optimization (PSO) and Genetic Algorithms (GA) does not depend on parameters that are tailored to the algorithm including mutation rates, crossover probabilities, or inertia weights. The only parameters in TLBO are the pop size (size of the population) and the iteration count, making it simpler to implement as well as tune.

• b. Balanced Exploration and Exploitation: The two diverse phases in TLBO, the teacher phase (also known as exploration phase) and learner phase (also known as exploitation), provide a balanced approach to searching the solution space. The teacher phase ensures the population is guided towards promising regions, while the learner phase allows for local refinement, helping the algorithm avoid premature convergence to suboptimal solutions.

• c. Fast Convergence: TLBO has been shown to converge more rapidly compared to other metaheuristic algorithms because of its dual-phase learning mechanism. The ongoing enhancement of solutions during both the teacher phase (exploration) and the learner phase (exploitation) serves to expedite the search process, making it particularly suitable for problems where computational efficiency is critical.

• d. Wide Applicability: Owing to its simplicity and effectiveness, the application of Teaching–Learning-Based Optimization (TLBO) has achieved notable success across a range of disciplines, particularly in engineering design, scheduling, machine learning, and many more. Its parameter-less nature reduces the complexity of adaptation to different problem types, ensuring that a broad variety of optimization difficulties are handled.

TLBO in hybrid optimization

When used in conjunction with Grey Wolf Optimizer (GWO), TLBO’s strengths in local exploitation complement GWO’s exploration abilities. GWO, being an exploration-heavy algorithm, efficiently navigates large, complex parameter spaces, but can sometimes fall short in fine-tuning solutions, especially in later stages when the population begins to converge. This is where TLBO’s learner phase shines by providing a mechanism for refining solutions without requiring additional parameters or tuning. The teaching phase of TLBO further supports the search by guiding the population towards the best-known solution, maintaining diversity in the search process.

By combining GWO and TLBO, the resulting hybrid algorithm benefits from GWO’s effective exploration of the parameter space and TLBO’s efficient exploitation, ensuring a well-rounded and robust optimization process. This hybrid approach is particularly advantageous for solving multimodal, high-dimensional problems where balancing the phase of exploration and the phase of exploitation is an important factor for finding a global optima (global optimum). Furthermore, the simplicity that TLBO offers ensures that the computational overhead introduced by the hybridization remains minimal, making it an efficient and influential instrument for resolving composite optimization problems.

GWO excels in exploration due to its mechanisms like encircling and hunting but can suffer from premature convergence and weak exploitation. TLBO, on the other hand, is parameter-free and effective in exploitation through its teacher and learner phases but may lack robust exploration. The hybrid GWO-TLBO leverages their complementary strengths—GWO’s dynamic exploration and TLBO’s refined exploitation—while addressing their respective weaknesses, such as improving convergence reliability and balancing search efficiency.

The Grey Wolf Optimizer (GWO) emulates the innate leadership pack structure and hunting tactics of grey wolves, whereas Teaching–Learning-Based Optimization (TLBO) leverages a teacher-student framework to improve learning within a population-based context. In this hybrid algorithm, we combine GWO’s exploration/exploitation phases with the TLBO’s teaching and learning mechanisms to maintain an equilibrium for global as well as local search. The pseudocode for hybrid GWO and TLBO is shown in Fig. 4.

Fig. 4

Psuedo code for the proposed algorithm (Hybrid GWO-TLBO).

Explanation

• I. Initialization

  • a. Input Parameters:

    • i. N: This is the pop size (population) wolves the (number of wolves).

    • ii. Max_iter: This is the termination conditions or maximum iteration limit.

  • b. Initialize random population of wolves:

    • i. Each wolf X_j acts as a potential to the optimization challenge, represented in a vector form in the searching space.

    • ii. j = 1, 2…,Nj, where N represents the population size or wolves (number of wolves).

  • c. Initialize the alpha, beta, and delta wolves:

    • i. X_α: Signifies the wolf with optimal fitness (best resolution so far).

    • ii. X_β: Signifies the alternate best wolf.

    • iii. X_δ: Signifies the tertiary best wolf.

      These three wolves guide the rest of the wolves toward the optimal solution.

• II. While the stopping condition is not met

  This iterative process will persist until a specified termination criterion is met, such as achieving the maximum allowable iterations, denoted as Max_iter, or attaining a predefined level of solution accuracy.

• III. Phase 1: GWO Phase

  The GWO phase encompasses both exploration and exploitation: it involves seeking out new regions within the parameter space while also focusing on refining and optimizing the current best solutions.

  For each wolf X_j:

  • a. Calculate the fitness:

    • 1. Each wolf’s position represents a potential solution, and its quality being estimated using a fitness function (specific to problem being optimized). Higher fitness (for maximization problems) or lower fitness (for minimization problems) indicates a better solution.

  • b. Update alpha, beta, delta based on fitness:

    • 1. If a wolf’s fitness is improved than the present alpha (optimal solution), update X_α.

    • 2. Similarly, update X_β and X_δ with the alternate and tertiary best wolves.

  • c. Calculate exploration/exploitation coefficients A and C:

    • 1. Coefficient A: Controls the wolf’s exploration/exploitation balance. If ∣A∣ ≥ 1, the algorithm emphasizes exploration (searching new regions of the parameter space). If ∣A∣ < 1, it emphasizes exploitation (refining the current best solutions).

    • 2. Coefficient C: A randomly generated number that regulates the extent of influence exerted by the alpha, beta, and delta wolves on the movement patterns of the other wolves.

  • d. Update the position of each wolf using exploration/exploitation equations:

    • 1. Exploration (∣A∣ ≥ 1):

      Wolves are updated to move randomly away from the alpha, beta, or delta positions. This helps them explore new regions.

      The wolf’s new position is influenced by a random direction, which encourages divergence and exploration of the parameter space.

    • 2. Exploitation (∣A∣ < 1):

      Wolves are updated to move towards the alpha, beta, or delta wolves (best solutions so far), encouraging convergence towards the optimal solution.

      This is done using equations that reduce the distance between the wolves and the best solutions.

• IV. Phase 2: TLBO Phase

  The TLBO phase helps further refine the population using Teaching and Learning mechanisms.

  • a. Teaching Phase:

    • 1. The teacher is defined as the wolf with the optimal solution, X_α.

    • 2. For each wolf X_j, adjust its location in accordance with the position of the teacher:

      • a. The underlying concept is that the teacher has the capacity to enhance the performance of the wolves, who are regarded as students.

      • b. The new position of X_j is calculated as:

        $${X}_{j}={X}_{j}+rand\left(\right)\times {(X}_{{\alpha }}-{T}_{f}\times {X}_{mean}$$

        where rand() represents a random value within the range of 0 to 1, T_f is the teaching factor, which take on the values of 1 or 2, controlling how much the teacher influences the wolf, X_mean represents the average of all wolves’ positions (mean solution).

        This equation encourages wolves to move closer to the teacher, improving their fitness.

    • b. Learning Phase:

      • 1. In the learning phase, each wolf learns by interacting with another randomly selected wolf X_j from the population.

      • 2. For each wolf X_i:

        • i. If X_i is worse (has a lower fitness) than X_j, it learns from X_j and moves towards it. This encourages weak wolves to move toward better solutions.

        • ii. Otherwise, X_i moves away from X_j to travel other regions of the parameter space, maintaining diversity within the population.

• V. Update the positions of alpha, beta, delta as per the new fitness values

  • 1. After completing the GWO and TLBO phases, re-evaluate the fitness of the wolves that have been updated.

  • 2. Update the X_α, X_β, and X_δ positions based on the new best, second-best (alternate-best), and third-best (tertiary-best) wolves.

• VI. Increment iteration counter

  Update the iteration count t=t+1.

• VII. Return the best solution found, X_α

  Upon fulfilling the termination criterion, either by reaching the maximum iteration count, denoted as Max_iter, or by discovering an acceptable solution, the algorithm returns X_α, signifying the most optimal solution identified throughout the search process

Analysis and testing of standard benchmark functions (CEC 2014, CEC 2017 and CEC 2022)

CEC-2014

The proposed hybrid GWO-TLBO algorithm is introduced and evaluated using standard benchmark functions^99,176 for performance comparison. The functions are classified into three primary groups: unimodal (UM), which includes functions F1 through F7; multimodal (MM), covering functions F8 to F13; and fixed-dimensional (FD), consisting of functions F14 to F23Mathematical expression of the above said functions, are detailed in the following tables (as shown in Tables 2, 3, and 4) for unimodal, multimodal, and fixed-dimensional functions, respectively. Three-dimensional representations of the functions (F1 to F23) are illustrated respectively (as illustrated in Figs. 5, 6, and 7) for unimodal, multimodal, and fixed-dimensional functions.

Table 2 Mathematical Expressions for Standard Unimodal benchmark functions (CEC-2014).

Table 3 Mathematical expressions for standard multimodal benchmark functions.

Table 4 Mathematical expressions for standard fixed dimension benchmark functions.

Fig. 5

Uni Modal functions-3D view curves.

Fig. 6

Multi modal functions-3D view curves.

Fig. 7

Fixed dimension functions-3D view curves.

CEC-2017

The proposed hybrid GWO-TLBO algorithm is introduced and evaluated using standard benchmark functions¹⁷⁷ for performance comparison. The example functions are illustrated in Fig. 8 and the details for the CEC 2017 benchmark functions are presented in Table 5.

Fig. 8

Test functions for CEC 2017.

Table 5 CEC 2017 benchmark functions.

CEC-2022

The proposed hybrid GWO-TLBO algorithm is introduced and evaluated using standard benchmark functions¹⁷⁸ for performance comparison. The functions are illustrated in Fig. 9 and the details for the CEC 2022 benchmark functions are presented in Table 6.

Fig. 9

Test functions for CEC 2022.

Table 6 CEC 2022 benchmark functions.

Results and discussion

CEC 2014: The hybrid GWO-TLBO algorithm was verified to a variety of benchmark functions to assess its performance. This included seven unimodal (UM) which are functions ranging from F1 to F7, five multimodal (MM) which are functions ranging from F8 to F13, and the rest ten fixed-dimension (FD) which are functions ranging from F14 to F23, across different dimensions. The tests were conducted with a maximum iteration of value 500 and trial runs of 30. The results for the UM functions are reported, including the quartile-based results for these functions across various dimensions are presented in Tables 7, 8 and 9. Figures 10, 11, 12, 13, 14, 15, 16, 17, 18, and 19 displays the parameter space, position history, trajectory, average fitness and convergence curve, for the Unimodal (UM) functions and Multimodal (MM) functions (CEC 2014) for different dimensions (30, 50, 100), highlighting the fast convergence of the GWO-TLBO. The UM functions were particularly useful for evaluating the capability of the proposed GWO-TLBO algorithm in finding the global optima, and outcomes indicate the usefulness of GWO-TLBO consistently outperformed many classical methods. Further, Figs. 20 and 21 shows the parameter space, position history, trajectory, average fitness and convergence curve for the fixed dimension standard benchmark functions (CEC 2014).

Table 7 Quartile results of Unimodal (F1 to F8) and Multimodal Benchmark Functions (F9 to F13) (30 Dimensions).

Table 8 Quartile results of Unimodal (F1 to F8) and Multimodal Benchmark Functions (F9 to F13) (50 Dimensions).

Table 9 Quartile results of unimodal and multimodal benchmark functions (100 dimensions).

Fig. 10

Parameter space, position history, trajectory, average fitness and convergence curve for Standard benchmark functions (F1–F2) for 30 dimensions (d = 30).

Fig. 11

Parameter space, position history, trajectory, average fitness and convergence curve for Standard benchmark functions (F3–F7) for 30 dimensions (d = 30).

Fig. 12

Parameter space, position history, trajectory, average fitness and convergence curve for Standard benchmark functions (F8–F11) for 30 dimensions (d = 30).

Fig. 13

Parameter space, position history, trajectory, average fitness and convergence curve for Standard benchmark functions (F12–F13) for 30 dimensions (d = 30).

Fig. 14

Parameter space, position history, trajectory, average fitness and convergence curve for Standard benchmark functions (F1–F5) for 50 dimensions (d = 50).

Fig. 15

Parameter space, position history, trajectory, average fitness and convergence curve for Standard benchmark functions (F6–F10) for 50 dimensions (d = 50).

Fig. 16

Parameter space, position history, trajectory, average fitness and convergence curve for Standard benchmark functions (F1–F13) for 50 dimensions (d = 50).

Fig. 17

Parameter space, position history, trajectory, average fitness and convergence curve for Standard benchmark functions (F1–F5) for 100 dimensions (d = 100).

Fig. 18

Parameter space, position history, trajectory, average fitness and convergence curve for Standard benchmark functions (F6–F10) for 100 dimensions (d = 100).

Fig. 19

Parameter space, position history, trajectory, average fitness and convergence curve for Standard benchmark functions (F11–F13) for 100 dimensions (d = 100).

Fig. 20

Parameter space, position history, trajectory, average fitness and convergence curve for Standard benchmark functions (F14–F18).

Fig. 21

Parameter space, position history, trajectory, average fitness and convergence curve for Standard benchmark functions (F19–F23).

For 30 dimensions: Table 7 represents the best score, mean score and standard deviation score for the Unimodal and Multimodal Standard Benchmark Functions (CEC 2014) for the dimension count of 30 (d = 30).

For 50 dimensions: Table 8 represents the best score, mean score and standard deviation score for the Unimodal and Multimodal Standard Benchmark Functions (CEC 2014) for 50 dimensions (d = 50).

For 100 dimensions: Table 9 represents the best score, mean score and standard deviation score for the Unimodal and Multimodal Benchmark Functions (CEC 2014) for the dimension count of 100 (d = 100).

Fixed Dimension Standard Benchmark Function Analysis: Table 10 represents the best score, mean score and standard deviation score for the fixed dimension of the standard benchmark functions (CEC 2014).

Table 10 Test result of fixed dimension of the standard benchmark functions (F14 to F23).

Further, the proposed algorithm is tested and compared against tvarious algorithms including LSHADE_EpSin¹³⁸, EBOwithCMAR¹³⁹, JSO¹⁴⁰, LSHADE_SPACMA¹⁴¹ and the analysis is presented in Table 11.

Table 11 Comparison of various algorithms CEC 2014.

CEC 2017: The algorithms compared in Table 12 provide a comprehensive overview of their respective performances across key metrics. Table 12 compares the performance of five algorithms: LSHADE_EpSin¹³⁸, EBOwithCMAR¹³⁹, JSO¹⁴⁰, LSHADE_SPACMA¹⁴¹, and GWO-TLBO. The table highlights their effectiveness across various optimization metrics, providing a detailed benchmark to evaluate their relative strengths and weaknesses.

Table 12 Comparison of various algorithms CEC 2017.

Figures 22, 23, 24, 25, 26, 27 present an in-depth analysis of the GWO-TLBO (Grey Wolf Optimizer—Teaching Learning-Based Optimization) hybrid approach. These figures showcase its performance across various scenarios, focusing on aspects such as convergence behavior, optimization accuracy, and robustness. The visual representation emphasizes the effectiveness of the GWO-TLBO method in addressing complex optimization challenges.

Fig. 22

Search history, trajectory, average fitness and convergence curve for CEC 2017 on GWO-TLBO.

Fig. 23

Search history, trajectory, average fitness and convergence curve for CEC 2017 on GWO-TLBO.

Fig. 24

Search history, trajectory, average fitness and convergence curve for CEC 2017 on GWO-TLBO.

Fig. 25

Search history, trajectory, average fitness and convergence curve for CEC 2017 on GWO-TLBO.

Fig. 26

Search history, trajectory, average fitness and convergence curve for CEC 2017 on GWO-TLBO.

Fig. 27

Search history, trajectory, average fitness and convergence curve for CEC 2017 on GWO-TLBO.

CEC 2022: The comparison in Table 13 provides a comparative analysis of five algorithms— LSHADE_EpSin¹³⁸, EBOwithCMAR¹³⁹, JSO¹⁴⁰, LSHADE_SPACMA¹⁴¹, and GWO-TLBO—based on the benchmark functions of the CEC 2022 competition. This evaluation highlights the algorithms’ performance in addressing the complex optimization problems defined by the competition standards.

Table 13 Comparison of various algorithms CEC 2022.

Figures 28, 29, 30 illustrate the performance of the GWO-TLBO algorithm on the benchmark functions of the CEC 2022 competition. These figures provide a visual analysis of the algorithm’s convergence trends, accuracy, and stability, demonstrating its effectiveness in solving challenging optimization problems.

Fig. 28

Search history, trajectory, average fitness and convergence curve for CEC 2022 on GWO-TLBO.

Fig. 29

Search history, trajectory, average fitness and convergence curve for CEC 2022 on GWO-TLBO.

Fig. 30

Search history, trajectory, average fitness and convergence curve for CEC 2022 on GWO-TLBO.

Experimental study on engineering design challenges

In real-world design challenges¹⁷⁹, it’s often difficult to achieve optimal results due to the complexity involved. This complexity usually comes from various constraints, such as equality and inequality conditions, which need to be considered during the optimization process. Solutions generated by optimization algorithms are typically classified as either feasible or infeasible, depending on how well they satisfy these constraints. To discover the finest possible solutions efficiently and with minimal computational effort, many approaches may utilize the combination of strengths of diverse algorithms. In this study, eleven constrained engineering design challenges are selected and the proposed hybrid GWO-TLBO algorithm was evaluated on these said challenges along with different algorithms including LSHADE_EpSin¹³⁸, EBOwithCMAR¹³⁹, JSO¹⁴⁰, LSHADE_SPACMA¹⁴¹. The details of these challenges are depicted in Table 14, with solution and computational times shown in Tables 15 and 16.

Table 14 Details of Engineering based designs (Special 1–Special 11).

Table 15 Obtained score/fitness from proposed GWO-TLBO optimization and other algorithms (Design_1 to Design_11).

Table 16 Proposed GWO-TLBO computational time in seconds.

Solution and computational times shown in Tables 15 and 16 for the Engineering design challenges

Engineering challenge—three bar truss (special 1)

To assess the effectiveness of the proposed hybrid GWO-TLBO algorithm in solving engineering design challenges, it was applied to the optimization of a Three-Bar Truss system configuration, as seen in Fig. 31^180,181. When comparing the outcomes, as represented in Table 17, the hybrid GWO-TLBO algorithm surpasses its performance in contrast with existing metaheuristic solutions, demonstrating its clear advantages. The Convergence curve for grey wolf optimization and hybrid GWO-TLBO is present in Fig. 32. The three-bar truss challenge is outlined mathematically as follows:

Fig. 31

Engineering design challenge for a three-bar truss (Special 1).

Table 17 Assessment of the proposed hybrid algorithm GWO-TLBO in case of Special 1.

Fig. 32

Convergence curve comparison for three bar truss challenge.

Let us consider,

$$\overrightarrow{t}=\left[{t}_{1},{t}_{2}\right]=\left[{A}_{1},{A}_{2}\right]$$

(1)

Minimize,

$$f\left(\overrightarrow{t}\right)=\left(2\sqrt{2}{t}_{1}+{t}_{2}\right)\times l$$

(2)

Subject to,

$${g}_{1}\left(\overrightarrow{t}\right)=\frac{\sqrt{2}{t}_{1}+{t}_{2}}{\sqrt{2}{t}_{1}^{2}+2{t}_{1}{t}_{2}}P-\sigma \le 0$$

(3)

$${g}_{2}\left(\overrightarrow{t}\right)=\frac{{t}_{2}}{\sqrt{2}{t}_{1}^{2}+2{t}_{1}{t}_{2}}P-\sigma \le 0$$

(4)

$${g}_{3}\left(\overrightarrow{t}\right)=\frac{1}{\sqrt{2}{t}_{2}+{t}_{1}}P-\sigma \le 0$$

(5)

Range of variables = 0 $\le$ ${t}_{1}$, ${t}_{2}\le l$

Here, l = 100 cm, P = 2 KN/${\text{cm}}^{2}$, $\sigma$ = 2 KN/${\text{cm}}^{2}$

Engineering design challenge—speed reducer (special 2)

The design challenge for speed reducers stands out as one of the most demanding tasks in optimization. It encompasses seven design variables, six of which are continuous, and is subject to eleven constraints. The key aim here is the minimization of the speed reducer weight, i.e. as minimum as could be obtained, while keeping factors like internal stress, shaft deflection, and the twisting and stress on the surface of the gear teeth should be within acceptable limits. Figure 33 illustrates the seven design variables (t1–t7). The Convergence curve for grey wolf optimization and hybrid GWO-TLBO is present in Fig. 34. The mathematical setup for the problem is described below, and the outcomes of the proposed hybrid algorithm of GWO-TLBO, in disparity to other metaheuristic algorithms, are shown in Table 18.

Fig. 33

Engineering design challenge- Speed Reducer (Special 2).

Fig. 34

Convergence curve Comparison for speed reducer challenge.

Table 18 Assessment of the proposed hybrid algorithm GWO-TLBO in case of Special 2.

$$\text{Minimize}, f\left(\overrightarrow{t}\right)=0.7854{t}_{1}{t}_{2}\left(3.3333{t}_{3}^{2}+14.9334{t}_{3}-43.0934\right)-1.508{t}_{1}\left({t}_{6}^{2}+{t}_{7}^{2}\right)+7.4777\left({t}_{6}^{3}+{t}_{7}^{3}\right)+0.7854\left({t}_{4}{t}_{6}^{2}+{t}_{5}{t}_{7}^{2}\right)$$

(6)

Subject to,

$${r}_{1}\left(\overrightarrow{t}\right)=\frac{27}{{t}_{1}{t}_{2}^{2}{t}_{3}}-1\le 0$$

(7)

$${r}_{2}\left(\overrightarrow{t}\right)=\frac{397.5}{{t}_{1}{t}_{2}^{2}{t}_{3}^{2}}-1\le 0$$

(8)

$${r}_{3}\left(\overrightarrow{t}\right)=\frac{1.93{t}_{4}^{3}}{{t}_{2}{t}_{3}{t}_{6}^{4}}-1\le 0$$

(9)

$${r}_{4}\left(\overrightarrow{t}\right)=\frac{1.93{t}_{5}^{3}}{{t}_{2}{t}_{3}{t}_{7}^{4}}-1\le 0$$

(10)

$${r}_{5}\left(\overrightarrow{t}\right)=\frac{1}{110{t}_{6}^{3}}\sqrt{(\frac{745.0{t}_{4}}{{t}_{2}{t}_{3}}}{)}^{2}+16.9\times 1{0}^{6}-1\le 0$$

(11)

$${r}_{6}\left(\overrightarrow{t}\right)=\frac{1}{85{t}_{7}^{3}}\sqrt{(\frac{745.0{t}_{5}}{{t}_{2}{t}_{3}}}{)}^{2}+157.5\times 1{0}^{6}-1\le 0$$

(12)

$${r}_{7}\left(\overrightarrow{t}\right)=\frac{{t}_{2}{t}_{3}}{40}-1\le 0$$

(13)

$${r}_{8}\left(\overrightarrow{t}\right)=\frac{5{t}_{2}}{{t}_{1}}-1\le 0$$

(14)

$${r}_{9}\left(\overrightarrow{t}\right)=\frac{{t}_{1}}{12{t}_{2}}-1\le 0$$

(15)

$${r}_{10}\left(\overrightarrow{t}\right)=\frac{1.5{t}_{6}+1.9}{12{t}_{2}}-1\le 0$$

(16)

$${r}_{11}\left(\overrightarrow{t}\right)=\frac{1.1{t}_{7}+1.9}{{t}_{5}}-1\le 0$$

(17)

Here,

$$\begin{aligned} & 2.6 \le t_{1} \le 3.6, 0.7 \le t_{2} \le 0.8,17 \le t_{3} \le 28,7.3 \\ & \le t_{4} \le 8.37.8 \le t_{5} \le 8.3,2.9 \le t_{6} \le 3.9, 5 \le t_{7} \le 5.5 \\ \end{aligned}$$

Engineering design challenge—pressure vessel (PV) (special 3)

The optimization challenge for the pressure vessel (PV) design had initially being investigated by Kramer and Kannan in 1994¹⁸², focuses on minimizing overall costs, including those for welding, forming, and materials. The vessel has a cylindrical shape with hemispherical ends on both sides, and the design involves four key parameters, as represented in Fig. 35. The Convergence curve for grey wolf optimization and hybrid GWO-TLBO is present in Fig. 36. The mathematical expression for this particular is challenge provided in below. Table 19 presents a comparison of the hybrid GWO-TLBO algorithm’s performance with other existing metaheuristic algorithms.

$${\text{Let}}\,{\text{us}}\,{\text{contemplate}},\vec{t} = \left[ {t_{1} t_{2} t_{3} t_{4} } \right] = \left[ {T_{s} T_{h} RL} \right]$$

(18)

$${\text{Minimizing}},f\left( {\vec{t}} \right) = 0.6224t_{1} t_{3} t_{4} + 1.7781t_{2} t_{3}^{2} + 3.1661t_{1}^{2} t_{4} + 19.84t_{1}^{2} t_{3}$$

(19)

Subject to,

$$g_{1} \left( {\vec{t}} \right) = - t_{1} + 0.0193t_{3} \le 0$$

(20)

$$g_{2} \left( {\vec{t}} \right) = t_{3} + 0.00954t_{3} \le 0$$

(21)

$$g_{3} \left( {\vec{t}} \right) = - \pi t_{3}^{2} t_{4} - \frac{4}{3}\pi t_{3}^{3} + 1296000 \le 0$$

(22)

$$g_{4} \left( {\vec{t}} \right) = t_{4} - 240 \le 0$$

(23)

Fig. 35

Pressure vessel (PV) optimal design (Special 3).

Fig. 36

Convergence curve Comparison for the challenge of pressure vessel design.

Table 19 Assessment of the proposed hybrid algorithm GWO-TLBO in case of Special 3.

Adjustable ranges are,

$$0 \le t_{1} \le {99};0 \le t_{2} \le {99};{1}0 \le t_{3} \le {2}00;{1}0 \le t_{4} \le {2}00$$

(24)

Engineering design challenge—compression/tension spring (special 4)

The primary goal of this problem is to reduce the weight of the spring while adhering to essential constraints, including shear stress limits, allowable deflection, geometric specifications, and surge frequency requirements. Achieving this balance is crucial to ensure the spring performs efficiently and safely under operational conditions. This design challenge considers three continuous variables and four nonlinear inequality restrictions. Figure 37 illustrates the design challenge variables, while Eqs. (29)–(31) describe the mathematical formulation. The Convergence curve for grey wolf optimization and hybrid GWO-TLBO is present in Fig. 38. A comparison of the hybrid GWO-TLBO algorithm’s performance with other existing metaheuristic methods is presented in Table 20.

$${\text{Consider}},\vec{s} = \left[ {s_{1} s_{2} s_{3} } \right] = \left[ {dDN} \right]$$

(25)

$${\text{Minimize}},f\left( s \right) = \left( {s_{3} + 2} \right)s_{2} s_{1}^{2}$$

(26)

Fig. 37

Compression/tension spring challenge (special 4).

Fig. 38

Convergence curve Comparison for spring design challenge.

Table 20 Assessment of the proposed hybrid algorithm GWO-TLBO in case of Special 4.

Subject to,

$$g_{1} \left( s \right) = 1 - \frac{{s_{2}^{3} s_{3} }}{{71785s_{1}^{4} }} \le 0$$

(27)

$${g}_{2}\left(s\right)=\frac{4{s}_{2}^{2}-{s}_{1}{s}_{2}}{12566\left({s}_{2}{s}_{1}^{3}-{t}_{1}^{4}\right)}+\frac{1}{5108{s}_{1}^{2}}\le 0$$

(28)

$${g}_{3}\left(s\right)=1-\frac{140.45{s}_{1}}{{s}_{2}^{2}{s}_{3}}\le 0$$

(29)

$${g}_{4}\left(s\right)=\frac{{s}_{1}+{s}_{2}}{1.5}-1\le 0$$

(30)

Variable ranges, 0.005 $\le$ ${s}_{1}\le$ 2.00, 0.25 $\le$ ${t}_{2}\le$ 1.30, 2.00 $\le$ ${s}_{3}\le$ 15.0.

Engineering design challenge—welded beam (WB) (special 5)

The main aim of this design challenge is to lower the construction costs associated with a welded beam. This must be accomplished while meeting seven specific constraints and considering four distinct design variables, as illustrated in Fig. 39. Successfully navigating these parameters is essential to optimize both cost-effectiveness and structural integrity. The mathematical expression of the design has been laid out in equations below. The Convergence curve for grey wolf optimization and hybrid GWO-TLBO is present in Fig. 40. Table 21 provides a comparison of the hybrid GWO-TLBO algorithm’s performance against other existing metaheuristic methods.

Fig. 39

Design challenge for welded beam (Special 5).

Fig. 40

Convergence curve Comparison for welded beam design challenge.

Table 21 Assessment of the proposed hybrid algorithm GWO-TLBO in case of Special 5.

Let us consider,

$$\overrightarrow{t}=\left[{t}_{1}{t}_{2}{t}_{3}{t}_{4}\right]=\left[hltb\right]$$

(31)

Minimize,

$$f\left(\overrightarrow{t}\right)=1.10471{t}_{1}^{2}{t}_{2}+0.04811{t}_{3}{t}_{4}\left(14.0+{t}_{2}\right)$$

(32)

Subject to,

$${g}_{1}\left(\overrightarrow{t}\right)=\tau \left(\overrightarrow{t}\right)-{\tau }_{maxi}$$

(33)

$${g}_{2}\left(\overrightarrow{t}\right)=\sigma \left(\overrightarrow{t}\right)-{\sigma }_{maxi}$$

(34)

$${g}_{3}\left(\overrightarrow{t}\right)=\delta \left(\overrightarrow{t}\right)-{\delta }_{maxi}$$

(35)

$${g}_{4}\left(\overrightarrow{t}\right)={t}_{1}-{t}_{4}\le 0$$

(36)

$${g}_{5}\left(\overrightarrow{t}\right)={P}_{i}-{P}_{c}\left(\overrightarrow{t}\right)\le 0$$

(37)

$${g}_{6}\left(\overrightarrow{t}\right)=0.125-{t}_{1}\le 0$$

(38)

$${g}_{7}\left(\overrightarrow{t}\right)=1.10471{t}_{1}^{2}+0.04811{t}_{3}{t}_{4}\left(14.0+{t}_{2}\right)-5.0\le 0$$

(39)

Range of Variables = 0.1 $\le$ ${t}_{1}\le$ 2; 0.1 $\le$ ${t}_{2}\le$ 1; 0.1 $\le$ ${t}_{3}\le$ 10; 0.1 $\le$ ${t}_{4}\le$ 2.

Here,

$$\tau \left( {t_{1} } \right) = \sqrt {(\overline{\tau })^{2} + 2\overline{\tau }\overline{\overline{\tau }} \frac{{t_{2} }}{2R} + (\overline{\overline{\tau }} )^{2} ,}$$

(40)

$$\overline{\tau } = \frac{{P_{i} }}{{\sqrt 2 t_{1} t_{2} }},\overline{\overline{\tau }} = \frac{MR}{J},M = P_{i} \left( {L + \frac{{t_{2} }}{2}} \right),$$

(41)

$$R=\sqrt{\frac{{t}_{2}^{2}}{4}+{\left(\frac{{t}_{1}+{t}_{3}}{2}\right)}^{2}},$$

(42)

$$J=2\left\{\sqrt{2}{t}_{1}{t}_{2}\left[\frac{{t}_{2}^{2}}{4}+{\left(\frac{{t}_{1}+{t}_{3}}{2}\right)}^{2}\right]\right\}$$

(43)

$$\sigma \left(\overrightarrow{t}\right)=\frac{6{P}_{i}L}{{t}_{4}{t}_{3}^{2}},\delta \left(\overrightarrow{y}\right)=\frac{6{P}_{i}{L}^{3}}{E{t}_{2}^{2}{t}_{4}}$$

(44)

$${P}_{c}\left(\overrightarrow{t}\right)=\frac{4.013E\frac{\sqrt{{t}_{3}^{2}{t}_{4}^{6}}}{36}}{{L}^{2}}\left(1-\frac{{t}_{3}}{2L}\sqrt{\frac{E}{4G}} \right)$$

(45)

$$P_{i} = 6000lb,L = 14in,G = 12 \times 10^{6} psi,E = 30 \times 1^{6} psi\,\tau \max i_{{maxi_{{maxi}} }}$$

Engineering design challenge—rolling element bearing (special 6)

The key aim of optimizing the design of rolling element bearings is to enhance their dynamic load capacity. By focusing on this improvement, the goal is to ensure that the bearings can withstand greater loads while maintaining performance and reliability. Achieving a higher dynamic load capacity is crucial for extending the lifespan of the bearings and improving the overall efficiency of the machinery they support. The design details, involving 10 decision variables, are depicted in Fig. 41. Important factors include the ball diameter (DIMB) the number of balls (Nb) and pitch diameter (DIMP), along with the coefficients for the curvature of the inner and outer channels. The Convergence curve for grey wolf optimization and hybrid GWO-TLBO is present in Fig. 42. A comparison of the proposed hybrid GWO-TLBO algorithm in contrast with existing metaheuristic algorithms is depicted in Table 22. The design optimization can be expressed mathematically as follows:

Fig. 41

Challenge for Rolling element bearing design (Special 6).

Fig. 42

Convergence curve Comparison for rolling element bearing challenge.

Table 22 Assessment of the proposed hybrid algorithm GWO-TLBO in case of Special 6.

Maximize,

$${C}_{D}={f}_{c}{N}^\frac{2}{3}DI{M}_{B}^{1.8}$$

(46)

If, $DIM\le 25.4mm$

$${C}_{D}=3.647{f}_{C}{N}^\frac{2}{3}DI{M}_{B}^{1.4}$$

(47)

If, $DIM\ge 25.4mm$

Subject to,

$${r}_{1}\left(x\right)=\frac{{\theta }_{0}}{2{\mathit{sin}}^{-1}\left(\frac{DI{M}_{B}}{DI{M}_{MAX}}\right)}-N+1\ge 0$$

(48)

$${r}_{2}(x)=2DI{M}_{B}-{K}_{DI{M}_{MIN}}(DIM-\mathit{dim})\ge 0$$

(49)

$${r}_{3}(x)={K}_{DI{M}_{MAX}}(DIM-\mathit{dim})\ge 0$$

(50)

$${r}_{4}\left(x\right)=\beta {B}_{W}-DI{M}_{B}\le 0$$

(51)

$${r}_{5}(x)=DI{M}_{MAX}-0.5(DIM+\mathit{dim})\ge 0$$

(52)

$${r}_{6}(x)=(0.5+re)(DIM+\mathit{dim})\ge 0$$

(53)

$${r}_{7}\left(x\right)=0.5\left(DIM-DI{M}_{MAX}-DI{M}_{B}\right)-\alpha DI{M}_{B}\ge 0$$

(54)

$${r}_{8}\left(x\right)={f}_{I}\ge 0.515$$

(55)

$${r}_{9}\left(x\right)={f}_{0}\ge 0.515$$

(56)

$$\text{Here}, {f}_{c}=37.91{\left[1+{\left\{1.04{\left(\frac{1-\varepsilon }{1+\varepsilon }\right)}^{1.72}{\left(\frac{{f}_{I}\left(2{f}_{0}-1\right)}{{f}_{0}\left(2{f}_{I}-1\right)}\right)}^{0.41}\right\}}^\frac{10}{3}\right]}^{-0.3}\times \left[\frac{{\varepsilon }^{0.3}{\left(1-\varepsilon \right)}^{1.39}}{{\left(1+\varepsilon \right)}^\frac{1}{3}}\right]{\left[\frac{2{f}_{I}}{2{f}_{I}-1}\right]}^{0.41}$$

(57)

$$\begin{aligned} \theta_{0} & = 2\pi - 2\cos^{ - 1} \left( {\frac{{\left[ {\left\{ {(DIM - \dim )/2 - 3\left( {t/4} \right)} \right\}^{2} + \left( {\frac{DIM}{2} - \frac{t}{4} - DIM_{B} } \right)^{2} - \left\{ {\dim /2 + \frac{t}{4}} \right\}^{2} } \right]}}{{2\left\{ {(DIM - \dim )/2 - 3\left( {t/4} \right)} \right\}\left\{ {\frac{D}{2} - \frac{t}{4} - DIM_{B} } \right\}}}} \right) \\ \varepsilon & = \frac{{DIM_{B} }}{{DIM_{MAX} }},f_{I} = \frac{{R_{I} }}{{DIM_{B} }},f_{0} = \frac{{R_{0} }}{{DIM_{B} }},t = DIM - \dim - 2DIM_{B} \\ \end{aligned}$$

(58)

$$0.5\left(DIM+\text{dim}({)}_{MAX}\left(DIM+\text{dim}\left(\right)\left(DIM-\text{dim}({)}_{B}\left(DIM-\text{dim}\left(\right)\right)\right)\right)\right)$$

(59)

$$DIM=160;\mathit{dim}=90;{B}_{W}=30;{R}_{I}={R}_{0}=11.033;0.515\le {f}_{I}\text{and}{f}_{0}\le 0.6$$

$$0.4\le {K}_{DI{M}_{MIN}}\le \text{0.5,0.6}\le {K}_{DI{M}_{MAX}}\le \text{0.7,0.3}\le re\le \text{0.1,0.02}\le re\le \text{0.1,0.6}\le \beta \le 0.85$$

Engineering design challenge—multi disk clutch break Special 7

The main goal of the design optimization challenge for the Multi-Disc Clutch Brake (MDCB) is to decrease its weight while maintaining functionality. By achieving a lighter design, the aim is to enhance overall system performance and efficiency, allowing for better handling and reduced energy consumption. This weight reduction is essential for applications where space and weight constraints are critical, ensuring that the MDCB can operate effectively without compromising its braking capabilities. The design details are illustrated in Fig. 43, and Table 23 provides an evaluation of the hybrid GWO-TLBO algorithm’s performance in contrast with existing metaheuristic method. Five important design variables has been considered, which includes the disc thickness (Th), friction surface (Sf), inner radius (Rin), outer radius (Ro), and actuating force (Fac). The Convergence curve for grey wolf optimization and hybrid GWO-TLBO is present in Fig. 44. The mathematical formulation for the optimization can be expressed as follows:

Fig. 43

Challenge for Multi disk clutch break design.

Table 23 Assessment of the proposed hybrid algorithm GWO-TLBO in case of Special 7.

Fig. 44

Convergence curve Comparison for multi disk clutch brake challenge.

Minimize,

$$f\left({R}_{in},{R}_{O},{S}_{f},Th\right)=\pi Th\gamma \left({R}_{0}^{2}-{R}_{in}^{2}\right)\left({S}_{f}+1\right)$$

(60)

$$\begin{aligned} & R_{o} \in 90,91, \ldots ..110;R_{in} \in 60,61,62 \ldots .80;F_{ac} \in 600,610,620,1000; \\ & Th \in 1,1.5,2,2.5,3;S_{f} \in 2,3,4,5,6,7,8,9 \\ \end{aligned}$$

Subject to;

$${t}_{1}={R}_{0}-{R}_{in}-\Delta R\ge 0$$

(61)

$${t}_{2}={L}_{MAX}-\left({S}_{f}+1\right)\left(Th+\alpha \right)\ge 0$$

(62)

$${t}_{3}=P{M\pi }_{max}$$

(63)

$${t}_{4}=P{M{\pi }_{SR}max}_{max}$$

(64)

$${t}_{5}={Y}_{S{R}_{MAX}}-{Y}_{SR}\ge 0$$

(65)

$${t}_{6}={b}_{MAX}-b\ge 0$$

(66)

$${t}_{7}=D{C}_{h}-D{C}_{f}\ge 0$$

(67)

$${t}_{8}=b\ge 0$$

(68)

$$P{M}_{\pi }=\frac{{F}_{ac}}{\Pi \left({R}_{0}^{2}-{R}_{in}^{2}\right)}$$

(69)

Here,

$$\begin{aligned} Y_{SR} & = \frac{{2\pi n\left( {R_{0}^{3} - R_{in}^{3} } \right)}}{{90\left( {R_{0}^{2} - R_{in}^{2} } \right)}} \\ b & = \frac{{i_{x} \pi n}}{{30\left( {DC_{h} + DC_{f} } \right)}} \\ \end{aligned}$$

(70)

Engineering design challenge—gear train (special 8)

In this hybrid approach combining Grey Wolf Optimization (GWO) and Teaching–Learning-Based Optimization (TLBO), the objective is to minimize both the gear teeth ratio and its associated scalar value. By effectively reducing these parameters, the method aims to enhance the efficiency and performance of the gear system. Achieving a lower gear teeth ratio can lead to smoother operation and improved torque transmission, while the scalar value reduction contributes to optimization, potentially resulting in weight savings and better mechanical efficiency. The choice of explicit variables is based upon how many teeth each gear has. Figure 45 highlights the optimal design strategies for this problem, while the performance difference presented in Table 24 compares hybrid GWO-TLBO algorithm in contrast to existing metaheuristic optimization techniques. The Convergence curve for grey wolf optimization and hybrid GWO-TLBO is present in Fig. 46. The optimization can be mathematically modeled and expressed as:

Fig. 45

Challenge for gear train design.

Fig. 46

Convergence curve Comparison for gear train challenge.

Table 24 Assessment of the proposed hybrid algorithm GWO-TLBO in case of Special 8.

Let’s consider,

$$\overrightarrow{t}=\left[{t}_{1}{t}_{2}{t}_{3}{t}_{4}\right]=\left[ABCD\right]$$

(71)

Minimize,

$$f\left(\overrightarrow{t}\right)={\left(\frac{1}{6.931}-\frac{{t}_{3}{t}_{4}}{{t}_{1}{t}_{4}}\right)}^{2}$$

(72)

Subject to; $12\le {t}_{1},{t}_{2},{t}_{3},{t}_{4}\le 60$

Engineering design challenge—belleville spring (Special 9)

The goal of the Belleville spring design, as depicted in Fig. 47, aims at lessening the overall mass of the said Belleville spring, which involves both a discrete variable, which represents the spring thickness, and numerous continuous variable quantity. The model needs to satisfy constraints such as, deflection, the height-to-deflection ratio, compressive tension, as well as limits on external and internal diameters, the spring’s slope and the height-to-maximum height ratio. Table 25 offers an evaluation to the hybrid GWO-TLBO algorithm’s performance in contrast with optimization methods. The Convergence curve for grey wolf optimization and hybrid GWO-TLBO is present in Fig. 48. The optimization challenge could be mathematically modelled and expressed as follows:

Fig. 47

Engineering design challenge-Belleville spring (Special 9).

Table 25 Assessment of the proposed hybrid algorithm GWO-TLBO in case of Special 9.

Fig. 48

Convergence curve Comparison for belleville spring challenge.

Minimize,

$$f\left(t\right)=0.07075\pi \left({D}_{e}^{2}-{D}_{i}^{2}\right)x$$

(73)

Subject to;

$${b}_{1}\left(t\right)=G-\frac{4P{\lambda }_{max}}{\left(1-{\delta }^{2}\right)\alpha {D}_{e}\left[\delta ({S}_{H}-\frac{\lambda max}{2}[]\right]}$$

(74)

$${b}_{2}(t)=(\frac{4P{\lambda }_{max}}{\left(1-{\delta }^{2}\right)\alpha {D}_{e}{\left[\left({S}_{H}-\frac{\lambda }{2}\right)\left({S}_{H}-\lambda \right)x+{x}^{3}\right]MAX}_{{\lambda }_{max}}}$$

(75)

$${b}_{3}\left(t\right)={\lambda }_{1}-{\lambda }_{max}$$

(76)

$${b}_{4}\left(t\right)=H-{S}_{H}-t\ge 0$$

(77)

$${b}_{5}\left(t\right)={D}_{MAX}-{D}_{e}\ge 0$$

(78)

$${b}_{6}\left(t\right)={D}_{e}-{D}_{i}\ge 0$$

(79)

$${b}_{7}\left(t\right)=0.3-\frac{{S}_{H}}{{D}_{e}-{D}_{i}}\ge 0$$

(80)

Here, $d=\frac{6}{p\times \mathit{ln}J}\left(\frac{J-1}{\mathit{ln}J}-1\right)$; $\alpha =\frac{6}{\pi \times \mathit{ln}J}\times {\left(\frac{J-1}{J}\right)}^{2}$; $\mu =\frac{6}{\pi \times \mathit{ln}J}\times \left(\frac{J-1}{2}\right)$

$${P}_{Max}=5400lb$$

$$P=30e6psi,\delta =0.3,{\lambda MAX}_{max}$$

$$J=\frac{{D}_{e}}{{D}_{i}};{\lambda }_{1}=f\left(a\right)a;a=\frac{{S}_{H}}{t}$$

Engineering design challenge—cantilever beam (CB) (Special 10)

The beam design model for Cantilever beam (CB), shown in Fig. 49, is focused on reducing the beam’s weight to its lowest possible value. In this case, five structural variables are considered, while keeping the beam’s thickness fixed. Table 26 shows a comparison that validates the effectiveness along with advantages of the hybrid GWO-TLBO tactic when compared to other popular optimization techniques. The Convergence curve for grey wolf optimization and hybrid GWO-TLBO is present in Fig. 50. The optimization challenge could be mathematically expressed for the model of this design challenge as follows:

Fig. 49

Challenge for cantilever beam design (Special 10).

Table 26 Assessment of the proposed hybrid algorithm GWO-TLBO in case of Special 10.

Fig. 50

Convergence curve Comparison for cantilever beam challenge.

$$\text{Let's\,consider}, \overrightarrow{t}=\left[{t}_{1}{t}_{2}{t}_{3}{t}_{4}{t}_{5}\right]$$

(81)

$$\text{Minimize}, f\left(\overrightarrow{t}\right)=0.6224\left({t}_{1}+{t}_{2}+{t}_{3}+{t}_{4}+{t}_{5}\right),$$

(82)

$$\text{Subject\,to}, g\left(t\right)=\frac{61}{{t}_{1}^{3}}+\frac{37}{{t}_{2}^{3}}+\frac{19}{{t}_{3}^{3}}+\frac{7}{{t}_{4}^{3}}+\frac{1}{{t}_{5}^{3}}\le 1$$

(83)

Variable ranges are, $0.01\le {t}_{1},{t}_{2},{t}_{3},{t}_{4},{t}_{5}\le 100$

Engineering design challenge—I beam (special 11)

This nonlinear design optimization challenge, shown in Fig. 51, involves four key variables: bs1 (flange thickness), bs2 (web thickness), bs3 (flange width), and bs4 (beam thickness). The design is constrained by the beam’s cross-sectional dimensions and dynamic deflection under the prearranged force. Table 27 compares the hybrid GWO-TLBO algorithm with other existing methods, showing how it performs. The Convergence curve for grey wolf optimization and hybrid GWO-TLBO is present in Fig. 52. The optimization challenge could be mathematically expressed for this problem, as described by Coello and Christiansen¹⁸³, is as follows:

Fig. 51

I-Beam engineering design challenge (Special 11).

Table 27 Assessment of the proposed hybrid algorithm GWO-TLBO in case of Special 11.

Fig. 52

Convergence curve Comparison for I-beam problem.

Firstly minimize,

$${f}_{1}({b}_{s})=2{b}_{s2}{b}_{s4}+{b}_{s3}\left({b}_{s1}-2{b}_{s4}\right)$$

(84)

$${f}_{2}({b}_{s})=\frac{60000}{{b}_{s3}{\left({b}_{s1}-2{b}_{s4}\right)}^{3}+2{b}_{s3}{b}_{s4}[4{b}_{s4}^{2}+3{b}_{s1}+\left({b}_{s1}-2{b}_{s4}\right)]}$$

(85)

Subject to,

$$g({b}_{s})=16-\frac{18000{b}_{s1}}{{b}_{s3}{\left({b}_{s1}-2{b}_{s4}\right)}^{3}+2{b}_{s3}{b}_{s4}[4{b}_{s4}^{2}+3{b}_{s1}+\left({b}_{s1}-2{b}_{s4}\right)]}-\frac{15000{b}_{s2}}{{\left({b}_{s1}-2{b}_{s4}\right)}^{3}{b}_{s3}^{3}+2{b}_{s4}{b}_{s2}^{3}}\ge 0$$

(86)

$$10 \le b_{s1} \le 80;10 \le b_{s2} \le 50;0.9 \le b_{s3} \le 5;0.9 \le b_{s4} \le 5$$

The Computational Analysis for all the Engineering problem designs has been conducted under Section “Experimental study on engineering design challenge” and all the experimental studies has been carried in Lenovo Legion 5 Pro Gen 8, AMD Ryzen 7 7745HX 8 core 16 threads 3.2 GHz, 32 GB DDR5 Ram 5200 MHz.

Sensitivity analysis

In optimization studies under benchmarking functions such as CEC 2014, CEC 2017, and CEC 2022, diversity analysis as depicted in Tables 28, 29 and 30 for CEC 2014, 2017 and 2022 respectively, evaluates the population’s spatial distribution over the search space, highlighting the algorithm’s ability to maintain a balance between convergence and exploration. Exploration/exploitation analysis as depicted in Tables 31, 32, and 33 for CEC 2014, 2017 and 2022 respectively, investigates the algorithm’s dynamic behavior in exploring new regions and intensifying the search in promising areas, crucial for navigating complex multimodal landscapes. Sensitivity analysis as depicted in Tables 34, 35 and 36 for CEC 2014, 2017 and 2022 respectively, examines the impact of algorithmic parameters on performance, identifying critical parameters that significantly influence convergence speed and solution quality. Together, these analyses provide comprehensive insights into the algorithm’s robustness and adaptability across diverse problem landscapes.

Analysis data of GWO-TLBO for CEC-2014

Diversity analysis

Table 28 Diversity Analysis of GWO-TLBO for CEC-2014.

Exploration/exploitation analysis

Table 29 Diversity analysis of GWO-TLBO for CEC-2017.

Sensitivity analysis

Table 30 Diversity analysis of GWO-TLBO for CEC-2022.

Analysis data of GWO-TLBO for CEC-2017

Diversity analysis

Table 31 Exploration/Exploitation Analysis of GWO-TLBO for CEC-2014.

Exploration/exploitation analysis

Table 32 Exploration/exploitation analysis of GWO-TLBO for CEC-2017.

Sensitivity analysis

Table 33 Exploration/exploitation analysis of GWO-TLBO for CEC-2022.

Analysis data of GWO-TLBO for CEC-2022

Diversity analysis

Table 34 Sensitivity analysis of GWO-TLBO for CEC-2014.

Exploration/exploitation analysis

Table 35 Sensitivity analysis of GWO-TLBO for CEC-2017.

Sensitivity analysis

Table 36 Sensitivity analysis of GWO-TLBO for CEC-2022.

Future work

An objective function for optimizing the threshold voltage of the supercapacitor bank’s switching mechanism has been modelled, we need to consider several parameters that influence the system’s performance. The primary goal of this optimization is to maximize the power delivery efficiency and extend the supercapacitor discharge period, while maintaining a stable output voltage.

Let’s define the objective function f(V_th1,V_th2) as a weighted sum of the key parameters to be maximized or minimized:

$$f({V}_{th1},{V}_{th2})={\alpha }_{1}\cdot {T}_{d}({V}_{th1},{V}_{th2})+{\alpha }_{2}\cdot {E}_{u}({V}_{th1},{V}_{th2})+{\alpha }_{3}\cdot {V}_{S}({V}_{th1},{V}_{th2})-{\alpha }_{4}\cdot {P}_{out}({V}_{th1},{V}_{th2})-{\alpha }_{5}(L-{P}_{out}\left({V}_{th1},{V}_{th2}\right))$$

where V_th1 is the First Threshold Voltage, V_th2 is the Second Threshold Voltage, T_d is the discharge time, E_u is the Energy Utilization, P_out is the Power Output, V_s is the Voltage Stability, L is the Load Demands, T_d(V_th1,V_th2) is the discharge time as a function of the threshold voltages, E_u(V_th1,V_th2) is the energy utilization efficiency as a function of the threshold voltages, V_s(V_th1,V_th2) is the voltage stability as a function of the threshold voltages, P_out(V_th1,V_th2) is the power output at different voltages, L is the required load demand, and ∣L − P_out(V_th1,V_th2)∣ minimizes the deviation between load demand and power output, and α₁,α₂,α₃,α₄,α₅ are weighting factors that reflect the importance of each parameter.

Further, the system has physical and operational constraints, which must be respected.

Conclusions

This article presents a novel optimization algorithm called hybrid GWO-TLBO, which has been designed for confront an extensive range of optimization problems (including Standard Benchmark Functions and Engineering challenges). The algorithm combines the strategic behavior of grey wolves while hunting their prey from the Grey Wolf Optimizer (GWO) with the structured learning process based on Teaching-Learning-Based Optimization (TLBO). This blend of natural behaviors provides an enhancement to the capability of the algorithm’s ability to both explore the parameter space as well as exploit new resolutions. GWO-TLBO is appraised on twenty three standard benchmarks and an array of real-world engineering problems, focusing on its ability to find the best solutions, how quickly it converges, and how well it handles different problems with different dimensions. The algorithm was evaluated for its capacity to avoid common pitfalls like premature convergence, ensuring it explores and exploits parameter spaces effectively. Computational tests further confirmed that GWO-TLBO consistently outperforms GWO algorithm. In summary, the findings indicate that the GWO-TLBO method demonstrates exceptional effectiveness, delivering solutions that are both quicker and more precise. This is particularly evident in intricate engineering problems, showcasing its capability as a powerful optimization tool. Its robust performance suggests that GWO-TLBO could significantly enhance decision-making processes in various engineering applications, making it a valuable asset for tackling complex design challenges. The proposed method is however is tested for standard benchmark function and various standard engineering problems, but it cannot be denied that the algo has the potential to perform well when it comes to solving electrical engineering problems for example, it could be the optimal location of the STATCOM in IEEE bus systems, optimization of various parameters of electric vehicle, etc. Author is currently working prolonging the delivery output of supercapacitors in electric vehicles and hopes the proposed algorithm will perform better for this application as well.