Introduction

The power system (PS) comprises three components: generation, transmission and distribution. The distribution system (DS) is one of the most vital components of the PS and is responsible for transporting and delivering electrical power from the transmission system to the customers. However, a portion of the electric energy generated was wasted as PLoss, mainly in the radial distribution system (RDS), impacted the far-end customers’ voltage profile and reliability. Energy needs have become increasingly important due to technological advancement and shifting global conditions. Even routine daily tasks were dependent on electricity1. As a result, the electricity demand is growing exponentially, but the supply of fossil fuels is declining. Additionally, since its commission, the distribution infrastructures have not been improved. Because the government owns the entire PS network in vertically integrated utility systems, nobody is concerned about the system’s voltage profile, power factors, and reactive power consumption, impacting system efficiency and overloading. These problems plaguing traditional PS networks have influenced using renewable energy resources in the RDS2.

Integrating renewable energy sources into the RDS has various technical, environmental, and economic benefits, apart from fulfilling the required demand for electric energy. The enhancement of the voltage profile, reduction of active PLoss and reactive PLoss, and improvement of system dependability, security, and power quality are only a few technological advantages3. The environmental benefits include lowering investment risk and greenhouse gas emissions, which reduce the earth’s warming. Reducing operating expenses and maintenance costs and delaying investments in transmission and distribution facility upgrades are some economic advantages of renewable energy resources4. Shunt capacitors (SCs) have several crucial functions in distribution networks (DNs). They are electrical components linked in parallel with the load or distribution feeder. Their primary function is to offer reactive power adjustment in addition to power factor improvement, voltage regulation, grid stability, increased load capacity, voltage flicker reduction and loss reduction5. The electrical DNs’ performance, dependability, and effectiveness are benefits that can all be enhanced by integrating DGs and SCs simultaneously into the RDS instead of placing DGs and SCs separately into the RDS. In6, the DG is defined as the generation of electric power from any resources in a smaller capacity than the central generating plants that allow interconnection at the near end of the customers. As per the generation and consumption of active and reactive power, the DGs are categorised into four types, as shown in Fig. 17.

Fig. 1
figure 1

Different types of DGs based on injection and consumption of active and reactive power.

Full size image

With incorporating DGs into the RDS as one of the prominent solutions, numerous recent research studies have been carried out using different optimisation techniques considering various single and multi-objective functions. In8, the Dingo Optimization Algorithm is introduced to optimise DG placement into the DN, particularly SPV. The verification of the effectiveness of the OT is needed to obtain the primary objectives of improving performance and reducing environmental effects, especially greenhouse gas (GHG) emissions. It is implemented in the IEEE-33 bus system and Ajinde 62-bus system. A few authors have also worked on integrating single and multiple DG’s using different OTs to find optimal location and size, which helps reduce PLoss and improve voltage profiles9,10,11,12,13. In14, the authors reviewed various papers on incorporating DGs into RDS using different algorithms and summarised significant findings.

In9, using the PSO optimising technique, they have presented the optimal sizing and placing of DGs into the Nigeria Ayepe distribution feeder of the Ibadan Electricity Distribution Company (IBEDC). The authors aim to reduce PLoss and improve the voltage profile. The authors employed improved analytical methods to locate optimally and size DGs into the various test systems. The paper focuses on PLoss and voltage profile improvement15. An Artificial Ecosystem Optimizer (AEO) is used for optimal DG allocation16. Four objective functions include active/reactive PLoss, voltage profile improvement and system stability index using the Jellyfish Search Algorithm (JSA) proposed in17. Using the Coot Optimization Algorithm (COA), the optimal placement of the SPV Generators and their intermittency of solar radiation was studied18.

In19, the authors suggest a novel approach to reducing power system congestion by integrating wind farms. By optimising wind farm placement and generator rescheduling using the Cuckoo search algorithm, congestion costs are effectively minimised compared to other heuristic approaches. In20, the authors suggest a hybrid HHO-SCA algorithm for home energy management that improves exploration and exploitation capabilities while efficiently scheduling smart appliances to reduce energy bills and the Peak-to-Average Ratio. In21, Modified Grey Wolf optimisation is implemented for power system congestion management with solar PV integration. To minimise operational costs and system risk resulting from uncertainties22, suggests a hybrid optimisation method for scheduling a hybrid power system that considers battery storage, electric vehicles, and renewable energy sources. Even the authors in23 used the Gravitational Search Algorithm to maximise generator outputs by integrating wind farms, generators and bus sensitivity.

Hybrid enhanced grey wolf optimiser and particle swarm optimisation (EGWO-PSO) algorithms are used for optimal placement and sizing of DGs and Capacitor banks (CBs) in RDN and artificial hummingbird algorithm (AHA) for optimal location and sizes of DGs24,25. Various algorithms used in the optimal order and sizing of the DGs are Grasshopper Optimization Algorithm, improved elephant herding optimisation26, and the backtracking search optimisation algorithm27. In28, they emphasise optimal sizing and placement of the DGs using the Multi-Objective Whale Optimisation Algorithm (MOWOA) in the RDS. The main objectives are to reduce the PLoss, maximise the techno-economic benefits of the RDS, and improve the voltage profile.

In29, the Firefly Algorithm (FA), Cuckoo Search Algorithm (CSA), and Shark Smell Optimization (SSO) are utilised to optimally site and size SCs for actual PLoss reduction and voltage profile improvement. The authors in30 focus on the Bacterial Foraging Optimization Algorithm (BFOA) OT for sizing capacitors into RDS and minimising the PLoss. The authors in31 exploited the opposition-based competitive swarm optimiser (OCSO) algorithm, and32 proposed an improved atom search optimisation (IASO) algorithm to minimise the annual operating cost. Also, the authors in33 focused on the optimal placement of the shunt capacitors to minimise power loss and enhance voltage profiles.

The above authors have incorporated DGs and SCs separately into the RDS; however, few authors have proposed incorporating both DGs and SCs simultaneously, as given in34,35. The proposed model ingeniously integrates competitive search optimisation (CSO) with fuzzy and chaotic theory to improve the voltage profile and power efficiency by integrating DGs and SCs into the power system36,37. By combining both, the performance of the RDS is improved, and stability is enhanced. After reviewing the above papers, which mainly highlight incorporating DGs and SCs for reducing PLoss and improving voltage, a few authors considered annual operating costs for constant power load38,39. However, some of the works that urged me to write this paper are (i) considering different types of the real-time load of the distribution system, (ii) comparing results of four different types of optimisation techniques, (iii) knowing the cost of the DGs, SCs, total operating costs, and total saving from the PLoss using MEWOA algorithm. The rest of the paper is structured as follows: Sect. 2 introduces the optimal DG placement problem formulation. Section 3 presents the locations of the DGs and SCs using the VSI. Section 4 briefly describes the proposed algorithm and its application steps. Sections 5 and 6 sequentially provide results & discussion, and a conclusion.

Problem formulation

Objective function (OF)

With the simultaneous allocation of DGs and SCs in RDS, the objective function’s goal is to decrease the PLoss and improve the voltage profile. This issue can be mathematically expressed as follows:

\(\hbox{min} [{f_1}(x)]\)

$$relyingto\mathop \{ \nolimits_{{g(x) \leqslant 0}}^{{h(x)=0}}$$
(1)

It is necessary to optimise the OF represented by \({f_1}(x)\)PLoss. OF is dependent on variable x, which may be control variables like active and reactive PLoss of DG and SC or state variables like voltage magnitude at various buses40. The functions represent the equality and inequality requirements of the issue \(\:h\left(x\right)\:=\:0\) and \(\:g\left(x\right)\:\le\:0\) respectively. Different OF optimised are as follows:

Minimising the active PLoss

The shallow voltage profile in the RDS generates more losses than the transmission system. The following equation calculates the active PLoss in the RDS.

$$_{{{P_{Loss}}={R_{ij}} * \frac{{P_{j}^{2}+Q_{j}^{2}}}{{|{V_j}{|^2}}}}}$$
(2)

where \(\:{R}_{ij}\) represents the resistance between buses i and j; \(\:{P}_{j}\) and \(\:{Q}_{j}\) are the real and reactive power flowing in the nodes j and \(\:{V}_{j}\) Is the voltage at the bus j. The sum of all branch losses yields the system’s overall real PLoss\(\:{(P}_{TL})\) as expressed below:

$${P_{TL}}=\sum\limits_{{n=1}}^{N} {{P_{Loss}}}$$
(3)

Where N represents the number of buses.

So, the OF of the active PLoss is given below:

$$_{{O{F_{AL}}=\hbox{min} ({P_{TL}})}}$$
(4)

Minimising the reactive PLoss

The formula for calculating the reactive PLoss of any branch is

$${Q_{Loss}}=\;{I_{ij}}\;x\;\frac{{(P_{j}^{2}+Q_{j}^{2})}}{{|{V_j}{|^2}}}$$
(5)

The sum of all branch losses yields the system’s overall reactive PLoss \(\:{(Q}_{TL})\) as expressed below:

$${Q_{TL}}=\sum\limits_{{n=1}}^{N} {{Q_{Loss}}}$$
(6)

So, the OF of the reactive PLoss is given below:

$$O{F_{RL}}=\hbox{min} ({Q_{TL}})$$
(7)

Cost analysis

Incorporating one or more DGs and SCs into the RDS reduces the overall active PLoss. The cost-based analysis is conducted using the mathematical model, and the costs for DGs (\(\:{C}_{DG})\), SCs (\(\:{C}_{SC})\), total operating expenses (\(\:{C}_{TO})\) and annual energy losses (\(\:{C}_{EL})\) are determined as shown below: All the constants and paraments shown in Table 1 are taken from41.

Table 1 Parameters and constants of cost analysis.
Full size table
$${C_{EL}}={P_{PT}}({k_{cp}}+{k_{ce}} * {k_{lf}} * 8760) \$$$
(8)

Where \(\:{P}_{TL}\) Is the real PLoss of the system; \(\:{k}_{cp}\) is the cost of the PLoss in $/kW/year, \(\:{k}_{ce}\) is the energy cost in $/kWh/year and the loss factor, respectively.

The cost of DG output power is calculated as follows:

$${C_{DG}}={k_1} * P_{{DG}}^{2}+{k_2} * {P_{DG}}+{k_3}\$$$
(9)

Where \({P_{DG}}\)is the power output of the DG, \(\:{\text{k}}_{1\:}\), \(\:{\text{k}}_{2\:}\) and \(\:{\text{k}}_{3\:}\)are constants.

The cost of the shunt capacitor bank (SC) is calculated as follows:

$${\operatorname{C} _{SC}}={k_{S1}}*{N_S}+\sum\limits_{{n=1}}^{{{N_S}}} {({k_{S2}}} *{Q_{SC}})\$$$
(10)

Where \(\:{N}_{s}\) is the number of shunt capacitor banks installed in the RDS, \(\:{Q}_{sc}\) is the sizing of the reactive power in kVAr and \(\:{k}_{s1}\) & \(\:{k}_{s2}\) are the constants.

The total operating cost is calculated using the following formula:

$${C_{TO}}=0.07*{P_{TL}}+\sum\limits_{{n=1}}^{{{N_D}}} {({k_5}*{P_{DG}})} +\sum\limits_{{n=1}}^{{{N_S}}} {({k_6}*{Q_{SC}})} \$$$
(11)

The energy savings were determined by comparing the cost of energy loss before and after the integration of the DG/SC into the RDS, as given below:

$${C_{EL}}=\frac{{{C_{EL}} - {C_{EL0}}}}{{{C_{EL0}}}}*100$$
(12)

Where the \(\:{C}_{EL0}\) represent the cost of energy loss before integration of the DG/SC.

Constraints

Any bus voltage must not exceed the defined maximum and minimum voltages and must be kept within the prescribed range of ± 5% of the rated value to supply reliable power to customers42. The voltage at each system bus should maintain the following requirements:

$$0.95\; \leqslant \;{V_n}\; \leqslant \;1.05\;$$
(13)

Where \(\:{V}_{n}\) is the voltage at any bus n.

Regarding DG and SC placements and capacity, the suggested solution complies with all system requirements. The total power generated by the DGs should not exceed the total power demand of the system43. Consequently, the reactive power introduced by the shunt capacitor bank must be within the limits of minimum and maximum as follows:

$${P_{DG,\;min}} \leqslant {P_{DG}} \leqslant \;{P_{DG,\;max}}$$
(14)

Where \(\:{P}_{DG,\:min}\) is the minimum limits of the DG capabilities and \(\:{P}_{DG,\:max}\) is the maximum limit of the DG capabilities

$${Q_{SC,\;min}} \leqslant {Q_{SC}} \leqslant \;{Q_{SC,max}}$$
(15)

The total amount of power produced in the PS equals the total amount consumed and lost44. Power balance is how it is expressed and is formulated as follows:

$${P_{Gen}}=\sum\limits_{{n=1}}^{{{N_D}}} {{P_{DG,n}}} ={P_{Demand}}+{P_{Loss}}$$
(16)
$${Q_{Gen}}=\sum\limits_{{n=1}}^{{{N_S}}} {{Q_{DG,n}}} ={Q_{Demand}}+{Q_{Loss}}$$
(17)

Where \({P_{Gen}}\)& \({Q_{Gen}}\) are the active and reactive power generated by Traditional power generators, \({P_{Demand}}\)& \({Q_{Demand}}\)are the total active and reactive power required by customers.

Location of DGs and SCs using voltage stability index

VSI is an essential indicator that provides information on the likelihood of voltage collapse in PS. This index can be used to assess a system’s voltage stability margins or to identify weak buses or weak lines. Apart from this, VSI can find the best location for the DERs45. The simplified PS model is shown in Fig. 2, and the VSI is calculated as per Eq. 18. The step of locating the optimal location of the DERs is provided in Fig. 3.

\(VSI=2*|V_{1}^{2}|*|V_{2}^{2}| - |V_{2}^{4}| - 2*|V_{2}^{2}|*\{ P_{2}^{{}}R_{{12}}^{{}}+Q_{2}^{{}}X_{{12}}^{{}}\} +Z_{{12}}^{2}*\{ P_{2}^{2}+Q_{2}^{2}\}\) (18)

Where V1 & V2 are the voltages at bus 1 and bus 2, respectively, Z12 is the line’s impedance between buses 1 and 2.

Fig. 2
figure 2

Simplified PS model.

Full size image
Fig. 3
figure 3

Simple steps to calculate the VSI.

Full size image

Algorithms

A metaheuristic method called the multi-population evolution whale optimisation algorithm (MEWOA) is an improved version of the whale optimisation algorithm motivated by the predation strategies of humpback whales46. They engage in three stages of predation: encircling prey, bubble net attack, and prey search. However, because global exploration was not present at the later end of the iteration, the authors created improved methods they call “MEWOA.” This algorithm resolves the drawback of converging into local optima47. Therefore, depending on the fitness value, this enhanced method divides the whale population into three categories. Individuals with poor fitness are presumed to be remote. They are classified as belonging to the exploratory sub-population, which calls for the ability to conduct global exploration. In contrast, those with good fitness are classified as belonging to the exploitative sub-population, which calls for the ability to perform local exploitation48. The remaining individuals are classified as belonging to the modest sub-population, which falls between good and poor fitness. Here, exploitation and exploration need to be balanced. Based on the three sub-population groups, the respective group updates their optimal position using the following equations49. In exploration sub-populations, their search range is increased by the global exploration ability provided by Eq. 19.

$$ran1=rand[0,1]+1$$
(19)
$$P(i+1)=P(i)\,ran1$$
(20)

Where i is the present iteration number, is the element-by-element multiplication and \(ran1\) is a random number between [0,1]. In exploitative sub-populations, their search range is increased by deep local search around the current optimal solution as provided by Eq. 2150.

$$ran2=2 \bullet rand[0,1]$$
(21)
$$P(i+1)={P^*}(i) \bullet ran2$$
(22)

In modest sub-populations, their position is updated as given in Eq. 2251.

$$P(i+1)=\left\{ {\begin{array}{*{20}{c}} {\mathop P\limits^{ \wedge } (i){\text{ if fit(}}\mathop P\limits^{ \wedge } {\text{(i)) is better than fit(P(i))}}} \\ {P(i){\text{ else }}} \end{array}} \right.$$
(23)

Where \(\mathop P\limits^{ \wedge } (i)=lb+Ub - P(i)\). lb is the lower bound, ub is the upper bound condition, and the updated position is based on OBL. \({\text{fit()}}\)is the objective function\(\:.\) The simplified flowchart of this algorithm is shown in Fig. 4, and Fig. 5 shows the pseudo-code of the MEWOA52.

Fig. 4
figure 4

Simplified flowchart of MEWOA.

Full size image
Fig. 5
figure 5

Pseudocode of MEWOA.

Full size image

Result and discussion

The proposed method is evaluated on Indian 28 and IEEE 69 buses to determine its efficacy and validity. The primary OF includes active/reactive PLoss reduction, voltage profile improvement, annual cost saving, and total operating cost reduction. The MEWOA evaluates the RDS’s effectiveness. The proposed MEWOA was compared against other well-known optimisation methods, including the GOA, WOA, and DA, considering different load models such as CP, IND, RES, COM, CI, and CZ. Electrical loads classified as CP maintain constant power consumption despite variations in voltage and current. It can be found in several power electronics equipment with a specified power rating. Their constant power helps maintain the PS’s reliability. The total amount of electricity a typical household uses is called a RES. The RES load models will have different daily consumptions such as lighting, heating, television, etc. IND loads pertain to the electrical power consumption of heavy machinery and equipment. Their power demands various and required specialised control and protection systems to safeguard the equipment from damage. The COM load models are those used in commercial areas such as restaurants, business stores, non-industrial loads, etc. The CI load models are those irrespective of voltage variation; their current supply remains constant, and loads with constant impedance irrespective of the voltage and frequency variation are known as CZ loads. The MATLAB 2020(a) environment is used to run the simulation. The various simulated results are categorised as follows:

Simulation results for the Indian 28 bus system

The 28-test system consists of 28 buses and 27 branches. The system operates at 11 kV, 761.040 kW, & 776.143 kVAr real and reactive power demand of CP, respectively. Similarly, different load models with real and reactive power demands are 751.254 kW & 507.979 kVAr, 712.421 kW & 582.513kVAr, 683.011 kW & 609.365 kVAr, 708.355 kW & 722.663 kVAr, and 659.581 kW & 672.904 kVAr are considered for IND, RES, COM, CI, and CZ respectively. VSI is used for siting of DGs & SCs optimally in the RDS. The single-line diagram of the 28-test system is shown in Fig. 6. Single-line diagram of the Indian 28-bus Test system incorporating DG location. The line and bus data related to the 28-test system are referred from40,41.

Base case

In this case, the DGs and SCs are not integrated into the RDS. The system is evaluated using different algorithms, and the results are presented here. The minimum \({P_{TL}}\)= 45.54 kW, \({Q_{TL}}\) = 30.4482 kVAr for the IND load model, and the maximum \({P_{TL}}\) = 68.82 kW and \({Q_{TL}}\)= 46.014 kVAr for the CP load model. The \(\:{\text{V}\text{S}\text{I}\:}_{\text{m}\text{i}\text{n}}\:(p.u)\) and \(\:{\text{V}\text{I}\:}_{\text{m}\text{i}\text{n}}\:(p.u)\:\)are provide as 0.7152 and 0.9123 respectively. The details of simulated results are presented in Table 2.

Fig. 6
figure 6

Single line diagram of Indian 28 bus test system incorporating DG.

Full size image

Case 1 integration of 1 DG (Type C) and 1 SC

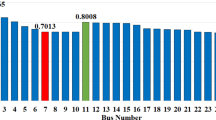
The optimal location to place a single DG (type C), according to VSI, was location 7. With integrating 1 DG, it is observed that the minimum \({P_{TL}}\)= 6.17 kW and \({Q_{TL}}\) = 3.59 kVAr for the IND models and the maximum in \({P_{TL}}\) = 8.69 kW and \({Q_{TL}}\)= 4.69 kVAr for CP. The \(\:{\text{V}\text{S}\text{I}\:}_{\text{m}\text{i}\text{n}}\:(p.u)\) = 0.9244 and \(\:{\text{V}\text{I}\:}_{\text{m}\text{i}\text{n}}\:(p.u)\:=0.9806\). Compared to the base case, it is observed that active PLoss & reactive gPLoss have drastically decreased with the integration of a single DG (Type C). The simulated results and PLoss reduction are presented in Table 2. Among the four algorithms, results obtained by the MEWOA are observed as superior. To further validate and verify the simulated results, it is compared with the other methods from previous works of literature. A comparison in Table 2 demonstrates that the suggested method best fits the optimal allocation and sizing of the DGs and significantly reduces PLoss. Figure 7 shows the improved voltage profile using the proposed methods compared to others.

Fig. 7
figure 7

Voltage profile of 28 bus system (1 DG + 1SC) for CP.

Full size image
Table 2 Simulation result of 28 bus test system considering various load models (Case 1).
Full size table

Simulation results for IEEE 69 test system

The efficacy of the MEWOA is implemented and verified using the IEEE 69 test system. The single-line diagram of the 69-bus incorporating the DGs and SCs location is shown in Fig. 8. Different parameters, such as active and reactive PLoss, are analysed for six different types of loads. The line and bus data of the 69-test system is referred to in33.

Base case

In this case, the integration of DGs and SCs is not considered. The base case system voltage is 13.8 kV, and active and reactive power demands are 3801.49 kW & 2694.60 kVAr, 3767.41 kW & 2046.78 kVAr, 3632.30 kW & 2226.22 kVAr, 3530.10 kW & 2290.92 kVAr, 3618.16 kW & 2564.43 kVAr and 3448.76 kW & 2444.18 kVAr for CP, IND, RES, COM, CI, and CZ respectively. The \(VS{I_{\hbox{min} }}{\text{(p}}{\text{.u)}}\) and \({V_{\hbox{min} }}{\text{(p}}{\text{.u)}}\)are provided as 0.6822 and 0.9172, respectively. The details of the simulated results are presented in Table 3.

Table 3 Simulation result of 69 bus test system considering various load models (Case 1).
Full size table

Case 1: integration of single DG (Type C) and single SC

Using VSI, 11, 17 & 61 buses are identified as the optimal location for placing DGs and SCs in the IEEE 69 bus test system. To validate and verify the superiority of the proposed method, a single DG and an SC are placed at bus location 61. The simulated results are presented in Table 3. The minimum \({P_{TL}}\)= 19.93 kW, \({Q_{TL}}\) = 12.98 kVAr is observed for the COM load model and the maximum \({P_{TL}}\) = 23.169 kW and \({Q_{TL}}\) = 14.42 kVAr is observed for the CP load model. The improved \(VS{I_{\hbox{min} }}{\text{(p}}{\text{.u)}}\)and \({V_{\hbox{min} }}{\text{(p}}{\text{.u)}}\) are observed as 0.8942 and 0.9724, respectively. Compared to other techniques, the suggested methods have significantly decreased PLoss, which has improved the voltage profile and stability of the RDS system.

Fig. 8
figure 8

Single line diagram of IEEE 69 Test system incorporating DGs and SCs location.

Full size image

Case 2: integration of two DGs (Type C) and two SCs

In this case, 2 DGs and 2 SCs are integrated into the RDS at bus locations 11 and 61, respectively. In this situation, DGs inject real power into the system, whereas SCs inject reactive power. Table 4 shows the outcomes of \({P_{TL}}\)all load models’ minimum voltage profiles and VSI values. The minimum values of \({P_{TL}}\)= 8.71 kW, \({Q_{TL}}\)= 8.05 kVAr. The results of this study unambiguously demonstrate that adding 2 DGs together with 2 SCs reduces PLoss and improves the voltage profile and VSI values. Additionally, it is seen that Case-2 significantly outperforms Case-1 in terms of PLoss reduction, voltage profile, and VSI.

Table 4 Simulation result of 69 bus test system considering various load models (Case 2).
Full size table

Case 3: integrating three DGs (Type C) and three SCs

In this case, 3 DGs and 3 SCs are positioned on 11, 17, and 61, which are identified as the optimal location using VSI. The sizing of the DGs and SCs was carried out using MEWOA techniques. The simulated outcomes are presented in Table 5. It is depicted in Table 5 that the system performance has been drastically improved after placing 3 DGs and 3 SCs into the RDS. Additionally, it is confirmed that placing DGs in numerous locations enhances system performance. The minimum \({P_{TL}}\)= 3.83 kW, \({Q_{TL}}\) = 6.43 kVAr for COM, and maximum \({P_{TL}}\) = 4.29 kW and \({Q_{TL}}\) = 6.76 kVAr for the CP load model. The improved \(VS{I_{\hbox{min} }}\) & \({V_{\hbox{min} }}\) are 0.9594 pu & 0.9944 pu respectively. The convergence curve for 3DGs + 3 SCs is shown in Fig. 9.

Table 5 Simulation result of 69 bus test system considering various load models (Case 3).
Full size table

Cost benefit analysis using different load models and different optimisation techniques

The PLoss has significantly decreased with integrating the DGs and SCs into RDS, allowing more beneficial work to be done and thereby reducing the cost of energy loss. Different parameters such as cost of energy loss (CEL), cost of DG units (CDG), cost of Shunt Capacitors (CSC) and total operating cost (CTO) are considered to check the efficacy and robustness of the proposed method. The proposed method is implemented for two test systems as follows:

Fig. 9
figure 9

Convergence curve for 3DGs + 3SCs.

Full size image

Indian 28 test system

The 28-test system is integrated with one pair of DG and SC, and the different cost functions, such as the cost of energy loss per annum \(({C_{EL}})\), cost of DG \(({C_{DG}})\), cost of SC (\({C_{SC}}\)), and total operating cost (\({C_{TO}}\)), are analysed. The cost analysis is implemented for different load models such as CP, IND, RES, COM, CI & CZ. Afterwards, these load models are further compared using different algorithms. The details of cost analysis for other load models & different methods are presented in Table 6.

With the integration of 1 DG and 1 SC, the minimum cost saving from energy loss per year (\({C_{EL}}\)) is saved for the IND load model with \({C_{EL}}\)= 0.37 thousand dollars and the maximum cost saving is observed for the CP load model with \({C_{EL}}\)= 0.52 thousand dollars. Similarly, the total operating cost saved for IND is \({C_{TO}}\) =11.18 thousand dollars and \({C_{TO}}\)= 11.40 thousand dollars for CP load models. Regarding percentage cost saving, RES has 86.42% and 87.37% for CP load models.

Table 6 Economic cost analysis for integration of 1 DG.
Full size table

IEEE 69 test system

The MEWOA analyses and optimizes the IEEE 69-bus RDS when allocating various DG-SC pairs. Here, one, two, and three DG-SC pairs are considered to check the effectiveness of different load models. The details of simulated results for different load models and algorithms are presented in Tables 7, 8, 9, respectively. Table 7 depicts that when a single pair of DG-SC is injected into the system, the CEL decrease drastically to 1.4 thousand dollars from 13.58 thousand dollars for CP using the proposed methods. The percentage of energy saved is 87.90% for the CP load model. Similarly, Table 8 presents that when two pair of DGs-SCs are connected to the RDS, the CEL decrease to 0.61 from 13.58 thousand dollars for CP load models, which is the maximum energy saving in terms of cost. When three pairs of DGs-SCs are injected into the system, the CEL is further reduced to 0.26 from 13.58 for CP load models, as shown in Table 9. Therefore, comparing with the different methods, it is observed that the proposed method provides superior results. It can also be concluded that, with the injection of an optimum pair of DGs-SCs, the energy losses in terms of cost are minimized to a great extent. The percentage reduction for injection of 2 DGs-SCs and three pairs of DGs-SCs are 95.51 and 98.10, respectively. The voltage profiles for integrating 3 DGs and 3 SCs using different algorithms are shown in Figs. 10, 11 shows the PLoss reduction in percentage for other load models.

Table 7 Economic cost analysis for integration of 1pair of DG and SC for 69 Bus.
Full size table
Table 8 Economic cost analysis for integration of 2 pairs of DGs and SCs for 69 Bus.
Full size table
Table 9 Economic cost analysis for integration of 3 pairs of DGs and SCs for 69 Bus.
Full size table
Fig. 10
figure 10

Voltage profile of 69 bus RDS with different load models and different algorithms.

Full size image
Fig. 11
figure 11

Different load demand along with its PLoss reduction in percentage in 69 bus system.

Full size image

Statistical evaluation of several load models with MEWOA

Data collection, analysis, interpretation, presentation, and organisation are various topics covered in the study area of statistics, a subfield of mathematics. It offers a collection of strategies and procedures for summarizing data, drawing conclusions from it, and assessing uncertainty. The optimisation methods are based on several nature-inspired algorithms, and random values are considered to start their search. As a result, several iterations of the optimisation procedures are required to obtain the actual optimal values. So, to minimise the cost of energy loss (\({C_{EL}}\)), all four algorithms execute 50 separate runs with each specific load model. The objective is to decrease the cost of energy loss. Different statistical parameters considered are minimum (\(Mi{n_{CEL}}\)), maximum (\(Ma{x_{CEL}}\)), mean value (\(Mea{n_{CEL}}\)), median (\(Media{n_{CEL}}\)), mode (\(Mod{e_{CEL}}\)), standard deviation (\({\sigma _{CEL}}\)), variance (\({\sigma ^2}_{{CEL}}\)), and statistical error of the (\({C_{EL}}\)) function.

Indian 28 test systems

Considering integrating only one DG at bus location 7, this test system executed 50 runs each for four algorithms such as MEWOA, WOA, GOA & DA. The results obtained are constants in their respective algorithm, and results depends on various load models. Among the four algorithms, as presented in Table 10, MEWOA algorithm is providing the optimal results with \(Mi{n_{CEL}}\)= 0.4020. Though this test system is smaller, the results obtained for the \({C_{EL}}\)almost remain constant for all four algorithms. The standard deviation as presented in the following Table 10, clearly indicates mostly zero for all the algorithms.

Table 10 Statistical analysis of 28 bus systems with one DG considering different algorithms and load models.
Full size table

IEEE 69 test systems

As the test system is a bit larger than the previous one, here considered integrating 3 DGs and 3 SCs. In this system, the obtained \(Mi{n_{CEL}}\)= 0.2311 for the COM load model and is provided by the MEWOA algorithm. The deviation is minimum for the IND load obtained with MEWOA algorithms. Hence, it is very clear that the MEWOA is best OT for obtaining optimal sizing of DGs and SCs. The results obtained are tabulated in Table 11.

Table 11 Statistical analysis of 28 bus systems with one DG considering different algorithms and load models.
Full size table

Conclusion

The Indian 28 test Systems and IEEE-69 Test System are used to confirm the various placements of the DGs and SCs within the DN. The MEWOA algorithm is used to compare the efficiency of optimising PLoss and the annual energy savings from PLoss, together with the other three algorithms: WOA, GOA, and DA. Six different load models are applied to the systems: industrial, commercial, constant impedance, constant current, and residential. According to the simulated results, the suggested MEWOA algorithm significantly reduces active and reactive PLoss, the cost of energy loss, and overall operating costs. Even the system stability and voltage profile have been enhanced. In light of these findings, the suggested methodology has considerable technological and financial benefits and can be used to tackle optimisation issues in various distribution systems. Uncertainties of renewable DGs and load needs to be considered in order to asses the performance in detailed way. Further, various storage devices integration along with electric vehicle charging stations and its uncertainties consideration in future scope of work.